1 Introduction

Non-Newtonian materials as compared to viscous liquids are more efficient in various physiological, engineering and industrial processes. Asphalts, biological solutions, paints and glues are some examples of nonlinear materials. More specifically, most of the liquids used in food and chemical industries are non-Newtonian liquids [1, 2]. Consequently, numerous relations were introduced in the literature to analyze the rheological properties of nonlinear materials. Cross-fluid model is one of these relations, which describes the shear-thinning features of liquids. Hayat et al. [3] considered properties of cross-material flow for stretched surface. Khan et al. [4] numerically analyzed heat transfer characteristics for cross-fluid. Khan et al. [5] securitized properties of static–moving wedge for cross-material. Manzur et al. [6] studied aspects of opposing and assisting flow for radiative cross-fluid. Sultan et al. [7] reported rheological analysis for 3D flow cross-fluid in the presence of nanomaterials.

A chemical reaction takes place, when the evident number of molecules of countable chemical species assumes a new form by changing the configuration of these atoms. Several reaction systems [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] comprise homogeneous/heterogeneous reactions, for example, in combustion, biochemical frameworks and catalysis. Heterogeneous reactions take place in different phase space (e.g., solid–gas space), while the homogeneous reactions have the same phase space. Furthermore, chemical reactions are applied as the part of applications such as food processing, rusting of iron, fog formation and several others. The aspects of nanoparticles and chemical mechanisms on generalized Burgers fluid flow over stretched surface have been inspected by Khan et al. [29]. Khan et al. [30] performed homogeneous–heterogeneous reactions and nonlinear thermal radiation solved numerically by a variable thicked surface. Sadiq et al. [31] observed chemically radiating flow toward heated surface of Maxwell liquid. Mahanthesh et al. [32] detected the properties of radiative flow by utilizing nanoparticles across permeable vertical plate. Hayat et al. [33] studied about reaction and convective flow between two rotating disks. Kumar et al. [34] analyzed the heat–mass transport behavior of chemically reacting of two different Casson and Maxwell fluids. Ramesh et al. [35] deliberated features of revised no mass flux relation and chemical phenomenon for Maxwell nanoliquid. Tangent hyperbolic nanofluid over stretched surface deliberated with the aspects of entropy generation and activation energy by Khan et al. [36]. Aspects of chemical mechanisms for 3D time-dependent flow of Maxwell fluid have been examined by Imtiaz et al. [37]. Khan et al. [38] considered the binary chemical reaction and activation energy for 3D cross-fluid.

Inspired by the overhead literature review, we have numerically computed the rheological behavior of cross-fluid subjected to revised heat flux relation. Furthermore, convective conditions are accounted in the modeling. More specifically, such features of cross-fluid have not yet been addressed in the literature. Numerical procedure is employed for simulations. Nature of significant parameters is elaborated graphically.

2 Modeling

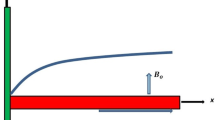
Let us formulate 2D time-dependent radiative flow of incompressible cross-fluid subjected to convectively heated surface. Moreover, coordinate frame in this physical problem is chosen in such a manner that x-axis coordinates extend in direction of axial surface and r-axis is perpendicular to it which is shown in Fig. 1. More specifically, Lorentz’s force is applied to control the motion of liquid. Besides, Brownian movement, radiation, thermophoresis, Brownian movement and convective conditions are accounted in the mathematical modeling. Furthermore, we have considered heated fluid at temperature \(T_{\text{f}}\) which is in contact with cylinder. An assumption is made that the sheet is in contact with a hot fluid at temperature \(T_{\text{f}}\). The flow analysis of cross-liquid is carried out subject to chemical processes.

Fig. 1
figure 1

Physical configuration

Full size image

The analysis of quartic autocatalysis for isothermal process is given by

$$E + 2F \to 3F,\,\;\;\;{\text{rate}} = k_{1} G_{\text{a}} G_{\text{b}}^{2} ,$$
(1)

while the catalytic surface for isothermal reaction in a single process and first order is

$$E \to F,\quad {\text{rate}} = k_{\text{s}} G_{\text{a}} ,$$
(2)

Taking into consideration the aforesaid assumptions, the governing hydromagnetic flow of cross-fluid can be written into the forms given below:

$$\frac{\partial }{\partial x}\left( {ru} \right) + \frac{\partial }{\partial r}\left( {rv} \right) = 0,$$
(3)
$$\begin{aligned} \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial r} = & \frac{{\partial U_{\text{e}} }}{\partial t} + U_{\text{e}} \frac{{\partial U_{\text{e}} }}{\partial x} + \frac{\nu }{r}\frac{\partial u}{\partial r}\left[ {\frac{1}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial r}} \right)^{n} }}} \right] \\ & \quad + \nu \frac{\partial }{\partial r}\left[ {\frac{{\tfrac{\partial u}{\partial r}}}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial r}} \right)^{n} }}} \right] - \frac{{\sigma^{ * } B^{2} \left( t \right)}}{\rho }\left( {u - U_{\text{e}} } \right), \\ \end{aligned}$$
(4)
$$\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial r} = \alpha_{\text{m}} \left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r}} \right] - \frac{1}{{\left( {\rho c} \right)_{\text{f}} }}\frac{{\partial q_{\text{r}} }}{\partial r} + \frac{{Q_{0} }}{{(\rho c)_{\text{f}} }}(T - T_{\infty } ),$$
(5)
$$\frac{{\partial G_{a} }}{\partial t} + u\frac{{\partial G_{a} }}{\partial x} + v\frac{{\partial G_{a} }}{\partial r} = D_{A} \left( {\frac{{\partial^{2} G_{a} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial G_{a} }}{\partial r}} \right) - k_{1} G_{a} G_{b}^{2} ,$$
(6)
$$\frac{{\partial G_{\text{b}} }}{\partial t} + u\frac{{\partial G_{\text{b}} }}{\partial x} + v\frac{{\partial G_{\text{b}} }}{\partial r} = D_{\text{B}} \left( {\frac{{\partial^{2} G_{\text{b}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial G_{\text{b}} }}{\partial r}} \right) + k_{1} G_{\text{a}} G_{\text{b}}^{2} ,$$
(7)

with

$$\begin{aligned} & u = U_{\text{w}} \left( {x,\,t} \right) = \frac{2cx}{1 - \beta t},\,v = V_{\text{w}} \left( t \right) = - \frac{{ab_{0} s}}{{\sqrt {1 - \beta t} }},k\frac{\partial T}{\partial r} = - h_{\text{f}} \left[ {T_{\text{w}} - T} \right] ,\\ & \qquad D_{\text{A}} \frac{{\partial G_{\text{a}} }}{\partial r} = k_{\text{s}} G_{\text{a}} ,\, \, D_{\text{B}} \frac{{\partial G_{\text{b}} }}{\partial r} = - K_{\text{s}} G_{\text{a}} \,\,{\text{at}}\,\, \, r = b\left( t \right) \\ \end{aligned}$$
(8)
$$u \to U_{\text{e}} \left( {x,t} \right) = \frac{2ax}{1 - \beta t},\quad T \to T_{\infty } ,\quad G_{\text{a}} \to G_{0} ,\quad G_{\text{b}} \to 0,\quad {\text{as}}\,\,\,r \to \infty ,$$
(9)

where

$$q_{\text{r}} = - \frac{{16\sigma^{ * } }}{{3k^{ * } }}T^{3} \frac{\partial T}{\partial r}.$$
(10)

Substituting Eq. (10) in Eq. (5), we get

$$\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial r} = \alpha_{m} \left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r}} \right] + \frac{1}{{\left( {\rho c} \right)_{f} }}\frac{\partial }{\partial r}\left( {\frac{{16\sigma^{ * } }}{{3k^{ * } }}T^{3} \frac{\partial T}{\partial r}} \right) + \frac{{Q_{0} }}{{(\rho c)_{f} }}(T - T_{\infty } ),$$
(11)

Employ

$$\begin{aligned} & u = \frac{2ax}{1 - \beta t} \, f^{{^{\prime } }} \left( \eta \right),\,\nu = - \frac{{ab_{0} }}{{\sqrt {1 - \beta t} }}\frac{f\left( \eta \right)}{\sqrt \eta },\,\eta = \left( {\frac{r}{{b_{0} }}} \right)^{2} \frac{1}{1 - \beta t}, \\ & \quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}, \, \phi \left( \eta \right) = \frac{{G_{\text{a}} }}{{G_{0} }},\,\vartheta \left( \eta \right) = \frac{{G_{\text{b}} }}{{G_{0} }}. \\ \end{aligned}$$
(12)

Equation (3) is justified trivially, whereas Eqs. (4)–(11) yield

$$\begin{aligned} & \left[ {1 + \left( {1 - n} \right)\,\left( {{\text{We }}f^{{^{\prime \prime } }} } \right)^{n} } \right]\,f^{{^{\prime \prime \prime } }} \eta + \left[ {1 + \left( {1 - \frac{n}{2}} \right)\,\left( {{\text{We }}f^{{^{\prime \prime } }} } \right)^{n} } \right]\,f^{{^{\prime \prime } }} + \left[ {Re\left( {ff^{{^{\prime \prime } }} - f^{{^{\prime } 2}} + 1} \right)} \right. \\ & \left. {\quad - A\left( {f^{{^{\prime } }} + \eta f^{{^{\prime \prime } }} - 1} \right) - M^{2} Re\left( {f^{{^{\prime } }} - 1} \right)} \right]\,\left[ {1 + \left( {{\text{We }}f^{{^{\prime \prime } }} } \right)^{n} } \right]^{2} = 0, \\ \end{aligned}$$
(13)
$$\begin{aligned} & \eta \theta^{{^{\prime \prime } }} + \left( {1 + \mathop {\Pr }\limits \text{Re} f - \mathop {\Pr }\limits A\eta } \right)\,\theta^{{^{\prime } }} + \frac{2}{{3N_{\text{R}} }}\left[ {\left( {1 + \left( {\theta_{\text{w}} - 1} \right)\theta } \right)^{3} \left( {2\eta \theta^{{^{\prime \prime } }} + \theta^{{^{\prime } }} } \right)} \right. \\ & \quad \left. { + 6\left( {1 + \left( {\theta_{\text{w}} - 1} \right)\theta } \right)^{2} \left( {\theta_{\text{w}} - 1} \right)\eta \left( {\theta^{{^{\prime } }} } \right)^{2} } \right] + \mathop {\Pr }\limits \lambda \theta = 0, \\ \end{aligned}$$
(14)
$$\frac{1}{\text{Sc}}\left[ {\phi^{{^{\prime } }} + \eta \phi^{{^{\prime \prime } }} } \right] - A\phi^{{^{\prime } }} \eta + \text{Re} f\phi^{{^{\prime } }} - K\phi \vartheta^{2} = 0,$$
(15)
$$\frac{\varepsilon }{\text{Sc}}\left[ {\vartheta^{{^{\prime } }} + \eta \vartheta^{{^{\prime \prime } }} } \right] - A\vartheta^{{^{\prime } }} \eta + \text{Re} f\vartheta^{{^{\prime } }} + K\phi \vartheta^{2} = 0$$
(16)
$$f\left( 1 \right) = s,\, \, f^{{^{\prime } }} \left( 1 \right) = \lambda_{1} ,\,f^{{^{\prime } }} \left( \infty \right) \to 1,$$
(17)
$$\theta^{{^{\prime } }} \left( 1 \right) = - \gamma \left[ {1 - \theta \left( 1 \right)} \right],\,\theta \left( \infty \right) \to 0,$$
(18)
$$\phi^{{^{\prime } }} \left( 1 \right) = K_{\text{s}} \phi \left( 1 \right),\,\phi \left( \infty \right) \to 1,$$
(19)
$$\varepsilon \vartheta^{{^{\prime } }} \left( 1 \right) = - K_{\text{s}} \vartheta \left( 1 \right),\,\vartheta \left( \infty \right) \to 0,$$
(20)

The mathematical forms of variables appearing in Eqs. (13)–(20) are expressed as follows

$$\begin{aligned} & {\text{We}} = \frac{{2\varGamma rU_{\text{e}} \, }}{{b_{0}^{2} \left( {1 - \beta t} \right)}},\,\mathop {\Pr }\limits = \frac{\nu }{{\alpha_{\text{m}} }},\,{\text{Sc}} = \frac{\nu }{{D_{\text{B}} }},\,A = \frac{{b_{0}^{2} \beta }}{4\nu },\,Re = \frac{{ab_{0}^{2} }}{2v},\,\varepsilon = \frac{{D_{\text{B}} }}{{D_{\text{A}} }}, \\ & \quad M^{2} = \frac{{\sigma B_{0}^{2} }}{2\rho a}\left( {1 - \beta t} \right),\,\lambda = \frac{{Q_{0} }}{{a(\rho c)_{\text{f}} }},\,\theta_{\text{w}} = \frac{{T_{\text{w}} }}{{T_{\infty } }},\,\lambda_{1} = \frac{c}{a},\,K = \frac{{k_{1} G_{0}^{2} \left( {1 - \beta t} \right)\,b_{0}^{2} }}{4\nu }. \\ \end{aligned}$$
(21)

Dimensional forms of \(\left( {C_{\text{f}} } \right)\) and \(\left( {\text{Nu}} \right)\) are

$$C_{\text{f}} = \frac{{\tau_{rx} \;|_{r = b\left( t \right)} }}{{\tfrac{1}{2}\rho U_{\text{e}}^{2} }},$$
(22)
$${\text{Nu}} = \frac{{b\left( t \right)\,q_{\text{w}} \;|_{r = b\left( t \right)} }}{{2k\left( t \right)\,\left( {T_{\text{w}} - T_{\infty } } \right)}} + q_{\text{r}} ,$$
(23)

where

$$\tau_{rx} = \left. {\mu_{0} \frac{\partial u}{\partial r}\left[ {\frac{1}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial r}} \right)^{n} }}} \right]} \right|_{r = b\left( t \right)} ,$$
(24)
$$q_{\text{w}} = \left. { - k\left( {\frac{\partial T}{\partial r}} \right)} \right|_{r = b\left( t \right)} + \left. {q_{\text{r}} } \right|_{r = b\left( t \right)} .$$
(25)

After the utilization of Eqs. (24) and (25), the simplified form of Eqs. (22) and (23) is

$$C_{\text{f}} Re_{x} \frac{x}{b\left( t \right)} = f^{{^{\prime \prime } }} \left( 1 \right)\,\left[ {1 + \left( {{\text{We}}f^{{^{\prime \prime } }} \left( 1 \right)} \right)^{n} } \right]^{ - 1} ,$$
(26)
$${\text{Nu}} = - \theta^{\prime}(1)\left[ {1 + \frac{4}{{3N_{\text{R}} }}\left\{ {\left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\,\theta \left( 1 \right)} \right]^{3} } \right\}} \right]$$
(27)

where \(Re_{x} = ax^{2} /\nu .\)

3 Results and discussion

Our main emphasis in this section is to analyze the physical importance of involved parameters that directly affect the cross-liquid velocity, temperature and mass concentration fields. Furthermore, we have discussed the significance of rheological parameters on \(\left( {C_{\text{f}} } \right)\) and \(\left( {\text{Nu}} \right)\). More specifically, Figs. 2, 3, 4, 5, 6, 7, 8 and 9 are drafted to get insight of the pertinent variables like local Weissenberg number (\({\text{We}}\)), time-dependent parameter \((A)\), suction parameter \((s)\), power law index \((n)\), thermal Biot number \((\gamma )\), Reynolds number \((\text{Re} )\), Prandtl number \((\Pr )\), radiation parameter \(\left( {N_{\text{R}} } \right)\), heterogeneous strength of reaction parameter \(\left( {K_{\text{s}} } \right)\) and Schmidt number \(\left( {\text{Sc}} \right)\).

Fig. 2
figure 2

(a), (b) \(f^{'} \left( \eta \right)\) profile via \({\text{We}}\) and \(A.\)

Full size image
Fig. 3
figure 3

(a), (b) \(f^{'} \left( \eta \right)\) profile via \(Re\) and \(M\)

Full size image
Fig. 4
figure 4

(a), (b) \(f^{'} \left( \eta \right)\) profile via \(s\) and \(n\)

Full size image
Fig. 5
figure 5

(a), (b) \(\theta \left( \eta \right)\) profile via \(A\) and \(Re\)

Full size image
Fig. 6
figure 6

(a), (b) \(\theta \left( \eta \right)\) profile via \(\Pr\) and \(\gamma .\)

Full size image
Fig. 7
figure 7

(a), (b) \(\theta \left( \eta \right)\) profile via \(N_{\text{R}}\) and \(\lambda\)

Full size image
Fig. 8
figure 8

(a), (b) \(\phi \left( \eta \right)\) profile via \(A\) and \(Re\)

Full size image
Fig. 9
figure 9

(a), (b) \(\phi \left( \eta \right)\) profile via \(K_{\text{s}}\) and \({\text{Sc}}\)

Full size image

Figure 2(a, b) is plotted for the physical importance of \({\text{We}}\) and \(A\) on \(f^{{^{\prime } }} (\eta )\) for stretching cylinder (\(\lambda_{1} = 1.5\)) and shrinking cylinder (\(\lambda_{1} = - 0.5\)). Clearly, velocity of cross-liquid and associated layer thickness declines against \({\text{We}}\) and \(A\) larger stretching cylinder (\(\lambda_{1} = 1.5\)), while liquid velocity rises against shrinking (\(\lambda_{1} = - 0.5\)) case. From a physical point of view, \({\text{We}}\) is ratio between relaxation time and specific process time. Consequently, rising estimations of \({\text{We}}\) intensifies relaxation time as a result velocity of cross-liquid deteriorates for stretching cylinder (\(\lambda_{1} = 1.5\)). Impact of \(Re\) and \(M\) on \(f^{{^{\prime } }} (\eta )\) is depicted in Fig. 3(a,b). From these figures, it is perceived that velocity of cross-liquid and momentum boundary layer rises against \(Re\) and \(M\) for shrinking cylinder (\(\lambda_{1} = - 0.5\)) case, while opposite trend is detected for stretching cylinder (\(\lambda_{1} = 1.5\)). Physically, Lorentz’s forces intensify with larger values of \(M\). More specifically, Lorentz force acts as resistive force, which deteriorates the liquid velocity of cross-fluid. Figure 4(a, b) shows the behavior of suction parameter \(\left( s \right)\) and power law index \(\left( n \right)\) for \(f^{{^{\prime } }} (\eta )\). Clearly, one can detect from graphical data that velocity of cross-liquid and associated layer thickness declines against larger suction parameter \(\left( s \right)\) for stretching cylinder (\(\lambda_{1} = 1.5\)), while opposite phenomenon is detected for shrinking cylinder (\(\lambda_{1} = - 0.5\)). Moreover, it is observed that cross-liquid velocity \(f^{{^{\prime } }} (\eta )\) boots via larger power law index \(\left( n \right)\) for stretching cylinder (\(\lambda_{1} = 1.5\)), whereas reverse trend is detected for shrinking cylinder (\(\lambda_{1} = - 0.5\)).

Figure 5(a, b) elaborates the significance of \(A\) and \(Re\) on \(\theta (\eta )\) for stretching (\(\lambda_{1} = 1.5\)) and shrinking cylinder (\(\lambda_{1} = - 0.5\)). Decreasing trend of \(\theta (\eta )\) is noticed for larger \(A\) and \(Re\). Figure 6(a, b) discloses the characteristics of \(\Pr\) and \(\gamma\) against \(\theta (\eta )\). A rise in \(\gamma\) yields decreasing trend of \(\theta (\eta )\), whereas reverse behavior of \(\Pr\) via \(\theta (\eta )\). From mathematical point of view, \(\Pr\) is ratio between kinematic viscosity (momentum diffusivity) and thermal diffusivity. Consequently, thermal diffusivity of cross-liquids boosts for intensifying values of \(\Pr\) as a result thermal field declines. Furthermore, for larger values of \(\gamma\), less resistance is faced by the thermal wall which intensifies the convective mechanism of heat transportation. Features of \(N_{\text{R}}\) and \(\lambda\) against \(\theta (\eta )\) are elaborated in Fig. 7(a,b). As expected, \(\theta (\eta )\) and allied thermal layer increase with larger values of \(\lambda\) for stretching (\(\lambda_{1} = 1.5\)) and shrinking cylinder (\(\lambda_{1} = - 0.5\)), while opposite behavior is detected against \(N_{\text{R}}\). In fact, larger quantity of heat has produced due to an upsurge in heat generation parameter (\(\lambda\)). Therefore, thermal field (\(\theta (\eta )\)) rises.

Figure 8(a, b) delineates the impact of \(A\) and \(Re\) on \(\phi (\eta )\). For higher estimation of these non-dimensional parameters, the concentration of cross-liquid \(\phi (\eta )\) rises. Figure 9(a,b) portrays the physical significance of \(K_{\text{s}}\) and \({\text{Sc}}\) on concentration field of cross-liquid \(\phi (\eta )\) for stretching (\(\lambda_{1} = 1.5\)) and shrinking cylinder (\(\lambda_{1} = - 0.5\)). We have observed from these sketches that \(\phi (\eta )\) intensifies for larger estimations \(K_{\text{s}}\) and \({\text{Sc}}\).

Numerical data for skin friction \(\left( {C_{\text{f}} Re\frac{x}{b\left( t \right)}} \right)\) and Nusselt number \(\left( {\text{Nu}} \right)\) have been computed for stretching (\(\lambda_{1} = 1.5\)) and shrinking cylinder (\(\lambda_{1} = - 0.5\)) in Tables 1 and 2. One can detect from Table 1 that \(\left( {C_{\text{f}} Re\frac{x}{b\left( t \right)}} \right)\) boosted via \(M\) and \(\text{Re}\), whereas \(\left( {C_{\text{f}} Re\frac{x}{b\left( t \right)}} \right)\) deteriorates against \(A\) and \(M\) for shrinking cylinder (\(\lambda_{1} = - 0.5\)). Furthermore, quite opposite trend of \(\left( {C_{\text{f}} Re\frac{x}{b\left( t \right)}} \right)\) is observed for stretching (\(\lambda_{1} = 1.5\)) cylinder. Table 2 is prepared to visualize the characteristics of Nusselt number \(\left( {\text{Nu}} \right)\) against \(A\), \(\Pr\), \(\gamma\), \(\theta_{\text{w}}\), \(\text{Re}\), \(M\) and \(N_{\text{R}}\). Clearly, \(\left( {\text{Nu}} \right)\) intensified via larger \(\Pr\), \(\gamma\), \(\theta_{\text{w}}\), \(\text{Re}\) and \(M\); however, it reduces through \(A\).

Table 1 Computational outcomes of surface drag forces \(\left( {Re^{1/2} C_{fx} } \right)\)
Full size table
Table 2 Computational outcomes for rate of heat transfer (\(Re^{ - 1/2} {\text{Nu}}\))
Full size table

4 Conclusions

The research work presented in this physical model elaborates the aspects of hydromagnetic cross-fluid by considering cylindrical surface. Moreover, convectively heated surface and nonlinear radiation effects were considered in the problem formulation. We have following noteworthy outcomes from aforementioned analysis: stretching cylinder (\(\lambda_{1} = 1.5\)), while liquid velocity rises against shrinking (\(\lambda_{1} = - 0.5\))

  • Cross-liquid velocity \(\left( {f^{{^{\prime } }} \left( \eta \right)} \right)\) deteriorates for larger \(We,\,\text{Re} ,M\) and \(A\) in case of stretching cylinder (\(\lambda_{1} = 1.5\)), while the reverse trend is detected for shrinking (\(\lambda_{1} = - 0.5\)).

  • Thermal field intensifies for heat generation and Biot number \(\left( \gamma \right)\).

  • Larger \(\left( {\Pr } \right)\) yields higher temperature \(\left( {\theta \left( \eta \right)} \right)\).

  • An increment in Pr corresponds to lower temperature and larger heat transfer rate.

  • The concentration profile was decreased with the higher values of the homogeneous reaction parameter \(k_{1}\).

  • Skin friction \(\left( {Re^{1/2} C_{fx} } \right)\) decays via larger \({\text{We}}\) and \(A\), whereas it enhances when \({\text{We}}\) and \(A\) are increased.