Perturbation effects in the generalized circular restricted three-body problem

Abstract

We study numerically the existence and stability of a test particle around the equilibrium points in the circular restricted three-body problem, and is generalized to include the effects in both primaries, oblateness and radiation together with P–R drag, small perturbations σ and ɛ′ given in the Coriolis and centrifugal forces α and β, respectively. The primaries are a neutron eclipsing binary system, which consists of bright oblate-stars possessing P–R drag. In the numerical exploration of the binary systems (Kruger 60 and Achird), we computed the radiation factors q_i (i = 1, 2) and the dimensionless velocity of light c_d which is a component of the P–R drag. It is interesting to note that, the involved parameters influence the position and stability of the triangular points. It is also observed that theses points are unstable due to the presence of a positive real part of the complex roots.

1 Introduction

It is no longer new that one of the most interesting and important topics in celestial mechanics as well as in dynamical astronomy is, the classical problem of the circular restricted three-body problem (CR3BP for short). The problem is defining a test particle having an infinitesimal mass under the gravitational attraction of two primary bodies, which move in circular orbits around their common center of gravity [1]. In realistic applications, this problem expands in many fields of research from chaos theory and molecular physics to planetary physics, stellar systems or even to galactic dynamics. This tells why this topic remains an active and stimulating area of research.

In recent times, several modifications of the R3BP have been proposed, most of which focus on investigating the character of the motion of infinitesimal mass in the Solar and Stellar Systems. All these modifications include additional types of forces, which are in general included in the total potential function of the classical R3BP in an attempt to take into consideration more dynamical parameters of the physical system and therefore make the study of the motion of the test particle more realistic and generalized.

The classical R3BP describes a setup in which the two main bodies are assumed to be spherically symmetric. However, in our Stellar and Solar Systems, several celestial bodies, such as Saturn, Jupiter and several degenerate stars have been found to be sufficiently oblate, prolate or triaxial. The shape of a celestial body should be taken into account in order that the dynamical exploration of the particular system to be more realistic. The investigations of problems involving oblateness of one or both primaries have been extensively studied in past years. Examples are studies all conducted in 2012 by [1,2,3,4]. The first is a variable mass circular restricted problem, the second is an elliptic restricted problem while the third examined the Robe’s circular R3BP, when the first primary is an oblate spheroid. Studies that are more recent include papers of [5,6,7,8].

Another interesting perturbing case is the model when a test particle moves in the vicinity of a radiating primary under the combined influence of both radiation and gravitational forces. This problem, according to [9, 10] is known as the photogravitational R3BP. A characteristic example is the motion of a dust grain in the vicinity of a binary stellar system in which one or even both main bodies are emitting radiation thus exerting light pressure to the dust grain. Solar sailing, an experimental method of spacecraft propulsion, uses radiation pressure from the Sun as a motive force. Also, in cosmic formation, radiation pressure has had a major effect on the development of the cosmos, from the birth of the universe to ongoing formation of stars and shaping of clouds of dust and gases on a wide range of scales.

The effects of the radiation pressure on the motion of the test particle have been investigated by several authors, e.g. [11,12,13,14,15,16,17]. However, in these papers, the light radiation force was defined, taken into account just one of the three components of the light pressure field, which is due to the central force: the gravitation and the radiation pressure. The other two components are arising from the Doppler shift and the absorption and subsequent re-emission of the incident radiation. These last two components constitute the so-called Poynting–Robertson (P–R) effect [18, 19]. The Poynting–Robertson effect act as an orbital perturbations and affects the orbits and trajectories of small bodies, all spacecrafts and all natural bodies (comets, asteroids, dust grains, gas molecules) and can cause dust grains to either leave the Solar system or spiral into the Sun. If the drag effects of the Sun’s radiation pressure on the spacecraft of the Viking program had been ignored, the spacecraft would have missed Mars orbit by 15,000 km (Eugene Hecht).

In incorporating the P–R effect, several authors such as [20,21,22,23,24] have under different assumptions studied the R3BP.

Finally, in the classical R3BP, the test particle is assumed to move, only under the mutual gravitational force of the primaries, but in practice, Coriolis and centrifugal forces are effective and small perturbations affect these forces. Examples include: small deviation of disc stars in circular orbits and motion of a close artificial satellite of the Earth perturbed by the atmospheric friction and the oblateness of the Earth. [25] studied the effect of small perturbations in the Coriolis and centrifugal forces when both primaries are oblate spheroid and are radiating as well, while [16] generalized the restricted problem to include the effects of perturbations in the Coriolis and centrifugal forces.

Sequel to the paper by [24], which took into account effects of oblateness and the P–R drag of the smaller primary, on the motion around triangular equilibrium points. Our aim in the present paper is to study the positions and stability of triangular equilibrium points under effects of small perturbations in the Coriolis and centrifugal forces when both primaries are radiating oblate spheroids coupled with the P–R drag emanating from both primaries.

The paper organization is as follows: Sect. 2 describes the equations of motion. The existence of triangular equilibrium points is discussed in Sect. 3, while Sect. 4 shows numerical applications. Section 5 examines the stability of these triangular points and Sect. 6 shows the results and discussion. Finally, Sect. 7 summarizes the conclusions of the paper.

2 Equations of motion

Let m₁ and m₂ be the masses of bigger and smaller primaries, respectively, while we denote the mass of the test particle by m. Suppose (x, y, z) be the coordinates of m in a rotating barycentric co-ordinate system 0 xyz relative to an inertial system with angular velocity n. Following the terminologies of [1], the equations of motion of the test body in the gravitating field of the primaries, is given by

$$ \begin{aligned} & \ddot{x} - 2\dot{y} = x - \frac{{\left( {1 - \mu } \right)\,\left( {x + \mu } \right)}}{{r_{1}^{3} }} - \frac{{\mu \left( {x + \mu - 1} \right)}}{{r_{2}^{3} }} \\ & \ddot{y} + 2\dot{x} = y\left( {1 - \frac{1 - \mu }{{r_{1}^{3} }} - \frac{\mu }{{r_{2}^{3} }}} \right) \\ & \ddot{z} = z\left( { - \frac{1 - \mu }{{r_{1}^{3} }} - \frac{\mu }{{r_{2}^{3} }}} \right) \\ \end{aligned} $$

(1)

where

$$ r_{1}^{2} = (x + \mu )^{2} + y^{2} + z^{2} ,\;r_{2}^{2} = (x + \mu - 1)^{2} + y^{2} + z^{2} , $$

(2)

r₁ and r₂ are the distances of the third body from the primaries while μ is the mass parameter and is defined as $\mu = \frac{{m_{2} }}{{m_{1} + m_{2} }}$.

Now, if we consider the primaries to be sources of radiation, and suppose that F_g and F_p are the gravitational and radiation forces acting on a particle. Then the resultant force on the particle is given by [9],

$$ F = F_{g} - F_{p} = F_{g} \left( {1 - \frac{{F_{p} }}{{F_{g} }}} \right) = qF_{g} , $$

where q is the factor characterizing radiation effects.

If the solar radiation flood fluctuations and a shadow effect of the planet are neglected, then q is assumed a constant. Depending upon the value of q, the reduced particle mass is positive, negative or zero. In the case where the gravitation prevails, q > 0. The modified equations of motion (1) with the allowance for the radiation force of the primaries, becomes

$$ \begin{aligned} & \ddot{x} - 2\dot{y} = x - \frac{{\left( {1 - \mu } \right)\left( {x + \mu } \right)q_{1} }}{{r_{1}^{3} }} - \frac{{\mu \left( {x + \mu - 1} \right)q_{2} }}{{r_{2}^{3} }} \\ & \ddot{y} + 2\dot{x} = y\left( {1 - \frac{{\left( {1 - \mu } \right)q_{1} }}{{r_{1}^{3} }} - \frac{{\mu q_{2} }}{{r_{2}^{3} }}} \right) \\ & \ddot{z} = z\left( { - \frac{{\left( {1 - \mu } \right)q_{1} }}{{r_{1}^{3} }} - \frac{{\mu q_{2} }}{{r_{2}^{3} }}} \right) \\ \end{aligned} $$

(3)

where q_i(i = 1, 2) represent radiation factors of the bigger and smaller primaries, respectively, and are such that $0 < 1 - q_{i} < < \,1\,\,\left( {i = 1,2} \right),$ and are the ratios of the radiation pressure force to the gravitational force of the primaries.

Equations (3) only took into account the radiation force owning to the gravitation and the radiation pressure. Incorporating the forces arising from the Doppler shift and, the absorption and subsequent re-emission of the incident radiation when the primaries are oblate spheroid, the derived equations of motion of the test particle in conformity with [24], have the form:

$$ \begin{aligned} & \ddot{x} - 2n\dot{y} = n^{2} x - \frac{{(1 - \mu )(x + \mu )q_{1} }}{{r_{1}^{3} }} - \frac{{3(1 - \mu )A_{1} (x + \mu )q_{1} }}{{2r_{1}^{5} }} - \frac{{\mu q_{2} (x + \mu - 1)}}{{r_{2}^{3} }} - \frac{{3\mu (x + \mu - 1)A_{2} q_{2} }}{{2r_{2}^{5} }} \\ & \quad - \frac{{W_{1} }}{{r_{1}^{2} }}\left[ {\frac{(x + \mu )}{{r_{1}^{2} }}\{ (x + \mu )\dot{x} + y\dot{y} + z\dot{z}\} + \dot{x} - ny} \right] - \frac{{W_{2} }}{{r_{2}^{2} }}\left[ {\frac{(x + \mu - 1)}{{r_{2}^{2} }}\{ (x + \mu - 1)\dot{x} + y\dot{y} + z\dot{z}\} + \dot{x} - ny} \right], \\ & \ddot{y} + 2n\dot{x} = n^{2} y - \frac{{(1 - \mu )yq_{1} }}{{r_{1}^{3} }} - \frac{{3(1 - \mu )yA_{1} q_{1} }}{{2r_{1}^{5} }} - \frac{{\mu q_{2} y}}{{r_{2}^{3} }} - \frac{{3\mu yA_{2} q_{2} }}{{2r_{2}^{5} }} \\ & \quad - \frac{{W_{1} }}{{r_{1}^{2} }}\left[ {\frac{y}{{r_{1}^{2} }}\{ (x + \mu )\dot{x} + y\dot{y} + z\dot{z}\} + \dot{y} + n(x + \mu )} \right] - \frac{{W_{2} }}{{r_{2}^{2} }}\left[ {\frac{y}{{r_{2}^{2} }}\{ (x + \mu - 1)\dot{x} + y\dot{y} + z\dot{z}\} + \dot{y} + n(x + \mu - 1)} \right], \\ & \ddot{z} = - \frac{{(1 - \mu )z\,q_{1} }}{{r_{1}^{3} }} - \frac{{3(1 - \mu )zA_{1} q_{1} }}{{2r_{1}^{5} }} - \frac{{\mu q_{2} z}}{{r_{2}^{3} }} - \frac{{3\mu zA_{2} q_{2} }}{{2r_{2}^{5} }} - \frac{{W_{1} }}{{r_{1}^{2} }}\left[ {\frac{z}{{r_{1}^{2} }}\{ (x + \mu )\dot{x} + y\dot{y} + z\dot{z}\} + \dot{z}} \right] \\ & \quad - \frac{{W_{2} }}{{r_{2}^{2} }}\left[ {\frac{z}{{r_{2}^{2} }}\{ (x + \mu - 1)\dot{x} + y\dot{y} + z\dot{z}\} + \dot{z}} \right]. \\ \end{aligned} $$

(4)

where

$$ \begin{aligned} & n^{2} = 1 + \frac{3}{2}A_{1} + \frac{3}{2}A_{2} ,A_{i} = \frac{{AE_{i}^{2} - AP_{i}^{2} }}{{5R^{2} }}\left( {i = 1,2} \right), \\ & W_{1} = \frac{{(1 - \mu )(1 - q_{1} )}}{{c_{d} }},\quad W_{2} = \frac{{\mu (1 - q_{2} )}}{{c_{d} }}. \\ \end{aligned} $$

(5)

A_i(0 < A_i < < 1) are the oblateness coefficients of the primaries and are defined [26] in terms of the distance between the primaries R, the equatorial radii AE_i and polar radii AP_i of m_i. c_d is the dimensionless velocity of light while W_i(i = 1, 2) are the P–R drag of the bigger and smaller primaries, respectively.

Next, we introduce small perturbations in the Coriolis and centrifugal forces with the help of the parameters α and β. Then, the generalized equations of motion under combined effects of radiation, P–R drag, oblateness and small perturbations in the Coriolis and centrifugal forces, in the xy-orbital plane is described by the equations

$$ \begin{aligned} & \ddot{x} - 2n\alpha \dot{y} = \varOmega_{x} , \\ & \ddot{y} + 2n\alpha \dot{x} = \varOmega_{y} , \\ \end{aligned} $$

(6)

where

$$ \begin{aligned} & \varOmega_{x} = n^{2} \beta x - \frac{{(1 - \mu )(x + \mu )q_{1} }}{{r_{1}^{3} }} - \frac{{3(1 - \mu )A_{1} (x + \mu )q_{1} }}{{2r_{1}^{5} }} - \frac{{\mu q_{2} (x + \mu - 1)}}{{r_{2}^{3} }} - \frac{{3\mu (x + \mu - 1)A_{2} q_{2} }}{{2r_{2}^{5} }} \\ & \; - \frac{{W_{1} }}{{r_{1}^{2} }}\left[ {\frac{(x + \mu )}{{r_{1}^{2} }}\{ (x + \mu )\dot{x} + y\dot{y} + z\dot{z}\} + \dot{x} - ny} \right] - \frac{{W_{2} }}{{r_{2}^{2} }}\left[ {\frac{(x + \mu - 1)}{{r_{2}^{2} }}\{ (x + \mu - 1)\dot{x} + y\dot{y} + z\dot{z}\} + \dot{x} - ny} \right], \\ \end{aligned} $$

$$ \begin{aligned} & \varOmega_{y} = n^{2} \beta y - \frac{{yq_{1} }}{{r_{1}^{3} }} - \frac{{3(1 - \mu )A_{1} yq_{1} }}{{2r_{1}^{5} }} - \frac{{\mu yq_{2} }}{{r_{2}^{3} }} - \frac{{3\mu A_{2} yq_{2} }}{{2r_{2}^{5} }} \\ & \quad - \frac{{W_{1} }}{{r_{1}^{2} }}\left[ {\frac{y}{{r_{1}^{2} }}\{ (x + \mu )\dot{x} + y\dot{y} + z\dot{z}\} + \dot{x} - ny} \right] - \frac{{W_{2} }}{{r_{2}^{2} }}\left[ {\frac{y}{{r_{2}^{2} }}\{ (x + \mu - 1)\dot{x} + y\dot{y} + z\dot{z}\} + \dot{x} - ny} \right], \\ \end{aligned} $$

$\alpha = 1 + \sigma$: $\left| \sigma \right| < < 1$ and $\beta = 1 + \varepsilon^{\prime}$: $\left| {\varepsilon^{\prime}} \right| < < 1$.

Next, we discuss the positions of triangular equilibrium points of the third body.

3 Position of triangular equilibrium points

The coordinates of triangular equilibrium points are found by solving the equations $\varOmega_{x} = 0$ and $\varOmega_{y} = 0$ provided $y \ne 0$. That is, they are the solutions of the equations

$$ \begin{aligned} & n^{2} \beta x - \frac{{(1 - \mu )(x + \mu )q_{1} }}{{r_{1}^{3} }} - \frac{{3(1 - \mu )A_{1} (x + \mu )q_{1} }}{{2r_{1}^{5} }} - \frac{{\mu q_{2} (x + \mu - 1)}}{{r_{2}^{3} }} - \frac{{3\mu (x + \mu - 1)A_{2} q_{2} }}{{2r_{2}^{5} }} \\ & \quad + \frac{{W_{1} ny}}{{r_{1}^{2} }} + \frac{{W_{2} ny}}{{r_{2}^{2} }} = 0, \\ \end{aligned} $$

(7)

and,

$$ \left[ {n^{2} \beta - \frac{{(1 - \mu )\,q_{1} }}{{r_{1}^{3} }} - \frac{{3(1 - \mu )q_{1} A_{1} }}{{2r_{1}^{5} }} - \frac{{\mu q_{2} }}{{r_{2}^{3} }} - \frac{{3\mu A_{2} q_{2} }}{{2r_{2}^{5} }}} \right]y - \frac{{W_{1} n\,(x + \mu )}}{{r_{1}^{2} }} - \frac{{W_{2} n\,(x + \mu - 1)}}{{r_{2}^{2} }} = 0 $$

(8)

Now, when the P–R drag effect and oblateness factors are ignored, Eqs. (7) and (8) become:

$$ \begin{aligned} & x\left[ {\beta - \frac{{(1 - \mu )q_{1} }}{{r_{1}^{3} }} - \frac{{\mu q_{2} }}{{r_{2}^{3} }}} \right] - (1 - \mu )\mu \left[ {\frac{{q_{1} }}{{r_{1}^{3} }} - \frac{{q_{2} }}{{r_{2}^{3} }}} \right] = 0, \\ & \quad \beta - \frac{{(1 - \mu )\,q_{1} }}{{r_{1}^{3} }} - \frac{{\mu q_{2} }}{{r_{2}^{3} }} = 0. \\ \end{aligned} $$

When the above equations are solved, we get

$$ r_{1} = \left( {\frac{{q_{1} }}{\beta }} \right)^{{\frac{1}{3}}} ,\quad r_{2} = \left( {\frac{{q_{2} }}{\beta }} \right)^{{\frac{1}{3}}} . $$

(9)

Equations (9) are the solutions of Eqs. (2) when $z = 0$, which is the photogravitational set up when both primaries are radiation sources. Hence, when P–R drag and oblateness of the primaries are present (i.e. $A_{i} \ne 0 \quad W_{i} \ne 0$), we can with the help of (9) assume the solutions of Eqs. (7) and (8), to be

$$ r_{1} = \left( {\frac{{q_{1} }}{\beta }} \right)^{{\frac{1}{3}}} + \varepsilon_{1} ,\quad r_{2} = \left( {\frac{{q_{2} }}{\beta }} \right)^{{\frac{1}{3}}} + \varepsilon_{2} ;\quad \varepsilon_{i} < < 1\quad \left( {i = 1,2} \right) $$

(10)

Now, the x-coordinate of the triangular point is found by solving $r_{1}^{2} = (x + \mu )^{2} + y^{2}$ and $r_{2}^{2} = (x + \mu - 1)^{2} + y^{2}$ simultaneously, to get

$$ x = \frac{1}{2} - \mu + \frac{{r_{1}^{2} - r_{2}^{2} }}{2} $$

(11)

On substituting Eqs. (10) in (11), yields

$$ x = \frac{1}{2} - \mu + \frac{{q_{1}^{{\frac{2}{3}}} - q_{2}^{{\frac{2}{3}}} }}{{2\beta^{{\frac{2}{3}}} }} + \left( {\frac{{q_{1} }}{\beta }} \right)^{{\frac{1}{3}}} \varepsilon_{1} - \left( {\frac{{q_{2} }}{\beta }} \right)^{{\frac{1}{3}}} \varepsilon_{2} $$

(12)

From $y^{2} = r_{1}^{2} - (x + \mu )^{2} ,$ we get

$$ y = \pm y_{0} \left[ {1 + \frac{1}{{2y_{0}^{2} \,\beta^{{\frac{1}{3}}} }}\left( {q_{1}^{{\frac{1}{3}}} \varepsilon_{1} + q_{2}^{{\frac{1}{3}}} \varepsilon_{2} } \right) - \frac{1}{{2y_{0}^{2} \,\beta }}\left( {q_{1}^{{\frac{2}{3}}} - q_{2}^{{\frac{2}{3}}} } \right)\,\left( {q_{1}^{{\frac{1}{3}}} \varepsilon_{1} - q_{2}^{{\frac{1}{3}}} \varepsilon_{2} } \right)} \right] $$

(13)

where

$$ y_{0} = \pm \frac{1}{2}\left[ { - 1 + \frac{1}{{2\,\beta^{{\frac{2}{3}}} }}\left( {q_{1}^{{\frac{1}{3}}} + q_{2}^{{\frac{1}{3}}} } \right) + \frac{1}{{2\,\beta^{{\frac{4}{3}}} }}\left( {q_{1}^{{\frac{2}{3}}} - q_{2}^{{\frac{2}{3}}} } \right)^{2} } \right]^{{\frac{1}{2}}} $$

Now, substituting Eqs. (5), (10), (12), and (13) and into Eqs. (7) and (8), we neglect products of ɛ_i, A_i and W_i(i = 1, 2), we get the respective equations:

$$ a_{1} \varepsilon_{1} + b_{1} \varepsilon_{2} = c_{1} $$

(14)

$$ a_{2} \varepsilon_{1} + b_{2} \varepsilon_{2} = c_{2} $$

(15)

where

$$ \begin{aligned} & a_{1} = 3x_{0} \,q_{1}^{{\frac{ - 1}{3}}} \beta^{{\frac{4}{3}}} \left( {1 - \mu } \right) + 3\mu q_{1}^{{\frac{ - 1}{3}}} \beta^{{\frac{4}{3}}} \left( {1 - \mu } \right) \\ & \quad b_{1} = 3\mu x_{0} q_{2}^{{\frac{ - 1}{3}}} \beta^{{\frac{4}{3}}} - 3\mu q_{2}^{{\frac{ - 1}{3}}} \beta^{{\frac{4}{3}}} \left( {1 - \mu } \right) \\ & c_{1} = \frac{3}{2}\beta \,\left( { - x_{0} + x_{0} q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} - x_{0} \mu q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} + \mu q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} - \mu^{2} q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} } \right)A_{1} + \frac{3}{2}\beta \left( { - x_{0} + } \right.x_{0} \mu q_{2}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} \\ & \quad + \left. {\mu^{2} q_{2}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} - \mu q_{2}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} } \right)A_{2} - y_{0} q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} \left( {W_{1} + W_{2} } \right) \\ \end{aligned} $$

$$ \begin{aligned} & a_{2} = 3y_{0} q_{1}^{{\frac{ - 1}{3}}} \beta^{{\frac{4}{3}}} \left( {1 - \mu } \right) \\ & b_{2} = 3\mu y_{0} q_{2}^{{\frac{ - 1}{3}}} \beta^{{\frac{4}{3}}} \\ & c_{2} = \frac{3}{2}\beta y_{0} \left( { - 1 + q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} - \mu q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} } \right)A_{1} + \frac{3}{2}\beta y_{0} \left( { - 1 + \mu q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} } \right)A_{2} + \left( {x_{0} + \mu } \right)q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} W_{1} \\ & \qquad + \left( {x_{0} + \mu - 1} \right)q_{1}^{{\frac{ - 2}{3}}} \beta^{{\frac{2}{3}}} W_{2} \\ \end{aligned} $$

For simplicity, we express $q_{i} = 1 - \delta_{i} \left( {i = 1,2} \right)$ where δ_i are very small. Substituting these in Eqs. (12) and (13), we have

$$ x = \frac{1}{2} - \mu - \frac{1}{3}\delta_{1} + \frac{1}{3}\delta_{2} + \varepsilon_{1} - \varepsilon_{2} \quad {\text{and}}\quad y = \pm \frac{\sqrt 3 }{2}\left( {1 - \frac{4}{9}\varepsilon^{\prime} - \frac{2}{9}\delta_{1} - \frac{2}{9}\delta_{2} + \frac{1}{{2y_{0}^{2} }}\left( {\varepsilon_{1} + \varepsilon_{2} } \right)} \right) $$

(16)

where $x_{0} = \frac{1}{2} - \mu - \frac{1}{3}\delta_{1} + \frac{1}{3}\delta_{2}$ and $y_{0} = \pm \frac{\sqrt 3 }{2}\left( {1 - \frac{4}{9}\varepsilon^{\prime} - \frac{2}{9}\delta_{1} - \frac{2}{9}\delta_{2} } \right).$

Now, using the relations:

$$ \varepsilon_{1} = \frac{{b_{2} c_{1} - b_{1} c_{2} }}{{a_{1} b_{2} - a_{2} b_{1} }},\quad \varepsilon_{2} = \frac{{a_{1} c_{2} - a_{2} c_{1} }}{{a_{1} b_{2} - a_{2} b_{1} }}. $$

The values of ɛ₁ and ɛ₂ are

$$ \begin{aligned} \varepsilon_{1} & = - \frac{{A_{2} }}{2} - \frac{{W_{1} }}{3\sqrt 3 (1 - \mu )} - \frac{{2W_{2} }}{3\sqrt 3 (1 - \mu )}, \\ \varepsilon_{2} & = - \frac{{A_{1} }}{2} + \frac{{2W_{1} }}{3\mu \sqrt 3 } + \frac{{W_{2} }}{3\mu \sqrt 3 }. \\ \end{aligned} $$

(17)

These equations have been obtained by neglecting products of ɛ_i, A_i, ∂_i and W_i(i = 1, 2)

Now, we substitute Eqs. (17) in (16), to get

$$ \begin{aligned} & x_{4} = \frac{1}{2} - \mu - \frac{1}{3}\delta_{1} + \frac{1}{3}\delta_{2} + \frac{{A_{1} }}{2} - \frac{{A_{2} }}{2} - \frac{{W_{1} (2 - \mu )}}{3\mu \sqrt 3 (1 - \mu )} - \frac{{W_{2} (1 + \mu )}}{3\mu \sqrt 3 (1 - \mu )} \\ & y_{4} = \pm \left[ {\frac{\sqrt 3 }{2}\left( {1 - \frac{4}{9}\varepsilon^{\prime} - \frac{2}{9}\delta_{1} - \frac{2}{9}\delta_{2} - \frac{{A_{1} }}{3} - \frac{{A_{2} }}{3}} \right) + \frac{{W_{1} (2 - 3\mu )}}{9\mu (1 - \mu )} + \frac{{W_{2} (1 - 3\mu )}}{9\mu (1 - \mu )}} \right] \\ \end{aligned} $$

(18)

Equations (18) give the coordinates of the triangular equilibrium points of the system under investigation. Since r₁ ≠ r₂, the two points defined by (18) form scalene triangles with the primaries. These points are denoted by $L_{4,5} (x_{4} , \pm y_{4} )$, and are called the triangular equilibrium points by virtue of the two triangles they form with lines joining the primaries. The positions depend on the mass ratio, small perturbation in the centrifugal force, oblateness, radiation pressures and P–R drag of the primaries.

4 Numerical applications

In order to show the effects of parameters involved in the position and stability of triangular equilibrium points, we consider the binaries system Kruger 60 and Achird. We first compute the dimensionless velocity of light c_d using the relation $c_{d} = \frac{c}{{\sqrt {\frac{{\gamma \left( {M_{1} + M_{2} } \right)}}{a}} }}$ [27], where 'c' is the velocity of light, 'γ' is the gravitational constant, 'a' the binary separation, and M₁ and M₂ are the masses of primaries. Then, we obtain the ratios δ_i and consequently radiation factors q_i by means of relation $q = 1 - \frac{A\kappa L}{a\rho M}$ [28] and $\delta_{2} = \delta_{1} \frac{{L_{2} M_{1} }}{{L_{1} M_{2} }}$ [29], taking κ = 1 on the basis of Stefan-Boltzmann’s law. L_i, M_i refer to luminosity and masses of the primaries, and a and ρ are the radius and density of a moving body; κ is the radiation pressure efficiency factor of a star; $A = \frac{3}{16\pi CG}$ is a constant. In C.G.S system, $A = 2.9838 \times 10^{ - 5} .$ We suppose that the dust grain has a radius and density a = 2 × 10^-2cm and ρ = 1.4g c⁻³,  respectively. All these necessary qualities are listed in the Table 1.

Table 1 Computation of q_i(i = 1, 2) and c_d for Kruger 60 and Achird binary system

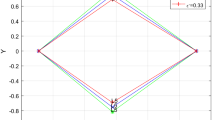
Using the software Mathematica, Table 1 and Eq. (18), we locate numerically the positions of triangular points given in Tables 2, 3, 4, 5. Figure 1 and 2 are the graph of Table 2 and 4 for the triangular points of the binaries system Kruger 60 and Achird.

Table 2 Effects of oblateness and Coriolis forces on L_4,5 for μ = 0.3937, c_d = 46,393.84,  0 < 1 − q_i < < 1 and 0 ≤ A_i ≤ 0.2

Table 3 Effects of radiation pressure on L_4,5 for μ = 0.3937, ɛ^′ = 0.003, c_d = 46,393.84,  0 < 1 − q_i < < 1 and 0 ≤ A_i ≤ 0.2

Table 4 Effects of oblateness and Coriolis forces onL_4,5 for μ = 0.3949, c_d = 67675.52,  0 < 1 − q_i < < 1 and 0 ≤ A_i ≤ 0.2

Table 5 Effects of radiation pressure on L_4,5 for μ = 0.3949,  ɛ^′ = 0.003,  c_d = 67675.52,  0 < 1 − q_i < < 1 and 0 ≤ A_i ≤ 0.2

Fig. 1

Showing the effect of oblateness and Coriolis forces on L_4,5 for Kruger 60

Fig. 2

Showing the effect of oblateness and Coriolis forces on L_4,5 for Achird

In the next section, we investigate the stability of triangular points.

5 Stability of triangular equilibrium points

We now examine the stability of an equilibrium configuration, that is, its ability to restrain the body motion in its vicinity. To do so, we displace the third body a little from an equilibrium point with a small velocity. If its motion is a rapid departure from the vicinity of the point, we call such a position an unstable one. However, if the body merely oscillates about the point, it is said to be a stable position. Let the position of an equilibrium point be denoted by (a₀, b₀) and consider a small displacement (ξ, η) from the point such that x = a₀ + ξ and y = b₀ + η. Substituting these values in (6), we obtain the variational equations

$$ \begin{aligned} & \ddot{\xi } - 2n\alpha \dot{\eta } = (U_{{x\dot{x}}} )^{0} \dot{\xi } + (U_{{x\dot{y}}} )^{0} \dot{\eta } + (U_{xx} )^{0} \xi + (U_{xy} )^{0} \eta \\ & \ddot{\eta } + 2n\alpha \dot{\xi } = (U_{{y\dot{x}}} )^{0} \dot{\xi } + (U_{{y\dot{y}}} )^{0} \dot{\eta } + (U_{yx} )^{0} \xi + (U_{yy} )^{0} \eta \\ \end{aligned} $$

(19)

Here, only linear terms in ξ and η have been taken. The second order partial derivatives of U are denoted by subscripts. The superscript o indicates that the derivatives are to be evaluated at the equilibrium point (a₀, b₀).

The characteristic equation corresponding to Eqs. (19) is

$$ \left| \begin{aligned} \lambda^{2} - \lambda U^{0}_{{x\dot{x}}} - U^{0}_{xx} \quad - 2n\alpha \lambda - \lambda U^{0}_{{x\dot{y}}} - U^{0}_{xy} \hfill \\ \hfill \\ \hfill \\ 2n\alpha \lambda - \lambda U^{0}_{{y\dot{x}}} - U^{0}_{yx} \quad \lambda^{2} - \lambda U^{0}_{{y\dot{y}}} - U^{0}_{yy} \hfill \\ \end{aligned} \right| = 0 $$

That is,

$$ \lambda^{4} + a\lambda^{3} + b\lambda^{2} + c\lambda + d = 0 $$

(20)

where

$$ \begin{aligned} & a = - (U_{{y\dot{y}}}^{0} + U_{{x\dot{x}}}^{0} ) \\ & b = 4n^{2} \alpha^{2} + U_{{x\dot{x}}}^{0} U_{{y\dot{y}}}^{0} - U_{xx}^{0} - U_{yy}^{0} - (U_{{x\dot{y}}}^{0} )^{2} \\ & c = U_{{x\dot{x}}}^{0} U_{yy}^{0} + U_{xx}^{0} U_{{y\dot{y}}}^{0} + 2nU_{xy}^{0} - 2nU_{yx}^{0} - U_{{y\dot{x}}}^{0} U_{xy}^{0} - U_{yx}^{0} U_{{x\dot{y}}}^{0} \\ & d = U_{xx}^{0} U_{yy}^{0} - U_{yx}^{0} U_{xy}^{0} \\ \end{aligned} $$

Evaluating the second order partial derivatives at the equilibrium points, we obtain

$$ \begin{aligned} U_{{x\dot{x}}}^{0} &= - (x_{0} + \mu )^{2} W_{1} - W_{1} - (x_{0} + \mu - 1)^{2} W_{2} - W_{2} \\ U_{{x\dot{y}}}^{0} &= - (x_{0} + \mu )y_{0} W_{1} - (x_{0} + \mu - 1)y_{0} W_{2} = U_{{y\dot{x}}}^{0} {\text{say}} \\ U_{{y\dot{y}}}^{0} &= - (y_{0}^{2} + 1)W_{1} - (y_{0}^{2} + 1)W_{2} \\ U_{xx}^{0} &= 3x_{0}^{2} - 3\mu^{2} + 3\mu + \left( {2x_{0}^{2} + 4\mu x_{0} + 2\mu^{2} - 2\mu^{2} x_{0} - 4\mu^{2} x_{0} - 2\mu^{3} } \right)\delta_{1} \\ & \quad + \left( {2\mu x_{0}^{2} + 2\mu^{3} + 4\mu^{2} x_{0} - 4\mu x_{0} - 4\mu^{2} + 2\mu } \right)\delta_{2} + \left( {5x_{0}^{2} - 5\mu^{2} + 5\mu } \right)\varepsilon^{\prime} \\ & \quad + \left( {\mu + 5x_{0}^{2} + 10\mu x_{0} + 5\mu^{2} - 5\mu x_{0}^{2} - 10\mu^{2} x_{0} - 5\mu^{3} } \right)\frac{3}{2}A_{1} \\ & \quad + \left( {1 + 4\mu + 5\mu x_{0}^{2} + 5\mu^{3} + 10\mu^{2} x_{0} - 10\mu x_{0} - 10\mu^{2} } \right)\frac{3}{2}A_{2} \\ & \quad + \left( {3 - 3\mu - 15\mu^{2} + 15\mu^{3} + 6x_{0} - 15x_{0}^{2} - 30\mu x_{0} + 15\mu x_{0}^{2} + 30\mu^{2} x_{0} } \right)\varepsilon_{1} \\ & \quad + \left( { - 12\mu + 30\mu^{2} - 15\mu^{3} - 6x_{0} - 15\mu x_{0}^{2} + 30\mu x_{0} - 30\mu^{2} x_{0} } \right)\varepsilon_{2} \\ & \quad - \left( {2x_{0} y_{0} + 2\mu y_{0} } \right)\,W_{1} - \left( {2x_{0} y_{0} + 2\mu y_{0} - 2y_{0} } \right)W_{2} \\ \end{aligned} $$

$$ \begin{aligned} & U_{xy}^{0} = 3x_{0} y_{0} + \left( {2x_{0} y_{0} - 2\mu y_{0} - 2\mu x_{0} y_{0} - 2\mu^{2} y_{0} } \right)\delta_{1} + \left( {2\mu x_{0} y_{0} + 2\mu^{2} y_{0} - 2\mu y_{0} } \right)\delta_{2} \\ & \quad + \left( {x_{0} y_{0} + \mu y_{0} - \mu x_{0} y_{0} - \mu^{2} y_{0} } \right)\frac{15}{2}A_{1} + \left( {\mu x_{0} y_{0} + \mu^{2} y_{0} - \mu y_{0} } \right)\frac{15}{2}A_{2} + 5\left( {x_{0} y_{0} } \right)\varepsilon^{\prime} \\ & \quad + \left( {3y_{0} + \frac{{3x_{0} }}{{2y_{0} }} - 15x_{0} y_{0} - 15\mu y_{0} + 15\mu x_{0} y_{0} + 15\mu^{2} y_{0} } \right)\varepsilon_{1} + \left( { - 3y_{0} + \frac{{3x_{0} }}{{2y_{0} }} + 15\mu y_{0} - 15\mu x_{0} y_{0} - 15\mu^{2} y_{0} } \right)\varepsilon_{2} \\ & \quad + \left( {1 - 2y_{0}^{2} } \right)W_{1} + \left( {1 - 2y_{0}^{2} } \right)W_{2} \\ \end{aligned} $$

$$ \begin{aligned} & U_{yx}^{0} = 3x_{0} y_{0} + + \left( {2x_{0} y_{0} - 2\mu y_{0} - 2\mu x_{0} y_{0} - 2\mu^{2} y_{0} } \right)\delta_{1} + \left( {2\mu x_{0} y_{0} + 2\mu^{2} y_{0} - 2\mu y_{0} } \right)\delta_{2} \\ & \quad + \left( {x_{0} y_{0} + \mu y_{0} - \mu x_{0} y_{0} } \right.\left. { - \mu^{2} y_{0} } \right)\frac{15}{2}A_{1} + \left( {\mu x_{0} y_{0} + \mu^{2} y_{0} - \mu y_{0} } \right)\frac{15}{2}A_{2} + 5\left( {x_{0} y_{0} } \right)\varepsilon^{\prime} \\ & \quad + \left( {3y_{0} + \frac{{3x_{0} }}{{2y_{0} }} - 15x_{0} y_{0} - 15\mu y_{0} + 15\mu x_{0} y_{0} } \right.\left. { + 15\mu^{2} y_{0} } \right)\varepsilon_{1} + \left( { - 3y_{0} + \frac{{3x_{0} }}{{2y_{0} }} + 15\mu y_{0} - 15\mu x_{0} y_{0} - 15\mu^{2} y_{0} } \right)\varepsilon_{2} + 2\left( {x_{0} + \mu } \right)^{2} W_{1} - W_{1} + 2\left( {x_{0} + \mu - 1} \right)^{2} W_{2} - W_{2} \\ & U_{yy}^{0} = 3y_{0}^{2} + \left( {2y_{{^{0} }}^{2} - 2\mu y_{{^{0} }}^{2} } \right)\delta_{1} + \left( {2\mu y_{{^{0} }}^{2} } \right)\delta_{2} + \left( {5y_{0}^{2} } \right)\varepsilon^{\prime} + \left( {\mu + 5y_{0}^{2} - 5\mu y_{0}^{2} } \right)\frac{3}{2}A_{1} \\ & \quad \left( {1 - \mu + 5\mu y_{0}^{2} } \right)\frac{3}{2}A_{2} + \left( {6 - 3\mu - 15y_{0}^{2} + 15\mu y_{0}^{2} } \right)\varepsilon_{1} + \left( {3 + 3\mu - 15\mu y_{0}^{2} } \right)\varepsilon_{2} + \left( {2x_{0} y_{0} + 2\mu y_{0} } \right)W_{1} + \left( {2x_{0} y_{0} + 2\mu y_{0} - 2y_{0} } \right)W_{2} \\ \end{aligned} $$

6 Results and discussion

Substituting for $U_{{x\dot{x}}}^{0} ,U_{{x\dot{y}}}^{0} ,U_{{y\dot{y}}}^{0} ,U_{{y\dot{x}}}^{0} ,U_{xx}^{0} ,U_{xy}^{0} ,U_{yy}^{0}$, and $\varOmega_{yx}^{0} ,$ in the characteristic Eq. (20), we get

$$ \begin{aligned} & a = 3W_{1} + 3W_{2} \\ & b = 1 + 8\sigma - 5\varepsilon^{\prime} - \frac{3}{2}A_{1} \left( {1 - 2\mu } \right) + \frac{3}{2}A_{2} \left( { - 1 + 2\mu } \right) + \frac{{W_{1} }}{\sqrt 3 } - \frac{{W_{2} }}{\sqrt 3 } \\ & c = - \frac{{W_{1} }}{4}\left( {12 + 9\mu } \right) - \frac{{W_{2} }}{4}\left( {21 - 9\mu } \right) \\ & d = \frac{27}{4}\mu \left( {1 - \mu } \right) + \frac{45}{2}\mu \left( {1 - \mu } \right)\varepsilon^{\prime} + \frac{3}{2}\mu \left( {1 - \mu } \right)\delta_{1} + \frac{3}{2}\mu \left( {1 - \mu } \right)\delta_{2} + \frac{117}{4}\mu \left( {1 - \mu } \right)A_{1} + \frac{117}{4}\mu \left( {1 - \mu } \right)A_{2} \\ & \quad + \frac{{27W_{1} }}{{4\sqrt 3 \left( {1 - \mu } \right)}}\left( { - 3\mu^{2} + 5\mu - 2} \right) + \frac{{27W_{2} }}{{4\sqrt 3 \left( {1 - \mu } \right)}}\left( { - 3\mu^{2} + 4\mu - 1} \right) \\ \end{aligned} $$

The characteristic equation roots (λ_1,2,3,4) are computed numerically for the motion of a test particle in the neighborhood of a binary star in Table 6 and 7. In particular, the binaries system, “Kruger 60 and Achird” are suitable model for our problem.

Table 6 Roots of the characteristic Eq. (20) for Kruger 60 with varying parameters of radiation, oblateness and P–R drag for μ = 0.3937, c_d = 46393.84, 0 ≤ 1 − q_i ≤ 1 and 0 ≤ A_i ≤ 0.2

Table 7 Roots of the characteristic Eq. (20) for Achird with varying parameters of radiation, oblateness and P–R drag for μ = 0.3949, c_d = 67675.52, 0 ≤ 1 − q_i ≤ 1 and 0 ≤ A_i ≤ 0.2

The triangular equilibrium points have also been established in Eqs. (18) forming scalene triangles with the line joining the primaries, and are calculated using the values of the binary system (Kruger 60 and Achird) as in Tables 2, 3, 4, 5 for varying oblateness, radiation pressure force and effects of the Coriolis force. These are shown graphically in Figs. 1 and 2. It found that both increases in the Coriolis force and the oblateness parameter cause decrease in the equilibrium points. The points L_4,5 is observed to shift in the direction of the bigger primary and towards the line joining the primaries with increasing perturbations.

7 Conclusions

We have modelled Eqs. (6), the motion in the circular R3BP of a test particle under the assumption of both bodies, oblate radiating stars possessing P–R drag given in the literature. The equations are affected by the mass ratio, radiation pressure, oblateness and small perturbation in the Coriolis and centrifugal force. These points are different from those of the classical R3BP of [1], and those obtained by [3, 16, 25].

The triangular equilibrium points L_4,5 under the joint action of perturbing forces are seen to be unstable in the presence of the P–R drag, while in their absence, they are conditionally stable.

Also, the stability of these points has been investigated for (Kruger 60 and Achird) as in Tables 6 and 7, these roots as shown above reveals the existence of at least one complex root with positive real part. Hence, we conclude that the triangular equilibrium points are unstable in the Lyapunov sense due to the presence of at least one complex root of Eq. (20) having positive real part.

This research work has produced significant results and is the backdrop for space technology, man-made satellites are modeled and built as test particles in orbits of celestial bodies. Results considering the shape of the Earth and radiation effect of the Sun, in the Sun-Earth-Satellites system are examples.