1 Background of the problem and review recap

Multi-level programming (MLP) problem is an important class of mathematical programming problems (MPPs) that has an in-built hierarchical structure (level-wise) within the problem with more than two levels. Such problems are more suitable for modeling real-world problems as most complex real problems have a hierarchical structure within them. Bi-level programming problem (BLPP) is a reduced case of MLP problem with only two hierarchical levels. MLP problems have the essential characteristic of having interacting decision-making units in the hierarchy, and each decision-maker (DM) is interested in optimizing their objectives and satisfying a standard set of constraints. A comprehensive literature review and analysis on MLP problems and BLPPs have already been detailed by Lachhwani and Dwivedi [1]. In mathematical format, a multi-level linear programming problem (MLLP problem) can be described as:

$$\begin{gathered} \mathop {Max}\limits_{{\overline{X}_{1} }} \left\{ {Z_{1} (X) = C_{11} \overline{X}_{1} + C_{11} \overline{X}_{2} + ... + C_{1T} \overline{X}_{T} } \right\}\;\;\;\left( {1st\;level} \right) \hfill \\ \mathop {Max}\limits_{{\overline{{X_{2} }} }} \left\{ {Z_{2} (X) = C_{21} \overline{X}_{1} + C_{22} \overline{X}_{2} + ... + C_{2T} \overline{X}_{T} } \right\}\;\;\;\left( {2nd\;level} \right) \hfill \\ . \hfill \\ . \hfill \\ \mathop {Max}\limits_{{\overline{{X_{T} }} }} \left\{ {Z_{T} (X) = C_{T1} \overline{X}_{1} + C_{T2} \overline{X}_{2} + ... + C_{TT} \overline{X}_{T} } \right\}\;\;\;\left( {T - th\;level} \right) \hfill \\ \end{gathered}$$
$${\text{Subject}}\;{\text{to}},\;\overline{{{\text{A}}_{{l{1}}} }} \;\overline{X}_{1} + \overline{{{\text{A}}_{{l{2}}} }} \;\overline{X}_{2} + ... + \overline{{{\text{A}}_{{l{\text{T}}}} }} \;\overline{{X{\kern 1pt} }}_{T} ( \le , = , \ge ){\kern 1pt} {\kern 1pt} b_{i} { ;1} \le l \le p$$
$${\text{and}}\;\overline{X}_{1} \ge 0,\,\overline{X}_{2} \ge 0,\,...,\overline{X}_{T} \ge 0.$$
(1)

where \(\overline{X}_{1} ,\,\overline{X}_{2} ,\,...,\,\overline{X}_{T}\) are respective set of controlling decision variables at each level. \(Z_{t} (\overline{X} {)} = C_{t1} \overline{X}_{1} + C_{t2} \overline{X}_{2} + ... + C_{tT} \overline{X}_{T}\), \(1 \le t \le T\) is the linear objective function at t-th level DM and other notations have the usual meanings.

Over the last fifteen years, a tremendous amount of research has been carried out in developing new solution methodologies for MLP problems and their other extension problems i.e. MLMOLP problems (multi-level multiobjective linear programming problems), MLMONLP problem (multi-level multi-objective non-linear programming problem), MLMOLFP/MLMOL + FP problem(multi-level multiobjective linear/linear plus fractional programming problem), etc. Some notable recent research contributions are: Pramanik et al. [2] developed and demonstrated a solution technique for solving multi-level multiobjective linear plus fractional programming problems (MLMOL + FP problems). Lachhwani [3] modified the existing FGP methodology for obtaining solutions to MLMOLFP problems comparatively with very less computations. Osman et al. [4] proposed a solution technique for solving MLMOP problem with parameters involved as fuzzy demands. Liu and Yang [5] developed a new technique for solving MLMOLP problem.

In the present era, fuzzy and intuitionistic data are used in the decision-making and problem formulation process of MLP problems due to the availability of rough information (vague and imprecise) to decision-makers. Many scholars have suggested important solution methodologies for fuzzy mathematical programming problems (FMPPs) i.e. Fuzzy LPPs, Fuzzy MOPPs, Fuzzy BLPPs, Fuzzy MLP problems, etc. Some of the research contributions which involve the use of integral transform technique in solving FMPP are: Peraei et al. [6] used the concept of Melin transform for solving FLPP. NA Alauden and MY Sanar [7] used Melin transform for de-fuzzification of fuzzy numbers in solving FLPPs. But the fuzzy theory has a major drawback of ignoring two other aspects of information i.e. indeterminacy and falsity in formulating membership functions. To eliminate the shortcomings of the fuzzy set (Zadeh [8]) and intuitionistic fuzzy theory (Atanassov [9]), Smarandache [10] introduced neutrosophic set theory—theory with three parts of information i.e. truthiness, falsity, and indeterminacy. This theory plays a vital role in describing industrial problems having vague and indeterminate information. Nowadays, MPPs are extended towards new and active research areas ‘under neutrosophic environment’. Many researchers have suggested new research ideas on MPPs in the neutrosophic environment: Ye [11] suggested a novel technique for LPPs with N numbers. Mohamed et al. [12] suggested a method for solving integer programming problems with trapezoidal N numbers. Abdel-Basset et al. [13] suggested a new type of ranking function for N numbers for conversion of N numbers into equivalent crisp values and proposed to apply this new ranking function to solve the fully neutrosophic (IVTrN numbers) linear programming problems (LPPs). Pramanik and Banerjee [14] developed a solution technique for MOLP problem under N number environment. Pramanik and Dey [15] suggested another solution technique for solving two-level programming problems (BLPPs) under N number environments. Bera and Mahapatra [16] developed a new simplex method (big-M method for N numbers) to solve real-life problems formulated as neutrosophic LPPs. Darehmiraki [17] proposed a new parametric ranking function to solve neutrosophic linear programming problems. Basumatary and Broumi [18] proposed a new type of neutrosophic MPP with parameters as interval-valued triangular N numbers. Khatter [19] proposed a solution approach to solve neutrosophic LP problem with a possibilistic mean. Maiti et al. [20] proposed a technique based on goal programming for MLMOP problem under N numbers. Lachhwani [21] suggested an algorithm for solving fully neutrosophic MLMOLP problems with all coefficients and parameters as trapezoidal N numbers. Ahmad [22] suggested a solution technique for MOPP under neutrosophic environment with application in the pharmaceutical supply chain planning problems. Recently, Tamilarasi and Paulraj [23] used Melin transform for de-neutrosophication of triangular type N numbers for developing the technique for linear programming problems.

The entire literature on MPPs under neutrosophic environment reveals that most of the researchers used ranking method, accuracy function value, score function values, etc. for the de-neutrosophication of N numbers. Except for Tamilarasi and Paulraj [23] who used Melin transform on triangular type N numbers), the literature does not provide any use of integral transform for de-neutrosophication of N numbers till now. This motivates us to extend the use of important integral transform i.e. Laplace transform for de-neutrosophication of fully N numbers i.e. interval values trapezoidal neutrosophic numbers (IVTrpN numbers) in solving more complex multi-level programming problems. The present study of fully neutrosophic MLLP problem with Laplace transform has not been studied in the literature. This makes the proposed study unique and novel in this research area. The main objectives of the paper:

  1. 1.

    To propose a novel method of defining proportional probability density function for IVTrpN numbers and de-neutrosophication of IVTrpN numbers with the use of Laplace transform.

  2. 2.

    To propose an improved solution algorithm for MLLP problem with IVTrpN numbers as coefficients/ parameters in objective functions and constrained functions.

In abstract form, the present paper describes a unique solution methodology for generalized multi-level linear programming involving coefficient parameters in an objective at each level as well as constraints as interval-valued trapezoidal neutrosophic numbers (IVTrp N numbers), based on Laplace transform. In this approach, we first propose to associate the probability density function to each membership function of each IVTrpN numbers and obtain an equivalent output value of each N numbers using Laplace transform. After that, the multi-level structure of the crisp problem is tackled by formulating separate membership functions for each objective function at each level and decision variables up to the (T-1) level with their best values. A simple solution model is formulated to obtain a satisfactory solution of MLLP problem under neutrosophic environment with the help of usual goal programming. Further, a comparative study is also carried out between the use of the Laplace transform and Melin transform (as suggested by Tamilarasi and Paulraj [23]) for de-neutrosophication of SVTrN numbers. Numerical example and solution of complex real problem are illustrated to show the functionality and applicability of the proposed improved approach.

This paper is organized as: in the first section of the paper, a background of the problem along with a review recap on specific MPPs and MPPs under neutrosophic environment are suggested. In Sect. 2, literature review analysis is suggested in tabular form on different solution techniques for MLP problems and extension problems under N number environment. Based on this review analysis, the research gap and significance of the proposed technique are also discussed. Some preliminaries on neutrosophic numbers (N numbers) are described in the next section. The proposed algorithm for MLLP problem with N numbers is presented in detail in Sect. 4. The introduction of proportional probability density functions to each N number and the use of the Laplace transform for finding equivalent crisp values of N numbers are discussed in Sects. 4.1 and 4.2 respectively. The step-by-step process and a flow chart of the proposed algorithm for solving MLP problems with IVTrpN numbers are also suggested in the same section. Further, a comparative study is also carried out between the use of the Laplace transform and Melin transform (as suggested by Tamilarasi and Paulraj [23]) for de-neutrosophication of N numbers in Sect. 5. In Sect. 6, a numerical example is illustrated with the proposed technique to show its computational simplicity and uniqueness in solving MLP problems with IVTrpN numbers. The application of the proposed technique in solving the real problem is described in the same section. Concluding remarks and future research directions are discussed in the last section.

2 Review analysis and identification of research gap

As detailed in the previous section it can be seen that ‘MPP under N number environment’ is a new area of research and limited number of research scholars have contributed in this area. In continuation of the literature review on solving different types of MPPs with N numbers can be described in tabular form (Table 1). From Table 1, it is evident that researchers preferably used score functions or accuracy functions as ranking methods to convert N numbers. But recently Tamilarasi and Paulraj [23] used Melin transform for de-neutrosophication of triangular type N numbers for developing the technique for linear programming problems. This motivates us to extend the use of important integral transform i.e. Laplace transform for de-neutrosophication of interval values trapezoidal neutrosophic numbers (IVTrpN numbers) in solving more complex multi-level linear programming problems. Further, in the above literature review and analysis, it can be observed that no researcher has proposed a solution method for MLP problems with IVTrpN numbers using Laplace transform. In all, the proposed algorithm is improved and unique for solving MLP problems under N number environment.

Table 1 Comparison of research contributions on MP problems with fuzzy and/ or N numbers
Full size table

3 Neutrosophic set theory—preliminaries

Neutrosophic set theory is a paradigm shift from traditional fuzzy and intuitionistic fuzzy set theory which includes three major parts of information i.e. truthiness, indeterminacy, and falsity information. This N set theory is used to analyze imprecise and inaccurate information. In literature, this theory was extended with properties of N set and neutrosophic statistics by Smarandache ([24, 25]) respectively. Some preliminaries on N numbers and related terms are described as:

Definition 1

(Smarandache [10]): a neutrosophic set A in X is characterized as \(A = \left\{ {x:\;\mu_{A}^{T} (x),\;\sigma_{A}^{T} (x),\;\upsilon_{A}^{T} (x),\;x \in X} \right\}\) where \(\mu_{A}^{T} (x),\;\sigma_{A}^{T} (x),\;\upsilon_{A}^{T} (x) \in \left( {0,\;1} \right)\) represents degree of membership for truthiness, indeterminacy and falsity parts of information respectively along with condition.

$$0^{ + } \le Sup\;\mu_{A}^{T} (x) + \;Sup\;\sigma_{A}^{T} (x) + \;Sup\;\upsilon_{A}^{T} (x) \le 3^{ - }$$

Definition 2

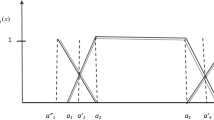
(Interval valued trapezoidal neutrosophic number IVTrpN number) (Abdel-Basset et al. [13]) Let \(\mu_{{\widetilde{a}}} ,\;\sigma_{{\widetilde{a}}} ,\;\upsilon_{{\widetilde{a}}} \in [0,\;1]\) and \(a_{i} \in R\), \(R\) the real numbers and \(a_{1} \le \;a_{2} \le \;a_{3} \le \;a_{4}\). Then an interval-valued trapezoidal neutrosophic number is given as: \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} );\;[\mu_{{\widetilde{a}}}^{L} ,\;\mu_{{\widetilde{a}}}^{U} ],\;[\sigma_{{\widetilde{a}}}^{L} ,\;\sigma_{{\widetilde{a}}}^{U} ],\;[\upsilon_{{\widetilde{a}}}^{L} ,\;\upsilon_{{\widetilde{a}}}^{U} ]} \right\rangle\) whose membership function for truthiness, indeterminacy and falsity are

$$\mu_{{\widetilde{a}}} (x) = \left\{ {\begin{array}{*{20}c} {\mu_{{\widetilde{a}}}^{U} \left( {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} \right),} & {a_{1} \le x \le a_{2} ,} \\ {\mu_{{\widetilde{a}}}^{U} ,} & {a_{2} \le x \le a_{3} ,} \\ {\mu_{{\widetilde{a}}}^{U} \left( {\frac{{a_{4} - x}}{{a_{4} - a_{3} }}} \right),} & {a_{3} \le x \le a_{4} ,} \\ {0,} & {{\text{otherwise}},} \\ \end{array} } \right.$$
(2)
$$\sigma_{{\widetilde{a}}} (x) = \left\{ {\begin{array}{*{20}c} {\frac{{a_{2} - x + \sigma_{{\widetilde{a}}}^{L} (x - a_{1} )}}{{a_{2} - a_{1} }},} & {a_{1} \le x \le a_{2} ,} \\ {\sigma_{{\widetilde{a}}}^{L} ,} & {a_{2} \le x \le a_{3} ,} \\ {\frac{{x - a_{3} + \sigma_{{\widetilde{a}}}^{L} (a_{4} - x)}}{{a_{4} - a_{3} }},} & {a_{3} \le x \le a_{4} ,} \\ {1,} & {{\text{otherwise}},} \\ \end{array} } \right.$$
(3)
$$\upsilon_{{\widetilde{a}}} (x) = \left\{ {\begin{array}{*{20}c} {\frac{{a_{2} - x + \upsilon_{{\widetilde{a}}}^{L} (x - a_{1} )}}{{a_{2} - a_{1} }},} & {a_{1} \le x \le a_{2} ,} \\ {\upsilon_{{\widetilde{a}}}^{L} ,} & {a_{2} \le x \le a_{3} ,} \\ {\frac{{x - a_{3} + \upsilon_{{\widetilde{a}}}^{L} (a_{4} - x)}}{{a_{4} - a_{3} }},} & {a_{3} \le x \le a_{4} ,} \\ {1,} & {{\text{otherwise}},} \\ \end{array} } \right.$$
(4)

In view of this definition, there is not much significance of \(\mu_{{\widetilde{a}}}^{L} ,\;\sigma_{{\widetilde{a}}}^{U}\) and \(\upsilon_{{\widetilde{a}}}^{U}\) in achieving membership values. Therefore for simplicity, we here assume \(\mu_{{\widetilde{a}}}^{U} = \mu_{{\widetilde{a}}} ,\;\sigma_{{\widetilde{a}}}^{L} = \sigma_{{\widetilde{a}}}\) and \(\upsilon_{{\widetilde{a}}}^{L} = \upsilon_{{\widetilde{a}}}\). Accordingly, IVTrp N numbers are rewritten as:

$$\widetilde{a} = \left\langle {(a_{1} ,a_{2} ,a_{3} ,a_{4} );\mu_{{\widetilde{a}}}^{{}} ,\sigma_{{\widetilde{a}}}^{{}} ,\upsilon_{{\widetilde{a}}}^{{}} } \right\rangle .$$
(5)

Definition 3

(Single valued triangular neutrosophic number SVTrN number) (Tamilarasi and Paulraj [23]) Let \(\mu_{{\widetilde{a}}} ,\;\sigma_{{\widetilde{a}}} ,\;\upsilon_{{\widetilde{a}}} \in [0,\;1]\) and \(a_{i} \in R\), \(R\) the real numbers and \(a_{1} \le \;a_{2} \le \;a_{3}\). Then a single valued triangular neutrosophic number is given as: \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} );\mu_{{\widetilde{a}}}^{{}} ,\;\sigma_{{\widetilde{a}}}^{L} ,\;\upsilon_{{\widetilde{a}}}^{L} } \right\rangle\) whose membership function for truthiness, indeterminacy and falsity are

$$\mu_{{\widetilde{a}}} (x) = \left\{ {\begin{array}{*{20}c} {\mu_{{\widetilde{a}}}^{{}} \left( {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} \right),} & {a_{1} \le x \le a_{2} ,} \\ {\mu_{{\widetilde{a}}}^{{}} ,} & {x = a_{2} ,} \\ {\mu_{{\widetilde{a}}}^{{}} \left( {\frac{{a_{4} - x}}{{a_{4} - a_{3} }}} \right),} & {a_{2} \le x \le a_{3} ,} \\ {0,} & {{\text{otherwise}}{.}} \\ \end{array} } \right.$$
(6)
$$\sigma_{{\widetilde{a}}} (x) = \left\{ {\begin{array}{*{20}c} {\frac{{a_{2} - x + \sigma_{{\widetilde{a}}}^{{}} (x - a_{1} )}}{{a_{2} - a_{1} }},} & {a_{1} \le x \le a_{2} ,} \\ {\sigma_{{\widetilde{a}}}^{{}} ,} & {x = a_{2} ,} \\ {\frac{{x - a_{3} + \sigma_{{\widetilde{a}}}^{{}} (a_{4} - x)}}{{a_{4} - a_{3} }},} & {a_{2} \le x \le a_{3} ,} \\ {1,} & {{\text{otherwise}}{.}} \\ \end{array} } \right.$$
(7)
$$\upsilon_{{\widetilde{a}}} (x) = \left\{ {\begin{array}{*{20}c} {\frac{{a_{2} - x + \upsilon_{{\widetilde{a}}}^{{}} (x - a_{1} )}}{{a_{2} - a_{1} }},} & {a_{1} \le x \le a_{2} ,} \\ {\upsilon_{{\widetilde{a}}}^{{}} ,} & {x = a_{2} ,} \\ {\frac{{x - a_{2} + \upsilon_{{\widetilde{a}}}^{{}} (a_{3} - x)}}{{a_{3} - a_{2} }},} & {a_{2} \le x \le a_{3} ,} \\ {1,} & {{\text{otherwise}}{.}} \\ \end{array} } \right.$$
(8)

Definition 4

(Score function) (Khatter [19]): the score function for the interval valued neutrosophic number \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} );\;[\mu_{{\widetilde{a}}}^{L} ,\;\mu_{{\widetilde{a}}}^{U} ],\;[\sigma_{{\widetilde{a}}}^{L} ,\;\sigma_{{\widetilde{a}}}^{U} ],\;[\upsilon_{{\widetilde{a}}}^{L} ,\;\upsilon_{{\widetilde{a}}}^{U} ]} \right\rangle\) is defined as:

$$S(\widetilde{a}) = \frac{1}{16}(a_{1} + a_{2} + a_{3} + a_{4} )(1 + \mu_{{\widetilde{a}}}^{L} + \mu_{{\widetilde{a}}}^{U} - \sigma_{{\widetilde{a}}}^{L} - \sigma_{{\widetilde{a}}}^{U} - \upsilon_{{\widetilde{a}}}^{L} - \upsilon_{{\widetilde{a}}}^{U} + 1).$$
(9)

Definition 5

(Accuracy function) (Khatter [19]): accuracy function for IVTrp N number \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} );\;[\mu_{{\widetilde{a}}}^{L} ,\;\mu_{{\widetilde{a}}}^{U} ],\;[\sigma_{{\widetilde{a}}}^{L} ,\;\sigma_{{\widetilde{a}}}^{U} ],\;[\upsilon_{{\widetilde{a}}}^{L} ,\;\upsilon_{{\widetilde{a}}}^{U} ]} \right\rangle\) is defined as:

$$A(\widetilde{a}) = \frac{1}{8}(a_{1} - a_{2} - a_{3} + a_{4} )(1 + \mu_{{\widetilde{a}}}^{L} + \mu_{{\widetilde{a}}}^{U} - \upsilon_{{\widetilde{a}}}^{L} - \upsilon_{{\widetilde{a}}}^{U} + 1).$$
(10)

Definition 6

(Ranking function for interval valued trapezoidal N number) (Abdel-Basset et al. [13]): ranking function for IVTrpN number Let \(\tilde{a} = (a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} ,;\;\mu_{{\tilde{a}}} ,\;\sigma_{{\tilde{a}}} ,\;\upsilon_{{\tilde{a}}} )\), then corresponding ranking function for maximization purpose is defined as:

$$R(\tilde{a}) = \left( {\frac{{a_{1} + a_{4} + 2(a_{3} + a_{4} )}}{2}} \right) + \left( {\mu_{{\tilde{a}}} - \sigma_{{\tilde{a}}} - \upsilon_{{\tilde{a}}} } \right).$$
(11)

It is important to mention that score function, accuracy function and ranking function are used to convert N numbers into equivalent crisp values.

4 Proposed improved solution technique for MLLP problem with IVTrpN numbers

In this part of the paper, we describe the proposed solution methodology for MLLP problem with IVTrpN numbers in three subsections ahead. Firstly, we propose to associate proportional probability density function (p.d.f.) and introduce the use of Laplace transform on p.d.f. to obtain the equivalent crisp value of the corresponding IVTrpN numbers in the following subsections:

4.1 Proportional probability density function to membership functions

Here, we propose to associate proportional p.d.f. corresponding to its truthiness, indeterminacy and falsity membership functions of IVTrpN number \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} );\;\mu_{{\widetilde{a}}}^{{}} ,\;\sigma_{{\widetilde{a}}}^{{}} ,\;\upsilon_{{\widetilde{a}}}^{{}} } \right\rangle\). For this, let \(f_{1} (x)\), \(f_{2} (x)\), \(f_{3} (x)\) be the p.d.f. corresponding to membership functions \(\mu_{{\widetilde{a}}}^{{}} ,\;\sigma_{{\widetilde{a}}}^{{}} \;\), \(\upsilon_{{\widetilde{a}}}^{{}}\) respectively. Then \(f_{1} (x) = k_{1} \mu_{{\widetilde{a}}}^{{}} (x)\), \(f_{2} (x) = k_{2} \sigma_{{\widetilde{a}}}^{{}} (x)\;\) and \(f_{3} (x) = k_{3} \upsilon_{{\widetilde{a}}}^{{}} (x)\) where \(k_{1}\), \(k_{2}\) and \(k_{3}\) are constants to be obtained using properties of p.d.f.

(i) \(\int\limits_{ - \infty }^{\infty } {f_{1} (x)dx = 1} \Rightarrow k_{1} \left[ {\int\limits_{{a_{1} }}^{{a_{2} }} {\mu_{{\widetilde{a}}} \left( {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} \right)dx + \int\limits_{{a_{2} }}^{{a_{3} }} {\mu_{{\widetilde{a}}} dx} + \int_{{a_{3} }}^{{a_{4} }} {\mu_{{\widetilde{a}}} \left( {\frac{{a_{4} - x}}{{a_{4} - a_{3} }}} \right)dx} } } \right] = 1\)

$$\Rightarrow k_{1} \left[ { - a_{1} \mu_{{\widetilde{a}}} - \frac{{a_{1}^{2} \mu_{{\widetilde{a}}} }}{{2( - a_{1} + a_{2} )}} + \frac{{a_{2}^{2} \mu_{{\widetilde{a}}} }}{{2( - a_{1} + a_{2} )}} + ( - a_{2} + a_{3} )\mu_{{\widetilde{a}}} + a_{4} \mu_{{\widetilde{a}}} + \frac{{a_{3}^{2} \mu_{{\widetilde{a}}} }}{{2( - a_{3} + a_{4} )}} - \frac{{a_{4}^{2} \mu_{{\widetilde{a}}} }}{{2( - a_{3} + a_{4} )}}} \right] = 1$$
$${\text{This}}\;{\text{will}}\;{\text{give}}\;{\text{us}}\;k_{1} = - \frac{2}{{(a_{1} + a_{2} - a_{3} - a_{4} )\mu_{{\widetilde{a}}} }}.$$
(12)

(ii) \(f_{2} (x) = k_{2} \sigma_{{\widetilde{a}}} (x)\), then \(\int\limits_{ - \infty }^{\infty } {f_{2} (x)dx = 1}\)

$$\Rightarrow k_{2} \left[ {\int\limits_{{a_{1} }}^{{a_{2} }} {\left( {\frac{{a_{2} - x + \sigma_{{\widetilde{a}}} (x - a_{1} )}}{{a_{2} - a_{1} }}} \right)dx + \int\limits_{{a_{2} }}^{{a_{3} }} {\sigma_{{\widetilde{a}}} dx} + \int_{{a_{3} }}^{{a_{4} }} {\left( {\frac{{x - a_{3} + \sigma_{{\widetilde{a}}} (a_{4} - x)}}{{a_{4} - a_{3} }}} \right)dx} } } \right] = 1$$
$$\Rightarrow k_{2} \left[ {( - a_{2} + a_{3} )\sigma_{{\widetilde{a}}} - \frac{1}{2}(a_{1} - a_{2} )(1 + \sigma_{{\widetilde{a}}} ) - \frac{1}{2}(a_{3} - a_{4} )(1 + \sigma_{{\widetilde{a}}} )} \right] = 1.$$
$${\text{It}}\;{\text{give}}\;{\text{us}}\;k_{2} = - \frac{2}{{(a_{1} - a_{2} + a_{3} - a_{4} ) + \sigma_{a} (a_{1} + a_{2} - a_{3} - a_{4} )}}.$$
(13)

(iii) Similarly for \(f_{3} (x) = k_{3} \upsilon_{{\widetilde{a}}} (x)\) and \(\int\limits_{ - \infty }^{\infty } {f_{3} (x)dx = 1}\) which yield

$$k_{3} = - \frac{2}{{(a_{1} - a_{2} + a_{3} - a_{4} ) + \upsilon_{a} (a_{1} + a_{2} - a_{3} - a_{4} )}}.$$
(14)

Now let \(f(x)\) be the complete probability density function of IVTrpN number [defined in (5)] in consideration of all membership functions, then \(f(x)\) can be defined as:

$$f(x) = \lambda_{1} f_{1} (x) + \lambda_{2} f_{2} (x) + \lambda_{3} f_{3} (x)$$
$$i.e.\;\;f(x) = \lambda_{1} k_{1} \mu_{{\widetilde{a}}}^{{}} (x) + \lambda_{2} k_{2} \sigma_{{\widetilde{a}}}^{{}} (x) + \lambda_{3} k_{3} \upsilon_{{\widetilde{a}}}^{{}} (x)$$
(15)

where \(\lambda_{1} ,\,\lambda_{2} ,\,\lambda_{3} \in [0,1]\) are relative weights to different functions selected by decision maker in accordance with preference information available to DM with condition \(\lambda_{1} + \lambda_{2} + \lambda_{3} = 1\).

4.2 Use of Laplace transform

Integral transform is normally used to convert a hard function into a simple one according to functional specifications. The integral transform of a specifically defined linear function is associated with the unique equivalent value of that function. Here we propose to use Laplace Transform on proportional complete probability density function to obtain an equivalent value of N number.

Definition 7

Laplace transform of function \(f(x)\) (\(0 < x < \infty\)) of class ‘A’ is defined as

$$L_{X} (s) = \int\limits_{0}^{\infty } {e^{ - sx} f(x)dx} ,$$

Whenever it exists. Here \(f(x)\) is complete probability density function associated with IVTrpN number and X denotes the random variable corresponding to the IVTrpN numbers. Laplace Transform has the unique property of one-to-one correspondence in two domains \((x,s)\) i.e. \(f(x) \leftrightarrow L_{X} (s)\). This property is taken as a tool for finding equivalent value for each of IVTrpN number with the assumption of least value of s, i.e. \(s = 1\). Laplace transform of p.d.f. of IVTrpN number (12) can be described as:

$$L_{X} (s) = \int\limits_{0}^{\infty } {e^{ - sx} } [\lambda_{1} f_{1} (x) + \lambda_{2} f_{2} (x) + \lambda_{3} f_{3} (x)]dx$$
$$\begin{gathered} \Rightarrow L_{X} (s) = \frac{{2\lambda_{1} }}{{(a_{3} + a_{4} - a_{1} - a_{2} )\mu_{{\widetilde{a}}} }}\left[ {\int\limits_{{a_{1} }}^{{a_{2} }} {e^{ - sx} \mu_{{\widetilde{a}}} \left( {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} \right)dx + \int\limits_{{a_{2} }}^{{a_{3} }} {e^{ - sx} \mu_{{\widetilde{a}}} dx} + \int_{{a_{3} }}^{{a_{4} }} {e^{ - sx} \mu_{{\widetilde{a}}} \left( {\frac{{a_{4} - x}}{{a_{4} - a_{3} }}} \right)dx} } } \right] \hfill \\ - \frac{{2\lambda_{2} }}{{(a_{1} - a_{2} + a_{3} - a_{4} + \sigma_{{\widetilde{a}}} a_{1} + \sigma_{{\widetilde{a}}} a_{2} - \sigma_{{\widetilde{a}}} a_{3} - \sigma_{{\widetilde{a}}} a_{4} )}}\left[ {\int\limits_{{a_{1} }}^{{a_{2} }} {e^{ - sx} \left( {\frac{{a_{2} - x + \sigma_{{\widetilde{a}}} (x - a_{1} )}}{{a_{2} - a_{1} }}} \right)dx + \int\limits_{{a_{2} }}^{{a_{3} }} {e^{ - sx} \sigma_{{\widetilde{a}}} dx} } } \right. \hfill \\ + \left. {\int_{{a_{3} }}^{{a_{4} }} {e^{ - sx} \left( {\frac{{x - a_{3} + \sigma_{{\widetilde{a}}} (a_{4} - x)}}{{a_{4} - a_{3} }}} \right)dx} } \right] \hfill \\ - \frac{{2\lambda_{3} }}{{(a_{1} - a_{2} + a_{3} - a_{4} + \upsilon_{{\widetilde{a}}} a_{1} + \upsilon_{{\widetilde{a}}} a_{2} - \upsilon_{{\widetilde{a}}} a_{3} - \upsilon_{{\widetilde{a}}} a_{4} )}}\left[ {\int\limits_{{a_{1} }}^{{a_{2} }} {e^{ - sx} \upsilon_{{\widetilde{a}}} \left( {\frac{{a_{2} - x + \upsilon_{{\widetilde{a}}} (x - a_{1} )}}{{a_{2} - a_{1} }}} \right)dx + \int\limits_{{a_{2} }}^{{a_{3} }} {e^{ - sx} \upsilon_{{\widetilde{a}}} dx} } } \right. \hfill \\ + \left. {\int_{{a_{3} }}^{{a_{4} }} {e^{ - sx} \left( {\frac{{x - a_{3} + \upsilon_{{\widetilde{a}}} (a_{4} - x)}}{{a_{4} - a_{3} }}} \right)dx} } \right] \hfill \\ \end{gathered}$$
$$\begin{gathered} \Rightarrow L_{X} (s) = \frac{{2\lambda_{1} }}{{(a_{3} + a_{4} - a_{1} - a_{2} )\mu_{{\widetilde{a}}} }}\left[ {\mu_{{\widetilde{a}}} \left( {\frac{{e^{{ - a_{2} s}} - e^{{ - a_{3} s}} }}{s}} \right) - \mu_{{\widetilde{a}}} \frac{{e^{{ - (a_{1} + a_{2} )s}} (e^{{a_{2} s}} + e^{{a_{1} s}} (1 + a_{1} s - a_{2} s))}}{{(a_{1} - a_{2} )s^{2} }}} \right. \hfill \\ \left. { + \mu_{{\widetilde{a}}} \frac{{e^{{ - (a_{3} + a_{4} )s}} ( - e^{{a_{3} s}} + e^{{a_{4} s}} (1 + a_{3} s - a_{4} s))}}{{(a_{3} - a_{4} )s^{2} }}} \right] \hfill \\ - \frac{{2\lambda_{2} }}{{(a_{1} - a_{2} + a_{3} - a_{4} + \sigma_{{\widetilde{a}}} a_{1} + \sigma_{{\widetilde{a}}} a_{2} - \sigma_{{\widetilde{a}}} a_{3} - \sigma_{{\widetilde{a}}} a_{4} )}}\left[ {\frac{{e^{{ - (a_{1} + a_{2} )s}} ( - e^{{ - a_{2} s}} ( - 1 - a_{1} s + a_{2} s + \sigma_{{\widetilde{a}}} )}}{{(a_{1} - a_{2} )s^{2} }}} \right. \hfill \\ + \frac{{e^{{ - (a_{1} + a_{2} )s}} (e^{{a_{1} s}} ( - 1 + \sigma_{{\widetilde{a}}} - a_{1} s\sigma_{{\widetilde{a}}} + a_{2} s\sigma_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )s^{2} }} + \frac{{e^{{ - (a_{3} + a_{4} )s}} ( - e^{{ - a_{3} s}} ( - 1 + a_{3} s - a_{4} s + \sigma_{{\widetilde{a}}} ))}}{{(a_{3} - a_{4} )s^{2} }} \hfill \\ + \left. {\frac{{e^{{ - (a_{3} + a_{4} )s}} (e^{{a_{4} s}} ( - 1 + \sigma_{{\widetilde{a}}} + a_{3} s\sigma_{{\widetilde{a}}} - a_{4} s\sigma_{{\widetilde{a}}} ))}}{{(a_{3} - a_{4} )s^{2} }} + \frac{{(e^{{ - a_{2} s}} - e^{{ - a_{3} s}} )\sigma_{{\widetilde{a}}} }}{s}} \right] \hfill \\ - \frac{{2\lambda_{3} }}{{(a_{1} - a_{2} + a_{3} - a_{4} + \upsilon_{{\widetilde{a}}} a_{1} + \upsilon_{{\widetilde{a}}} a_{2} - \upsilon_{{\widetilde{a}}} a_{3} - \upsilon_{{\widetilde{a}}} a_{4} )}}\left[ {\frac{{e^{{ - (a_{1} + a_{2} )s}} (e^{{ - a_{2} s}} ( - 1 - a_{1} s + a_{2} s + \upsilon_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )s^{2} }}} \right. \hfill \\ + \frac{{e^{{ - (a_{1} + a_{2} )s}} (e^{{a_{1} s}} ( - 1 + \upsilon_{{\widetilde{a}}} - a_{1} s\upsilon_{{\widetilde{a}}} + a_{2} s\upsilon_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )s^{2} }} + \frac{{e^{{ - (a_{3} + a_{4} )s}} ( - e^{{ - a_{3} s}} ( - 1 + a_{3} s - a_{4} s + \upsilon_{{\widetilde{a}}} ))}}{{(a_{3} - a_{4} )s^{2} }} \hfill \\ + \left. {\frac{{e^{{ - (a_{3} + a_{4} )s}} (e^{{a_{4} s}} ( - 1 + \upsilon_{{\widetilde{a}}} + a_{3} s\upsilon_{{\widetilde{a}}} - a_{4} s\upsilon_{{\widetilde{a}}} ))}}{{(a_{3} - a_{4} )s^{2} }} + \frac{{(e^{{ - a_{2} s}} - e^{{ - a_{3} s}} )\upsilon_{{\widetilde{a}}} }}{s}} \right] \hfill \\ \end{gathered}$$
(16)

In order to find equivalent crisp values E(\(\widetilde{a}\)) of each of neutrosophic coefficient/parameter of the problem with minimum mathematical computation, here we have considered the least value of s i.e. s = 1. It is to be noted that E(\(\widetilde{a}\)) only represents the corresponding equivalent crisp value of N number.

For s = 1, the corresponding equivalent value will be as:

$$\begin{gathered} E(\widetilde{a}) = \frac{{2\lambda_{1} }}{{(a_{3} + a_{4} - a_{1} - a_{2} )}}\left[ {\frac{{e^{{ - a_{1} - a_{2} - a_{3} - a_{4} }} (( - a_{1} + a_{2} )e^{{a_{1} + a_{2} + a_{3} }} + (a_{1} - a_{2} )e^{{a_{1} + a_{2} + a_{4} }} }}{{(a_{1} - a_{2} )(a_{3} - a_{4} )}}} \right. \hfill \\ + \left. {\frac{{e^{{ - a_{1} - a_{2} - a_{3} - a_{4} }} ((a_{3} - a_{4} )e^{{a_{1} + a_{3} + a_{4} }} + ( - a_{3} + a_{4} )e^{{a_{2} + a_{3} + a_{4} }} ))}}{{(a_{1} - a_{2} )(a_{3} - a_{4} )}}} \right] \hfill \\ + \frac{{2\lambda_{2} }}{{(a_{2} - a_{3} + a_{4} - \sigma_{{\widetilde{a}}} a_{2} + \sigma_{{\widetilde{a}}} a_{3} + \sigma_{{\widetilde{a}}} a_{4} - a_{1} (1 + \sigma_{{\widetilde{a}}} )}}\left[ {\frac{{e^{{ - (a_{1} + a_{2} )}} ( - e^{{ - a_{2} }} ( - 1 - a_{1} + a_{2} + \sigma_{{\widetilde{a}}} )}}{{(a_{1} - a_{2} )}}} \right. \hfill \\ + \frac{{e^{{ - (a_{1} + a_{2} )}} (e^{{a_{1} }} ( - 1 + \sigma_{{\widetilde{a}}} - a_{1} \sigma_{{\widetilde{a}}} + a_{2} \sigma_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )}} + \frac{{e^{{ - (a_{3} + a_{4} )}} ( - e^{{ - a_{3} }} ( - 1 + a_{3} - a_{4} + \sigma_{{\widetilde{a}}} ))}}{{(a_{3} - a_{4} )}} \hfill \\ + \left. {\frac{{e^{{ - (a_{3} + a_{4} )}} (e^{{a_{4} }} ( - 1 + \sigma_{{\widetilde{a}}} + a_{3} \sigma_{{\widetilde{a}}} - a_{4} \sigma_{{\widetilde{a}}} ))}}{{(a_{3} - a_{4} )}} + \frac{{(e^{{ - a_{2} }} - e^{{ - a_{3} }} )\sigma_{{\widetilde{a}}} }}{1}} \right] \hfill \\ + \frac{{2\lambda_{3} }}{{(a_{2} - a_{3} + a_{4} - \upsilon_{{\widetilde{a}}} a_{2} + \upsilon_{{\widetilde{a}}} a_{3} + \upsilon_{{\widetilde{a}}} a_{4} - a_{1} (1 + \upsilon_{{\widetilde{a}}} )}}\left[ {\frac{{e^{{ - (a_{1} + a_{2} )}} ( - e^{{ - a_{2} }} ( - 1 - a_{1} + a_{2} + \upsilon_{{\widetilde{a}}} )}}{{(a_{1} - a_{2} )}}} \right. \hfill \\ + \frac{{e^{{ - (a_{1} + a_{2} )}} (e^{{a_{1} }} ( - 1 + \upsilon_{{\widetilde{a}}} - a_{1} \upsilon_{{\widetilde{a}}} + a_{2} \upsilon_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )}} + \frac{{e^{{ - (a_{3} + a_{4} )}} ( - e^{{ - a_{3} }} ( - 1 + a_{3} - a_{4} + \upsilon_{{\widetilde{a}}} ))}}{{(a_{3} - a_{4} )}} \hfill \\ + \left. {\frac{{e^{{ - (a_{3} + a_{4} )}} (e^{{a_{4} }} ( - 1 + \upsilon_{{\widetilde{a}}} + a_{3} \upsilon_{{\widetilde{a}}} - a_{4} \upsilon_{{\widetilde{a}}} ))}}{{(a_{3} - a_{4} )}} + \frac{{(e^{{ - a_{2} }} - e^{{ - a_{3} }} )\upsilon_{{\widetilde{a}}} }}{1}} \right] \hfill \\ \end{gathered}$$
(17)

This gives the unique equivalent value corresponding to each of IVTrpN number, therefore it is proposed to use this equivalent value for the purpose of converting the problem into crisp problem.

4.3 Improved solution of MLLP problems with interval valued TrpN numbers: Laplace transform approach

In this section, we apply the proportional p.d.f. to each N number and Laplace transform on complete p.d.f. to obtain equivalent crisp values in solving MLLP problem under N number environment in following manner:

Mathematically MLLP problem with interval valued trapezoidal N numbers is described in matrix form as:

$$\begin{gathered} \mathop {Max/Min\;}\limits_{{\overline{X}_{1} }} \left\{ {\widetilde{{Z_{1} }}(\overline{X} ) = \widetilde{{C_{11} }}\overline{X}_{1} + \widetilde{{C_{12} }}\overline{X}_{2} + ... + \widetilde{{C_{1T} }}\overline{X}_{T} } \right\} \hfill \\ \mathop {Max/Min\;}\limits_{{\overline{X}_{2} }} \left\{ {\widetilde{{Z_{2} }}(\overline{X} ) = \widetilde{{C_{21} }}\overline{X}_{1} + \widetilde{{C_{22} }}\overline{X}_{2} + ... + \widetilde{{C_{2T} }}\overline{X}_{T} } \right\} \hfill \\ . \hfill \\ . \hfill \\ \mathop {Max/Min\;}\limits_{{\overline{{X_{T} }} }} \left\{ {\widetilde{{Z_{T} }}(\overline{X} ) = \widetilde{{C_{T1} }}\overline{X}_{1} + \widetilde{{C_{T2} }}\overline{X}_{2} + ... + \widetilde{{C_{TT} }}\overline{X}_{T} } \right\} \hfill \\ \end{gathered}$$
$${\text{Subject}}\;{\text{to}},\;\widetilde{{A_{1} }}\overline{X}_{1} + \widetilde{{A_{2} }}\overline{X}_{2} + ... + \widetilde{{A_{T} }}\overline{X}_{T} ( \le , = , \ge )\widetilde{b}$$
$${\text{And}}\;\overline{X}_{1} ,\overline{X}_{2} ,...,\overline{X}_{T} \ge 0.$$
(18)

where \(\widetilde{{A_{j} }} = \left[ {\widetilde{{a_{ij} }}} \right]\), \(\widetilde{b} = [\widetilde{{b_{ij} }}]\), \(1 \le i \le T;1 \le j \le T\) and superscript ~ indicates all coefficients/parameters are IVTrp N number in format \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} );\;\mu_{{\widetilde{a}}} ,\;\sigma_{{\widetilde{a}}} ,\;\upsilon_{{\widetilde{a}}} } \right\rangle\).With the techniques discussed in Sects. 4.1 and 4.2, these interval valued trapezoidal neutrosophic coefficients/parameters are translated into equivalent crisp values as given in Eq. (14), then accordingly MLLP problem with IVTrp N numbers reduces into equivalent crisp problem as:

$$\begin{gathered} \mathop {Max/Min\;}\limits_{{\overline{{X_{1} }} }} \left\{ {[E(\widetilde{{C_{11} }})]\overline{X}_{1} + [E(\widetilde{{C_{12} }})]\overline{X}_{2} + \,[E(\widetilde{{C_{13} }})]\overline{X}_{3} + \,... + [E(\widetilde{{C_{1T} }})]\overline{X}_{T} } \right\} \hfill \\ \mathop {Max/Min\;}\limits_{{\overline{X}_{2} }} \left\{ {[E(\widetilde{{C_{21} }})]\overline{X}_{1} + [E(\widetilde{{C_{22} }})]\overline{X}_{2} + \,[E(\widetilde{{C_{23} }})]\overline{X}_{3} + \,... + [E(\widetilde{{C_{2T} }})]\overline{X}_{T} } \right\} \hfill \\ . \hfill \\ . \hfill \\ \mathop {Max/Min\;}\limits_{{\overline{X}_{T} }} \left\{ {[E(\widetilde{{C_{T1} }})]\overline{X}_{1} + [E(\widetilde{{C_{T2} }})]\overline{X}_{2} + \,[E(\widetilde{{C_{T3} }})]\overline{X}_{3} + \,... + [E(\widetilde{{C_{TT} }})]\overline{X}_{T} } \right\} \hfill \\ \end{gathered}$$
$${\text{Subject}}\;{\text{to}},\;\widetilde{{A_{1} }}\overline{X}_{1} + \widetilde{{A_{2} }}\overline{X}_{2} + ... + \widetilde{{A_{T} }}\overline{X}_{T} ( \le , = , \ge )\widetilde{b}$$
$${\text{And}}\;\;\;\overline{X}_{1} ,\overline{X}_{2} ,...,\overline{X}_{T} \ge 0.$$
(19)

where \(E(\widetilde{{C_{11} }}),\;E(\widetilde{{C_{12} }}),\;...,E(\widetilde{{C_{1T} }});\) …\(E(\widetilde{{C_{T1} }}),\;E(\widetilde{{C_{T2} }}),\;...,E(\widetilde{{C_{T2} }});\) \(A(\widetilde{{a_{1ij} }});\,A(\widetilde{{a_{2ij} }})\,,...,A(\widetilde{{a_{Tij} }})\) and \(\widetilde{{b_{j} }}\) are corresponding equivalent values of parameters and coefficients obtained by technique discussed in Sect. 4. Now, to tackle the multi-level structure of crisp problem (16), we extend the modified approach suggested by Lachhwani [3] for a multi-level single objective linear programming problem. For this, we estimate the ideal values of each objective function at each level (\(\overline{{Z_{t} }}\) and \(\underline{{Z_{t} }}\)) of the crisp problem (19). Then, we construct the linear membership functions for each objective function with individual maximum and minimum values as:

$$M_{{_{t} }} (Z_{t} (\overline{X} )) = \left\{ {\begin{array}{*{20}c} 1 & {if\;{\text{Z}}_{t} (\overline{X} ) \ge \overline{{Z_{t} }} } \\ {\frac{{Z_{t} (\overline{X} ) - \underline{{Z_{t} }} }}{{\overline{{Z_{t} }} - \underline{{Z_{t} }} }}} & {if\;\underline{{Z_{t} }} \le Z_{t} (\overline{X} ) \le \overline{{Z_{t} }} } \\ 0 & {if\;{\text{Z}}_{t} (\overline{X} ) \le \underline{{Z_{t} }} } \\ \end{array} } \right.\;\;\;\forall {\text{ t}} = 1,2,..,T$$
(20)

Further, in order to avoid decision deadlock in between of different levels due to multi-level structure we construct the linear membership function for the decision vector \(X_{1}\) (up to T-1 levels) as:

$$N_{{X_{t} }} (X_{t} ) = \left\{ {\begin{array}{*{20}c} 1 & {for\;X_{t} \ge \overline{{X_{t} }} } \\ {\frac{{X_{t} - \underline{{X_{t} }} }}{{\overline{{X_{t} }} - \underline{{X_{t} }} }}} & { \, for\;\underline{{X_{t} }} \le X_{t} \le \overline{{X_{t} }} } \\ 0 & {for\;X_{t} \le \underline{{X_{t} }} } \\ \end{array} } \right.\;\;\forall {\text{ t}} = 1,2,..,T - 1$$
(21)

where \(\overline{{X_{t} }}\) and \(\underline{{X_{t} }}\) are considered as respective values of decision vectors at t-th level (\(\forall {\text{ t}} = 1,2,..,T - 1\)) which yield the maximum and minimum values of crisp objective functions (\(\overline{{Z_{t} }} (\overline{X} )\) and \(\underline{{Z_{t} }} (\underline{X} )\)) of problem (19). The flexible membership goals [(22) and (23)] having aspired level unity and negative deviational variables only can be described as:

$$M_{{_{t} }} (Z_{t} (\overline{X} )) + d_{{Z_{t} }}^{ - } \ge 1\;\;\;1 \le t \le T$$
(22)
$$N_{{X_{t} }} (X_{t} ) + d_{t}^{ - } \ge 1\;\;\;1 \le t \le T - 1$$
(23)

Now using the simplest version of goal programming, the solution model based on proposed algorithm for MLLP problem with IVTrpN numbers can be given as:

4.3.1 Solution model

$$\min \lambda = \sum\limits_{t = 1}^{T} {d_{{Z_{t} }}^{ - } } + \sum\limits_{t = 1}^{T - 1} {d_{t}^{ - } }$$
$${\text{Subject}}\;{\text{to}},\; - \overline{{Z_{t} }} + Z_{t} + d_{{Z_{t} }}^{ - } (\overline{{Z_{t} }} - \underline{{Z_{t} }} ) \ge 0\;\;\;1 \le t \le T$$
$$- \overline{{X_{t} }} + X_{t} + d_{t}^{ - } (\overline{{X_{t} }} - \underline{{X_{t} }} ) \ge {\mathbf{0}}$$
$$\widetilde{{A_{1} }}\overline{X}_{1} \, + \widetilde{{A_{2} }}\overline{X}_{2} + ... + \widetilde{{A_{T} }}\overline{X}_{T} \,( \le ,\, = ,\, \ge )\,\widetilde{b}$$
$${\text{And}}\;\;\;\overline{X}_{1} ,\overline{X}_{2} ,...,\overline{X}_{T} \ge 0.$$
(24)

With the above discussion, the proposed improved solution methodology for MLLP problem with IVTrpN numbers can be summarised in the following stepwise algorithm:

  1. 1.

    Obtain the corresponding probability density function for each membership function and complete probability density function of IVTrpN numbers as described in sub-Sect. 4.1.

  2. 2.

    Set the value \(\lambda_{1} ,\,\lambda_{2} ,\,\lambda_{3} \in [0,1]\) as per the decision maker’s information on the relative importance of truthiness, intuitionistic and falsity of information and write a complete p.d.f. of each N numbers as given in (15).

  3. 3.

    Obtain the equivalent value (17) of each p.d.f. using Laplace transform as given in sub-Sect. 4.2.

  4. 4.

    Convert each interval-valued trapezoidal neutrosophic coefficient and parameters of MLLP problem into corresponding crisp values using equivalent function values and convert the problem into an equivalent crisp problem (19).

  5. 5.

    Estimate ideal values for each objective function at each level along with ideal values of decision variables (up to T-1 levels) irrespective of multi-level structure.

  6. 6.

    Construct the fuzzy linear membership function for each objective function (for T levels) and the decision variables (up to T-1 levels) as defined in Eqs. (20) and (21), respectively.

  7. 7.

    Formulate the solution model (24) for this reduced problem.

  8. 8.

    Solve solution model (24) with programming technique or software tool to obtain a satisfactory solution of MLLP problem with IVTrpN numbers.

The flow chart of the proposed algorithm for MLP problems under N number environment can be presented (in Fig. 1) as:

Fig. 1
figure 1

Flow chart of proposed algorithm

Full size image

5 Comparison between laplace and melin transform on SVTrN numbers

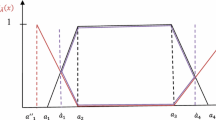
Tamilarasi and Paulraj [23] used Melin transform for de-neutrosophication (converting neutrosophic numbers into equivalent crisp values) of single valued triangular neutrosophic (SVTrN) numbers for developing the technique for linear programming problems. In this section, we explore the use of the Laplace Transform on SVTrN numbers and compare the problem’s coefficients/parameters as SVTrN numbers with that obtained through the Melin Transform as given by Tamilarasi and Paulraj [23].

Let \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} );\mu_{{\widetilde{a}}}^{{}} ,\;\sigma_{{\widetilde{a}}}^{{}} ,\;\upsilon_{{\widetilde{a}}}^{{}} } \right\rangle\) be SVTrN numbers (as defined in Definition 3) given as coefficients/parameters of the problem under consideration. Let \(f_{1} (x)\),\(f_{2} (x)\),\(f_{3} (x)\) be the p.d.f. corresponding to membership functions \(\mu_{{\widetilde{a}}} ,\sigma_{{\widetilde{a}}}\), \(\upsilon_{{\widetilde{a}}}^{{}}\) respectively then these p.d.f. can be described (Tamilarasi and Paulraj [23]) as:

$$f_{1} (x) = \left\{ {\begin{array}{*{20}c} {\left( {\frac{{2(x - a_{1} )}}{{(a_{2} - a_{1} )(a_{3} - a_{1} )}}} \right),} & {a_{1} \le x \le a_{2} ,} \\ {\frac{2}{{(a_{3} - a_{1} )}},} & {x = a_{2} ,} \\ {\left( {\frac{{2(a_{3} - x)}}{{(a_{3} - a_{2} )(a_{3} - a_{1} )}}} \right),} & {a_{2} \le x \le a_{3} ,} \\ {0,} & {{\text{otherwise}}{.}} \\ \end{array} } \right.$$
(25)
$$f_{2} (x) = \left\{ {\begin{array}{*{20}c} {\frac{{a_{2} - x + \sigma_{{\widetilde{a}}}^{{}} (x - a_{1} )}}{{a_{2} - a_{1} }}\frac{2}{{(a_{3} - a_{1} )(1 + \sigma_{{\widetilde{a}}}^{{}} )}},} & {a_{1} \le x \le a_{2} ,} \\ {\sigma_{{\widetilde{a}}} \frac{2}{{(a_{3} - a_{1} )(1 + \sigma_{{\widetilde{a}}} )}},} & {x = a_{2} ,} \\ {\frac{{x - a_{3} + \sigma_{{\widetilde{a}}} (a_{4} - x)}}{{a_{4} - a_{3} }}\frac{2}{{(a_{3} - a_{1} )(1 + \sigma_{{\widetilde{a}}} )}},} & {a_{2} \le x \le a_{3} ,} \\ {0,} & {{\text{otherwise}}{.}} \\ \end{array} } \right.$$
(26)
$$f_{3} (x) = \left\{ {\begin{array}{*{20}c} {\frac{{a_{2} - x + \upsilon_{{\widetilde{a}}}^{{}} (x - a_{1} )}}{{a_{2} - a_{1} }}\frac{2}{{(a_{3} - a_{1} )(1 + \upsilon_{{\widetilde{a}}}^{{}} )}},} & {a_{1} \le x \le a_{2} ,} \\ {\upsilon_{{\widetilde{a}}} \frac{2}{{(a_{3} - a_{1} )(1 + \upsilon_{{\widetilde{a}}} )}},} & {x = a_{2} ,} \\ {\frac{{x - a_{2} + \upsilon_{{\widetilde{a}}} (a_{3} - x)}}{{a_{3} - a_{2} }}\frac{2}{{(a_{3} - a_{1} )(1 + \upsilon_{{\widetilde{a}}} )}},} & {a_{2} \le x \le a_{3} ,} \\ {0,} & {{\text{otherwise}}{.}} \\ \end{array} \, } \right.$$
(27)

Accordingly, probability density function for single valued triangular neutrosophic (SVTrN) number \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} );\mu_{{\widetilde{a}}}^{{}} ,\;\sigma_{{\widetilde{a}}}^{{}} ,\;\upsilon_{{\widetilde{a}}}^{{}} } \right\rangle\) can be described as:

$$f(x) = \lambda f_{1} (x) + (1 - \lambda )f_{2} (x) + (1 - \lambda )f_{3} (x)$$
(28)

Now, we apply Laplace transform on p.d.f. (28) of SVTrN number of the problem in following manner as:

$$\begin{aligned} \Rightarrow L_{X} (s) = & \frac{2\lambda }{{(a_{3} - a_{1} )}}\left[ {\frac{{e^{{ - (a_{1} + a_{2} )s}} ( - e^{{a_{2} s}} + e^{{a_{1} s}} (1 - a_{1} s + a_{2} s))}}{{(a_{1} - a_{2} )s^{2} }} + \frac{{e^{{ - (a_{2} + a_{3} )s}} ( - e^{{a_{2} s}} + e^{{a_{3} s}} (1 + a_{2} s - a_{3} s))}}{{(a_{2} - a_{3} )s^{2} }}} \right] \\ & \; - \frac{2(1 - \lambda )}{{(a_{3} - a_{1} )(1 + \upsilon_{{\widetilde{a}}} )}}\left[ {\frac{{e^{{ - (a_{2} + a_{3} )s}} ( - e^{{ - a_{2} s}} + e^{{a_{3} s}} (1 + a_{2} s - a_{3} s))(1 - \upsilon_{{\widetilde{a}}} )}}{{(a_{2} - a_{3} )s^{2} }}} \right. \\ & \; + \left. {\frac{{e^{{ - (a_{1} + a_{2} )s}} ( - e^{{a_{2} s}} ( - 1 - a_{1} s + a_{2} s + \upsilon_{{\widetilde{a}}} ) + e^{{a_{1} s}} ( - 1 - a_{1} s\upsilon_{{\widetilde{a}}} + a_{2} s\upsilon_{{\widetilde{a}}} + \upsilon_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )s^{2} }}} \right] \\ & \; - \frac{2(1 - \lambda )}{{(a_{3} - a_{1} )(1 + \sigma_{{\widetilde{a}}} )}}\left[ {\frac{{e^{{ - (a_{2} + a_{3} )s}} ( - e^{{ - a_{2} s}} + e^{{a_{3} s}} (1 + a_{2} s - a_{3} s))(1 - \sigma_{{\widetilde{a}}} )}}{{(a_{2} - a_{3} )s^{2} }}} \right. \\ & \; + \left. {\frac{{e^{{ - (a_{1} + a_{2} )s}} ( - e^{{a_{2} s}} ( - 1 - a_{1} s + a_{2} s + \sigma_{{\widetilde{a}}} ) + e^{{a_{1} s}} ( - 1 - a_{1} s\sigma_{{\widetilde{a}}} + a_{2} s\sigma_{{\widetilde{a}}} + \upsilon_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )s^{2} }}} \right] \\ \end{aligned}$$
(29)

For s = 1, the corresponding equivalent value will be as:

$$\begin{aligned} E(\widetilde{a}) = & \frac{2\lambda }{{(a_{3} - a_{1} )}}\left[ {\frac{{e^{{ - (a_{1} + a_{2} )}} ( - e^{{a_{2} }} + e^{{a_{1} }} (1 - a_{1} + a_{2} ))}}{{(a_{1} - a_{2} )}} + \frac{{e^{{ - (a_{2} + a_{3} )}} ( - e^{{a_{2} }} + e^{{a_{3} }} (1 + a_{2} - a_{3} ))}}{{(a_{2} - a_{3} )}}} \right] \\ & \; - \frac{2(1 - \lambda )}{{(a_{3} - a_{1} )(1 + \upsilon_{{\widetilde{a}}} )}}\left[ {\frac{{e^{{ - (a_{2} + a_{3} )}} ( - e^{{ - a_{2} }} + e^{{a_{3} }} (1 + a_{2} - a_{3} ))(1 - \upsilon_{{\widetilde{a}}} )}}{{(a_{2} - a_{3} )}}} \right. \\ & \; + \left. {\frac{{e^{{ - (a_{1} + a_{2} )}} ( - e^{{a_{2} }} ( - 1 - a_{1} + a_{2} + \upsilon_{{\widetilde{a}}} ) + e^{{a_{1} }} ( - 1 - a_{1} \upsilon_{{\widetilde{a}}} + a_{2} \upsilon_{{\widetilde{a}}} + \upsilon_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )}}} \right] \\ & \; - \frac{2(1 - \lambda )}{{(a_{3} - a_{1} )(1 + \sigma_{{\widetilde{a}}} )}}\left[ {\frac{{e^{{ - (a_{2} + a_{3} )}} ( - e^{{ - a_{2} }} + e^{{a_{3} }} (1 + a_{2} - a_{3} ))(1 - \sigma_{{\widetilde{a}}} )}}{{(a_{2} - a_{3} )}}} \right. \\ & \; + \left. {\frac{{e^{{ - (a_{1} + a_{2} )}} ( - e^{{a_{2} }} ( - 1 - a_{1} + a_{2} + \sigma_{{\widetilde{a}}} ) + e^{{a_{1} }} ( - 1 - a_{1} \sigma_{{\widetilde{a}}} + a_{2} \sigma_{{\widetilde{a}}} + \upsilon_{{\widetilde{a}}} ))}}{{(a_{1} - a_{2} )}}} \right] \\ \end{aligned}$$
(30)

This quickly gives equivalent crisp values corresponding to SVTrN numbers \(\widetilde{a} = \left\langle {(a_{1} ,\;a_{2} ,\;a_{3} );\mu_{{\widetilde{a}}}^{{}} ,\;\sigma_{{\widetilde{a}}}^{{}} ,\;\upsilon_{{\widetilde{a}}}^{{}} } \right\rangle\) by the Laplace transform which can be used in converting coefficients/parameters (SVTrN numbers) of the concern problem into corresponding equivalent crisp values. On the other hand, Tamilarasi and Paulraj [23] used Melin transform (with s = 2) on SVTrN numbers which yield the following equivalent crisp values as:

$$E(\widetilde{a}) = \lambda \left\{ {\frac{{(a_{1} + a_{2} + a_{3} )}}{3}} \right\} + (1 - \lambda )\left\{ {\frac{{\sigma_{{\widetilde{a}}} (a_{1} + a_{2} + a_{3} ) + 2(a_{1} + a_{3} ) - a_{2} }}{{3(1 + \sigma_{{\widetilde{a}}} )}}} \right\} + (1 - \lambda )\left\{ {\frac{{\upsilon_{{\widetilde{a}}} (a_{1} + a_{2} + a_{3} ) + 2(a_{1} + a_{3} ) - a_{2} }}{{3(1 + \upsilon_{{\widetilde{a}}} )}}} \right\}$$
(31)

If we compare these results [(30) and (31)], it can be easily observed that both the transform gives equivalent crisp values corresponding to N numbers which are required to convert such problems (like MLLP problem with IVTrN numbers, LPP with SVTrN numbers, etc.) into corresponding crisp problems. This comparison shows that the proposed methodology based on the Laplace transform for MLLP problem with IVTrN numbers is improved in terms of computational difficulties than Melin Transform on single valued triangular neutrosophic numbers (SVTrNNs). Further, it shows that the Laplace transform can also be applied on SVTrN numbers for converting into their crisp values.

6 Numerical illustration and application of proposed solution technique in real world problem

6.1 Numerical illustrations

In this section, we illustrate one numerical example in following stepwise manner to show the functionality of algorithm for MLLP problems with IVTrpN numbers:

Example 1

A maximization type tri-level linear programming problem under N number environment is considered as:

$$\mathop {Max}\limits_{{x_{1} ,x_{2} }} \left\{ {Z_{1} (X) = \widetilde{{c_{11} }}x_{1} + \widetilde{{c_{12} }}x_{2} + \widetilde{{c_{13} }}x_{3} + \widetilde{{c_{14} }}x_{4} } \right\}\;\;\;\left( {1st\;level} \right)$$
$$\mathop {Max}\limits_{{x_{3} }} \left\{ {Z_{2} (X) = \widetilde{{c_{21} }}x_{1} + \widetilde{{c_{22} }}x_{2} + \widetilde{{c_{23} }}x_{3} + \widetilde{{c_{24} }}x_{4} } \right\}\;\;\;\left( {2nd\;level} \right)$$
$$\mathop {Max}\limits_{{x_{4} }} \left\{ {Z_{3} (X) = \widetilde{{c_{31} }}x_{1} + \widetilde{{c_{32} }}x_{2} + \widetilde{{c_{33} }}x_{3} + \widetilde{{c_{34} }}x_{4} } \right\}\;\;\;\left( {3rd\;level} \right)$$
$${\text{Subject}}\;{\text{to}},\;\widetilde{{a_{11} }}x_{1} + \widetilde{{a_{12} }}x_{2} + \widetilde{{a_{13} }}x_{3} + \widetilde{{a_{14} }}x_{4} \, \le 50$$
$$\widetilde{{a_{21} }}x_{1} + \widetilde{{a_{22} }}x_{2} - \widetilde{{a_{23} }}x_{3} + \widetilde{{a_{24} }}x_{4} \, \le \,100$$
$$\widetilde{{a_{31} }}x_{1} + \widetilde{{a_{32} }}x_{2} + \widetilde{{a_{33} }}x_{3} + \widetilde{{a_{34} }}x_{4} \, \le \,200$$
$${\text{and}}\;x_{1} ,x_{2} ,x_{3} ,x_{4} \ge 0$$

where coefficients in the objective function and constraint are IVTrpN numbers format respectively as: \(\widetilde{Z}_{i} = \sum\limits_{j = 1}^{4} {\left\langle {(c_{ij}^{1} ,\,c_{ij}^{2} ,\,c_{ij}^{3} ,\,c_{ij}^{4} );\mu_{{\widetilde{c}_{ij} }} ,\sigma_{{\widetilde{c}_{ij} }} ,\upsilon_{{\widetilde{c}_{ij} }} } \right\rangle } \,x_{j}\)

$${\text{and}}\;\widetilde{a}_{ij} = \left\langle {(a_{ij}^{1} ,a_{ij}^{2} ,a_{ij}^{3} ,a_{ij}^{4} ),\mu_{{\widetilde{a}_{ij} }} ,\sigma_{{\widetilde{a}_{ij} }} ,\upsilon_{{\widetilde{a}_{ij} }} } \right\rangle \;\;\;\;\forall j = 1,2,3,4;\;\;i = 1,2;$$
$$\begin{aligned} \widetilde{Z}_{1} = & \left\langle {(1,\,1.5,\,2.5,\,4),0.25,0.75,0.25} \right\rangle x_{1} + \left\langle {(2,2.5,3,5),0.25,0.75,0.25} \right\rangle x_{2} \\ & \; + \left\langle {(2.5,\,3.0,\,3.5,\,6);0.20,0.80,0.20} \right\rangle x_{3} + \left\langle {(2.5,\,3,\,3.5,\,6);0.20,0.80,0.20} \right\rangle x_{4} \\ \end{aligned}$$
$$\begin{aligned} \widetilde{Z}_{2} = & \left\langle {(0.5,\,1.5,\,2.5,\,4.5);0.20,0.80,0.20} \right\rangle x_{1} + \left\langle {(1.5,\,2.5,\,3,\,5.5);0.20,0.80,0.20} \right\rangle x_{2} \\ & \; + \left\langle {(2,\,3,\,3.5,\,6.5);0.20,0.80,0.20} \right\rangle x_{3} + \left\langle {(2.5,\,3.5,\,4,\,5.5);0.20,0.80,0.20} \right\rangle x_{4} \\ \end{aligned}$$
$$\begin{aligned} \widetilde{Z}_{3} = & \left\langle {(0.5,\,1.5,\,2.5,\,4.5);0.25,0.75,0.25} \right\rangle x_{1} + \left\langle {(1.5,\,2.5,\,3,\,5.5);0.25,0.75,0.25} \right\rangle x_{2} \\ & \; + \left\langle {(2,\,3,\,3.5,\,4.5);0.20,0.80,0.20} \right\rangle x_{3} + \left\langle {(2.5,\,3.5,\,4,\,6);0.20,0.80,0.20} \right\rangle x_{4} \\ \end{aligned}$$

Subject to,

$$\begin{gathered} \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.20,0.80,0.50} \right\rangle x_{1} + \left\langle {(1.5,\,1.75,\,2.0,\,6.50);0.40,0.50,0.30} \right\rangle x_{2} \hfill \\ \, + \left\langle {(1.0,\,1.75,\,2.0,\,6.75);0.20,0.80,0.30} \right\rangle x_{3} + \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.30,0.60,0.20} \right\rangle x_{4} \, \le \,50 \hfill \\ \end{gathered}$$
$$\begin{gathered} \left\langle {(2.0,\,2.5,\,3.0,\,11.5);0.30,0.80,0.50} \right\rangle x_{1} + \left\langle {(1.5,\,1.75,\,2.0,\,6.50);0.30,0.50,0.40} \right\rangle x_{2} \hfill \\ \, + \left\langle {(1.0,\,1.75,\,2.0,\,6.75);0.30,0.80,0.20} \right\rangle x_{3} + \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.20,0.50,0.20} \right\rangle x_{4} \, \le \,100 \hfill \\ \end{gathered}$$
$$\begin{gathered} \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.40,0.70,0.20} \right\rangle x_{1} + \left\langle {(1.5,\,1.75,\,2.0,\,6.50);0.40,0.50,0.30} \right\rangle x_{2} \hfill \\ \, + \left\langle {(1.0,\,1.75,\,2.0,\,6.75);0.30,0.70,0.20} \right\rangle x_{3} + \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.40,0.60,0.30} \right\rangle x_{4} \, \le \,200 \hfill \\ \end{gathered}$$
$${\text{and}}\;\;\;x_{1} ,\;x_{2} ,\;x_{3} ,\;x_{4} \ge \,0\,$$

With the proposed approach in a stepwise manner as:

Step 1 we obtain the corresponding proportional p.d.f. of each N number coefficient in each objective function and constraint as discussed in Sect. 4.1. For this, we use MATLAB software and the values of \(k_{1}\), \(k_{2}\) and \(k_{3}\) for each N number coefficient of objectives and constraints are tabulated (Tables 2 and 3) as:

Table 2 Values of \(k_{1}\), \(k_{2}\) and \(k_{3}\) for each N number coefficient of objective functions
Full size table
Table 3 Values of \(k_{1}\), \(k_{2}\) and \(k_{3}\) for each N number coefficient of constraint coefficients
Full size table

Step 2 setting the values of \(\lambda_{1} ,\,\lambda_{2}\) and \(\lambda_{3}\) for each of IVTrpN numbers present as coefficient in objective and constraint as:\(\lambda_{1} = 0.20,\,\lambda_{2} = 0.50\),\(\lambda_{3} = 0.30\) for each N numbers coefficients in each objective and \(\lambda_{1} = 0.30,\,\lambda_{2} = 0.40\), \(\lambda_{3} = 0.30\) for each N numbers coefficients in each of constraint respectively. With these values, the complete p.d.f. of each N number coefficient can be given as:

$$\begin{gathered} \mathop {f_{{Z_{1} }} (X)}\limits_{{x_{1} ,\;x_{2} }} = [0.40\mu_{{\widetilde{a}}}^{{}} (x_{1} ) + 0.1429\sigma_{{\widetilde{a}}}^{{}} (x_{1} ) + 0.15\upsilon_{{\widetilde{a}}}^{{}} (x_{1} )]x_{1} + [0.4444\mu_{{\widetilde{a}}}^{{}} (x_{2} ) + 0.1408\sigma_{{\widetilde{a}}}^{{}} (x_{2} ) + 0.1364\upsilon_{{\widetilde{a}}}^{{}} (x_{2} )]x_{2} \hfill \\ { + }[0.40\mu_{{\widetilde{a}}}^{{}} (x_{3} ) + 0.1250\sigma_{{\widetilde{a}}}^{{}} (x_{3} ) + 0.1200\upsilon_{{\widetilde{a}}}^{{}} (x_{3} )]x_{3} + [0.5714\mu_{{\widetilde{a}}}^{{}} (x_{4} ) + 0.1887\sigma_{{\widetilde{a}}}^{{}} (x_{4} ) + 0.1875\upsilon_{{\widetilde{a}}}^{{}} (x_{4} )]x_{4} \hfill \\ \end{gathered}$$
$$\begin{gathered} \mathop {f_{{Z_{2} }} (X)}\limits_{{x_{3} }} = [0.40\mu_{{\widetilde{a}}}^{{}} (x_{1} ) + 0.20\sigma_{{\widetilde{a}}}^{{}} (x_{1} ) + 0.20\upsilon_{{\widetilde{a}}}^{{}} (x_{1} )]x_{1} + [0.4571\mu_{{\widetilde{a}}}^{{}} (x_{2} ) + 0.1951\sigma_{{\widetilde{a}}}^{{}} (x_{2} ) + 0.1778\upsilon_{{\widetilde{a}}}^{{}} (x_{2} )]x_{2} \hfill \\ { + }[0.50\mu_{{\widetilde{a}}}^{{}} (x_{3} ) + 0.1613\sigma_{{\widetilde{a}}}^{{}} (x_{3} ) + 0.1579\upsilon_{{\widetilde{a}}}^{{}} (x_{3} )]x_{3} + [0.50\mu_{{\widetilde{a}}}^{{}} (x_{4} ) + 0.1613\sigma_{{\widetilde{a}}}^{{}} (x_{4} ) + 0.1579\upsilon_{{\widetilde{a}}}^{{}} (x_{4} )]x_{4} \hfill \\ \end{gathered}$$
$$\begin{gathered} \mathop {f_{{Z_{3} }} (X)}\limits_{{x_{4} }} = [0.32\mu_{{\widetilde{a}}}^{{}} (x_{1} ) + 0.1481\sigma_{{\widetilde{a}}}^{{}} (x_{1} ) + 0.1412\upsilon_{{\widetilde{a}}}^{{}} (x_{1} )]x_{1} + [0.3556\mu_{{\widetilde{a}}}^{{}} (x_{2} ) + 0.1455\sigma_{{\widetilde{a}}}^{{}} (x_{2} ) + 0.1297\upsilon_{{\widetilde{a}}}^{{}} (x_{2} )]x_{2} \hfill \\ { + }[0.6667\mu_{{\widetilde{a}}}^{{}} (x_{3} ) + 0.2273\sigma_{{\widetilde{a}}}^{{}} (x_{3} ) + 0.2308\upsilon_{{\widetilde{a}}}^{{}} (x_{3} )]x_{3} + [0.50\mu_{{\widetilde{a}}}^{{}} (x_{4} ) + 0.1613\sigma_{{\widetilde{a}}}^{{}} (x_{4} ) + 0.1579\upsilon_{{\widetilde{a}}}^{{}} (x_{4} )]x_{4} \hfill \\ \end{gathered}$$

Subject to,

$$\begin{gathered} [0.60\mu_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} ) + 0.0941\sigma_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} ) + 0.0857\upsilon_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} )]x_{1} + [0.2857\mu_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} ) + 0.1085\sigma_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} ) + 0.0949k_{3} \upsilon_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} )]x_{2} \hfill \\ { + }[0.50\mu_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} ) + 0.0777\sigma_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} ) + 0.0822\upsilon_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} )]x_{3} + [0.40\mu_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} ) + 0.1067\sigma_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} ) + 0.1091\upsilon_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} )]x_{4} \le 50 \hfill \\ \end{gathered}$$
$$\begin{gathered} [0.20\mu_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} ) + 0.0471\sigma_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} ) + 0.0429\upsilon_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} )]x_{1} + [0.3810\mu_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} ) + 0.1085\sigma_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} ) + 0.0876\upsilon_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} )]x_{2} \hfill \\ { + }[0.3333\mu_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} ) + 0.0777\sigma_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} ) + 0.0896\upsilon_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} )]x_{3} + [0.60\mu_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} ) + 0.1143\sigma_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} ) + 0.1091\upsilon_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} )]x_{4} \le 100 \hfill \\ \end{gathered}$$
$$\begin{gathered} [0.30\mu_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} ) + 0.10\sigma_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} ) + 0.1091\upsilon_{{\widetilde{{a_{11} }}}}^{{}} (x_{1} )]x_{1} + [0.2857\mu_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} ) + 0.1085\sigma_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} ) + 0.0949\upsilon_{{\widetilde{{a_{12} }}}}^{{}} (x_{2} )]x_{2} \hfill \\ { + }[0.3333\mu_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} ) + 0.0825\sigma_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} ) + 0.0896\upsilon_{{\widetilde{{a_{13} }}}}^{{}} (x_{3} )]x_{3} + [0.30\mu_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} ) + 0.1067\sigma_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} ) + 0.10\upsilon_{{\widetilde{{a_{14} }}}}^{{}} (x_{4} )]x_{4} \le 200 \hfill \\ \end{gathered}$$
$${\text{and}}\;\;\;x_{1} ,\;x_{2} ,\;x_{3} ,\;x_{4} \ge \,0\,$$

Step 4 in this step. We obtain the equivalent value of each p.d.f. using Laplace Transform as given in (14). For this, we use MATHEMATICA© software and equivalent crisp problem as:

$$\mathop {Max}\limits_{{x_{1} ,x_{2} }} \left\{ {Z_{1} (X) = 0.0627x_{1} + 0.0213x_{2} + 0.0102x_{3} + 0.0137x_{4} } \right\}\;\;\;\left( {1st\;level} \right)$$
$$\mathop {Max}\limits_{{x_{3} }} \left\{ {Z_{2} (X) = 0.0041x_{1} + 0.0052x_{2} + 0.0103x_{3} + 0.0103x_{4} } \right\}\;\;\;\left( {2nd\;level} \right)$$
$$\mathop {Max}\limits_{{x_{4} }} \left\{ {Z_{3} (X) = 0.0556x_{1} + 0.0297x_{2} + 0.0321x_{3} + 0.0102x_{4} } \right\}\;\;\;\left( {3rd\;level} \right)$$
$${\text{Subject}}\;{\text{to}},\;0.0156x_{1} + 0.0169x_{2} + 0.0155x_{3} + 0.0208x_{4} \le 50$$
$$0.0013x_{1} + 0.0064x_{2} + 0.0204x_{3} + 0.0164x_{4} \le 100$$
$$0.0165x_{1} + 0.0147x_{2} + 0.0181x_{3} + 0.0163x_{4} \, \le \,200$$
$${\text{and}}\;\;\;x_{1} ,\;x_{2} ,\;x_{3} ,\;x_{4} \ge 0$$

Step 5 calculating the ideal values (maximum and minimum values) for each objective function at each level along with ideal values of decision variables (up to T-1 levels) (as shown in Table 4).

Table 4 Maximum and minimum values of objective functions and corresponding decision variables
Full size table

Step 6 construct membership functions for each objective functions at each level and decision variables (i.e. \(x_{1} ,\;x_{2} \;x_{3}\)) of first two levels as defined in Eqs. (17) and (18) respectively as shown below:

$$\begin{gathered} F_{{_{1} }} (Z_{1} (\overline{X} )) = \frac{{0.0627x_{1} + 0.0213x_{2} + 0.0102x_{3} + 0.0137x_{4} - 0}}{200.9615 - 0} \hfill \\ F_{{_{2} }} (Z_{2} (\overline{X} )) = \frac{{0.0041x_{1} + 0.0052x_{2} + 0.0103x_{3} + 0.0103x_{4} - 0}}{33.22581 - 0} \hfill \\ \end{gathered}$$
$$F_{{_{3} }} (Z_{3} (\overline{X} )) = \frac{{0.0556x_{1} + 0.0297x_{2} + 0.0321x_{3} + 0.0102x_{4} - 0}}{178.2051 - 0};$$
$$F_{{x_{1} }} (x_{1} ) = \frac{{x_{1} - 0}}{3205.128 - 0};\;F_{{x_{3} }} (x_{3} ) = \frac{{x_{3} - 0}}{3.225806 - 0}$$

Step 7 with these values, solution model (21) for MLLP problem with IVTrpN numbers can be given as:

$$\min \lambda = d_{1}^{ - } + d_{2}^{ - } + d_{3}^{ - } + d_{{x_{1} }}^{ - } + d_{{x_{3} }}^{ - }$$
$${\text{Subject}}\;{\text{to}},\;0.0627x_{1} + 0.0213x_{2} + 0.0102x_{3} + 0.0137x_{4} + 200.9615d_{1}^{ - } \ge 200.9615$$
$$0.0041x_{1} + 0.0052x_{2} + 0.0103x_{3} + 0.0103x_{4} + 33.22581d_{2}^{ - } \ge 33.22581$$
$$0.0556x_{1} + 0.0297x_{2} + 0.0321x_{3} + 0.0102x_{4} + 178.2051d_{3}^{ - } \ge 178.2015$$

\(x_{1} + 3205.128d_{{x_{1} }}^{ - } \ge 3205.128\)

$$x_{3} + 33.22581d_{{x_{1} }}^{ - } \ge 33.22581$$
$$0.0156x_{1} + 0.0169x_{2} + 0.0155x_{3} + 0.0208x_{4} \, \le \,50$$
$$0.0013x_{1} + 0.0064x_{2} + 0.0204x_{3} + 0.0164x_{4} \, \le \,100$$
$$0.0165x_{1} + 0.0147x_{2} + 0.0181x_{3} + 0.0163x_{4} \, \le \,200$$

\({\text{and}}\;\;\;x_{1} ,x_{2} ,x_{3} ,x_{4} ,d_{1}^{ - } ,d_{2}^{ - } ,d_{3}^{ - } ,d_{{x_{1} }}^{ - } ,d_{{x_{3} }}^{ - } \ge 0\).

Solving this programming problem model with LINGO© tool, we obtain the satisfactory solution to the original problem: \(\lambda = 0.6214752,\) \(x_{1} = 3172.115,\) \(x_{2} = 0,\) \(x_{3} = 33.22581,\) \(x_{4} = 0\) with the objective function values as: \(\widetilde{{Z_{11} }} = 199.2305,\) \(\widetilde{{Z_{2} }} = 13.34790,\) and \(\widetilde{{Z_{3} }} = 177.4362\).

6.2 Application of proposed solution technique in real world problem

Multi-level programming approaches under neutrosophic environment have can be used in solving real world problem e.g. Luo et al. [26] applied different approach with N number in solving a pricing decision-making case of satellite image data products. Proposed solution algorithm can be applied in solving complex real problems arising in day-to-day life. Here, formulation of production problem as MLLP problem with N numbers and its solution with proposed technique is described as:

Let us consider a real problem of ‘XYZ’ production firm producing mainly three types of products P, Q and R. This firm has three hierarchical levels of functioning namely manufacturing unit (1st level), distributor (2nd level) and retailer (3rd unit). At each level, the firm has different objective functions (say \(Z_{1} (X)\), \(Z_{2} (X)\), \(Z_{3} (X)\)) as: at manufacturing unit, maximization of market share of product of firm; at distributor level, maximization of sales revenue of product and at 3rd level, maximization of profit on net product cost. There are different decision variables involved in decision making such as \(x_{1}\)- profit on product P, \(x_{2}\)- profit on product Q and \(x_{3}\)- profit on product R. Besides these, coefficients in each objective function and each constraint are in the form of interval valued trapezoidal N numbers. This real production problem can be formulated in mathematical format as:

$$\mathop {Max}\limits_{{x_{1} }} \left\{ \begin{gathered} Z_{1} (X) = \left\langle {(1.0,\,1.75,\,2.0,\,6.75);0.20,0.80,0.30} \right\rangle x_{1} + \left\langle {(1.5,\,1.75,\,2.0,\,6.50);0.30,0.50,0.40} \right\rangle x_{2} \hfill \\ + \left\langle {(1.0,\,1.75,\,2.0,\,6.75);0.30,0.70,0.20} \right\rangle x_{3} \hfill \\ \end{gathered} \right\}\;\;\;\left( {1st\;level} \right)$$
$$\mathop {Max}\limits_{{x_{2} }} \left\{ \begin{gathered} Z_{2} (X) = \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.40,0.70,0.20} \right\rangle x_{1} + \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.20,0.80,0.50} \right\rangle x_{2} \hfill \\ + \left\langle {(1.5,\,1.75,\,2.0,\,6.50);0.40,0.50,0.30} \right\rangle x_{3} \hfill \\ \end{gathered} \right\}\;\;\;\left( {2nd\;level} \right)$$
$$\mathop {Max}\limits_{{x_{3} }} \left\{ \begin{gathered} Z_{3} (X) = \left\langle {(1.5,1.75,2.0,6.25);0.40,0.60,0.30} \right\rangle x_{1} + \left\langle {(1.0,1.75,2.0,6.75);0.30,0.70,0.20} \right\rangle x_{2} \hfill \\ + \left\langle {(1.5,1.75,2.0,6.25);0.20,0.80,0.50} \right\rangle x_{3} \hfill \\ \end{gathered} \right\}\;\;\;\left( {3rd\;level} \right)$$
$$\begin{gathered} {\text{Subject to}},\;\left\langle {(0.5,1.5,2.5,4.5);0.20,0.80,0.20} \right\rangle x_{1} + + \left\langle {(1.5,2.5,3,5.5);0.20,0.80,0.20} \right\rangle x_{2} \hfill \\ + \left\langle {(1.0,1.75,2.0,6.75);0.20,0.80,0.30} \right\rangle x_{3} + \left\langle {(1.5,1.75,2.0,6.25);0.30,0.60,0.20} \right\rangle x_{4} \, \le 850 \hfill \\ \end{gathered}$$
$$\begin{gathered} \left\langle {(2,3,3.5,6.5);0.20,0.80,0.20} \right\rangle x_{1} + \left\langle {(2.0,2.5,3.0,11.5);0.30,0.80,0.50} \right\rangle x_{2} \hfill \\ + \left\langle {(1.0,1.75,2.0,6.75);0.30,0.80,0.20} \right\rangle x_{3} + \left\langle {(1.5,1.75,2.0,6.25);0.20,0.50,0.20} \right\rangle x_{4} \, \le 900 \hfill \\ \end{gathered}$$
$$\begin{gathered} \left\langle {(1.5,\,1.75,\,2.0,\,6.50);0.30,0.50,0.40} \right\rangle x_{1} + \left\langle {(1.0,\,1.75,\,2.0,\,6.75);0.30,0.80,0.20} \right\rangle x_{2} \hfill \\ \, + \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.40,0.70,0.20} \right\rangle x_{3} + \left\langle {(1.5,\,1.75,\,2.0,\,6.25);0.40,0.60,0.30} \right\rangle x_{4} \, \le \,1100 \hfill \\ \end{gathered}$$
$${\text{and}}\;x_{1} ,x_{2} ,x_{3} ,x_{4} \ge 0$$

Using the step 1 of proposed solution technique, the values of \(k_{1}\), \(k_{2}\) and \(k_{3}\) for each N number coefficient of objectives and constraints are obtained (Tables 5 and 6) as:

Table 5 Values of \(k_{1}\), \(k_{2}\) and \(k_{3}\) for each N number coefficient of objective functions
Full size table
Table 6 Values of \(k_{1}\), \(k_{2}\) and \(k_{3}\) for each N number coefficient of constraint
Full size table

Thereafter, with the values \(\lambda_{1} = 0.20,\,\lambda_{2} = 0.50\), \(\lambda_{3} = 0.30\) and \(\lambda_{1} = 0.30,\,\lambda_{2} = 0.40\), \(\lambda_{3} = 0.30\) for N numbers coefficient in objective function and constraint respectively, the complete p.d.f. of each coefficient as mentioned in step 2 of algorithm can be obtained and accordingly their equivalent value can be obtained using Laplace Transform as given in (14) and mentioned in step 4. With these equivalent values of each N numbers, we convert the problem into equivalent crisp problem as:

$$\mathop {Max}\limits_{{x_{1} }} \left\{ {Z_{1} (X) = 0.0155x_{1} + 0.0064x_{2} + 0.0204x_{3} } \right\}\;\;\;\;\;\left( {1st\;level} \right)$$
$$\mathop {Max}\limits_{{x_{2} }} \left\{ {Z_{2} (X) = 0.0165x_{1} + 0.0156x_{2} + 0.0147x_{3} } \right\}\;\;\;\left( {2nd\;level} \right)$$
$$\mathop {Max}\limits_{{x_{3} }} \left\{ {Z_{3} (X) = 0.0163x_{1} + 0.0181x_{2} + 0.0156x_{3} } \right\}\;\;\;\left( {3rd\;level} \right)$$
$${\text{Subject}}\;{\text{to}},\;\;\;0.0627x_{1} + 0.0213x_{2} + 0.0155x_{3} \le 850$$
$$0.0102x_{1} + 0.0041x_{2} + 0.0204x_{3} \le \,900$$
$$0.0052x_{1} + 0.0103x_{2} + 0.0556x_{3} \le \,1100$$
$${\text{and}}\;\;\;x_{1} ,x_{2} ,x_{3} ,x_{4} \ge 0$$

Solving this crisp problem irrespective of level structure, we obtain the ideal values of decision variables and objective function and formulate the linear membership function for each objective function and variables (up to T-1 level i.e. \(x_{1} ,\;x_{2}\)). Finally, we have the solution model for MLLP problem with IVTrp N numbers as:

$$\min \lambda = d_{1}^{ - } + d_{2}^{ - } + d_{3}^{ - } + d_{{x_{1} }}^{ - } + d_{{x_{3} }}^{ - }$$
$${\text{Subject}}\;{\text{to}},\;\;\;0.0155x_{1} + 0.0064x_{2} + 0.0204x_{3} + 524.1711d_{1}^{ - } \ge 524.1711$$
$$0.0165x_{1} + 0.0156x_{2} + 0.0147x_{3} + 670.4845d_{2}^{ - } \ge 670.4845$$
$$0.0163x_{1} + 0.0181x_{2} + 0.0156x_{3} + 757.0840d_{3}^{ - } \ge 757.0840$$

\(x_{1} + 8870.892d_{{x_{1} }}^{ - } \ge 8870.892\)

$$x_{2} + 29483.81d_{{x_{2} }}^{ - } \ge 29483.81$$
$$0.0627x_{1} + 0.0213x_{2} + 0.0155x_{3} \le 8\,50$$
$$0.0102x_{1} + 0.0041x_{2} + 0.0204x_{3} \le \,900$$
$$0.0052x_{1} + 0.0103x_{2} + 0.0556x_{3} \le \,1100$$
$${\text{and}}\;\;\;\;\;x_{1} ,x_{2} ,x_{3} ,d_{1}^{ - } ,d_{2}^{ - } ,d_{3}^{ - } ,d_{{x_{1} }}^{ - } ,d_{{x_{2} }}^{ - } \ge 0$$

Solving this programming problem model with simplex method or LINGO© tool, we obtain the satisfactory solution to the original problem: \(\lambda = 1.082608\) \(x_{1} = 0.001104,\) \(x_{2} = 29483.81,\) \(x_{3} = 14322.24\) with the objective function values as: \(\widetilde{{Z_{11} }} = 480.8702,\) \(\widetilde{{Z_{2} }} = 670.4844,\) and \(\widetilde{{Z_{3} }} = 757.0840\).

7 Concluding remarks and future research directions

This paper presents an improved and unique solution technique for MLLP problem with interval-valued trapezoidal neutrosophic numbers (IVTrpN numbers). The unique feature of the proposed technique is the use of proportional p.d.f. to each N number and use of Laplace transform to convert problem into crisp problem. Besides this, proposed technique is comparatively simpler with reduced number of computational steps as there is no use of ranking function, score function, accuracy function etc. values of N numbers in the de-neutrosophication process of N numbers. However, proposed technique has limitation of computation difficulties of Laplace transform of associated p.d.f. but this limitation can be dealt with the use of computing software like MATHEMATICA, MATLAB and LINGO. The proposed technique can be extended for the solution of more complex problems like MOP problems, BLP problems, MLMOP problems etc. by the future researchers.