1 Introduction

Multi-level programming problems (MLPPs) occur in hierarchical decision making organizations where a DM is present at each level of decision making and is assigned the task of optimizing one or more objective functions. Also, every DM has independent control over a set of decision variables (Baky 2010). Since an MLPP involves multiple DMs who generally have conflicting objectives, the DMs must co-operate with each other to obtain a compromise optimal solution for the overall benefit of the organization. In particular, if an MLPP has 2 levels it is called bi-level programming problem (BLPP). In most real world situations, the values to be assigned to the parameters cannot be precisely known due to incomplete and ambiguous information. To address this problem, parameters have been interpreted as fuzzy data which is represented as fuzzy sets (Baky et al. 2014).

Goal programming (GP) (Charnes et al. 1955) is a very important mathematical tool suitable for obtaining optimal solution of multi objective programming problems involving conflicting objectives. Goal programming when applied to a programming problem with fuzzy parameters is termed as fuzzy goal programming (FGP). GP has been widely used to solve various types of optimization problems such as BLPPs, fractional BLPPs, MLPPs, fractional MLPPs, multi-objective MLPPs, and decentralized fractional BLPP (Pramanik 2012; Pramanik and Dey 2011; Pramanik et al. 2012; Baky 2010; Dey et al. 2014a).

The disadvantage of fuzzy sets is its inability to efficiently represent imprecise and inconsistent information as it considers only the truth membership function (Zadeh 1965). Intuitionistic fuzzy set (Atanassov 1986) is a modification of fuzzy sets which considered both the truth and falsity membership functions. But still it had some drawbacks in depicting human like decision making. Group decision making with fuzzy sets and intuitionistic fuzzy sets has been discussed in Banaeian et al. (2018) and Liu et al. (2018). Some recent developments on group decision making has been discussed in Morente-Molinera et al. (2018, 2019) and Pérez et al. (2018). In 1998, a new type of set called neutrosophic set was introduced by Smarandache (1998) to deal with decision making problems which involved incomplete, inconsistent and indeterminate information. Here indeterminacy is considered as an independent factor which has a major contribution in decision making. Neutrosophic set helps in human-like decision making by considering truth, falsity and indeterminacy membership functions. Wang et al. (2010) introduced single valued neutrosophic set (SVNS) to solve practical problems. Application of SVNS can be found in a vast range of decision making problems such as multi criteria decision making problems (Biswas et al. 2014a, b; Broumi and Smarandache 2014), educational problems (Mondal and Pramanik 2015), social problems (Pramanik and Chakrabarti 2013) etc.

The notion of neutrosophic number (NN) and its basic properties were established by Smarandache (2013), in which indeterminacy plays a pivotal role. Ye (2016a) investigated ranking of NNs based on possibility degree in multi-attribute group decision making (MAGDM) strategy. Another MAGDM strategy with NNs was formulated by Ye (2017) where bidirectional measure was applied. Kong et al. (2015) developed misfire fault diagnosis technique in gasoline engines using distance measure of NNs and cosine function based similarity measure. Ye (2016b) developed a method for fault diagnosis of steam turbine with the help of exponential similarity measure of NNs. Ye et al. (2017) analysed joint roughness coefficient taking the help of NN functions. NN generalized weighted power averaging operator formulated by Liu and Liu (2018) is applied to MAGDM in NN environment. Zheng et al. (2017) applied NN generalized hybrid weighted averaging operator to MAGDM problems. Mondal et al. (2018) approached MAGDM problems in NN environment through NN-Harmonic mean aggregation operators. Shi and Ye (2017) presented the cosine measures of linguistic neutrosophic numbers and used it in MAGDM with NNs. Ye (2018b) developed a multi attribute decision making strategy using the expected value in hesitant neutrosophic linguistic number and its similarity measure. Various other works related to uncertainty has also been studied (Liu et al. 2019; Zhang 2012; Zhang and Zhang 2012; Zhang et al. 2012a, b, c, 2014a, b, 2015a, b, c, 2016, 2017a, b, 2018a, b, c, d, e, f, Zhang et al. 2019a, b, c, d; Zhang and Liang 2013). Pramanik et al. (2017) addressed teacher selection problem using bidirectional projection measure in NN environment. Ye (2018a) employed a linear programming strategy in NN environment to solve optimization problems with NNs. Ye et al. (2018) have also solved non-linear programming problems in NN environment. Banerjee and Pramanik (2018) grounded the linear programming problem with single objective in NN environment with the help of goal programming. Here, the coefficients of the objectives along with the constraint coefficients have been taken to be NNs in the form of \(c + dI\), where c, d are real numbers and indeterminacy is represented by I. Pramanik and Banerjee (2018) broadened the notion of article Banerjee and Pramanik (2018) to multi-objective linear programming problem in NN environment. Also Pramanik and Dey (2018) formulated solution method to linear bi-level programming problem in NN environment.

In this paper, we have considered NNs in the form \(M = c + dI\) where c and d are real numbers and I symbolizes indeterminacy. c denotes the determinate or sure part of M and dI denotes the indeterminate or unsure part of M. I is also called the non-numerical indeterminacy (or literal indeterminacy) (Smarandache 2015) The method proposed in this paper helps to solve MLMOLPP in NN environment where the DMs present in various levels usually have conflicting objectives. The parameters for the problem are considered as NNs in the form \(c + dI\) where indeterminacy is an independent factor which plays a crucial part in decision making. Since decision making in real life problems involves indeterminate information so NNs can better represent them compared to other parameters in uncertain environment such as fuzzy numbers and intuitionistic fuzzy numbers.

A GP based strategy to solve MLMOLPP with NNs is proposed in this paper. Firstly, the NNs are transformed into interval numbers and hereby the given problem gets converted into a MLMOLPP with interval parameters. The target interval of each objective function is formed through interval programming technique and then the goal achieving functions are constructed to achieve the target goals. Each DM allows some possible relaxation on the variable controlled by him/her to avoid decision deadlock and obtain an optimal compromise solution of the MLMOLPP. Then a GP model is constructed to solve the MLMOLPP with NNs. Lastly the efficacy of the strategy discussed is demonstrated through a numerical illustration.

The remaining part of this paper is arranged in the following manner. Some preliminary notions regarding interval numbers and neutrosophic numbers are presented in Sect. 2. Section 3 deals with the formulation of the MLMOLPP with NNs. Section 4 elaborate the proposed GP strategy. In Sect. 5 the proposed strategy is applied to an illustrative numerical example to clarify its applicability. The article comes to an end with the concluding remarks and further fields of study presented in Sect. 6.

2 Preliminaries

Some elementary concepts regarding interval numbers and neutrosophic numbers have been discussed under this section head.

2.1 Interval numbers (Moore 1998)

An interval number on the real line R is denoted as \(N = [N^{L} ,\;N^{U} ] = \{ n:N^{L} \le n \le N^{U} ,\;n \in R\} ,\) where \(N^{L}\) and \(N^{U}\) represent the left and right limit of the interval number \(N\) on \(R.\)

Definition 1

Let \(m(N)\) denotes the midpoint and \(w(N)\) denotes the width of the interval number \(N\) Then \(m(N) = \frac{1}{2}(N^{L} + N^{U} )\) and \(w(N) = (N^{U} - N^{L} ).\)

Definition 2

The definition of scalar multiplication on \(N\) is as follows:

$$\lambda N = \left\{ {\begin{array}{*{20}l} {[\lambda N^{L} ,\,\lambda N^{U} ],} & {\quad \lambda \ge 0} \\ {[\lambda N^{U} ,\,\lambda N^{L} ],} & {\quad \lambda \le 0} \\ \end{array} } \right..$$

Definition 3

Absolute value of N is defined in the following way:

$$|N| = \left\{ {\begin{array}{*{20}l} {[N^{L} ,\,N^{U} ],\;\;N^{L} \ge 0} \\ {[0,\max ( - N^{L} ,N^{U} )],\;\;N^{L} < 0 < N^{U} } \\ {[ - N^{U} , - N^{L} ],\;\;N^{U} \le 0} \\ \end{array} } \right..$$

Definition 4

The binary operation ‘*’ between two interval numbers \(N_{1} = [N_{1}^{L} ,\;N_{1}^{U} ]\) and \(N_{2} = [N_{2}^{L} ,\;N_{2}^{U} ]\) can be defined as

$$N_{1} *N_{2} = \{ n_{1} *n_{2} :n_{1} \in N_{1} ,n_{2} \in N_{2} \} \quad {\text{where}}\;\;N_{1}^{L} \le n_{1} \le N_{1}^{U} ,\,N_{2}^{L} \le n_{2} \le N_{2}^{U} .$$

In particular

$$\begin{gathered} N_{1} + N_{2} = [N_{1}^{L} + N_{2}^{L} ,N_{1}^{U} + N_{2}^{U} ] \hfill \\ N_{1} - N_{2} = [N_{1}^{L} - N_{2}^{U} ,N_{1}^{U} - N_{2}^{L} ] \hfill \\ N_{1} \times N_{2} = [\min (N_{1}^{L} \times N_{2}^{L} ,N_{1}^{L} \times N_{2}^{U} ,N_{1}^{U} \times N_{2}^{L} ,N_{1}^{U} \times N_{2}^{U} ),\;\max (N_{1}^{L} \times N_{2}^{L} ,N_{1}^{L} \times N_{2}^{U} ,N_{1}^{U} \times N_{2}^{L} ,N_{1}^{U} \times N_{2}^{U} )] \hfill \\ N_{1} /N_{2} = \left\{ {\begin{array}{*{20}l} {[N_{1}^{L} ,N_{1}^{U} ] \times \left[ {\frac{1}{{N_{2}^{U} }},\frac{1}{{N_{2}^{L} }}} \right]\;or} \\ {[\min (N_{1}^{L} /N_{2}^{L} ,N_{1}^{L} /N_{2}^{U} ,N_{1}^{U} /N_{2}^{L} ,N_{1}^{U} /N_{2}^{U} ),\;\max (N_{1}^{L} /N_{2}^{L} ,N_{1}^{L} /N_{2}^{U} ,N_{1}^{U} /N_{2}^{L} ,N_{1}^{U} /N_{2}^{U} )]\;if\;0 \notin N_{2} } \\ {undefined\;if\;0 \in N_{2} } \\ \end{array} } \right.. \hfill \\ \end{gathered}$$

2.2 Neutrosophic number (Smarandache 2013)

A neutrosophic number is denoted as \(M = c + dI\), where c and d are real (or complex) numbers and \(I \in [I^{L} ,I^{U} ]\) denotes indeterminacy. Also \(0.I = I\) and I ^ n = I for integer \(n \ge 1.\) Here \(c\) is called the determinate part of \(M\) and \(dI\) is the indeterminate part of \(M\). So \(M\) can be written as

$$M = c + dI = c + d[I^{L} ,I^{U} ] = [c + dI^{L} ,c + dI^{U} ] = [M^{L} ,M^{U} ]\quad ({\text{say}}).$$

Here we consider \(c\) and \(d\) to be real numbers.

Now the operations on NNs follow from the operations on interval numbers.

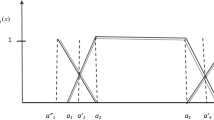
Let an NN be considered as \(M = 2 + 4I,\) where 2 represents the determinate part and \(4I\) represents the indeterminate part. Let it be assumed that \(I \in [0,1]\), so \(M\) transforms into an interval number \(M = [2,6].\)

Graphical representation of NN is shown in Fig. 1.

Fig. 1
figure 1

Graphical representation of 3 Neutrosophic Numbers with \(I \in [0,1]\)

Full size image

3 Formulation of MLMOLPP with NN parameters

In an MLMOLPP, each decision level has a DM associated with it and multiple objective functions have to be optimized at each level. Here we consider that the objective coefficients together with the constraint coefficients are NNs.

We consider here a hierarchical structure consisting of q (> 2) levels. The kth level decision maker DMk controls the decision variable \(w_{k} ,\,\,k = 1,2, \ldots ,q\) where \(w = (w_{1} ,w_{2} , \ldots ,w_{q} )\). A MLMOLPP with NNs where the objective function is to be minimized can be written as:

[1st level]

$$\mathop {\hbox{min} }\limits_{{w_{1} }} Z_{1} (w) = \mathop {\hbox{min} }\limits_{{w_{1} }} \,(Z_{11} (w),Z_{12} (w), \ldots ,Z_{{1p_{1} }} (w))$$
(1)

[2nd level]

$$\mathop {\hbox{min} }\limits_{{w_{2} }} Z_{2} (w) = \mathop {\hbox{min} }\limits_{{w_{2} }} \,(Z_{21} (w),Z_{22} (w), \ldots ,Z_{{2p_{2} }} (w))$$
(2)
$$\begin{array}{*{20}c} . \\ . \\ . \\ \end{array}$$

[qth level]

$$\mathop {\hbox{min} }\limits_{{w_{q} }} Z_{q} (w) = \mathop {\hbox{min} }\limits_{{w_{q} }} \,(Z_{q1} (w),Z_{q2} (w), \ldots ,Z_{{qp_{q} }} (w))$$
(3)

Subject to

$$w \in G = \left\{ {w = (w_{1} ,w_{2} , \ldots ,w_{q} ) \in R^{q} |\sum\limits_{j = 1}^{q} {(a_{lj} + I_{lj} d_{lj} )w_{j} \ge \alpha_{l} + I_{l} \beta_{l} ,\,w \ge 0,l = 1,2, \ldots ,p} } \right\} \ne \phi$$
(4)

where

$$Z_{kr} (w) = \sum\limits_{j = 1}^{q} {(c_{krj} + I_{krj} b_{krj} )} w_{j} + (\gamma_{kr} + I_{kr} \delta_{kr} )\quad (k = 1,2, \ldots ,q;\,\,r = 1,2, \ldots ,p_{k} )$$
(5)

Here \(I_{lj} \in [I_{lj}^{L} ,I_{lj}^{U} ],\,I_{krj} \in [I_{krj}^{L} ,I_{krj}^{U} ],\,I_{kr} \in [I_{kr}^{L} ,I_{kr}^{U} ]\) and \(a_{lj} ,d_{lj} ,\alpha_{l} ,\beta_{l} ,c_{krj} ,b_{krj} ,\gamma_{kr} ,\delta_{kr} ,I_{lj}^{L} ,I_{lj}^{U} ,I_{krj}^{L} ,I_{krj}^{U} ,I_{kr}^{L} ,I_{kr}^{U}\) are real numbers. \(p_{k} \,\) is the number of objective functions for DMk\((k = 1,2, \ldots ,q)\) and \(l\) is the number of constraints.

Now from Eq. (5) we get

$$\begin{aligned} Z_{kr} (w) & = \sum\limits_{j = 1}^{q} {(c_{krj} + I_{krj} b_{krj} )} w_{j} + (\gamma_{kr} + I_{kr} \delta_{kr} ) \\ & = \sum\limits_{j = 1}^{q} {\left[ {\left( {c_{krj} + I_{krj}^{L} b_{krj} } \right)w_{j} ,\;\left( {c_{krj} + I_{krj}^{U} b_{krj} } \right)w_{j} } \right]} + \left[ {\left( {\gamma_{kr} + I_{kr}^{L} \delta_{kr} } \right),\;\left( {\gamma_{kr} + I_{kr}^{U} \delta_{kr} } \right)} \right] \\ & = \left[ {\sum\limits_{j = 1}^{q} {\left( {c_{krj} + I_{krj}^{L} b_{krj} } \right)w_{j} ,\;\sum\limits_{j = 1}^{q} {\left( {c_{krj} + I_{krj}^{U} b_{krj} } \right)w_{j} } } } \right] + \left[ {\left( {\gamma_{kr} + I_{kr}^{L} \delta_{kr} } \right),\;\left( {\gamma_{kr} + I_{kr}^{U} \delta_{kr} } \right)} \right] \\ & = \left[ {\sum\limits_{j = 1}^{q} {\left( {c_{krj} + I_{krj}^{L} b_{krj} } \right)w_{j} + \left( {\gamma_{kr} + I_{kr}^{L} \delta_{kr} } \right)} ,\sum\limits_{j = 1}^{q} {\left( {c_{krj} + I_{krj}^{U} b_{krj} } \right)w_{j} + \left( {\gamma_{kr} + I_{kr}^{U} \delta_{kr} } \right)} } \right] \\ & = \left[ {C_{kr}^{L} (w),C_{kr}^{U} (w)} \right] \\ \end{aligned}$$
(6)

where \(\sum\limits_{j = 1}^{q} {(c_{krj} + I_{krj}^{L} b_{krj} )w_{j} + } (\gamma_{kr} + I_{kr}^{L} \delta_{kr} ) = C_{kr}^{L} (w)\) and \(\sum\limits_{j = 1}^{q} {(c_{krj} + I_{krj}^{U} b_{krj} )w_{j} + } (\gamma_{kr} + I_{kr}^{U} \delta_{kr} ) = C_{kr}^{U} (w)\)

Similarly, the constraints in Eq. (4) is reduced as

$$\begin{aligned} \sum\limits_{j = 1}^{q} {(a_{lj} + I_{lj} d_{lj} )w_{j} \ge \alpha_{l} + I_{l} \beta_{l} } \quad (l = 1,2, \ldots ,p) \hfill \\ \Rightarrow \left[ {\sum\limits_{j = 1}^{q} {(a_{lj} + I_{lj}^{L} d_{lj} )w_{j} ,} \sum\limits_{j = 1}^{q} {(a_{lj} + I_{lj}^{U} d_{lj} )w_{j} } } \right] \ge \left[ {\alpha_{l} + I_{l}^{L} \beta_{l} ,\alpha_{l} + I_{l}^{U} \beta_{l} } \right] \hfill \\ \ge [B_{l}^{L} ,B_{l}^{U} ] \hfill \\ \end{aligned}$$
(7)

where \(\alpha_{l} + I_{l}^{L} \beta_{l} = B_{l}^{L}\) and \(\alpha_{l} + I_{l}^{U} \beta_{l} = B_{l}^{U} .\)

4 A goal programming strategy to solve MLMOLPP with NN parameters

The minimization type MLMOLPP with neutrosophic numbers is rewritten as:

[1st level]

$$\mathop {\hbox{min} }\limits_{{w_{1} }} Z_{1r} (w) = \left[ {C_{1r}^{L} (w),C_{1r}^{U} (w)} \right]\quad (r = 1,2, \ldots ,p_{1} )$$
(8)

[2nd level]

$$\mathop {\hbox{min} }\limits_{{w_{2} }} Z_{2r} (w) = \left[ {C_{2r}^{L} (w),C_{2r}^{U} (w)} \right]\quad (r = 1,2, \ldots ,p_{2} )$$
(9)
$$\begin{array}{*{20}c} . \\ . \\ . \\ \end{array}$$

[qth level]

$$\mathop {\hbox{min} }\limits_{{w_{q} }} Z_{qr} (w) = \left[ {C_{qr}^{L} (w),C_{qr}^{U} (w)} \right]\quad (r = 1,2, \ldots ,p_{q} )$$
(10)

Subject to

$$\begin{aligned} \left[ {\sum\limits_{j = 1}^{q} {\left( {a_{lj} + I_{lj}^{L} d_{lj} } \right)w_{j} ,} \sum\limits_{j = 1}^{q} {\left( {a_{lj} + I_{lj}^{U} d_{lj} } \right)w_{j} } } \right] \ge \left[ {B_{l}^{L} ,B_{l}^{U} } \right] \hfill \\ w = (w_{1} ,w_{2} , \ldots ,w_{q} ) \ge 0 \hfill \\ l = 1,2, \ldots ,p \hfill \\ \end{aligned}$$

Proposition 1

(Shaocheng 1994) Suppose\(\sum\nolimits_{k = 1}^{n} {[e_{1}^{k} ,e_{2}^{k} ]z_{k} \ge [f_{1} ,f_{2} ],}\)then\(\sum\nolimits_{k = 1}^{n} {[e_{2}^{k} ]} z_{k} \ge f_{1} ,\,\sum\nolimits_{k = 1}^{n} {[e_{1}^{k} ]z_{k} \ge f_{2} }\)are the inequalities which provide the maximum and minimum value ranges respectively.

For acquiring the best optimal solution of \(Z_{kr} (w)\,,\) (the rth objective function of the kth level DM), \(k = 1,2,\ldots ,q;\,\,r = 1,2,\ldots ,p_{k}\),we solve the following problem according to Ramadan (1996) as given below:

$$\hbox{min} C_{kr}^{L} (w)\quad (k = 1,2, \ldots ,q;\,\;r = 1,2,\ldots ,p_{k} )$$
(11)

Subject to

$$\begin{aligned} \sum\limits_{j = 1}^{q} {\left( {a_{lj} + I_{lj}^{U} d_{lj} } \right)w_{j} } \ge B_{l}^{L} \hfill \\ w = (w_{1} ,w_{2} , \ldots ,w_{q} ) \ge 0 \hfill \\ l = 1,2, \ldots ,p\, \hfill \\ \end{aligned}$$
(12)

Let the rth objective function of the kth level DM denoted by \(Z_{kr} (w),\) acquires its best solution at \(w_{kr}^{B} = (w_{kr1}^{B} ,w_{kr2}^{B} ,\ldots ,w_{krq}^{B} ),\,\,\,\,\,\,(k = 1,2,\ldots ,q;\,\,r = 1,2,\ldots ,p_{k} )\) and let \(Z_{kr}^{B}\) denote the best objective value of \(Z_{kr} (w).\)

The worst optimal solution of \(Z_{kr} (w)\,,\,\,\,\,\,(k = 1,2,\ldots ,q;\,\,r = 1,2,\ldots ,p_{k} )\) is obtained by solving the following problem as given by Ramadan (1996).

$$\hbox{min} C_{kr}^{U} (w)\quad (k = 1,2,\ldots ,q;\,r = 1,2,\ldots ,p_{k} )$$
(13)

Subject to

$$\begin{aligned} \sum\limits_{j = 1}^{q} {\left( {a_{lj} + I_{lj}^{L} d_{lj} } \right)w_{j} } \ge B_{l}^{U} \hfill \\ w = (w_{1} ,w_{2} ,\ldots ,w_{q} ) \ge 0 \hfill \\ l = 1,2,\ldots ,p\, \hfill \\ \end{aligned}$$
(14)

Let the worst solution of \(Z_{kr} (w)\) be obtained at \(w_{kr}^{W} = (w_{kr1}^{W} ,w_{kr2}^{W} ,\ldots ,w_{krq}^{W} ),\,\,\,\,\,\,(k = 1,2,\ldots ,q;\,\,r = 1,2,\ldots ,p_{k} )\) and \(Z_{kr}^{W}\) denote the worst objective value of \(Z_{kr} (w)\).

So the optimal value of \(Z_{kr} (w)\) in interval form is \([Z_{kr}^{B} ,\,Z_{kr}^{W} ].\)

Let it be assumed that the objective function \(Z_{kr} (w)\) has its target interval \([Z_{kr}^{*B} ,\,Z_{kr}^{*W} ]\) as considered by the DM.

The objective function \(Z_{kr} (w)\) has the target level considered as follows:

$$C_{kr}^{U} (w) \ge Z_{kr}^{*B}$$
(15)
$$C_{kr}^{L} (w) \le Z_{kr}^{*W} \quad (k = 1,2,\ldots ,q;\,\,r = 1,2,\ldots ,p_{k} )$$
(16)

Hence the goal achievement functions for \(Z_{kr} (w)\) can be written as:

$$- C_{kr}^{U} (w) + D_{kr}^{U} = - Z_{kr}^{*B}$$
(17)
$$C_{kr}^{L} (w) + D_{kr}^{L} = Z_{kr}^{*W} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(k = 1,2,\ldots ,q;\,\,r = 1,2,\ldots ,p_{k} )$$
(18)

where \(D_{kr}^{U} > 0,\,D_{kr}^{L} > 0\) represent the deviational variables.

Solution of the GP model presented below provides the best solution for the kth level (\(k = 1,2,\ldots ,q\)) DM.

$$\begin{aligned} \hbox{min} \theta \hfill \\ {\text{Subject}}\;{\text{to}} \hfill \\ - C_{kr}^{U} (w) + D_{kr}^{U} = - Z_{kr}^{*B} \hfill \\ C_{kr}^{L} (w) + D_{kr}^{L} = Z_{kr}^{*W} \hfill \\ \sum\limits_{j = 1}^{q} {(a_{lj} + I_{lj}^{U} d_{lj} )w_{j} } \ge B_{l}^{L} \hfill \\ \sum\limits_{j = 1}^{q} {(a_{lj} + I_{lj}^{L} d_{lj} )w_{j} } \ge B_{l}^{U} \hfill \\ \theta \ge D_{kr}^{U} \,,\,\theta \ge D_{kr}^{L} \hfill \\ D_{kr}^{U} ,D_{kr}^{L} ,w_{j} \ge 0 \hfill \\ r = 1,2,\ldots ,p_{k} \,;\,\,l = 1,2,\ldots ,p\,;\,j = 1,2,\ldots ,q \hfill \\ \end{aligned}$$
(19)

In MLMOLPP, the objectives of various level DMs are usually conflicting in nature. So it is necessary for the DMs to cooperate with each other so as to attain a compromise optimal solution for the overall benefit of the organization (Dey et al. 2014b).

Let \(w_{k}^{B} = (w_{k1}^{B} ,w_{k2}^{B} ,\ldots ,w_{kq}^{B} )\) be the best solution of kth level DM. The decision variable which is in control of the kth level DM is \(w_{kk}^{B}\). To cooperate with other level DMs, the kth level DM allows some upper and lower preference bounds on the variable \(w_{kk}^{B}\). Let \(l_{kk}\) and \(u_{kk}\) be the respective lower and upper preference bounds suggested by the kth level DM. Therefore, we can write

$$w_{kk}^{B} - l_{kk} \le w_{kk}^{B} \le w_{kk}^{B} + u_{kk} ,\quad k = 1,2,\ldots ,q$$
(20)

Finally, we develop a GP model for MLMOLPP with neutrosophic number structured as follows:

GP model:

$${\text{Min S}} = \sum\limits_{r = 1}^{{p_{1} }} {\left( {\tau_{1r}^{U} D_{1r}^{U} + \tau_{1r}^{L} D_{1r}^{L} } \right)} + \sum\limits_{r = 1}^{{p_{2} }} {\left( {\tau_{2r}^{U} D_{2r}^{U} + \tau_{2r}^{L} D_{2r}^{L} } \right)} + \cdots + \sum\limits_{r = 1}^{{p_{q} }} {\left( {\tau_{qr}^{U} D_{qr}^{U} + \tau_{qr}^{L} D_{qr}^{L} } \right)}$$
(21)

Subject to

$$\begin{aligned} - C_{kr}^{U} (w) + D_{kr}^{U} = - Z_{kr}^{*B} \hfill \\ C_{kr}^{L} (w) + D_{kr}^{L} = Z_{kr}^{*W} \hfill \\ \sum\limits_{j = 1}^{q} {\left( {a_{lj} + I_{lj}^{U} d_{lj} } \right)w_{j} } \ge B_{l}^{L} \hfill \\ \sum\limits_{j = 1}^{q} {\left( {a_{lj} + I_{lj}^{L} d_{lj} } \right)w_{j} } \ge B_{l}^{U} \hfill \\ w_{kk}^{B} - l_{kk} \le w_{kk}^{B} \le w_{kk}^{B} + u_{kk} \, \hfill \\ w_{j} ,\,D_{kr}^{U} ,D_{kr}^{L} ,\tau_{kr}^{U} ,\,\tau_{kr}^{L} \ge 0 \hfill \\ k = 1,2,\ldots ,q;\,\,r = 1,2,\ldots ,p_{k} ;\,\,l = 1,2,\ldots ,p;\,\;j = 1,2,\ldots ,q \hfill \\ \end{aligned}$$

Here \(\tau_{kr}^{U} ,\,\tau_{kr}^{L} \,\,(k = 1,2,\ldots ,q)\) denote the numerical weights of the corresponding deviational variables as recommended by the DMs.

4.1 Algorithm for the proposed strategy to solve MLMOLPP with NNs

  • Step 1: The original MLMOLPP with NNs is converted into MLMOLPP with interval numbers as in Eqs. (8–10) along with the reduced constraints (7).

  • Step 2: For each objective function the individual best and worst solutions are obtained using Eqs. (11–14).

  • Step 3: The goal achievement functions are constructed using Eqs. (17–18).

  • Step 4: The best solution for each level DM is obtained using the GP model (19).

  • Step 5: The DMs assign upper and lower preference bounds as given in Eq. (20).

  • Step 6: GP model (21) is formed and its solution provides the required values of the decision variables.

The flowchart framework for solving the MLMOLPP with NNs is presented in Fig. 2.

Fig. 2
figure 2

Flowchart depicting the proposed solution method

Full size image

5 Numerical illustration

A numerical problem is provided to clarify the steps of the proposed strategy to obtain the solution of MLMOLPP with NNs. Here it is considered that \(I \in [0,1].\)

1st level DM:

$$\mathop {\hbox{min} }\limits_{{x_{1} }} \left\{ \begin{aligned} Z_{11} (x) = [1 + 2I]x_{1} + [3 + 4I]x_{2} + [7 + 5I]x_{3} + [1 + 3I] \hfill \\ Z_{12} (x) = [3 + 4I]x_{1} + [5 + 9I]x_{2} + [2 + 3I]x_{3} + [2 + 4I] \hfill \\ \end{aligned} \right.$$

2nd level DM:

$$\mathop {\hbox{min} }\limits_{{x_{2} }} \left\{ \begin{aligned} Z_{21} (x) = [5 + 6I]x_{1} + [8 + 9I]x_{2} + [1 + 4I]x_{3} \hfill \\ Z_{22} (x) = [9 + 8I]x_{1} + [5 + 4I]x_{2} + [1 + 2I]x_{3} + [6 - 7I] \hfill \\ \end{aligned} \right.$$

3rd level DM:

$$\mathop {\hbox{min} }\limits_{{x_{3} }} \left\{ \begin{aligned} Z_{31} (x) = [5 - 2I]x_{1} + [3 - I]x_{2} + [9 + 4I]x_{3} \hfill \\ Z_{32} (x) = [10 - 4I]x_{1} + [5 - 4I]x_{2} + [2 + 3I]x_{3} + [2 + 5I] \hfill \\ \end{aligned} \right.$$

Subject to

$$\begin{aligned} \hfill [4 + 2I]x_{1} + [3 + 7I]x_{2} + [1 + 5I]x_{3} \ge [15 + 10I] \hfill \\ [6 + I]x_{1} + [ - 2 + 4I]x_{2} + [6 + 2I]x_{3} \ge [5 + 3I] \hfill \\ x_{1} ,x_{2} ,x_{3} \ge 0 \hfill \\ \end{aligned}$$

Table 1 presents the transformed problem for 1st level DM and Table 2 presents the best and worst solutions for 1st level DM.

Table 1 Problem formulation for best and worst solution of 1st level DM
Full size table
Table 2 Best and worst solutions for 1st level DM
Full size table

Hence the target objective functions can be taken as:

$$\begin{aligned} x_{1} + 3x_{2} + 7x_{3} + 1 \le 22.75 \hfill \\ 3x_{1} + 7x_{2} + 12x_{3} + 4 \ge 4 \hfill \\ 3x_{1} + 5x_{2} + 2x_{3} + 2 \le 49 \hfill \\ 7x_{1} + 14x_{2} + 5x_{3} + 6 \ge 7 \hfill \\ \end{aligned}$$

The goal functions with targets are:

$$\begin{aligned} x_{1} + 3x_{2} + 7x_{3} + 1 + D_{11}^{L} = 22.75 \hfill \\ - 3x_{1} - 7x_{2} - 12x_{3} - 4 + D_{11}^{U} = - 4 \hfill \\ 3x_{1} + 5x_{2} + 2x_{3} + 2 + D_{12}^{L} = 49 \hfill \\ - 7x_{1} - 14x_{2} - 5x_{3} - 6 + D_{12}^{U} = - 7 \hfill \\ \end{aligned}$$

The best solution of 1st level DM is obtained using GP model (19) as \(x_{1} = 6.25,\,x_{2} = 0,\,x_{3} = 0\)

The 2nd level problem is transformed into 2 linear programming problems as given in Table 3. The solutions of these 2 LPPs which give the best and worst solutions for 2nd level DM are given in Table 4.

Table 3 Problem formulation for best and worst solution of 2nd level DM
Full size table
Table 4 Best and worst solutions for 2nd level DM
Full size table

Hence the target objective functions can be taken as:

$$\begin{aligned} 5x_{1} + 8x_{2} + x_{3} \le 68 \hfill \\ 11x_{1} + 17x_{2} + 5x_{3} \ge 3 \hfill \\ 9x_{1} + 5x_{2} + x_{3} - 1 \le 81 \hfill \\ 17x_{1} + 9x_{2} + 3x_{3} + 6 \ge 2 \hfill \\ \end{aligned}$$

The goal functions with targets are:

$$\begin{aligned} 5x_{1} + 8x_{2} + x_{3} + D_{21}^{L} = 68 \hfill \\ - 11x_{1} - 17x_{2} - 5x_{3} + D_{21}^{U} = - 3 \hfill \\ 9x_{1} + 5x_{2} + x_{3} - 1 + D_{22}^{L} = 81 \hfill \\ - 17x_{1} - 9x_{2} - 3x_{3} - 6 + D_{22}^{U} = - 2 \hfill \\ \end{aligned}$$

The best solution of 2nd level DM is obtained using GP model (19) as \(x_{1} = 3.0714,\,x_{2} = 0,\,x_{3} = 12.714\)

Table 5 presents the transformed problems for finding the best and worst solution of 3rd level DM. Table 6 depicts the best and worst solutions for 3rd level DM.

Table 5 Problem formulation for best and worst solution of 3rd level DM
Full size table
Table 6 Best and worst solutions for 3rd level DM
Full size table

Hence the target objective functions can be taken as:

$$\begin{aligned} 3x_{1} + 2x_{2} + 9x_{3} \le 27 \hfill \\ 5x_{1} + 3x_{2} + 13x_{3} \ge 4 \hfill \\ 6x_{1} + x_{2} + 2x_{3} + 2 \le 58 \hfill \\ 10x_{1} + 5x_{2} + 5x_{3} + 7 \ge 4 \hfill \\ \end{aligned}$$

The goal functions with targets are:

$$\begin{aligned} 3x_{1} + 2x_{2} + 9x_{3} + D_{31}^{L} = 27 \hfill \\ - 5x_{1} - 3x_{2} - 13x_{3} + D_{31}^{U} = - 4 \hfill \\ 6x_{1} + x_{2} + 2x_{3} + 2 + D_{32}^{L} = 58 \hfill \\ - 10x_{1} - 5x_{2} - 5x_{3} - 7 + D_{32}^{U} = - 4 \hfill \\ \end{aligned}$$

The best solution of 3rd level DM is obtained using GP model (19) as \(x_{1} = 2.846,\,x_{2} = 4.53846,\,x_{3} = 0\)

Suppose the preference bounds offered by the 1st level DM on \(x_{1}\), the decision variable under his/her control, is taken as \(6.25 - 1.25 \le x_{1} \le 6.25 + 1.25.\) Similarly, the preference bounds set by the 2nd level DM on the decision variable \(x_{2}\) is taken as \(0 \le x_{2} \le 0 + 2\) and the 3rd level DM assigns preference bounds on the decision variable \(x_{3}\) as \(0 \le x_{3} \le 0 + 2.\)

The best solution point of each level DM and the preference bounds imposed by them are presented in Table 7.

Table 7 Best solution points for the level DMs and the preference bounds imposed
Full size table

The solution of the GP model described below is the optimal compromise solution of the original given problem.

GP model:

$${\text{Min}}\frac{1}{12}\left( {D_{11}^{L} + D_{11}^{U} + D_{12}^{L} + D_{12}^{U} + D_{21}^{L} + D_{21}^{U} + \,D_{22}^{L} + D_{22}^{U} + D_{31}^{L} + D_{31}^{U} + D_{32}^{L} + D_{32}^{U} } \right)$$
(22)

Subject to

$$\begin{aligned} x_{1} + 3x_{2} + 7x_{3} + 1 + D_{11}^{L} = 22.75 \hfill \\ - 3x_{1} - 7x_{2} - 12x_{3} - 4 + D_{11}^{U} = - 4 \hfill \\ 3x_{1} + 5x_{2} + 2x_{3} + 2 + D_{12}^{L} = 49 \hfill \\ - 7x_{1} - 14x_{2} - 5x_{3} - 6 + D_{12}^{U} = - 7 \hfill \\ 5x_{1} + 8x_{2} + x_{3} + D_{21}^{L} = 68 \hfill \\ - 11x_{1} - 17x_{2} - 5x_{3} + D_{21}^{U} = - 3 \hfill \\ 9x_{1} + 5x_{2} + x_{3} - 1 + D_{22}^{L} = 81 \hfill \\ - 17x_{1} - 9x_{2} - 3x_{3} - 6 + D_{22}^{U} = - 2 \hfill \\ 3x_{1} + 2x_{2} + 9x_{3} + D_{31}^{L} = 27 \hfill \\ - 5x_{1} - 3x_{2} - 13x_{3} + D_{31}^{U} = - 4 \hfill \\ 6x_{1} + x_{2} + 2x_{3} + 2 + D_{32}^{L} = 58 \hfill \\ - 10x_{1} - 5x_{2} - 5x_{3} - 7 + D_{32}^{U} = - 4 \hfill \\ 6x_{1} + 10x_{2} + 6x_{3} \ge 15 \hfill \\ 7x_{1} + 2x_{2} + 8x_{3} \ge 5 \hfill \\ 4x_{1} + 3x_{2} + x_{3} \ge 25 \hfill \\ 6x_{1} - 2x_{2} + 6x_{3} \ge 8 \hfill \\ 5 \le x_{1} \le 7.5 \hfill \\ 0 \le x_{2} \le 2 \hfill \\ 0 \le x_{3} \le 2 \hfill \\ x_{1} ,x_{2} ,x_{3} \ge 0\,\, \hfill \\ D_{1i}^{L} \,,D_{1i}^{U} ,D_{2i}^{L} ,D_{2i}^{U} ,D_{3i}^{L} ,D_{3i}^{U} \, \ge 0\, \hfill \\ i = 1,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{aligned}$$

Solving GP model (22), we obtain the solution point as (6.25, 0, 0). The compromise optimal range of the objective functions obtained using this solution point are shown in Table 8.

Table 8 Compromise optimal range of the objective functions
Full size table

5.1 Sensitivity analysis

For different choices of the preference bounds, the solution points obtained by solving the GP model (22) are shown in Table 9.

Table 9 Solution points obtained for various preference bounds
Full size table

6 Comparison with other existing methods

The proposed method solves Multi-Level Multi-Objective Linear Programming Problem with the parameters as neutrosophic numbers in the form c + dI, where c and d are real numbers and I denotes indeterminacy. But there exists no other method in the literature for solving Multi-Level Multi-Objective Linear Programming Problem with neutrosophic numbers in the form c + dI. This is the first approach in neutrosophic number environment.

Some research articles dealing with Multi-Level Multi-Objective Linear Programming Problem (MLMOLPP) are mentioned here. Liu and Yang (2018) used interactive programming approach to solve MLMOLPP. Pramanik et al. (2015) deals with the solution of multi- level linear plus linear fractional programming with multiple objective functions using Fuzzy Goal Programming (FGP) approach. MLMOLPP has been solved using FGP by Baky (2010). Lachhwani (2014) solved MLMOLPP using FGP approach in a simpler way than Baky (2010). In all these articles the parameters are crisp numbers. So the parameter environments of these papers are different than our paper.

Multi-Level Multi-Objective Programming Problem which involves fuzzy parameters in the objectives and right hand side of constraints has been solved by Abou-El-Enien and El-Feky (2018). Here the compromise solution of the problem has been obtained using TOPSIS approach. Stochastic fuzzy multi-level multi-objective fractional programming problem has been solved by Osman et al. (2017) using FGP approach. Here the chance-constrained approach with dominance possibility criteria and level cuts are used to transform the fuzzy problem into an equivalent crisp problem. Emam et al. (2016) discussed a solution method to multi-level multi-objective quadratic programming problem with the constraint parameters as trapezoidal fuzzy numbers. The method proposed in this article uses linear ranking to convert the fuzzy numbers into crisp numbers and then uses interactive approach to obtain the satisfactory solution. A solution procedure of multi-level multi-objective fractional programming problem with fuzzy demands has been discussed by Osman et al. (2018) using FGP approach. In all these research articles, the parameters are considered as fuzzy numbers.

So it can be observed that till now no paper in the literature deals with MLMOLPP with neutrosophic numbers in the form c + dI. Since the parameter environment of our paper does not match with that of other research articles, for this reason direct comparison with relative methods does not arise.

7 Conclusion

The paper presents a GP strategy to solve MLMOLPP with neutrosophic numbers. The NNs are firstly converted into interval numbers and the problem thus gets changed into an MLMOLPP with interval parameters. Interval programming technique is employed to obtain the target interval of each objective function. Goal achievement functions are constructed to attain the target goals. Since in an MLMOLPP, a situation of decision deadlock may arise owing to conflicting objectives, each level DM provides preference bounds on the decision variables controlled by him/her. GP strategy is then employed to obtain the compromise optimal solution of the MLMOLPP with NNs. A numerical example is solved to clarify the applicability and efficiency of this strategy. The method discussed here can be applied in decision making in large hierarchical organizations where multiple DMs having conflicting objectives are involved. Real decision making process can be better represented through neutrosophic numbers as it considers all aspects of decision making i.e., truth, falsity and indeterminacy. Here indeterminacy is considered as an independent factor which has a key role in decision making. The novelty of the method lies in its simplicity and efficient handling of indeterminate data.

No comparison is done as the developed strategy is the first attempt to solve MLMOLPP in NN environment. The goal programming strategy discussed here can be useful to solve real problems in a vast range of fields which include agriculture, transportation, bio-fuel production etc. in NN environment.