High-Order Compact Finite Difference Scheme for Pricing Asian Option with Moving Boundary Condition

Abstract

In this paper, an unconditionally stable compact finite difference scheme for the solution of linear convection–diffusion equation is proposed. In the proposed scheme, second derivative approximations of the unknowns are eliminated with the unknowns itself and their first derivative approximations while retaining the fourth order accuracy and tri-diagonal nature of the scheme. Proposed compact finite difference scheme which is fourth order accurate in spatial variable and second or lower order accurate in temporal variable depending on the choice of weighted time average parameter is applied to Asian option partial differential equation. A diagonally dominant system of linear equation is obtained from the proposed scheme which can be efficiently solved. Two numerical examples are given to demonstrate the efficiency and accuracy of the proposed compact finite difference scheme.

Introduction

Asian options [1], as one of the example of exotic options, first appeared in 1987 when the Bankers Trust Tokyo (hence the name Asian options) office developed a commercially used pricing formula for options on the average crude oil price. Asian options, having lower volatility than their underlying asset because of their averaging feature, are considered as an economical financial instrument for hedging purpose. So the study of Greeks (hedging parameters) is also important in the case of Asian options. In practice, most Asian options use the arithmetic average [2]. Since the probability distribution of the sum of log-normally distributed random variables is analytically intractable, the problem of pricing arithmetic Asian options does not have a closed form solution. Therefore various numerical techniques have been applied to price the Asian options.

Let us review some existing literature for Asian options. Vecer [3] characterized Asian options by a one-dimensional partial differential equation (PDE) which could be applied to both discrete and continuous average Asian options. He applied classical finite difference scheme to solve the Asian options PDE. Marcozzi [4] provided variational methods for pricing the Asian options. A theoretical framework is given by Marcozzi in his paper as numerical analysis of a finite element implementation. He provided the method to find the price of Asian options which has early exercise feature. Dubois and Lelievre [5] applied classical finite difference scheme to the Asian options PDE with moving boundary condition and showed that their method is much faster than the method presented in [3]. D’halluin et al. [6] gave a semi-Lagrangian approach to price continuously observed fixed strike Asian options. In this paper, a one-dimensional partial integro differential equation (PIDE) has been solved at each time step and solution is updated using semi-Lagrangian time stepping. Rogers and Shi [7] obtained lower-bounds for both types of Asian options. Lower bound formulas in [7] restrict the option’s maturity to exactly 1 year. This limitation has been removed by Chen and Lyuu [8] and Rogers–Shi formula is extended to general maturities. Recently, Kumar et al. [9] presented a numerical study of Asian options with radial basis functions based on finite differences scheme.

The growing popularity of compact finite different schemes in recent years have brought about a renewed interest towards the finite difference schemes. High-order compact schemes leads to a system of equations with coefficient matrix having smaller band width as compared to classical finite difference schemes. High-order compact finite difference schemes which consider not only the value of the function but also those of its first or higher derivatives as unknowns at each discretization point have been extensively studied and widely used to compute problems involving compressible flows [10], computational aeroacoustic [11] and several other practical applications [12]. High-order compact finite difference schemes have also been used in computational finance in order to compute the option prices, for e.g. During et al. [13] discussed the convergence of high-order compact finite difference schemes for European options by solving nonlinear Black–Scholes equation. Zhao et al. [14] discussed the high-order compact finite difference schemes for pricing American options. Tangman et al. [15] discussed the high-order compact finite difference schemes for numerical pricing of European and American options under Black–Scholes model.

There exist a vast literature of compact finite difference schemes for convection–diffusion equations [16,17,18]. For e.g. in [16, 17], modified differential equation approach is used to derive the high-order accurate first and second derivative approximations and the truncation error is compactly approximated. In these paper, original second order differential equation is considered as an auxiliary relation and original equation is differentiated in order to get the expressions for higher derivatives. Deriving compact schemes using modified differential approach for variable coefficient PDEs is difficult in general. A fourth order accurate compact finite difference scheme for convection–diffusion equation is proposed by Rigal [18]. He eliminated the highest order term in Taylor series in order to get a fourth order accurate compact finite difference scheme.

In this paper, we propose an unconditionally stable fourth-order compact finite difference scheme for the solution of linear convection–diffusion equation. The main contribution of the manuscript are as follows:

• Proposed compact finite difference scheme does not require the original equation as an auxiliary equation. In the proposed compact finite difference scheme, second derivative approximations of the unknowns are eliminated with the unknowns itself and their first derivative approximations while retaining the fourth order accuracy and tri-diagonal nature of the scheme.

• Proposed compact finite difference approximations are compared with the classical finite difference approximations and Padé approximation for second derivative using Fourier analysis and it is observed that proposed compact finite difference approximation have better resolution characteristics.

• Proposed compact finite difference scheme is applied to Asian option PDE and it is proved that proposed scheme is unconditionally stable for suitable choice of weighted time average parameter. Particular Asian option PDE with moving boundary condition is taken to reduce the computational cost significantly.

• Moreover, efficiency of the proposed compact finite difference scheme is compared to the central difference scheme by calculating the CPU time for a given accuracy and it is observed that proposed compact finite difference scheme is significantly efficient than central difference scheme.

The rest of the paper is organized as follows. In the next section, continuous arithmetic Asian options PDE is given. In the following section, compact finite difference approximations for first and second derivatives are discussed. Fourier analysis for different finite difference schemes is also discussed in this section. Stability of the proposed scheme for a convection–diffusion equation is also proved in this section. Before the concluding section, numerical results for arithmetic Asian options with compact finite difference scheme are given and obtained results are compared with the existing literature. Finally, conclusion of this paper is given and future work is proposed.

Mathematical Model

The price of continuous arithmetic average fixed strike Asian call option can be obtained from the solution of following two-dimensional PDE [1]

$$\begin{aligned} \frac{\partial V}{\partial t}+\frac{1}{2}\sigma ^2S^2\frac{\partial ^2 V}{\partial S^2}+rS\frac{\partial V}{\partial S}+S\frac{\partial V}{\partial I}-rV=0, \end{aligned}$$

(2.1)

with the final condition

$$\begin{aligned} V(S,I,T)= max\left( \frac{I}{T}-K,0\right) , \end{aligned}$$

(2.2)

where r is interest rate, T is the time to expiration, K is the stock price and $\sigma$ is the volatility of underlying asset and

$$\begin{aligned} I(t)=\int _0^t S(x)dx. \end{aligned}$$

Well-posedness of the boundary value formulation of a fixed strike Asian option is discussed in [19]. For more details about the existence and uniqueness of the solution of Asian option PDE (2.1), one can see [19] and references therein. Using the change of variables discussed in [7]

$$\begin{aligned} z=\frac{K-I/T}{S},\quad V(S,I,t)=Sv(z,t), \end{aligned}$$

(2.3)

above two dimensional PDE can be transformed into one dimensional PDE

$$\begin{aligned} \begin{aligned} -\frac{\partial v}{\partial t}&=\frac{1}{2}\sigma ^2z^2\frac{\partial ^2v}{\partial z^2}-\left( \frac{1}{T}+rz\right) \frac{\partial v}{\partial z},\\ v(z,T)&=max(-z,0). \\ \end{aligned} \end{aligned}$$

(2.4)

Now, using the change of variables [5]

$$\begin{aligned} z=x-\frac{t}{T},\quad u(x,t)=v(z,t), \end{aligned}$$

(2.5)

in PDE (2.4), we get

$$\begin{aligned} \begin{aligned} -\frac{\partial u}{\partial t}&=\frac{1}{2}\sigma ^2\left( x-\frac{t}{T}\right) ^2\frac{\partial ^2u}{\partial x^2}-r\left( x-\frac{t}{T}\right) \frac{\partial u}{\partial x},\\ v(x,T)&=max(1-x,0). \\ \end{aligned} \end{aligned}$$

(2.6)

The value of Asian option for $I \ge KT$ is given as [20]

$$\begin{aligned} V(S,I,t)=\frac{S}{rT}(1-e^{-r(T-t)})+\left( \frac{I}{T}-K\right) e^{-r(T-t)}. \end{aligned}$$

(2.7)

By using Eqs. (2.3) and (2.5) in above equation, we get

$$\begin{aligned} u(x,t)=\frac{1}{rT}(1-e^{-r(T-t)})-\left( x-\frac{t}{T}\right) e^{-r(T-t)}, \quad x \le \frac{t}{T}. \end{aligned}$$

(2.8)

So we find solution of Eq. (2.6) for $x>\frac{t}{T}$ using (2.8) as boundary condition at $x=t/T$. From Fig. 1, it is evident that using (2.8) as boundary condition at $x=t/T$ reduces the computation significantly. Hence, we have the following PDE

$$\begin{aligned} \begin{aligned} -\frac{\partial u}{\partial t}&=\frac{1}{2}\sigma ^2\left( x-\frac{t}{T}\right) ^2\frac{\partial ^2u}{\partial x^2}-r\left( x-\frac{t}{T}\right) \frac{\partial u}{\partial x},\quad (x,t)\in (t/T,\infty ) \times (0,T),\\ u(x,T)&=max(1-x,0),\quad x\in [1,\infty ),\\ u\left( \frac{t}{T},t\right)&=\frac{1}{rT}\left( 1-e^{-r(T-t)}\right) , \quad t\in (0,T],\\ \lim _{x\rightarrow \infty }u(x,t)&=0,\quad t\in [0,T]. \end{aligned} \end{aligned}$$

(2.9)

It can be seen from Eq. (2.9) that left boundary condition is varying as time is changing. This is depicted in Fig. 1. We propose an unconditionally stable compact finite difference scheme for the solution of above Eq. (2.9). In order to solve the above PDE numerically, domain $(t/T,\infty )$ is truncated to $\varOmega =(t/T,L)$ for a fixed constant L and $u(L,t)=0$ is chosen. It is discussed in [21] that truncation of domain leads to a negligible error in the price of option. Hence, we consider the following PDE throughout the paper:

$$\begin{aligned} \begin{aligned} -\frac{\partial u}{\partial t}&=\frac{1}{2}\sigma ^2\left( x-\frac{t}{T}\right) ^2\frac{\partial ^2u}{\partial x^2}-r\left( x-\frac{t}{T}\right) \frac{\partial u}{\partial x},\quad (x,t)\in (t/T,L) \times (0,T),\\ u(x,T)&=max(1-x,0),\quad x\in [1,L),\\ u\left( \frac{t}{T},t\right)&=\frac{1}{rT}\left( 1-e^{-r(T-t)}\right) , \quad t\in (0,T],\\ u(L,t)&=0,\quad t\in [0,T]. \end{aligned} \end{aligned}$$

(2.10)

After getting the solution u(x, t) of above PDE, spline interpolation is used to find the price of the Asian option. The relation between the price of Asian option $\left( V(S,I,0)\right)$ and the solution of above PDE $\left( u(x,t)\right)$ is written as:

$$\begin{aligned} \hbox {price}=S_{0}u\left( \frac{K}{S_{0}},0\right) , \end{aligned}$$

where $S_{0}$ is the stock price and K is the strike price.

Fig. 1

Grid with moving boundary condition for pricing of arithmetic average Asian option

Compact Finite Difference Scheme

To begin with, we discuss the compact finite difference approximations for first and second derivatives in this section.

Fourth-Order Compact Finite Difference Approximations for First and Second Derivatives

In this section, we derive fourth order accurate second derivative approximation of unknowns with the help of unknowns itself and their first derivative approximation. From Taylor series, second-order accurate central difference approximation for first derivative can be written as follows

$$\begin{aligned} \varDelta _{x}u_{i}=\frac{u_{i+1}-u_{i-1}}{2\delta x}, \end{aligned}$$

(3.1)

and similarly second order accurate central difference approximation for second derivative can be written as

$$\begin{aligned} \varDelta ^2_{x}u_{i}=\frac{u_{i+1}-2u_{i}+u_{i-1}}{\delta x^2}, \end{aligned}$$

(3.2)

where $\delta x$ is the grid size along x-direction and $u_{i}$ is the value of $u(x_{i})$ at a typical grid point $x_{i}$. Now, fourth-order accurate compact finite difference approximation for first derivative [22] (Padé scheme for first derivative) can be written as

$$\begin{aligned} \frac{1}{4}u_{x_{i-1}}+u_{x_{i}}+\frac{1}{4}u_{x_{i+1}}= \frac{1}{\delta x}\left[ -\frac{3}{4}u_{i-1}+\frac{3}{4}u_{i+1}\right] , \end{aligned}$$

(3.3)

where $u_{x_{i}}$ is first derivative approximation of unknown u at grid point $x_{i}$. Similarly, fourth-order accurate compact finite difference approximation for second derivative [22] (Padé scheme for second derivative) can be written as

$$\begin{aligned} \frac{1}{10}u_{xx_{i-1}}+u_{xx_{i}}+\frac{1}{10}u_{xx_{i+1}} = \frac{1}{\delta x^2}\left[ \frac{6}{5}u_{i-1}-\frac{12}{5}u_{i}+\frac{6}{5}u_{i+1}\right] , \end{aligned}$$

(3.4)

where $u_{xx_{i}}$ is second derivative approximation of unknown u at grid point $x_{i}$. If $u_{x_{i}}$ are also considered as a variable then from Eq. (3.3), we obtain

$$\begin{aligned} \frac{1}{4}u_{xx_{i-1}}+u_{xx_{i}}+\frac{1}{4}u_{xx_{i+1}}= \frac{1}{\delta x}\left[ -\frac{3}{4}u_{x_{i-1}}+\frac{3}{4}u_{x_{i+1}}\right] . \end{aligned}$$

(3.5)

Eliminating $u_{xx_{i-1}}$ and $u_{xx_{i+1}}$ from Eqs. (3.4) and (3.5), we obtain second derivative approximation as follows

$$\begin{aligned} u_{xx_{i}}=2\frac{u_{i+1}-2u_{i}+u_{i-1}}{\delta x^2}-\frac{u_{x_{i+1}}-u_{x_{i-1}}}{2\delta x}. \end{aligned}$$

(3.6)

Using Eqs. (3.1) and (3.2) in above Eq. (3.6), we obtain

$$\begin{aligned} u_{xx_{i}}=2\varDelta ^2_{x}u_{i}-\varDelta _{x}u_{x_{i}}. \end{aligned}$$

(3.7)

In Eq. (3.7), $u_{x_{i}}$ is obtained from Eq. (3.3). It is observed that Eqs. (3.3) and (3.7) provides fourth-order accurate compact approximations for first and second derivatives. The elimination of second order derivatives was initially proposed by Adam [23, 24]. In case of non-periodic boundary conditions, additional compact relations are required at the boundary points. For the additional boundary formulations of various orders, one can see [24, 25]. It is shown in Fig. 2 that less number of grid points are required to obtain high-order accuracy as compared to central difference. We compare the proposed compact finite difference approximations with central difference approximations as follows.

Fig. 2

Number of required grid points for various order of accuracy for first derivative approximation using central difference approximation and compact finite difference approximation

Fourier Analysis

Fourier analysis is a classical technique to compare two difference schemes in numerical analysis. Fourier analysis of a finite difference scheme quantifies the resolution characteristics of the difference approximation. By resolution characteristics, we mean that the accuracy with which difference schemes represents the exact value over the full grid. For more details about the Fourier analysis of finite difference approximations, one can see [22].

Fourier analysis for first derivative approximation If we denote the wave number by $\omega$ and modified wave number for first derivative approximation by $\omega '$, then for fourth-order accurate compact finite difference approximation given in Eq. (3.3)

$$\begin{aligned} \omega '=\frac{3\sin (\omega )}{2+\cos (\omega )}. \end{aligned}$$

(3.8)

For second-order accurate central finite difference approximation

$$\begin{aligned} \omega '=\sin (\omega ), \end{aligned}$$

(3.9)

and for fourth-order accurate central finite difference approximation

$$\begin{aligned} \omega '=\frac{-\sin \left( 2\omega \right) }{6}+\frac{4\sin (\omega )}{3}. \end{aligned}$$

(3.10)

In Fig. 3a modified wave numbers are plotted with respect to the wave numbers for exact differentiation ($\omega '=\omega$), fourth-order accurate compact finite difference approximation (Eq. (3.8)), second-order accurate classical finite difference approximation (Eq. (3.9)) and fourth-order accurate classical finite difference approximation (Eq. (3.10)). It can be seen from Fig. 3a that fourth-order accurate compact finite difference approximation has better resolution characteristics as compared to the classical finite difference approximations.

Fourier analysis for second derivative approximation If we denote modified wave number for second derivative approximation by $\omega ''$, then for fourth-order accurate compact finite difference approximation given in Eq. (3.7)

$$\begin{aligned} \omega ''=\frac{5-4\cos (\omega )-\cos ^{2}(\omega )}{2+\cos (\omega )}. \end{aligned}$$

(3.11)

For fourth-order accurate compact finite difference Padé approximation given in Eq. (3.4)

$$\begin{aligned} \omega ''=\frac{12(1-\cos (\omega ))}{2+\cos (\omega )}. \end{aligned}$$

(3.12)

For second-order accurate central finite difference approximation

$$\begin{aligned} \omega ''=2-2\cos (\omega ), \end{aligned}$$

(3.13)

and for fourth-order accurate central finite difference approximation

$$\begin{aligned} \omega ''=\frac{\cos (2\omega )}{6}-\frac{8\cos (\omega )}{3}+\frac{5}{2}. \end{aligned}$$

(3.14)

In Fig. 3b modified wave numbers are plotted with respect to the wave numbers for exact differentiation ($\omega ''=\omega ^{2}$), compact finite difference approximation for second derivative (Eq. (3.12)), classical finite difference second-order approximation (Eq. (3.13)) and classical finite difference fourth-order approximation (Eq. (3.14)). It can be seen from Fig. 3b that compact finite difference approximation has better resolution characteristics as compared to the classical finite difference approximation.

Fig. 3

Modified wave number and wave number for various finite difference schemes: a first derivative approximation, b second derivative approximation

Fully Discrete Problem

Asian option PDE  (2.9) can be written as a one-dimensional linear convection–diffusion equation of the form

$$\begin{aligned} \frac{\partial u}{\partial t}=p(x,t)\frac{\partial u}{\partial x}+q(x,t)\frac{\partial ^2 u}{\partial x^2}, \end{aligned}$$

(3.15)

with the given initial and boundary conditions, where $p(x,t)=r(x-\frac{t}{T})$ and $q(x,t)=\frac{1}{2}\sigma ^2(x-\frac{t}{T})^2$. Now we discretize the Eq. (3.15) in finite domain $(x,t) \in (\varOmega \times (0,T])$. We use $\theta$ method for temporal semi-discretization, $0 \le \theta \le 1$, ($\theta =0$ for forward Euler, $\theta =1$ for backward Euler, and $\theta =1/2$ for Crank–Nicolson scheme) and compact finite difference approximations discussed above for spatial discretization of the PDE (3.15). If $U^{m}_{n}$ represents the approximation of the solution of Eq. (3.15) at $(x_{n},t_{m})$ then Eq. (3.15) can be written in discrete form as follows

$$\begin{aligned} \frac{U^{m+1}_{n}-U^{m}_{n}}{\delta t}=\left[ (1-\theta )q_{n}^{m}U_{xx_{n}}^{m}+\theta q_{n}^{m+1}U_{xx_{n}}^{m+1}\right] +\left[ (1-\theta ) p_{n}^{m}U_{x_{n}}^{m}+\theta p_{n}^{m+1}U_{x_{n}}^{m+1}\right] .\nonumber \\ \end{aligned}$$

(3.16)

Using the second derivative approximation given in Eq. (3.7) in above equation

$$\begin{aligned} \frac{U^{m+1}_{n}-U^{m}_{n}}{\delta t}= & {} \left[ (1-\theta )q_{n}^{m}\left( 2 \varDelta _{x}^2 U_{n}^{m}-\varDelta _{x}U_{x_{n}}^{m}\right) +\theta q_{n}^{m+1}\left( 2 \varDelta _{x}^2 U_{n}^{m+1}-\varDelta _{x}U_{x_{n}}^{m+1}\right) \right] \nonumber \\&+\left[ (1-\theta ) p_{n}^{m}U_{x_{n}}^{m}+\theta p_{n}^{m+1}U_{x_{n}}^{m+1}\right] , \end{aligned}$$

(3.17)

where $1 \le n \le N$, $1 \le m \le M$ and N, M are the number of grid points in space and time direction respectively. By rearranging the terms, we get

$$\begin{aligned}{}[1-2\theta q_{n}^{m+1} \delta t \varDelta _{x}^2]U^{m+1}_{n}= & {} [1+2q_{n}^{m}(1-\theta )\delta t \varDelta _{x}^2]U^{m}_{n}+\theta \delta t[p_{n}^{m+1}-q_{n}^{m+1}\varDelta _{x}]U_{x_{n}}^{m+1}\nonumber \\&+\,(1-\theta )\delta t[p_{n}^{m}-q_{n}^{m}\varDelta _{x}]U_{x_{n}}^{m}. \end{aligned}$$

(3.18)

The above scheme is fourth order accurate in spatial variable and second order accurate (for $\theta =0.5$) in temporal variable. It is observed that proposed compact finite difference scheme requires only three grid points to achieve fourth order accuracy in spatial variable. Proposed compact finite difference scheme is implicit in nature and it will be proved in following section that proposed scheme is unconditionally stable for $0.5 \le \theta \le 1$.

Stability Analysis

Stability analysis is very crucial aspect for the solution of time dependent problems using numerical algorithms. Since the coefficients of the Eq. (2.9) are polynomial in x and t, they will always be bounded in max norm for a discrete problem. Hence, principle of frozen coefficients can be used in order to prove the stability for variable coefficient PDE (3.15). Stability analysis using classical central difference scheme for constant coefficient problems is discussed in [26] and for variable coefficient problems by using the principle of frozen coefficients in [27]. We carry out von-Neumann stability analysis for the difference scheme (3.18) as follows.

Theorem 1

(Stability) The difference scheme (3.18) is unconditionally stable for $0.5 \le \theta \le 1.$

Proof

Let $U_{n}^{m}=b^{m}e^{im\omega }$ where $\omega =2 \pi \delta x/\lambda$ is the phase angle with wavelength $\lambda$ and $b^{m}$ is the amplitude at time level m then from Eqs. (3.9), (3.13) and (3.8) we can write

$$\begin{aligned} \varDelta _{x}U_{n}^{m}= & {} i \frac{\sin (\omega )}{\delta x}U^{m}_{n}, \end{aligned}$$

(3.19)

$$\begin{aligned} \varDelta _{x}^{2}U_{n}^{m}= & {} \frac{2\cos (\omega )-2}{\delta x^2}U^{m}_{n}, \end{aligned}$$

(3.20)

$$\begin{aligned} U_{x_{n}}^{m}= & {} i \frac{3\sin (\omega )}{\delta x(2+\cos (\omega ))}U^{m}_{n}, \end{aligned}$$

(3.21)

where $i=\sqrt{-1}$. Using relation (3.19)–(3.21) in the difference scheme (3.18), we get

$$\begin{aligned} \left[ 1-4q\theta \delta t \left( \frac{\cos (\omega )-1}{\delta x^2}\right) \right] u^{m+1}_{n}= & {} \left[ 1+4q(1-\theta ) \delta t \left( \frac{\cos (\omega )-1}{\delta x^2}\right) \right] u^{m}_{n}\nonumber \\&+\,\theta \delta t\left[ \left( q\frac{\sin (\omega )}{\delta x}+ip\right) \frac{3\sin (\omega )}{\delta x(2+\cos (\omega ))}\right] u_{n}^{m+1}\nonumber \\&+\,(1-\theta ) \delta t\left[ \left( q\frac{\sin (\omega )}{\delta x}+ip\right) \frac{3\sin (\omega )}{\delta x(2+\cos (\omega ))}\right] u_{n}^{m}.\nonumber \\ \end{aligned}$$

(3.22)

Then amplification factor $A_{F}$ can be written as

$$\begin{aligned} A_{F}=\frac{1+(1-\theta ) \delta t \left[ \left( q\frac{\cos ^{2}(\omega )+4\cos (\omega )-5}{\delta x^2(2+\cos (\omega ))}\right) +i\left( p\frac{3\sin (\omega )}{\delta x(2+\cos (\omega ))}\right) \right] }{1-\theta \delta t \left[ \left( q\frac{\cos ^{2}(\omega )+4\cos (\omega )-5}{\delta x^2(2+\cos (\omega ))}\right) +i\left( p\frac{3\sin (\omega )}{\delta x(2+\cos (\omega ))}\right) \right] }. \end{aligned}$$

(3.23)

If

$$\begin{aligned} P= & {} \delta t\left( q\frac{\cos ^{2}(\omega )+4\cos (\omega )-5}{\delta x^2(2+\cos (\omega ))}\right) , \\ Q= & {} \delta t\left( p\frac{3\sin (\omega )}{\delta x(2+\cos (\omega ))}\right) , \end{aligned}$$

then

$$\begin{aligned} A_{F}=\frac{1+(1-\theta ) (P+iQ)}{1-\theta (P+iQ)}. \end{aligned}$$

(3.24)

This implies

$$\begin{aligned} |A_{F}|^2=\frac{(1+P-\theta P)^2+(1-\theta )^2Q^2}{(1-\theta P)^2+\theta ^2Q^2}. \end{aligned}$$

(3.25)

$|A_{F}| \le 1$ is required for stability condition, hence

$$\begin{aligned} (P^2+Q^2)(1-2\theta )+2P \le 0. \end{aligned}$$

(3.26)

It is observed that $P \le 0$ because

$$\begin{aligned} \left( \frac{\cos ^{2}(\omega )+4\cos (\omega )-5}{\delta x^2(2+\cos (\omega ))}\right) \le 0 \quad \forall \ \omega \in [0,2\pi ]. \end{aligned}$$

Inequality (3.26) is satisfied if

$$\begin{aligned} (1-2 \theta ) \le 0 \Rightarrow \theta \ge 0.5. \end{aligned}$$

Hence difference scheme (3.18) is unconditionally stable in the sense of von-Neumann for $0.5 \le \theta \le 1$.

Solution to Algebraic System

Solution of algebraic system associated with the difference scheme (3.18) is discussed in this section. If we denote

$$\begin{aligned} \mathbf U ^{m}=(U_{1}^{m},U_{2}^{m},\ldots ,U_{N}^{m})^T \quad \hbox {and} \quad \mathbf U _{x}^{m}=(U_{x_{1}}^{m},U_{x_{2}}^{m},\ldots ,U_{x_{N}}^{m})^T, \end{aligned}$$

then system of equations corresponding to the difference scheme (3.18) can be written in matrix form as follows

$$\begin{aligned} A\mathbf U ^{m+1}=F(\mathbf U ^{m},\mathbf U _{x}^{m},\mathbf U _{x}^{m+1}). \end{aligned}$$

(3.27)

The matrix A is a diagonally dominant, tri-diagonal matrix which leads to an efficient solution of system of equations. The value of $\mathbf U _{x}^{m}$ can be obtained by solving a tri-diagonal system of equations from Eq. (3.3). The main problem is due to the presence of $\mathbf U _{x}^{m+1}$ on the right hand side of the Eq. (3.27). For this reason, we use correcting to convergence approach [28] which is summarized in the following algorithm.

Algorithm for Correcting to Convergence Approach

• 1. Start with $\mathbf U ^{m}$.

• 2. Obtain $\mathbf U _{x}^{m}$ using Eq. (3.3).

• 3. Take $\mathbf U ^{m+1}_{old}=\mathbf U ^{m}$, $\mathbf U _{x_{old}}^{m+1}=\mathbf U _{x}^{m}$.

• 4. Correct to $\mathbf U ^{m+1}_{new}$ using Eq. (3.27).

• 5. If $\Vert \mathbf U ^{m+1}_{new}-\mathbf U ^{m+1}_{old}\Vert$ < tolerance, then $\mathbf U ^{m+1}_{new}=\mathbf U ^{m+1}_{old}$.

• 6. Obtain $\mathbf U _{x_{new}}^{m+1}$ using Eq. (3.3).

• 7. $\mathbf U ^{m+1}_{old}=\mathbf U ^{m+1}_{new}$, $\mathbf U ^{m+1}_{x_{old}}=\mathbf U ^{m+1}_{x_{new}}$ and go to step 4. Stopping criterion for inner iteration is taken $tolerance=10^{-12}$ in above approach.

Numerical Results

Two numerical examples are given in this section in order to show the accuracy and efficiency of the proposed compact finite difference scheme. For temporal semi-discretization, $\theta =0.5$ is used for both the examples.

Example 1

Linear convection–diffusion equation.

Table 1 Error in discrete $\ell _2$ norm and rate of convergence in temporal variable for Example 1 when $\delta x=\frac{1}{64}$

Table 2 Error in discrete $\ell _2$ norm and rate of convergence in spatial variable for Example 1 when $\delta t = \delta x^2$

Our goal for this example is to show that the proposed compact finite difference scheme is second order accurate in temporal variable and fourth order accurate in spatial variable. We consider the following convection–diffusion equation:

$$\begin{aligned} \frac{\partial u}{\partial t}= & {} \frac{1}{2}\frac{\partial u}{\partial x}+\frac{1}{2}\frac{\partial ^2 u}{\partial x^2}, \quad x \in (0,1),\ t \in (0,1],\nonumber \\ u(x,0)= & {} e^{x},\quad x \in (0,1),\nonumber \\ u(0,t)= & {} e^{t},\quad u(1,t)=e^{1+t},\ t \in (0,1]. \end{aligned}$$

(4.1)

Exact solution for the above Eq. (4.1) is given as $u(x,t)=e^{x+t}$. Let $e(\delta x)$ denotes the discrete $\ell _{2}$ norm error between the numerical solution and the exact solution at final time with respect to grid size $\delta x$, then rate of convergence $\eta$ can be written

$$\begin{aligned} \eta =\log _{2}\left[ \frac{e(\delta x)}{e(\delta x/2)}\right] . \end{aligned}$$

(4.2)

For a vector $z=(z_{1}, z_{2},\ldots , z_{s})^T$, discrete $\ell _2$ norm is given as

$$\begin{aligned} |z|_{\ell _2}=\left[ \delta x \sum _{i=1}^{s}|z_{i}|^2\right] ^{1/2}. \end{aligned}$$

In Table 1, error between the exact and numerical solution in discrete $\ell _2$ norm is given at $T=1$ for fixed grid size $\delta x=\frac{1}{64}$. It is evident from the table that when $\delta t$ is reduced to half of its value, error is reduced by a factor of $\frac{1}{4}$. In this way it is proved that proposed compact finite difference scheme is second order accurate in temporal variable.

Fig. 4

Efficiency: CPU time and discrete $\ell _{2}$ error using central difference schemes and proposed compact finite difference scheme for Example 1

Table 3 Comparison of price of arithmetic average Asian call option by various methods for different volatilities and interest rates for $S=100$ and $T=1$

Table 2 shows the error between the exact and numerical solution in discrete $\ell _2$ norm for $\delta t =\delta x^2$. Error in discrete $\ell _2$ norm between exact and numerical solution is computed for various grid size $(\delta x)$ values and it is observed that when $\delta x$ is reduced to half of its value, error is reduced by a factor of $\frac{1}{16}$. This proves that proposed compact finite difference scheme is fourth order accurate in spatial variable.

Efficiency of proposed compact finite difference scheme for Example 1 Efficiency of the proposed schemes, i.e. the computation time to obtain a given accuracy, is an important point in our comparison with finite difference schemes. This is machine as well as programming dependent. All the computations are done using MATLAB on a computer with Intel core i7 CPU@ 3.10 GHz. In order to compare the efficiency of the proposed scheme, we compute the error between the exact and numerical solution in discrete $\ell _{2}$ norm for $N=50,70,90,110,130$ and CPU time using central difference scheme and proposed compact finite difference scheme. In Fig. 4, error and CPU time is presented and it is shown in the figure that for a given accuracy, proposed compact finite difference scheme is significantly efficient as compared to the central difference scheme.

Example 2

Asian option.

Numerical results for fixed strike arithmetic average Asian call options are given in this example. We chose number of intervals J for $x > 1$ such that result should be independent of J. It is given in [5] that $J=N/2$ is sufficient to guarantee that price of Asian option will not depend on value of $x_{max}$. We also compute Greeks using the proposed compact finite difference scheme for Asian options. For e.g. Delta values ($\varDelta ^{num}$) at $t=0$ for Asian options can be calculated by

$$\begin{aligned} Delta(\varDelta ^{num})=u\left( \frac{K}{S_{0}},0\right) -\frac{K}{S_{0}}\frac{\partial u}{\partial x}\left( \frac{K}{S_{0}},0 \right) . \end{aligned}$$

(4.3)

We apply the proposed compact finite difference scheme to the Asian option PDE with the parameters, $S_{0}=100$, $T=1$ for various values of volatility $(\sigma )$, interest rates (r) and strike prices (K). Results obtained from these parameters for Asian option PDE are given in Table 3 and compared with the results given in [29, 30]. Lower and upper bounds for different Asian options are taken from [7]. Price of Asian option using the proposed compact scheme is obtained with $N=512$ in all cases. It is observed from the Table 3 that results obtained from proposed compact finite difference scheme are in a good agreement with the existing literature. In Fig. 5, price of arithmetic average Asian call option with the parameters $S_{0}=100$, $T=1$ and various values of r and $\sigma$ versus strike price is plotted.

Now, proposed compact finite difference scheme is applied to the Asian option PDE for small and large volatilities at different strike prices (K) with the parameters, $S_{0}=100$, $T=1$, $r=0.09$. The values of Asian option and their comparison with the results in [29,30,31] are given in Table 4. From the Table 4, it is observed that proposed compact finite difference scheme is accurate for small and large both type of volatilities. Figure 6 shows the price of arithmetic average Asian call option versus strike price for different values of $\sigma$ and $S_{0}=100$, $T=1$, $r=0.09$.

In Table 5, price of Asian option obtained from proposed compact finite difference scheme for large maturity time $(T=3)$ at different strike prices (K) and volatilities with the parameters, $S_{0}=100$, $T=1$, $r=0.09$ are given. The values of Asian option are compared with the results in [9, 29, 32, 33]. From the Table 5, it is observed that proposed compact finite difference scheme is accurate for large maturity time also.

Fig. 5

Price of arithmetic average Asian call option with the parameters $S_{0}=100$, $T=1$ and various values of r and $\sigma$ versus strike price: a$\sigma =0.1$, b$\sigma =0.2$, c$\sigma =0.3$

Table 4 Comparison of price of arithmetic average Asian call option by various methods for different volatilities for $S_{0}=100$, $r=0.09$ and $T=1$

Fig. 6

Price of arithmetic average Asian call option with the parameters $S_{0}=100$, $T=1$, $r=0.09$ and various values $\sigma$ versus strike price

Table 5 Comparison of price of arithmetic average Asian call option by various methods for different volatilities for $S_{0}=100$, $r=0.09$ and $T=3$

Table 6 Comparison of value of Delta ($\varDelta ^{num}$) for $S_{0}=100$, $r=0.05$, $K=100$ and $T=1$. Delta value for finite difference (FD estimate), finite difference with control variate (FD with CV), path-wise derivatives (PW estimate), path-wise derivatives with control variate (PW with CV) are taken from [34]

Fig. 7

Efficiency: CPU time to obtain a given accuracy and discrete $\ell _{2}$ error using central difference schemes and proposed compact finite difference scheme for Asian option PDE

The relation between the option prices and the Delta values is given in Eq. (4.3). In Table 6, Delta $(\varDelta ^{num})$ values for Asian option obtained from proposed compact finite difference scheme for the parameters, $S_{0}=100$, $K=100$, $T=1$, $r=0.05$ are given. Results obtained from proposed compact finite difference scheme are compared with [34] and it is observed that proposed compact finite difference scheme is accurate for the computation of hedging parameters (Delta) also.

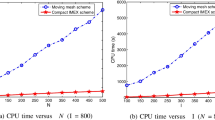
Efficiency of proposed compact finite difference scheme for Asian option PDE We discuss the CPU time taken to obtain a given accuracy and discrete $\ell ^2$ norm error using central difference scheme and proposed compact finite difference scheme for Asian option PDE. In Fig. 7, $\ell _{2}$ error represents the error between the numerical solution and reference solution for $K=100$, $S_{0}=100$, $\sigma =0.05$, $r=0.15$ and $T=1$ in discrete $\ell _{2}$ norm. Reference solution is computed for same parameters with $N=2048$. We compute the error and corresponding CPU time at grid points N=10, 20, 30, 40, 50 using central difference scheme and proposed compact finite difference scheme. Since the convection and diffusion coefficients of the Asian option PDE (2.9) are variables in x and t and grid is changing at each time step, matrices and their inverses are computed at each time step. It is shown in Fig. 7 that for a given accuracy, proposed compact finite difference scheme is significantly efficient as compared to the central difference scheme.

Conclusion and Future Work

An unconditionally stable compact finite difference scheme is proposed to solve the linear convection–diffusion equation. In the proposed scheme, second derivative approximations of the unknowns are eliminated with the unknowns itself and their first derivative approximations while retaining the tri-diagonal nature of the scheme. Fourier analysis of the difference schemes is presented and it is concluded that proposed compact finite difference approximations have better resolution characteristics as compared to classical finite difference schemes. It is also proved that proposed compact finite difference scheme is unconditionally stable. Proposed compact finite difference scheme is applied to Asian option PDE and a diagonally dominant system of linear equations is obtained which can be solved using Thomas algorithm efficiently. Efficiency of the proposed compact finite difference scheme is compared to the central difference scheme by calculating the CPU time for a given accuracy and it is observed that proposed compact finite difference scheme is significantly efficient than central difference scheme. Since the proposed compact finite difference scheme is easily extendable for the two dimensional problems in a similar manner, we would like to extend the proposed compact finite difference scheme for two dimensional problems.