Second-order IMEX scheme for a system of partial integro-differential equations from Asian option pricing under regime-switching jump-diffusion models

Abstract

This paper studies an implicit-explicit (IMEX) finite difference scheme for solving a system of moving boundary partial integro-differential equations (PIDEs) which arises in Asian option pricing under regime-switching jump-diffusion models. First, the moving boundary PIDEs are recast into a fixed boundary problem of the PIDEs. Then the IMEX scheme is proposed to solve the problem and the second-order convergence rates are proved. Numerical examples are carried out to validate the theoretical results.

1 Introduction

Denote a complete probability space with risk-neutral measure by $({\Omega },\mathcal {F},\mathbb {P})$ and assume that the price of the underlying asset S_t follows the state-dependent regime-switching jump-diffusion model under risk-neutral measure

$$ \begin{array}{@{}rcl@{}} \frac{dS_{t}}{S_{t}}&=&\left[r\left( \chi(t)\right) - \delta\left( \chi(t)\right)-\lambda\left( \chi(t)\right)\alpha\left( \chi(t)\right)\right]dt+\sigma\left( \chi(t)\right) dW_{t}\\&&+\left[\eta\left( \chi(t)\right)-1\right]d\aleph_{t}, \end{array} $$

(1)

where W_t is a standard Brownian motion under the risk-neutral measure $\mathbb {P}$, χ(t) is a continuous-time finite-state Markov chain with state space {c₁,c₂,…,c_d}. Assume that at each state $\chi (t)=c_{k}, k\in \mathbb {D}\equiv \{1,2,\ldots ,d\}$, the interest rates $r\left (c_{k}\right )=r_{k}$, dividend yields $\delta \left (c_{k}\right )=\delta _{k}$ and volatilities $\sigma \left (c_{k}\right )=\sigma _{k}$ are nonnegative constants. ℵ_t denotes a Poisson jump process with the intensity $\lambda \left (c_{k}\right )=\lambda _{k}\geq 0$, the amplitude $\eta \left (c_{k}\right )-1=\eta _{k}-1$, and the expectation of the random amplitude $\alpha \left (c_{k}\right )=\alpha _{k}=E\left (\eta _{k}-1\right )$, where $\eta _{k}=e^{Y\left (c_{k}\right )}=e^{Y_{k}}$, and the jump sizes Y_k for $k\in \mathbb {D}$ are independent random variables with density functions

$$ \begin{array}{@{}rcl@{}} f_{k}(y)=\frac{1}{{{\varrho}}_{k}\sqrt{2\pi}}\exp\left[-\frac{(y-\mu_{k})^{2}}{2{{{\varrho}}_{k}^{2}}}\right], \end{array} $$

(2)

where ϱ_k > 0 and μ_k ≥ 0 are the constants depending solely on the regime state c_k for $k\in \mathbb {D}$. Let $\mathbf {A}=\left (a_{k\ell }\right )_{k,\ell \in \mathbb {D}}$ be the generator matrix of the Markov chain process whose elements are constants satisfying a_kℓ ≥ 0 for k≠ℓ and $k,\ell \in \mathbb {D}$, and ${\sum }_{\ell =1}^{d}a_{k\ell }=0$ for $k\in \mathbb {D}$. Finally, all sources of randomness in this model, χ(t), W_t and ℵ_t are assumed to be conditionally independent.

This paper studies the numerical method for pricing Asian options. For Asian option pricing using PDE approach, it is studied under the geometric Brownian motion models (see, e.g., Zvan et al. [20], Večeř [17], Dubois and Lelièvre [4], Ma and Zhou [11], Roul [2], and the references therein), and under the regime-switching models (Boyle and Draviam [1], Ma and Zhou [12]). However, such problem under the regime-switching jump-diffusion models remains to be insufficient in the literature and the governing equation is a system of two-dimensional PIDEs. Dang et al. [5] decouple the PIDE system and solve the decoupled PIDEs by the numerical methods — finite difference methods for time variable and finite element methods for space variable. However, the convergence rates are not given in their paper. Ma and Wang [13] transform the two-dimensional PIDEs into a one-dimensional moving boundary problem of the PIDEs, then construct the moving mesh methods for solving the problem. Denote

$$ \begin{array}{@{}rcl@{}} M_{t}={{\int}_{0}^{t}}S_{l}dl. \end{array} $$

(3)

Then the value of the continuous arithmetic average Asian options is defined by

$$ \begin{array}{@{}rcl@{}} V\left( S_{t},M_{t},t;k\right)=e^{-r_{k}(T-t)}\mathbb{E}_{t}\left[\max\left( M_{T}/T-K,0\right)\right], \quad k\in\mathbb{D}, \end{array} $$

(4)

where $\mathbb {E}_{t}$ represents the conditional expectation at t, K the fixed strike price and T the maturity date. Then the value function of the Asian option satisfies the following system of PIDEs

$$ \begin{array}{@{}rcl@{}} && \frac{\partial V(S,M,t;k)}{\partial t}+\frac{{\sigma^{2}_{k}}S^{2}}{2}\frac{\partial^{2}V(S,M,t;k)}{\partial S^{2}}+\left( r_{k}-\delta_{k}-\lambda_{k}\alpha_{k}\right)S\frac{\partial V(S,M,t;k)}{\partial S} \\ &&+S\frac{\partial V(S,M,t;k)}{\partial M}-(r_{k}+\lambda_{k}-a_{kk})V(S,M,t;k)+\lambda_{k}{\int}_{-\infty}^{+\infty}V(e^{y}S,M,t;k)f_{k}(y)dy \\ && +\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}V(S,M,t;\ell)=0, \quad k\in\mathbb{D}, \end{array} $$

(5)

with terminal condition $V(S,M,T;k)=\max \limits \left (M/T-K,0\right )$ and boundary condition $V(S,-\infty ,t;k)=0$ for $k\in \mathbb {D}$, where S and M are dummy variables. As asserted by [11,12,13], each equation in (5) is a two-dimensional problem and there is no diffusion in the M direction. These facts would arise many difficulties in the numerical solutions and analysis with the standard finite difference methods.

Motivated by the works (see Zvan et al. [20], Večeř [17], Dubois and Lelièvre [4]), Ma and Wang [13] recast the system of PIDEs (5) into a moving boundary problem of one-dimensional PIDEs. First, they construct an explicit solution to (5) in the region M ≥ KT for all t ≤ T as follows

$$ \begin{array}{@{}rcl@{}} V(S,M,t;k) = \left( \frac{M}{T} - K\right)e^{-r_{k}(T-t)} + \frac{S}{(\delta_{k}-r_{k})T}\left( e^{-r_{k}(T-t)} - e^{-\delta_{k}(T-t)}\right), k\in\mathbb{D}.\!\!\!\!\!\!\\ \end{array} $$

(6)

Then using transformation of variables, for $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} x=\frac{T-\tau}{T}+\frac{K-M/T}{S}, \quad G(x,\tau;k)=\frac{V(S,M,T-\tau;k)}{S}, \quad \tau=T-t, \end{array} $$

(7)

the formula (6) becomes

$$ \begin{array}{@{}rcl@{}} G(x,\tau;k)&=&-\left( x-\frac{T-\tau}{T}\right)e^{-r_{k}\tau} \\ &&+ \frac{1}{(\delta_{k}-r_{k})T}\left( e^{-r_{k}\tau}-e^{-\delta_{k}\tau}\right), \quad x\in\left( -\infty,\frac{T-\tau}{T}\right], \end{array} $$

(8)

and the system of PIDEs (5) is rewritten as, for $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} && \frac{\partial G(x,\tau;k)}{\partial \tau}-\frac{1}{2}{\sigma^{2}_{k}}\left( x-\frac{T-\tau}{T}\right)^{2}\frac{\partial^{2}G(x,\tau;k)}{\partial x^{2}}\\ &&+(r_{k}-\delta_{k}-\lambda_{k}\alpha_{k})\left( x-\frac{T-\tau}{T}\right)\frac{\partial G(x,\tau;k)}{\partial x} \\ &&+(\lambda_{k}+\delta_{k}+\lambda_{k}\alpha_{k}-a_{kk})G(x,\tau;k)-\lambda_{k}{\int}_{-\infty}^{+\infty}e^{y}G\left( \frac{x-\frac{T-\tau}{T}}{e^{y}}+\frac{T-\tau}{T},\tau;k\right)f_{k}(y)dy \\ &&-\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}G(x,\tau;\ell)=0, \quad x\in\left( \frac{T-\tau}{T},+\infty\right), \quad \tau\in(0,T], \end{array} $$

(9)

with initial and boundary conditions

$$ \begin{array}{@{}rcl@{}} && G(x,0;k)=0, \quad x\in[1,+\infty), \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} &&G\left( \frac{T-\tau}{T},\tau;k\right)=\frac{1}{(\delta_{k}-r_{k})T}\left( e^{-r_{k}\tau}-e^{-\delta_{k}\tau}\right), \quad \tau\in(0,T], \end{array} $$

(11)

$$ \begin{array}{@{}rcl@{}} &&G(+\infty,\tau;k)=0, \quad \tau\in(0,T]. \end{array} $$

(12)

Since the problems (9)–(12) contain a moving boundary, then Ma and Wang [13] develop the moving mesh methods for solving the problems and the convergence rates of first-order in time and second-order in space are also proved by them. For solving PIDEs, the implicit-explicit (IMEX) finite difference schemes are efficient tools which discretize the integral term of the PIDEs explicitly, treat other terms implicitly and therefore can avoid the inversion of the dense matrices in the computation. The IMEX schemes are proposed to solve the PIDEs arising in the pricing of European and American options under jump-diffusion models (see, e.g., [3, 6,7,8,9,10, 15, 16, 18, 19]). To the best of my knowledge, this paper is the first time in the literature to study the IMEX scheme for Asian option pricing. Moreover, the convergence analysis of the studied IMEX scheme is significantly different from the literature and also different from the moving mesh methods.

The remaining of the paper is organized as follows: In Section 2, we construct an IMEX scheme for solving the system of PIDEs arising in the regime-switching jump-diffusion Asian option pricing and prove the convergence rates; In Section 3, we provide numerical examples to confirm the theoretical results. In the final section, we conclude the paper.

2 IMEX scheme and convergence rates

For aim of computation, the semi-infinite domain $\left [\frac {T-\tau }{T},+\infty \right )$ is truncated into a finite one ${\Omega }_{\tau }\equiv \left [\frac {T-\tau }{T},X\right ]$ with an appropriate value of X such that G(X,τ;k) ≈ 0.

Since x ∈Ω_τ, we normalize the variable x as $\theta =\frac {x-\frac {T-\tau }{T}}{X-\frac {T-\tau }{T}}$ which implies that 𝜃 ∈ [0,1] for any τ ∈ (0,T]. Denote $u(\theta ,\tau ;k)\equiv G\left (\frac {T-\tau }{T}+\theta \left (X-\frac {T-\tau }{T}\right ),\tau ;k\right )$, then it is easy to derive that

$$ \begin{array}{@{}rcl@{}} \frac{\partial G(x,\tau;k)}{\partial\tau}&=&\frac{\partial u(\theta,\tau;k)}{\partial\tau}+\frac{1-\theta}{T}\frac{\partial G(x,\tau;k)}{\partial x}, \end{array} $$

(13)

$$ \begin{array}{@{}rcl@{}} \frac{\partial G(x,\tau;k)}{\partial x}&=&\frac{1}{X-\frac{T-\tau}{T}}\frac{\partial u(\theta,\tau;k)}{\partial\theta}, \end{array} $$

(14)

$$ \begin{array}{@{}rcl@{}} \frac{\partial^{2} G(x,\tau;k)}{\partial x^{2}}&=&\frac{1}{\left( X-\frac{T-\tau}{T}\right)^{2}}\frac{\partial^{2} u(\theta,\tau;k)}{\partial\theta^{2}}. \end{array} $$

(15)

Plugging the above identities into (9), we obtain that, for $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} \frac{\partial u(\theta,\tau;k)}{\partial \tau}&=&\phi(\theta,\tau;k)\frac{\partial^{2} u(\theta,\tau;k)}{\partial \theta^{2}}+\psi(\theta,\tau;k)\frac{\partial u(\theta,\tau;k)}{\partial \theta} \\ &&- (\lambda_{k}+\delta_{k}+\lambda_{k}\alpha_{k}-a_{kk})u(\theta,\tau;k)\\&&+\lambda_{k}{\int}_{-\infty}^{+\infty}e^{y}u\left( \frac{\theta}{e^{y}},\tau;k\right)f_{k}(y)dy \\ &&+ \sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}u(\theta,\tau;\ell), \quad \theta\in(0,1), \quad \tau\in(0,T], \end{array} $$

(16)

with initial and boundary conditions

$$ \begin{array}{@{}rcl@{}} u(\theta,0;k)&=&0, \quad \theta\in[0,1], \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} u\left( 0,\tau;k\right)&=&\frac{1}{(\delta_{k}-r_{k})T}\left( e^{-r_{k}\tau}-e^{-\delta_{k}\tau}\right), \quad \tau\in(0,T], \end{array} $$

(18)

$$ \begin{array}{@{}rcl@{}} u(1,\tau;k)&=&0, \quad \tau\in(0,T].\end{array} $$

(19)

where

$$ \begin{array}{@{}rcl@{}} \begin{cases}\phi(\theta,\tau;k)=\frac{1}{2}{\sigma^{2}_{k}}\theta^{2},\\ \psi(\theta,\tau;k)=\frac{\theta-1}{T}\frac{1}{X-\frac{T-\tau}{T}}-(r_{k}-\delta_{k}-\lambda_{k}\alpha_{k})\theta. \end{cases} \end{array} $$

We below study the IMEX scheme to solve the system of PIDEs (16) and define the uniform spatial and time meshes as follows:

$$ \begin{array}{@{}rcl@{}} \theta_{i}=i{\Delta} \theta,& i=0,1,\ldots,I; \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} \tau_{n}=n{\Delta} \tau,& n=0,1,\ldots,N, \end{array} $$

(21)

where I and N are the number of meshes in the 𝜃 and τ directions, and ${\Delta } \theta =\frac {1}{I}$ and ${\Delta } \tau =\frac {T}{N}$ are the meshsizes.

Denote $\xi =\frac {\theta _{i}}{e^{y}}$, then the integral term in (16) can be discretized at mesh point (𝜃_i,τ_n;k) as follows, for $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} &&{\int}_{-\infty}^{+\infty}e^{y}u\left( \frac{\theta_{i}}{e^{y}},\tau_{n};k\right)f_{k}(y)dy \\ &&={\int}_{\ln\theta_{i}}^{+\infty}e^{y}u\left( \frac{\theta_{i}}{e^{y}},\tau_{n};k\right)f_{k}(y)dy+{\int}_{-\infty}^{\ln\theta_{i}}e^{y}u\left( \frac{\theta_{i}}{e^{y}},\tau_{n};k\right)f_{k}(y)dy \\ &&={\int}_{\ln\theta_{i}}^{+\infty}e^{y}u\left( \frac{\theta_{i}}{e^{y}},\tau_{n};k\right)f_{k}(y)dy \\ &&={{\int}_{0}^{1}}\frac{\theta_{i}}{\xi^{2}}u(\xi,\tau_{n};k)f_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)d\xi \\ &&\approx\sum\limits_{j=1}^{I}{\int}_{\theta_{j-1}}^{\theta_{j}}\left[\frac{\theta_{i}}{\xi^{2}}\frac{\xi-\theta_{j}}{\theta_{j-1}-\theta_{j}}u(\theta_{j-1},\tau_{n};k)f_{k}\left( \ln\frac{\theta_{i}}{\xi}\right) \right.\\ &&\left.\quad+ \frac{\theta_{i}}{\xi^{2}}\frac{\xi-\theta_{j-1}}{\theta_{j}-\theta_{j-1}}u(\theta_{j},\tau_{n};k)f_{k}\left( \ln\frac{\theta_{i}}{\xi}\right) \right]d\xi\equiv\mathcal{I}u(\theta_{i},\tau_{n};k). \end{array} $$

(22)

where we have used the piecewise linear interpolation for function u:

$$ \begin{array}{@{}rcl@{}} u(\xi,\tau_{n};k)\approx\frac{\xi-\theta_{j}}{\theta_{j-1}-\theta_{j}}u(\theta_{j-1},\tau_{n};k)+\frac{\xi-\theta_{j-1}}{\theta_{j}-\theta_{j-1}}u(\theta_{j},\tau_{n};k), \theta_{j-1}\leq\xi\leq\theta_{j}.\\ \end{array} $$

(23)

It is easy to calculate that, for $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} &&{\int}_{\theta_{j-1}}^{\theta_{j}}\frac{\theta_{i}}{\xi^{2}}\frac{\xi-\theta_{j}}{\theta_{j-1}-\theta_{j}}f_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)d\xi \\ &&=-{\int}_{\theta_{j-1}}^{\theta_{j}}\frac{\theta_{i}}{\xi}\frac{\xi-\theta_{j}}{\theta_{j-1}-\theta_{j}}f_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)d\ln\frac{\theta_{i}}{\xi} \\ &&=-\exp\left( \mu_{k}+\frac{{{{\varrho}}^{2}_{k}}}{2}\right){\int}_{\theta_{j-1}}^{\theta_{j}}\frac{\xi-\theta_{j}}{\theta_{j-1}-\theta_{j}}dF_{k}\left( \ln\frac{\theta_{i}}{\xi}\right) \\ &&=\exp\left( \mu_{k}+\frac{{{{\varrho}}^{2}_{k}}}{2}\right)\left[F_{k}\left( \ln\frac{\theta_{i}}{\theta_{j-1}}\right)-\frac{{\int}_{\theta_{j-1}}^{\theta_{j}}F_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)d\xi}{\theta_{j}-\theta_{j-1}}\right], \end{array} $$

(24)

where F_k(⋅) is the distribution function for a normal random variable with expectation $\mu _{k}+{{{\varrho }}^{2}_{k}}$ and variance ${{{\varrho }}^{2}_{k}}$.

Similarly we have, for $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} &&{\int}_{\theta_{j-1}}^{\theta_{j}}\frac{\theta_{i}}{\xi^{2}}\frac{\xi-\theta_{j-1}}{\theta_{j}-\theta_{j-1}}f_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)d\xi \\ &=&-\exp\left( \mu_{k}+\frac{{{{\varrho}}^{2}_{k}}}{2}\right)\Bigg[F_{k}\left( \ln\frac{\theta_{i}}{\theta_{j}}\right)-\frac{{\int}_{\theta_{j-1}}^{\theta_{j}}F_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)d\xi}{\theta_{j}-\theta_{j-1}}\Bigg], \end{array} $$

(25)

For ease of presentation, we introduce the finite difference operators. Denote by

$$ \begin{array}{@{}rcl@{}} (u_{i})_{\overline{\theta}}=\frac{u_{i}-u_{i-1}}{\Delta \theta},\quad (u_{i})_{\theta}=\frac{u_{i+1}-u_{i}}{\Delta \theta}, \end{array} $$

(26)

the backward difference and the forward difference operators respectively. Then, the first-order central difference for function u at 𝜃 = 𝜃_i can be expressed as

$$ (u_{i})_{\widehat{\theta}}=\frac{(u_{i+1})_{\overline{\theta}}+(u_{i})_{\overline{\theta}}}{2} =\frac{u_{i+1}-u_{i-1}}{2{\Delta} \theta}, $$

(27)

and the second-order central difference for function u at 𝜃 = 𝜃_i as

$$ (u_{i})_{\theta \overline{\theta}}=\frac{u_{i+1}-2u_{i}+u_{i-1}}{\Delta \theta^{2}}. $$

(28)

Denote the approximation of u(𝜃_i,τ_n;k) by ${u_{i}^{n}}(k)$, i.e., ${u_{i}^{n}}(k)\approx u(\theta _{i},\tau _{n};k)$. Then the system of PIDEs (16) can be discretized as the following IMEX scheme, for i = 1,2,…,I − 1; n = 1,2,…,N − 1 and $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} \frac{3u^{n+1}_{i}(k)-4{u^{n}_{i}}(k)+u^{n-1}_{i}(k)}{2{\Delta}\tau}&=&\phi(\theta_{i},\tau_{n+1};k)\left( u^{n+1}_{i}(k)\right)_{\theta \overline{\theta}}\\&&+\psi(\theta_{i},\tau_{n+1};k)\left( u^{n+1}_{i}(k)\right)_{\widehat{\theta}} \\ &&- (\lambda_{k}+\delta_{k}+\lambda_{k}\alpha_{k}-a_{kk})u^{n+1}_{i}(k)\\ &&+\lambda_{k}\left( 2\mathcal{I}{u^{n}_{i}}(k)-\mathcal{I}u^{n-1}_{i}(k)\right) \\ &&+ 2\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}{u^{n}_{i}}(\ell)-\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}u^{n-1}_{i}(\ell),\\ \end{array} $$

(29)

with

$$ \begin{array}{@{}rcl@{}} {u^{0}_{i}}(k)&=&0, \quad i=0,1,\ldots,I, \end{array} $$

(30)

$$ \begin{array}{@{}rcl@{}} {u^{n}_{0}}(k)&=&\frac{1}{(\delta_{k}-r_{k})T}\left( e^{-r_{k}n{\Delta}\tau}-e^{-\delta_{k}n{\Delta}\tau}\right), \quad n=0,1,\ldots,N, \end{array} $$

(31)

$$ \begin{array}{@{}rcl@{}} {u^{n}_{I}}(k)&=&0, \quad n=0,1,\ldots,N, \end{array} $$

(32)

where

$$ \begin{array}{@{}rcl@{}} \mathcal{I}{u^{n}_{i}}(k)&\equiv&\exp\left( \mu_{k}+\frac{{{{\varrho}}^{2}_{k}}}{2}\right)\sum\limits_{j=1}^{I}u^{n}_{j-1}(k)\left[F_{k}\left( \ln\frac{\theta_{i}}{\theta_{j-1}}\right)\!-\frac{{\int}_{\theta_{j-1}}^{\theta_{j}}F_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)d\xi}{\theta_{j}-\theta_{j-1}}\right]\\ &&- \exp\left( \mu_{k} + \frac{{{{\varrho}}^{2}_{k}}}{2}\right)\sum\limits_{j=1}^{I}{u^{n}_{j}}(k)\left[\!F_{k}\left( \ln\frac{\theta_{i}}{\theta_{j}}\right)\!-\frac{{\int}_{\theta_{j-1}}^{\theta_{j}}F_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)d\xi}{\theta_{j}-\theta_{j-1}}\right], \end{array} $$

(33)

similarly, we have $\mathcal {I}u^{n-1}_{i}(k)$. After solving (29), we can use the correspondence $u(\theta ,\tau ;k)\equiv G\left (\frac {T-\tau }{T}+\theta \left (X-\frac {T-\tau }{T}\right ),\tau ;k\right )$ and relations (7) to get the final Asian option prices.

It can be seen from (29) that this numerical scheme involves three time levels where the integral terms and the regime terms are treated explicitly. To proceed the computations, we therefore need two initial conditions on the zeroth and first time levels, the zeroth time level is given by (30) and the first time level can be derived as follows. Using the system of PIDEs (16) and the initial condition (17), applying Taylor expansion, we obtain that, for $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} u(\theta,\tau_{1};k)&=&u(\theta,\tau_{0};k)+{\Delta}\tau\frac{\partial u(\theta,\tau_{0};k)}{\partial \tau}+\mathcal{O}({\Delta}\tau^{2}) \\ &=&\mathcal{O}({\Delta}\tau^{2}), \end{array} $$

(34)

which means that the initial condition for the first time level can be computed through, for $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} {u^{1}_{i}}(k)=0, \quad i=0,1,\ldots,I, \end{array} $$

(35)

with the truncation error $\mathcal {O}({\Delta }\tau ^{2})$.

We below provide the convergence analysis for the scheme (29). We shall use the mesh-dependent norm for spatial direction:

$$ \|\mathbf{\zeta}\|=\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}{\zeta_{i}^{2}}\right]^{1/2}, $$

(36)

where ζ = [ζ₁,ζ₂,…,ζ_I− 1]^′.

To prove the convergence rates, we need the following Lemma 2.1 which is well established in the literature.

Lemma 2.1

(Discrete Gronwall inequality). Let Δτ > 0 and suppose that $w(\mathcal {N}), \rho (\mathcal {N})$ are nonnegative sequences while $\rho (\mathcal {N})$ is non-decreasing. Then, if

$$ w(\mathcal{N})\leq\rho(\mathcal{N})+C{\Delta}\tau\sum\limits_{n=1}^{\mathcal{N}-1}w(n), \quad \forall\mathcal{N}\in\mathbb{N}, $$

(37)

then

$$ w(\mathcal{N})\leq\rho(\mathcal{N})e^{C{\Delta}\tau\mathcal{N}}, \quad \forall\mathcal{N}\in\mathbb{N}, $$

(38)

where C is a positive constant.

Theorem 2.1

Denote the computational error by, for i = 1,2,…,I − 1; n = 1,2,…,N; $k\in \mathbb {D}$,

$$ {e^{n}_{i}}(k)\equiv u(\theta_{i},\tau_{n};k)-{u^{n}_{i}}(k), $$

(39)

and the error vector by

$$ e^{n}(k)\equiv [{e^{n}_{1}}(k),{e^{n}_{2}}(k),\ldots,e^{n}_{I-1}(k)]^{\prime}. $$

(40)

Then, the convergence rate of the IMEX scheme (29) with initial and boundary conditions (30)–(32) and (35) is estimated by, for $\mathcal {N}=1,2,\ldots ,N$,

$$ \begin{array}{@{}rcl@{}} \sum\limits_{k=1}^{d}\|e^{\mathcal{N}}(k)\|^{2}\leq \mathcal{O}\left( {\Delta}\tau^{2}+{\Delta} \theta^{2}\right)^{2}. \end{array} $$

(41)

Proof

Define the local truncation error $\eta ^{n+1}_{i}(k)$, for i = 1,2,…,I − 1; n = 1,2,…,N − 1 and $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} &&\frac{3u(\theta_{i},\tau_{n+1};k)-4u(\theta_{i},\tau_{n};k)+u(\theta_{i},\tau_{n-1};k)}{2{\Delta}\tau} \\ &&=\phi(\theta_{i},\tau_{n+1};k)\left( u(\theta_{i},\tau_{n+1};k)\right)_{\theta \overline{\theta}}+\psi(\theta_{i},\tau_{n+1};k)\left( u(\theta_{i},\tau_{n+1};k)\right)_{\widehat{\theta}} \\ &&\quad- (\lambda_{k}+\delta_{k}+\lambda_{k}\alpha_{k}-a_{kk})u(\theta_{i},\tau_{n+1};k)+\lambda_{k}\left( 2\mathcal{I}u(\theta_{i},\tau_{n};k)-\mathcal{I}u(\theta_{i},\tau_{n-1};k)\right) \\ &&\quad+ 2\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}u(\theta_{i},\tau_{n};\ell)-\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}u(\theta_{i},\tau_{n-1};\ell)+\eta^{n+1}_{i}(k). \end{array} $$

(42)

Performing Taylor expansion at mesh point (𝜃_i,τ_n+ 1;k), since all terms in (42) are the second-order approximations of the corresponding terms in (16) around (𝜃_i,τ_n+ 1;k), then using the system of PIDEs (16), it is trivial to obtain that

$$ \begin{array}{@{}rcl@{}} \eta^{n+1}_{i}(k)=\mathcal{O}({\Delta} \tau^{2}+{\Delta} \theta^{2}). \end{array} $$

(43)

Then subtracting (29) from (42) yields, for i = 1,2,…,I − 1; n = 1,2,…,N − 1; $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} \frac{3e^{n+1}_{i}(k)-4{e^{n}_{i}}(k)+e^{n-1}_{i}(k)}{2{\Delta}\tau}&=&\phi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i}(k)\right)_{\theta \overline{\theta}}+\psi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i}(k)\right)_{\widehat{\theta}} \\ &&- (\lambda_{k}+\delta_{k} + \lambda_{k}\alpha_{k} - a_{kk})e^{n+1}_{i}(k) + \lambda_{k}\left( 2\mathcal{I}{e^{n}_{i}}(k) - \mathcal{I}e^{n-1}_{i}(k)\right) \\ &&+ 2\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}{e^{n}_{i}}(\ell)-\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}e^{n-1}_{i}(\ell)+\eta^{n+1}_{i}(k), \end{array} $$

(44)

Moreover we know that

$$ \begin{array}{@{}rcl@{}} {e^{0}_{i}}(k)=0, {e^{n}_{0}}(k)=0, {e^{n}_{I}}(k)=0, {e^{1}_{i}}(k)=\mathcal{O}({\Delta}\tau^{2}). \end{array} $$

(45)

Multiplying (44) by ${\Delta }\theta e^{n+1}_{i}(k)$ and summing up for i = 1,2…,I − 1 give that, for n = 1,2,…,N − 1 and $k\in \mathbb {D}$,

$$ \begin{array}{@{}rcl@{}} &&\frac{\Big<3e^{n+1}(k)-4e^{n}(k)+e^{n-1}(k),{\Delta}\theta e^{n+1}(k)\Big>}{2{\Delta}\tau} \\ &&={\Delta}\theta\sum\limits_{i=1}^{I-1}\phi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i}(k)\right)_{\theta \overline{\theta}}e^{n+1}_{i}(k)+{\Delta}\theta\sum\limits_{i=1}^{I-1}\psi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i}(k)\right)_{\widehat{\theta}}e^{n+1}_{i}(k) \\ &&\quad- (\lambda_{k}+\delta_{k}+\lambda_{k}\alpha_{k}-a_{kk}){\Delta}\theta\sum\limits_{i=1}^{I-1}\left( e^{n+1}_{i}(k)\right)^{2} \\ &&\quad+ \lambda_{k}\left( 2{\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\mathcal{I}{e^{n}_{i}}(k)-{\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\mathcal{I}e^{n-1}_{i}(k)\right) \\ &&\quad+ 2\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}\left( {\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k){e^{n}_{i}}(\ell)\right)-\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}\left( {\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)e^{n-1}_{i}(\ell)\right) \\ &&\quad+ {\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\eta^{n+1}_{i}(k), \end{array} $$

(46)

where < ⋅,⋅ > denotes inner product.

Using the relation 2 < 3a − 4b + c,a >= ∥a∥² −∥b∥² + ∥2a − b∥² −∥2b − c∥² + ∥a − 2b + c∥², the term on the left-hand side of (46) can be estimated as

$$ \begin{array}{@{}rcl@{}} &&\frac{\Big<3e^{n+1}(k)-4e^{n}(k)+e^{n-1}(k),{\Delta}\theta e^{n+1}(k)\Big>}{2{\Delta}\tau} \\ &&=\frac{1}{4{\Delta}\tau}\left[\|e^{n+1}(k)\|^{2}-\|e^{n}(k)\|^{2}+\|2e^{n+1}(k)-e^{n}(k)\|^{2}-\|2e^{n}(k)-e^{n-1}(k)\|^{2} \right.\\ &&\quad\left.+ \|e^{n+1}(k)-2e^{n}(k)+e^{n-1}(k)\|^{2}\right] \\ &&\geq \frac{1}{4{\Delta}\tau}\left[\|e^{n+1}(k)\|^{2} - \|e^{n}(k)\|^{2}+\|2e^{n+1}(k)-e^{n}(k)\|^{2} - \|2e^{n}(k)-e^{n-1}(k)\|^{2}\right],\\ \end{array} $$

(47)

We now estimate the right-hand side of (46) term by term. Using the discrete Green formula (see, e.g., [14]) and identities (45), the first term can be estimated as

$$ \begin{array}{@{}rcl@{}} &&{\Delta}\theta\sum\limits_{i=1}^{I-1}\phi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i}(k)\right)_{{\theta}\overline{\theta}}e^{n+1}_{i}(k) \\ &&=-{\Delta}\theta\sum\limits_{i=1}^{I}\left[\phi(\theta_{i},\tau_{n+1};k)e^{n+1}_{i}(k)\right]_{\overline{\theta}}\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}}-\phi(\theta_{i},\tau_{n+1};k)e^{n+1}_{i}(k)\left( e^{n+1}_{i}(k)\right)_{\theta}|_{i=0} \\ &&\quad+ \phi(\theta_{i},\tau_{n+1};k)e^{n+1}_{i}(k)\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}}|_{i=I} \\ \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&=-{\Delta}\theta\sum\limits_{i=1}^{I}\left[\phi(\theta_{i},\tau_{n+1};k)e^{n+1}_{i}(k)\right]_{\overline{\theta}}\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}} \\ &&=-{\Delta}\theta\sum\limits_{i=1}^{I}\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}}\left[\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}}\phi(\theta_{i},\tau_{n+1};k)+e^{n+1}_{i-1}(k)\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\right] \\ &&\leq -{\Delta}\theta\sum\limits_{i=1}^{I}\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}}e^{n+1}_{i-1}(k)\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}. \end{array} $$

(48)

Also we obtain that

$$ \begin{array}{@{}rcl@{}} &&{\Delta}\theta\sum\limits_{i=1}^{I-1}\phi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i}(k)\right)_{\theta \overline{\theta}}e^{n+1}_{i}(k) \\ &&=-{\Delta}\theta\sum\limits_{i=1}^{I}\left[\phi(\theta_{i},\tau_{n+1};k)e^{n+1}_{i}(k)\right]_{\overline{\theta}}\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}} \\ &&=-{\Delta}\theta\sum\limits_{i=1}^{I}\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}}\left[\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}}\phi(\theta_{i-1},\tau_{n+1};k)+e^{n+1}_{i}(k)\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\right] \\ &&\leq -{\Delta}\theta\sum\limits_{i=1}^{I}\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}}e^{n+1}_{i}(k)\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}. \end{array} $$

(49)

Adding (48) and (49) together gives

$$ \begin{array}{@{}rcl@{}} &&{\Delta}\theta\sum\limits_{i=1}^{I-1}\phi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i}(k)\right)_{\theta \overline{\theta}}e^{n+1}_{i}(k) \\ &&\leq -\frac{1}{2}{\Delta}\theta\sum\limits_{i=1}^{I}\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\left( e^{n+1}_{i-1}(k)+e^{n+1}_{i}(k)\right)\left( e^{n+1}_{i}(k)\right)_{\overline{\theta}} \\ &&=-\frac{1}{2}\sum\limits_{i=1}^{I}\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\left( \left( e^{n+1}_{i}(k)\right)^{2}-\left( e^{n+1}_{i-1}(k)\right)^{2}\right) \\ &&=-\frac{1}{2}\sum\limits_{i=1}^{I}\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\left( e^{n+1}_{i}(k)\right)^{2}+\frac{1}{2}\sum\limits_{i=1}^{I}\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\left( e^{n+1}_{i-1}(k)\right)^{2} \\ &&=-\frac{1}{2}\sum\limits_{i=1}^{I-1}\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\left( e^{n+1}_{i}(k)\right)^{2}+\frac{1}{2}\sum\limits_{i=0}^{I-1}\left( \phi(\theta_{i+1},\tau_{n+1};k)\right)_{\overline{\theta}}\left( e^{n+1}_{i}(k)\right)^{2} \\ \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&=-\frac{1}{2}\sum\limits_{i=1}^{I-1}\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\left( e^{n+1}_{i}(k)\right)^{2}+\frac{1}{2}\sum\limits_{i=1}^{I-1}\left( \phi(\theta_{i+1},\tau_{n+1};k)\right)_{\overline{\theta}}\left( e^{n+1}_{i}(k)\right)^{2} \\ &&= \frac{1}{2}\sum\limits_{i=1}^{I-1}\left( \left( \phi(\theta_{i+1},\tau_{n+1};k)\right)_{\overline{\theta}}-\left( \phi(\theta_{i},\tau_{n+1};k)\right)_{\overline{\theta}}\right)\left( e^{n+1}_{i}(k)\right)^{2} \\ &&= \frac{{\sigma^{2}_{k}}}{2}{\Delta}\theta\sum\limits_{i=1}^{I-1}\left( e^{n+1}_{i}(k)\right)^{2}\leq C_{1}\|e^{n+1}(k)\|^{2}. \end{array} $$

(50)

where $C_{1}\equiv \frac {1}{2}\max \limits _{k\in \mathbb {D}}{\sigma ^{2}_{k}}$.

Shifting the index, using Cauchy-Schwartz inequality and identities (45), the second term can be estimated as

$$ \begin{array}{@{}rcl@{}} &&{\Delta}\theta\sum\limits_{i=1}^{I-1}\psi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i}(k)\right)_{\widehat{\theta}}e^{n+1}_{i}(k) \\ &&=\frac{1}{2}\sum\limits_{i=1}^{I-1}\psi(\theta_{i},\tau_{n+1};k)\left( e^{n+1}_{i+1}(k)-e^{n+1}_{i-1}(k)\right)e^{n+1}_{i}(k) \\ &&=\frac{1}{2}\sum\limits_{i=1}^{I-1}\psi(\theta_{i},\tau_{n+1};k)e^{n+1}_{i+1}(k)e^{n+1}_{i}(k)-\frac{1}{2}\sum\limits_{i=1}^{I-1}\psi(\theta_{i+1},\tau_{n+1};k)e^{n+1}_{i}(k)e^{n+1}_{i+1}(k) \\ &&=\frac{1}{2}\sum\limits_{i=1}^{I-1}\left( \psi(\theta_{i},\tau_{n+1};k)-\psi(\theta_{i+1},\tau_{n+1};k)\right)e^{n+1}_{i}(k)e^{n+1}_{i+1}(k) \\ &&\leq \frac{\Delta\theta}{2}\sum\limits_{i=1}^{I-1}\left|r_{k}-\delta_{k}-\lambda_{k}\alpha_{k}-\frac{1}{XT-T+\tau_{n+1}}\right|\frac{\left( e^{n+1}_{i}(k)\right)^{2}+\left( e^{n+1}_{i+1}(k)\right)^{2}}{2} \\ &&\leq C_{2}{\Delta}\theta\sum\limits_{i=1}^{I-1}\frac{\left( e^{n+1}_{i}(k)\right)^{2} + \left( e^{n+1}_{i+1}(k)\right)^{2}}{2} \!\leq\! C_{2}{\Delta}\theta\sum\limits_{i=1}^{I-1}\left( e^{n+1}_{i}(k)\right)^{2} = C_{2}\left\|e^{n+1}(k)\right\|^{2},\!\\ \end{array} $$

(51)

where $C_{2}\equiv \frac {1}{2}\max \limits _{\tau \in [0,T],k\in \mathbb {D}}\left |r_{k}-\delta _{k}-\lambda _{k}\alpha _{k}-\frac {1}{XT-T+\tau }\right |$.

The third term can be estimated as

$$ \begin{array}{@{}rcl@{}} -(\lambda_{k}+\delta_{k}+\lambda_{k}\alpha_{k}-a_{kk}){\Delta}\theta\sum\limits_{i=1}^{I-1}\left( e^{n+1}_{i}(k)\right)^{2}\leq0. \end{array} $$

(52)

Using the triangle and Cauchy-Schwartz inequalities, we obtain that

$$ \begin{array}{@{}rcl@{}} &&{\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\mathcal{I}{e^{n}_{i}}(k) \\ &&\leq\left|{\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\mathcal{I}{e^{n}_{i}}(k)\right| \\ &&\leq \exp\left( \mu_{k}+\frac{{{{\varrho}}^{2}_{k}}}{2}\right)\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}|e^{n+1}_{i}(k)|\left( \sum\limits_{j=1}^{I}|e^{n}_{j-1}(k)|\cdot\left|{\int}_{\theta_{j-1}}^{\theta_{j}}\frac{\xi-\theta_{j}}{\theta_{j-1}-\theta_{j}}dF_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)\right|\right) \right.\\ &&\left.\quad+ {\Delta}\theta\sum\limits_{i=1}^{I-1}|e^{n+1}_{i}(k)|\left( \sum\limits_{j=1}^{I}|{e^{n}_{j}}(k)|\cdot\left|{\int}_{\theta_{j-1}}^{\theta_{j}}\frac{\xi-\theta_{j-1}}{\theta_{j}-\theta_{j-1}}dF_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)\right|\right) \right] \\ &&\leq \exp\left( \mu_{k}+\frac{{{{\varrho}}^{2}_{k}}}{2}\right)\|e^{n+1}(k)\| \left\{\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}\left( \sum\limits_{j=1}^{I}|e^{n}_{j-1}(k)|\cdot\left|{\int}_{\theta_{j-1}}^{\theta_{j}}\frac{\xi-\theta_{j}}{\theta_{j-1}-\theta_{j}}dF_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)\right|\right)^{2}\right]^{1/2} \right.\\ &&\left.\quad+ \left[{\Delta}\theta\sum\limits_{i=1}^{I-1}\left( \sum\limits_{j=1}^{I}|{e^{n}_{j}}(k)|\cdot\left|{\int}_{\theta_{j-1}}^{\theta_{j}}\frac{\xi-\theta_{j-1}}{\theta_{j}-\theta_{j-1}}dF_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)\right|\right)^{2}\right]^{1/2} \right\} \\ &&=\exp\left( \mu_{k}+\frac{{{{\varrho}}^{2}_{k}}}{2}\right)\|e^{n+1}(k)\| (\mathbb{I}_{1}+\mathbb{I}_{2}), \end{array} $$

(53)

where the meanings of $\mathbb {I}_{1}$ and $\mathbb {I}_{2}$ are obvious.

Applying Lipschitz continuity and inequality $\left ({\sum }_{i=1}^{I}a_{i}\right )^{2}\leq I{\sum }_{i=1}^{I}{a^{2}_{i}}$, we derive that

$$ \begin{array}{@{}rcl@{}} \mathbb{I}_{1}&\leq&\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}\left( \sum\limits_{j=1}^{I}|e^{n}_{j-1}(k)|\cdot\left|{\int}_{\theta_{j-1}}^{\theta_{j}}dF_{k}\left( \ln\frac{\theta_{i}}{\xi}\right)\right|\right)^{2}\right]^{1/2} \\ &=&\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}\left( \sum\limits_{j=1}^{I}|e^{n}_{j-1}(k)|\cdot\left|F_{k}\left( \ln\frac{\theta_{i}}{\theta_{j}}\right)-F_{k}\left( \ln\frac{\theta_{i}}{\theta_{j-1}}\right)\right|\right)^{2}\right]^{1/2} \\ &\leq&\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}\left( \sum\limits_{j=1}^{I}|e^{n}_{j-1}(k)|\cdot L_{k}(\theta_{j}|\theta_{i})\cdot\left|\theta_{j}-\theta_{j-1}\right|\right)^{2}\right]^{1/2} \\ &\leq&\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}{L^{2}_{k}}(\theta_{i}){\Delta}\theta^{2}\left( \sum\limits_{j=1}^{I}|e^{n}_{j-1}(k)|\right)^{2}\right]^{1/2} \\ &\leq&\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}{L^{2}_{k}}(\theta_{i}){\Delta}\theta^{2}I \sum\limits_{j=1}^{I}\left( e^{n}_{j-1}(k)\right)^{2}\right]^{1/2}, \end{array} $$

(54)

where $L_{k}(\theta _{i})=\max \limits _{1\leq j\leq I}L_{k}(\theta _{j}|\theta _{i})$ and L_k(𝜃_j|𝜃_i) is Lipschitz constant in the range [𝜃_j− 1,𝜃_j] by fixing 𝜃_i, for $k\in \mathbb {D}$.

Define ${C_{3}^{2}}\equiv \max \limits _{1\leq i\leq I-1,k\in \mathbb {D}}{L^{2}_{k}}(\theta _{i})$ and noting that Δ𝜃I = 1 and Δ𝜃(I − 1) < 1, it therefore follows from (54) that

$$ \begin{array}{@{}rcl@{}} \mathbb{I}_{1}\leq C_{3}\left[{\Delta}\theta\sum\limits_{i=1}^{I-1}1\cdot{\Delta}\theta \sum\limits_{j=1}^{I}\left( e^{n}_{j-1}(k)\right)^{2}\right]^{1/2}\leq C_{3}\|e^{n}(k)\|. \end{array} $$

(55)

Similarly we have

$$ \begin{array}{@{}rcl@{}} \mathbb{I}_{2}\leq C_{4}\|e^{n}(k)\|. \end{array} $$

(56)

where C₄ is a positive constant.

Combining (55) and (56) into (53), we have

$$ \begin{array}{@{}rcl@{}} {\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\mathcal{I}{e^{n}_{i}}(k)\leq C_{5}\|e^{n+1}(k)\|\|e^{n}(k)\|, \end{array} $$

(57)

where $C_{5}\equiv (C_{3}+C_{4})\max \limits _{k\in \mathbb {D}}\exp \left (\mu _{k}+\frac {{{{\varrho }}^{2}_{k}}}{2}\right )$.

Similarly we derive that

$$ \begin{array}{@{}rcl@{}} -{\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\mathcal{I}e^{n-1}_{i}(k)&\leq&\left|{\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\mathcal{I}e^{n-1}_{i}(k)\right| \\ &\leq& C_{6}\|e^{n+1}(k)\|\|e^{n-1}(k)\|, \end{array} $$

(58)

where C₆ is a positive constant.

Using Cauchy-Schwartz inequality, the fifth term can be estimated as

$$ \begin{array}{@{}rcl@{}} \sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}\left( {\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k){e^{n}_{i}}(\ell)\right)\leq\|e^{n+1}(k)\|\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}\|e^{n}(\ell)\|. \end{array} $$

(59)

Similarly we have

$$ \begin{array}{@{}rcl@{}} -\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}\left( {\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)e^{n-1}_{i}(\ell)\right)\leq\|e^{n+1}(k)\|\sum\limits_{\ell=1,\ell\neq k}^{d}a_{k\ell}\|e^{n-1}(\ell)\|. \end{array} $$

(60)

Using Cauchy-Schwartz inequality, the last term can be estimated as

$$ \begin{array}{@{}rcl@{}} {\Delta}\theta\sum\limits_{i=1}^{I-1}e^{n+1}_{i}(k)\eta^{n+1}_{i}(k)\leq\|e^{n+1}(k)\|\|\eta^{n+1}(k)\|. \end{array} $$

(61)

Combining (47), (50), (51), (52), (57), (58), (59), (60) and (61) with (46), we obtain that

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{4{\Delta}\tau}\Bigg[\|e^{n+1}(k)\|^{2}-\|e^{n}(k)\|^{2}+\|2e^{n+1}(k)-e^{n}(k)\|^{2}-\|2e^{n}(k)-e^{n-1}(k)\|^{2}\Bigg] \\ &&\leq C_{1}\|e^{n+1}(k)\|^{2}+C_{2}\left\|e^{n+1}(k)\right\|^{2}+2C_{5}\lambda_{k}\|e^{n+1}(k)\|\|e^{n}(k)\|+C_{6}\lambda_{k}\|e^{n+1}(k)\|\|e^{n-1}(k)\| \\ &&\quad+ \|e^{n+1}(k)\|{\sum}_{\ell=1,\ell\neq k}^{d}a_{k\ell}\left( 2\|e^{n}(\ell)\|+\|e^{n-1}(\ell)\| \right)+\|e^{n+1}(k)\|\|\eta^{n+1}(k)\| \\ &&\leq \left( C_{1}+C_{2}+C_{5}\lambda_{k}+\frac{C_{6}\lambda_{k}}{2}+1\right)\|e^{n+1}(k)\|^{2}+C_{5}\lambda_{k}\|e^{n}(k)\|^{2}+\frac{C_{6}\lambda_{k}}{2}\|e^{n-1}(k)\|^{2} \\ &&\quad+ \frac{\left[\sum\nolimits_{\ell=1,\ell\neq k}^{d}a_{k\ell}\left( 2\|e^{n}(\ell)\|+\|e^{n-1}(\ell)\| \right)\right]^{2}}{2}+\frac{1}{2}\|\eta^{n+1}(k)\|^{2} \\ &&\leq \left( C_{1}+C_{2}+C_{5}\lambda_{k}+\frac{C_{6}\lambda_{k}}{2}+1\right)\|e^{n+1}(k)\|^{2}+C_{5}\lambda_{k}\|e^{n}(k)\|^{2}+\frac{C_{6}\lambda_{k}}{2}\|e^{n-1}(k)\|^{2} \\ &&\quad+ \frac{(d-1)\sum\nolimits_{\ell=1,\ell\neq k}^{d}a^{2}_{k\ell}\left( 2\|e^{n}(\ell)\|+\|e^{n-1}(\ell)\| \right)^{2}}{2}+\frac{1}{2}\|\eta^{n+1}(k)\|^{2} \\ &&\leq C_{8}\|e^{n+1}(k)\|^{2}+C_{5}C_{7}\|e^{n}(k)\|^{2}+\frac{C_{6}C_{7}}{2}\|e^{n-1}(k)\|^{2} \\ &&\quad+ (d-1)\sum\limits_{\ell=1,\ell\neq k}^{d}a^{2}_{k\ell}\left( 4\|e^{n}(\ell)\|^{2}+\|e^{n-1}(\ell)\|^{2} \right)+\frac{1}{2}\|\eta^{n+1}(k)\|^{2}, \end{array} $$

(62)

where $C_{7}\equiv \max \limits _{k\in \mathbb {D}}\lambda _{k}$ and $C_{8}\equiv C_{1}+C_{2}+C_{5}C_{7}+\frac {C_{6}C_{7}}{2}+1$.

Define $C_{9}\equiv \max \limits _{\ell \neq k}a^{2}_{k\ell }$, we derive that

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{k=1}^{d}\sum\limits_{\ell=1,\ell\neq k}^{d}a^{2}_{k\ell}\left( 4\|e^{n}(\ell)\|^{2}+\|e^{n-1}(\ell)\|^{2} \right) \\ &&\leq 4C_{9}\sum\limits_{k=1}^{d}\sum\limits_{\ell=1,\ell\neq k}^{d}\|e^{n}(\ell)\|^{2}+C_{9}\sum\limits_{k=1}^{d}\sum\limits_{\ell=1,\ell\neq k}^{d}\|e^{n-1}(\ell)\|^{2} \\ &&=4C_{9}\sum\limits_{k=1}^{d}\left( \sum\limits_{\ell=1}^{d}\|e^{n}(\ell)\|^{2}-\|e^{n}(k)\|^{2}\right)+C_{9}\sum\limits_{k=1}^{d}\left( \sum\limits_{\ell=1}^{d}\|e^{n-1}(\ell)\|^{2}-\|e^{n-1}(k)\|^{2}\right) \\ &&=4C_{9}(d-1)\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2}+C_{9}(d-1)\sum\limits_{k=1}^{d}\|e^{n-1}(k)\|^{2}. \end{array} $$

(63)

Using (63) and summing up (62) for index $k\in \mathbb {D}$, we obtain that

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{4{\Delta}\tau}\sum\limits_{k=1}^{d}\Bigg[\|e^{n+1}(k)\|^{2}-\|e^{n}(k)\|^{2}+\|2e^{n+1}(k)-e^{n}(k)\|^{2}-\|2e^{n}(k)-e^{n-1}(k)\|^{2}\Bigg] \\ &&\leq C_{8}\sum\limits_{k=1}^{d}\|e^{n+1}(k)\|^{2}+C_{5}C_{7}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2}+\frac{C_{6}C_{7}}{2}\sum\limits_{k=1}^{d}\|e^{n-1}(k)\|^{2} \\ &&\quad+ (d-1)\sum\limits_{k=1}^{d}\sum\limits_{\ell=1,\ell\neq k}^{d}a^{2}_{k\ell}\left( 4\|e^{n}(\ell)\|^{2}+\|e^{n-1}(\ell)\|^{2} \right)+\frac{1}{2}\sum\limits_{k=1}^{d}\|\eta^{n+1}(k)\|^{2} \\ &&\leq C_{8}\sum\limits_{k=1}^{d}\|e^{n+1}(k)\|^{2}+C_{10}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2}+C_{11}\sum\limits_{k=1}^{d}\|e^{n-1}(k)\|^{2}+\frac{1}{2}\sum\limits_{k=1}^{d}\|\eta^{n+1}(k)\|^{2},\\ \end{array} $$

(64)

where C₁₀ ≡ 4C₉(d − 1)² + C₅C₇ and $C_{11}\equiv C_{9}(d-1)^{2}+\frac {C_{6}C_{7}}{2}$.

Summing up (64) for n from 1 to $\mathcal {N}-1$, for $1\leq \mathcal {N}\leq N$, we have

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{4{\Delta}\tau}\sum\limits_{k=1}^{d}\Bigg[\|e^{\mathcal{N}}(k)\|^{2}-\|e^{1}(k)\|^{2}+\|2e^{\mathcal{N}}(k)-e^{\mathcal{N}-1}(k)\|^{2}-\|2e^{1}(k)-e^{0}(k)\|^{2}\Bigg] \\ &&\leq C_{8}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|e^{n+1}(k)\|^{2}+C_{10}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2} \\ &&\quad+ C_{11}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|e^{n-1}(k)\|^{2}+\frac{1}{2}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|\eta^{n+1}(k)\|^{2} \\ &&\leq C_{8}\sum\limits_{k=1}^{d}\|e^{\mathcal{N}}(k)\|^{2}+C_{8}\sum\limits_{n=2}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2}+C_{10}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2} \\ &&\quad+ C_{11}\sum\limits_{n=0}^{\mathcal{N}-2}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2}+\frac{1}{2}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|\eta^{n+1}(k)\|^{2}, \end{array} $$

(65)

which implies that

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{4{\Delta}\tau}\sum\limits_{k=1}^{d}\Bigg[\|e^{\mathcal{N}}(k)\|^{2}-\|e^{1}(k)\|^{2}-\|2e^{1}(k)-e^{0}(k)\|^{2}\Bigg] \\ &&\leq C_{8}\sum\limits_{k=1}^{d}\|e^{\mathcal{N}}(k)\|^{2}+C_{12}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2}+\frac{1}{2}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|\eta^{n+1}(k)\|^{2}, \end{array} $$

(66)

where C₁₂ ≡ C₈ + C₁₀ + C₁₁.

For small time meshsize Δτ such that ${\Delta }\tau <\frac {1}{4C_{8}}$, it follows from (66) that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{k=1}^{d}\|e^{\mathcal{N}}(k)\|^{2} & \leq& \frac{1}{1-4C_{8}{\Delta}\tau}\left( \sum\limits_{k=1}^{d}\|e^{1}(k)\|^{2}+\sum\limits_{k=1}^{d}\|2e^{1}(k)-e^{0}(k)\|^{2}\right) \\ &&+ \frac{4{\Delta}\tau}{1 - 4C_{8}{\Delta}\tau}\left( C_{12}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2} + \frac{1}{2}\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|\eta^{n+1}(k)\|^{2}\right).\\ \end{array} $$

(67)

Recall that $\frac {1}{1-4C_{8}{\Delta }\tau }=1+4C_{8}{\Delta }\tau +(4C_{8}{\Delta }\tau )^{2}+\cdots$, and incorporating higher-order term into the truncation error term, we derive that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{k=1}^{d}\|e^{\mathcal{N}}(k)\|^{2} & \leq& C\left[\sum\limits_{k=1}^{d}\|e^{1}(k)\|^{2}+\sum\limits_{k=1}^{d}\|2e^{1}(k)-e^{0}(k)\|^{2} \right.\\ &&\left.+ {\Delta}\tau\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|e^{n}(k)\|^{2}+{\Delta}\tau\sum\limits_{n=1}^{\mathcal{N}-1}\sum\limits_{k=1}^{d}\|\eta^{n+1}(k)\|^{2}\right] , \end{array} $$

(68)

where C is a positive constant.

From (45), we know that ${\sum }_{k=1}^{d}\|e^{1}(k)\|^{2}=\mathcal {O}({\Delta }\tau ^{2})^{2}$ and ${\sum }_{k=1}^{d}\|e^{0}(k)\|^{2}=0$, noting that ${\Delta }\tau \mathcal {N}\leq T$, applying the discrete Gronwall inequality to (68), and using the estimation of the truncation error (43), we prove that, for $1\leq \mathcal {N}\leq N$,

$$ \begin{array}{@{}rcl@{}} \sum\limits_{k=1}^{d}\|e^{\mathcal{N}}(k)\|^{2} \leq \mathcal{O}({\Delta}\tau^{2}+{\Delta}\theta^{2})^{2}. \end{array} $$

(69)

where we complete the proof. □

3 Numerical examples

In this section, we conduct several numerical examples to verify the theoretical results studied in this paper. The model parameters used in the computation are given in the corresponding examples. The codes are run in MATLAB R2014a on a PC with the configuration: AMD, CPU A10-9600P@2.40GHz and 24.0GB RAM.

Since the exact solution of the problem is unknown, we shall use the following formulas given by Ma and Zhou [11] to calculate the convergence rates for time and space. To this end, let u^I,N(k) for $k\in \mathbb {D}$, be the computational solutions at τ = T of the studied numerical scheme with respect to the number of 𝜃-direction meshes I and time meshes N, then the continuous form of the computational solutions $\widetilde {u}^{I,N}(\theta ,T;k)$ can be obtained by applying the cubic spline interpolation to u^I,N(k). When we test the convergence rates for 𝜃-direction, we may fix the number N and vary I, and use the following log-formula with respect to three consecutive levels I = I₁,I₂,I₃ (see Ma and Zhou [11]),

$$ \text{Convergence rate for space }\theta=\frac{\log \frac{I_{1}\|u^{I_{1}, N}(k)-\widetilde{u}^{I_{2},N}(k)\|}{I_{2} \|u^{I_{2},N}(k) -\widetilde{u}^{I_{3},N}(k)\|}} {\log\frac{I_{3}}{I_{2}}}, $$

(70)

where the norm ∥⋅∥ is defined by (36), and $\widetilde {u}^{I,N}(k)$ can be obtained by calculating the values of $\widetilde {u}^{I,N}(\theta ,T;k)$ on spatial mesh of the previous adjacent level. Similarly, we can define the convergence rate for time direction (see Ma and Zhou [11]),

$$ \text{Convergence rate for time $\tau$}=\frac{\log \frac{N_{1}\|u^{I, N_{1}}(k)-u^{I,N_{2}}(k)\|}{N_{2}\|u^{I,N_{2}}(k) -u^{I,N_{3}}(k)\|}} {\log\frac{N_{3}}{N_{2}}}. $$

(71)

Example 3.1

We use this example to test the convergence rates of the studied IMEX scheme (29) with initial conditions (30), (35) and boundary conditions (31), (32). Functions f_k (k = 1,2) are given by (2) and other model parameters are given by X = 1.5, r₁ = r₂ = 0.05, σ₁ = 0.15, σ₂ = 0.25, δ₁ = δ₂ = 0, T = 1, λ₁ = 1, λ₂ = 2, μ₁ = μ₂ = − 0.1, ϱ₁ = ϱ₂ = 0.3, − a₁₁ = a₁₂ = a₂₁ = −a₂₂ = 1.

From Tables 1 and 2, we observe that the second-order convergence rates in both time and space are consistent with theoretical findings in Theorem 2.1.

Table 1 Convergence rates for time for Example 3.1

Table 2 Convergence rates for space for Example 3.1

Example 3.2

We use this example to test the convergence rates of the studied IMEX scheme (29) with initial conditions (30), (35) and boundary conditions (31), (32). Functions f_k (k = 1,2,3) are given by (2) and other model parameters are given by X = 1.5, r₁ = r₂ = r₃ = 0.05, σ₁ = 0.2, σ₂ = 0.15, σ₃ = 0.25, δ₁ = δ₂ = δ₃ = 0, T = 1, λ₁ = 1, λ₂ = 5, λ₃ = 2, μ₁ = − 0.1, μ₂ = − 0.15, μ₃ = − 0.05, ϱ₁ = 0.3, ϱ₂ = 0.25, ϱ₃ = 0.35, a₁₂ = a₁₃ = a₂₁ = a₂₃ = a₃₁ = a₃₂ = 1/3, a₁₁ = a₂₂ = a₃₃ = − 2/3.

From Tables 3 and 4, we observe that the second-order convergence rates are still consistent with theoretical findings in Theorem 2.1.

Table 3 Convergence rates for time for Example 3.2

Table 4 Convergence rates for space for Example 3.2

Example 3.3

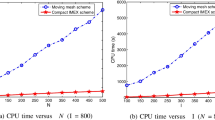
In this example, we compare the IMEX scheme studied in this paper with the moving mesh method in Ma and Wang [13] for the 3-state regime-switching jump-diffusion model, the model parameters are given by Example 3.2. Therefore, we transform the computational solution u(𝜃,τ;k) from (16) into V (S,M,t;k) via the following variable transformations

$$ \begin{array}{@{}rcl@{}} V(S,M,t;k)=S u(\theta,T-t;k), \quad \theta=\frac{K-M/T}{S(X-t/T)}. \end{array} $$

(72)

We calculate the value V (S₀,M₀,0;k) with K = 100 and M₀ = 0. Moreover, the IMEX method of this paper uses time meshes 400 and spatial meshes 400, and the moving mesh method [13] uses time meshes 800 and spatial meshes 400 to obtain the results that have two digit accuracy after decimal point.

From Table 5, we observe that the IMEX method of this paper uses less mesh nodes while achieving almost the same accuracy as the moving mesh method in [13]. The reasons for these facts are just that the convergence rate of the moving mesh method is first-order in time direction and our IMEX method is second-order.

Table 5 Prices for Asian options at t = 0 for Example 3.3

4 Conclusions

This paper studies an IMEX scheme for solving moving boundary problem of the PIDEs which arises in Asian option pricing under the regime-switching jump-diffusion models. The moving boundary problem of the PIDEs is recast into the fixed boundary problem and the IMEX scheme is constructed to solve the problem. Compared to the moving mesh method (for Asian option pricing under the regime-switching jump-diffusion models, it is the first time in the literature to study the convergence rates of the numerical methods), the IMEX method studied in this paper achieves the second-order convergence rates in both time and space.