1 Introduction

Engaging in regular physical activity decreases risk of obesity, chronic diseases and improves longevity [40]. To date, much of the evidences linking activity to disease in large studies have relied on self-report questionnaires to assess physical activity [1, 39]. Such questionnaires provide reasonable estimates for time spent in structured exercise, but questionnaires are subject to measurement error [36] and do not provide precise estimates for lower intensity activities of daily living or sedentary time. The gold-standard approach to measure energy expenditure is doubly labeled water [12], but it is expensive and time-consuming in practice and does not provide estimates of time in different postures (e.g., sitting vs. standing) or intensities (e.g., light vs. vigorous). To get around these difficulties, many recent health studies use wearable accelerometer-based devices. These devices are fairly inexpensive and convenient for participants to wear for multiple days or weeks. They can collect and store acceleration signals at relatively high frequencies (e.g., 80 Hz) in 3-axes for weeks. Freedson et al. [19] provide a detailed review for the application of these devices.

There are two main categories of statistical considerations for accelerometer data. The first is that an algorithm is needed to translate the acceleration signal into estimates of metrics that are of use to physical activity and health researchers (e.g., time spent sitting vs. standing, in light, moderate or vigorous intensity activity). Because the monitors could generate over 10,000 observations per person per day, specific statistical software is required to process the raw data. The second is that, once summary estimates of time spent in particular activity intensities or behaviors are obtained, researchers in physical activity and health are interested in the relationships between different types of activities across days and weeks or even within a day. Thus, our statistical methods should postulate the association pattern. This manuscript will provide a brief overview of methods to estimate activity based on acceleration signals, but will primarily focus on reviewing statistical methods for analyzing the summary data obtained from these devices over days and weeks.

The manuscript is organized as follows. Section 2 describes methods to translate acceleration signals to estimates of physical activity behaviors, and Sect. 3 discusses longitudinal data methods to analyze the data. Functional data analysis to handle minute-by-minute physical activity information is discussed in Sect. 4. Concluding remarks are given in Sect. 5.

2 Translating Acceleration Signals to Estimates of Physical Activity Behavior

Some research-based activity monitors provide estimates of behavior within the device using proprietary software. For example, the activPAL device (www.paltech.plus.com), which is taped in the front of the thigh, uses 1- to 3-axis accelerometers to measure the angle of the thigh and movement. Based on the measurements, the software generates the estimate of body posture and movement in three categories: sitting, standing, and stepping. The software also estimates energy expenditure (metabolic equivalent, MET) using the following equation [25]:

$$\begin{aligned} \mathrm{MET}\cdot h^{-1}=1.4\times d+(4-1.4)\times (c/120)\times d, \end{aligned}$$
(1)

where c represents the number of steps per minute and d is activity duration (in hours). Table 1 displays a sample dataset obtained from the activPAL device [51]. Based on the MET level, the intensity of activity can be categorized to sedentary (\(1\le \mathrm{MET}<2\)), light (\(2\le \mathrm{MET}<3\)), moderate (\(3\le \mathrm{MET}<6\)), and vigorous (\(\mathrm{MET}\ge 6\)) [11].

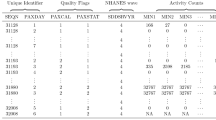
Table 1 Sample data obtained from the ActivPAL device [51]
Full size table

Other research-based monitors (e.g., ActiGraph [www.actigraphcorp.com]) provide output files with the “raw” acceleration data and then researchers select algorithm to process the data into summary estimates. In the first-generation devices, the monitors collect and store one data signal, in an arbitrary unit called an “activity count”, each minute in the vertical axis only. As previous mentioned, the devices now capture and store acceleration signals in 3-axes at 80 Hz. The processing of ActiGraph raw acceleration data to activity counts can be refereed to Brønd and Arvidsson [6] and the vector magnitude counts from 3-axes are studied by Howe et al. [26]. Table 2 shows a sample activity counts dataset collected from an ActiGraph device [14]. Moreover, Bai et al. [3] summarize a general workflow to translate the acceleration signal into the variables with research interests. Several pathways are involved in this workflow. For example, linear regression models are developed to estimate thresholds (or cut-points) that define activity intensity categories [18]. Machine learning algorithms are also studied to derive a group of measurements for physical activity including “time active” and activity intensity [2, 3]. A comprehensive evaluation of existing methods is beyond the scope of this paper, but have been summarized by others [13].

Table 2 Sample signal data obtained from the ActiGraph device [14]
Full size table

The increasing of the quality in the signal and the sophistication in data processing methods should increase the accuracy and precision of the estimates, but also increase the computational burden and there is a need for software that can handle this complex data. Many R packages [41] are developed to sort the raw data. Domelen et al. [15] and Domelen [14] develop the packages accelerometry and nhanesaccel to process data collected from the National Health and Nutrition Examination Survey [48]. Choi et al. [10] and Geraci [20] propose the packages PhysicalActivity and pawacc to analyze Actigraph data, respectively. Zhang et al. [51] develop the package PAactivPAL for activPAL data, and Zhang et al. [52] propose the PASenseWear to handle BodyMedia records. van Hees et al. [49] develop the package GGIR to process and analyze raw accelerometer data collected from multiple types of devices.

3 Longitudinal Data Analysis

Standard statistical approaches such as group comparison (e.g., t-test), correlation coefficient, and regression can be directly used to analyze sorted physical activity data [25]. However, regular statistical methods do not take advantage of these newly developed instruments. Accelerometer data are generally collected by following up individuals over days or weeks, the trend and association for activity variables across different time points are also the statistical problems of great research interests. Once the activity data are summarized into daily summary measures, data recorded over multiple days or weeks can be viewed as longitudinal data. One such study, Kozey-Keadle et al. [28] and Kozey-Keadle et al. [29] evaluate the trend of physical activity outcomes (e.g., total daily energy expenditure), and health factors (e.g., cardiorespiratory fitness, body weight) across several weeks.

Moreover, additional complexities in longitudinal data analysis arise from multivariate outcomes and varying variable types. Keadle et al. [27] suggest that a complete description of an individual’s pattern of physical activity requires specification of multiple variables. They discuss a set of 48 metrics generated from activPAL data, where 20 of them are for sedentary behavior, 16 metrics are for light activities, and 12 metrics are for moderate to vigorous physical activity (MVPA).

To model the trend and association for activity outcomes across time points, longitudinal data methods such as linear mixed models can be implemented [17]. Li et al. [32] propose a multivariate longitudinal data model to jointly analyze the multiple measurements from a physical activity study. In this study, participants have one day’s wearable device records across 5 weeks. The recorded information involves eight variables: (1) daily sedentary hours (continuous); (2) energy expenditure (continuous); (3) proportion of sedentary time greater than 20 min; (4) proportion of active time greater than 5 min; (5) number of daily standing up behaviors (count); (6) number of daily steps (count); (7) whether daily MVPA time is greater than one hour (binary); (8) whether the highest energy expenditure rate measured by METs in 10 min is greater than 3 (binary). The joint model for continuous data \((\ell =1,2)\) is

$$\begin{aligned} Y_{ij}^{(\ell )}=X_{ij}^{(\ell )}\beta ^{(\ell )}+Z_{ij}^{(\ell )}u_i^{(\ell )} +\epsilon _{ij}^{(\ell )}, \end{aligned}$$

where \(Y_{ij}^{(\ell )}\) is the \(\ell ^{th}\) outcome at week j for subject i, \(X_{ij}^{(\ell )}\) and \(Z_{ij}^{(\ell )}\) are covariate vectors for fixed and random effects, \(\beta ^{(\ell )}\) is a vector of fixed effect coefficients, \(u_i^{(\ell )}\) is a vector of correlated random effects, and \(\epsilon _{ij}^{(\ell )}\) is independent random noise with normal distribution. For proportional data \((\ell =3,4)\), the Beta regression framework [16] is used and its mean \(\mu _{ij}^{(\ell )}\) given \(X_{ij}^{(\ell )}\), \(Z_{ij}^{(\ell )}\) and \(u_i^{(\ell )}\) has

$$\begin{aligned} \mathrm{logit}\{\mu _{ij}^{(\ell )}\}=X_{ij}^{(\ell )}\beta ^{(\ell )}+Z_{ij}^{(\ell )}u_i^{(\ell )}, \end{aligned}$$

Poisson distribution with log link function is employed to model the count data \((\ell =5,6)\)

$$\begin{aligned} \log \{\mu _{ij}^{(\ell )}\}=X_{ij}^{(\ell )}\beta ^{(\ell )}+Z_{ij}^{(\ell )}u_i^{(\ell )}, \end{aligned}$$

and the binary data \((\ell =7,8)\) are postulated by binomial distribution with logit link function

$$\begin{aligned} \mathrm{logit}\{\mu _{ij}^{(\ell )}\}=X_{ij}^{(\ell )}\beta ^{(\ell )}+Z_{ij}^{(\ell )}u_i^{(\ell )}. \end{aligned}$$

The joint model further assumes that given the random effects \(u_i^{(\ell )}\)\((\ell =1,\ldots ,8)\), the observations across all visits and different types of responses are independent. Therefore, the association pattern across all visits and response variables are established by the correlation structures among the random effects. To handle model estimation, this study develops an efficient algorithm, which combines the idea of penalized quasilikelihood framework [5, 23] and the expectation/conditional maximization either algorithm (ECME, [35, 44]).

The proposed joint model can be applied to fit the wearable device data. The results show that four responses, energy expenditure levels, number of daily steps, whether daily MVPA time is greater than one hour, and whether the highest energy expenditure rate measured by METs in 10 min is greater than 3, will be improved in the exercise treatment group. Therefore, the analysis demonstrates the health benefits for physical activity intervention on population level.

The model of the correlation structure can also facilitate the study among typical subgroups of research interests. For example, a study focuses on the longitudinal pattern of sedentary time and energy expenditure in a subgroup of active participants whose first week records have: (1) the proportion of long sedentary bout is less than \(20\%\); (2) the proportion of long active bouts is more than \(30\%\); (3) more than 40 times of daily standing up; (4) more than 6000 daily steps; (5) more than 1 h daily MVPA time; (6) more than 3 METs for the most intensive activities in 10 min. A naive solution for this problem is to analyze the individuals who meet those criteria. However, the physical activity study only has a small sample, and there could be few or even none of the individuals meet all of the criteria. On the other hand, the proposed joint model can handle this issue. Statistically, the mean sedentary time and energy expenditure can be expressed in a conditional expectation formulation as follows:

$$\begin{aligned} E\left\{ {Y_{ij}^{(\ell )}\Big |Y_{i1}^{(3)}<0.2,Y_{i1}^{(4)}\ge 0.3,Y_{i1}^{(5)}\ge 40,Y_{i1}^{(6)}\ge 6000,Y_{i1}^{(7)}=1,Y_{i1}^{(8)}=1}\right\} , \end{aligned}$$

where \(\ell =1,2\). The conditional expectation can be estimated based on the joint model via Monte Carlo samplings. In this application, the estimates suggest that the active participants in the first week would have lower sedentary time than other subjects across all five weeks. In addition, for those active participants, the exercise treatment would help them to have faster decreasing rate in sedentary time through weeks comparing to the control group. A reasonable explanation is that the supervised structured exercise training leads to further reductions in sedentary behaviors. For energy expenditure levels in those exercise treatment participants, the active ones have higher outcome than the inactive ones for the first week but the difference is gradually decreasing. In particular, active subjects have decreased energy expenditure across weeks. In this study, all participants in the exercise groups completes the same amount of exercise each week (\(\sim 200\) min) regardless of their baseline activity status. This is a standard practice in such trials to ensure all participants complete the same dose. However, the evaluation of the conditional expectation based on the joint model suggests that active participants at baseline decrease their energy expenditure as a result of the standard intervention. The data analysis suggests that future studies could consider personalized exercise programs based on initial activity status to promote increases in energy expenditure for all participants.

4 Functional Data Analysis

When research interest focuses on minute-by-minute temporal pattern of physical activity over a period of monitoring time, the functional data [24, 38, 42, 43] framework can be applied to our data analysis. Physical activity information obtained by wearable device is often summarized into time intervals by every 1 or 5 or 10 min. For a univariate response, Schrack et al. [45] explore smoothing curves for activity counts per minute across 24-h by different age groups. Goldsmith et al. [22] discuss a functional data analysis method to explore the pattern of diurnal activity profile (aggregated into 10-min intervals) in children. In the following sections, we discuss the utility of functional data models to handle multivariate, multilevel, and excess zero features in analyzing physical activity data.

4.1 Multivariate Functional Data Analysis

Similar to longitudinal data analysis, the joint modeling of multiple aspects of physical activity is useful for health studies. Li et al. [30] propose a functional data method to jointly model energy expenditure and interruptions to sedentary behavior across 36 five-minute intervals. The energy expenditure is a continuous measurement skewed to the right. The interruptions to sedentary behavior is a binary variable to indicate whether sedentary behavior was interrupted at least once in an interval. The joint functional data model is

$$\begin{aligned} d_\mathrm{tr}\{Y_{i}(t);\lambda \}= & {} \mu (t)+\mathbf{U}_{i}(t) +\epsilon _{yi}(t);\\ \mathrm{logit}[\hbox {pr}\{W_i(t)=1|\mathbf{V}_{i}(t)\}]= & {} \nu (t)+\mathbf{V}_{i}(t), \end{aligned}$$

where \(\{Y_i(t),W_i(t)\}\) denotes continuous and binary outcomes at time interval t for subject i, \(d_\mathrm{tr}(\cdot ;\lambda )\) is the Box-Cox transformation function with transformation parameter \(\lambda \), \(\mu (t)\) and \(\nu (t)\) are fixed effect curves, \(\mathbf{U}_{i}(t)\) and \(\mathbf{V}_{i}(t)\) are correlated random effect curves, and \(\epsilon _{yi}(t)\) denotes independent random noise. The model assumes that given \(\mathbf{U}_{i}(t)\) and \(\mathbf{V}_{i}(t)\), the paired observations are independent for all t, and thus, the correlation structure between the two outcomes is postulated by the random effect curves \(\mathbf{U}_{i}(t)\) and \(\mathbf{V}_{i}(t)\). The two random effect curves are further modeled by principal components as

$$\begin{aligned} \mathbf{U}_{i}(t)= \sum _{\ell =1}^{k_y} f_{y,\ell }(t) \alpha _{yi,\ell }; \ \mathbf{V}_{i}(t)= \sum _{\ell =1}^{k_w} f_{w,\ell }(t) \alpha _{wi,\ell }, \end{aligned}$$

where \(k_y\) and \(k_w\) are the number of principal components, \(f_{y,\ell }(t)\) and \(f_{w,\ell }(t)\) are orthogonal principal component functions, and \(\alpha _{yi,\ell }\) and \(\alpha _{wi,\ell }\) are principal component scores. \(\alpha _{yi,\ell }\)\((\ell =1,\ldots ,k_y)\) and \(\alpha _{wi,\ell ^*}\)\((\ell ^*=1,\ldots ,k_w)\) are set to be correlated to establish the association for two outcomes.

To analyze the data obtained from the physical activity study [28], the multivariate functional data model has \(Y_i(t)\) to be METs minus 1.24 for subject i in the tth time interval. \(W_i(t)=1\) if sedentary behavior is interrupted at least once in the tth time interval and is zero otherwise. The study displays that the energy expenditure increases dramatically at about 15 min before the MVPA bout, and then decreases to the starting level by an hour after the bout. The probability of interrupting sedentary behavior follows the similar pattern. In addition, it is of interest to compare the energy expenditure level for a participant with/without consecutive sedentary behavior interruptions in the previous 10 min. This is equivalent to estimate the conditional expectation

$$\begin{aligned}&E\{Y_i(t)|W_i(t-1)=1,W_i(t-2)=1\} \ \ \ \text {and} \ \ \ \\&E\{Y_i(t)|W_i(t-1)=0,W_i(t-2)=0\}. \end{aligned}$$

The fitted model shows that without previous sedentary behavior interruptions, the energy expenditure is higher around the MVPA bout. On the other hand, the simulation study illustrates that if the association structure between energy expenditure and sedentary behavior interruptions is ignored (i.e., two outcomes are assumed to be independent), the estimation would lead to biased conclusion.

4.2 Multilevel Functional Data Analysis

Physical activity information can be collected by accelerometer device over several days, and thus, the functional data can be multilevel for daily observations nested in days and days nested in subjects. Goldsmith et al. [21] propose a generalized multilevel functional data model to study physical activity response observed by 144 ten-minute intervals per subject per day for 5 days. The model is

$$\begin{aligned} g[\mu _{ij}(t)] = \beta _0(t) + \sum _{k=1}^{p} x_{ij,k}\beta _k(t) + b_i(t) + \nu _{ij}(t), \end{aligned}$$

where \(\mu _{ij}(t)\) represents the mean curve for functional response \(Y_{ij}(t)\) for subject i on day j at time interval t, given covariate \(x_{ij,k}\), subject-specific random effect curve \(b_i(t)\) and day-specific random effect curve \(\nu _{ij}(t)\), \(g(\cdot )\) is a known link function, \(\beta _k(t)\) are fixed effect coefficient functions corresponding to the scalar covariates \(x_{ij,k}\), p is the dimension of covariates. This model is estimated by a Bayesian method.

Li et al. [31] work on a more complicated functional data structure for energy expenditure (METs) measured by every 5 min. The dataset is collected from 5 days a week (Monday through Friday) for 5 separated weeks. Therefore, the hierarchical data structure has daily observations nested in weeks and weeks nested in subjects. The study uses a three-level functional data model to handle the issue. The model is

$$\begin{aligned} Y_{ijk}(t)&=\mu _{\cdot \cdot }(t)+\mu _{j\cdot }(t)+ \mu _{\cdot k}(t)+\mu _{jk}(t)+{\varvec{\xi }}_i(t) + {\varvec{\eta }}_{ij}(t)\\&\quad + {\varvec{\zeta }}_{ik}(t)+ {\varvec{\gamma }}_{ijk}(t)+\epsilon _{ijk}(t), \end{aligned}$$

where \(\mu _{\cdot \cdot }(t)\) is the population mean curve, \(\mu _{j\cdot }(t)\), \(\mu _{\cdot k}(t)\), and \(\mu _{jk}(t)\) are week-specific, day-specific, and week\(\times \)day interaction mean curves, \({\varvec{\xi }}_i(t)\), \({\varvec{\eta }}_{ij}(t)\), \({\varvec{\zeta }}_{ik}(t)\) and \({\varvec{\gamma }}_{ijk}(t)\) are mutually independent subject-specific, week-within-subject, day-within-subject, and week\(\times \)day interaction-within-subject random effect curves, and \(\epsilon _{ijk}(t)\) denotes random noise. The model can be estimated by an extension of the ECME algorithm, and the estimation approach can be used to handle incomplete functional data. This work also suggests to use Wald test to handle hypothesis tests for mean curves.

There are many other methodology developments involving multilevel functional data model to analyze physical activity data. For example, Xiao et al. [50] propose a covariate-dependent functional model to quantify the lifetime circadian rhythm of physical activity; Shou et al. [46] discuss a structured functional principal component analysis method to handle multiple levels of variation generated by nested and crossed study designs.

4.3 Functional Data Analysis with Excess Zero

Physical activity information aggregated by 1- or 5- or 10-min intervals is featured by excess zeros for variables such as numbers of steps and standing-up behaviors. This issue is the result of massive inactive intervals recorded by wearable devices, where no movement signal is captured. To assess the data with excess zeros, Bai et al. [4] propose a two-stage model. The first stage is to model \(A_i(t)\) as a binary factor to indicate whether subject i is active at time interval t. \(A_i(t)=1\) represents active time interval, while \(A_i(t)=0\) indicates inactive time interval. The second stage is to model \(Y_i(t)\) as a non-negative variable (e.g., activity counts or number of steps) conditioning on \(A_i(t)=1\). The model is

$$\begin{aligned} \mathrm{logit} [\hbox {pr}\{A_i(t) = 1 | Z_i(t),H_i(t)\}] = \beta _0(t) + Z_i(t)^{\mathrm{T}}\beta _1 + H_i(t)^{\mathrm{T}}\beta _2(t), \end{aligned}$$

and given \(A_i(t) = 1\),

$$\begin{aligned} \log \{Y_i(t)\} = \gamma _0(t) + Z_i(t)^{\mathrm{T}}\gamma _1 + H_i(t)^{\mathrm{T}}\gamma _2(t) + \epsilon _i(t), \end{aligned}$$

where \(Z_i(t)\) and \(H_i(t)\) are time-invariant and time-varying covariates, respectively, \(\beta _0(t)\) and \(\gamma _0(t)\) are time-varying intercepts, \(\beta _1\) and \(\gamma _1\) are time-invariant coefficients, \(\beta _2(t)\) and \(\gamma _2(t)\) are time-varying coefficients, and \(\epsilon _i(t)\) has \(E\{\epsilon _i(t)\}=0\). The two-stage model can be estimated by solving estimation equations.

Li et al. [33] extend the definition of time intervals from two categories (inactive and active) to three categories (inactive, partially active and active). This extension can cover a wide range of activity combinations. For example, in a 5-min interval, a wearer can be inactive for 2 min and walk for 3 min. To implement this setting, this study defines \(C_{i}(t)\) for subject i at time interval t where \(C_{i}(t)\in \{1,2,3\}\) represents inactive, partially active, and completely active intervals, respectively. \(P_{i}(t)\) is the proportion of active behavior in time interval t with \(P_{i}(t)=0\) when \(C_{i}(t) = 1\), \(0<P_{i}(t)<1\) when \(C_{i}(t) = 2\), and \(P_{i}(t)=1\) when \(C_{i}(t) = 3.\)\(Y_{i}(t)\) denotes energy expenditure rate with \(Y_{i}(t)=0\) when \(C_{i}(t) = 1\) and \(Y_{i}(t)>0\) otherwise. The proposed method uses the continuation-ratio model suggested by Molenberghs and Verbeke [37] to model the ordinal outcome \(C_{i}(t)\). The Beta regression is employed to model proportional outcome \(P_i(t)\). The Box-Cox transformation is applied to handle skewed \(Y_{i}(t)\). The joint model is

$$\begin{aligned} \mathrm{logit}[ \hbox {pr}\{C_i(t)>\ell | C_i(t)\ge \ell ,\mathbf{U}_{C_{\ell },i}(t)\}]= & {} \mu _{C_{\ell }}(t)+\mathbf{U}_{C_{\ell },i}(t) , \qquad \ell =1,2, \\ \mathrm{logit}[E\{P_i(t)|C_i(t)=2,\mathbf{U}_{P,i}(t)\}]= & {} \mu _P(t)+\mathbf{U}_{P,i}(t) ,\\ d_\mathrm{tr}\{Y_{i}(t) |C_i(t)\ge 2, \mathbf{U}_{Y,i}(t);\lambda \}= & {} \mu _{Y_1}(t)+I\{C_i(t)=3\}\mu _{Y_2}(t)\\&+\mathbf{U}_{Y,i}(t) +\epsilon _{Y,i}(t), \end{aligned}$$

where \(\mu _{C_{\ell }}(t)\), \(\mu _P(t)\), and \(\mu _{Y_{\ell }}(t)\) are fixed effect curves, \(\mathbf{U}_{C_{\ell },i}(t)\), \(\mathbf{U}_{P,i}(t)\) and \(\mathbf{U}_{Y,i}(t)\) are random effect curves, \(\lambda \) is transformation parameter and \(\epsilon _{Y,i}(t)\) denotes random noise. The model can be estimated by an ECME procedure. The algorithm iteratively runs a Newton-Raphson estimation step, an EM estimation step and a principal component selection step.

The model to handle excess zeros can facilitate efficient estimation of the energy expenditure rate for active behaviors, physical activity energy expenditure (PAEE). In the application from Li et al. [33], there exists a relationship for \(Y_i(t)+1.25 = 1.25\times \{1-P_i(t)\} + P_i(t)\mathrm{{PAEE}}_i(t),\) and thus the term \(Y_i(t)/P_i(t)\) represents energy expenditure rate for active behaviors \((\mathrm{{PAEE}}-1.25)\). A typical research interest is to explore the PAEE in a 5-min interval with active behaviors use more than 2.5 min, which is equivalent to study the conditional expectation \(E\{Y_i(t)/P_i(t)|C^{(1)}_i(t)=1,P_i(t)>0.5\}\). Based on the model estimation from the model, the PAEE rate increases significantly at about 10 min before the MVPA bout, and returns to the initial level after an hour from the bout.

5 Discussion

We have reviewed the statistical methods to analyze physical activity data obtained from wearable accelerometer-based devices. The large-scale raw data can be summarized by useful algorithms and R packages. Longitudinal data methods provide appropriate estimation on responses followed by days and weeks. The applications of function data approaches demonstrate their utilities to model the activity pattern across minute-by-minute intervals. These methods can be extended to handle more complicated accelerometer data with multi-sensors to collect physiologic variables such as skin temperature and heat flux.

One potential limitation for our discussed methods is that we require the physical activity data to be accurate and complete. Staudenmayer et al. [47] suggest that measurement error/misclassification and missing data problems could lead to biased conclusion in physical activity studies. Measurement error/misclassification issue occurs when accelerometer device may not accurately detect real behavior. Missing data are common for non-compliance reasons in randomized trials. Missing data problem may also arise if wearers take off the monitor for bathing or water activities. Statistical methods (e.g., [7,8,9, 34]) to handle these issues can be employed to obtain valid inference conclusions.