1 Introduction

The ordinary form of the differential equations is considered very important for the researcher community due to the assortment of applications in technology, science, and engineering. The recent work is related to the nonlinear Emden–Fowler model (NEFM) known as a singular differential model, which is considered complicated because of its stiffer nature. The researchers applied many analytical and numerical tools in different decades to solve the NEFM. The NEFM has been programmatic in many areas of fluid dynamics, population growth, pattern creation system and chemical reactors. The NEFM is mathematically written as (Sabir 2020a, 2020b; Adel et al. 2020; Sabir et al. 2020a; Li et al. 2017):

$$\left\{ \begin{array}{l} \frac{{d^{2} v}}{{dt^{2} }} + \frac{\xi }{t}\frac{dv}{{dt}} + h(t)z(v) = 0, \xi \ge 1 \hfill \\ v(0) = \varepsilon ,\,\,\,\,\,\,\,\frac{dv(0)}{{dt}} = 0, \hfill \\ \end{array} \right.$$
(1)

where \(\xi\) is the value of the shape factor, for \(h(t) = 1\), the NEFM takes the form of Lane–Emden singular model (LESM), mathematically written as:

$$\left\{ \begin{array}{l} \frac{{d^{2} v}}{{dt^{2} }} + \frac{\xi }{t}\frac{dv}{{dt}} + z(v) = 0, \xi \ge 1 \hfill \\ v(0) = \varepsilon ,\,\,\,\,\,\,\,\frac{dv(0)}{{dt}} = 0. \hfill \\ \end{array} \right.$$
(2)

The celebrated LESM presented in the above Eq. (2) presented by a famous astrophysicists H. Lane along with R. Emden. This LESM is applied in the modeling of spherical gas cloud, mathematical physics, structure of polytropic star, stellar configuration, self-gravitating gas clouds and in the modeling of cluster galaxies (Ahmad et al. 2017; Singh et al. 2019a; Abbas et al. 2019; Li et al. 2018). The function \(z(v)\) shows several forms of the LESM like as \(z(v) = v^{r}\) is considered a most prominent form. It is perceived that the LESM is identified as a linear equation for the values of r = 0 and 1, else it depicts nonlinear performance. The LESM of second kind presents the isothermal gas sphere for \(z(v) = e^{v}\). Few other forms of \(z(v)\) express the nonlinearity, like \(\sin v/\cos v,\,\sinh v\) and \(\cosh v,\) etc. The LESM becomes white dwarf by taking \(z(v) = \left( {v^{2} - C} \right)^{1.5}\) proposed by Chandrasekhar (Chandrasekhar 1967). The LESM has a variety of applications in dusty fluid models (Flockerzi and Sundmacher 2011), physical sciences (Mandelzweig and Tabakin 2001), gaseous star (Luo et al. 2016), electromagnetic theory (Khan et al. 2015), catalytic reactions (Rach et al. 2014), sublinear neutral factor (Dv{z}urina et al. 2020), isotropic continuous media (Radulescu and Repovs 2012), morphogenesis investigations (Ghergu and Radulescu 2007), quantum/classical mechanics (Ramos 2003) and oscillating magnetic systems (Dehghan and Shakeri 2008).

The singular systems are not easy to solve because of stiff nature and only a few numerical and analytic schemes found in the literature to solve these models. Some testified approaches to handle these models are the Adomian decomposition method proposed by Shawagfeh (Shawagfeh 1993). Sabir et al. (2020) solved a 3rd singular functional system using the differential transformation approach. Romas et al. (Ramos 2008) proposed the series scheme to solve the LESM analytically. Singh et al. (2019b) discussed Haar wavelet based collocation approach to solve the LESM. Saeed et al. (2017) implemented the Haar Adomian approach in order to solve the fractional nonlinear LESM. Dizicheh et al. (2020) suggested the Legendre spectral wavelet approach to solve the nonlinear LESM. Hashemi et al. (Hashemi et al. 2017) proposed the LESM using the group preserving and reproduced kernel approaches. Bender et al. (Bender et al. 1989) derived a perturbative approach to evade the singular point difficulty. Nouh (Nouh 2004) discussed the singular models using the power series as well as Pade approximation schemes and many more (Angelov et al. Oct. 2018; Angelov and Gu 2019; Sabir et al. 2022a, 2022b; Raja et al. 2018; Botmart et al. 2022).

The model based on the pantograph differential (PD) equation is considered significant due to its enormous submissions in the variety of biological and scientific works, like as, dynamical population system, communication system, control problems, light absorption in the stellar matter, engineering, economical models, transport, electronic systems, quantum mechanics, propagation systems and infectious diseases (Li and Liu 2000; Kuang and ed., 1993; Zhao 1995; Li et al. 2014; Niculescu 2001; Vanani et al. 2011). Many numerical and analytical tools have been implemented to solve such models, as the Direchlet series approach has been functional to solve the PD model analytically (Liu and Li 2004), differential transformation one-dimensional approach has been implemented to solve the nonlinear higher order multiple PD system (Koroma et al. 2013), the Taylor approximate polynomial has been used to solve the PD system (Sezer and Şahin 2008) and many other approaches have been introduced to solve PD system, see References (Keskin et al. 2007; Derfel and Iserles 1997; Abazari and Abazari 2009; Saadatmandi and Dehghan 2009; Benhammouda et al. 2014; Widatalla and Koroma 2012; Feng 2013).

The intension of the present research is to design a nonlinear third order (NTO) pantograph Emden–Fowler system (PEFS), i.e., (NTO-PEFS) together with its two forms. The solution of the designed system based equations have been proposed based Levenberg–Marquardt backpropagation (LMB) neural network. The system based on singular models has huge importance in the field of science and engineering, e.g., chemical reactor fields, theory of boundary layer, network flow in biology and optimization control (Shah, et al. 2020; Umar et al. 2020a; Umar et al. 2020b; Jadoon, et al. 2020; Jadoon 2020; Bukhari et al. 2020; Ahmad 2020; Mehmood et al. 2020; Raja et al. 2020).

The highlighted geographies of the current research are presented as:

  • The design of a novel NTO-PEFS is presented with its two forms using the typical form of the NEFM and the PD model together with the details of the singular points, shape factors and pantographs.

  • The solution of both the forms based novel NTO-PEFS have been numerically presented by applying the strength of the LMB neural network approach.

  • A reference-based dataset using the exact solutions with the proposed neural network approach is conventional for each form of the novel NTO-PEFS.

  • The matching/overlapping of the proposed outcomes establishes the worth of the LMB neural network approach to solve the novel NTO-PEFS.

  • The LMB neural network approach performance using the comparative studies based on mean square error (MSE), correlation, error histograms (EHs) and regression metrics is also provided.

The other paper is planned as: The construction of NTO-PEFS together with its both forms is given in Sect. 2. The design of the novel NTO-PEFS based problems are given in Sect. 3. The LMB neural network approach, essential description, and numerical solutions of the novel NTO-PEFS via LMB neural network approach is given in Sect. 4. The final statements are provided in the final Sect.

2 Structure of the novel NTO-PEFS

Two different forms based on the novel NTO-PEFS are provided in this section. The novel NTO-PEFS structure is provided with the shape factors, pantographs and singularity for both of the types. The boundary conditions (BCs) of the novel NTO-PEFS are found using the terminology of the typical NEFM. To derive the novel NTO-PEFS, the mathematical construction is provided as (Guirao et al. 2020; Sabir et al. 2022c, 2020b):

$$\left\{ \begin{gathered} t^{{ - q_{1} }} \frac{{d^{\alpha } }}{{dt^{\alpha } }}\left( {t^{{q_{1} }} \frac{{d^{\gamma } }}{{dt^{\gamma } }}} \right)u(\beta t) + h_{1} (t)z_{1} (u,v) = l(t), \hfill \\ t^{{ - q_{2} }} \frac{{d^{\alpha } }}{{dt^{\alpha } }}\left( {t^{{q_{2} }} \frac{{d^{\gamma } }}{{dt^{\gamma } }}} \right)v(\beta t) + h_{2} (t)z_{2} (u,v) = m(t), \hfill \\ \end{gathered} \right.$$
(3)

where \(q_{1}\) and \(q_{2}\) are chosen as positive and real, \(h_{1} (t)\) and \(h_{2} (t)\) are the given values of the function, \(l(t)\) and \(m(t)\) are the forcing functions, \(\beta\) shows the pantographs, \(z_{1} (u,v)\) and \(z_{2} (u,v)\) are the functions of u and v. To construct the NTO-PEFS, the values can be selected as:

$$\left\{ \begin{array}{ll} q_{1} + m_{1} = 3,\,\, & q_{1} ,\,\,m_{1} \ge 1 \hfill \\ q_{2} + m_{2} = 3,\,\, & q_{2} ,\,\,m_{2} \ge 1. \hfill \\ \end{array} \right.$$
(4)

The following possibilities can be chosen as:

$$q_{1} = 2, m_{1} = 1,$$
(5)
$$q_{2} = 2, m_{2} = 1.$$
(6)

Using the Eqs. (5) and (6), the system (3) is categorized in two forms as:

2.1 1st form of the novel NTO-PEFS

System (3) takes the form by using the Eq. (5) is

$$\left\{ \begin{gathered} t^{{ - q_{1} }} \frac{{d^{2} }}{{dt^{2} }}\left( {t^{{q_{1} }} \frac{d}{dt}} \right)u(\beta t) + h_{1} (t)z_{1} (u,v) = l(t), \hfill \\ t^{{ - q_{2} }} \frac{{d^{2} }}{{dt^{2} }}\left( {t^{{q_{2} }} \frac{d}{dt}} \right)v(\beta t) + h_{2} (t)z_{2} (u,v) = m(t), \hfill \\ \end{gathered} \right.$$
(7)

The derivative form of the Eq. (7) is given as:

$$\left\{ \begin{gathered} \frac{{d^{2} }}{{dt^{2} }}\left( {t^{{q_{1} }} \frac{d}{dt}} \right)u(\beta t) = \beta^{3} t^{{q_{1} }} \frac{{d^{3} }}{{dt^{3} }}u(\beta t) + 2\beta^{2} q_{1} t^{{q_{1} - 1}} \frac{{d^{2} }}{{dt^{2} }}u(\beta t) + \beta q_{1} (q_{1} - 1)t^{{q_{1} - 2}} \frac{d}{dt}u(\beta t), \hfill \\ \frac{{d^{2} }}{{dt^{2} }}\left( {t^{{q_{2} }} \frac{d}{dt}} \right)v(\beta t) = \beta^{3} t^{{q_{2} }} \frac{{d^{3} }}{{dt^{3} }}u(\beta t) + 2\beta^{2} q_{2} t^{{q_{2} - 1}} \frac{{d^{2} }}{{dt^{2} }}u(\beta t) + \beta q_{2} (q_{2} - 1)t^{{q_{2} - 2}} \frac{d}{dt}u(\beta t), \hfill \\ \end{gathered} \right.$$
(8)

Using the Eq. (8), the simplified form of the Eq. (7) is taken as:

$$\left\{ \begin{gathered} \beta^{3} \frac{{d^{3} }}{{dt^{3} }}u(\beta t) + \frac{{2\beta^{2} q_{1} }}{t}\frac{{d^{2} }}{{dt^{2} }}u(\beta t) + \frac{{\beta q_{1} (q_{1} - 1)}}{{t^{2} }}\frac{d}{dt}u(\beta t) + h_{1} (t)z_{1} (u,v) = l(t), \hfill \\ \beta^{3} \frac{{d^{3} }}{{dt^{3} }}v(\beta t) + \frac{{2\beta^{2} q_{2} }}{t}\frac{{d^{2} }}{{dt^{2} }}v(\beta t) + \frac{{\beta q_{2} (q_{2} - 1)}}{{t^{2} }}\frac{d}{dt}v(\beta t) + h_{2} (t)z_{2} (u,v) = m(t). \hfill \\ \end{gathered} \right.$$
(9)

The associated BCs are written as:

$$\left\{ \begin{gathered} u(0) = A_{1} ,\,\,\,\frac{du(0)}{{dt}} = 0,\,\,\,\,\frac{{d^{2} u(0)}}{{dt^{2} }} = 0, \hfill \\ v(0) = A_{2} ,\,\,\,\frac{dv(0)}{{dt}} = 0,\,\,\,\,\frac{{d^{2} v(0)}}{{dt^{2} }} = 0. \hfill \\ \end{gathered} \right.$$
(10)

The system (9) and (10) shows the first form of the novel NTO-PEFS. For both u(t) and v(t), the parameters of the pantographs are noticed in the 1st, 2nd and 3rd factor and the singular points appeared twice at \(t = 0\,\,{\text{and}}\,\,t^{2} = 0\,\). The shape factors are \(2q_{1}\) and \(q_{1} (q_{1} - 1)\) for u(t), while \(2q_{2}\) and \(q_{2} (q_{2} - 1)\) for v(t) respectively. It is observed for \(q_{1} = q_{2} = 1\), the 3rd factor vanishes, and the shape factor value becomes 2.

2.2 2nd form of the novel NTO-PEFS

System (3) takes the form by using the Eq. (6) is

$$\left\{ \begin{gathered} t^{{ - q_{1} }} \frac{d}{dt}\left( {t^{{q_{1} }} \frac{{d^{2} }}{{dt^{2} }}} \right)u(\beta t) + h_{1} (t)z_{1} (u,v) = l(t), \hfill \\ t^{{ - q_{2} }} \frac{d}{dt}\left( {t^{{q_{2} }} \frac{{d^{2} }}{{dt^{2} }}} \right)v(\beta t) + h_{2} (t)z_{2} (u,v) = m(t), \hfill \\ \end{gathered} \right.$$
(11)

The derivative form of the Eq. (11) is given as:

$$\left\{ \begin{gathered} \frac{d}{dt}\left( {t^{{q_{1} }} \frac{{d^{2} }}{{dt^{2} }}} \right)u(\beta t) = \beta^{3} t^{{q_{1} }} \frac{{d^{3} }}{{dt^{3} }}u(\beta t) + \beta^{2} q_{1} t^{{q_{1} - 1}} \frac{{d^{2} }}{{dt^{2} }}u(\beta t), \hfill \\ \frac{d}{dt}\left( {t^{{q_{2} }} \frac{{d^{2} }}{{dt^{2} }}} \right)v(\beta t) = \beta^{3} t^{{q_{2} }} \frac{{d^{3} }}{{dt^{3} }}u(\beta t) + \beta^{2} q_{2} t^{{q_{2} - 1}} \frac{{d^{2} }}{{dt^{2} }}u(\beta t), \hfill \\ \end{gathered} \right.$$
(12)

Using the Eq. (12), the simplified form of the Eq. (11) is taken as:

$$\left\{ \begin{gathered} \beta^{3} \frac{{d^{3} }}{{dt^{3} }}u(\beta t) + \frac{{\beta^{2} q_{1} }}{t}\frac{{d^{2} }}{{dt^{2} }}u(\beta t) + h_{1} (t)z_{1} (u,v) = l(t), \hfill \\ \beta^{3} \frac{{d^{3} }}{{dt^{3} }}v(\beta t) + \frac{{\beta^{2} q_{2} }}{t}\frac{{d^{2} }}{{dt^{2} }}v(\beta t) + h_{2} (t)z_{2} (u,v) = m(t). \hfill \\ \end{gathered} \right.$$
(13)

The associated BCs are written as:

$$\left\{ \begin{gathered} u(0) = A_{1} ,\,\,\,\frac{du(0)}{{dt}} = B_{1} ,\,\,\,\,\frac{{d^{2} u(0)}}{{dt^{2} }} = 0, \hfill \\ v(0) = A_{2} ,\,\,\,\frac{dv(0)}{{dt}} = B_{2} ,\,\,\,\,\frac{{d^{2} v(0)}}{{dt^{2} }} = 0. \hfill \\ \end{gathered} \right.$$
(14)

The system (13) and (14) shows the second form of the novel NTO-PEFS. \(q_{1}\) and \(q_{2}\) are the shape factor and pantograph expressions appear twice in the first and second terms of the Eq. (11). For both u(t) and v(t), the parameters of pantographs are noticed in the 1st and 2nd forms of novel NTO-PEFS, while the single singular point and shape factor are also noticed in other terms of presented NTO-PEFS.

3 Methodology

The methodology based on the LMB neural network approach consists of two stages; in the first stage, essential explanations are provided to create the dataset for the proposed LMB neural network approach, whereas in the second stage, an execution procedure for the proposed LMB neural network approach is defined.

As compared to traditional deterministic numerical and analytical solution techniques, the intelligent computing based proposed LMB are recently introduced mythologies for solving the ODEs/PDEs based problems without even interfering in to simple system by the use transformation. Normally in these methods, whole solution starts from an element known as artificial neuron, which is responsible for picking up the input and then multiplying this input with the suitable weights to get the results continually adding them with the involvement of log-sigmoidal activation function. These solution approximation methodologies consist of three basic layers i.e., input layer, hidden layer and output layer.

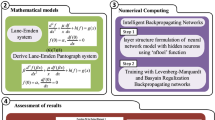
Implementing/execution of these type of computing solvers is exploited in the presented study by utilizing the strength of LMB neural network to scrutinize the solution of novel nonlinear third order (NTO) pantograph Emden–Fowler system (PEFS), i.e., (NTO-PEFS) together with its two forms. These network models represent the highly nonlinear ODEs terms and with ease to handle the singularity as well as delay. Thus the proposed LMB based neural networks provides an alternate, precise and reliable solution methodology for NTO-PEFS. Also, the presented technique produces unmatched fast convergent outcomes with reliability and stability as compared to other existing traditional techniques due to nonlinearity, singularity and delays. The approximate solutions obtained by these methods are seem generally reliable, stable, and swift convergence. The proposed neural networks methods proved to be accurate, reliable and robust having the capabilities to predict the expected feature outcomes based on testing, training and validation processes. Recently, several researchers have been considering intelligent computing algorithms/paradigms for solving nonlinear stiff systems arising in variety of domain of applied science and technology (Fig. 1).

In this study, Fig. 2 shows the process of the workflow and the reference results, i.e., datasets of LMB neural network approach. Figure 3 represents a single neuron system in neural network approach, while the proposed LMB neural network approach is executed using ‘nftool’ in the Matlab software package along with the setting of suitable testing data, hidden neurons, validation/training data and learning schemes. The settings of parameter of the networks, i.e., percentage of 80, 10 and 10 of arbitrary selected samples for respective training, testing and validation sets, 10 number of hidden neurons, single input and two vectors, is done with care, exhaustive simulation, experience and knowledge of the solver as well as optimization paradigm. The best compromise between accuracy and complexity to avoid the over-fitting/under-fitting scenarios is incorporated for finding the solution NTO-PEFS with proposed LMB based neural networks. Additionally, the exact solution of NTO-PEFS are used as reference dataset for LMB because of non-availability of numerical method that can simultaneous handle the nonlinearity, singularity as well as pantograph types of the delay.

Fig. 1
figure 1

Workflow design of the LMB neural network for NTO-PEFS

Full size image
Fig. 2
figure 2

Designed construction based on single neuron

Full size image
Fig. 3
figure 3

LMB neural network for NTO-PEFS

Full size image

4 Numerical interpretations

Six different variants of both the forms of the novel NTO-PEFS treated numerically through the LMB neural network. The examples (1–3) show the first form, while the rest of the examples show the second form.

Example 1:

Consider the doubly singular nonlinear third order pantograph Emden–Fowler system is shown as:

$$\left\{ \begin{array}{l} \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}u\left( \frac{t}{2} \right) + \frac{1}{t}\frac{{d^{2} }}{{dt^{2} }}u\left( \frac{t}{2} \right) + \frac{1}{{t^{2} }}\frac{d}{dt}u\left( \frac{t}{2} \right) + u(t)v(t) = \frac{11}{2} - t^{6} , \hfill \\ \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}v\left( \frac{t}{2} \right) + \frac{1}{t}\frac{{d^{2} }}{{dt^{2} }}v\left( \frac{t}{2} \right) + \frac{1}{{t^{2} }}\frac{d}{dt}v\left( \frac{t}{2} \right) - u(t)v(t) = - \frac{11}{2} + t^{6} , \hfill \\ \end{array} \right.$$
(15)

associated to the BCs

$$u(0) = v(0) = 1,\,\,\frac{du(0)}{{dt}} = \frac{dv(0)}{{dt}} = \,\frac{{d^{2} u(0)}}{{dt^{2} }} = \frac{{d^{2} v(0)}}{{dt^{2} }} = \,\,0.$$

The true/exact form of the solution is \(\left[ {1 + t^{3} ,1 - t^{3} } \right].\)

Example 2:

Suppose the doubly singular third order pantograph Emden–Fowler system involving exponential function is shown as:

$$\left\{ \begin{array}{l} \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}u\left( \frac{t}{2} \right) + \frac{1}{t}\frac{{d^{2} }}{{dt^{2} }}u\left( \frac{t}{2} \right) + \frac{1}{{t^{2} }}\frac{d}{dt}u\left( \frac{t}{2} \right) + u(t)v(t) = \frac{9}{2}e^{\frac{t}{2}} + \frac{11}{4}te^{\frac{t}{2}} \hfill \\ + \frac{13}{{32}}t^{2} e^{\frac{t}{2}} + \frac{1}{64}t^{3} e^{\frac{t}{2}} + 1 - t^{6} e^{2t} , \\ \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}v\left( \frac{t}{2} \right) + \frac{1}{t}\frac{{d^{2} }}{{dt^{2} }}v\left( \frac{t}{2} \right) + \frac{1}{{t^{2} }}\frac{d}{dt}v\left( \frac{t}{2} \right) - u(t)v(t) = - \frac{9}{2}e^{\frac{t}{2}} - \frac{11}{4}te^{\frac{t}{2}} \hfill \\ - \frac{13}{{32}}t^{2} e^{\frac{t}{2}} - \frac{1}{64}t^{3} e^{\frac{t}{2}} - 1 + t^{6} e^{2t} , \\ \end{array} \right.$$
(16)

associated to the BCs

$$u(0) = 1,\,\,\frac{du(0)}{{dt}} = 0,\,v(0) = 1,\,\frac{dv(0)}{{dt}} = \,\frac{{d^{2} u(0)}}{{dt^{2} }} = \frac{{d^{2} v(0)}}{{dt^{2} }} = \,\,0.$$

The true solutions of Eq. (16) are \(\left[ {1 + t^{3} e^{t} ,1 - t^{3} e^{t} } \right].\)

Example 3:

Consider the doubly singular nonlinear third order pantograph Emden–Fowler system having trigonometric function is shown as:

$$\left\{ \begin{array}{l} \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}u\left( \frac{t}{2} \right) + \frac{1}{t}\frac{{d^{2} }}{{dt^{2} }}u\left( \frac{t}{2} \right) + \frac{1}{{t^{2} }}\frac{d}{dt}u\left( \frac{t}{2} \right) + u(t)v(t) = \frac{9}{2}\cos \left( \frac{t}{2} \right) - \frac{11}{4}t\sin \left( \frac{t}{2} \right) \hfill \\ - \frac{13}{{32}}t^{6} \cos \left( \frac{t}{2} \right) + \frac{1}{64}t^{3} \sin \left( \frac{t}{2} \right) + 1 - t^{6} \cos^{2} t, \hfill \\ \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}v\left( \frac{t}{2} \right) + \frac{1}{t}\frac{{d^{2} }}{{dt^{2} }}v\left( \frac{t}{2} \right) + \frac{1}{{t^{2} }}\frac{d}{dt}v\left( \frac{t}{2} \right) - u(t)v(t) = - \frac{9}{2}\cos \left( \frac{t}{2} \right) + \frac{11}{4}t\sin \left( \frac{t}{2} \right) \hfill \\ + \frac{13}{{32}}t^{6} \cos \left( \frac{t}{2} \right) + \frac{1}{64}t^{3} \sin \left( \frac{t}{2} \right) - 1 + t^{6} \cos^{2} t, \hfill \\ \end{array} \right.$$
(17)

associated to the BCs

$$u(0) = v(0) = 1,\,\,\frac{du(0)}{{dt}} = \frac{dv(0)}{{dt}} = \,\frac{{d^{2} u(0)}}{{dt^{2} }} = \frac{{d^{2} v(0)}}{{dt^{2} }} = \,\,0.$$

The exact/true solution of Eq. (17) is \(\left[ {1 + t^{3} \cos t,1 - t^{3} \cos t} \right].\)

Example 4:

Consider a singular nonlinear third order pantograph Emden–Fowler system having trigonometric function is shown as:

$$\left\{ \begin{array}{l} \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}u\left( \frac{t}{2} \right) + \frac{1}{4t}\frac{{d^{2} }}{{dt^{2} }}u\left( \frac{t}{2} \right) + u(t)v(t) = - \frac{1}{8}\cos \left( \frac{t}{2} \right) - \frac{1}{4t}\sin \left( \frac{t}{2} \right) + 1 - \sin^{2} t, \hfill \\ \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}v\left( \frac{t}{2} \right) + \frac{1}{4t}\frac{{d^{2} }}{{dt^{2} }}v\left( \frac{t}{2} \right) - u(t)v(t) = \frac{1}{8}\cos \left( \frac{t}{2} \right) + \frac{1}{4t}\sin \left( \frac{t}{2} \right) - 1 + \sin^{2} t. \hfill \\ \end{array} \right.$$
(18)

associated to the BCs

$$u(0) = v(0) = 1,\,\,\frac{du(0)}{{dt}} = 1,\,\frac{dv(0)}{{dt}} = - 1,\,\,\frac{{d^{2} u(0)}}{{dt^{2} }} = \frac{{d^{2} v(0)}}{{dt^{2} }} = \,\,0.$$

The exact/true solution of (18) is \(\left[ {1 + \sin t,1 - \sin t} \right].\)

Example 5:

Consider a singular nonlinear third order pantograph Emden–Fowler system having exponential function is shown as:

$$\left\{ \begin{array}{l} \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}u\left( \frac{t}{2} \right) + \frac{1}{4t}\frac{{d^{2} }}{{dt^{2} }}u\left( \frac{t}{2} \right) + u(t)v(t) = 1 + t^{2} + 2t - t^{6} e^{2t} + \frac{{t^{3} }}{64}e^{\frac{t}{2}} + \frac{{5t^{2} }}{16}e^{\frac{t}{2}} + \frac{3t}{2}e^{\frac{t}{2}} + \frac{3}{2}e^{\frac{t}{2}} , \hfill \\ \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}v\left( \frac{t}{2} \right) + \frac{1}{4t}\frac{{d^{2} }}{{dt^{2} }}v\left( \frac{t}{2} \right) - u(t)v(t) = - 1 - t^{2} - 2t + t^{6} e^{2t} - \frac{{t^{3} }}{64}e^{\frac{t}{2}} - \frac{{5t^{2} }}{16}e^{\frac{t}{2}} - \frac{3t}{2}e^{\frac{t}{2}} - \frac{3}{2}e^{\frac{t}{2}} . \hfill \\ \end{array} \right.$$
(19)

associated to the BCs

$$u(0) = v(0) = 1,\,\,\frac{du(0)}{{dt}} = \,\frac{dv(0)}{{dt}} = 1,\,\,\frac{{d^{2} u(0)}}{{dt^{2} }} = \frac{{d^{2} v(0)}}{{dt^{2} }} = \,\,0.$$

The exact/true solution of (19) is \(\left[ {1 + t + t^{3} e^{t} ,1 + t - t^{3} e^{t} } \right].\)

Example 6:

Consider a singular nonlinear third order pantograph Emden–Fowler system having exponential function is shown as:

$$\left\{ \begin{array}{l} \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}u\left( \frac{t}{2} \right) + \frac{1}{4t}\frac{{d^{2} }}{{dt^{2} }}u\left( \frac{t}{2} \right) + u(t)v(t) = \frac{5}{2} + t^{2} + 2t - t^{6} , \hfill \\ \frac{1}{8}\frac{{d^{3} }}{{dt^{3} }}v\left( \frac{t}{2} \right) + \frac{1}{4t}\frac{{d^{2} }}{{dt^{2} }}v\left( \frac{t}{2} \right) - u(t)v(t) = - \frac{5}{2} - t^{2} - 2t + t^{6} . \hfill \\ \end{array} \right.$$
(20)

associated to the BCs

$$u(0) = v(0) = 1,\,\,\frac{du(0)}{{dt}} = \,\frac{dv(0)}{{dt}} = 1,\,\,\frac{{d^{2} u(0)}}{{dt^{2} }} = \frac{{d^{2} v(0)}}{{dt^{2} }} = \,\,0.$$

The exact/true solution of (19) is \(\left[ {1 + t + t^{3} ,1 + t - t^{3} } \right].\)

The proposed results are calculated based LMB neural network in 0 to 1 with 0.01 step size for each problem of novel NTO-PEFS. LMB neural network is implemented to solve all examples of both forms of the novel NTO-PEFS given in the system (15–20) using ‘nftool’ with 80% training data, 10 neurons and 10% testing/validation based LMB optimization scheme. The designed neural network is obtainable in Fig. 3.

The obtained numerical result through LMB neural network for all examples of both forms of the novel NTO-PEFS are presented in Figs. Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 ,20. The NTO-PEFS results for the state of transition/ performance are plotted in Figs. 4 and 5. The MSE for training, testing, best curve and validation are presented for each example of both the categories of the novel NTO-PEFS are drawn in Fig. 4. The best performances are calculated at epochs 364, 634, 72, 204, 1000 and 453 are calculated around 2.8447 × 10–10, 4.7013 × 10–09, 7.0144 × 10–10, 7.4597 × 10–12, 1.8709 × 10–10 and 3.7001 × 10–10, respectively. The gradient and Mu value of LMB are performed for each example of both forms are [9.9733 × 10–08, 9.9905 × 10–08, 9.9014 × 10–08, 9.9279 × 10–08, 3.8021 × 10–07 and 9.9857 × 10–08] and [10–08, 10–08, 10–09, 10–11, 10–08 and 10–08] plotted in Fig. 5. These plots specify the correctness, as well as convergence of the LMB neural networks for each example of both form of the NTO-PEFS. Figures 6–11 authenticate the fitting plots for each example of both form of the NTO-PEFS. These Figures designate the results comparison obtained by the LMB neural network with the reference dataset of exact solutions for each example of both form of the NTO-PEFS. The testing/training and validation of the LMB neural network lie around 10–04 to 10–06 each example of both form of the NTO-PEFS. Figure 12 shows the plots of the error histograms (EHs) to examine the error investigation using the input/output grids for each example of both form of the NTO-PEFS. The EHs with zero-line reference are calculated 8.90 × 10–06, − 7.7 × 10–07, -2.0 × 10–06, −4.2 × 10–07, − 5.3 × 10–06 and 1.5 × 10–05 for all examples of the novel NTO-PEFS.

Fig. 4
figure 4

Performance curves for MSE using the designed LMB neural network for both the categories of the third order nonlinear pantograph Emden–Fowler model

Full size image
Fig. 5
figure 5

State transition for both the categories of the novel NTO-PEFS

Full size image
Fig. 6
figure 6

Comparison of LMB neural network of Example-1 for novel NTO-PEFS based category 1

Full size image
Fig. 7
figure 7

Comparison of LMB neural network of Example-2 for novel NTO-PEFS based category 1

Full size image
Fig. 8
figure 8

Comparison of LMB neural network of Example-3 for novel NTO-PEFS based category 1

Full size image
Fig. 9
figure 9

Comparison of LMB neural network of Example-1 for novel NTO-PEFS based category 2

Full size image
Fig. 10
figure 10

Comparison of LMB neural network of Example-2 for novel NTO-PEFS based category 2

Full size image
Fig. 11
figure 11

Comparison of LMB neural network of Example-3 for novel NTO-PEFS based category 2

Full size image
Fig. 12
figure 12

EHs for LMB neural network of Example-3 for both the categories of the novel NTO-PEFS

Full size image

The regression investigations are plotted in Figs. 13–18 for each example of both form of the NTO-PEFS. These investigations via co-relation are applied to conduct the regression analysis. It is seen that correlation values (R) are found to be 1, that indicates the perfect system, which clearly shows the correctness of LMB-neural network for the novel NTO-PEFS. Furthermore, the MSE convergence is achieved for validation, training, testing, backpropagation procedures, performance executed epochs are shown in Tables 1 for NTO-PEFS.

Fig. 13
figure 13

Regression for Example-1 based category 1

Full size image
Fig. 14
figure 14

Regression for Example-2 based category 1

Full size image
Fig. 15
figure 15

Regression for Example-3 based category 1

Full size image
Fig. 16
figure 16

Regression for Example-1 based category 2

Full size image
Fig. 17
figure 17

Regression for Example-2 based category 2

Full size image
Fig. 18
figure 18

Regression for Example-3 based category 2

Full size image
Table 1 LMB neural network for both the categories of the novel NTO-PEFS
Full size table

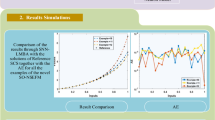
The proposed results (LMB neural network) have been compared for all examples of both categories of the novel NTO-PEFS is given in Fig. 19. The first category results are provided based Examples 1–3 are provided in Fig. 19a–b, whereas the second form is provided in Fig. 19c–d. It is observed that the obtained outcomes overlapped to the exact solutions for both forms of the novel NTO-PEFS. This results comparison indicates the precision and excellence of the designed LMB neural network scheme. The AE values for all examples of the novel NTO-PEFS is plotted in Fig. 20. Examples 1–3 indicate the AE values are plotted in Fig. 20 (a-b), whereas Examples 4–6 are drawn in Fig. 20 (c-d). It is observed that AE values for Example 1–3 based form 1 for u(t) and v(t) lie in the interval [10–04, 10–06]. Whereas the AE values for Example 1, 2 and 3 based form 1 for uinput [10–04, 10–07]. These obtained outcomes improve the worth of the designed LMB neural network approach.

Fig. 19
figure 19

Result assessment through the LMB neural network for both the categories of the novel NTO-PEFS

Full size image
Fig. 20
figure 20

AE for both the categories of the for novel NTO-PEFS

Full size image

5 Conclusions

In this research study, a novel third order nonlinear pantograph Emden–Fowler system is designed successfully along with its two forms. The descriptions of the shape factor, pantographs and singular points are also provided for the designed model. The singular systems are always difficult to solve due to the nature of singularity and when the pantograph term is involved with the singular models then it becomes more stiffer in nature, Therefore, stochastic numerical schemes can be applied to solve such models as these schemes are familiar to solve various difficult and harder nature problems. Three different examples of both forms are presented based on the designed model and numerically treated by using efficient designed LMB neural networks. The reference 80% data are used for training, while for both validation and testing outputs, the data are used 10% along with 10 hidden numbers of neurons. To check the precision and perfection, the matching of the achieved simulations from the proposed LMB neural network scheme with the reference solutions is performed. One can prove the values based absolute error are close to 10–04 to 10–08 for each problem to solve the designed NTO-PEFS using the stochastic procedures. For convergence processes, the values based on mean square error of training, testing, validation, and best curve are indicated for each example of the novel NTO-PEFS. The correlation values are applied to form the regression studies are also examined. The gradient together with the LMB are considered for the novel NTO-PEFS. Furthermore, the precision is further verified using the numerical/graphical demonstrations of regression and convergence plots on MSE index.

In the future, various types of differential and fractional singular systems (Fateh et al. 2019; Khan et al. 2021a, 2021b; Qureshi and Yusuf 2020; Sabir et al. 2022d; Umar et al. 2020c; Qureshi et al. 2020) can be assembled using the traditional Emden–Fowler system and solved by the strength of the supervised form of the neural networks.