1 Introduction

During the sixteenth century, the research in the area of differential models shows the introduction of a specific type of differential model; namely delay differential (DD) model. The literature of delay differential models offers substantial contribution to solving real-life problems. These contributions can be seen in the several applications of DDEs in a myriad of physical phenomena, for instance, transport and propagation, communication network model, economical systems, and population dynamics engineering system, [1,2,3,4,5]. In an extensive research, Forde [5] illustrates the solutions using delay differential equations of mathematical biology, whereas Beretta and Kuang [6] utilize the delay-dependent factors of DDEs to control their geometric constancy. Forde solves the DDEs in mathematical biology [7], in the study of DD models, delay/non-delay differential models were solved by Chapra [8] applying the Runge–Kutta method. Rangkuti and Noorani [9] provided exact solutions while taking help of both variation iterations coupled technique, as well as the Taylor series. Frazier solved second-order DDEs by using the wavelet Galerkin method [10].

This research study uses pantograph delay differential equations (PD-DEs), a certain type of proportional delay differential equation which has multifarious applications considerably in mathematical models of broad problems in applied science and technology [11, 12]. Based on the significance of PD-DEs, several numerical, as well as analytical techniques, have been posited. Methods used to solve PD-DEs in literature include, but are not limited to, Collocation [13], multi-wavelets Galerkin [14], Taylor operation [15], modified Chebyshev collocation [16], multistep block [17], fully geometric mesh one-leg [18], the partially truncated Euler–Maruyama [19], Laplace decomposition [20] methods and numerous other methodologies [21,22,23,24,25,26,27], while non-traditional computing procedures are also implemented for solving PD-DEs including neuro-heuristic computational intelligence [28], Bernstein neural network [29], neuro-swarm intelligent computing [30], computational intelligence approach to pantograph delay differential system [31], backpropagated artificial neural networks for pantograph differential models [32] and machine learning approach for pantograph ODEs systems [33]. Beside these Pantograph models, researchers have exhibited keen interest in solving the ‘singular problems.’ The Lane–Emden singular system (LESS) is one such valuable and recognized model. LESS explains a good deal of physical phenomena such as cooling of radiators, clouds, cluster galaxies, polytrophic stars and many other physical problems. The LESSs have benefited numerous fields of study, including, physical sciences [34], oscillating magnetic problem [35], electromagnetic problem [36], mathematical physics [37], study of gaseous star [38], catalytic diffusion in chemical reaction [39], stellar structure model [40], quantum mechanics [41] and isotropic media [42]. Alongside these deterministic solver, stochastic methods based in artificial intelligence have been utilized exhaustively in different applications [43,44,45,46,47,48,49]. A few of these solver for singular system include Thomas–Fermi system of atomic physics [50,51,52], Lane–Emden and Emden–Fowler based system models in astrophysics [30, 53,54,55], doubly singular system [56] and thermal analysis of human head model [57]. Based on our examination of relevant literature, up till now, no researcher has made use of the applied AI techniques for the recently introduced model based on integration of singular and proportional delay system, named as Lane–Emden pantograph delay differential equations (LE–PDDEs). This encourages motivation for the authors to explore or exploit the said AI algorithms to solve recently reported nonlinear singular LE–PDDEs equation.

Enlisted below are certain prominent characteristics or features of the proposed research:

  • An innovative application of backpropagated intelligent networks (BINs) is introduced for numerical treatment of nonlinear, singular, delay differential models.

  • The BINs comprising of Levenberg–Marquardt backpropagation networks (LMBNs) and Bayesian regularization backpropagation networks (BRBNs) are designed effectively for Lane–Emden pantograph delay differential equations (LE–PDDEs).

  • The mean squared error (MSR) as a figure of merit is exploited for the training, testing and validation of LMRNs and BRBNs for estimated modeling of the LE–PDDEs-based system.

  • The superior accomplishment of the developed methodologies via LMBNs and BRBNs is certified through assessment on error histograms, regression measures and index of mean squared error.

The rest of the study is organized in this paper as follows: Sect. 2 describes the overview of system model based on LE–PDDEs. In Sect. 3, numerical experimentation with interpretations of the outcomes is given, while the conclusions are provided in Sect. 4 with potential future applications of presented methodology.

2 Lane–Emden Pantograph Delay Differentiation Equations

Given below is the standard form of LESS [30, 53,54,55]

$$ \begin{gathered} \frac{{d^{2} f}}{{dx^{2} }} + \frac{\mu }{x}\frac{df}{{dx}} + h(f) = g(x), \hfill \\ f(0) = \alpha ,\,\,\frac{df(0)}{{dx}} = 0, \hfill \\ \end{gathered} $$
(1)

where µ shows the shape parameters, x = 0 be the location of the singularity ,while α denotes a constant value.

Inspired from Eq. (1), introducing the proportional delay as reported in [58], the LE–PDDEs-based system is given as follows

$$ \begin{gathered} \beta \frac{{d^{2} f(\beta x)}}{{dx^{2} }} + \frac{\mu }{x}\frac{df(\beta x)}{{dx}} + h(f) = g(x), \hfill \\ f(0) = \alpha ,\,\,\frac{df(0)}{{dx}} = 0, \hfill \\ \end{gathered} $$
(2)

where β represents the pantograph factor in a singular system.

The three different variants of LE–PDDEs are chosen in the presented analysis of the proposed methodology as follows:

Problem 2.1

Consider nonlinear LE–PDDE equation in (2) for µ = 3, β = 0.5, h(f) = f2 and g(x) = x8 + 2x4 + 3x2 + 1 as follows [58]

$$ \begin{gathered} 0.5\frac{{d^{2} f(0.5x)}}{{dx^{2} }} + \frac{3}{x}\frac{df(0.5x)}{{dx}} + f^{2} (x) = x^{8} + 2x^{4} + 3x^{2} + 1, \hfill \\ f(0) = 1,\,\frac{df(0)}{{dx}} = 0. \hfill \\ \end{gathered} $$
(3)

The reference exact solution of (3) is provided as:

$$ f(x) = 1 + x^{4} . $$
(4)

Problem 2.2

We consider in this case, the LE–PDDEs Eq. (2) for µ = 3, β = 0.5, h(f) = ef and g(x) = e(1+x3) + 3.75 × as follows [58]

$$ \begin{gathered} 0.5\frac{{d^{2} f(0.5x)}}{{dx^{2} }} + \frac{3}{x}\frac{df(0.5x)}{{dx}} + e^{f} = e^{{1 + x^{3} }} + 3.75x, \hfill \\ f(0) = 1,\,\,\,\frac{df(0)}{{dx}} = 0. \hfill \\ \end{gathered} $$
(5)

The reference exact solution of (4, 5) is written as:

$$ f(x) = 1 + x^{3} . $$
(6)

Problem 2.3

Suppose in this case, the LE–PDDEs (2) for µ = 3, β = 0.5, h(f) = x−2 and g(x) = -0.05cos(0.5x) + sec2x –

3x−1sin(0.5x) as follows [58]

$$ \begin{gathered} 0.5\frac{{d^{2} f(0.5x)}}{{dx^{2} }} + \frac{3}{x}\frac{df(0.5x)}{{dx}} + x^{ - 2} = - 0.05\cos (0.5x) \hfill \\ + \sec^{2} x - \frac{3}{x}\sin (0.5x)\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ f(0) = 1,\,\,\,\,\frac{df(0)}{{dx}} = 0. \hfill \\ \end{gathered} $$
(7)

The reference solution of (7) is provided as:

$$ f(x) = \cos x. $$
(8)

3 Numerical Computing with Discussion

We present here the numerical experimentation with necessary discussion on solving LE–PDDEs using proposed LMBNs and BRBNs.

The methodology adopted in the presented study is illustrated in the flowchart in Fig. 1, while the outcomes of the numerical experimentation conducted by using LMBNs and BRBNs to solve the three selected problems on LE–PDDEs as presented in Eqs. (3–8) are provided along with necessary interpretations. Using backpropagation based networks incorporating Levenberg–Marquardt and Bayesian regularization schemes for training of weights by implementation of function in Matlab neural networks modeling toolbox through ‘nftool’ routine. Figure 2 manifests the design of networks by nine neurons having log-sigmoid transfer function in the hidden layers.

Fig. 1
figure 1

Process blocks of methodology for solving LE–PDDEs

Full size image
Fig. 2
figure 2

Architecture of proposed LMBN and BRBNs

Full size image

For all three Problems 2.1–2.3 of LE–PDDEs, the dataset has been developed while making use of Eqs. (4), (5), (6) and (8) for 201 inputs in interval [0, 2] for both LMBN and BRBNs. The developed dataset was divided randomly in three parts: the first 15% for testing, the second 15% for the validation, whereas the last 70% are utilized for training of the networks. As can be seen in Fig. 2, the fitting tool through ‘nftool’ routine based on two-layered structure of feed forward networks is applied to provide solutions for the all 03 problems of LE–PDDEs.

In the three LE–PDDEs, i.e., Problem 2.1 to Problem 2.3, respective results of LMBN and BRBNs are listed in Tables 1 and 2, which portrayed the performance in relation to fitness on MSE, epochs, training/testing/validation performance, backpropagation measures and time duration. For LMBNs, the values of performance are around 10–10, however, for BRBNs, the performance values are 10–12 to 10–11. The corresponding values of MSE for training, validation and testing of LMBNs are about 10–10 and about 10–12 to 10–11 for BRBNs. The algorithms complexity in the form of executing time utilized for training of weights of both backpropagated networks is also listed in Tables 1 and 2 for all three problems. Both backpropagation methodologies LMBN and BRBNs show almost similar computational time. Generally, these outcomes manifest similar, consistent, accuracy in finding the numerical solution of LE–PDDEs.

Table. 1. Outcomes of lmbns for numerical treatment of nonlinear singular LE–PDDEs
Full size table
Table. 2 Outcomes of BRBNs for numerical treatment of nonlinear singular LE–PDDEs
Full size table

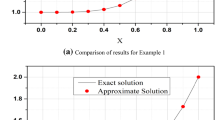
Figs. 3 and 4 manifest the results of MSE-based objective function, performance of testing validation and training process, state transition index, regression outcomes of LMBN and BRBNs for LE–PDDEs as presented in Problem 2.1. However, Figs. 5 and 6 exhibit the approximate solutions with error dynamics, i.e., difference between proposed results and available exact solutions. Consequently, the outcomes of LMBN and BRBNs for LE–PDDEs in problems 2.2 and 4.3 are put forth, respectively, in Figs. 7, 8, 9, 10, 11, 12, 13 and 14.

Fig. 3
figure 3

The results of LMBNs for LE–PDDE of Problem 2.1a convergence curves, b transition states, c histograms d regression index

Full size image
Fig. 4
figure 4

The results of BRBNs for LE–PDDE in Problem 2.1a convergence curves, b transition states, c, histograms, d regression index

Full size image
Fig. 5
figure 5

Comparison of results for LMBNs in case of LE–PDDE in Problem 2.1

Full size image
Fig. 6
figure 6

Comparison of results for BRBNs in case of LE–PDDE in Problem 2.1

Full size image
Fig. 7
figure 7

The results of LMBNs for LE–PDDE of Problem 2.2a convergence curves, b transition states, c histograms, d regression index

Full size image
Fig. 8
figure 8

The results of BRBNs for LE–PDDE of Problem 2.2a convergence curves, b transition states, c histograms, d regression index

Full size image
Fig. 9
figure 9

Comparison of results for LMBNs in case of LE–PDDE in Problem 2.2

Full size image
Fig. 10
figure 10

Comparison of results for BRBNs in case of LE–PDDE in Problem 2.2

Full size image
Fig. 11
figure 11

The results of LMBNs for LE–PDDE of Problem 2.3a convergence curves, b transition states, c histograms, d regression index

Full size image
Fig. 12
figure 12

The results of BRBNs for LE–PDDE of Problem 2.3a convergence curves, b transition states, c histograms, d regression index

Full size image
Fig. 13
figure 13

Comparison of results for LMBNs in case of LE–PDDE in Problem 2.3

Full size image
Fig. 14
figure 14

Comparison of results for BRBNs in case of LE–PDDE in Problem 2.3

Full size image

In connection with training, validation and testing against epochs, the performance of MSE is exhibited in Figs. 3a, 4a, 7a, 8a, 11a and 12a about the developed problems (respectively, for 2.1, 2.2 and 2.3) of LE–PDDE. It can be observed that optimum curves of the networks are obtained at 1000, 1000 and 168 epochs having respective MSE approximately 10–10 to 10–09, 10–10 to 10–09 and 10–10 to 10–09 for LMBNs, whereas 1000, 662 and 201 epochs with MSE about 10–10 to 10–09, 10–11 to 10–10 and 10–12 to 10–11 for BRBNs for respective problems 2.1 to 2.3.

The sub-Figs. 3b, 4b, 7b, 8b, as well as 11b and 12b, layout the gradient index and parameter Mu of backpropagation procedure in LMBNs for LE -PDDEs in each of the problems 2.1, 2.2 and 2.3, respectively. The approximate values 10–08 to 10–06 and 10–09 to 10–07 of gradient and Mu values for Levenberg–Marquardt-based backpropagation, on the other hand, the corresponding values for BRBNs are about 10–07 to 10–08 and 10–10 to 10–07. The reasonably stable performance of BRBNs over LMBNs is indicated via a slight change in the parameters of gradient index and Mu.

The dissimilarity of estimated solutions of LMBNs and BRBNs from reference solutions is revealed in Figs. 5, 6, 9, 10, 13 and 14 for respective 2.1 to 2.3 problems. These solutions indicate the consistency in both results with 5–7 decimal precision. Furthermore, it can be inferred that performance of LMBNs for LE–PDDE in Problem 2.2 is comparatively less effective as compared to BRBNs whereas the reliable and viable performance of BRBNs is attained for all three variants of LE–PDDEs.

Histogram-based error analysis has been carried out for the pair LMBN and BRBNs, and the outcome of the error analysis for LE–PDDEs in problems 2.1, 2.2 and 2.3 is figuratively described for each system, in the following Figs 3c, 4c, 7c, 8c, 11c and 12c, respectively. For LMBNs, the value is found to be close to 10–06 to 10–07, however, value for BRBNs is 10–06 to 10–08 of the error bin with reference to desire optimal value of zero. It is shown clearly from the results that there is only a miniscule variance in the performance for LE–PDDE for both methodologies; small error values (better) are obtained using BRBNs over LMBNs.

For the complete and evident inferences, the regression analysis intended for training, testing, validation for both LMBNs and BRBNs. Figs. 3d, 4d, 7d, 8d and 11d, 12d for LE–PDDEs in problems 2.1, 2.2 and 2.3, respectively, show the results of regression index. For LMBNs, as well as BRBNs, the value of correlation is very close to unity, i.e., R = 1, for almost each variant of LE–PDDE.

The analysis is continued further for the scenario of the LE–PDDEs other than those presented in problems 2.1 to 2.3 without known exact solutions or reference numerical solutions. In these scenarios, we are unable to get the training target for an equation, e.g., nonlinear singular Thomas Fermi equation [51], nonlinear fractional Riccati equation [59], nonlinear singular Flierl–Petviashivili equations [60], etc. Thus, we cannot implement the proposed LMBNs, as well as BRBNs, straightforwardly, however, unsupervised versions of these neural networks as reported in [61, 62] can be exploited for finding the solution in such scenarios of LE–PDDEs.

4 Conclusions

The present research looks into the pursuit of intelligent backpropagated networks exploiting the Levenberg–Marquardt and Bayesian Regularization optimization mechanism to discover the solution of recently introduced nonlinear, singular and delay systems known as nonlinear second order Lane–Emden pantograph delay differential equations. Based on acknowledged standard results, i.e., available exact solutions, for the variants of LE–PDDEs, a dataset for training, testing, in addition to, validation was formed. The two different types of intelligent backpropagated networks via LMBNs and BRBNs are employed on a given dataset for approximate modeling of the LE–PDDEs-based systems on fitness through mean squared error. The performance of the developed intelligent backpropagated algorithms LMBNs and BRBNs on LE–PDDEs is authenticated by attaining a good agreement, i.e., a close matching, with the available solutions and additionally validated using regression analyses and error histograms. Beside the reasonably precise solutions of LE–PDDE proposed LMBNs and BRBNs, simple concept, implementations ease, stability, convergence, robustness, extendibility and applicability are other key advantages.

In future, one should investigate in Bernstein and Legendre ANNs, as well as deep version of LMBNs and BRBNs along with their proof of theoretical convergence such that these methodologies can be exploited effectively to solve variety of nonlinear systems of paramount interest [29, 63,64,65,66,67,68]. Additionally, the proposed LMBNs and BRBNs, as well as the deep versions of both intelligence computing paradigms, can be extended to be applicable for singularly perturb variants of LE–PDDEs.