Stability Analysis of Second Order Impulsive Differential Equations

Abstract

In this paper, we apply the strongly continuous cosine family of bounded linear operators to study the explicit representation of solutions for second order linear impulsive differential equations, and we give sufficient conditions for asymptotical stability of solutions. In addition we study the exponential stability of the linear perturbed problem. Existence and uniqueness of solutions of the initial value problem for nonlinear second order impulsive differential equations is obtained and we present Ulam–Hyers–Rassias stability results. Examples are provided to illustrate the applicability of our results.

1 Introduction

The states of many evolutionary processes are often subject to instantaneous perturbations and experience abrupt changes at certain moments of time. Usually the duration of the changes is very short and negligible in comparison with the duration of the process considered so as a result it is natural to study differential equations with instantaneous impulses. The mathematical investigation of impulsive ordinary differential equations began with Milman and Myshkis [1] where some general concepts of systems with an impulse effect were given and also results for the stability of solutions were presented. Inspired by [1] a number of results on the qualitative analysis for impulsive differential equations appeared in the literature, see [2,3,4,5,6,7].

As a very important branch of control theory, stability has a wide range of applications in various fields, such as nonlinear control, biological mathematics, gene network, chaos control and synchronization, etc. To study the approximate behaviors in dynamic systems, stability is a first question which one needs to study. In 1986, Hopfield reapplies the energy function to neural networks, and studies the asymptotic behavior of neural networks. This work pioneered neural optimization computing and associative memory, precedent for neural optimization calculations and associative memory, and plays an important role in the worldwide upsurge of neural network [8]. In particular, it is well known that exponential stability is closely related to Lyapunov exponents, exponential dichotomies, periodic solutions and so on, and the notion of exponential dichotomy plays a central role in the Hadamard-Perron theory of invariant manifolds for dynamical systems. In addition, some prior contributions have shown the relationship between exponential dichotomy and Hyers–Ulam stability for linear continuous/discrete differential systems, see [9,10,11,12,13]. Therefore, our work can broaden some of the results on other topics related to stability.

In [5], Samoilenko and Perestyuk considered the following linear impulsive system with constant coefficients,

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx}{dt}=Ax,\quad t\ne \tau _{i},\\&\Delta x(\tau _{i})=Bx, \end{aligned} \right. \end{aligned}$$

(1)

where A and B are constant matrices, $\tau _{i}$ are impulsive points, and $\tau _{i}\rightarrow \infty$ as $i\rightarrow \infty$. They assume that A and B are interchangeable, and, in Theorem 32, they obtained asymptotically stable result of (1) provided that

$$\begin{aligned} \max _{j}\lambda _{j}(A)+\frac{1}{\theta _{0}}\ln \max _{j}|1+\lambda _{j}(B)|<0, \end{aligned}$$

and some other conditions, where $\theta _{0}$ is a related constant, $\lambda _{j}(\cdot )$ denotes the eigenvalue. Then they also considered a special class of nonconstant coefficients linear impulsive system

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx}{dt}=Ax+P(t)x,\quad t\ne \tau _{i},\\&\Delta x(\tau _{i})=Bx+I_{i}x, \end{aligned} \right. \end{aligned}$$

(2)

in Theorem 12 and achieved the stable result if the solutions of linear system (1) are stable and

$$\begin{aligned} \int _{t_{0}}^{\infty }\Vert P(t)\Vert dt<\infty \quad \text {and} \quad \prod _{\tau _{i}>t_{0}}(1+\Vert I_{i}\Vert )<\infty . \end{aligned}$$

Following the linear problems, naturally, in Theorem 39, they considered the stability of solutions for first order approximation of nonlinear impulsive system, that is

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx}{dt}=Ax+g(t,x),\quad t\ne \tau _{i},\\&\Delta x(\tau _{i})=Bx+I_{i}x. \end{aligned} \right. \end{aligned}$$

(3)

Up to date, the literature concentrates on the stability of first order impulsive system. For existence and stability results on first order impulsive differential equations, one can see [5, 7, 14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. In [19] the authors considered general first order non-instantaneous impulsive ordinary differential equations and they obtain the stability of zero solutions of linear problems, the exponential stability of perturbed problems, existence, uniqueness of solutions and Ulam–Hyers–Rassias stability of nonlinear systems.

Inspired by the above results, in this paper, we aim to generalize the three results above to second order impulsive differential equations. We study the following initial problems of second order impulsive differential equations.

(i): Asymptotical stability of second order linear impulsive differential equations

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t),\quad t\in (t_{i},t_{i+1}],\quad i\in \mathbb {N},\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-}),\quad i\in \mathbb {N},\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-}),\quad i\in \mathbb {N},\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

(4)

where A, $B_{1}$ and $B_{2}$ are constant $n\times n$ matrixes satisfying $AB_{1}=B_{1}A$, $AB_{2}=B_{2}A$, $B_{1}B_{2}=B_{2}B_{1}$, $0=t_{0}<t_{1}<\cdots<t_{i}<\cdots$ and $t_{i}\rightarrow \infty$ are impulsive points.

(ii): Exponential stability of the linear perturbed problem

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+P(t)u(t),\quad t\in (t_{i},t_{i+1}],\quad i\in \mathbb {N},\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-}),\quad i\in \mathbb {N},\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-}),\quad i\in \mathbb {N},\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

(5)

where A, $B_{1}$, $B_{2}$, $t_{i}$ are as in (4) and P is a continuous matrix in $\mathbb {R}^{+}$ outside $t_{i}$.

(iii): Existence, uniqueness and Ulam–Hyers–Rassias stability of solutions for nonlinear second order impulsive differential equations

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+f(t,u(t)),\quad t\in (t_{i},t_{i+1}],\quad i\in \mathbb {N},\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-}),\quad i\in \mathbb {N},\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-}),\quad i\in \mathbb {N},\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

(6)

where A, $B_{1}$, $B_{2}$, $t_{i}$ are as in (4) and $f:[0,+\infty )\times \mathbb {R}^{n}\rightarrow \mathbb {R}^{n}$ is continuous.

Section 2 presents some lemmas and corollaries needed in the paper. In Sect. 3, we derive an explicit expression of (4) via mathematical induction, and then we consider the asymptotical stability of (4). Section 4 is devoted to the exponentially stability of (5). Finally, in Sect. 4, we study existence and uniqueness of solutions for (6) using the contraction mapping principle, and then we discuss the Ulam–Hyers–Rassias stability of solutions. In addition examples are provided to illustrate the applicability of our results.

2 Preliminary

In this section, we consider initial value problems of the second order linear differential equation

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t),\quad 0\le t\le T,\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

(7)

and the second order linear nonhomogeneous differential equation

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+f(t),\quad 0\le t\le T,\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

(8)

where X is a Banach space, A is the infinitesimal generator of a uniformly continuous cosine family C(t) on X, $u_{0}, u_{1}\in D(A)$ and $f:[0,T]\rightarrow \mathbb {R}$ is continuous.

Lemma 2.1

(see [32]) Let A be an operator such that $R(\lambda ^{2};A)$ exists in the half plane $\Re \lambda >\omega$, C(t) an operator valued function strongly continuous in $t\ge 0$ and such that

$$\begin{aligned} ||C(t)||\le C_{0}e^{\omega t}\quad (t\ge 0). \end{aligned}$$

Assume that, for each $u\in X$,

$$\begin{aligned} \int _{0}^{\infty } e^{-\lambda t}C(t)udt=\lambda R(\lambda ^{2}; A)u\quad (\Re \lambda >\omega ). \end{aligned}$$

(9)

Then the Cauchy problem (7) is uniformly well posed in $t\ge 0$, and C(|t|) is the solution operator of (7).

Lemma 2.2

(see [32]) Let A be a bounded linear operator in a Banach space E. Then the Cauchy problem (7) is uniformly well posed in $-\infty<t<+\infty$. The cosine function C(t) generated by A is given by

$$\begin{aligned} C(t)=\sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n}, \end{aligned}$$

(10)

and the series (10) is uniformly convergent on compact subsets of $-\infty<t<+\infty$. The other propagator S(t) is given by

$$\begin{aligned} S(t)=\sum _{n=0}^{\infty }\frac{t^{2n+1}}{(2n+1)!}A^{n}, \end{aligned}$$

(11)

and the series (11) converging in the same sense of (10).

Proof

We prove this result using Lemma 2.1. Therefore, the first task is to show that $R(\lambda ^{2};A)$ exists in a certain half plane. Now A is an bounded linear operator, and we assume that $||A||\le M$; here M is a positive constant. By Neumman’s theorem, we see that the operator $\lambda ^{2}I-A$ is regular if $|\lambda ^{2}|>M$. Hence $R(\lambda ^{2};A)$ exists in the half plane $\Re \lambda >M^{\frac{1}{2}}$. Define the cosine functions C(t) as in (10). Since $||A||\le M$ we see that C(t) is well-defined, and C(t) is an operator valued function strongly continuous in $t\ge 0$, and

$$\begin{aligned} ||C(t)||\le C_{0}e^{M^{\frac{1}{2}}t}\quad (t\ge 0). \end{aligned}$$

We verify next that C(t) defined by (10) satisfied (9). Let $u\in D(A)=E$, and $T>0$. Now A is a closed operator. Using a well known result on closed operators [33] and integration by parts, we have

$$\begin{aligned} \begin{aligned}&A\cdot \frac{1}{\lambda }\int _{0}^{T}e^{-\lambda t}\cdot \sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n}udt= \frac{1}{\lambda }\int _{0}^{T}e^{-\lambda t}\cdot \sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n+1}udt \\&\quad = \sum _{n=0}^{\infty }\frac{1}{\lambda }\left[ e^{-\lambda T}\frac{T^{2n+1}}{(2n+1)!}A^{n+1}u+\lambda \int _{0}^{T}e^{-\lambda t}\frac{t^{2n+1}}{(2n+1)!}A^{n+1}udt\right] \\&\quad = \sum _{n=0}^{\infty }\frac{1}{\lambda }\left[ e^{-\lambda T}\frac{T^{2n+1}}{(2n+1)!}A^{n+1}u+\lambda e^{-\lambda T}\frac{T^{2n+2}}{(2n+2)!}A^{n+1}u\right. \\&\qquad \left. +\lambda ^{2}\int _{0}^{T}e^{-\lambda t}\frac{t^{2n+2}}{(2n+2)!}A^{n+1}udt\right] . \end{aligned} \end{aligned}$$

Let $T\rightarrow \infty$ and we have

$$\begin{aligned} A\cdot \frac{1}{\lambda }\int _{0}^{\infty }e^{-\lambda t}\cdot \sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n}udt= & {} \lambda ^{2}\cdot \frac{1}{\lambda }\int _{0}^{\infty }e^{-\lambda t}\cdot \sum _{n=0}^{\infty }\frac{t^{2n+2}}{(2n+2)!}A^{n+1}udt \\= & {} \lambda ^{2}\cdot \frac{1}{\lambda }\int _{0}^{\infty }e^{-\lambda t}\left( \sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n}u-u\right) dt \\= & {} \lambda ^{2}\cdot \frac{1}{\lambda }\int _{0}^{\infty }e^{-\lambda t}\cdot \sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n}udt-u, \end{aligned}$$

and hence,

$$\begin{aligned} (\lambda ^{2}I-A)\cdot \frac{1}{\lambda }\int _{0}^{\infty }e^{-\lambda t}\cdot \sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n}udt=u\quad (\Re \lambda >M^{\frac{1}{2}}). \end{aligned}$$

Let $u\in D(A)\subset E$. Since A is a closed, densely defined operator, for all $u\in E$, there exists a sequence $\{u_{k}\}\subset D(A)$ such that

$$\begin{aligned} u_{k}\rightarrow u \end{aligned}$$

in the norm of E. For all $u_{k}\in D(A)$ we have

$$\begin{aligned} (\lambda ^{2}I-A)\cdot \frac{1}{\lambda }\int _{0}^{\infty }e^{-\lambda t}\cdot \sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n}u_{k}dt=u_{k}\quad (\Re \lambda >M^{\frac{1}{2}}). \end{aligned}$$

Taking the limit of both sides with respect to k, we have

$$\begin{aligned} (\lambda ^{2}I-A)\cdot \frac{1}{\lambda }\int _{0}^{\infty }e^{-\lambda t}\cdot \sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A^{n}udt=u\quad (\Re \lambda >M^{\frac{1}{2}}). \end{aligned}$$

Therefore, by Lemma 2.1, the Cauchy problem (7) is uniformly well posed in $-\infty<t<+\infty$, and C(t) is a solution operator of (7) with $u(0)=u_{0}$, $u'(0)=0$. Now, $S(t)u_{1}=\int _{0}^{t}C(s)u_{1}ds$, in other words,

$$\begin{aligned} S(t)=\sum _{n=0}^{\infty }\frac{t^{2n+1}}{(2n+1)!}A^{n}, \end{aligned}$$

which converges in the same sense of (10) is the solution operator of (7) with $u(0)=0$, $u'(0)=u_{1}$. $\square$

Remark 2.1

If we assume the existence of square roots of A and the existence of the inverse of square roots of A, then the series (10) and (11) in Theorem 2.2 can be expressed as

$$\begin{aligned} C(t)=\cosh A^{\frac{1}{2}}t, \end{aligned}$$

and

$$\begin{aligned} S(t)=A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}t, \end{aligned}$$

respectively.

For A a constant matrix we have the following corollary.

Corollary 2.1

Let A be a nonsingular constant matrix, and the square roots of A exist. Then the Cauchy problem (7) is uniformly well posed in $-\infty<t<+\infty$, and the solutions of (7) is given by

$$\begin{aligned} u(t)=\cosh A^{\frac{1}{2}}t u_{0}+A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}t u_{1}. \end{aligned}$$

(12)

Remark 2.2

Although the square roots of A are not unique, the expression (12) is well-defined. In fact, if $A_{1}$ and $A_{2}$ both are the square roots of A and satisfy the assumptions of Corollary 2.1, we have

$$\begin{aligned} \cosh A_{1}t u_{0}=\sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A_{1}^{2n}=\sum _{n=0}^{\infty }\frac{t^{2n}}{(2n)!}A_{2}^{2n}=\cosh A_{2}t u_{0}, \end{aligned}$$

and

$$\begin{aligned} A_{1}^{-1}\sinh A_{1}t u_{0}=\sum _{n=0}^{\infty }A_{1}^{-1}\frac{t^{2n+1}}{(2n+1)!}A_{1}^{2n}=\sum _{n=0}^{\infty }\frac{t^{2n+1}}{(2n+1)!}A_{2}^{2n}=A_{2}^{-1}\sinh A_{2}t u_{0}. \end{aligned}$$

Lemma 2.3

(see [32]) Assume that $u_{0}, u_{1}\in D(A)$ and $f(t)\in D(A)$, f(t), Af(t) are continuous in $0\le t\le T$. Then the following initial value problem

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+f(t),\\&u(0)=u_{0},\quad u'(0)=u_{1} \end{aligned} \right. \end{aligned}$$

has a solution

$$\begin{aligned} u(t)=C(t)u_{0}+S(t)u_{1}+\int _{0}^{t}S(t-s)f(s)ds,\quad 0\le t\le T, \end{aligned}$$

where $C(t),t\in \mathbb {R}$ is a strongly continuous cosine family in X with infinitesimal generator A and associated sine function $S(t), t\in \mathbb {R}$.

Lemma 2.4

(see [5, 34]) Let X be a Banach space with norm $||\cdot ||$ and let F be a mapping of the ball $||x||\le h$ (here $h>0$) in the space X into the space X and assume

$$\begin{aligned} ||F(x)-F(y)||\le \rho ||x-y||,\quad 0<\rho <1; \end{aligned}$$

here $x,y \in X$. Also assume

$$\begin{aligned} ||F(0)||\le h(1-\rho ). \end{aligned}$$

Then the mapping F has a unique fixed point $x_{0}$ (i.e. $F(x_{0})=x_{0}$).

Lemma 2.5

(see [19]) Let $|\cdot |$ be a norm on $\mathbb {R}^{n}$ and B be an $n\times n$ matrix. Then for any $\varepsilon >0$ there exists $T_{B,\varepsilon }\ge 1$ such that $||B^{k}||\le T_{B,\varepsilon }(\rho (B)+\varepsilon )^{k}$, where $\rho (B)$ is the spectral radius of B.

Lemma 2.6

(see [35]) Let u(t), k(t, s) and its partial derivative $k_{t}(t,s)$ be nonnegative continuous functions for $\alpha \le s \le t$, and suppose

$$\begin{aligned} u(t)\le a+\int _{\alpha }^{t}k(t,s)u(s)ds,\quad t\ge \alpha , \end{aligned}$$

where $a\ge 0$ is a constant. Then

$$\begin{aligned} u(t)\le a \exp \Big (\int _{\alpha }^{t}k(t,s)ds\Big ),\quad t\ge \alpha . \end{aligned}$$

Lemma 2.7

For any $a>0$, $0<t_{0}< t_{1}< t_{2}<\cdots< t_{k}< \cdots <\infty$ and

$$\begin{aligned} \lim _{i\rightarrow \infty }\inf (t_{i+1}-t_{i})\ne 0. \end{aligned}$$

Then

$$\begin{aligned} \sum _{i=1}^{+\infty }e^{-at_{i}}\le \frac{1}{\lambda a}, \end{aligned}$$

here $\lambda =\inf \{t_{i+1}-t_{i}|i\in \mathbb {N}\}$.

Proof

Note

$$\begin{aligned} \lambda \sum _{i=1}^{+\infty } e^{-at_{i}} \le \sum _{i=1}^{+\infty }(t_{i+1}-t_i)e^{-at_{i}}\le \sum _{i=1}^{+\infty } \int _{t_i}^{t_{i+1}}e^{-at}dt\le \frac{1}{a}. \end{aligned}$$

This implies the result. $\square$

3 Solutions of Linear Second Order Impulsive Differential Equations

In this section, we present an expression of the solution of the second order linear impulsive system

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t),\quad t\in (t_{i},t_{i+1}],\quad i\in \mathbb {N},\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-}),\quad i\in \mathbb {N},\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-}),\quad i\in \mathbb {N},\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

where A, $B_{1}$ and $B_{2}$ are constant $n\times n$ matrixes satisfying $AB_{1}=B_{1}A$, $AB_{2}=B_{2}A$, $B_{1}B_{2}=B_{2}B_{1}$, $0=t_{0}<t_{1}<\cdots<t_{i}<\cdots$ and $t_{i}\rightarrow \infty$ are impulsive points, and we discuss the stability of solutions. For the sake of convenience in writing, we always set $A^{\frac{1}{2}}t=x$, $A^{\frac{1}{2}}t_{i}=x_{i}$, $I+\frac{B_{1}+B_{2}}{2}=A_{1}$,$\frac{B_{1}-B_{2}}{2}=A_{2}$,

$$\begin{aligned} \cosh xu_{0}+A^{-\frac{1}{2}}\sinh xu_{1}=H(x),\ \cosh xu_{0}-A^{-\frac{1}{2}}\sinh xu_{1}=G(x). \end{aligned}$$

Theorem 3.1

For all $t\in (t_{k},t_{k+1}]$, the solution u(t) of (4) with initial value condition $u(0)=u_{0}$, $u'(0)=u_{1}$ is given as follows:

$$\begin{aligned} u(t)=\left\{ \begin{aligned}&A_{1}^{k}H(x)+A_{1}^{k-1}A_{2}\sum \limits _{1\le i_{11}\le k}G(x-2x_{i_{11}})+A_{1}^{k-2}A_{2}^{2}\\&\quad \sum \limits _{1\le i_{21}<i_{22}\le k}H(x-2x_{i_{22}}+2x_{i_{21}})\\&\quad + \cdots +A_{1}A_{2}^{k-1}\sum \limits _{1\le i_{k-1,1}< i_{k-1,2}<\cdots<i_{k-1,k-1}\le k}\\&\quad G(x-2x_{i_{k-1,k-1}}+2x_{i_{k-1,k-2}}-\cdots -2x_{i_{k-1,1}})\\&\quad +A_{2}^{k}H(x-2x_{k}+2x_{k-1}-\cdots +2x_{1}),\quad \text {if k is even},\\&A_{1}^{k}H(x)+A_{1}^{k-1}A_{2}\sum \limits _{1\le i_{11}\le k}G(x-2x_{i_{11}})+A_{1}^{k-2}A_{2}^{2}\\&\quad \sum \limits _{1\le i_{21}<i_{22}\le k}H(x-2x_{i_{22}}+2x_{i_{21}}) \\&\quad + \cdots +A_{1}A_{2}^{k-1}\sum \limits _{1\le i_{k-1,1}< i_{k-1,2}<\cdots <i_{k-1,k-1}\le k} \\&\quad H(x-2x_{i_{k-1,k-1}}+2x_{i_{k-1,k-2}}-\cdots -2x_{i_{k-1,1}})\\&\quad +A_{2}^{k}G(x-2x_{k}+2x_{k-1}-\cdots +2x_{1}),\quad \text {if k is odd}. \end{aligned} \right. \end{aligned}$$

(13)

Proof

We use mathematical induction to show the result. For the case of $k=0$, Corollary 2.1 shows (13) holds. Without loss of generality, assume (13) holds for $k=2i$, that is

$$\begin{aligned} \begin{aligned} u(t) = \,&A_{1}^{2i}H(x)+A_{1}^{2i-1}A_{2}\sum \limits _{1\le i_{11}\le k}G(x-2x_{i_{11}})+A_{1}^{2i-2}A_{2}^{2}\\&\quad \sum \limits _{1\le i_{21}<i_{22}\le k}H(x-2x_{i_{22}}+2x_{i_{21}}) + \cdots \\&+A_{1}A_{2}^{2i-1}\sum \limits _{1\le i_{k-1,1}< i_{k-1,2}<\cdots <i_{k-1,k-1}\le k}G(x-2x_{i_{k-1,k-1}}+2x_{i_{k-1,k-2}}\\&-\cdots -2x_{i_{k-1,1}}) +A_{2}^{2i}H(x-2x_{k}+2x_{k-1}-\cdots +2x_{1}), \quad t\in (t_{2i},t_{2i+1}]. \end{aligned} \end{aligned}$$

(14)

Next we show that (13) holds for $k=2i+1$. By a direct calculation, we have

$$\begin{aligned}&\cosh (x-x_{i})H(y(x))(I+B_{1})+A^{-\frac{1}{2}}\sinh (x-x_{i})H'(y(x_{i}))(I+B_{2})\nonumber \\&\quad =A_{1}H(y(x))+A_{2}G(x-x_{i}-y(x_{i})), \end{aligned}$$

(15)

$$\begin{aligned}&\cosh (x-x_{i})G(y(x))(I+B_{1})+A^{-\frac{1}{2}}\sinh (x-x_{i})G'(y(x_{i}))(I+B_{2})\nonumber \\&\quad =A_{1}G(y(x))+A_{2}H(x-x_{i}-y(x_{i})), \end{aligned}$$

(16)

where $y(x)=x-$const. Hence for all $t\in (t_{2i+1},t_{2i+2}]$, from Corollary 2.1, we have

$$\begin{aligned} u(t)=\cosh (x-x_{2i+1})u(t_{2i+1})(I+B_{1})+A^{-\frac{1}{2}}\sinh (x-x_{2i+1})u(t_{2i+1})(I+B_{2}). \end{aligned}$$

(17)

Combine (14), (15), (16) with (17), so we see (13) holds for $k=2i+1$. $\square$

Remark 3.1

Obviously, if $A_{2}=0$, i.e., $B_{1}=B_{2}$, then for all $t\in (t_{k},t_{k+1}]$, we have

$$\begin{aligned} u(t)=A_{1}^{k}H(x); \end{aligned}$$

(18)

if $A_{1}=0$, that is $B_{1}=-2I-B_{2}$, then for all $t\in (t_{k},t_{k+1}]$, we have

$$\begin{aligned} u(t)=\left\{ \begin{aligned}&A_{2}^{k}G(x-2x_{k}+2x_{k-1}-\cdots +2x_{1}),\quad \text {if}\,k\,\text {is\,odd},\\&A_{2}^{k}H(x-2x_{k}+2x_{k-1}-\cdots +2x_{1}),\quad \text {if}\,k\,\text {is\,even}; \end{aligned} \right. \end{aligned}$$

if $A_{1}=A_{2}$, i.e., $B_{2}=-I$, this means $u'(t_{i})=0$, where $t_{i}\in (0,t)$ are impulsive points. Then for all $t\in (t_{k},t_{k+1}]$, we have

$$\begin{aligned} u(t)=(I+B_{1})^{k}\cosh (x-x_{k})\prod \limits _{i=2}^{k}\cosh (x_{i}-x_{i-1})\left( \cosh x_{1}u_{0}+A^{-\frac{1}{2}}\sinh x_{1}u_{1}\right) ; \end{aligned}$$

if $A_{1}=-A_{2}$, that is $B_{1}=-I$, this means $u(t_{i})=0$, where $t_{i}\in (0,t)$ are impulsive points. Then for all $t\in (t_{k},t_{k+1}]$, we have

$$\begin{aligned} u(t)=(I+B_{2})^{k}\sinh (x-x_{k})\prod \limits _{i=2}^{k}\cosh (x_{i}-x_{i-1})\left( \sinh x_{1}u_{0}+A^{-\frac{1}{2}}\cosh x_{1}u_{1}\right) . \end{aligned}$$

Definition 3.1

The zero solution of the second order impulsive initial value problem is called stable if for any $\varepsilon >0$ there exists $\delta (t_{0},\varepsilon )>0$ such that if $||u_{0}||+||u_{1}||<\delta (t_{0},\varepsilon )$ then $||u(t,t_{0},u_{0},u_{1})||+||u'(t,t_{0},u_{0},u_{1})||<\varepsilon$. The zero solution of the second order impulsive initial value problem is called asymptotically stable if it is stable and attractive, that is

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }u(t,t_{0},u_{0},u_{1})=\lim \limits _{t\rightarrow \infty }u'(t,t_{0},u_{0},u_{1})=0. \end{aligned}$$

Now we give sufficient conditions to guarantee the stability of (4).

Theorem 3.2

Assume that the following conditions hold

$$\begin{aligned} \rho \left( I+\frac{B_{1}+B_{2}}{2}\right) +\rho \left( \frac{B_{1}-B_{2}}{2}\right)<1,\qquad \lim _{t\rightarrow \infty }\inf \frac{i(0,t)}{t}=p<\infty ; \end{aligned}$$

(19)

here i(0, t) is the number of impulsive points which belong to (0, t). Then (4) is asymptotically stable provided that the following inequality

$$\begin{aligned} \Upsilon =\sqrt{\rho (A)}+p\ln \left( \rho \left( I+\frac{B_{1}+B_{2}}{2}\right) +\rho \left( \frac{B_{1}-B_{2}}{2}\right) \right) <0 \end{aligned}$$

(20)

is satisfied.

Proof

For all $t\ge 0$, from Lemma 2.2, we find

$$\begin{aligned} S(t)=A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}t, \end{aligned}$$

and

$$\begin{aligned} C(t)=\cosh A^{\frac{1}{2}}t. \end{aligned}$$

Making use of Lemma 2.5, for $t\ge 0$, and any constant a, we have

$$\begin{aligned} \Vert A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}(t-2a)\Vert \le T_{A,\varepsilon } \sum _{n=0}^{\infty }\frac{|t-2a|^{2n+1}}{(2n+1)!}(\rho (A)+\varepsilon )^{n}, \end{aligned}$$

if $t-2a\ge 0$, then we have

$$\begin{aligned} \begin{aligned} \Vert A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}(t-2a)\Vert&\le T_{A,\varepsilon } \sum _{n=0}^{\infty }\frac{(t-2a)^{2n+1}}{(2n+1)!}(\rho (A)+\varepsilon )^{n}\\&\le \frac{T_{A,\varepsilon }}{\sqrt{\rho (A)+\varepsilon }} e^{\sqrt{\rho (A)+\varepsilon }(t-2a)}\\&\le \frac{T_{A,\varepsilon }}{\sqrt{\rho (A)+\varepsilon }} e^{\sqrt{\rho (A)+\varepsilon }t}, \end{aligned} \end{aligned}$$

(21)

if $t-2a\le 0$, we find

$$\begin{aligned} \begin{aligned} \Vert A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}(t-2a)\Vert&\le T_{A,\varepsilon } \sum _{n=0}^{\infty }\frac{(2a-t)^{2n+1}}{(2n+1)!}(\rho (A)+\varepsilon )^{n}\\&\le \frac{T_{A,\varepsilon }}{\sqrt{\rho (A)+\varepsilon }} e^{\sqrt{\rho (A)+\varepsilon }(2a-t)}. \end{aligned} \end{aligned}$$

(22)

Similarly,

$$\begin{aligned} \Vert \cosh A^{\frac{1}{2}}(t-2a)\Vert \le T_{A,\varepsilon } \sum _{n=0}^{\infty }\frac{|t-2a|^{2n}}{(2n)!}(\rho (A)+\varepsilon )^{n}, \end{aligned}$$

if $t-2a\ge 0$, then we have

$$\begin{aligned} \begin{aligned} \Vert \cosh A^{\frac{1}{2}}(t-2a)\Vert&\le T_{A,\varepsilon } \sum _{n=0}^{\infty }\frac{|t-2a|^{2n}}{(2n)!}(\rho (A)+\varepsilon )^{n}\\&\le T_{A,\varepsilon } e^{\sqrt{\rho (A)+\varepsilon }(t-2a)}\\&\le T_{A,\varepsilon } e^{\sqrt{\rho (A)+\varepsilon }t}, \end{aligned} \end{aligned}$$

(23)

if $t-2a\le 0$, we get

$$\begin{aligned} \begin{aligned} \Vert \cosh A^{\frac{1}{2}}(t-2a)\Vert&\le T_{A,\varepsilon } \sum _{n=0}^{\infty }\frac{|t-2a|^{2n}}{(2n)!}(\rho (A)+\varepsilon )^{n}\\&\le T_{A,\varepsilon } e^{\sqrt{\rho (A)+\varepsilon }(2a-t)}. \end{aligned} \end{aligned}$$

(24)

Next we show that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }u(t,0,u_{0},u_{1})=0. \end{aligned}$$

(25)

It follows from Lemma 2.5, (13), (21), (22), (23) and (24) that

$$\begin{aligned}&||u(t,0,u_{0},u_{1})|| \nonumber \\&\quad \le 2\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} T_{A,\varepsilon }\Vert A_{1}^{k}\Vert e^{\sqrt{\rho (A)+\varepsilon }t}(||u_{0}||+||u_{1}||)\nonumber \\&\qquad +2C_{k}^{1}\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} T_{A,\varepsilon }||A_{1}^{k-1}A_{2}||e^{\sqrt{\rho (A)+\varepsilon }t}(||u_{0}||+||u_{1}||)\nonumber \\&\qquad +\cdots \nonumber \\&\qquad +2C_{k}^{k-1}\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} T_{A,\varepsilon }||A_{1}A_{2}^{k-1}||e^{\sqrt{\rho (A)+\varepsilon }t}(||u_{0}||+||u_{1}||)\nonumber \\&\qquad +2\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} T_{A,\varepsilon }||A_{2}^{k}||e^{\sqrt{\rho (A)+\varepsilon }t}(||u_{0}||+||u_{1}||)\nonumber \\&\quad \le \Delta _{1} e^{\sqrt{\rho (A)+\varepsilon }t}\Bigg [(\rho (A_{1})+\varepsilon )^{k}+C_{k}^{1}(\rho (A_{1})+\varepsilon )^{k-1}(\rho (A_{2})+\varepsilon )\nonumber \\&\qquad +\cdots +C_{k}^{k-1}(\rho (A_{1})+\varepsilon )(\rho (A_{2})+\varepsilon )^{k-1}+(\rho (A_{2})+\varepsilon )^{k}\Bigg ](||u_{0}||+||u_{1}||)\nonumber \\&\quad \le \Delta _{1} e^{\sqrt{\rho (A)+\varepsilon }t}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}(||u_{0}||+||u_{1}||)\nonumber \\&\quad =\Delta _{1} e^{\big (\sqrt{\rho (A)+\varepsilon }+\frac{k}{t}\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )\big )t}(||u_{0}||+||u_{1}||), \end{aligned}$$

(26)

where $\Delta _{1}=2\max \{\frac{1}{\sqrt{\rho (A)+\varepsilon }},\sqrt{\rho (A)+\varepsilon }\}T_{\varepsilon }^{3}$, $T_{\varepsilon }=\max \{T_{A,\varepsilon },T_{A_{1},\varepsilon },T_{A_{2},\varepsilon }\}$ and $k=i(0,t)$ is the number of impulsive points which belong to (0, t). If (19) holds, we have

$$\begin{aligned} \frac{i(0,t)}{t}>p-\varepsilon \end{aligned}$$

for any $t>0$ large enough. Consequently, using $\rho \left( I+\frac{B_{1}+B_{2}}{2}\right) +\rho \left( \frac{B_{1}-B_{2}}{2}\right) < 1$ and (26), we have

$$\begin{aligned} ||u(t,0,u_{0},u_{1})||\le \Delta _{1} e^{\big (\sqrt{\rho (A)+\varepsilon }+(p-\varepsilon )\ln (\rho \left( I+\frac{B_{1}+B_{2}}{2}\right) +\rho \left( \frac{B_{1}-B_{2}}{2}\right) +2\varepsilon )\big )t}(||u_{0}||+||u_{1}||). \end{aligned}$$

(27)

For $\varepsilon >0$ sufficiently small, from (20), we have

$$\begin{aligned} \sqrt{\rho (A)+\varepsilon }+(p-\varepsilon )\ln \big (\rho \left( I+\frac{B_{1}+B_{2}}{2}\right) +\rho \left( \frac{B_{1}-B_{2}}{2}\right) +2\varepsilon \big )<\frac{\Upsilon }{2}<0. \end{aligned}$$

Thus, from (27), we have that

$$\begin{aligned} ||u(t,0,u_{0},u_{1})||\le \Delta _{1}e^{\frac{\Upsilon }{2}t}(||u_{0}||+||u_{1}||), \end{aligned}$$

for any $t>0$ large enough. Hence, (25) holds. Since for $t\in (t_{k},t_{k+1}]$,

$$\begin{aligned} \begin{aligned} \Vert A^{\frac{1}{2}}\sinh A^{\frac{1}{2}}(t-2a)\Vert&\le T_{A,\varepsilon }\sum _{n=1}^{\infty }\frac{|t-2a|^{2n-1}}{(2n-1)!}(\rho (A)+\varepsilon )^{n}\\&\le T_{A,\varepsilon } \sqrt{\rho (A)+\varepsilon }e^{\sqrt{\rho (A)+\varepsilon }t}, \end{aligned} \end{aligned}$$

where $a=t_{i_{j}}-t_{i_{j-1}}+\cdots \pm t_{i_{1}}$, $i<i_{1}<i_{2}<\cdots <i_{j}\le k$. Using the same method as that of $u(t,0,u_{0},u_{1})$, we also have

$$\begin{aligned} \Vert u'(t,t_{0},u_{0},u_{1})\Vert \le \Delta _{1}e^{\frac{\Upsilon }{2}t}(||u_{0}||+||u_{1}||). \end{aligned}$$

(28)

for any $t>0$ large enough. Therefore,

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }u'(t,t_{0},u_{0},u_{1})=0. \end{aligned}$$

$\square$

Remark 3.2

Theorem 3.2 show that second order differential systems instable can be stable by adding an impulsive impact.

In the following example we provide an application of Theorem 3.2.

Example 3.1

Consider (4) with

$$\begin{aligned} A= \begin{pmatrix} \frac{1}{9} &{}\quad 0\\ 0 &{}\quad \frac{1}{16} \end{pmatrix}, \quad B_{1}=B_{2}= \begin{pmatrix} -\frac{1}{2} &{}\quad 0\\ 0 &{}\quad -\frac{1}{2} \end{pmatrix}, \end{aligned}$$

(29)

and the initial value

$$\begin{aligned} u_{0}= \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \quad u_{1}= \begin{pmatrix} 1\\ 0 \end{pmatrix} \end{aligned}$$

(30)

respectively. Let $t_{i}=i$. Clearly, (19) holds. In addition, we have

$$\begin{aligned} \Upsilon =\sqrt{\rho (A)}+p\ln \left( \rho \left( I+\frac{B_{1}+B_{2}}{2}\right) +\rho \left( \frac{B_{1}-B_{2}}{2}\right) \right) \approx -0.36<0. \end{aligned}$$

Hence, Theorem 3.2 implies the solution of (4) with (29) and (30) is asymptotical stability. Indeed, from (18), the solution of (4) with (29) and (30) is

$$\begin{aligned} u(t)= \begin{pmatrix} \hat{u}(t)\\ \overline{u}(t) \end{pmatrix} = \begin{pmatrix} {\frac{1}{2}}&{}\quad 0\\ 0 &{}\quad {\frac{1}{2}} \end{pmatrix}^{[t]} \begin{pmatrix} 3\sinh \frac{t}{3}\\ \cosh \frac{t}{4} \end{pmatrix}. \end{aligned}$$

(31)

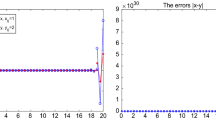
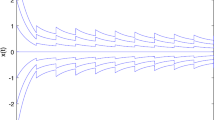
It is easy to see u(t) is asymptotical stability in $[0,+\infty )$ (see Fig. 1).

Fig. 1

Red line denotes $\overline{u}(t)$ and blue line denotes $\hat{u}(t)$ in (31), respectively

4 Second Order Linear Perturbed Problem

In this section, we study the exponential stability of the linear perturbed problem

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+P(t)u(t),\quad t\in (t_{i},t_{i+1}],\quad i\in \mathbb {N},\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-}),\quad i\in \mathbb {N},\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-}),\quad i\in \mathbb {N},\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

where A, $B_{1}$, $B_{2}$, $t_{i}$ are as in (4) and P is a continuous matrix in $\mathbb {R}$ outside $t_{i}$.

To this end, we present an explicit solutions of the following second order linear nonhomogeneous initial value problem

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+f(t),\quad t\in (t_{i},t_{i+1}],\quad i\in \mathbb {N},\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-}),\quad i\in \mathbb {N},\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-}),\quad i\in \mathbb {N},\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

(32)

here $f:(t_{i},t_{i+1}]\rightarrow \mathbb {R}$ is continuous.

Theorem 4.1

For all $t\in (t_{k},t_{k+1}]$, the solutions u(t) of (32) have the following form

$$\begin{aligned} \begin{aligned} u(t)&=W(A,t,u_{0},u_{1})+\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)f(s)ds \\&\quad +A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)f(s)ds, \end{aligned} \end{aligned}$$

(33)

where $W(A,t,u_{0},u_{1})$ is the solution of the initial value problem (4), and

$$\begin{aligned} \begin{aligned}&W_{i}(A,t,s)=A_{1}^{k-i}A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}(t-s)-A_{1}^{k-i-1}A_{2}A^{-\frac{1}{2}}\sum \limits _{i+1\le i_{11}\le k}\sinh A^{\frac{1}{2}}(t-2t_{i_{11}}+s)\\&\quad +A_{1}^{k-i-2}A_{2}^{2}A^{-\frac{1}{2}}\sum \limits _{i+1\le i_{21}<i_{22}\le k}\sinh A^{\frac{1}{2}}(t-2t_{i_{22}}+2t_{i_{21}}-s)+\cdots +(-1)^{k-i-1}A_{1}A_{2}^{k-i-1}\\&A^{-\frac{1}{2}}\sum \limits _{i+1\le i_{k-1,1}< i_{k-1,2}<\cdots <i_{k-1,k-1}\le k}\sinh A^{\frac{1}{2}}(t-2t_{i_{k-1,k-1}}+2t_{i_{k-1,k-2}}-\cdots \pm 2t_{i_{k-1,1}}\mp s)\\&\quad +(-1)^{k-i}A_{2}^{k-i}A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}(t-2t_{k}+2t_{k-1}-\cdots \pm 2t_{i+1}\mp s),\quad i=0,1,\cdots ,k-1. \end{aligned} \end{aligned}$$

Proof

It follows from Lemma 2.3 that (33) holds for $k=0$. Without loss of generality, assume that (33) holds for $k=2m-1$, that is

$$\begin{aligned} u(t)=&A_{1}^{2m-1}H(x)+A_{1}^{2m-2}A_{2}\sum \limits _{1\le i_{11}\le 2m-1}G(x-2x_{i_{11}})+A_{1}^{2m-3}A_{2}^{2}\nonumber \\&\quad \sum \limits _{1\le i_{21}<i_{22}\le 2m-1}H(x-2x_{i_{22}}+2x_{i_{21}}) \nonumber \\&+ \cdots +A_{1}A_{2}^{2m-2}\sum \limits _{1\le i_{k-1,1}< i_{k-1,2}<\cdots <i_{k-1,k-1}\le 2m-1}H(x-2x_{i_{k-1,k-1}}\nonumber \\&\quad +2x_{i_{k-1,k-2}}-\cdots -2x_{i_{k-1,1}})\nonumber \\&+A_{2}^{2m-1}G(x-2x_{k}+2x_{k-1}-\cdots +2x_{1})+\sum _{i=0}^{2m-2}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)f(s)ds\nonumber \\&+A^{-\frac{1}{2}}\int _{t_{2m-1}}^{t}\sinh A^{\frac{1}{2}}(t-s)f(s)ds. \end{aligned}$$

(34)

Note

$$\begin{aligned} \begin{aligned}&(I+B_{1})\cosh A^{\frac{1}{2}}(t-t_{k})\sinh A^{\frac{1}{2}}(t_{k}-2a+s)+(I+B_{2})\sinh A^{\frac{1}{2}}(t-t_{k})\\&\quad \cosh A^{\frac{1}{2}}(t_{k}-2a+s)\\&\quad =A_{1}\sinh A^{\frac{1}{2}}(t-2a+s)-A_{2}\sinh A^{\frac{1}{2}}(t-2t_{k}+2a-s), \end{aligned} \end{aligned}$$

(35)

where a is an arbitrary constant. Thus combining (35), (34) with Lemma 2.3, we see that (33) holds for $k=2m$. $\square$

Definition 4.1

System (32) is uniformly exponentially stable if there exists $N>0$ and $\alpha >0$ such that the solution of (32) satisfies the estimate

$$\begin{aligned} ||u(t)||\le Ne^{-\alpha t},\quad ||u'(t)||\le Ne^{-\alpha t},\quad t\in [0,+\infty )\backslash \{t_{i}\},\quad i\in \mathbb {N}. \end{aligned}$$

Theorem 4.2

Assume that (19) hold. Suppose

$$\begin{aligned} ||P(t)||<(\rho (A_{1})+\rho (A_{2}))^{i}, \quad \forall t\in (t_{i},t_{i+1}],\quad i\in \mathbb {N} \end{aligned}$$

and p in (19) satisfies

$$\begin{aligned} \Theta =\frac{\Delta _{1}}{2}+\sqrt{\rho (A)}+p\ln (\rho (A_{1})+\rho (A_{2}))<0. \end{aligned}$$

(36)

Then, the solution of (5) is exponentially stable.

Proof

According to Theorem 4.1, the solution u(t) of (5) can be expressed in the following form,

$$\begin{aligned} \begin{aligned} u(t) =&W(A,t,u_{0},u_{1})+\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)P(s)u(s)ds\\&+A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)P(s)u(s)ds. \end{aligned} \end{aligned}$$

(37)

Following the proof process of (26), we have

$$\begin{aligned} ||W(A,t,u_{0},u_{1})||\le \Delta _{1} e^{\sqrt{\rho (A)+\varepsilon }t}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}(||u_{0}||+||u_{1}||). \end{aligned}$$

(38)

Next, we give an estimate on $||W_{i}(A,t,s)||$. For all $i<i_{1}< i_{2}<i_{3}\le k$, if $t-2t_{i_{2}}+2t_{i_{1}}-s \ge 0$, $t-2t_{i_{3}}+2t_{i_{2}}-2t_{i_{1}}+s\ge 0$, we have

$$\begin{aligned}&t-2t_{i_{2}}+2t_{i_{1}}-s \le t-s, \\&t-2t_{i_{3}}+2t_{i_{2}}-2t_{i_{1}}+s\le t-s. \end{aligned}$$

If $t-2t_{i_{2}}+2t_{i_{1}}-s \le 0$, $t-2t_{i_{3}}+2t_{i_{2}}-2t_{i_{1}}+s\le 0$, we have

$$\begin{aligned}&2t_{i_{2}}-2t_{i_{1}}-t+s \le t-s, \\&2t_{i_{3}}-2t_{i_{2}}+2t_{i_{1}}-t-s\le t-s. \end{aligned}$$

Therefore, for any $i<i_{1}<i_{2}<\cdots <i_{j}\le k$, we have

$$\begin{aligned} |t-2t_{i_{j}}+2t_{i_{j-1}}-\cdots \pm 2t_{i_{1}}\mp s|\le t-s. \end{aligned}$$

(39)

Hence, making use of Lemma 2.5 and (39), we deduce

$$\begin{aligned} \begin{aligned} ||A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}(t-2a\pm s)||&\le T_{A,\varepsilon }\sum _{n=0}^{\infty }\frac{|t-2a\pm s|^{2n+1}}{(2n+1)!}(\rho (A)+\varepsilon )^{n}\\&\le T_{A,\varepsilon }\sum _{n=0}^{\infty }\frac{(t-s)^{2n+1}}{(2n+1)!}(\rho (A)+\varepsilon )^{n}\\&\le \frac{T_{A,\varepsilon }}{\sqrt{\rho (A)+\varepsilon }} e^{\sqrt{\rho (A)+\varepsilon }(t-s)}, \end{aligned} \end{aligned}$$

(40)

where $a=t_{i_{j}}-t_{i_{j-1}}+\cdots \pm t_{i_{1}}$, $i<i_{1}<i_{2}<\cdots <i_{j}\le k$. Therefore, using (40) and Lemma 2.5, for $s\in (t_{i},t_{i+1}]$, $i\in \mathbb {N}$, we find

$$\begin{aligned} \begin{aligned} ||W_{i}(A,t,s)||&\le \frac{T_{A,\varepsilon }}{\sqrt{\rho (A)+\varepsilon }}\Big (||A_{1}^{k-i}||+C_{k-i}^{1}||A_{1}^{k-2}A_{2}||+\\&\quad \cdots +C_{k-i}^{k-i-1}||A_{1}A_{2}^{k-2}||+||A_{2}^{k-i}||\Big )e^{\sqrt{\rho (A)+\varepsilon }(t-s)}\\&\le \frac{T_{\varepsilon }^{3}}{\sqrt{\rho (A)+\varepsilon }}\Big (\rho (A_{1})+\rho (A_{2})+2\varepsilon \Big )^{k-i}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}.\\ \end{aligned} \end{aligned}$$

(41)

Therefore, using (38), (40) and (41), we have

$$\begin{aligned} ||u(t)||&\le ||W(A,t,u_{0},u_{1})||+\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}\Vert W_{i}\Vert \cdot ||P(s)u(s)||ds\nonumber \\&\quad +\int _{t_{k}}^{t}||A^{-\frac{1}{2}}\sinh A^{\frac{1}{2}}(t-s)||\cdot ||P(s)u(s)||ds\nonumber \\&\le \Delta _{1} e^{\sqrt{\rho (A)+\varepsilon }t}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}(||u_{0}||+||u_{1}||)\nonumber \\&\quad +\frac{T_{\varepsilon }^{3}}{\sqrt{\rho (A)+\varepsilon }}\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k-i}\nonumber \\&\quad e^{\sqrt{\rho (A)+\varepsilon }(t-s)}\Vert P(s)u(s)\Vert ds\nonumber \\&\quad +\frac{T_{A,\varepsilon }}{\sqrt{\rho (A)+\varepsilon }}\int _{t_{k}}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}\Vert P(s)u(s)\Vert ds\nonumber \\&\le \Delta _{1} e^{\sqrt{\rho (A)+\varepsilon }t}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}(||u_{0}||+||u_{1}||)\nonumber \\&\quad +\frac{T_{\varepsilon }^{3}}{\sqrt{\rho (A)+\varepsilon }}\int _{0}^{t}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}\Vert u(s)\Vert ds\nonumber \\&\le \Delta _{1} e^{\sqrt{\rho (A)+\varepsilon }t}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}(||u_{0}||+||u_{1}||)\nonumber \\&\quad +\frac{T_{\varepsilon }^{3}}{\sqrt{\rho (A)+\varepsilon }}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{\frac{k(t-s)}{t}}\Vert u(s)\Vert ds\nonumber \\&\le \Delta _{1}e^{\theta t}(\Vert u_{0}\Vert +\Vert u_{1}\Vert )+\frac{T_{\varepsilon }^{3}}{\sqrt{\rho (A)+\varepsilon }}\int _{0}^{t}e^{\theta (t-s)}\Vert u(s)\Vert ds, \end{aligned}$$

(42)

where

$$\begin{aligned} \theta =\sqrt{\rho (A)+\varepsilon }+\frac{k}{t}\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon ). \end{aligned}$$

Multiply both sides of (42) by $e^{-\theta t}$, and we find

$$\begin{aligned} e^{-\theta t}||u(t)||\le \Delta _{1}(||u_{0}||+||u_{1}||)+\frac{\Delta _{1}}{2}\int _{0}^{t}e^{-\theta s}||u(s)||ds. \end{aligned}$$

Using Bellman’s inequality, we have

$$\begin{aligned} e^{-\theta t}||u(t)||\le \Delta _{1}(||u_{0}||+||u_{1}||) e^{\frac{\Delta _{1}}{2}t}, \end{aligned}$$

hence,

$$\begin{aligned} ||u(t)||\le \Delta _{1}(||u_{0}||+||u_{1}||)e^{(\theta +\frac{\Delta _{1}}{2})t}. \end{aligned}$$

(43)

It follows from condition (36) that one can choose $\varepsilon$ small enough such that

$$\begin{aligned} \sqrt{\rho (A)+\varepsilon }+\frac{k}{t}\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )+\frac{\Delta _{1}}{2}\le \frac{\Theta }{2}<0. \end{aligned}$$

Then, (43) implies

$$\begin{aligned} ||u(t)||\le \Delta _{1}(||u_{0}||+||u_{1}||)e^{\frac{\Theta }{2}t}\rightarrow 0\quad \hbox { for }\quad t\rightarrow \infty . \end{aligned}$$

(44)

Since

$$\begin{aligned} \begin{aligned} \Vert \cosh A^{\frac{1}{2}}(t-2a\pm s)\Vert&\le \sum _{n=0}^{\infty }\frac{|t-2a\pm s|^{2n}}{(2n)!}\Vert A^{n}\Vert \\&\le T_{A,\varepsilon }\sum _{n=0}^{\infty }\frac{(t-s)^{2n}}{(2n)!}(\rho (A)+\varepsilon )^{n}\\&\le T_{A,\varepsilon }e^{\sqrt{\rho (A)+\varepsilon }(t-s)},\quad t\in (t_{k},t_{k+1}], \end{aligned} \end{aligned}$$

(45)

where $a=t_{i_{j}}-t_{i_{j-1}}+\cdots \pm t_{i_{1}}$, $i<i_{1}<i_{2}<\cdots <i_{j}\le k$, using a similar method used in the process of (44), we also can show that

$$\begin{aligned} ||u'(t)||\rightarrow 0\quad \hbox { for }\quad t\rightarrow \infty , \end{aligned}$$

(46)

we omit the details. It follows from (44), (46) that the solution of (5) is exponentially stable. $\square$

5 Existence, Uniqueness and Ulam–Hyers–Rassias Stability of Solutions for Nonlinear Problem

In this section, we study the existence, uniqueness and Ulam–Hyers–Rassias stability of solutions for second order semilinear impulsive differential equations

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+f(t,u(t)),\quad t\in J'=J\,{\setminus }\,\{t_{i}\},\quad i\in \mathbb {N},\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-}),\quad i\in \mathbb {N},\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-}),\quad i\in \mathbb {N},\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

where A, $B_{1}$, $B_{2}$, $t_{i}$ are as in (4) and $f:J'\times \mathbb {R}^{n}\rightarrow \mathbb {R}^{n}$ is continuous, $J=[0,+\infty )$. In addition, we assume the impulsive points fulfill

$$\begin{aligned} \lim _{i\rightarrow \infty }(t_{i+1}-t_{i})\ne 0. \end{aligned}$$

Let $PC(I,\mathbb {R}^{n})$ denote the Banach space of piecewise continuous on interval I, that is $PC(I,\mathbb {R}^{n})=\{u:I\rightarrow \mathbb {R}^{n}|u\in C((t_{k-1},t_{k}],\mathbb {R}^{n})$ for $k\in \mathbb {N}$ and there exists $u(t_{k}^{-})$ and $u(t_{k}^{+}), k\in \mathbb {N}$ with $u(t_{k})=u(t_{k}^{-}) \}$ equipped with the Chebyshev PC-norm $||u||_{PC}:=\sup \{||u(t)||:t\in I\}$, $PCB(I,\mathbb {R}^{n})$ is the Banach space of all bounded functions in $PC(I,\mathbb {R}^{n})$ equipped with the Bielecki PCB-norm $||u||_{PCB}:=\sup \{||u(t)||e^{-\omega t}:t\in I\}$ for some $\omega \in \mathbb {R}$.

Consider the following second order linear nonhomogeneous initial value problem

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+f(t),\quad t\in J',\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-})+g_{i},\quad i=1,2,\cdots ,m,\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-})+g_{i},\quad i=1,2,\cdots ,m,\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

(47)

where A, $B_{1}$, $B_{2}$, $t_{i}$ are as in (4), and $f:J\rightarrow \mathbb {R}^{n}$ is continuous, $g_{1},g_{2},\cdots ,g_{m}$ is a number sequence.

Theorem 5.1

If $t\in (t_{k},t_{k+1}]$, then the solutions u(t) of linear impulsive differential equations (47) is given as follows:

$$\begin{aligned} \begin{aligned} u(t)&= \overline{W}(A,t)+W(A,t,u_{0},u_{1})+\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)h(s)ds\\&\quad +A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)h(s)ds, \end{aligned} \end{aligned}$$

where $W(A,t,u_{0},u_{1})$, $W_{i}(A,t,s)$ is given in (33) and

$$\begin{aligned} \begin{aligned} \overline{W}(A,t)=&\sum _{i=1}^{k}g_{i}\Big ( A_{1}^{k-i}H(x-x_{i})+A_{1}^{k-i-1}A_{2}\sum _{i<j_{11}\le k}G(x-2x_{j_{11}}+x_{i})\\&+A_{1}^{k-i-2}A_{2}^{2}\sum _{i<j_{21}<j_{22}\le k}H(x-2x_{j_{22}}+2x_{j_{21}}-x_{i})+\cdots +A_{2}^{k-i}\\&G(x-2x_{k}+2x_{k-1}-\cdots \pm x_{i})(or H(x-2x_{k}+2x_{k-1}-\cdots \pm x_{i}))\Big ). \\ \end{aligned} \end{aligned}$$

(48)

Proof

The proof is essentially similar to that of Theorem 4.1, so we omit it. $\square$

We list for convenience the following assumption.

(H) $f\in C(J\times \mathbb {R}^{n},\mathbb {R}^{n})$ and there exists a constant $L_{f}>0$ such that

$$\begin{aligned} ||f(t,y_{2})-f(t,y_{1})||\le L_{f}||y_{2}-y_{1}||, \end{aligned}$$

for all $t\in J$ and $y_{1},y_{2}\in \mathbb {R}^{n}$. Moreover $||f||_{\infty }:=\max _{t\in J} ||f(t,0)||<\infty$.

Theorem 5.2

Suppose that (H), (19) hold, and for any fixed $0<\varepsilon \le 1$ used in Lemma 2.5, $L_{f}$ satisfies

$$\begin{aligned} L_{f}\le \frac{\rho (A)+\varepsilon }{T_{\varepsilon }^{3}} \end{aligned}$$

(49)

Then (6) has a unique solution $u\in PCB(J,\mathbb {R}^{n})$ and $\omega =\sqrt{\rho (A)+1}$.

Proof

For all $t\in (t_{k},t_{k+1}]$, we define the mapping $S:PC(J,\mathbb {R}^n)\rightarrow PC(J,\mathbb {R}^n)$ by

$$\begin{aligned} \begin{aligned} Su(t)=W(A,t,&u_{0},u_{1})+\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)f(s,u(s))ds\\&+A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)f(s,u(s))ds. \end{aligned} \end{aligned}$$

Clearly, $S:PC(J,\mathbb {R}^n)\rightarrow PC(J,\mathbb {R}^n)$ is continuous. From Theorem 4.1, the solution of (6) is equivalent to the fixed point of S.

For any $u,\overline{u} \in PCB(J,\mathbb {R}^{n})$ and $t\in (t_{k},t_{k+1}]$, according to condition (H) and (41), we have

$$\begin{aligned} \begin{aligned} ||S\overline{u}-Su||&=||\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)\big (f(s,\overline{u}(s))-f(s,u(s))\big )ds\\&\quad +A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)\big (f(s,\overline{u}(s))-f(s,u(s))\big )ds||\\&\le \frac{L_{f}T_{\varepsilon }^{3}}{\sqrt{\rho (A)+\varepsilon }}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}ds\Vert \overline{u}-u\Vert _{PCB}\\&\le \frac{L_{f}T_{\varepsilon }^{3}}{\rho (A)+\varepsilon }e^{\sqrt{\rho (A)+\varepsilon }t}\Vert \overline{u}-u\Vert _{PCB} \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} e^{-\sqrt{\rho (A)+1}t}||S\overline{u}-Su||<\frac{L_{f}T_{\varepsilon }^{3}}{\rho (A)+\varepsilon }\Vert \overline{u}-u\Vert _{PCB}. \end{aligned}$$

From (49), $S:PCB(J,\mathbb {R}^{n})\rightarrow PC(J,\mathbb {R}^{n})$ is a contraction mapping. Also, we have

$$\begin{aligned} \begin{aligned} ||S0||&\le ||W(A,t,u_{0},u_{1})||+||\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)f(s,0)ds||\\&\quad +||A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)f(s,0)ds||\\&\le \Delta _{1}e^{\frac{\Upsilon }{2}t}(||u_{0}||+||u_{1}||)+\frac{T_{\varepsilon }^{3}\Vert f\Vert _{\infty }}{\sqrt{\rho (A)+\varepsilon }}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}ds\\&\le \Delta _{1}e^{\frac{\Upsilon }{2}t}(||u_{0}||+||u_{1}||)+\frac{T_{\varepsilon }^{3}\Vert f\Vert _{\infty }}{\rho (A)+\varepsilon }e^{\sqrt{\rho (A)+\varepsilon }t}\\&\le \Delta _{1}(\Vert u_{0}\Vert +\Vert u_{1}\Vert )+\frac{T_{\varepsilon }^{3}\Vert f\Vert _{\infty }}{\rho (A)+\varepsilon }e^{\sqrt{\rho (A)+1}t}, \end{aligned} \end{aligned}$$

which implies

$$\begin{aligned} e^{-\sqrt{\rho (A)+1}t}||S0||\le \Delta _{1}(||u_{0}||+||u_{1}||)+\frac{T_{\varepsilon }^{3}\Vert f\Vert _{\infty }}{\rho (A)+\varepsilon }. \end{aligned}$$

Thus

$$\begin{aligned} ||S0||_{PCB}\le \Delta _{1}(||u_{0}||+||u_{1}||)+\frac{T_{\varepsilon }^{3}\Vert f\Vert _{\infty }}{\rho (A)+\varepsilon }. \end{aligned}$$

From Lemma 2.4, $S:PCB(J,\mathbb {R})\rightarrow PCB(J,\mathbb {R})$ has a unique fixed point, which is the solution of system (6). $\square$

Let $\varepsilon ^{*}>0$, $\psi >0$ and $\varphi (t)\in PC(J,\mathbb {R}_{+})$ be a nondecreasing function. We consider the following inequalities:

$$\begin{aligned} \left\{ \begin{aligned}&||v''(t)-Av(t)-f(t,v(t))||\le \varepsilon ^{*} (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{i}\varphi (t),\quad t\in (t_{i},t_{i+1}], \quad i\in \mathbb {N}\\&\Delta v(t_{i})-B_{1}v(t_{i}^{-})\le \varepsilon ^{*}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{i}\psi ,\quad i\in \mathbb {N},\\&\Delta v'(t_{i})-B_{2}v'(t_{i}^{-})\le \varepsilon ^{*}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{i}\psi ,\quad i\in \mathbb {N}. \end{aligned} \right. \end{aligned}$$

(50)

and we take the vector space

$$\begin{aligned} X:=PC^{2}(J,\mathbb {R}^{n}). \end{aligned}$$

Definition 5.1

The equation (6) is Ulam–Hyers–Rassias stable with respect to $(\varphi ,\psi )$, if there exists constants c, $\overline{c}>0$ such that for each function $\hat{v}\in X$ satisfying (50), there exists a solution $v\in X$ of (6) with

$$\begin{aligned}&||\hat{v}(t)-v(t)||\le \varepsilon ^{*} c(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{i}(\varphi (t)+\psi ),\quad t\in (t_{i},t_{i+1}], \end{aligned}$$

(51)

$$\begin{aligned}&||\hat{v}'(t)-v'(t)||\le \varepsilon ^{*} \overline{c}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{i}(\varphi (t)+\psi ),\quad t\in (t_{i},t_{i+1}].\qquad \end{aligned}$$

(52)

Remark 5.1

A function $\hat{v}\in X$ is a solution of (50) if and only if there is $G\in X$, and a sequence $g_{i}$, $i\in \mathbb {N},$ such that:

(a) $||G(t)||\le \varepsilon ^{*}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{i} \varphi (t)$, $t\in (t_{i},t_{i+1}]$,   $i\in \mathbb {N}$,

      $||g_{i}||\le \varepsilon ^{*}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{i}\psi$, $t\in (t_{i},t_{i+1}]$,   $i\in \mathbb {N}$;

(b) $\hat{v}''(t)=A\hat{v}(t)+f(t,\hat{v}(t))+G(t)$,   $t\in (t_{i},t_{i+1}]$,   $i\in \mathbb {N}$;

(c) $\Delta \hat{v}(t_{i})=B_{1}\hat{v}(t_{i}^{-})+g_{i}$,   $i\in \mathbb {N}$;

(d) $\Delta \hat{v}'(t_{i})=B_{2}\hat{v}'(t_{i}^{-})+g_{i}$,   $i\in \mathbb {N}$.

Theorem 5.3

Assume that all the assumptions in Th 5.2 hold (so the solution of (6) is unique), and there exists a constant $\tau >0$ such that

$$\begin{aligned} \int _{0}^{t}e^{-\sqrt{\rho (A)}s}\varphi (s)ds\le \tau \varphi (t),\quad \forall t\ge 0, \end{aligned}$$

(53)

and p is as in (16) and $L_{f}$ satisfies

$$\begin{aligned} \Theta =\frac{\Delta _{1}L_{f}}{2}+\sqrt{\rho (A)}+p\ln (\rho (A_{1})+\rho (A_{2}))<0. \end{aligned}$$

(54)

Then the equation (6) is Ulam–Hyers–Rassias stable with respect to $(\varphi ,\psi )$.

Proof

Let $\hat{v}\in X$ be a solution of (50), and from Remark 5, $\hat{v}(t)$ satisfies the following impulsive differential equation

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=Au(t)+f(t,u(t))+G(t),\quad t\in (t_{i},t_{i+1}],\quad i\in \mathbb {N},\\&u(t^{+}_{i})=u(t_{i}^{-})+B_{1}u(t_{i}^{-})+g_{i},\quad i\in \mathbb {N},\\&u'(t_{i}^{+})=u'(t_{i}^{-})+B_{2}u'(t_{i}^{-})+g_{i},\quad i\in \mathbb {N},\\&u(0)=u_{0},\quad u'(0)=u_{1}, \end{aligned} \right. \end{aligned}$$

(55)

here G(t) and $g_{i}$ satisfy

$$\begin{aligned}&||G(t)||\le \varepsilon ^{*}(\rho (A_{1})+\rho (A_{2}))^{i}\varphi (t),\quad t\in (t_{i},t_{i+1}], \end{aligned}$$

(56)

$$\begin{aligned}&||g_{i}||\le \varepsilon ^{*}(\rho (A_{1})+\rho (A_{2}))^{i}\psi . \end{aligned}$$

(57)

Using Theorem 5.1 we have

$$\begin{aligned} \begin{aligned} \hat{v}(t)&= \overline{W}(A,t)+W(A,t,u_{0},u_{1})+\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)\big (f(s,\hat{v}(s))+G(s)\big )ds\\&\quad +A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)\big (f(s,\hat{v}(s))+G(s)\big )ds,\quad t\in (t_{k},t_{k+1}]. \end{aligned} \end{aligned}$$

From (40) and (45), for any $t\ge 0$, we have

$$\begin{aligned}&||H(x-2a\pm x_{i})||\le 2\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} T_{A,\varepsilon }e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}(||u_{0}||+||u_{1}||),\nonumber \\ \end{aligned}$$

(58)

$$\begin{aligned}&||G(x-2a\pm x_{i})||\le 2\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} T_{A,\varepsilon }e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}(\Vert u_{0}\Vert +\Vert u_{1}\Vert ),\nonumber \\ \end{aligned}$$

(59)

where $a=t_{i_{j}}-t_{i_{j-1}}+\cdots \pm t_{i_{1}}$, $i<i_{1}<i_{2}<\cdots <i_{j}\le k$. Hence, using (58), (59), for any $t\in (t_{k},t_{k+1}]$, we have

$$\begin{aligned} \begin{aligned}&||\overline{W}(A,t)||\\&\quad \le \sum _{i=0}^{k}2||g_{i}||\Bigg [T_{\varepsilon }^{2}(\rho (A_{1})+\varepsilon )^{k-i}\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}\\&\qquad +C_{k-i}^{1}T_{\varepsilon }^{3} (\rho (A_{1})+\varepsilon )^{k-i-1}(\rho (A_{2})+\varepsilon )\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}\\&\qquad +\cdots +T_{\varepsilon }^{2}(\rho (A_{2})+\varepsilon )^{k-i}\max \left\{ \frac{1}{\sqrt{\rho (A)+\varepsilon }},1\right\} e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}\Bigg ](||u_{0}||+||u_{1}||)\\&\quad \le \varepsilon ^{*}\psi \Delta _{1}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}(||u_{0}||+||u_{1}||)\sum _{i=1}^{k}e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}. \end{aligned} \end{aligned}$$

(60)

Let u(t) be the unique solution of (6) (see Theorem 5.2). Then using Lemma 2.7, (40), (41), (53), (56), (57) and (60), for all $t\in (t_{k},t_{k+1}]$, we have

$$\begin{aligned} ||u-\hat{v}||&=||\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)\Big (f(s,u(s))-f(s,\hat{v}(s))-G(s)\Big )ds\nonumber \\&\quad +A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)\Big (f(s,u(s))-f(s,\hat{v}(s))-G(s)\Big )ds-\overline{W}(A,t)||\nonumber \\&\le ||\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)\Big (f(s,u(s))-f(s,\hat{v}(s))\Big )ds||\nonumber \\&\quad +||A^{-\frac{1}{2}}\int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)\Big (f(s,u(s))-f(s,\hat{v}(s))\Big )ds||\nonumber \\&\quad +||\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}}W_{i}(A,t,s)G(s)ds||+||A^{-\frac{1}{2}}\nonumber \\&\quad \int _{t_{k}}^{t}\sinh A^{\frac{1}{2}}(t-s)G(s)ds||+||\overline{W}(A,t)||\nonumber \\&\le \frac{L_{f}T_{\varepsilon }^{3}}{\sqrt{\rho (A)+\varepsilon }}\sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}} (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k-i}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}||u-\hat{v}||ds\nonumber \\&\quad +\frac{L_{f}T_{\varepsilon }}{\sqrt{\rho (A)+\varepsilon }}\int _{t_{k}}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}||u-\hat{v}||ds\nonumber \\&\quad +\frac{\varepsilon ^{*}T_{\varepsilon }^{3}}{\sqrt{\rho (A)+\varepsilon }} (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}\varphi (s)ds\nonumber \\&\quad +\varepsilon ^{*}\psi \Delta _{1}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}(||u_{0}||+||u_{1}||)\sum _{i=1}^{k}e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}\nonumber \\&\le \frac{\Delta _{1}L_{f}}{2}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}||u-\hat{v}||ds+\frac{\varepsilon ^{*}\Delta _{1}}{2} (\rho (A_{1})\nonumber \\&\quad +\rho (A_{2})+2\varepsilon )^{k}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}\varphi (s)ds\nonumber \\&\quad +\frac{\varepsilon ^{*}\psi \Delta _{1}}{\lambda \sqrt{\rho (A)+\varepsilon }}(||u_{0}||+||u_{1}||)(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}e^{\sqrt{\rho (A)+\varepsilon }t}\nonumber \\&\le \frac{\Delta _{1}L_{f}}{2}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}||u-\hat{v}||ds +\frac{\varepsilon ^{*}\Delta _{1}\tau }{2}(\rho (A_{1})\nonumber \\&\quad +\rho (A_{2})+2\varepsilon )^{k}e^{\sqrt{\rho (A)+\varepsilon }t}(\varphi (t)+\psi )\nonumber \\&\quad +\frac{\varepsilon ^{*}\Delta _{1}}{\lambda \sqrt{\rho (A)+\varepsilon }}(||u_{0}||+||u_{1}||)(\varphi (t)+\psi )(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}e^{\sqrt{\rho (A)+\varepsilon }t}, \end{aligned}$$

(61)

here $\lambda$ is the minimum length of the interval, i.e. $\lambda =\inf \{t_{i+1}-t_{i}|i\in \mathbb {N}\}$. Multiply both sides of (61) by $e^{-\sqrt{\rho (A)+\varepsilon }t}$ and we find

$$\begin{aligned} \begin{aligned} e^{-\sqrt{\rho (A)+\varepsilon }t}||u-\hat{v}||&\le \frac{\Delta _{1}L_{f}}{2}\int _{0}^{t}e^{-\sqrt{\rho (A)+\varepsilon }s}||u-\hat{v}||ds\\&\quad +\varepsilon ^{*}(\varphi (t)+\psi )\left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) \\&\qquad (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}. \end{aligned} \end{aligned}$$

Since $\varphi \in PC(J,\mathbb {R}_{+})$ is a nondecreasing function, using Bellman’s inequality, we have

$$\begin{aligned} \begin{aligned} e^{-\sqrt{\rho (A)+\varepsilon }t}||u-\hat{v}||&\le \varepsilon ^{*}(\varphi (t)+\psi )\left( \frac{\Delta _{1}\tau }{2} +\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) (\rho (A_{1})\\&\quad +\rho (A_{2})+2\varepsilon )^{k}e^{\frac{\Delta _{1}L_{f}t}{2}}, \end{aligned} \end{aligned}$$

(62)

which implies

$$\begin{aligned} ||u-\hat{v}||&\le \varepsilon ^{*}(\varphi (t)+\psi )\left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) \\&\quad e^{\big (\sqrt{\rho (A)+\varepsilon }+\frac{\Delta _{1}L_{f}}{2}+\frac{k}{t}\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )\big )t}. \end{aligned}$$

Making use of (19), there exists $T>0$, such that

$$\begin{aligned} \frac{i(0,t)}{t}>p-\varepsilon \end{aligned}$$

for any $t>T$. In addition, according to (54), one can choose $\varepsilon >0$ small enough such that

$$\begin{aligned} \sqrt{\rho (A)+\varepsilon }+\frac{\Delta _{1}L_{f}}{2}+(p-\varepsilon )\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )<\frac{\Theta }{2}<0. \end{aligned}$$

Therefore, we have

$$\begin{aligned} ||u-\hat{v}||\le \left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) \varepsilon ^{*}(\varphi (t)+\psi ) \end{aligned}$$

(63)

for any $t>T$ and $t\in (t_{k},t_{k+1}]$.

In the case of $t\le T$ and $t\in (t_{k},t_{k+1}]$, from (62), we have

$$\begin{aligned} ||u-\hat{v}||&\le \varepsilon ^{*}(\varphi (t)+\psi )\left( \frac{\Delta _{1}\tau }{2} +\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) \\&\quad (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}e^{\big (\sqrt{\rho (A)+\varepsilon }+\frac{\Delta _{1}L_{f}}{2}\big )T}. \end{aligned}$$

Hence, (51) holds for

$$\begin{aligned} \begin{aligned} c&=\min \left\{ \left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{-k},\right. \\&\left. \qquad \left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) e^{\left( \sqrt{\rho (A)+\varepsilon }+\frac{\Delta _{1}L_{f}}{2}\right) T}\right\} . \end{aligned} \end{aligned}$$

Similarly, for any $t\in (t_{k},t_{k+1}]$, we also have

$$\begin{aligned} \begin{aligned} ||\overline{W}'(A,t)||&\le 2\varepsilon ^{*} \psi \max \left\{ \sqrt{\rho (A)+\varepsilon },\frac{1}{\sqrt{\rho (A)+\varepsilon }}\right\} T_{\varepsilon }^{3}(||u_{0}||+||u_{1}||)\Bigg (\rho (A_{1})\\&\quad +\rho (A_{2})+2\varepsilon \big )^{k} \sum _{i=1}^{k}e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}\\ =&\varepsilon ^{*} \psi \Delta _{1}\left( \rho (A_{1})+\rho (A_{2})+2\varepsilon \right) ^{k} (||u_{0}||+||u_{1}||)\\&\quad \sum _{i=1}^{k}e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}, \end{aligned} \end{aligned}$$

(64)

hence, making use of (56), (57) and (64), we have

$$\begin{aligned} \begin{aligned} ||u'-\hat{v}'||&\le T_{\varepsilon }^{3}L_{f} \sum _{i=0}^{k-1}\int _{t_{i}}^{t_{i+1}} (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k-i}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}||u-\hat{v}||ds\\&\quad +L_{f}T_{\varepsilon }\int _{t_{k}}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}||u-\hat{v}||ds\\&\quad +\varepsilon ^{*}T_{\varepsilon }^{3} (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}\varphi (s)ds\\&\quad +\varepsilon ^{*}\psi \Delta _{1}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}(||u_{0}||+||u_{1}||)\sum _{i=1}^{k}e^{\sqrt{\rho (A)+\varepsilon }(t-t_{i})}\\&\le \frac{\Delta _{1}L_{f}}{2}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}||u-\hat{v}||ds+\frac{\varepsilon ^{*}\Delta _{1}}{2} (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}\\&\qquad \int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}\varphi (s)ds\\&\quad +\frac{\varepsilon ^{*}\psi \Delta _{1}}{\lambda \sqrt{\rho (A)+\varepsilon }}(||u_{0}||+||u_{1}||)(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}e^{\sqrt{\rho (A)+\varepsilon }t}\\&\le \frac{\Delta _{1}L_{f}t}{2}\int _{0}^{t}e^{\sqrt{\rho (A)+\varepsilon }(t-s)}||u'-\hat{v}'||ds\\&\quad +\frac{\varepsilon ^{*}\Delta _{1}\tau }{2}(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}e^{\sqrt{\rho (A)+\varepsilon }t}(\varphi (t)+\psi )\\&\quad +\frac{\varepsilon ^{*}\Delta _{1}}{\lambda \sqrt{\rho (A)+\varepsilon }}(||u_{0}||+||u_{1}||)(\varphi (t)+\psi )(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}e^{\sqrt{\rho (A)+\varepsilon }t}\\&\le \varepsilon ^{*}(\varphi (t)+\psi )\big (\frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\big ) (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}e^{\sqrt{\rho (A)+\varepsilon }t}\\&\quad +\frac{\Delta _{1}L_{f}t}{2}e^{\sqrt{\rho (A)+\varepsilon }t}\int _{0}^{t}e^{-\sqrt{\rho (A)+\varepsilon }s}||u'-\hat{v}'||ds. \end{aligned} \end{aligned}$$

Multiply both sides by $e^{-\sqrt{\rho (A)+\varepsilon }t}$ and we have

$$\begin{aligned} \begin{aligned}&e^{-\sqrt{\rho (A)+\varepsilon }t}||u'-\hat{v}'||\le \varepsilon ^{*}(\varphi (t)+\psi )\left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{2}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) \\&\quad (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k}+\frac{\Delta _{1}L_{f}t}{2}\int _{0}^{t}e^{-\sqrt{\rho (A)+\varepsilon }s}||u'-\hat{v}'||ds,\\ \end{aligned} \end{aligned}$$

hence, by Lemma 2.6 we have

$$\begin{aligned} \begin{aligned} e^{-\sqrt{\rho (A)+\varepsilon }t}||u'-\hat{v}'||&\le \varepsilon ^{*}(\varphi (t) +\psi )\left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) \\&\quad (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k} e^{\frac{\Delta _{1}L_{f}t^{2}}{2}},\\ \end{aligned} \end{aligned}$$

so

$$\begin{aligned} ||u'-\hat{v}'||&\le \varepsilon ^{*}(\varphi (t)+\psi )\left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) \nonumber \\&\quad e^{\frac{\Delta _{1}L_{f}t^{2}}{2}+k\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )+\sqrt{\rho (A)+\varepsilon }t}. \end{aligned}$$

(65)

Note

$$\begin{aligned} \begin{aligned}&\frac{\Delta _{1}L_{f}t^{2}}{2}+k\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )+\sqrt{\rho (A)+\varepsilon }t\\&\quad \le \Big (\frac{\Delta _{1}L_{f}}{2}+\frac{k}{t}\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )+\sqrt{\rho (A)+\varepsilon }\Big )t,\quad t\le 1, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\frac{\Delta _{1}L_{f}t^{2}}{2}+k\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )+\sqrt{\rho (A)+\varepsilon }t\\&\quad \le \Big (\frac{\Delta _{1}L_{f}}{2}+\frac{k}{t}\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )+\sqrt{\rho (A)+\varepsilon }\Big )t^{2},\quad t\ge 1. \end{aligned} \end{aligned}$$

Therefore, from (54), we can choose $\varepsilon >0$ small enough such that

$$\begin{aligned} e^{\frac{\Delta _{1}L_{f}t^{2}}{2}+k\ln (\rho (A_{1})+\rho (A_{2})+2\varepsilon )+\sqrt{\rho (A)+\varepsilon }t}\le 1, \end{aligned}$$

for any $t>T$ large enough. Therefore, using the same method as in the previous proof, we have

$$\begin{aligned} ||u'-\hat{v}'||\le \overline{c}\varepsilon ^{*}(\varphi (t)+\psi )(\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{k},\quad t\in (t_{k},t_{k+1}], \end{aligned}$$

(66)

which implies (52) holds for

$$\begin{aligned} \begin{aligned} \overline{c}&=\min \Bigg \{\left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) (\rho (A_{1})+\rho (A_{2})+2\varepsilon )^{-k},\\&\left( \frac{\Delta _{1}\tau }{2}+\frac{\Delta _{1}(||u_{0}||+||u_{1}||)}{\lambda \sqrt{\rho (A)+\varepsilon }}\right) e^{\big (\sqrt{\rho (A)+\varepsilon }+\frac{\Delta _{1}L_{f}}{2}\big )T}\Bigg \}. \end{aligned} \end{aligned}$$

Hence, system (6) is Ulam–Hyers–Rassias stable with respect to $(\varphi ,\psi )$. $\square$

Example 5.1

Consider the second order impulsive differential equation (6) with $f(t,u(t))=\frac{\sqrt{2}}{2}\sin u(t)$, $t_{i}=i$, $i=0,1,2,\cdots$ and

$$\begin{aligned} A= \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 2 \end{pmatrix}, \quad B_{1}=B_{2}= \begin{pmatrix} e^{-3}-1 &{}\quad 0\\ 0 &{}\quad e^{-3}-1 \end{pmatrix}, \end{aligned}$$

and the initial value

$$\begin{aligned} u_{0}= \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \quad u_{1}= \begin{pmatrix} 1\\ 0 \end{pmatrix}. \end{aligned}$$

Define

$$\begin{aligned} \sin u(t)&=(\sin u_{1}(t),\sin u_{2}(t),\cdots ,\sin u_{n}(t))^{T},\\&\quad \forall u(t)=(u_{1}(t),u_{2}(t),\cdots ,u_{n}(t))^{T}\in \mathbb {R}^{n}. \end{aligned}$$

Let $\mathbb {R}^{m\times n}$ be the usual matrix space with the norm $||A||=\max \limits _{j}\sum _{i=1}^{m}|a_{i,j}|$, and set $\varepsilon =1$ in Lemma 2.5, then we can pick $T_{A,\varepsilon }=T_{A_{1},\varepsilon }=T_{A_{2},\varepsilon }=1$. Note

$$\begin{aligned} ||f(t,u)-f(t,v)||\le \frac{\sqrt{2}}{2}||u-v||, \end{aligned}$$

for all $u, v\in \mathbb {R}^{N}$. Thus conditions (19) and (49) hold, and (H) is fulfilled for $L_{f}=\frac{\sqrt{2}}{2}$. Hence, (6) has a unique solution $u\in PCB(J,\mathbb {R}^{n})$ with $\omega =\sqrt{3}$. Furthermore, let $\varphi (t)=e^{t}$, $\psi =1$, and $\tau =1$, and v(t) be a solution of (50). Then

$$\begin{aligned} \Theta =\frac{\Delta _{1}L_{f}}{2}+\sqrt{\rho (A)}+p\ln (\rho (A_{1})+\rho (A_{2}))=\frac{\sqrt{6}}{2}+\sqrt{2}-3<0. \end{aligned}$$

Then all the assumptions of Theorem 5.3 is fulfilled, and therefore equation (6) is Ulam–Hyers–Rassias stable with respect to $(e^{t},1)$.