Asymptotical stability of numerical methods for semi-linear impulsive differential equations

Abstract

This paper is concerned with asymptotical stability of a class of semi-linear impulsive ordinary differential equations. First of all, sufficient conditions for asymptotical stability of the exact solutions of semi-linear impulsive differential equations are provided. Under the sufficient conditions, some explicit exponential Runge–Kutta methods can preserve asymptotically stability without additional restriction on stepsizes. Moreover, it is proved that some explicit Runge–Kutta methods can preserve asymptotical stability without additional restriction on stepsizes under stronger conditions.

1 Introduction

The impulsive differential equations (IDEs) are widely applied in numerous fields of science and technology. Recently, the theory of IDEs has been an object of active research. Especially, the exact solutions of semi-linear IDEs have been widely studied (see Abada et al. 2009; Benchohra et al. 2006; Cardinali and Rubbioni 2008; Fan 2010; Friedli 1978; Fan and Li 2010; Liang et al. 2009). However, many IDEs cannot be solved analytically or their solving is more complicated. Hence, taking numerical methods is a good choice.

In recent years, the stability of numerical methods for IDEs has attracted more and more attention (see Liu et al. 2007, 2014; Liang et al. 2011; Ran et al. 2008; Wen and Yu 2011; Zhang and Liang 2014 etc). Stability of Runge–Kutta (RK) methods with the constant stepsize for scalar linear IDEs has been studied by Ran et al. (2008). RK methods with variable stepsizes for multidimensional linear IDEs have been investigated in Liu et al. (2007). Collocation methods for linear nonautonomous IDEs has been considered in Zhang and Liang (2014). An improved linear multistep method for linear IDEs has been investigated in Liu et al. (2012). Stability of the exact and numerical solutions of nonlinear IDEs has been studied by the Lyapunov method in Liang et al. (2011). Stability of RK methods for a special kind of nonlinear IDEs has been investigated by the properties of the differential equations without impulsive perturbations in Liu et al. (2014). Asymptotic stability of implicit Euler method for stiff IDEs in Banach space has been studied in Wen and Yu (2011). There are a lot of meaningful work on the numerical solution of impulsive differential equations, for example Ding et al. (2006, 2010), Liang et al. (2014), Liu and Zeng (2018), Wu et al. (2010), Wu and Ding (2012a, b) and Wu et al. (2019a, b). But, up to our knowledge, the numerical methods for impulsive semi-linear ordinary differential equations are still a blank field.

Exponential RK methods are widely applied to semi-linear ordinary differential equations without impulsive perturbations have been widely studied (see Calvo et al. 2000; Lawson 1967; Maset and Zennaro 2009; Ostermann and Daele 2007; Ostermann et al. 2006). Now the exponential RK methods are applied to the following equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} x'(t)=Lx(t)+f(t,x(t)),&{} t>t_0,\;t\ne \tau _k,\;k\in {\mathbb {Z}}^+,\\ x(\tau _k^+)=I_k(x(\tau _k)),&{} k\in {\mathbb {Z}}^+, \\ x(0^+)=x_0, \end{array}\right. } \end{aligned}$$

(1.1)

where $L\in {\mathbb {R}}^{d\times d}$, $f:(t_0,+\infty )\times \mathbb { R}^d\rightarrow {\mathbb {R}}^d$, $I_k:{\mathbb {R}}^d\rightarrow {\mathbb {R}}^d$, ${\mathbb {Z}}^+=\{1,2,\ldots \}$ and $\tau _k$ is a positive real constant and $\tau _k<\tau _{k+1}$ for arbitrary $k\in {\mathbb {Z}}^+$.

Outline of the rest of the paper is provided as follows. In Sect. 2, sufficient conditions for asymptotical stability of the exact solution of (1.1) are provided.

In Sect. 3, explicit Euler method, implicit Euler method and explicit exponential Euler are applied for two semi-linear IDEs to explore the stability of numerical methods. From the two numerical examples, the following two key questions which will be worked out in this article are presented. Are there some exponential RK methods which can preserve asymptotical stability of (1.1) without additional restrictions on stepsizes under the sufficient conditions which are provided in Sect. 2? Are there some RK methods which can preserve asymptotical stability of (1.1) without additional restrictions on stepsizes under stronger sufficient conditions?

In Sect. 4, it is proved that a class of explicit exponential RK methods can preserve asymptotical stability semi-linear IDEs without restriction on the stepsizes except that $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$, under the sufficient conditions which are provided in Sect. 2.

In Sect. 5, stronger sufficient conditions for asymptotical stability of the exact solution of (1.1) are provided first. Under these stronger sufficient conditions, asymptotical stability of RK methods for (1.1) is studied.

In Sect. 6, some conclusions are drafted.

2 Stability of IDEs

Assume that y(t) is the solution of the following equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} y'(t)=Ly(t)+f(t,y(t)),&{} t\ne \tau _k, k \in {\mathbb {Z}}^+, \\ y(\tau _k^+)=I_k(y(\tau _k)),&{} k \in {\mathbb {Z}}^+ , \\ y(0^+)=y_0, \end{array}\right. } \end{aligned}$$

(2.1)

and the functions f and $I_k$ satisfy the following properties, respectively:

$$\begin{aligned} \Vert f(t,x)-f(t,y)\Vert\le & {} \lambda \Vert x-y\Vert ,\;\forall t\in {\mathbb {R}}^+, \forall x,y\in {\mathbb {R}}^d, \end{aligned}$$

(2.2)

$$\begin{aligned} \Vert I_k(x)-I_k(y)\Vert\le & {} \gamma _k\Vert x-y\Vert , \;\forall x,y\in {\mathbb {R}}^d. \end{aligned}$$

(2.3)

Definition 2.1

(Bainov and Simeonov 1989; Samoilenko et al. 1995) The exact solution x(t) of  (1.1) is said to be

• 1. Stable if, for an arbitrary $\epsilon >0$, there exists a positive number $\delta =\delta (\epsilon )$ such that, for the solution y(t) of (2.1), $\Vert x_0-y_0\Vert <\delta$ implies

  $$\begin{aligned} \Vert x(t)-y(t)\Vert <\epsilon ,\;\forall \;t>t_0; \end{aligned}$$

• 2. Asymptotically stable, if it is stable and $\lim \limits _{t\rightarrow \infty }\Vert x(t)-y(t)\Vert =0.$

Theorem 2.2

Assume that there exists a positive constant ${\hat{C}}$ such that $\tau _{k}-\tau _{k-1}\le {\hat{C}}$, $k\in {\mathbb {Z}}^+$. The exact solution of (1.1) is asymptotically stable if there is a positive constant C such that

$$\begin{aligned} \gamma _k \mathrm{e}^{(\mu (L)+\lambda )(\tau _k-\tau _{k-1})}\le C<1, \end{aligned}$$

(2.4)

for arbitrary $k\in {\mathbb {Z}}^+$.

Proof

Define $\delta (t)=\Vert x(t)-y(t)\Vert ^2$. Obviously, we have

$$\begin{aligned} \begin{aligned} \delta '(t)&=2<x'(t)-y'(t),x(t)-y(t)> \\&=2<Lx(t)+f(t,x(t))-Ly(t)-f(t,y(t)),x(t)-y(t)>\\&\le 2\mu (L)\delta (t)+2\Vert f(t,x(t))-f(t,y(t))\Vert \Vert x(t)-y(t)\Vert \\&\le 2\mu (L)\delta (t)+2\lambda \Vert x(t)-y(t)\Vert \Vert x(t)-y(t)\Vert \\ \end{aligned} \end{aligned}$$

Since x(t) and y(t) are left continuous, we get

$$\begin{aligned} \delta (t)\le \mathrm{e}^{2(\mu (L)+\lambda )(t-\tau _k)}\delta (\tau _k^+),\;\;t\in (\tau _k,\tau _{k+1}], \end{aligned}$$

that is

$$\begin{aligned} \Vert x(t)-y(t)\Vert \le \mathrm{e}^{(\mu (L)+\lambda )(t-\tau _k)}\Vert x(\tau _k^+)-y(\tau _k^+)\Vert ,\;\;t\in (\tau _k,\tau _{k+1}], \end{aligned}$$

which implies

$$\begin{aligned} \Vert x(\tau ^+_{k+1})-y(\tau ^+_{k+1})\Vert= & {} \Vert I_{k+1}(x(\tau _{k+1}))-I_{k+1}(y(\tau _{k+1}))\Vert \\\le & {} \gamma _{k+1}\Vert x(\tau _{k+1})-y(\tau _{k+1})\Vert \\\le & {} \Vert x(\tau _{k}^+)-y(\tau _{k}^+)\Vert \gamma _{k+1}\mathrm{e}^{(\mu (L)+\lambda ) (\tau _{k+1}-\tau _{k})}. \end{aligned}$$

According to mathematical induction, we can get that, for $\forall \;t\in (\tau _k,\tau _{k+1}]$,

$$\begin{aligned} \Vert x(t)-y(t)\Vert&\le \Vert x_0-y_0\Vert (\gamma _1\mathrm{e}^{(\mu (L)+\lambda )(\tau _1-\tau _0)})\\&(\gamma _2\mathrm{e}^{(\mu (L)+\lambda )(\tau _2-\tau _1)}) (\gamma _{k} \mathrm{e}^{(\mu (L)+\lambda )(\tau _{k}-\tau _{k-1})}) \mathrm{e}^{(\mu (L)+\lambda ) (t-\tau _{k})}\\&\le C^{k}\Vert x_0-y_0\Vert \mathrm{e}^{(\mu (L)+\lambda ) (t-\tau _{k})} \\&\le C^{k}\Vert x_0-y_0\Vert {\hat{C}}_1, \end{aligned}$$

where ${\hat{C}}_1=\max \{1,\mathrm{e}^{(\mu (L)+\lambda ){\hat{C}}}\}$. Hence, for an arbitrary $\epsilon >0$, there exists $\delta =\frac{\epsilon }{{\hat{C}}_1}$ such that $\Vert x_0-y_0\Vert <\delta$ implies

$$\begin{aligned} \Vert x(t)-y(t)\Vert \le C^{k}\Vert x_0-y_0\Vert {\hat{C}}_1\le \Vert x_0-y_0\Vert {\hat{C}}_1<\epsilon \end{aligned}$$

for arbitrary $t\in (\tau _{k}, \tau _{k+1}]$, $k=0,1,2,\ldots$. And at the moments of impulsive effect $t=\tau _{k+1}, k=0,1,2,\ldots$, we can also obtain that

$$\begin{aligned} \Vert x(\tau _{k+1})-y(\tau _{k+1})\Vert \le C^{k}\Vert x_0-y_0\Vert {\hat{C}}_1<\epsilon , \end{aligned}$$

and

$$\begin{aligned} \Vert x(\tau ^+_{k+1})-y(\tau ^+_{k+1})\Vert \le C^{k+1}\Vert x_0-y_0\Vert <\epsilon . \end{aligned}$$

Therefore, the exact solution of (1.1) is stable. Obviously, for arbitrary $t\in (\tau _{k}, \tau _{k+1}]$, $k=0,1,2,\ldots$,

$$\begin{aligned} \Vert x(t)-y(t)\Vert \le C^{k}\Vert x_0-y_0\Vert {\hat{C}}_1\rightarrow 0,\;k\rightarrow \infty . \end{aligned}$$

At the moments of impulsive effect $t=\tau _{k+1}, k=0,1,2,\ldots$, we can also obtain that

$$\begin{aligned} \Vert x(\tau _{k+1})-y(\tau _{k+1})\Vert \le C^{k}\Vert x_0-y_0\Vert {\hat{C}}_1\rightarrow 0,\;k\rightarrow \infty , \end{aligned}$$

and

$$\begin{aligned} \Vert x(\tau ^+_{k+1})-y(\tau ^+_{k+1})\Vert \le C^{k+1}\Vert x_0-y_0\Vert \rightarrow 0,\;k\rightarrow \infty . \end{aligned}$$

Consequently, the exact solutions of (1.1) is asymptotically stable under the condition (2.4). $\square$

3 Two numerical examples

In this section, explicit Euler method, implicit Euler method and explicit exponential Euler are applied to semi-linear IDEs to explore the stability of numerical methods.

Example 3.1

Consider one-dimension semi-linear IDE:

$$\begin{aligned} {\left\{ \begin{array}{ll} x'(t)=-5x(t)+\sin (x(t)),&{} t>0,\;t\ne k,\;k\in {\mathbb {Z}}^+,\\ x(k^+)=18x(k),&{} k\in {\mathbb {Z}}^+,\\ x(0^+)=x_0, \end{array}\right. } \end{aligned}$$

(3.1)

and the same equation with another initial value

$$\begin{aligned} {\left\{ \begin{array}{ll} y'(t)=-5y(t)+\sin (y(t)),&{} t>0,\;t\ne k,\;k\in {\mathbb {Z}}^+,\\ y(k^+)=18y(k),&{} k\in {\mathbb {Z}}^+,\\ y(0^+)=y_0, \end{array}\right. } \end{aligned}$$

(3.2)

where $x_0$ and $y_0$ are real constants and $x_0\ne y_0$. By Theorem 2.2, we can obtain that the exact solution of (3.1) is asymptotically stable.

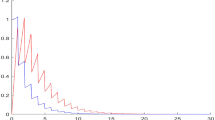
Figures 1, 2 and 3 are the numerical solutions and the absolute value of these errors between two different numerical solutions, which are obtained from explicit Euler method, implicit Euler method and explicit exponential Euler, respectively, when $x_0=1$, $y_0=2$, $h_k= h=\frac{1}{2}$, $k\in {\mathbb {N}}$.

First of all, we claim that the absolute value of these errors between two different numerical solutions obtained from explicit Euler method for (3.1) and (3.2) tend to infinite when the stepsize $h=\frac{1}{2}$ (see Fig. 1).

Fig. 1

Explicit Euler method for (3.1) and (3.2)

Fig. 2

Implicit Euler method for (3.1) and (3.2)

Fig. 3

Explicit exponential Euler method for (3.1) and (3.2)

To prove this, let us consider the explicit Euler method for (3.1):

$$\begin{aligned} \left\{ \begin{array}{lll} x_{k,l+1}=x_{k,l}+h(-5x_{k,l}+\sin (x_{k,l})), &{} \qquad k\in {\mathbb {N}},\;l=0,1,\ldots ,m-1,\\ x_{k+1,0}=18x_{k,m}, &{} \qquad k\in {\mathbb {N}},\\ x_{0,0}=x_0, \end{array} \right. \end{aligned}$$

(3.3)

and explicit Euler method for (3.2):

$$\begin{aligned} \left\{ \begin{array}{lll} y_{k,l+1}=y_{k,l}+h(-5y_{k,l}+\sin (y_{k,l})),&{} \qquad k\in {\mathbb {N}},\;l=0,1,\ldots ,m-1,\\ y_{k+1,0}=18y_{k,m}, &{} \qquad k\in {\mathbb {N}},\\ y_{0,0}=y_0, \end{array} \right. \end{aligned}$$

(3.4)

where $h=\frac{1}{m}$, $m\in {\mathbb {Z}}^+$, $x_{k,l}$ is an approximation to the exact solution $x(k+lh)$ and $x_{k,m}$ is an approximation to $x(k+1^-)$, $k\in {\mathbb {N}}, l=0,1,\ldots ,m-1$.

Obviously, when $h=\frac{1}{2}$, we can obtain that, for $l=0,1$,

$$\begin{aligned} |x_{k,l+1}-y_{k,l+1}|= & {} |(1-5h)(x_{k,l}-y_{k,l})+h(\sin (x_{k,l})-\sin (y_{k,l}))|\\\ge & {} |(1-5h)(x_{k,l}-y_{k,l})|-h|(\sin (x_{k,l})-\sin (y_{k,l}))|\\\ge & {} |(1-5h)(x_{k,l}-y_{k,l})|-h|x_{k,l}-y_{k,l}|\\= & {} \frac{3}{2} \cdot |x_{k,l}-y_{k,l}|-\frac{1}{2}\cdot |x_{k,l}-y_{k,l}|\\= & {} |x_{k,l}-y_{k,l}|, \end{aligned}$$

which implies that, for any $l=0,1,2$,

$$\begin{aligned} \begin{aligned} |x_{k,l}-y_{k,l}| \ge&\,18|x_{k-1,l}-y_{k-1,l}|\\ \ge&\,18^k|x_{0,l}-y_{0,l}|\\ \ge&\,18^k|x_{0}-y_{0}|\rightarrow \infty ,\;k\rightarrow \infty . \end{aligned} \end{aligned}$$

Second, we claim that the absolute value of these errors between two different numerical solutions, which are obtained from implicit Euler method for (3.1) and (3.2), tend to infinite when $h=\frac{1}{2}$ (see Fig. 1).

To prove this, let us consider implicit Euler method for (3.1)

$$\begin{aligned} \left\{ \begin{array}{lll} x_{k,l+1}=x_{k,l}+h(-5x_{k,l+1}+\sin (x_{k,l+1})), &{} \qquad k\in {\mathbb {N}},\;l=0,1,\ldots ,m-1,\\ x_{k+1,0}=18x_{k,m}, &{} \qquad k\in {\mathbb {N}},\\ x_{0,0}=x_0. \end{array} \right. \end{aligned}$$

(3.5)

and implicit Euler method for (3.2)

$$\begin{aligned} \left\{ \begin{array}{lll} y_{k,l+1}=y_{k,l}+h(-5y_{k,l+1}+\sin (y_{k,l+1})), &{} \qquad k\in {\mathbb {N}},\;l=0,1,\ldots ,m-1,\\ y_{k+1,0}=18y_{k,m}, &{} \qquad k\in {\mathbb {N}},\\ y_{0,0}=y_0. \end{array} \right. \end{aligned}$$

(3.6)

Obviously, when $h=\frac{1}{2}$, we can obtain that

$$\begin{aligned} \begin{aligned} |x_{k,l+1}-y_{k,l+1}| =&\,|x_{k,l}-y_{k,l}-5h(x_{k,l+1}-y_{k,l+1})+h(\sin (x_{k,l+1})-\sin (y_{k,l+1}))|\\ \ge&\,|x_{k,l}-y_{k,l}|-5h|x_{k,l+1}-y_{k,l+1}|-h|(\sin (x_{k,l+1})-\sin (y_{k,l+1}))|\\ \ge&\,|x_{k,l}-y_{k,l}|-6h|x_{k,l+1}-y_{k,l+1}|\\ =&\,|x_{k,l}-y_{k,l}|-3|x_{k,l+1}-y_{k,l+1}| \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} |x_{k,l+1}-y_{k,l+1}|\ge \frac{1}{4} \cdot |x_{k,l}-y_{k,l}|. \end{aligned}$$

Hence, for any $l=0,1,2$,

$$\begin{aligned} \begin{aligned} |x_{k,l}-y_{k,l}| \ge&\frac{18}{4^2} \cdot |x_{k-1,l}-y_{k-1,l}|\\ \ge&\left( \frac{9}{8}\right) ^k \cdot |x_{0,l}-y_{0,l}|\\ \ge&\left( \frac{9}{8}\right) ^k \cdot \frac{1}{4^2}\cdot |x_{0}-y_{0}|\rightarrow \infty ,\;k\rightarrow \infty . \end{aligned} \end{aligned}$$

It is different from the above two cases, we can easily prove that exponential explicit Euler method (see Fig. 3) for (3.1) is asymptotically stable for arbitrary $h=\frac{1}{m}$, $\forall m\in {\mathbb {Z}}^+$. By Corollary 4.4 of this paper, we also can obtain this point.

Example 3.2

Consider one-dimension semi-linear IDE:

$$\begin{aligned} {\left\{ \begin{array}{ll} x'(t)=4x(t)+\frac{\sqrt{x^2(t)+1}}{10}, &{} \qquad t>0,\;t\ne k,\;k\in {\mathbb {Z}}^+,\\ x(k^+)=\frac{x(k)}{80},&{} \qquad k\in {\mathbb {Z}}^+,\\ x(0^+)=x_0, \end{array}\right. } \end{aligned}$$

(3.7)

and the same equation with another initial value

$$\begin{aligned} {\left\{ \begin{array}{ll} y'(t)=4y(t)+\frac{\sqrt{y^2(t)+1}}{10} ,&{} \qquad t>0,\;t\ne k,\;k\in {\mathbb {Z}}^+,\\ y(k^+)=\frac{y(k)}{80},&{} \qquad k\in {\mathbb {Z}}^+,\\ y(0^+)=y_0, \end{array}\right. } \end{aligned}$$

(3.8)

where $x_0$ and $y_0$ are real constants and $x_0\ne y_0$ . By Theorem 2.2, we can obtain that the exact solution of (3.7) is asymptotically stable.

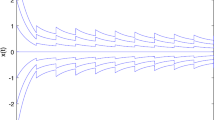
Figures 4, 5 and 6 are the numerical solutions and the absolute value of these errors between two different numerical solutions, which are obtained from explicit Euler method, implicit Euler method and explicit exponential Euler, respectively, when $x_0=1$, $y_0=2$, $h=\frac{1}{5}$.

Fig. 4

Explicit Euler method for (3.7) and (3.8)

Fig. 5

Explicit Euler method for (3.7) and (3.8)

Fig. 6

Explicit exponential Euler method for (3.7) and (3.8)

We claim that the absolute value of these errors between two different numerical solutions obtained from implicit Euler method for (3.7) and (3.8) tend to infinite when $h=\frac{1}{5}$.

To prove this, let us consider implicit Euler method for (3.7)

$$\begin{aligned} \left\{ \begin{array}{lll} x_{k,l+1}=x_{k,l}+h\left( 4x_{k,l+1}+\frac{\sqrt{x_{k,l+1}^2+1}}{10}\right) , &{}\qquad k\in {\mathbb {N}},\;l=0,1,\ldots ,m-1,\\ x_{k+1,0}=\frac{x_{k,m}}{80}, &{} \qquad k\in {\mathbb {N}},\\ x_{0,0}=x_0. \end{array} \right. \end{aligned}$$

(3.9)

and implicit Euler method for (3.8)

$$\begin{aligned} \left\{ \begin{array}{lll} y_{k,l+1}=y_{k,l}+h\left( 4y_{k,l+1}+\frac{\sqrt{y_{k,l+1}^2+1}}{10}\right) , &{} \qquad k\in {\mathbb {N}},\;l=0,1,\ldots ,m-1,\\ y_{k+1,0}=\frac{y_{k,m}}{80}, &{} \qquad k\in {\mathbb {N}},\\ y_{0,0}=y_0. \end{array} \right. \end{aligned}$$

(3.10)

Obviously, when $h=\frac{1}{5}$, we can obtain that

$$\begin{aligned} \begin{aligned} (1-4h)|x_{k,l+1}-y_{k,l+1}| =&\,|(x_{k,l}-y_{k,l})+\frac{h (\sqrt{x_{k,l+1}^2+1}-\sqrt{y_{k,l+1}^2+1})}{10}|\\ \ge&\,|x_{k,l}-y_{k,l}|-\frac{h|x_{k,l+1}-y_{k,l+1}|}{10} \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} |x_{k,l+1}-y_{k,l+1}|\ge \frac{50}{11} \cdot |x_{k,l}-y_{k,l}|. \end{aligned}$$

Hence, for any $l=0,1,2$,

$$\begin{aligned} \begin{aligned} |x_{k,l}-y_{k,l}| \ge&\left( \frac{50}{11}\right) ^5\cdot \frac{1}{80} \cdot |x_{k-1,l}-y_{k-1,l}|\\ \ge&\left( \frac{50}{11}\right) ^{5k}\cdot \frac{1}{80^k} \cdot |x_{0,l}-y_{0,l}|\\ \ge&\left( \frac{50}{11}\right) ^{5k}\cdot \frac{1}{80^k}\cdot |x_{0}-y_{0}|\rightarrow \infty ,\;k\rightarrow \infty . \end{aligned} \end{aligned}$$

On the other hand, it is easy to prove that both explicit Euler method (see Fig. 4) and exponential explicit Euler method (see Fig. 6) for (3.7) are asymptotically stable for arbitrary $h=\frac{1}{m}$, $\forall m\in {\mathbb {Z}}^+$. This point can also be obtained by Corollary 4.4 and Theorem 5.2 of this paper.

From Examples 3.1 and 3.2, we can see that explicit exponential Euler method can preserve asymptotically stability of the exact solutions of (3.1) and (3.7) for arbitrary $h=\frac{1}{m},\; m\in {\mathbb {Z}}^+$, but Runge–Kutta methods sometimes cannot preserve asymptotically stability without additional restriction on stepsizes. Naturally, the following two questions arise. Are there some exponential RK methods which can preserve asymptotical stability of (1.1) under the conditions of Theorem 2.2 without restrictions on stepsizes except that $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $m\in {\mathbb {Z}}^+$, $k\in {\mathbb {N}}$ ? Are there some RK methods which can preserve asymptotical stability of (1.1) without restrictions on stepsizes except that $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $m\in {\mathbb {Z}}^+$, $k\in {\mathbb {N}}$, under stronger conditions?

4 Stability of exponential RK methods

In this section, exponential RK methods for (1.1) can be constructed as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{k,l}^i=\mathrm{e}^{c_ih_kL}x_{k,l}+h_k\sum \limits _{i=1}^v a_{ij}(h_kL) f(t_{k,l}^j,X_{k,l}^j),&{}k\in {\mathbb {N}}, i=1,2,\ldots ,v,\\ x_{k,l+1}=\mathrm{e}^{h_kL}x_{k,l}+h_k \sum \limits _{i=1}^v b_i(h_kL) f(t_{k,l}^i,X_{k,l}^i),&{}l=0,1,2,\ldots ,m-1,\\ x_{k+1,0}=I_{k+1}(x_{k,m}),\\ x_{0,0}=x_0, \end{array}\right. } \end{aligned}$$

(4.1)

where $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $t_{k,l}=\tau _{k}+l h_k$, $t_{k,l}^i=t_{k,l}+c_ih_k$, $x_{k,l}$ is an approximation to the exact solution $x(t_{k,l})$, $x_{k,m}$ is an approximation to $x(\tau _{k+1}^-)$ and $X_{k,l}^i$ is an approximation to the exact solution $x(t_{k,l}^i)$, $k\in {\mathbb {N}}=\{0,1,2,\ldots \}, l=0,1,\ldots ,m-1, i=1,2,\ldots ,v$, v is referred to as the number of stages. The weights $b_i$, the abscissae $c_i=\sum \nolimits _{j=1}^v a_{ij}$ and the matrix $A=[a_{ij}]_{i,j=1}^s$ are denoted by (A, b, c). Now we introduce, for constant $\alpha$ (may be nonnegative), the $1\times v$-vector $\mathbf{b }(\alpha )$ of components

$$\begin{aligned} {\mathbf {b}}_i(\alpha ):=\sup _{M\in {\mathbb {R}}^{d\times d},\mu (M)\le \alpha }\Vert b_i(M)\Vert ,\;\;i=1,2,\ldots ,v \end{aligned}$$

and the $v\times v$-vector $\mathbf{A }(\alpha )$ whose elements are

$$\begin{aligned} {\mathbf {a}}_{ij}(\alpha ):=\sup _{M\in {\mathbb {R}}^{d\times d},\mu (M)\le \alpha }\Vert a_{ij}(M)\Vert ,\;\;i,j=1,2,\ldots ,v \end{aligned}$$

And the exponential RK methods for (2.1):

$$\begin{aligned} {\left\{ \begin{array}{ll} Y_{k,l}^i=\mathrm{e}^{c_ih_kL}y_{k,l}+h_k\sum \limits _{i=1}^v a_{ij}(h_kL) f(t_{k,l}^j,Y_{k,l}^j),&{}k\in {\mathbb {N}}, i=1,2,\ldots ,v,\\ y_{k,l+1}=\mathrm{e}^{h_kL}y_{k,l}+h_k \sum \limits _{i=1}^v b_i(h_kL) f(t_{k,l}^i,Y_{k,l}^i),&{}l=0,1,2,\ldots ,m-1,\\ y_{k+1,0}=I_{k+1}(y_{k,m}),\\ y_{0,0}=y_0. \end{array}\right. } \end{aligned}$$

(4.2)

Definition 4.1

The exponential RK methods (4.1) (or RK methods ) for impulsive differential equation (1.1) is said to be

• 1. stable, if $\exists M>0$, $m\ge M$, $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$,

  • (i) $I-zA$ is invertible for all $z=\alpha h_k$,

  • (ii) for an arbitrary $\epsilon >0$, there exists such a positive number $\delta =\delta (\epsilon )$ that, for the numerical solutions of (4.2), $\Vert x_0-y_0\Vert <\delta$ implies

    $$\begin{aligned} \max _{1\le l\le m}\Vert x_{k,l}-y_{k,l}\Vert <\epsilon ,\;\forall \; k\in {\mathbb {N}}, \end{aligned}$$

• 2. asymptotically stable, if it is stable and if there exists such a positive number $\delta _0$ that $\Vert x_0-y_0\Vert <\delta _1$ implies

  $$\begin{aligned} \lim \limits _{k\rightarrow \infty }\max _{1\le l\le m}\Vert x_{k,l}-y_{k,l}\Vert =0. \end{aligned}$$

Theorem 4.2

(Asymptotically stable) If the explicit exponential RK method (4.1) satisfies ${\mathbf {S}}(\alpha ,\beta )\le \mathrm{e}^{\alpha +\beta }$, where

$$\begin{aligned} {\mathbf {S}}(\alpha ,\beta )=\mathrm{e}^\alpha +\sum _{k=0}^{v-1}\beta ^{k+1}{\mathbf {b}}(\alpha ){\mathbf {A}}(\alpha )^{k}\mathrm{e}^{c\alpha }e,\;\alpha \in {\mathbb {R}},\beta \ge 0, \end{aligned}$$

then the explicit exponential RK method (4.1) for (1.1) is asymptotically stable, for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$.

Proof

Define

$$\begin{aligned} \begin{aligned}&\delta _{k,l}:=x_{k,l}-y_{k,l},\;\; k=0,1,2,\ldots ,\;l=0,1,\ldots ,m,\\&\Delta _{k,l}^i:=X_{k,l}^i-Y_{k,l}^i,\;\; k=0,1,2,\ldots ,\;\;l=0,1,\ldots ,m,\;\;i=1,2,\ldots ,v. \end{aligned} \end{aligned}$$

Hence, we have

$$\begin{aligned} \begin{aligned}&\delta _{k,l}=\mathrm{e}^{h_kL}\delta _{k,l-1}+h_k\sum _{i=1}^vb_i(h_kL)(f(t_{k,l}^i,X_{k,l}^i)-f(t_{k,l}^i,Y_{k,l}^i)),\\&\Delta _{k,l}^i=\mathrm{e}^{c_ih_kL}\delta _{k,l-1}+h_k\sum _{j=1}^{i-1}a_{ij}(h_kL)(f(t_{k,l}^i,X_{k,l}^j)-f(t_{k,l}^i,Y_{k,l}^j)),\\&\delta _{k+1,0}=I_{k+1}(x_{k,m})-I_{k+1}(y_{k,m}), \end{aligned} \end{aligned}$$

which imply that

$$\begin{aligned} \begin{aligned}&\Vert \delta _{k,l}\Vert \le \mathrm{e}^{\mu (h_kL)}\Vert \delta _{k,l-1}\Vert +h_k\lambda \sum _{i=1}^v\Vert b_i(h_kL)\Vert \Vert \Delta _{k,l}^i\Vert ,\\&\Vert \Delta _{k,l}^i\Vert \le \mathrm{e}^{c_i\mu (h_kL)}\Vert \delta _{k,l-1}\Vert +h_k\lambda \sum _{j=1}^{i-1}\Vert a_{ij}(h_kL)\Vert \Vert \Delta _{k,l}^j\Vert ,\\&\Vert \delta _{k+1,0}\Vert =\Vert I_{k+1}(x_{k,m})-I_{k+1}(y_{k,m})\Vert \le \gamma _{k+1}\Vert \delta _{k,m}\Vert , \end{aligned} \end{aligned}$$

where $\lambda$ and $\gamma _k$ are the Lipschitz constants of f and $I_k$, respectively, $\Delta _{k,l}$ is the $v\times 1$-vector of components $\Vert \Delta _{k,l}^i\Vert ,\;i=1,2,\ldots ,v$. Since the function ${\mathbf {b}}_i$ and ${\mathbf {a}}_{ij},i,j=1,2,\ldots v$, are nondecreasing, we can obtain that

$$\begin{aligned} \Vert \delta _{k,l+1}\Vert \le {\mathbf {S}}(h_k\mu (L),h_k\lambda )\Vert \delta _{k,l}\Vert \le \mathrm{e}^{(\mu (L)+\lambda )h_k}\Vert \delta _{k,l}\Vert , \end{aligned}$$

where $\mathbf{S }(\alpha ,\beta )=\mathrm{e}^\alpha +\sum _{k=0}^{v-1}\beta ^{k+1}\mathbf{b }^\mathrm{T}(\alpha )\mathbf{A }(\alpha )^{k}\mathrm{e}^{c\alpha }e,\;\alpha \in {\mathbb {R}},\beta \ge 0.$

Hence, for arbitrary $k=0,1,2,\ldots$ and $l=0,1,\ldots ,m$, we have

$$\begin{aligned} \Vert \delta _{k,l}\Vert \le \Vert \delta _{k,0}\Vert \mathrm{e}^{(\Vert L\Vert +\lambda ) lh_k}. \end{aligned}$$

Therefore, by the method of introduction and the condition (5.1), we can obtain that

$$\begin{aligned}&\Vert \delta _{k,l}\Vert \\&\quad \le \Vert x_0-y_0\Vert (\gamma _1\mathrm{e}^{(\Vert L\Vert +\lambda ) (\tau _1-\tau _0)}) (\gamma _2\mathrm{e}^{(\Vert L\Vert +\lambda ) (\tau _2-\tau _1)})\cdots (\gamma _{k}\mathrm{e}^{(\Vert L\Vert +\lambda ) (\tau _{k}-\tau _{k-1})}) \mathrm{e}^{(\Vert L\Vert +\lambda ){\hat{C}}}\\&\quad \le \Vert x_0-y_0\Vert C^{k} \mathrm{e}^{(\Vert L\Vert +\lambda ){\hat{C}}} \end{aligned}$$

which implies that the exponential RK method for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$ and $m\ge M$. $\square$

Along with the function ${\mathbf {S}}$, we consider also the function

$$\begin{aligned} S(\alpha ,\beta )=\mathrm{e}^\alpha +\sum _{k=0}^{v-1}\beta ^{k+1}b^\mathrm{T} (\alpha )A(\alpha )^{k}\mathrm{e}^{c\alpha }e,\;\alpha \in {\mathbb {R}},\beta \ge 0. \end{aligned}$$

Therefore, by Theorem 4.2, we immediately get the following corollary.

Corollary 4.3

If the explicit exponential RK method (4.1) satisfies

$$\begin{aligned} S(\alpha ,\beta )\le \mathrm{e}^{\alpha +\beta } \end{aligned}$$

(4.3)

and

$$\begin{aligned} b(\alpha )={\mathbf {b}}(\alpha ),\;\;and\;\;A(\alpha )={\mathbf {A}}(\alpha ), \end{aligned}$$

(4.4)

then the explicit exponential RK method (4.1) for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$.

For an IF method with an explicit underlying RK method (A, b, c), we have

$$\begin{aligned} S(\alpha ,\beta )=\mathrm{e}^\alpha \left( 1+\sum _{k=0}^{v-1}\beta ^{k+1}b^\mathrm{T}A^ke\right) ,\;\alpha ,\beta \in {\mathbb {R}}. \end{aligned}$$

Condition (4.3) holds if

$$\begin{aligned} b^\mathrm{T}A^ke\le \frac{1}{(k+1)!},\;k\ge {\mathbf {k}}, \end{aligned}$$

where ${\mathbf {k}}=\min \{k: k\in {\mathbb {N}}, b^\mathrm{T}A^ke\ne \frac{1}{(k+1)!}\}$. On the other hand, the condition (4.4) holds if

$$\begin{aligned} 0=c_1\le c_2\le \cdots \le c_v\le 1 \end{aligned}$$

(4.5)

and

$$\begin{aligned} b_i\ge 0\;\mathrm{and}\; a_{ij}\ge 0,\;i=1,\ldots ,i-1. \end{aligned}$$

(4.6)

Hence, by Corollary 4.3, we can obtain the following corollary.

Corollary 4.4

If the explicit exponential RK method (4.1) is IF method satisfies (4.5), (4.6) and

$$\begin{aligned} b^\mathrm{T}A^ke\le \frac{1}{(k+1)!},\;k\ge {\mathbf {k}}, \end{aligned}$$

where ${\mathbf {k}}=\min \{k\in \{0,1,2,\ldots \}|\; b^\mathrm{T}A^ke\ne \frac{1}{(k+1)!}\}$, then the explicit exponential RK method (4.1) for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$.

5 Stability of RK methods

In this section, stronger sufficient conditions for asymptotical stability of the exact solution of (1.1) are provided. Moreover, asymptotical stability of RK methods for (1.1) is studied under these conditions.

Since $\mu (L)\le \Vert L\Vert$, by Theorem 2.2, we can obtain the following corollary.

Corollary 5.1

Assume that there exists a positive constant ${\hat{C}}$ such that $\tau _{k}-\tau _{k-1}\le {\hat{C}}$, $k\in {\mathbb {Z}}^+$. The exact solution of (1.1) is asymptotically stable if there is a positive constant C such that

$$\begin{aligned} \gamma _k \mathrm{e}^{(\Vert L\Vert +\lambda )(\tau _{k+1}-\tau _k)}\le C<1, \end{aligned}$$

(5.1)

for arbitrary $k\in {\mathbb {Z}}^+$.

5.1 Explicit RK method

Consider the explicit Euler method for (1.1):

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{k,l+1}=x_{k,l}+h_kLx_{k,l}+h_k f(t_{k,l},x_{k,l}),~ k\in {\mathbb {N}},\;l=1,2,\ldots ,m-1,\\ x_{k+1,0}=x_{k,m}+I_{k+1}(x_{k,m}),\\ x_{0,0}=x_0. \end{array}\right. } \end{aligned}$$

(5.2)

Theorem 5.2

Under the conditions of Corollary 5.1, the explicit Euler method (5.2) for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $\forall m\in {\mathbb {Z}}^+$.

Proof

For arbitrary $k=0,1,2,\ldots$ and $l=0,1,\ldots ,m-1$, we can obtain

$$\begin{aligned} \Vert \delta _{k,l+1}\Vert&=\Vert x_{k,l}-y_{k,l}+h_kL(x_{k,l}-y_{k,l})+h_k f(t_{k,l},x_{k,l})-h_k f(t_{k,l},y_{k,l})\Vert \\&\le (1+h_k\Vert L\Vert )\Vert \delta _{k,l}\Vert +h_k\Vert f(t_{k,l},x_{k,l})- f(t_{k,l},y_{k,l})\Vert \\&\le (1+\Vert L\Vert h_k+ \lambda h_k)\Vert \delta _{k,l}\Vert \\&\le \mathrm{e}^{(\Vert L\Vert +\lambda )h_k}\Vert \delta _{k,l}\Vert . \end{aligned}$$

Hence, for arbitrary $k=0,1,2,\ldots$ and $l=0,1,\ldots ,m$, we have

$$\begin{aligned} \Vert \delta _{k,l}\Vert \le \Vert \delta _{k,0}\Vert \cdot \mathrm{e}^{(\Vert L\Vert +\lambda ) lh_k}. \end{aligned}$$

Consequently, by the method of introduction and the condition (5.1), we can obtain that

$$\begin{aligned} \Vert \delta _{k,l}\Vert&\le \Vert x_0-y_0\Vert \cdot (\gamma _1\mathrm{e}^{(\Vert L\Vert +\lambda )(\tau _1-\tau _0)})\cdots (\gamma _{k}\mathrm{e}^{(\Vert L\Vert +\lambda )(\tau _{k}-\tau _{k-1})}) \mathrm{e}^{(\Vert L\Vert +\lambda ) lh_k}\\&\le \Vert x_0-y_0\Vert C^{k}\mathrm{e}^{(\Vert L\Vert +\lambda ){\hat{C}}} \end{aligned}$$

which implies that the explicit Euler method (5.2) for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $\forall m\in {\mathbb {Z}}^+$. $\square$

The two-stage explicit Runge–Kutta methods have a Butcher tableau

$$\begin{aligned} \begin{array}{c|cc} 0 &{} 0&{}\quad 0\\ c_2&{} a_{21}&{} \quad 0\\ \hline &{}b_1&{}\quad b_2\\ \end{array} \end{aligned}$$

For brevity, the proofs of the following two theorems are omitted.

Theorem 5.3

Assume that all the coefficients of two-stage explicit Runge–Kutta methods are nonnegative, that is $a_{21}\ge 0$, $b_1\ge 0$ and $b_2\ge 0$, and

$$\begin{aligned} b_1+b_2=1,\;\;b_2c_2=\frac{1}{2}. \end{aligned}$$

Then the 2-stage explicit Runge–Kutta method for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $\forall m\in {\mathbb {Z}}^+$, under the conditions of Corollary 5.1.

The following two-stage second-order explicit Runge–Kutta methods all satisfy the conditions of Theorem 5.3.

$$\begin{aligned} \begin{array}{ccc} \begin{array}{c|cc} 0 &{}~ 0&{}\quad ~0\\ \frac{1}{2}&{}~ \frac{1}{2}&{}\quad ~0\\ \hline ~~~ &{}~0&{}\quad ~1\\ \end{array} &{} \begin{array}{c|cc} 0 &{}~ 0&{}\quad ~0\\ 1&{}~ 1&{}\quad ~0\\ \hline ~~~ &{}~\frac{1}{2}&{}\quad ~\frac{1}{2}\\ \end{array} &{} \begin{array}{c|cc} 0 &{}~ 0&{}\quad ~0\\ \frac{3}{4}&{}~ \frac{3}{4}&{}\quad ~0\\ \hline ~~~ &{}~\frac{1}{3}&{}\quad ~\frac{2}{3}\\ \end{array} \\ {\mathrm{Modified~ Euler~ Method}}~~~~ &{} {\mathrm{Heun's~ Method, order\; 2}}~~~~ &{} {\mathrm{Ralston's~ Method}} \end{array} \end{aligned}$$

The three-stage explicit Runge–Kutta methods have a Butcher tableau

$$\begin{aligned} \begin{array}{c|ccc} 0 &{} 0&{}\quad 0&{} \quad 0\\ c_2&{} a_{21}&{}\quad 0&{}\quad 0\\ c_3&{} a_{31}&{} \quad a_{32}&{}\quad 0\\ \hline &{}b_1&{}\quad b_2&{}\quad b_3\\ \end{array} \end{aligned}$$

Theorem 5.4

Under the conditions of Corollary 5.1 and all the coefficients of explicit Runge–Kutta methods are nonnegative ($a_{ij}\ge 0$ and $b_i\ge 0$, $1\le i,j\le 3$), the three-stage third-order explicit Runge–Kutta methods for (1.1) are asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $\forall m\in {\mathbb {Z}}^+$.

The following three-stage third-order explicit Runge–Kutta methods all satisfy the conditions of Theorem 5.4.

$$\begin{aligned} \begin{array}{ccc} \begin{array}{c|ccc} 0 &{}~~ 0&{}\quad ~~0&{}\quad ~~0\\ \frac{1}{3}&{}~~ \frac{1}{3}&{}\quad ~~0&{}\quad ~~0\\ \frac{2}{3}&{}~~0&{}\quad ~~ \frac{2}{3}&{}\quad ~~0\\ \hline ~~~ &{}~~\frac{1}{4}&{}\quad ~~0&{}\quad ~~\frac{3}{4}\\ \end{array}~~~~~~~~~~~~~~~~ &{} \begin{array}{c|ccc} 0 &{}~~ 0&{}\quad ~~0&{}\quad ~~0\\ \frac{2}{3}&{}~~ \frac{2}{3}&{}\quad ~~0&{}\quad ~~0\\ \frac{2}{3}&{}~~\frac{1}{3}&{}\quad ~~ \frac{1}{3}&{}\quad ~~0\\ \hline ~~~ &{}~~\frac{1}{4}&{}\quad ~~0&{}\quad ~~\frac{3}{4}\\ \end{array} \\ {\mathrm{Heun's~ Method, order\; 3}}~~~~~~~~~~~~ &{} ~~~~~~~~{\mathrm{Runge--Kutta~ Method, order\; 3}} \end{array} \end{aligned}$$

Consider the explicit four-stage RK methods for (1.1):

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{k,l}^1=x_{k,l},~~~~~~~~~~~~~~~~~~~~~~~~~~ k\in {\mathbb {N}},\;l=1,2,\ldots ,m-1,\\ X_{k,l}^2=x_{k,l}+h_ka_{21}(LX_{k,l}^1+f(t_{k,l}^1,X_{k,l}^1)),\\ X_{k,l}^3=x_{k,l}+h_k\sum \limits _{j=1}^2 a_{3j}(LX_{k,l}^j+f(t_{k,l}^1,X_{k,l}^j)),\\ X_{k,l}^4=x_{k,l}+h_k\sum \limits _{j=1}^3 a_{4j}(LX_{k,l}^j+f(t_{k,l}^j,X_{k,l}^j)),\\ x_{k,l+1}=x_{k,l}+h_k\sum \limits _{i=1}^4 b_i(LX_{k,l}^i+f(t_{k,l}^i,X_{k,l}^i)),\\ x_{k+1,0}=x_{k,m}+I_{k+1}(x_{k,m}),\\ x_{0,0}=x_0. \end{array}\right. } \end{aligned}$$

(5.3)

Theorem 5.5

Assume that all the coefficients of explicit Runge–Kutta method (5.3) are nonnegative ($a_{ij}\ge 0$ and $b_i\ge 0$, $1\le i, j \le 4$) and

$$\begin{aligned}&\sum \limits _ib_i=b_1+b_2+b_3+b_4=1, \end{aligned}$$

(5.4)

$$\begin{aligned}&\sum \limits _ib_ic_i=b_2c_2+b_3c_3+b_4c_4=\frac{1}{2},\end{aligned}$$

(5.5)

$$\begin{aligned}&\sum \limits _{i,j}b_ia_{ij}c_j=b_3a_{32}c_2+b_4a_{42}c_2+b_4a_{43}c_3=\frac{1}{6},\end{aligned}$$

(5.6)

$$\begin{aligned}&\sum \limits _{i,j,k}b_ia_{ij}a_{jk}c_k=b_4a_{43}a_{32}c_2=\frac{1}{24}. \end{aligned}$$

(5.7)

Then, under the conditions Corollary 5.1, the four-stage explicit Runge–Kutta method (5.3) for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $\forall m\in {\mathbb {Z}}^+$.

Proof

Obviously, for arbitrary $k=0,1,2,\ldots$ and $l=0,1,\ldots ,m-1$,

$$\begin{aligned} \Vert \Delta _{k,l}^1\Vert =\Vert \delta _{k,l}\Vert . \end{aligned}$$

(5.8)

Due to the condition (5.1), $a_{21}\ge 0$ and $c_2=a_{21}$, we have

$$\begin{aligned} \Vert \Delta _{k,l}^2\Vert&=\Vert x_{k,l}-y_{k,l}+h_k a_{21}(LX_{k,l}^1- LY_{k,l}^1+f(t_{k,l}^1,X_{k,l}^1)- f(t_{k,l}^1,Y_{k,l}^1)\Vert \\&\le (1+\Vert L\Vert h_k a_{21}+\lambda h_k a_{21})\Vert \delta _{k,l}\Vert \\&=(1+\Vert L\Vert h_k c_2+\lambda h_k c_2)\Vert \delta _{k,l}\Vert . \end{aligned}$$

Similarly, we can obtain that

$$\begin{aligned} \Vert \Delta _{k,l}^3\Vert&=\Vert x_{k,l}-y_{k,l}+h_k \sum \limits _{j=1}^2 a_{3j}(LX_{k,l}^j-LY_{k,l}^j+f(t_{k,l}^j,X_{k,l}^j)- f(t_{k,l}^j,Y_{k,l}^j))\Vert \\&\le \Vert \delta _{k,l}\Vert +(\Vert L\Vert +\lambda ) h_k a_{31}\Vert \Delta _{k,l}^1\Vert +(\Vert L\Vert +\lambda ) h_k a_{32}\Vert \Delta _{k,l}^2\Vert \\&\le (1+(\Vert L\Vert +\lambda ) h_k ( a_{31}+a_{32})+(\Vert L\Vert +\lambda )^2 h_k^2 a_{32} c_2) \Vert \delta _{k,l}\Vert \\&=(1+(\Vert L\Vert +\lambda )h_kc_3+(\Vert L\Vert +\lambda )^2 h_k^2 a_{32} c_2) \Vert \delta _{k,l}\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert \Delta _{k,l}^4\Vert&=\Vert x_{k,l}-y_{k,l}+h_k \sum \limits _{j=1}^3 a_{4j}(LX_{k,l}^j-LY_{k,l}^j+f(t_{k,l}^j,X_{k,l}^j)- f(t_{k,l}^j,Y_{k,l}^j))\Vert \\&\le \Vert \delta _{k,l}\Vert +h_k (\Vert L\Vert +\lambda )\sum \limits _{j=1}^3 a_{4j}\Vert \Delta _{k,l}^j\Vert \\&\le (1+ (\Vert L\Vert +\lambda )h_kc_4+(\Vert L\Vert +\lambda )^2 h_k^2(a_{42} c_2+a_{43}c_3)\\&\quad +(\Vert L\Vert +\lambda )^3 h_k^3a_{43}a_{32}c_2)\Vert \delta _{k,l}\Vert . \end{aligned}$$

By the conditions (5.4)–(5.7), the equality (5.8) and the above three inequalities, we can obtain

$$\begin{aligned} \Vert \delta _{k,l+1}\Vert&=\Vert x_{k,l}-y_{k,l}+h_k\sum _{i=1}^4 b_i (LX_{k,l}^i- LY_{k,l}^i+f(t_{k,l}^i,X_{k,l}^i)- f(t_{k,l}^i,Y_{k,l}^i))\Vert \\&\le \Vert \delta _{k,l}\Vert +h_k(\Vert L\Vert +\lambda ) \sum _{i=1}^4 b_i\Vert \Delta _{k,l}^i\Vert \\&\le (1+h_k(\Vert L\Vert +\lambda )(b_1+b_2+b_3+b_4)+h_k^2(\Vert L\Vert +\lambda ))^2(b_2c_2+b_3c_3+b_4c_4)\\&\qquad +h_k^3(\Vert L\Vert +\lambda )^3 (b_3 a_{32}c_2+b_4a_{42}c_2+b_4a_{43}c_3)+h_k^4(\Vert L\Vert +\lambda )^4a_{43}a_{32}c_2)\cdot \Vert \delta _{k,l}\Vert \\&= (1+(\Vert L\Vert +\lambda ) h_k+\frac{(\Vert L\Vert +\lambda )^2 h_k^2}{2}+\frac{(\Vert L\Vert +\lambda )^3h_k^3}{3!}+\frac{(\Vert L\Vert +\lambda )^4 h_k^4}{4!})\cdot \Vert \delta _{k,l}\Vert \\&\le \mathrm{e}^{(\Vert L\Vert +\lambda )h_k}\Vert \delta _{k,l}\Vert . \end{aligned}$$

Consequently, the four-stage explicit Runge–Kutta method (5.3) for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $\forall m\in {\mathbb {Z}}^+$. $\square$

Obviously, all the four-stage fourth-order explicit Runge–Kutta methods satisfy conditions (5.4)–(5.7) (see (Butcher 2003, p. 90) or (Hairer et al. 1993b, pp. 135–136)). Consequently, by Theorem 5.5, we immediately obtain the following corollary.

Corollary 5.6

Assume that all the coefficients of explicit Runge–Kutta method (5.3) are nonnegative ($a_{ij}\ge 0$ and $b_i\ge 0$, $1\le i, j \le 4$). Then, under the conditions Corollary 5.1, the four-stage fourth-order explicit Runge–Kutta method (5.3) for (1.1) is stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $\forall m\in {\mathbb {Z}}^+$.

The four-stage explicit Runge–Kutta methods have a Butcher tableau

$$\begin{aligned} \begin{array}{c|cccc} 0 &{} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ c_2&{} a_{21}&{}\quad 0&{}\quad 0&{}\quad 0\\ c_3&{} a_{31}&{}\quad a_{32}&{}\quad 0&{}\quad 0\\ c_4&{} a_{41}&{}\quad a_{42}&{}\quad a_{43}&{}\quad 0\\ \hline ~~~~ &{}~~b_1&{}\quad b_2&{}\quad b_3&{}\quad b_4\\ \end{array} \end{aligned}$$

The following classical four-stage fourth-order explicit Runge–Kutta method satisfies the conditions of Theorem 5.5 and Corollary 5.6.

$$\begin{aligned} \begin{array}{c|cccc} 0 &{} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \frac{1}{2} &{} \frac{1}{2} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \frac{1}{2} &{}0 &{}\quad \frac{1}{2} &{}\quad 0 &{}\quad 0\\ 1 &{}0 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ \hline ~~~~~ &{}~~\frac{1}{6}~~&{}\quad \frac{1}{3}~~&{}\quad \frac{1}{3}~~&{}\quad \frac{1}{6} \end{array} \end{aligned}$$

Remark 5.7

In fact, there are many four-stage explicit Runge–Kutta methods which are not of order 4 , but they satisfy conditions (5.4)–(5.7). The following method is an example which is not of order 4, however, it satisfies not only conditions (5.4)–(5.7), but also the conditions of Theorem 5.5.

$$\begin{aligned} \begin{array}{c|cccc} 0 &{} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \frac{1}{2} &{} \frac{1}{2} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \frac{1}{2} &{}0 &{}\quad \frac{1}{2} &{}\quad 0 &{}\quad 0\\ 1 &{}\frac{1}{3} &{}\quad \frac{1}{3}&{}\quad \frac{1}{3}&{}\quad 0\\ \hline ~~~~~ &{}~~\frac{1}{2}~~&{}\quad 0~~&{}\quad 0~~&{}\quad \frac{1}{2} \end{array} \end{aligned}$$

Unfortunately, we can not obtain the p-stage explicit Runge–Kutta methods of order p for $p\ge 5$, because of the Butcher Barriers as follows.

Theorem 5.8

(See Butcher 2003, Theorem 370, pp. 258–259) or (Hairer et al. 1993b, Theorem 5.1 p. 173) For $p\ge 5$, no explicit Runge–Kutta methods exist of order p with $s=p$ stages.

5.2 RK methods

Consider the following RK methods for (1.1):

$$\begin{aligned} \left\{ \begin{array}{lll} x_{k,l+1}=x_{k,l}+h\sum \limits _{i=1}^vb_i(LY_{k,l}^i+f(t_{k,l}^i,X_{k,l+1}^i)), &{}k\in {\mathbb {N}},\;l=0,1,\ldots ,m-1,\\ X_{k,l+1}^i=x_{k,l}+h\sum \limits _{j=1}^{v}a_{ij} (LX_{k,l}^j+f(t_{k,l}^j,X_{k,l+1}^j)), &{}k\in {\mathbb {N}},\;l=0,1,\ldots ,m-1,\\ x_{k+1,0}=I_{k+1}(x_{k,m}), &{}k\in {\mathbb {N}},\\ x_{0,0}=x_0. \end{array} \right. \nonumber \\ \end{aligned}$$

(5.9)

Lemma 5.9

(Butcher 1987; Dekker and Verwer 1984; Hairer et al. 1993b; Wanner et al. 1978) The $(\mathbf{j },\mathbf{k })$-Padé approximation to $\mathrm{e}^z$ is given by

$$\begin{aligned} \mathbf{R }(z)=\frac{P_\mathbf{j }(z)}{Q_\mathbf{k }(z)}, \end{aligned}$$

(5.10)

where

$$\begin{aligned} P_\mathbf{j }(z)= & {} 1+\frac{\mathbf{j }}{\mathbf{j }+\mathbf{k }}\cdot z+\frac{\mathbf{j }(\mathbf{j }-1)}{(\mathbf{j }+\mathbf{k })(\mathbf{j }+\mathbf{k }-1)}\cdot \frac{z^2}{2!}+\cdots +\frac{\mathbf{j } !\mathbf{k }!}{(\mathbf{j }+\mathbf{k })!}\cdot \frac{z^\mathbf{j }}{\mathbf{j } !}, \\ Q_\mathbf{k }(z)= & {} 1-\frac{\mathbf{k }}{\mathbf{j }+\mathbf{k }}\cdot z+\frac{\mathbf{k }(\mathbf{k }-1)}{(\mathbf{j }+\mathbf{k })(\mathbf{j }+\mathbf{k }-1)}\cdot \frac{z^2}{2!}+\cdots +(-1)^\mathbf{k }\cdot \frac{\mathbf{k }!\mathbf{j } !}{(\mathbf{j }+\mathbf{k })!}\cdot \frac{z^\mathbf{k }}{\mathbf{k }!}, \end{aligned}$$

with error

$$\begin{aligned} \mathrm{e}^z-\mathbf{R }(z)=(-1)^{\mathbf{k }}\cdot \frac{\mathbf{j }!\mathbf{k }!}{(\mathbf{j }+\mathbf{k })!(\mathbf{j }+\mathbf{k }+1)!}\cdot z^{\mathbf{j }+\mathbf{k }+1}+O(z^{j+k+2}). \end{aligned}$$

It is the unique rational approximation to $\mathrm{e}^z$ of order $\mathbf{j }+\mathbf{k }$, such that the degrees of numerator and denominator are $\mathbf{j }$ and $\mathbf{k }$, respectively.

Lemma 5.10

(Song et al. 2005; Yang et al. 2005; Wang and Qiu 2014) Assume that $\mathbf{R }(z)$ is the $(\mathbf{j },\mathbf{k })$-Padé approximation to $\mathrm{e}^z$. Then $\mathbf{R }(z)<\mathrm{e}^{z}$ for all $z>0$ if and only if $\mathbf{k }$ is even, when $z>0$.

Theorem 5.11

Assume that $\mathbf{R }(z)$ is the stability function of Runge–Kutta method (5.9) i.e.

$$\begin{aligned} \mathbf{R }(z)=1+zb^\mathrm{T}(I-zA)^{-1}e=\frac{P_\mathbf{j }(z)}{Q_\mathbf{k }(z)}. \end{aligned}$$

Under the conditions of Corollary 5.1, Runge–Kutta method (4.1) with nonnegative coefficients ($a_{ij}\ge 0$ and $b_i\ge 0$, $1\le i\le v$, $1\le j\le v$) for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$ and $m\ge M$, if $\mathbf{k }$ is even, where $M=\inf \{m: I-zA \;is\; invertible\; and\; (I-z_kA)^{-1}e\ge 0, z_k=(\Vert L\Vert +\lambda ) h_k, k\in {\mathbb {N}}, m\in {\mathbb {Z}}^+\}$.

Proof

Since $a_{ij}\ge 0$ and $b_i\ge 0$,$1\le i\le s$, $1\le j\le v$, we can obtain that

$$\begin{aligned} \Vert \Delta _{k,l}^i\Vert&=\Vert x_{k,l}-y_{k,l}+h_k \sum _{j=1}^{v}a_{ij}(LX_{k,l}^j-LY_{k,l}^j+f(t_{k,l}^j,X_{k,l}^j)-f(t_{k,l}^j,Y_{k,l}^j))\Vert \\&\le \Vert \delta _{k,l}\Vert +h_k \sum _{j=1}^{v}a_{ij}(\Vert L\Delta _{k,l}^j\Vert +\Vert f(t_{k,l}^j,X_{k,l}^j)-f(t_{k,l}^j,Y_{k,l}^j)\Vert )\\&\le \Vert \delta _{k,l}\Vert +(\Vert L\Vert +\lambda ) h_k \sum _{j=1}^{v}a_{ij}\Vert \Delta _{k,l}^j\Vert . \end{aligned}$$

And when $m\ge M$, $(I-z_kA)^{-1}e\ge 0, z_k=(\Vert L\Vert +\lambda ) h_k, k\in {\mathbb {Z}}^+$, so

$$\begin{aligned} {}[\Vert \Delta _{k,l}^i\Vert ]\le (I-z_k A)^{-1} e\Vert \delta _{k,l}\Vert \end{aligned}$$

where $[\Vert \Delta _{k,l}^i\Vert ]=(\Vert \Delta _{k,l}^1\Vert ,\Vert \Delta _{k,l}^2\Vert ,\ldots , \Vert \Delta _{k,l}^v\Vert )^\mathrm{T}$. By Lemmas 5.9 and 5.10, we can obtain

$$\begin{aligned} \Vert \delta _{k,l+1}\Vert&=\Vert x_{k,l}-y_{k,l}+h_k \sum _{j=1}^v b_i (LX_{k,l}^i- LY_{k,l}^i+f(t_{k,l}^i,X_{k,l}^i)- f(t_{k,l}^i,Y_{k,l}^i))\Vert \\&\le \Vert \delta _{k,l}\Vert +h_k \sum _{j=1}^v b_i (\Vert LX_{k,l}^i- LY_{k,l}^i\Vert +\Vert f(t_{k,l}^i,X_{k,l}^i)- f(t_{k,l}^i,Y_{k,l}^i)\Vert )\\&\le \Vert \delta _{k,l}\Vert +(\Vert L\Vert +\lambda ) h_k \sum _{j=1}^v b_i \Vert \Delta _{k,l}^i\Vert \\&=\Vert \delta _{k,l}\Vert +z_k b^\mathrm{T} [\Vert \Delta _{k,l}^i\Vert ]\\&\le (1+z_k b^\mathrm{T}(I-z_k A)^{-1}e) \Vert \delta _{k,l}\Vert \\&=\mathbf{R }((\Vert L\Vert +\lambda ) h_k) \Vert \delta _{k,l}\Vert \\&\le \mathrm{e}^{(\Vert L\Vert +\lambda ) h_k}\Vert \delta _{k,l}\Vert . \end{aligned}$$

Therefore, RK method (5.9) for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$ and $m\ge M$. $\square$

5.3 $\theta$-methods

Consider $\theta$-methods for (1.1):

$$\begin{aligned} \left\{ \begin{array}{lll} x_{k,l+1}=x_{k,l}+h_k(1-\theta )(Lx_{k,l}+f(t_{k,l},x_{k,l}))\\ ~~~~~~~~~~~+h_k\theta (Lx_{k,l+1}+f(t_{k,l+1},x_{k,l+1}))\\ x_{k+1,0}=I_{k+1}(x_{k,m}), \\ x_{0,0}=x_0, \end{array} \right. \end{aligned}$$

(5.11)

where $h_k=\frac{\tau _{k+1}-\tau _k}{m},\;\; m\ge 1,\; m$ is an integer, $k=0,1,2,\ldots$.

Lemma 5.12

(See Song et al. 2005) For $m>\Vert L\Vert +\lambda$ and $z_k=h_k(\Vert L\Vert +\lambda ),\;h=\frac{\tau _k-\tau _{k-1}}{m},\;m\in {\mathbb {Z}}^+$,$k\in {\mathbb {N}}$, then

$$\begin{aligned} \left( 1+\frac{z_k}{1-z_k\theta }\right) ^m\le \mathrm{e}^{h_k(\Vert L\Vert +\lambda )} \end{aligned}$$

if and only if $0\le \theta \le \varphi (1)$, where $\varphi (x)=\frac{1}{x}-\frac{1}{\mathrm{e}^x-1}$.

Theorem 5.13

Under the conditions of Corollary 5.1, if $0\le \theta \le \varphi (1)$, there is a positive M such that $\theta$ method for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$ and $m\ge M$ .

Proof

Obviously, we can obtain

$$\begin{aligned} \Vert \delta _{k,l+1}\Vert&=\Vert \delta _{k,l}+(1-\theta )h_k(Lx_{k,l}- Ly_{k,l}+f(t_{k,l},x_{k,l})- f(t_{k,l},y_{k,l})\Vert \\&\quad +\theta h_k(Lx_{k,l+1}- Ly_{k,l+1}+f(t_{k,l+1},x_{k,l+1})- f(t_{k,l+1},y_{k,l+1}))\Vert \\&\le (1+(1-\theta )(\Vert L\Vert +\lambda )h_k)\Vert \delta _{k,l}\Vert +\theta h_k\Vert L\Vert \Vert \delta _{k,l+1}\Vert \\&\quad +h_k\theta \Vert f(t_{k,l+1},x_{k,l+1})- f(t_{k,l+1},y_{k,l+1})\Vert \\&\le (1+(1-\theta )(\Vert L\Vert +\lambda ) h_k)\Vert \delta _{k,l}\Vert +\theta (\Vert L\Vert +\lambda )h_k\Vert \delta _{k,l+1}\Vert \end{aligned}$$

which implies

$$\begin{aligned} \Vert \delta _{k,l+1}\Vert \le \frac{1+(1-\theta )(\Vert L\Vert +\lambda ) h_k}{1-\theta (\Vert L\Vert +\lambda )h_k} \cdot \Vert \delta _{k,l}\Vert \end{aligned}$$

Therefore, by Lemma 5.12 and the method of introduction , we can obtain that

$$\begin{aligned} \Vert \delta _{k,l+1}\Vert \le \mathrm{e}^{(\Vert L\Vert +\lambda ) h_k} \Vert \delta _{k,l}\Vert \end{aligned}$$

Hence, $\theta$-method for (1.1) is asymptotically stable for $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$ and $m> \theta (\Vert L\Vert +\lambda )(\tau _{k+1}-\tau _k)$, $k\in {\mathbb {N}}$, if $0\le \theta \le \varphi (1)$. $\square$

6 Conclusions

There are three advantages of a class of explicit exponential RK methods (which satisfy the conditions Theorem 4.2 or Corollary 4.4) for semi-linear IDEs. First, they can preserve asymptotical stability of semi-linear IDEs under the conditions of Theorem 2.2 which are weaker than the conditions of Corollary 5.1. Second, they can preserve asymptotical stability semi-linear IDEs without restriction on the stepsizes except that $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$. Third, they are suitable for stiff problems.

On the other hand, classical four-order explicit RK method preserves asymptotical stability of semi-linear IDEs without restriction on the stepsizes except that $h_k=\frac{\tau _{k+1}-\tau _k}{m}$, $k\in {\mathbb {N}}$, $m\in {\mathbb {Z}}^+$, under the conditions of Corollary 5.1. And it does not need to compute $\mathrm{e}^{h_kL}$ and $\mathrm{e}^{c_ih_kL}$, $i=1,2,\ldots , v$, $k\in {\mathbb {N}}$.