DSM-DE: a differential evolution with dynamic speciation-based mutation for single-objective optimization

Abstract

A new differential evolution algorithm with two dynamic speciation-based mutation strategies (DSM-DE) is proposed to solve single-objective optimization problems. An explorative mutation “DE/seeds-to-seeds” and an exploitative mutation “DE/seeds-to-rand” are employed simultaneously in DSM-DE in the evolutionary process. A Dynamic Speciation Technique is designed to assist the two mutations in order to utilize the potential of selective portioning of critical individuals in the population. It dynamically divides the population into numbers of species whilst taking species seeds as centers. The best individuals for each species are used as base vectors in each species in the proposed mutation strategies. “DE/seeds-to-seeds” selects individuals from species seeds and current species to constitute difference vectors whereas “DE/seeds-to-rand” selects from the whole population. Thus the two mutation strategies can accelerate the convergence process without decreasing diversity of the population. Comparison results with four classic DE variants, one state-of-art DE variant and two improved non-DE variants on CEC2014, CEC2015 benchmark, and Lennard-Jones potential problem reveal that the overall performance of DSM-DE is better than that of the other seven DE algorithms. In addition, experiments also substantiate the effectiveness and superiority of two seeds-guided mutation strategies in DSM-DE.

1 Introduction

Differential evolution (DE) is a simple yet powerful algorithm firstly proposed by Storn and Price in 1997 [27]. It has attracted extensive attention of scholars to find new variants because of its excellent performance and has been used in various engineering fields [8, 23]. DE is a population-based stochastic search technique employing mutation, crossover, and selection operators at each generation to evolve the population to the global optimum. The classic DE employs “DE/rand/1/bin” mutation in which three parent vectors are randomly chosen from the current population. It is of robust capacity in exploring the whole solution space and locating the global optimal region but of less efficient convergence rate when exploiting the optimal solution. Greedy mutation strategies such as “DE/current-to-best/bin” and “DE/best/bin”, which utilize the best solution information in the current population, usually display higher convergence rate but less reliable. However, the reliability of the greedy mutation DE/current-to-pbest/bin [32] is highly improved by utilizing the information of p% good solutions and incorporating the archived inferior information into the mutation. In CoDE [31], SaDE [25], several well-studied mutation strategies are incorporated into these algorithms through various mechanisms to generate trial vectors.

In order to be successful, an improved DE variant needs to achieve a good balance between exploration and exploitation, where exploration is the algorithm’s capability of searching for new regions, whilst exploitation is the algorithm’s capability of searching for the neighboorhoods of the previously visited points [20]. To excavate potential of better information in the population and balance explorative and exploitative capacity of the algorithm, in this paper, two seeds-based mutation strategies “DE/seeds-to-seeds” and “DE/seeds-to-rand” are employed simultaneously in evolutionary process. Furthermore, the two mutation strategies greatly dependent on a specially designed population structure derived from Dynamic Speciation Technique (DST), which is mainly used to locate elicits in different regions of the search space and obtain a hierarchical population structure. Speciation [18] is a niching technique originally used to solve multimodal optimization problems. The fact that local optimal solutions quite close to the global optimal solution in terms of value or position exist commonly in many practical functions makes it difficult for classical DE to find the real global optimal solution in single-objective optimization. Thus using the grouping idea in speciation may be benefit to locate the real global optimal position accurately among numerous local optimal solutions.

Numerous experimental studies and theoretical analysis [5, 9, 22, 32] have been conducted to investigate mechanism of effects the setting of control parameters on the DE performance because there is no fixed parameter setting suitable for all kinds of problems or even different evolution phases of the same problem. For example, literature [1] comprehensively presented the parameter adaptation schemes in recent years. jDE [5] introduced two new parameters as possibilities to adjust F and CR and ZEPDE [9] generates F and CR according to Cauchy and Normal distribution and combines parameters adaptation with zoning. Parameter adaptation mechanism in this paper adopts a mechanism using Levy distribution. It can be categorized as deterministic parameter control because it adjusts parameters without feedback from the evolutionary search into account.

Finally, a novel DE variant with dynamic speciation-based mutation for single-objective optimization (DSM-DE) is designed. It is tested on two benchmarks CEC2014 [15] and CEC2015 [16] and Lennard-Jones problem to compare with other four classic DE variants, one state-of-art DE variant and two improved non-DE variants. The simulation results show that DSM-DE achieves an excellent optimization performance no matter in convergence speed or accuracy.

The layout of the rest of the paper is as follows: Sect. 2 gives a brief introduction of the classical DE algorithm. Section 3 reviews the related works on DE mutation strategies. Section 4 elaborates the algorithm with dynamic speciation-based mutations (DSM-DE). Comparative experiments results for the proposed algorithm are conducted in Sect. 5. Finally, a conclusion is made in Sect. 6.

2 Basic operations of DE

In this section, basic operations of DE dealing with the continuous optimization problem is introduced.

2.1 Initialization

The objective function $f(\overrightarrow{X}),\overrightarrow{X}=(x_1,x_2, \ldots x_D)\in R^D$ whose feasible solution space is $\varOmega =\prod _{i=1}^D[L_i,U_i]$ is assumed to be minimized in this paper. D is the dimension of the problem. DE algorithm aims at evolving the population to find the global optimal of the function. In classical DE, the initial population $\overrightarrow{X}_{i,0}=(x_{1,i,0},x_{2,i,0} \ldots x_{D,i,0})|i=1,2, \ldots NP$ is randomly generated by a uniform distribution within the search space constrained by the prescribed minimum and maximum parameter bounds $\overrightarrow{X}_{min}=(x_{1,min}, x_{2,min} \ldots x_{D,min})$ and $\overrightarrow{X}_{max}=(x_{1,max}, x_{2,max}, \ldots x_{D,max})$. NP is the population size. Mutation, crossover, and selection operations are adopted in a loop program after initialization.

2.2 Mutation

At each generation g, a mutant vector $\overrightarrow{V}_{i,g}$ is produced for each target vector $\overrightarrow{X}_{i,g}$ through the combination of different individuals in the population. The five most frequently used mutation operators are shown as follows:

“DE/rand/1”:

$$\begin{aligned} \overrightarrow{V}_{i,g}=\overrightarrow{X}_{r1,g}+F \varvec{\cdot }(\overrightarrow{X}_{r2,g}-\overrightarrow{X}_{r3,g}) \end{aligned}$$

(1)

“DE/best/1”:

$$\begin{aligned} \overrightarrow{V}_{i,g}= \overrightarrow{X}_{best,g}+F \varvec{\cdot }(\overrightarrow{X}_{r1,g}-\overrightarrow{X}_{r2,g}) \end{aligned}$$

(2)

“DE/rand-to-best/1”:

$$\begin{aligned} \overrightarrow{V}_{i,g}=\overrightarrow{X}_{i,g}+F \varvec{\cdot }(\overrightarrow{X}_{best,g}-\overrightarrow{X}_{i,g})+F\varvec{\cdot }(\overrightarrow{X}_{r1,g}-\overrightarrow{X}_{r2,g}) \end{aligned}$$

(3)

“DE/best/2”:

$$\begin{aligned} \overrightarrow{V}_{i,g}{=}\overrightarrow{X}_{best,g}+F \varvec{\cdot }(\overrightarrow{X}_{r1,g}-\overrightarrow{X}_{r2,g} )+F \varvec{\cdot }(\overrightarrow{X}_{r3,g}-\overrightarrow{X}_{r4,g}) \end{aligned}$$

(4)

“DE/rand/2”:

$$\begin{aligned} \overrightarrow{V}_{i,g}=\overrightarrow{X}_{r1,g}+F \varvec{\cdot }(\overrightarrow{X}_{r2,g}-\overrightarrow{X}_{r3,g})+F \varvec{\cdot }(\overrightarrow{X}_{r4,g}-\overrightarrow{X}_{r5,g}) \end{aligned}$$

(5)

Indices r0, r1, r2, r3, r4, and r5 are distinct integers randomly generated in the range [1, NP]. They are different from the index i. F is a positive control parameter used to scale the difference vector. $\overrightarrow{X}_{best,g}$ is the best individual in the population at generation g.

2.3 Crossover

After mutant vectors are generated, binomial crossover operator is implemented on $\overrightarrow{X}_{i,g}$ and $\overrightarrow{V}_{i,g}$ to generate trial vectors $\overrightarrow{U}_{i,g}=(u_{i,1,g},u_{i,2,g}, \ldots u_{i,D,g})$.

$$\begin{aligned} u_{i,j,g}= {\left\{ \begin{array}{ll} {v}_{i,j,g} &{} \text {if }rand_j(0,1) \leqslant CR\text { or }j={j}_{rand}\\ {x}_{i,j,g} &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(6)

where $i=1,2, \ldots NP$, $j=1,2, \ldots D$. $rand_j(0,1)$ is randomly chosen from 0 to 1 for each j and each i according to a uniform distribution. $j_{rand}$ is a random number between 1 and D newly generated for each i. The crossover probability $CR\in [0,1]$ scales the amount of changed components in a target vector. $j_{rand}$ keeps that at least one different parameter exists between the trial vector $\overrightarrow{U}_{i,g}$ and its target vector $\overrightarrow{X}_{i,g}$.

2.4 Selection

Competition is performed between target vector $\overrightarrow{X}_{i,g}$ and mutation vector $\overrightarrow{U}_{i,g}$ through selection operator and the individual with better fitness value enters the next generation.

$$\begin{aligned} \overrightarrow{X}_{i,g+1}= {\left\{ \begin{array}{ll} \overrightarrow{U}_{i,g} &{} \text {if }f(\overrightarrow{U}_{i,g}) \leqslant f(\overrightarrow{X}_{i,g})\\ \overrightarrow{X}_{i,g} &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(7)

3 Previous work related to DE

Firstly, this section introduces some mutation strategies in DE variants with single population. Then mutation strategies in structural population constructed by niching technique are listed. Finally, the original motivation to design DSM-DE is interpreted.

3.1 Mutation strategies in single population

Mutation operation randomly changes elements in target vector to generate a new individual, so it is critical in diversifying the population. Improving mutation strategy has become an important aspect in researchers’ study of DE. A well designed mutation strategy (both explorative and exploitative) will greatly improve the searching efficiency and accelerate the convergence of DE. DE/current-to-better/1 is proposed in [13], where p% better solutions are sampled by a Gaussian distribution to guide the search. UDE [26] selects parents according to fitness space criterion and design space criterion to enhance exploration and exploitation. Another operation that improved the selection of parents is ranking-based mutation strategy in DE with ranking-based mutation operators [11]. In order to utilize the information of good vectors, it selected parents proportionally according to their fitness rankings from current population in mutation operation. Moreover, many researchers combined several existing mutation strategies in their algorithms [9, 25] to make different mutant vectors compete with each other.

3.2 Mutation strategies in structural population

A structured EA refers to decentralizing the population into subpopulations which may have different evolutionary roles and can interact with each other. It is also an important method for DE algorithms. Neighborhood concept, which includes two categories namely index-based and distance-based, is extensively used to get a structural population.

3.2.1 Index-based neighborhood

Index-based neighborhood separates the population based on the code number or the fitness value of the individuals. Zheng [33] divided the current population into superior and inferior subpopulations based on evolution metrics. Mutation operations in the two subpopulations selected parent individuals from different population sets to make better use of superior individuals. Gao et al. [10] separated the population based on the solutions’ feasibility and parent individuals were selected from the $m\_{th}$ subpopulation and whole population. CMODE [30] used cooperative populations in their algorithm and adopted JADE’s mutation in each subpopulation. Cui et al. [7] split the population into three sub-populations based on fitness values and introduced three novel mutation strategies for each subpopulation. In [28], a multi-topology and a topology-dependent mutation strategy are combined to utilize the information of topology adaptation.

3.2.2 Distance-based neighborhood

Generally, distance-based neighborhood divides the population based on the Euclidean distance. Niching is a distance-based neighborhood technique commonly used in multimodal optimization to form a structural population. Cluster-based methods were also adopted to divide the population [24].

Sheldon and Suganthan [14] apply arithmetic recombination with speciation in their algorithm. Mutation with ensemble strategies were employed to enhance exploration and exploitation. Li et al. [19] utilize the clearing niche mechanism in the existing mutation strategies, in which the niche individuals are utilized as base vectors. A parent-centric mutation operator combined with synchronous population update rule was proposed by Biswas et al. [3] where the offspring was produced in the region of dominating parent updated by the dominated parent. Biswas et al. [4] integrated an improved information-sharing mechanism with DE algorithm for inducing efficient niching behavior. In mutation operator, the probability of picking relatively fitter individuals was higher than the less fit individuals lying closely to the target vector.

3.3 Motivation for the mutation strategies and DST

From the studies mentioned above, many DE variants with single population modified parent selection methods in mutation to utilize the information that can navigate the searching direction. In DE variants with structural population, hierarchical structure is mainly used for mutation operation to select useful information according to different criteria for classification i.e. generations, fitness values, code numbers or spatial distance etc. Constructing a structural population is an effective way to maintain the diversity since it could increase the selection diversity. In the author’s view, using distance-based neighborhood concept is a more suitable way to group the population compared to index-based neighborhood because a population structure that each subpopulation contains individuals which are different in fitness values but similar in spacial positions is wanted to fully utilize better individuals in different regions. In this paper, distance-based neighborhood concept is adopted in DST to construct the population structure. It is known that the idea of grouping population in DST is borrowed from speciation but the specific steps of DST are totally different from speciation. Here it is necessary to explain the differences between two techniques.

Firstly, sizes of species in DST are flexible and various while they are fixed and the same in speciation. Secondly, DST reduces a deterministic parameter $r_s$ in speciation, which denotes the radius from the species seeds to its boundary. DST selects as a number of closest individuals to the seeds to constitute species. Furthermore, speciation need to regenerate (discard) vectors if the number of vectors in boundary $r_s$ is more than (less than) the predefined species size while DST do not need this operation. Additionally, SDE runs a basic DE in each species independently to locate multiple optimal simultaneously. In DSM-DE, parent individuals in mutation are selected from different species.

The structure constructed by DST is served for the mutation process in our proposal. Two new mutation strategies both take the best individuals in each species as basic vectors under this structure so that the algorithm could exploitate better individuals located in different areas in the search space which play an important role in leading the searching direction and accelerating the convergence speed.

4 DSM-DE

In this section, DSM-DE utilizing two new mutation strategies is proposed. Firstly, the steps of DST designed to locate various better individuals in different regions are introduced. Secondly, the basic of DSM-DE two mutation strategies are presented. Two generated trial vectors compete with each other and the better one is used in the selection. Finally, the adaptive parameter control mechanism is introduced.

4.1 DST

In evolutionary process, a new population is generated at the end of each iteration. DST is designed to classify the new generated population at the beginning of each iteration. These species with different sizes can be identified by determining their own species seeds and calculating their own sizes. The steps of DST can be summarized as follows.

First of all, fitness values of all individuals and Euclidean distance between each two individuals in population P are calculated. Distance is computed using the following equation:

$$\begin{aligned} dist(\overrightarrow{X}^{(i)},\overrightarrow{X}^{(j)} )=\sqrt{\sum _{k=1}^D \left( x_k^{(i)}-x_k^{(j)}\right) ^{2}} \end{aligned}$$

(8)

where $\overrightarrow{X}^{(i)}=(x_1^{(i)},x_2^{(i)},\ldots , x_D^{(i)})$ and $\overrightarrow{X}^{(j)}=(x_1^{(j)},x_2^{(j)}, \ldots , x_D^{(j)})$ are D-dimensional vectors of real numbers representing two individuals i and j from population P. The minimum individual is removed as the first species seed from current population P to cells S which saves all species including their members. The next step is to evaluate size of the first species based on the percentage of the fitness value of the first seed using (9).

$$\begin{aligned} \begin{aligned} m(i)=round \left\{ \frac{valparents(i)-min(valparents)}{max(valparents)-min(valparents)}*\right. \\ \left. (S\_{max}-S\_{min})+S\_{min}pg{\phantom {\frac{valparents(i)-min(valparents)}{max(valparents)-min(valparents)}}} \right\} \end{aligned} \end{aligned}$$

(9)

where m(i) is size of the $i_{th}$ species, valparents is set of fitness values of the whole parent population, $S\_{max}$ and $S\_{min}$ are the maximum and minimum number of individuals in each species. Sizes of all species m(i) fall into the maximum and minimum boundary. $S\_{min}$ is set as 3 to guarantee there are alternatives for parent individuals in “DE/seeds-to-rand” mutation”, in which two parent vectors are selected from the current species. When $S\_{min}$ is less than 3, the second parent has only two or one option. Experiment results show that NP / 5 is the most appropriate number for $S\_{max}$. Additionally, $max(valparents)=min(valparents)$ indicates all individuals in the population have the same fitness values. Clearly, it is no sense to calculate m(i) using (9) because the calculated result will be infinite. Under this circumstance, $S\_{num}$ will be set as NP / 10 and all sizes of species will be same because a uniform species allocation is expected to obtain at this time. The formula that limits the species including at least $S\_{min}$ and not exceeding $S\_{max}$ individuals is of great importance to balance the species allocation i.e. a species with a fitter seed will have a smaller size. A species is formed after removing the nearest $m(i)-1$ individuals to the species seed measured by Euclidean distance from P into the $i_{th}$ species. When forming a new species, the best one among the rest individuals in population P is always selected as the seed of that species. Species is formed following the same steps mentioned above until population P becomes a empty set. Note that if the number of individuals left in population P is less than the calculated number m(i) when the last species is generated, the left number is assigned to m(i) to guarantee the total number of the population not to change. Algorithm 1 is the process of DST and Fig. 1 illustrates its sketch map. Obviously, species seeds with higher fitness will circle fewer individuals in their groups.

Fig. 1

Sketch map of Dynamic Speciation Technique

4.2 Mutation strategies

Two mutation strategies “DE/seeds-to-seeds” and “DE/seeds-to-rand” are implemented simultaneously to maintain explorative and exploitative capacity of the algorithm. Studies indicate that compared to the most frequently used classical mutation strategy “DE/rand/1”, greedy strategy “DE/best/2” has a higher convergence rate. However, incorporating the only best solution can also be a defect because the best individual may lead the population to wrong direction due to the resultant reduced population diversity. To avoid weakness of existing greedy strategies, two new mutation strategies are proposed to serve as the basic of the algorithm.

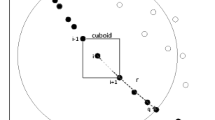
The first mutation “DE/seeds-to-seeds” is relatively exploitative. It is designed to accelerate convergence of the algorithm. Species seeds are elite individuals in the population so it will dominate the evolutionary process and lead the population into global optimum quickly. Figure 2 demonstrates this mutation in 2-Dimensional plane picture. Current seeds are taken as basic vectors and random seeds in other species will cooperate with random individuals in current species to give directions, guiding the currents seeds to promising areas. Since the two mutation strategies are both species dependent, it is necessary to indicate in which species the mutation operation is performed. Thus index is added i in the subscript to represent the current species. The first mutation strategy generate mutation vector in the $i_{th}$ species as follows:

“DE/seeds-to-seeds”:

$$\begin{aligned} \overrightarrow{V}_{{\varvec{i,j,g}}}=\overrightarrow{X}_{{\varvec{i,seedi,g}}} +{{\varvec{F}}}_{{{\varvec{i,j,g}}}} {\varvec{\cdot }} (\overrightarrow{{{\varvec{X}}}}_{{{\varvec{i,seedr1,g}}}} -\overrightarrow{{{\varvec{X}}}}_{{{\varvec{i,sr2,g}}}}) \end{aligned}$$

(10)

where j stands for $j_{th}$ individual in current species, $x_{i,seedi,g}$ is seed of the species current target vector belongs to, and $F_{i,j,g}$ denotes mutation factor that is updated at each generation adaptively. Indices seedr1 and sr2 are integers uniformly chosen from set of other $S\_num-1$ species seeds and current species respectively. On the one hand, it combines the best solution in current species and the best solution of other species, which leads to a fast convergence and guide the population to multiple promising regions. On the other hand, it does not merely rely on information provided by the best solution so it relieves the premature convergence problem.

Fig. 2

DE/seeds-to-seeds

Fig. 3

DE/seeds-to-rand

The second mutation “DE/seeds-to-rand” is relatively explorative. In this mutation, current species seeds are also taken as base vectors. The two individuals used to constitute difference vector are selected from the whole population randomly rather than be restricted in the species seeds set or current species. It is designed to diversify the population in later evolution stage and help the population jump out of local optimum because it expands searching ranges compared with the first mutation. Figure 3 illustrates this mutation in 2-dimensional plane picture. The more arbitrary combinations of individuals in this mutation make it could generate more beneficial directions to base vectors. A mutation vector is generated as follows:

“DE/seeds-to-rand”:

$$\begin{aligned} \overrightarrow{V}_{{{\varvec{i,j,g}}}}=\overrightarrow{X}_{{{\varvec{i,seedi,g}}}}+{{\varvec{F}}}_{{{\varvec{i,j,g}}}} {\varvec{\cdot }} \left( \overrightarrow{{{\varvec{X}}}}_{{{\varvec{i,r1,g}}}} -\overrightarrow{{{\varvec{X}}}}_{{{\varvec{i,r2,g}}}}\right) \end{aligned}$$

(11)

where $\overrightarrow{X}_{i,seedi,g}$ is seed of the species target vector belongs to, indices seedr1 and sr2 are integers both randomly chosen from the whole parent population. It increases randomness of the searching process and enhance the diversity of offspring population through involving individuals from the whole population.

At each generation, “DE/seeds-to-seeds” and “DE/seeds-to-rand” are employed to produce two offspring. Fitness values of the two offspring are compared and the better one could enter final selection process to against with target vector, which will promote search capacity and robustness of the algorithm because their explorative and exploitative characteristics are complementary. Experiments conducted in Sect. 5.3 illustrates that two mutation strategies can not be replaced by other strategies because of their powerful exploration and exploitation capability.

4.3 Parameter adaptation

Reference [17] adopted mutation based on Levy probability distribution. In this paper, Levy distribution is used to generate F and CR.

Levy distribution is a special case of Cauchy probability distribution. It will lead to larger variation and enable the evolution to discover a wider search space. Therefore, Levy distribution is used in F and CR adaptation to assist two mutation operations escaping from local optimal when the whole population is of highly cluster intensity. The location parameters $\mu _{F}$ and $\mu _{CR}$ are set to be 0.6 and 0.8 respectively. The standard deviation of the two parameters are both set to be 0.1. Experiments proved that DSM-DE are not sensitive to the feedback from previous generations thus fixed parameter setting do not impair the performance of DSM-DE. Conversely, it reduces calculation time and improves the program efficiency. The pseudo code of DSM-DE is presented in Algorithm 2.

4.4 The time complexity of DSM-DE

Compared with classical DE, DSM-DE demands additional computations on species division process. In each generation, DST is executed to divide the population into several subpopulations. Sorting the individuals based on fitness values will need NP log(NP) times. In order to find the nearest individuals to the species seeds, the Euclidean distances between each individuals are calculated. The average complexity of this process is $\hbox {O}(D\cdot NP \cdot (NP-1)/2$) [6] because of the symmetric property of the distance measure. The time complexity of classical DE is $\hbox {O}(Gmax \cdot NP \cdot D$) and the total time complexity of DSM-DE is $\hbox {O}(Gmax \cdot [ NP \cdot D + NP \cdot log (NP) + D \cdot NP \cdot (NP-1)/2]$) which can be simplified to $\hbox {O}(Gmax \cdot D \cdot NP^2$). It should be emphasized that the computational complexity of DSM-DE is mainly derived from the function evaluation when the function evaluation is costly. Furthermore, the additional computation cost by distance computing is proved to be negligible for the functions with costly evaluation.

5 Simulation results

In this section, comprehensive assessments for DSM-DE are carried out on CEC2014 and CEC2015 benchmark functions and Lennard-Jones potential problem by dividing the experiment results into three subsections. References [15, 16] introduced benchmark functions in CEC2014 and CEC2015 exhaustively. Section 5.1 compares the overall performance of DSM-DE with four classical DE variants. Section 5.2 compares DSM-DE with one state-of-art DE algorithm and two improved non-DE variants. Section 5.3 testifies the effectiveness and superiority of the two mutation strategies adopted in DSM-DE through designing DSM-DE variants as comparison.

5.1 Comparison with JADE, CoDE, SaDE, and jDE on 30-D, 50-D, and 100-D problems in CEC2014 and CEC2015 and 38 atom Lennard-Jones potential problem

JADE, CoDE, SaDE , jDE are four acknowledged classical DE variants that have been widely used in the literatures to do comparative experiments because of their excellent optimization performance. Four algorithms are employed the same parameters as in their original paper. All DE algorithms and variants of DSM-DE are programmed in MATLAB R2014a and run on a Windows 7 system.

In this experiment, five DE algorithms are tested on 30-D, 50-D, and 100-D problems in CEC2014 and CEC2015. The number of decision variables D is set to be 30, 50, and 100. MaxFES is set to be 300000 for 30-D, 500000 for 50-D, and 1000000 for 100-D. Each algorithm on each test function terminates when reaching MaxFES or the error value is smaller than 1E−08. Each algorithm is executed for 50 independent runs to obtain the average and standard variance error values. Non-parameter statistical analysis are conducted on the results to distinguish the optimization performance of different algorithms. The experiment results of average and standard error values of five algorithms on CEC2014 benchmarks (30-D and 50-D results on CEC2014 and all results on CEC2015 benchmarks are in the supplement due to the page limit) are presented in Table 2.

Table 1 Friedman’s test ranking of DSM-DE and four DE variants ON CEC2014 and CEC2015 functions

Table 2 Mean and standard deviation error value of JADE, CoDE, SaDE, jDE, AND DSM-DE on 100-D test functions in CEC2014 over 50 independent runs

Fig. 4

Evolution of the mean function error for DE variants on 30-D, 50-D, and 100-D benchmarks in CEC2014 and CEC2015

Firstly, Friedman’s test is implemented on the statistic results to see the overall performance of all compared algorithms. It could be observed from Table 1 that the overall performance of DSM-DE is the best among the compared algorithms both on lower or higher dimensional problems in CEC2014 and CEC2015. JADE ranks second except for 30-D test in CEC2015 and its performance is becoming relatively better with dimension increasing. CoDE ranks second or third in 30-D and 50-D test but it is exceeded by SaDE and jDE in 100-D test and ranks the last.

Wilcoxon signed-rank test is also implemented on the results at a 0.05 significance level and the overall results are recorded in the last three rows in Table 2. Comparison results on each function are given in supplementary. ‘$+$’, ‘−’, and ‘$=$’ denotes DSM-DE is better than, worse than, or equal to other algorithms respectively. Boldface font is used to indicate the best performance among five algorithms in terms of mean solution error. Figure 4 demonstrates convergence process for functions in different dimensions in CEC2014 and CEC2015 benchmarks. The figures graph mean error value curves for all five DE variants over 50 independent runs.

Unimodal functions In CEC2014 30-D test, global optimal solution of F2 is found by five algorithms and the global optimum of F3 is found by four algorithms except for JADE. But in 50-D and 100-D test, only JADE reaches the global optimum of F2. DSM-DE reduces the mean error value of F2 to 1E−07 in 50-D test and 1E−01 in 100-D test. Similarly, DSM-DE finds the global optimum of F3 in 30-D and 50-D test and reduces the mean error of F3 to 1E−05 in 100-D test. Other four algorithms only reach the global optimum in 30-D test. F3 is a rotated discus unimodal function that has a sensitive direction. DSM-DE is seeds-guided algorithm so it can tread on the heels of the evolutionary path of better solutions (i.e. the sensitive direction of the function) and diversify the population through selecting mutation individuals from a wider region at the same time. In CEC2015 30-D and 50-D tests, only DSM-DE and JADE find the global optimum of the rotated cigar function F2 which is smooth but with narrow ridge. Overall, JADE performs best on unimodal functions among five algorithms. DSM-DE is the second best but it performs better than JADE on rotated discus unimodal function.

Simple multimodal functions In CEC2014 30-D test, DSM-DE outperforms JADE on 7 functions and other three algorithms on 10 functions. It is worth pointing that there are 11 good results in 50-D test and 13 good results in 100-D test compared to CoDE on total 13 simple multimodal functions, which proves DSM-DE’s superiority in solving multimodal problems. In CEC2015, there are only 3 multimodal functions. DSM-DE performs better than JADE on F3 and F4 and it surpasses other three algorithms on all multimodal functions in all dimensional tests. Obviously, the overall performance of DSM-DE on basic multimodal functions is extremely better than other algorithms. It is not surprising to obtain these results. Most multimodal functions have a large number of local optima and it is easily to trapped in local optimum for most algorithms. DSM-DE is skilled in exploiting those huge amount of local optimums and diversifying the population with the perfect cooperation of the explorative and the exploitative mutation strategies. “seeds-to-seeds” mutation leads the population to promising area and “seeds-to-rand” mutation enable the evolution escape from local optimum through selecting parent individuals from larger ranges.

Hybrid functions In CEC2014 30-D test, DSM-DE is better than JADE on all 6 hybrid functions. It outperforms SaDE and jDE on 4 functions. In 50-D, DSM-DE also has overwhelming superiority compared to JADE, SaDE and jDE. In 100-D test, JADE is equally better with DSM-DE. Although DSM-DE is defeated by CoDE in 30-D test with 3 bad results and 2 good results, it succeeds CoDE in 50-D test with 3 good results and 1 bad result and in 100-D test with 6 good results.In CEC2015 test, DSM-DE gains a complete victory against JADE, SaDE, and jDE in 30-D test because it is significantly better than these three algorithms on all hybrid functions. Similarly, CoDE performs better than DSM-DE in 30 dimensional test, but it loses the dominance in 50-D and 100-D tests. Obviously, DSM-DE’s performance on higher dimension is remarkable. In summary, DSM-DE ranks second to CoDE and outperforms three other variants on lower dimensional functions. However, it surpasses CoDE and exhibits excellent performance on higher dimensional hybrid functions.

Composition functions In CEC2014, composition functions are made up of 3 or 5 functions. No method could reduce the mean error value of these functions below 1E+02. In 30-D test, CoDE performs best, which defeats other algorithms on five functions. SaDE ranks second and DSM-DE ranks third. In 50-D test, CoDE and jDE perform best and SaDE is surpassed by DSM-DE. In 100-D test, DSM-DE and JADE perform best and CoDE again loses its dominance. In CEC2015, DSM-DE is better than JADE, CoDE, SaDE and jDE on 4, 5, 5 and 6 functions respectively among 7 composition benchmarks in 30-D test. It is better than CoDE and SaDE on all composition functions in 100-D test. F12 is a composition function including 5 functions and DSM-DE wins four variants on all dimensional tests.

In summary, DSM-DE performs best on simple multimodal benchmarks in all dimensional tests. For other kinds of benchmarks, DSM-DE performs best on 50-D and 100-D tests in most cases. It ranks fourth on CEC2014 composition in 50-D test, which is not so desirable. Overall, the number of better results of DSM-DE is always more than worse results compared with four DE variants. JADE performs better on higher dimensional functions than on lower dimensional functions since the total good results are increasing and bad results are decreasing with the growth of dimension. CoDE, SaDE, and jDE perform much worse on higher dimension than on lower dimension. DSM-DE always keeps its leading position in all dimensional tests on two set of benchmarks.

In order to present the effectiveness of DSM-DE over real-world problems, it is tested on Lennard-Jones potential problem together with other four algorithms. Lennard-Jones Potential problem is a potential energy minimization problem, which deals with the minimization of molecular potential energy relating to pure Lennard-Jones cluster. It consists of numerous number of local minimum and have brought many optimizers to harsh tests. According to the description given in CEC2011 [29], an algorithm can be tested on this function for confirming its ability in conforming molecular structure. When such a structure is obtained, the atom has the minimum energy. In this experiment, a well-known atomic cluster with 38 atoms is considered, which means the problem dimension is 38 * 3. Thus, the maximum FES is set to be 38 * 3 * 10000. Each algorithm is executed for 50 independent runs to obtain the average and standard error values.

Table 3 Mean and standard deviation value of JADE, CoDE, SaDE, jDE, and DSM-DE on Lennard-Jones potential problem over 50 independent runs

Table 4 Results obtained by Wilcoxon’s test for DSM-DE, EFADE, EABC, and RW-GWC on 30-dimensional CEC2014 and CEC2015 functions

Table 3 illustrates the mean and standard deviation values optimized by four classic DE algorithms and DSM-DE through 50 independent runs. The optimum potential for the 38 atom Lennard-Jones cluster reported up to now is − 173.928427. It is clearly from the table that DSM-DE obtains the closest result to the optimum and SaDE ranks second. CoDE performs worst in solving this practical problem. Thus, this experiment demonstrates that the proposed method works in hard real life optimization problem.

5.2 Comparison with the state-of-art DE variant and non-DE algorithms

EFADE [21], EABC [12], and RW-GWC [2] are selected for comparison in this experiment. EFADE is the ensemble of fundamental DE and a fitness-adaptive mechanism. EABC includes four selection schemes to improve exploitation capability and convergence guided by the search process of onlooker bee. RW-GWC, which is a relatively new algorithm in the field of swarm intelligence, focuses on enhancing the search ability using random walk technique and a better leadership method. In the experiment, DSM-DE, EFADE and two non-DE variants are tested on 30-D functions in CEC2014 and CEC2015. We run EFADE on CEC2014 benchmark for 50 times to obtain the average and standard error values. However, the original codes of EABC and RW-GWC were not provided by the authors, so the results provided by these methods were directly taken from their references to conduct comparison (EABC was tested on CEC2015 and RW-GWC was tested on CEC2014, so DSM-DE can only be compared with them on the two benchmarks respectively).

Table 4 summarizes the Wilcoxon’s test results for DSM-DE and other three algorithms. $R^+$ and $R^-$ is the positive and negative rank sum respectively. It shows that DSM-DE obtains larger $R^+$ values than $R^-$ values no matter when it is compared with EFADE and EABC on CEC2014 or it is compared with RW-GWC on CEC2015 benchmark functions. The reason is that DSM-DE performs better than other three algorithms in most cases. Besides, p-values of EFADE and RW-GWC are all less than 0.05, which indicates that DSM-DE significantly surpasses these two algorithms. Although there is not 95% for us to conclude that DSM-DE is significantly better than EABC, the results of DSM-DE are competitive ($R^+$ is larger than $R^-$). In conclusion, DSM-DE outperforms the state-of-art DE variant EFADE and one non-DE variant RW-GWC and has comparable or even better optimization ability when comparing with EABC.

Table 5 Friedman’s test ranking of DSM-DE and its variants on 30-dimensional CEC2014 and CEC2015 functions

Table 6 Results obtained by Wilcoxon’s test for DSM-DE, DSM-DE1, DSM-DE2, and DSM-DE3 ON 30-dimensional CEC2014 and CEC2015 functions

Table 7 Adjusted p-values obtained by the post hoc methods for DSM-DE1, DSM-DE2, and DSM-DE3 on 30-dimensional CEC2014 and CEC2015 functions

5.3 Testifying the effectiveness and superiority of the two mutation strategies

To testify the mechanism of effect of the two mutation strategies in DSM-DE, three variants of DSM-DE which adopt different mutation combinations are designed in this experiment. Two frequently used strategies “DE/rand/1” and “DE/best/1” are introduced for comparison. “DE/best/1” takes internal individuals of each species as parent individuals. “DE/rand/1” selects parent individuals from the whole population. In this case, “DE/best/1” is more exploitative and “DE/rand/1” is more explorative. Each variant will combine an exploitative mutation and an explorative mutation as in DSM-DE. The first variant DSM-DE1 adopts “DE/best/1” and “DE/rand/1”. Similarly, DSM-DE2 adopts “DE/best/1” and “DE/seeds-to-rand/1”. DSM-DE3 employs “DE/seeds-to-seeds/1” and “DE/rand/1”. Except for employing different mutation strategies, other steps in these variants are rigorous the same as in DSM-DE. All variants are tested on 30-D functions in CEC2014 and CEC2015. The statistic results are given in supplementary due to pages limit.

Friedman’s ranking results of DSM-DE and three variants of DSM-DE are listed in Table 5. DSM-DE ranks first and DSM-DE2 ranks second in terms of the overall performance. Table 6 summarizes Wilcoxon’s test results for DSM-DE, which shows that DSM-DE obtains larger $R^+$ values than $R^-$ values compared to all variants. Clearly, DSM-DE is overly superior to the designed variants. The p values in Table 7 obtained by Bonferroni–Dunn’s, Holm’s and Hochberg’s procedures indicate that DSM-DE is significantly better than all variants with a level of significance $\alpha =0.05$.

The mean number of successful trial vectors generated by two mutations at each generation in 50 independent runs is recorded to observe the mechanism of effects of the mutation combinations. From the Wilcoxon signed-rank results, DSM-DE1, DSM-DE2, and DSM-DE3 all perform worse than DSM-DE on function 4 in CEC2014. The first line in Fig. 5 shows the evolutionary process of two mutation strategies on F4. There is a dominant strategy, i.e. the more exploitative mutation, for all variants, which means the successful rate of the exploitative mutation is always higher than that of the explorative mutation. The differences of DSM-DE and three variants is that the proportion gap of the two successful rates is decreasing in DSM-DE whereas it does not show no signs of decreasing in three variants. The gap in DSM-DE2 even shows to be increasing. For function 8 in CEC2014, DSM-DE1 and DSM-DE2 performs better than DSM-DE while DSM-DE3 performs worse than DSM-DE. In this case, it can be seen from the second line in Fig. 5 the proportion gap in DSM-DE and DSM-DE3 is increasing whereas DSM-DE1 and DSM-DE2 shows no signs of increasing.

Fig. 5

Mean number of successful trial vectors generated by two mutations in DSM-DE and three variants at each generation on F4 and F8

Experiments on other functions are also conducted and the records are given in supplementary. In most cases, the gap tendency of the two mutations affect the variants’ performance. Variants with decreasing proportion gap perform better than that with increasing gap. The results are reasonable because explorative mutation is used to expand the search scope and diversify the population. The algorithm is more likely to jump out of the local optimum with higher employment of explorative mutation because it is helpful in the later stage of evolution when the population is of highly cluster intensity. Thus, variants with higher successful rate of explorative mutation perform better. For the three variants, the number of trial vectors generated by explorative mutation in later evolution is usually small. It means the effect of explorative mutation is overly impaired by the dominant mutation in the final period. However, in DSM-DE, the successful rate of explorative mutation is increasing with the evolutionary process, which suggests that “DE/seeds-to-rand” is not totally surpassed by “DE/seeds-to-seeds”, so DSM-DE could continually generate better individuals in the later evolution. Therefore, the algorithm achieves a good balance of exploration and exploitation and the combination of the two mutations is perfect and irreplaceable.

6 Conclusion

Mutation is of great importance in collecting and allocating information. Good mutation strategies will highly improve the convergence rate and reliability of the DE algorithm. The mutation strategies “DE/seeds-to-seeds” and “DE/seeds-to-rand” in this paper accomplished this goal with the assistance of DST, which is designed to find better individuals located at different areas so that two mutation strategies can utilize the better individual’s location information to guide the evolution. Comparison experiments have shown that the combination of the two mutations achieves well balance between exploration and exploitation. DSM-DE is tested on a serious of benchmark functions and one well-known harsh real-world problem with four classical DE algorithms, one newly publicized DE variant and two improved non-DE algorithms. It demonstrates better performance in terms of convergence and accuracy compared with JADE, CoDE, SaDE, jDE, EFADE, RW-GWC, and EABC. It is worth to note that DSM-DE performs especially better on higher dimensional problems when compared with those DE variants. Although DSM-DE has shown promising results, the mechanisms of mutation strategies will be further studied in the future research in order to enhance the determining method of species sizes.