1 Introduction

Differential evolution (DE) is one of the most popular and efficient meta-heuristic optimization algorithms, which is proposed by Storn and Price (1995). It is very popular due to its simplicity and efficient convergence, and it has gained much success in a series of real applications, such as training neural network (Arce et al. 2018), object tracking (Nenavath et al. 2018) and other research and engineering fields. However, slow convergence rate and the loss of the diversity at the later stage of evolution are the key factors restricting the search performance, which makes DE algorithm get trapped in the local optimum and suffer the premature convergence. In recent years, many variants of DE algorithm have been put forward, which can mainly be categorized into the following 5 types:

  1. (1)

    Mutation strategies, which design new mutation strategies to guide the search process (Gong et al. 2013; Tang et al. 2017; Zheng et al. 2017; Cui et al. 2018; Sun et al. 2018; Zhang et al. 2019; Mohamed et al. 2019; Nadimi-Shahraki et al. 2020; Tan and Li 2021; Liu et al. 2021; Yu et al. 2021) or assemble different mutation operators based on the advantages of different mutation modes (Qin et al. 2009; Wang et al. 2011; Mallipeddi et al. 2011; Wu et al. 2016; Wu et al. 2018; Wei et al. 2019; Li et al. 2020a; Zhang et al. 2021a; Hu et al. 2021). Gong et al. (2013) proposed ranking-based mutation operators. Tang et al. (2017) presented a novel decentralizing and coevolving differential evolution (DCDE) algorithm. A novel “DE/current-to-SP-best-ring/1” mutation operation is also proposed in DCDE. Moreover, some researchers combined various mutation strategies based on the advantages of different mutation modes. Zheng et al. (2017) proposed a collective information-powered DE (CIPDE), a collective individual contained in the mutation operator of which is a linear combination of m individuals with optimal fitness values. Cui et al.(2018) put forward an adaptive multiple-elites-guided composite differential evolution algorithm with a shift mechanism (AMECoDEs). Sun et al.(2018) proposed a novel variant of DE with an individual-dependent mechanism that includes an individual-dependent parameter setting and an individual-dependent mutation strategy. Zhang et al. (2019) proposed a multi-layer competitive-cooperative (MLCC) framework to facilitate the competition and cooperation of multiple DEs. Mohamed et al. (2019) proposed the DE variants (EBDE, EBSHADE), in which three different individuals were ranked to participate in mutations, the difference being that the former’s individuals were randomly selected from the top p individuals and from the entire population, while the latter three individuals were all randomly chosen from the population. Nadimi-Shahraki et al. (2020) proposed an effective metaheuristic algorithm named multi-trial vector-based differential evolution (MTDE), which combined different search strategies in the form of trial vector producers. Tan and Li (2021) presented a mixed mutation strategy DE algorithm based on deep Q-network (DQN), named DEDQN, in which a deep reinforcement learning approach realized the adaptive selection of mutation strategy in the evolution process. Liu et al. (2021) proposed a niching differential evolution algorithm (NDE), which incorporated niching methods into differential evolution algorithm. Yu et al. (2021) presented a differential evolution algorithm based on the knee point (named DEAKP), in which the knee solution would guide the search direction of the algorithm. Qin et al. (2009) proposed a self-adaptive DE algorithm (SaDE). Wang et al. (2011) introduced a Composite Differential Evolution algorithm (CoDE). Mallipeddi et al. (2011) employed an ensemble of mutation strategies and control parameters with the DE (EPSDE). Wu et al. (2016) proposed a multi-population ensemble DE (MPEDE). Wu et al. (2018) focused on the high-level ensemble of different DE variants and proposed a new algorithm named EDEV. Wei et al.(2019) proposed a random perturbation modified differential evolution algorithm (PRMDE), which contained a new "DE/M_pBest-best/1" mutation operator. Li et al. (2020a) proposed an improved differential evolution algorithm with dual mutation strategies collaboration (DMCDE), in which an elite guidance mechanism and a mechanism of dual mutation strategies collaboration were introduced. Zhang et al. (2021a) put forward a new strategy adaptation method, named explicit adaptation scheme (Ea scheme), which separated multiple strategies and employs them on-demand. Hu et al. (2021) presented a multi-strategy co-evolutionary approach considering a dynamic adaptive selection mechanism and the combination of different characteristic mutation strategies.

  2. (2)

    Control parameters adaption or self-adaption strategies, which mainly focus on the adjustment strategies of the amplification factor and crossover probability. Nasimul et al. (2011) proposed a new Adaptive Differential Evolution algorithm (aDE), which adjusts the scaling factor (F) and the crossover probability (CR) adaptively according to the average fitness of parent population and the fitness of offspring individual. Ryoji et al. (2013) proposed a parameter adaptation technique for DE (SHADE) which uses a historical memory of successful control parameters to guide the selection of future control parameters. Gong et al. (2014) proposed a crossover rate repair technique for the adaptive DE algorithms (Rcr-JADE) based on successful parameters. Awad et al. (2016) proposed LSHADE-EpSin to enhance the performance of L-SHADE algorithm. In addition, some scholars have proposed adaptive strategies for the population size (Np). Awad et al. (2018) et al. proposed ensemble sinusoidal differential evolution with niching-based population reduction (called EsDEr-NR). Li et al. (2020b) proposed an enhanced adaptive differential evolution algorithm (EJADE), which introduced the crossover rate sorting mechanism and a dynamic population reduction strategy.

  3. (3)

    Both mutation strategies and control parameters strategies, which design the new mutation strategy and novel control parameters strategies simultaneously to improve the performance of algorithm. Cai et al. (2017) presented a neighborhood-adaptive DE (NaDE). A pool of index-based neighborhood topologies and a neighborhood-dependent directional mutation operator are introduced into NaDE. He et al. (2018) presented a novel DE variant with covariance matrix self-adaptation (DECMSA). Wang et al. (2017) proposed a self-adaptive differential evolution algorithm with improved mutation mode (IMMSADE) by improving “DE/rand/1”. Ali et al. (2017) presented adaptive guided differential evolution algorithm (AGDE). Ali et al. (2018) proposed an enhanced fitness-adaptive differential evolution algorithm with novel mutation (EFADE). Zhang et al. (2020) proposed an explicit exploitation and exploration capabilities (EEC) control method named selective-candidate framework with similarity selection rule (SCSS). Xu (2020) presented a novel dual-population adaptive differential evolution (DPADE) algorithm, in which a dual-population framework was employed and an adaptive technology was adopted to adjust two important control parameters and avoid the inappropriate parameters. Tian et al. (2020) proposed a high-performance DE (PDE) algorithm guided by information from individuals with potential. At each generation, the selection probability of each strategy in the strategy pool was determined by the strategy’s contribution to the improvement in fitness values. Zhang et al. (2021b) proposed a new multi-objective dynamic differential evolution algorithm with parameter self-adaptive strategies, named SA-MODDE. All components of the algorithm were synergically designed to reach its full potential, containing parental selection, mutation strategy, parameter setting, survival selection, constraint handling, and termination criteria.

  4. (4)

    Crossover strategies, which try to expand the search areas to keep the diversity of population. Guo et al. (2015) proposed a crossover operator utilizing eigenvectors of covariance matrix. Xu et al. (2015) proposed the superior-inferior crossover scheme. Cai et al. (2015) proposed hybrid linkage crossover. Ghosh et al. (2017) proposed the optional blending crossover scheme. Qiu et al. (2017) proposed a multiple exponential recombination.

  5. (5)

    Hybrid mechanisms, which mainly study the advantages of various evolutionary algorithms and have proposed hybrid algorithms of DE and other EAs. Li et al. (2012) proposed a new hybrid algorithm, called as differential evolution algorithm (DE)/artificial bee colony algorithm (ABC). Vaisakh et al. (2013) came up with a hybrid approach involving Differential Evolution (DE) and BFOA algorithm. Ponsich et al. (2013) hybridized DE with Tabu Search (TS). Le et al. (2013) merged differential evolution and harmony search. Nenavath et al. (2018) proposed a hybrid sine–cosine algorithm with differential evolution algorithm (Hybrid SCA-DE). Myszkowski et al. (2018) presented a hybrid Differential Evolution and Greedy Algorithm (DEGR). Wang et al. (2019) proposed a self-adaptive mutation differential evolution algorithm based on particle swarm optimization (DEPSO). Yildizdan and Baykan (2020) used the bat algorithm (MBA) algorithm in conjunction with the DE algorithm. Nguyen-Van et al. (2021) proposed a novel optimization algorithm as a cross-breed of the DE and the symbiotic organisms search (SOS). Houssein et al. (2021) proposed a hybrid algorithm: SMA combined to Adaptive Guided Differential Evolution Algorithm (AGDE) (SMA-AGDE). An opposition-based hybrid discrete optimization algorithm that a discrete and Opposition-Based Learning (OBL) version of the Moth-Flame Optimization (MFO) combined with the Differential Evolution (DE) algorithm was proposed by Ahmed et al. (2021). Chakraborty et al. (2021) presented a modified Whale optimization with the success history-based adaptive differential evolution (SHADE-WOA). The differential evolution and sine cosine algorithm based novel hybrid multi-objective evolutionary optimization methods were proposed by Altay and Alatas (2021).Although many kinds of DE variants have been proposed to improve the global optimization performance, they are still unavoidable for getting trapped in the local optima, especially for the complex problems, such as the problem with a very narrow valley from local optimum to global optimum, etc. Finding a proper balance between exploration and exploitation is the most challenging task in the development of any meta-heuristic algorithm due to the stochastic nature of the optimization process. In order to further balance the local exploitation and global exploration ability of DE, a differential evolution with superior-inferior mutation scheme (SIDE) is proposed.

The rest of the paper is structured as follows. Section 2 describes the background materials of DE. Section 3 is devoted to the proposed SIDE algorithm. Section 4 performs numerical experiments and comparisons using 32 benchmark functions of different properties, comparing with 8 DE variants and 4 non-DE-based algorithms. Finally, Sect. 5 presents the conclusions and future work.

2 Background materials of DE

DE is a population-based meta-heuristic global optimization algorithm and a competitive evolutionary algorithm (EA), especially in solving complex numerical optimization problems. Similar to the other evolution algorithms, DE also utilizes mutation, crossover and selection operators. For D-dimensional minimum optimization problems:

$$ \left\{ \begin{array}{l} \min \;f(x_{1} ,...,x_{D} ) \hfill \\ x_{j} \in [x_{j}^{L} ,x_{j}^{U} ],\forall j = 1, \ldots ,D \hfill \\ \end{array} \right. $$
(1)

where \(x_{j}^{L}\) and \(x_{j}^{U}\) are respectively the lower bound and upper bound of \(x_{j}\).

2.1 Mutation

A mutant vector \(V_{i}\) for each vector (called target vector here) is obtained by mutation operator based on scaling differences between randomly selected elements of the population to another element. There are many mutation operators available, and the classical one is “DE/rand/2”:

$$ V_{i}^{t} = X_{r1}^{t} + F \cdot (X_{r2}^{t} - X_{r3}^{t} ) + F \cdot (X_{r4}^{t} - X_{r5}^{t} ) $$
(2)

where \(F \in [0,2]\) is the scaling factor, \(i = \{ 1,\;2,\; \ldots \;,N_{p} \}\), \(N_{p}\) is the population size, t is the generation number, \(V_{i}^{t}\) is the mutant vector, \(r_{1} ,r_{2} ,r_{3} ,r_{4} ,r_{5} \in \{ 1,2,...,N_{p} \} \backslash \{ i\}\) are randomly generated, and \(r_{1} \ne r_{2} \ne r_{3} \ne r_{4} \ne r_{5}\).

2.2 Crossover

A trial vector can be constructed by performing crossover operator between a mutant vector and its associated target vector. The diversity of the population can be increased to expand the search area. The most commonly used binomial crossover constructs the trial vector in a random manner, as is described in Eq. (3).

$$ U_{i,j}^{t} = \left\{ \begin{array}{l} V_{i,j}^{t} \;\;\;if\;\;rand(0,1) \le CR\;\;or\;\;j = j_{rand} \hfill \\ X_{i,j}^{t} \;\;\;others\;\; \hfill \\ \end{array} \right.\;\;\; $$
(3)

where CR is the crossover probability in [0,1]. \(j_{rand}\) is randomly chosen from the set \(\{ 1,\;2,\; \ldots \;,\;D\}\), which guarantees that \(U_{i}^{t}\) has at least one component from \(V_{i}^{t}\).

2.3 Selection

The selection operator determines the survival of the better one between the target vector and the trial vector to the next generation. DE adopts a greedy strategy to determine whether the trial vector or the old target vector survives to the next generation. If and only if the trial vector \(U_{i}^{t}\) yields a better fitness value than the old target vector \(X_{i}^{t}\), then \(X_{i}^{t + 1}\) is updated by the trial vector \(U_{i}^{t}\). Otherwise, the old target vector \(X_{i}^{t}\) remains unchanged. The detailed selection scheme is as follows:

$$ X_{i}^{t + 1} = \left\{ \begin{array}{l} U_{i}^{t} \quad f(U_{i}^{t} ) < f(X_{i}^{t} ) \hfill \\ X_{i}^{t} \quad others \hfill \\ \end{array} \right. $$
(4)

3 SIDE algorithm

3.1 Superior-Inferior mutation scheme

The population diversity decreases rapidly, which leads to the failure of the clustered individuals to reproduce better individuals. Meanwhile, original DE has the weak local convergence ability. To further improve the local exploitation capability and global exploration capability of DE, a superior-inferior mutation scheme is proposed.

In superior-inferior mutation scheme, the superior individuals mainly guide the promising searching direction, and the inferior individuals can maintain population diversity in the evolution process. They have different effect to the mutation vector in the different milestones of optimization. The former increases emphasis on local search speeds up convergence without sacrificing the global properties of the algorithm; the latter is used to prevent the algorithm from becoming too local in its orientation, wasting precious function evaluations in pursuit of extremely small improvements.

The proposed superior-inferior mutation scheme is shown in Eq. (5).

$$ V_{i}^{t} = \omega_{i\_1}^{t} \cdot X_{best}^{t} + \gamma^{t} \cdot \omega_{i\_2}^{t} \cdot X_{worst}^{t} + F \cdot (X_{superior}^{t} - X_{i}^{t} ) + \gamma^{t} \cdot \omega_{i\_2}^{t} \cdot (X_{inferior}^{t} - X_{i}^{t} ) $$
(5)

where t is the generation counter, \(X_{best}^{t}\) and \(X_{worst}^{t}\) are respectively the best individual and worst individual at the current generation. \(X_{superior}^{t}\) and \(X_{inferior}^{t}\) are respectively the superior individual and inferior individual. \(X_{superior}^{t}\), \(X_{inferior}^{t}\) and \(X_{i}^{t}\) are distinct individuals. The fitness value of \(X_{superior}^{t}\) is better than the parent vector \(X_{i}^{t}\), and the fitness value of \(X_{inferior}^{t}\) is worse than the fitness of parent vector \(X_{i}^{t}\). \(\omega_{i\_1}^{t}\) and \(\omega_{i\_2}^{t}\) serve as a relative weight on local versus global search. if \(f(X_{i}^{t} ) > f_{mean}\), \(\omega_{i\_1}^{t} = 1\), \(\omega_{i\_2}^{t} = 0\), otherwise, \(\omega_{i\_1}^{t} = 0\), \(\omega_{i\_2}^{t} = 1\). \(f(X_{i}^{t} )\) is the fitness value of \(X_{i}^{t}\), \(f_{mean}\) is the mean fitness value. The larger \(\omega_{i\_1}^{t}\) is, the higher the relative emphasis puts on local search is. The larger \(\omega_{i\_2}^{t}\) is, the higher the relative emphasis puts on global search is. \(\gamma^{t}\) is the exploration factor, which also controls the relative emphasis putting on global search.

As far as the fitness value is concerned, the larger the better. The individuals are sorted in descending order according to the fitness of individuals. After fitness sorting, the top individual is the best, and the bottom individual is the worst. For the ith individual \(X_{i}^{t}\), it is the kth individual after sorting in Fig. 1. In our mutation scheme, \(X_{superior}^{t}\) is chosen from the superior set \(\{ X_{1} ,\; \ldots \;,\;X_{k - 1} \} {\kern 1pt} {\kern 1pt}\) randomly, and \(X_{inferior}^{t}\) is randomly chosen from the inferior set \(\{ X_{k + 1} ,\; \ldots \;,\;X_{{N_{p} }} \} {\kern 1pt} {\kern 1pt}\).

Fig. 1
figure 1

Superior-inferior mutation scheme

Full size image

3.2 Dynamic adjustment strategy of exploration factor \(\gamma\)

Population-based meta-heuristic optimization algorithms share a common feature regardless of their nature. The optimization process can be divided to two phases: exploration versus exploitation. In the exploration phase, searching the promising regions of the search space with a high rate is important. While, in the exploitation phase, random variations are considerably less than those in the exploration phase, which leads to lower the population diversity. Based on the above evolutionary property, to make full use of the role of the superior individual and the inferior individual, dynamic adjustment strategies of exploration factor are adopted.

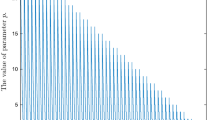
Inferior individual is mainly used to improve the diversity at the later stage of evolution. Therefore, the exploration factor is adjusted dynamically according to sine curve with the generations.

$$ \gamma^{t} = \sin ((t/T)^{2} ) $$
(6)

The dynamic adjustment curve of exploration factor are shown in the Fig. 2, which take 1000 iterations as an example.

Fig. 2
figure 2

The adjustment curve of exploration factor

Full size image

The flow diagram of SIDE is illustrated in Fig. 3.

Fig. 3
figure 3

The flow diagram of SIDE

Full size image

A detailed description of proposed SIDE algorithm is presented in Algorithm 1.

figure a

4 Numerical experiments and comparisons

4.1 Experiments setup

As shown in Table 1, a total of 32 benchmark test functions from literature (Suganthan et al. 2005; Liang et al. 2013; Awad et al. 2017) are used to perform performance comparison. The properties are as follows: f1–f10 and f13 are unimodal functions, f11 is step function, f12 is noise function, and others are multimodal functions.

Table 1 Benchmark test functions
Full size table

4.2 Time complexity

The time complexity is calculated as described in (Suganthan et al. 2005). The codes are implemented in Matlab 2015a and run on a PC with an Intel (R) Core (TM) i5-6500 CPU (3.20 GHz) and 8 GB RAM. The algorithm complexity at D = 10:10:200 is plotted in Fig. 4. In Fig. 4, \({T}_{0}\) denotes the running time of the following program:

$$ \begin{aligned}& for\;i = 1:1000000 \hfill \\& x = (double)5.55; \hfill \\& x = x + x;x = x./2;x = x*x;x = sqrt(x);x = \ln (x);x = \exp (x);y = x/x; \hfill \\ end \hfill \\ \end{aligned} $$
Fig. 4
figure 4

Time complexity (time in seconds)

Full size image

\({T}_{1}\) is the computing time just for Elliptic function for 200,000 evaluations at a certain dimension D. \({T}_{2}\) is the complete computing time for the algorithm with 200,000 evaluations of D dimensional Elliptic Function. \({T}_{2}\) is evaluated five times, and \({\widehat{T}}_{2}\) is used to denote the mean \({T}_{2}\). At last, the complexity of the algorithm is reflected by: \({T}_{0}\), \({T}_{1}\), \({\widehat{T}}_{2}\), \({(\widehat{T}}_{2}-{T}_{1})/{T}_{0}\).

4.3 Comparison with 8 DE variants and 4 non-DE-based algorithms

In order to verify the performance of proposed SIDE, SIDE was compared with 8 advanced DE algorithms which have been reported to have good performance, including MLCCDE (Zhang et al. 2019), EBDE (Mohamed et al. 2019), EDEV (Wu et al. 2018), EsDEr-NR (Awad et al. 2018), EJADE (Li et al. 2020b), IMMSADE (Wang et al. 2017), EFADE (Ali et al. 2018), DEPSO (Wang et al. 2019).

  • MLCCDE and EBDE are DEs with new mutation strategies.

  • EDEV is a composite DE with multiple mutation strategies and control parameters.

  • EsDEr-NR, EJADE, IMMSADE and EFADE are DEs with an improved mutation strategy and adaptive control parameters.

  • DEPSO is a hybrid algorithm of DE and particle swarm optimization (PSO).

  • SIDE is also compared with 4 non-DE-based algorithms, including Multi-Verse Optimizer (Mirjalili et al. 2016), Dragonfly algorithm (Mirjalili 2016), Gaining Sharing Knowledge (Ali et al. 2020) and Flow Direction Algorithm (Karami et al. 2021).

  • Multi-Verse Optimizer (MVO) is proposed based on three concepts in cosmology: white hole, black hole, and wormhole.

  • Dragonfly algorithm (DA): The main inspiration of DA originates from the static and dynamic swarming behaviour of dragonflies in nature.

  • Gaining Sharing Knowledge (GSK) mimics the process of gaining and sharing knowledge during the human life span.

  • Flow Direction Algorithm (FDA) mimics the flow direction to the outlet point with the lowest height in a drainage basin.

In our experiments, for all the compared algorithms,the associated control parameters are kept the same as the settings in their original papers, which is shown in Table 2. F = 0.1 and CR = 0.9 are set in SIDE.

Table 2 Parameters setting
Full size table

To have a reliable and fair comparison, the other common parameters are setting as follows: the population size is set as Np = 100, the maximum generation is set to T = 1000 and 30 independent runs are conducted.

4.3.1 Numerical analysis

In this subsection, the numerical results obtained by proposed SIDE are compared with other 12 state-of-the-art algorithms. In the following comparisons, we adopt the solution error (\(f(x) - f(x^{*} )\)) to evaluate the optimization performance, where \(x\) is the best solution obtained by algorithms in one run, \(x^{*}\) is the global optimum. The Mean and Standard Deviation (STD) of the solution error value are summed up in Tables 3, 4 and 5.

Table 3 The optimization results obtained by SIDE, 8 DE variants and 4 non-DE-based algorithms at D = 30 over independent 30 runs
Full size table
Table 4 The optimization results obtained by SIDE, 8 DE variants and 4 non-DE-based algorithms at D = 50 over independent 30 runs
Full size table
Table 5 The optimization results obtained by SIDE, 8 DE variants and 4 non-DE-based algorithms at D = 100 over independent 30 runs
Full size table

From Tables 3, 4 and 5, SIDE performs better than many compared algorithms and can obtain the global optimal solution on most of test functions, including unimodal functions (f1 − f2, f6 − f8, f10 − f11 and f13) and multimodal functions (f14 − f16, f17 − f18, f13, f24, f26, f28 and f30) in all dimensions. Especially, Rastrigin function (f14) has several local minima and it is highly multimodal; Griewank's function (f15) has a component that causes linkage among the dimensions; Ackley function (f18) is characterized by a nearly flat outer region and a large hole at the center; Non-Continuous Rastrigin’s Function (f28) is multi-modal, non-separable and asymmetrical function and the local optima’s number is huge. For these functions, DE is easy to suffer from premature convergence to be trapped in one of its many local minima. However, SIDE can find the global optimal solution on f14, f15, f18 and f28. The reason is that the superior-inferior mutation strategy and the dynamic adjustment strategy of exploration factor assist SIDE in realizing a better balance between local exploitation and global exploration. SIDE can maintain larger diversity to yield better performance. For noise quadric function f12, EJADE, EsDEr-NR and MLCCDE are the best at D = 30, D = 50 and D = 100, respectively. Rosenbrock function (f19) have global optimum lays inside a long, narrow, parabolic shaped flat valley, and it is challenging to find the global optimum. For f19, EJADE is the best at D = 30 and D = 50, and IMMSADE is the best at D = 100. Happy Cat function (f22) and HGBat function are multimodal and non-separable functions. For Happy Cat function (f22), MLCCDE is best in all dimensions. Griewank's function has a component that causes linkage among the dimensions and Rosenbrock function is very complex, therefore, expanded Griewank’s plus Rosenbrock’s function (f27) will be difficult to reach the global optimum. For f27, DEPSO is best in all dimensions. The Schaffer’s F7 function (f32) is non-separable, asymmetrical and the local optima’s number is huge. For f32, SIDE is the best in all dimensions.

The number of the best and the second best solution error results are listed in Fig. 5. From Fig. 5, SIDE has outstanding performance on most of test functions. SIDE obtains 23 best results out of 32 functions at D = 30, while MLCCDE, EBDE, EDEV, EsDEr-NR, EJADE, IMMSADE, EFADE, DEPSO, MVO, DA, GSK and FDA obtain 6, 1, 5, 4, 3, 6, 1, 8, 0, 0, 4 and 2 functions, respectively. SIDE keeps this obvious advantage in both 50-D and 100-D problems. However, for other compared algorithms, even for the 30-D dimensions, DEPSO only obtains at most in 8 out of 32 functions.

Fig. 5
figure 5

Number of cases on which each algorithm performs the best and the second best in the comparison

Full size image

To further show the performance clearly, we summarize the number of the global optimum graphically in Fig. 6. From the histogram in Fig. 6, for the 30-D dimensions, SIDE obtains 18 global optimums (8 unimodal functions + 10 multi-modal functions), MLCCDE, EBDE, EDEV, EsDEr-NR, EJADE, IMMSADE, EFADE, DEPSO, MVO, DA, GSK and FDA only obtain 5 (2 + 3), 0 (0 + 0), 5 (2 + 3), 3 (1 + 2), 1 (1 + 0), 6 (2 + 4), 1 (1 + 0), 7 (2 + 5), 0 (0 + 0), 0 (0 + 0), and 1 (0 + 1) out of 32functions, respectively. SIDE keeps this obvious advantage in both 50-D and 100-D problems. It is obviously that the performance superiority of IDE becomes gradually more significant with the increase of the problems’ dimension.

Fig. 6
figure 6

Number of cases on which each algorithm obtains the global optimum in the comparison

Full size image

In order to illustrate the distribution of the results of each algorithm, the box plots of function solutions of all the algorithms on 6 functions (1 unimodal function and 5 multimodal functions) for the 30-D and 100-D dimensions are depicted in Fig. 7, respectively. It can be seen that SIDE has more concentrated solution error values and fewer outliers compared with other algorithms. Therefore, it can be concluded that SIDE performs more stable than other algorithms on these problems.

Fig. 7
figure 7figure 7

Box plots of the result of solution error for functions f5, f14, f21, f26, f28 and f32

Full size image

Based on the above analysis, it is clear that the proposed SIDE performs well and it has a high exploitation ability and high performance in finding the global solution.

4.3.2 Convergence analysis

The Mean Number of Evolution Generations (MNEG) required to reach the specified convergence precision and the Success Rate (SR) are adopted to analyze the convergence properties. In our experiments, the specified convergence precision is set as 10–8. The MNEG and SR obtained by SIDE, 8 DE variants and 4 non-DE-based algorithms are described in Tables 6, 7 and 8, where “N/A” denotes Not Applicable. For some functions, all the algorithms cannot reach the specified convergence precision, so the MNEG and SR of these functions are omitted in the following tables.

Table 6 The MNEG and SR obtained by SIDE, 8 DE variants and 4 non-DE-based algorithms at D = 30 over independent 30 runs
Full size table
Table 7 The MNEG and SR obtained by SIDE, 8 DE variants and 4 non-DE-based algorithms at D = 50 over independent 30 runs
Full size table
Table 8 The The MNEG and SR obtained by SIDE, 8 DE variants and 4 non-DE-based algorithms at D = 100 over independent 30 runs
Full size table

From Tables 6, 7 and 8, we obvious that the MNEG of SIDE is much less than its competitors and the success rate is 100% on f1~f11, f13~f18, f20, f24, f26 and f28~f30 for all dimensions. It also can be seen that the SIDE has the better performance of convergence rate and outperformed some of other algorithms in terms of stability of solutions. The reasons are as follows: On one hand, the superior individuals guide the promising searching direction, so convergence rate will be faster. On the other hand, the dynamic adjustment strategy of exploration factor realizes a better balance of exploration and exploitation, hence SIDE can obtain the better optimization results in most of functions and has the better reliability. Based on the superior-inferior mutation scheme and the dynamic adjustment strategy of exploration factor, the proposed SIDE can better alleviate the premature convergence.

4.3.3 Non-parametric statistical tests

An performance comparison between SIDE and other 12 state-of-the-art algorithms is provided in the above comparisons. To further compare and analyze the solution quality from a statistical angle of different algorithms and to check the behavior of the stochastic algorithms, the results are compared using the following non-parametric statistical tests (Derrac et al. 2011):

  1. (1)

    Wilcoxon signed-rank test (to check the differences for each function);

  2. (2)

    The Friedman test and Kruskal_Wallis test (to obtain the final rankings of different algorithms for all functions);

  3. (3)

    Wilcoxon rank-sum test (to check the differences between SIDE and compared algorithms for all functions).

Wilcoxon's signed-rank test results at the 0.05 significance level for each function are shown in Fig. 8. Signs “ + ”, “−” and “≈” indicate the number of functions that SIDE is better than, worse than and similar to its competitor, respectively. The Friedman test and Kruskal–Wallis test results are plotted in Fig. 9. Wilcoxon's rank-sum test results are listed in Tables 9, 10 and 11. In Tables 9, 10 and 11, R + denotes the sum of ranks for the test problems in which the first algorithm performs better than the second algorithm, and R − represents the sum of ranks for the test problems in which the first algorithm performs worse than the second algorithm. Larger ranks indicate larger performance discrepancy. “Yes” indicates that the performance of SIDE is better than its competitor significantly.

Fig. 8
figure 8

The Wilcoxon's signed-rank test results with a significance level of 0.05 over 30 independent runs

Full size image
Fig. 9
figure 9

Non-parametric test results over 30 independent runs

Full size image
Table 9 The results of Wilcoxon rank-sum test at D = 30 over 30 independent runs
Full size table
Table 10 The results of Wilcoxon rank-sum test at D = 50 over 30 independent runs
Full size table
Table 11 The results of Wilcoxon rank-sum test at D = 100 over 30 independent runs
Full size table

In Fig. 8, SIDE at least outperforms all the compared DE variants in 17, 18, 18 out of 32 functions significantly at D = 30, D = 50 and D = 100, respectively.

Figure 9 shows the average ranks of SIDE and other algorithms according to Friedman test and Kruskal_Wallis test based on the solution error at D = 30, D = 50 and D = 100, respectively. No matter low-dimensional problems or high-dimensional problems, SIDE gets the first ranking among all algorithms, DEPSO is the second best for 30, 50 and 100 variables.

From a comparative analysis of the results from Tables 9, 10 and 11, it can be seen that SIDE obtains higher R + values than R − in all the cases. It also can be observed that SIDE outperforms all the compared DE variants and non-DE-based algorithms significantly. In addition, Figs. 7, 8 and Tables 9, 10 and 11 clearly show that the advantage of SIDE is more prominent as the number of dimensions increasing.

Overall, from the above analysis and comparisons, the proposed SIDE is better in term of searching quality, efficiency and robustness. It proves that SIDE greatly keeps the balance between the local optimization speed and the global optimization diversity.

4.4 Performance sensitivity to the population size N p

The impact of the population size Np on the performance of SIDE is also investigated. SIDE variants with Np = {50, 75, 125, 150, 175, 200, 225, 250} are compared with the SIDE with Np = 100. Friedman test results are shown in Fig. 10.

Fig. 10
figure 10

The Friedman test results at D = 30 over 30 independent runs

Full size image

Although SIDE with Np = 200 is best in Fig. 10, there is no obvious difference in performance in Table 12. In a word, SIDE is not sensitive to the population size Np.

Table 12 The results of Wilcoxon's rank-sum test over 30 independent runs
Full size table

4.5 Efficiency analysis of proposed algorithmic component

The proposed algorithm represents a combined effect of superior-inferior mutation scheme and the dynamic adjustment strategy of exploration factor γ. In order to investigate the efficiency of the proposed algorithmic components, some experiments are conducted. Five SIDE variants with γ = {0.2, 0.4, 0.6, 0.8, rand()} have been compared with the proposed SIDE on 32 benchmark functions benchmark at D = 30 over 30 independent runs.

Figure 11 shows the rankings of different SIDE variants of applying Friedman test and Kruskal–Wallis test between proposed SIDE and other compared five versions. From Fig. 11, the proposed SIDE is the best, SIDE with γ = {0.2, rand()} is the second best, followed by SIDE with γ = {0.4, 0.6, 0.8}. From Table 13, there is no obvious performance difference between SIDE and the five SIDE variants. But we can see that proposed SIDE obtains higher R + values than R − values in comparison with its other exploration factor γ. It proves that the superior-inferior mutation scheme has the biggest contribution to SIDE, followed by the dynamic adjustment strategy of γ. It also verifies that superior-inferior mutation scheme and the dynamic adjustment strategy of exploration factor balance the exploration capability and exploitation tendency better.

Fig. 11
figure 11

The Friedman test and Kruskal–Wallis test results at D = 30 over 30 independent runs

Full size image
Table 13 The results of Wilcoxon's rank-sum test between SIDE with γ = sin((t/T)2) and SIDE with γ = {0.2, 0.4, 0.6, 0.8, rand()} over 30 independent runs
Full size table

4.6 Adaptability analysis to high-dimensional problems

Wilcoxon's signed-rank test is performed to evaluate the adaptability to high-dimensional problems for each algorithm between its own 30 variables and 100 variables with the same maximum generation. From the statistical results in Fig. 12, it is easy to observe that:

  1. (1)

    The low-dimensional performance of a part of DE variants is significantly better than high-dimensional performance for all the test functions, including EBDE, EsDEr-NR, EFADE, MVO and GSK.

  2. (2)

    For MLCCDE, EDEV, EJADE and DA, the low-dimensional performance is better than high-dimensional performance in 31 out of 32 functions.

  3. (3)

    For SIDE, the low-dimensional performance is better than, worse than and similar to high-dimensional performance in 10, 4 and 18 out of 32 functions, respectively.

Fig. 12
figure 12

The Wilcoxon's signed-rank test results with a significance level of 0.05 over 30 independent runs. Signs “ + ”, “−” and “≈” indicate the number of functions that the performance of algorithm for low dimensional problems is better than, worse than and similar to the performance for high dimensional problems, respectively

Full size image

We can draw the conclusion that SIDE has the best adaptability to high-dimensional problems respectively.

4.7 Discussions on SIDE

The SIDE algorithm has a considerable ability to maintain its convergence rate, improve its diversity as well as advance its local tendency through a search process. Thus, the proposed SIDE shows competitive performance in terms of quality of solution, efficiency, convergence rate and robustness. The outstanding performance of SIDE stems from three aspects:

  1. 1.

    In the early stage of evolution, superior individual has larger weight, and it is used to guide the population evolving toward the promising solution and improve local exploitation capability.

  2. 2.

    In the later stage of evolution, inferior individual has larger weight, and it can expand the search area to improve population diversity to alleviate the premature convergence.

  3. 3.

    By adjusting the weight of exploration factor dynamically, there is a better balance between the local exploitation and global exploration to improve the global optimization capability of DE.

5 Conclusions

In order to further balance the convergence and diversity, a superior-inferior mutation scheme is proposed in the paper. Furthermore, novel dynamic weight adjustment strategy of superior individual and inferior individual are introduced according to the evolutionary property. Based on the above experiments, the effectiveness and efficiency of proposed algorithmic components are verified. Extensive numerical experiments and comparisons comparing with 8 advanced DE algorithms and 4 non-DE-based algorithms have demonstrated the high effectiveness of proposed SIDE. The advantages of proposed SIDE are more obvious as the number of dimensions increase.

As future work, novel control parameters optimization strategies will be studied to solve more complex engineering optimization problems. In addition, SIDE will be applied to various optimization fields, such as carrier aircraft landing sequencing, etc.