Introduction

The behavior of highly concentrated suspensions of long discontinuous fibers is of interest during composite manufacturing. Such materials can provide fiber volume fractions above 50%, desired for structural reasons, while providing the potential for net-shape manufacturing and forming techniques that are difficult to realize in systems with continuous fibers. The matrix material is usually softened to form the part and then re-solidified. To ensure that no clumps or wrinkles form while shaping the material on the tool surface, it is critical to understand the evolution of the microstructure and its effect on the effective viscosity.

In this work we limit the material forms containing (a) very high fiber volume fraction, (b) straight highly aligned discontinuous fibers. These two conditions are not mutually exclusive because the geometry dictates that to get maximum volume fraction, they will have to be highly aligned. Such materials can be made by material manufacturers. The fibers in considered materials are structural, have limited flexibility and are embedded in the material parallel to each other to maximize the reinforcing benefit. Tensile deformation will not introduce bending and deviation from this state. In this work, we will not address the behavior of such systems under compressive loads which may lead to fiber bending and loss of stability.

Previous work

Deformation of thermoplastic materials reinforced by high fiber volume fraction of fibers – both individual (continuous or discontinuous) or in textile form have been analyzed previously [1,2,3,4,5,6]. In this work we will limit our analysis to individual systems of discontinuous and aligned fibers. These systems are attractive as long and discontinuous fiber systems allow for material extension in the fiber direction improving material forming properties. At the same time, they are less studied than those reinforced with continuous or woven/stitched fiber systems that can undergo shearing deformations only [7,8,9].

During the forming process the fibers remain solid while the polymer matrix softens and/or melts creating a suspension. This suspension exhibits effective anisotropic viscous behavior and an effective anisotropic viscosity tensor is used to describe its deformation behavior at the macroscale [7]. This is postulated to depend on fiber’s length, aspect ratio, volumetric content and orientation. The effective constitutive behavior of the system can be described with the suspension parameters: resin viscosity, fiber aspect ratio, dimensions and fiber orientation state.

For structural performance, high fiber volume fractions are desirable. The system can realize high fiber volume fraction (over 50%) only when the fibers are all straight and aligned in one direction with the thin layer of polymer matrix lubricating the contacts between them. Based on this possible configuration, simple Representative Elementary Volume (RVE) models were created to estimate the effective properties [7]. It was noted that the effective viscosity of fiber reinforced material dramatically increases with the aspect ratio of fibers and also with the fiber volume fraction. This leads to requiring considerable forming forces and may cause [10] stability issues as the formed material cannot support compression forces in certain directions. There is some experimental work supporting these conclusions [8, 9].

The viscous squeeze flow model for the forming deformation depends on a “effective” viscous constitutive equation that relates the applied forces to the deformation rate. The constitutive relation may focus just on the linear viscous effect or more complex visco-elastic behavior. The formulated constitutive relation is then used within analytic or more likely numerical models [10,11,12,13] to simulate the forming process progression. The stress-strain rate relationship for simple in-plane deformation in fiber direction can be cast in a simple form [7].

$$ \left[\begin{array}{c}{\sigma}_L\\ {}{\sigma}_T\\ {}{\tau}_{LT}\end{array}\right]=\left[\begin{array}{ccc}{\mu}_{11}& {\mu}_{12}& 0\\ {}{\mu}_{12}& {\mu}_{22}& 0\\ {}0& 0& {\mu}_{66}\end{array}\right]\left[\begin{array}{c}{\dot{\varepsilon}}_L\\ {}{\dot{\varepsilon}}_T\\ {}{\dot{\varepsilon}}_{LT}\end{array}\right] $$
(1)

Where the parameters in the above matrix depend on effective viscosity components (longitudinal (η11), transverse (η22) and shearing (η12) as follows [7]:

$$ {\displaystyle \begin{array}{c}\begin{array}{c}{\mu}_{11}=4{\eta_{11}}^2/\left(4{\eta}_{11}-{\eta}_{22}\right)\\ {}{\mu}_{12}=2{\eta}_{11}{\eta}_{22}/\left(4{\eta}_{11}-{\eta}_{22}\right)\end{array}\\ {}\begin{array}{c}{\mu}_{22}=4{\eta}_{11}{\eta}_{22}/\left(4{\eta}_{11}-{\eta}_{22}\right)\\ {}{\mu}_{66}={\eta}_{12}\end{array}\end{array}} $$
(2)

Embedding this relation into a finite element formulation and having a constitutive form for the longitudinal (η11), longitudinal transverse (η22) and shearing (η12) effective viscosity, one can predict the forming deformation as shown in Fig. 1 though the approach still presents many challenges and is not ready for industrial deployment [11].

Fig. 1
figure 1

Simulation of stretch forming of a beam around a corner. (a) Geometry, (b) velocity field and longitudinal stress (fiber tension) [11]

Full size image

Microstructural model

Limitations

This work concentrates on the determination of effective viscosity values (mainly longitudinal extensional η11 and in-plane shear η12) using unit cell based micro-mechanics models. The continuum models used with constant material parameters is an approximation. In real materials, the viscous deformation is expected to be non-homogenous on the fiber length scale. The presence of solid fibers causes the local deformation rates in matrix material to be significantly higher than the nominal forming rates during shaping of such materials into a mold during the manufacturing process.

Thus, at the length scale of fiber diameter, based on the local arrangement of fibers the material behavior strongly varies with the location. On the macro-scale, we can assume that for “sufficiently large sample” the behavior averages to that provided by Eq. (1) and (2) with constant coefficients. For thin sheets of such materials about 0.1 mm, micrographs show that there are about 10 fiber diameters across the thickness. Any non-uniformity in behavior of material samples at the length scale of sheet thickness should be considered as significantly affecting the overall material properties for forming with such materials.

We expect that the non-uniformity in material parameters during forming itself will appear as a result of non-uniformity in material microstructure introduced during the production of the material. If there is a variation of material microstructure, there will be corresponding variation in “effective” properties on the length scale of interest because it is too small to allow perfect averaging.

To study this phenomenon we will relax the usual, but highly impractical, constraint of highly regular representative volume around a single fiber and we will introduce many fibers in the unit cell and examine the effect of slight deviations of these fiber arrangements in terms of end to end spacing between the fibers and fiber overlap distance on the macroscopic processing properties such as the global (mean) and local (standard deviation at certain length scale) effective viscosity values.

Approach

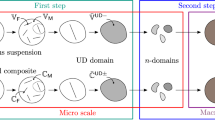
The hyper-concentrated fibrous system is expected to be highly oriented to achieve the desirable high fiber volume fraction. The material exhibits orthotropy related to the local fiber direction, usually transverse isotropy. The behavior in fiber length direction (L) significantly differs from the behavior in both transverse directions (T) as is evident from Fig. 2.

Fig. 2
figure 2

Coordinate system within the hyper-concentrated suspension of long, discontinuous slender fibers

Full size image

There are, strictly speaking, four deformation modes to be considered for the material microstructure shown in Fig. 2, however we are interested in thin sheet materials so we will only address the three deformation modes as shown schematically in Fig. 3.

Fig. 3
figure 3

Deformation modes of thermoplastic sheet reinforced by concentrated aligned discontinuous fibers: (a) longitudinal extension (b) transverse extension, (c) in-plane sheering deformation

Full size image

The sheet may be extended (or compressed) in the direction of fibers (a), across the fibers (b) or sheared in plane (L-T in Fig. 1). Applying the longitudinal extension (deformation mode (a)) requires significant relative in-plane slip between adjacent fibers and this obviously leads to magnified deformation rates as seen by the matrix material. Note that even the sheet extension may be accompanied by through-the-thickness deformation (to preserve volume) which in turn implies transverse shear deformation (Fig. 4) orthogonal to fibers which we did not consider in Fig. 3. The deformation rates within the resin are, again, magnified relative to the global ones computed from the deformation rate of the sheet. Thus, the effective viscosity components are much higher than the viscosity of the pure matrix.

Fig. 4
figure 4

Transverse deformation of fiber reinforced sheet. Change in thickness results in shearing deformation in resin surrounding the fibers

Full size image

To obtain η11 or η12 we will use unit cell micro-mechanical models as previously applied to periodic RVE [7] (Fig. 5). These utilize the fact that for high fiber volume fractions of reinforcement the fibers have to be well aligned. Using idealized fiber distribution, these models build a repetitive microstructure (in two- or three-dimensional space) as shown in Fig. 2. As each cell in this microstructure deforms in similar manner, one can force the relative motion of individual fibers and determine the resin flow needed for such a motion given a proper constitutive model for resin deformation. This can be accomplished using analytic solutions (exact or approximate) or even applying numerical models. Once the system of equations is formulated and solved, necessary required forces to induce those deformations can be determined.

Fig. 5
figure 5

Unit cell model for individual fiber and adjacent resin volume: (a) Two-dimensional, in plane shear (b) Three-dimensional, longitudinal extension

Full size image

Numerical modeling

Unit cell models were previously applied to both Newtonian and non-Newtonian (Carreau) fluids [7, 14]. However, the geometry of simple periodic unit cell is overly simplified to be seen as a representative structure as we know that the actual material will not be perfectly arranged. This is particularly important for the extensional flow in fiber direction which changes the spacing between fiber fragments. Additional simplifications are also excessive. Actually, the hexagonal “unit” cell as used in [7] cannot even be repeated spatially.

We will set a few simple requirements to build a unit cell model containing multiple fibers to evaluate the effective viscosity components. The unit cell allows for

  1. a)

    fiber overlap to be a random value between all fibers in the cell

  2. b)

    random gap distance between fiber ends

  3. c)

    flexibility in fiber arrangement and spacing in the transverse direction

To accommodate this, our unit cell will look similar as the one shown in Fig. 2 and will have parameters as shown (schematically) in Fig. 6:

Fig. 6
figure 6

Unit cell parameters and principal unknowns used in solution: both the gap distance between fiber ends, g and overlap distance o are random within certain range, the overlap actually depends on gaps (random) and the random value of first fiber offset is e. Fiber dimensions are length L, diameter d and spacing s dependent on desired fiber volume fraction. Individual fiber velocity is as shown on the right side and forces are transferred due to fluid shearing between individual neighboring fibers

Full size image

The size of a “unit” cell to be built for these requirements is unknown to begin with, though it must be more than five or seven fibers unlike in previous models. The actual size will be set later to make sure that at least the basic statistics of the predicted viscosity are invariant to further cell size increase and the size should not exceed the characteristic length of the system (the ply thickness in sheet materials) We will use the ply thickness as the size of our unit cell even if smaller cell size makes it possible to find mean values because of our interest in calculating the standard deviation of the effective property as well. The flexibility in fiber arrangement has been currently limited to square/hexagonal packing though many other configurations could be addressed within the framework.

Approach to compute effective viscosity

In our approach we generate a cell of aligned fibers, periodic in transverse directions as shown in Fig. 6. The actual example system is depicted in Fig. 2. For square and hex packing, the periodicity may be simply introduced by mirroring the fibers from one border of the cell to the opposite border. If perturbed positions are to be used, the boundary perturbations will need to be linked, too.

The extension is simulated by prescribing the velocity at the end fibers in the longitudinal direction (L in Fig. 2). This can be accomplished by two approaches: (i) periodic conditions at the cell ends or (ii) by simply “locking” the ends, keeping one end stationary and moving the other end with prescribed constant velocity.

We have opted for the second approach because the periodicity would put significant constraints on generation of fiber to fiber end gaps. The obvious effect of this second approach is that the cell must be sufficiently long; the value of which will be determined later.

The fibers in the system are now assumed to remain aligned and move in longitudinal direction with transverse plane contraction decreasing spacing s as needed to satisfy the incompressibility of the fluid as shown in Fig. 6. Each fiber i will act on its neighbor j through a force Fij. We will neglect inertia effects and write moment conservation for each fiber. For the highlighted fiber (i = 5) in Fig. 6 it will be simply

$$ {F}_{15}+{F}_{25}+{F}_{35}+{F}_{45}=0 $$
(3)

Similar equation may be written for every fiber in the system. Now, to determine velocity of fibers we need to realize that we can relate the forces with velocity difference between neighboring fibers i and j, resin viscosity η and their specific geometrical configuration:

$$ {F}_{ij}={F}_{ij}\left({v}_i-{v}_j,\eta, geometry\right) $$
(4)

We can substitute Eq. (4) in Eq. (3) for each fiber, constrain the velocities at the cell ends that are known and solve the system of equations. The actual simplicity or complexity of this system depends on how we model (or simplify) the resin viscosity and resin flow between fibers (fiber-fiber interaction).

Forces between two fibers

To create and model a fairly large fiber system which can be deformed in significant number of time steps, and to run the model for significant number of random realizations we need to accept limitation on reaction force between any two fibers which overlap in some cross section. In theory we might (for Newtonian fluids) just resolve the function in Eq. (4) by actually evaluating the resin flow by forcing the motion of a single fiber in some CFD package and evaluating the forces on other fibers by Stokes flow solver. This approach would, however, incur heavy performance penalty. To avoid this burden, we will use a simplified form of this expression. These simplifications stem from the geometric constraints of fiber bed with high fiber volume fraction: Fiber bed deformation can be essentially approximated by two modes:

  1. 1.

    Fibers slide relative to each other along the fiber direction. This happens when the system is extended in fiber direction or if the system shears in longitudinal/transverse plane. In both cases, there is relative shearing in the resin layer between fibers in which resin transfers the force from one fiber to its neighbor. As the flow is essentially unidirectional, the actual flow velocity profile may be easy to compute, but the coupling between multiple fibers may complicate this and we will approximate this further. Also, if system extends in fiber direction, cavitation flows may be possible to move the resin from between the fibers to growing spacing between their ends, but in this work we will not consider this additional physics as it is not trivial to address this in random fiber configurations.

  2. 2.

    The gap between fibers in transverse direction deforms from the original configuration but fibers remain parallel. Again, force is transferred by deforming resin layer but there is insignificant magnification. This is not necessary to model the system extension in transverse direction as it will not contribute to forces in longitudinal extension. Currently, we do not study this phenomenon and we accept previously reported relationships between effective shearing and transverse extensional viscosity [7].

We will model the first mentioned case to analyze extension and shear along fibers in a randomized “unit” cell. The force acting between two relatively sliding fibers must follow certain rules:

  1. i.

    It is directly proportional to resin viscosity, relative velocity of two fibers and the current length of the overlap oij.

  2. ii.

    It is inversely proportional to the distance between the fibers.

$$ {F}_{ij}={C}_{ij}\left({\alpha}_{ij}\right)\eta \frac{\left({v}_j-{v}_i\right)}{\left(s-d\right)}{o}_{ij} $$
(5)

This proportionality will require a coefficient Cij, which will be definitely dependent on the “angle of contact” between two fibers. Within this angle, the shearing flow is assumed to be controlled exclusively by the closest neighboring fibers and decoupled from motion of other surrounding fibers. For regular fiber cells this would be 90 degrees for quad and 60 degrees for hex spacing, for irregular cells some approximation will be called for (Fig. 7).

Fig. 7
figure 7

The flow cell is influenced only by two closest fibers. (a) Square arrangement (b) Hex arrangement and (c) General Arrangement. The determination by bi-sectors as shown in (c) has some limitations and this paper does not deal with cells randomized in the cross-section plane

Full size image

Note that once there is any non-uniformness in the cell, eq. (5) is an approximation. The true “decoupling” happens only for perfectly regular cells where it is ensured by the flow pattern symmetries/antisymmetries. As such, if we apply CFD approach to a selected random cell, we might see certain effect of general arrangement on Cij, resulting in some variation for same “angle of contact” value. As we consider only “regular cells” this influence can be ignored.

For regular cells, the coefficient can be determined by calculating one-dimensional shearing flow in the gap between fibers as was done before [7, 14] with various levels of detail. For such regular arrangements, it would not be necessary to build a 3D model of the unit cell. For fully random cell, however, the assumption does not quite hold. Modeling for such cells can be undertaken as it will provide not only the coefficients, but also information about their possible variation. However, CFD models would need to be fairly large and the evaluation would be daunting as the deformation/flow coupling would need to be included. For this work, we assume regular transverse arrangement, square or hex with uniform shearing throughout the flow domain which yields a very simple relation between force and velocity

$$ {F}_{ij}=\left({\alpha}_{ij}.d/2\right)\eta \frac{\left({v}_j-{v}_i\right)}{\left(s-d\right)}{o}_{ij} $$
(6)

Here, the angle αij is π/2 or π/3, for square and hexagonal arrangement, respectively. Note that for the fiber arrays regularly spaced in cross-section plane any inaccuracy in this coefficient just poses a multiplicative constant (of order 1) for effective viscosity values. Also note that for randomly spaced fibers – even in regular grid – it is not quite possible to decouple the flow between individual fiber pairs so we will be limited to applying Eq. (6) with Newtonian viscosity.

Extensional viscosity

To study the extensional behavior of a system with random fiber distribution, the unit cell is constructed as shown in Figs. 8 and 9. Notably, the cross section remains regular but in each chain of fibers the offset and gaps between fibers can be generated randomly as shown by the schematic on the right side in Fig. 8. One could also vary the location of the fiber chains or of the individual fibers within the chain, but in this work we did not apply that perturbation.

Fig. 8
figure 8

The square packed unit cell of short fibers. The cross-section arrangement is regular, but the individual fiber chains have randomly varying offset and gaps between fiber ends. Note that the latter influences the fiber spacing in cross section (the left schematic) if fiber volume fraction is prescribed

Full size image
Fig. 9
figure 9

The hexagonally packed unit cell of short fibers. Note that the cell is no longer orthogonal and two fibers are mirrored to two positions to accommodate hexagonal connectivity

Full size image

The viscosity is calculated by forcing a uniform extensional deformation by locking the fiber segments that cross one face of the unit cell and move the fiber segments that cross the opposite face of the unit cell with constant velocity. The net forces acting on the set of fixed fibers crossing one unit cell end are summed and divided by the corresponding cross-sectional area of the unit cell face to calculate the applied stress. Applied velocity divided by cell length provides the strain rate and the ratio of stress to strain is the viscosity.

Size of unit cell

There are two characteristic sizes of the unit cell. One is in the cross sectional direction, and is given by number of fiber chains considered. This size is limited by material thickness, and there cannot be more fibers in this direction than physically possible. The unit cell is periodic in the cross-sectional plane, and thus can be used to determine mean values for thicker material by repetition, though the standard deviation values depend on this size.

Along the fibers, the random non-uniform gaps prevent one from generating periodic structure along the fiber chains. Thus, one has to provide “sufficiently long” cell to overcome the effects of the fibers that are locked in the unit cell faces instead of proper periodic boundary conditions. One can select the in-plane dimensions to be very small but that does not necessarily reflect the larger system. Also, as random values are used for offsets and gaps, one should explore how the number of realizations influence the results.

In this section we address the following three questions:

  1. 1.

    How large should the periodic cell be in the cross-sectional plane to ensure that the predicted mean extensional viscosity is invariant? Obviously, sufficient increase in the cell size will reduce the standard deviation to zero but the physical system size, as, say, the ply thickness might be limited to 10 fibers, will limit the size of cell to be considered. We, however, need to determinate if the mean value will become constant before limiting size is reached otherwise the standard deviation would not be sufficient to describe the variability of the property. Also, free edge of the cell must be considered instead of a periodic BC if the physical system thickness is reached by a required single cell thickness.

  2. 2.

    How long should the cell be to predict invariant viscosity? Does the fact that the edges are locked and extended at fixed rate influence the result? Does the standard deviation reach invariant state in that case?

  3. 3.

    How many realizations are needed before the mean viscosity value and its standard deviations converge?

From computational viewpoint, one would like to keep the system as small as possible, but ensure that it is large enough to describe the randomness introduced in the unit cell due to the spacings (gaps) and overlaps between the fibers within the cell.

Number of realizations

To determine the necessary number of realizations, we executed the sequence of random generation of gaps and offsets, evaluated the viscosity in the initial configuration (the cell was not deformed) and processed the resulting data sets. These were then compared with the results from significantly larger data set. The studies were initially conducted for no end-to-end gaps and the presented results are for these cases unless stated otherwise.

The resulting standard deviation stabilized after 100 to 200 realizations, the mean value much sooner. Therefore, we chose to work with 200 realizations when standard deviation needed to be evaluated. Table 1 compares results from several 200 sample realizations with one containing 2000 sample realizations. These were run for 10 × 10 square cells with cell length equal to five fiber lengths.

Table 1 Comparison of mean relative viscosity w.r.t. resin voscosity and standard deviation obtained for several 200 sample sets and compared with one 2000 sample set
Full size table

The mean value for 200 samples is within 0.3% of the larger set, the standard deviation value within 5% which we consider as sufficient considering the assumptions used for this model. The relative viscosity is with respect to the viscosity of the matrix material. The introduction of end to end gaps between fibers slightly increases the variability of these values.

Size of cell

The previous evaluations were performed for 10 × 10 cells of certain length. Different cell sizes were considered to determine whether the predicted viscosity value depends on the cell size and what cell size is sufficient. The effect of the cell size is depicted in Fig. 10.

Fig. 10
figure 10

Relative extensional viscosity (Effective viscosity/Resin Viscosity) and standard deviation for 200 sample realizations of various sizes of square and hex cells at vf = 60%, L/d = 1000, no end-to-end gaps

Full size image

It is obvious that the mean value is steady from very small cell sizes (6 × 6 would do). The standard deviation still decreases after 6 × 6 cell size. It seems to plateau after 8 or 10 cells but it really keeps slowly decreasing. For infinite cell the standard deviation should (and does) go to zero. To determine how many fibers to consider for standard deviation we are limited by the material dimensions and, for the materials of interest we will consider the cell size to be 10 – the sheets will have 10 fibers across the thickness (fiber diameter ~ 10 μm so the sheet thickness will be ~0.1 mm). For other material thickness we would need to reevaluate the standard deviation.

Length of the “periodic” cell

The fibers which touch the top and bottom surface of the unit cell are locked. On one side they are stationary, the other side is moved by a prescribed velocity. This replaces the periodicity condition which is not suitable because of the variable end-to-end fiber gaps.

To eliminate the end effects, the cell must be sufficiently long. Figure 11 shows the predicted mean relative extensional viscosity as a function of unit cell length and maximal gap size. By gradually increasing the length of the cell we determined that (i) even for fairly short cell the effect is not dramatic and (ii) the Lcell/Lfiber of 5 or 6 is perfectly sufficient for extensional viscosity modeling and further extension of the cell length does not change the results significantly.

Fig. 11
figure 11

Mean relative extensional viscosity for 200 sample realizations for various unit cell lengths with no or 10% maximal end-to-end fiber gap (hex cells at vf = 60%, L/d = 1000)

Full size image

The effect of free boundary

It is easy to modify the described model to include the thickness limitation of 10 fiber layers (or whatever number is significant). Instead of mirrored periodic boundary, we do not include any contact and force transfer along the free boundaries (Fig. 12), reducing the periodicity to two boundaries out of the four.

Fig. 12
figure 12

Unit cell configuration with free boundary for square (left) and hexagonal (right) fiber arrangement. No force is transferred across the top and bottom boundaries which represent the material ply surfaces

Full size image

The results show similar trends as those with periodic boundaries. The free boundary demonstrates reduction of viscosity (“stiffness”) of the system. For hexagonal arrangement (vf = 60%, L/d = 1000) the relative viscosity decreases from 1.82 × 106 to 1.70 × 106 and for square arrangement from 2.34 × 106 to 2.21 × 106. The standard deviation scales almost proportionally, from 4.95 × 104 to 4.56 × 104 for hex packing and from 7.85 × 104 to 7.60 × 104 for square packing respectively. No significant changes in behavior of numerical model were observed.

The resulting viscosity distributions

In this section we will examine the dependence of effective viscosity on material and model parameters. Four “model” parameters are considered

  1. 1.

    Fiber arrangement within the unit cell

  2. 2.

    The relative size of end-to-end gap g (Fig. 6) relative to fiber length

  3. 3.

    Fiber aspect ratio L/D

  4. 4.

    Fiber volume fraction vf.

These are features of the physical material to be modeled and can be related to the physical values, but in the absence of the material, the effect may be studied to determine trends needed to optimize the material.

The effect of Fiber arrangement

In our model we have so far utilized only two regular arrangements, hexagonal and square. Both can be seen as an idealization and both could be perturbed to randomize the cell a bit more. As was already shown above, the values of effective extensional viscosity vary between these two cases with the square packing predicting higher values and wider distributions (higher standard deviation). Cumulative plot of predicted relative extensional viscosity values (vf = 60%, L/d = 1000, no gaps) is shown in Fig. 13. The plotted viscosity is the “initial viscosity” value, evaluated at the inception of deformation by applying the strain rate to undeformed (strain =0%) cell at time equal to zero.

Fig. 13
figure 13

Cumulative plot of predicted initial viscosity values (117 realizations), evaluated at the inception of deformation by applying the strain rate to undeformed cell at time equal to zero which depends on the unit cell configuration. Note that the square and hexagonal distributions do not overlap

Full size image

This shows that the square fiber arrangement model (i) predicts larger viscosity values and (ii) predicts wider distribution. Note that there is no overlap between the two distributions. It seems likely, though we cannot prove it rigorously, that the hex arrangement presents a lower bound. The square one is possibly an upper bound on the system stiffness (viscosity).

The effect of end-to-end fiber gaps

As long as the fiber volume fraction of suspension remains constant, the introduction of end-to end gaps – whether in the original random generation or by stretching the material as examined later – has two obvious effects on the mechanics:

  1. 1.

    The overlap between neighboring fibers decreases, reducing the viscous resistance (oij in Eq. (5)).

  2. 2.

    The distance between neighboring fibers (s-d in Eq. (5)) reduces, increasing viscous resistance of the system

As these two constitute competing mechanisms, the behavior on mean viscosity is uncertain unless we exercise the model. The results of such an exercise are shown in Fig. 14. Note that there is a limit on the gap size which is the dictated by the desired fiber volume fraction.

Fig. 14
figure 14

Relative initial viscosity evaluated at the inception of deformation by applying the strain rate to undeformed cell at time equal to zero as a function of end-to-end fiber gaps (vf = 60%, L/d = 1000). Low and High are determined using twice the standard deviation

Full size image

The figure shows that the dependence of mean viscosity value on gaps is not particularly strong, and for hex arrangement is insignificant. For smaller fiber volume fraction the trend may be actually reversed. However, it shows something that is not quite so obvious: The standard deviation increases significantly with the gaps, resulting in significant local variability. From forming perspective, this may have serious effects as a simple stretching might result in localized, very non-uniform deformations.

The effect of Fiber length

The L/D ratio’s effect has been studied previously for regular cells with the effect that the extensional viscosity scales with (L/D)2. This means that the system is rather resistant to extension for any but very short fibers. Our results are consistent with this reported finding (Fig. 15) [7]. They obviously correspond with eq. (5) as both the overlap and the relative velocity increase linearly with the fiber length, resulting in the quadratic growth.

Fig. 15
figure 15

Relative initial viscosity evaluated at the inception of deformation by applying the strain rate to undeformed cell at time equal to zero as a function of fiber aspect ratio (vf = 60%, L/d = 1000, square packing, no gaps). Power fit shows excellent correlation with reported results [7] and also that the relation extends to the standard deviation as well

Full size image

However, in addition to the verification of the known relationship of viscosity with aspect ratio, we can also show that the standard deviation in viscosity distribution follows the same trend, though it will shift to larger values with the introduction of gaps. This suggests that making the fibers longer (or shorter) does not result in more uniform forming properties.

The effect of Fiber volume fraction

Again, the relation is similar to the relation predicted by the previously reported deterministic models [7] (Fig. 16). The particular shape depends on fiber packing and the form accepted to describe fiber to fiber force.

Fig. 16
figure 16

Relative initial viscosity evaluated at the inception of deformation by applying the strain rate to undeformed cell at time equal to zero as a function of fiber volume fraction (L/d = 1000, no gaps). The same trend is seen for both the mean value and the standard deviation

Full size image

The standard deviation follows the same curve (within the accuracy of our 200 sample realization) as the mean value, so again the forming properties will not be more uniform if the fibers are more or less packed together. As the viscosity is inversely proportional to the fiber spacing (Eq. (5)) this is to be expected.

Viscosity and deformation

The initial fiber cell configuration is random within the constraints we have listed in previous sections. This includes the gaps between fiber ends which may be generated randomly. As the extension is applied, the structure, however, deforms in deterministic fashion, modifying the underlying geometrical arrangements as fibers slide past each other and their transverse distance reduces while the end-to-end gaps increase in size or are created. Thus, it is feasible that at the end of deformation the structure of fiber gaps may not be quite fully random.

As far as the transverse distance reduction is concerned, we assume that the cell is incompressible as the resin is incompressible and fiber deformation is neglected. To accommodate this, the distance between fiber chains is reduced as the material cell is extended. The cell is contracted uniformly in transverse directions. The contraction moves fibers closer to each other which would, in the end, cause the forces to become singular. In this work we avoided this situation by limiting the deformation to 10–15% extension.

During the actual deformation, the contraction would require some matrix redistribution which would, in turn, apply some additional forces on fiber segments. This is neglected within the current work.

In this section, we want to briefly examine two effects:

  1. 1.

    How does the extensional viscosity vary with the system deformation?

  2. 2.

    How does the microstructure develop during the deformation process?

Viscosity variation during the deformation process

For high fiber volume fraction (60%), the viscosity during the extension increases slightly as shown in Fig. 17. The contraction overrides the reduction in overlap length, more for square arrangement of cells. In that case, the fibers are closer and are approaching to touch each other much sooner.

Fig. 17
figure 17

Relative extensional viscosity during the deformation for Square and Hex cells at vf = 60%, L/d = 1000. These are individual realizations. Viscosity is related to the reduced cross-section

Full size image

With rising mean value, the standard deviation of viscosity remains similar to the initial distribution. The effects of free boundary appear to be limited to shifting the mean value as well.

The change of mean value during the deformation depends on the fiber microstructure arrangement and fiber volume fraction. Extension shortens the fiber overlaps – which decreases the effective viscosity but brings fibers closer to each other which increases the effective viscosity value. The relative effect of these two opposing phenomena depends on the fiber volume fraction. Thus, for high fiber volume fraction, the latter is more significant and there is increase of effective viscosity during deformation. For smaller fiber volume fraction (Fig. 18) the transverse distance between fibers is less important and the dependence is reduced. If we compute the behavior for even smaller fiber volume fractions than considered herein, the trend reverses and viscosity starts to decrease with the deformation as volume fraction drops.

Fig. 18
figure 18

Relative extensional viscosity during the deformation for Square and Hex cells at different fiber volume fractions, L/d = 1000. Viscosity is related to the reduced cross-section

Full size image

Microstructure variation during the deformation process

The evolution of the microstructure within the unit cell can be followed during the deformation process by tracking the fiber positions with time. This is shown in Fig. 19. The processing of the data is however non-trivial. The visual inspection reveals that

  1. 1.

    The end-to-end gaps extend fairly non-uniformly. For idealized periodic cell they would remain of the same size, in random cell some open more than others.

  2. 2.

    The short overlaps in neighboring chains tend to disappear. In other words, the ends show some propensity to align, which may have adverse effects on structural properties of the formed composite.

Fig. 19
figure 19

Hex fiber cell (at vf = 60%, L/d = 1000) in original configuration and after 10% longitudinal extension. Matching fibers are color coded. Careful look reveals that the gaps between fibers extend non-uniformly

Full size image

Other modes of deformation

The two-dimensional (sheet) anisotropic viscosity is defined by three values. These can be related to the extensional viscosity in fiber direction examined above, shearing viscosity in longitudinal and transverse plane and transverse extensional viscosity. The previous work [7] suggests that there is a simple (constant) relation between the last two values, so we will briefly look at the shearing behavior only.

Longitudinal-transverse shearing deformation and the unit cell

In this section we briefly examine the application of shearing deformation to the unit cell model we developed to see what effect the random cell structure has on shearing behavior. This is straightforward as the model can be modified to this purpose easily. We will for the time being assume that [7] is correct and the transverse extension would behave similarly.

Possible approaches

We want to utilize the same model we applied to extensional deformation. To apply shearing deformation to the cells shown in Fig. 8, one has two possible approaches as shown in Fig. 20:

  1. 1.

    Apply the shearing deformation along one of the walls while locking the opposite wall in place. At the same time apply periodicity at the ends. This approach has a drawback that the periodicity restricts the end-to-end fiber gaps as we need a periodic geometry in the longitudinal direction.

  2. 2.

    Apply the deformation as before but lock the end fibers to the shearing frame. This is of course over-constrained (stiffer) system, but one would expect that if the cell is made sufficiently long, the end effects will eventually become negligible.

Fig. 20
figure 20

Possible application of shear to the unit cell developed for extensional deformation

Full size image

We decided to implement approach 2 as we considered the unconstrained variation of gaps between fiber ends important.

Size of the unit cell

The end effects mean that the unit cell must be long enough to make them insignificant. The effect of the size was studied by evaluating the relative shearing viscosity for increasingly long cells (Fig. 20) In this case, the sample size was reduced to 20 realizations to save the computational time as the cells were becoming very large. This implies limited accuracy of standard deviation prediction which explains the rough curve for standard deviation in Fig. 21.

Fig. 21
figure 21

Model predicted relative shearing viscosity depending on the relative length of the unit cell

Full size image

The results suggest that the end effects require relatively long (and slow to model) unit cell. We opted for L/Lfiber = 20.

Resulting distribution

The behavior of relative shearing viscosity has been computed for the original random configuration. It corresponds reasonably to the previous models of periodic cells [7, 14]:

  • The magnification factor is moderate (~10)

  • There is no dependence on fiber aspect ratio

  • The dependence on fiber volume fraction is moderate unless getting close to maximal packing (Fig. 22)

Fig. 22
figure 22

Predicted relative shearing viscosity dependence on fiber volume fraction. Square packing, 10 × 10 cell, L/D = 1000, end-to-end gaps maximally 10% of fiber length with 20 realizations

Full size image

The random variations proved rather insignificant in the case of shearing viscosity:

  • The end-to-end gap slightly increased the viscosity (around target 60% fiber volume fraction) because of reduction of transverse fiber distance

  • The standard deviation is less than 1% of mean value.

This implies that there is little in local variability of shearing viscosity on the length scale of 10 fibers (material thickness) and that the effects of random distribution are far more significant for longitudinal extension.

Conclusions

We presented a micromechanical unit cell model to study the effective forming properties of highly concentrated suspension of long, discontinuous fibers based on the material microstructure. Compared to the previous work, the model is based on significantly larger and partially randomized unit cells and allows one to predict both the mean material response (effective viscosity) and its variability introduced by microstructural variability. The presented results analyze the effects of random fiber overlaps and end-to-end gaps, but other random parameters can be introduced into the model, for example perturbed fiber spacing to quantify the influence on the effective property.

We fully expected that the introduction of variability into the cell will produce variability in effective material parameters at certain unit cell length-scale, considered to be about 10 fiber diameters. This length-scale is physically related to the thickness of analyzed material and non-uniformity on this length scale cannot be easily smoothed out further during forming.

With respect to the extensional viscosity the variability proved to be significant. Moreover, it increases with additional material extensional deformation and such behavior may have significant effect on material forming.

The dependence of mean value on the usually considered material parameters (fiber aspect ratio, fiber volume fraction) was determined and shown to match the dependence predicted by previous models, using simple regular microcells [7]. The value of standard deviation seems to follow the same dependence as the mean value.

With respect to longitudinal-transverse shearing, the analyzed variability does not produce significant variability in the effective cell behavior and its dependence on random perturbation of material microstructure is virtually nonexistent. This result might transfer to transverse extension as argued before [7], but we did not study this mode of deformation as the presented model would require significant modification.

The studied random variations of the unit cell – end gaps and overlaps – are just a subset of possible geometrical disturbances. Two additional mechanisms to consider would be irregular fiber transverse spacing and fiber misalignment. The former can be added to our model. The latter may require numerical modeling.

Also note that we did not examine the effects of finite shearing deformation on end-to-end fiber gaps similar to the way we examined the effects of extension. Since that may have effects on material performance after forming, it should be definitely addressed despite the fact that the randomness effect on viscosity is negligible.