Machine learning assisted discovery of effective viscous material laws for shear-thinning fiber suspensions

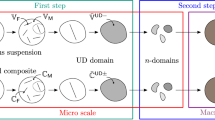
Abstract

In this article, we combine a Fast Fourier Transform based computational approach and a supervised machine learning strategy to discover models for the anisotropic effective viscosity of shear-thinning fiber suspensions. Using the Fast Fourier Transform based computational approach, we study the effects of the fiber orientation state and the imposed macroscopic shear rate tensor on the effective viscosity for a broad range of shear rates of engineering process interest. We visualize the effective viscosity in three dimensions and find that the anisotropy of the effective viscosity and its shear rate dependence vary strongly with the fiber orientation state. Combining the results of this work with insights from literature, we formulate four requirements a model of the effective viscosity should satisfy for shear-thinning fiber suspensions with a Cross-type matrix fluid. Furthermore, we introduce four model candidates with differing numbers of parameters and different theoretical motivations, and use supervised machine learning techniques for non-convex optimization to identify parameter sets for the model candidates. By doing so, we leverage the flexibility of automatic differentiation and the robustness of gradient based, supervised machine learning. Finally, we identify the most suitable model by comparing the prediction accuracy of the model candidates on the fiber orientation triangle, and find that multiple models predict the anisotropic shear-thinning behavior to engineering accuracy over a broad range of shear rates.

1 Introduction

1.1 State of the art

Viscosity models for fiber polymer suspensions are widely used in molding process simulations of composite parts [1], which play a major role in the lightweight design of engineering systems, i.e., in the automotive, aerospace, and energy sectors [2, 3]. Molding process simulations are an established tool in composite part engineering, partly because of the industrial benefits of digital twins [4] and virtual process chains [2, 5, 6]. In molding simulations for fiber reinforced plastics, accurate modeling of the suspension viscosity is crucial to predict various parameters of engineering interest. The suspension viscosity influences manufacturing process parameters [7, 8], as well as fiber orientation and fiber volume distributions [9]. Consequently, flow fields [10] and final part properties [10, 11] are also affected by the suspension viscosity. However, finding analytical models for the suspension viscosity is a challenging task, partly because of the locally inhomogeneous flow field inside the suspension, as well as the hydrodynamic interactions [12] and mechanical contacts [13] between the fibers. Furthermore, the suspension viscosity also depends strongly on the local microstructure, i.e., the fiber geometry [14], the fiber volume fraction [15], and the fiber orientation state [16]. As far as external influences are concerned, the loading direction, the shear rate [17, 18], and the melt temperature [19] also affect the suspension viscosity. Especially for suspensions with non-Newtonian solvents and fiber concentrations beyond the semi-delute regime, capturing the large variety of effects in a single analytical model is a difficult task.

Based on the work by Batchelor [20, 21] on fiber suspensions with Newtonian matrix behavior, Goddard [22, 23] proposed self-consistent analytical models of dilute and semi-dilute fiber suspensions with power-law shear-thinning matrix behavior. While the model predictions agree well with experimental results qualitatively, as found by Goddard [24] and Mobuchon et al. [25], quantitative accuracy can still be improved. Later, Souloumiac and Vincent [26] incorporated fiber orientation distributions into a self-consistent modeling approach for dilute, semi-dilute and concentrated fiber suspensions. However, in a comparison with experimental results in a convergent channel flow, the prediction accuracy of the model varies strongly with the shear rate and the fiber volume fraction. More recently, Ferec et al. [27] proposed semi-analytical and numerical self-consistent models for fiber suspensions with Ellis and Carreau-type matrix behavior. Even though the semi-analytical model was able to accurately replicate steady state solutions of a simple shear flow simulation, the models have yet to be successfully applied in other flow scenarios. Focusing on the concentrated and the hyperconcentrated regime, Pipes et al. [28,29,30,31] developed models of collimated fiber suspensions, including uniformly distributed fiber misalignments with an orientation averaging [32, 33] approach. The model predictions agree well with experimental results by Binding [34], but the applicability of the model is restricted to collimated fiber arrays. To improve existing molding simulation solvers through small modifications, Favaloro et al. [35] combined orientation averaging with a deformation mode and microstructure dependent informed isotropic viscosity, and successfully predicted the shell-core effect common in fiber suspension molding. However, the error of the model depends strongly on the applied deformation mode and approximated anisotropic viscosity. Thus, including recent developments [36, 37] it proves difficult to achieve high model prediction accuracy over the wide variety of application requirements in engineering systems.

In addition to the challenging analytical treatment, the investigation of fiber suspensions via rheological experiments is also difficult. Because of the transient effects during fiber suspension molding, including fiber breakage and change of orientation state, it is difficult to determine the suspension viscosity for a particular microstructure and load case [34, 38]. Furthermore, interaction of fibers with measurement devices [39] can affect the measured quantities.

In light of the analytical and experimental difficulties involved when studying the viscosity of fiber suspensions with non-Newtonian solvents, computational approaches provide insights and observations that are otherwise hard to obtain. Švec et al. [40] combined the lattice Boltzmann method for fluid flow, an immersed boundary procedure for the interaction between fluid and rigid particles, and a mass tracking algorithm for the free surface representation to simulate slump tests of a suspension of rigid spherical particles and fibers suspended in a Bingham-type fluid. In comparison with a slump test of pure matrix material, they observed a smaller spread and increased height in the slump test of the suspension, suggesting an increased effective yield stress. Using a Finite Element Method (FEM) based approach, Domurath et al. [41] investigated the rheological coefficients of the transversely isotropic fluid equation by Ericksen [32] in the context of rigid fibers suspended in a power-law fluid. In a simple shear flow, they found the model by Souloumiac and Vincent [26] to overpredict the orientation dependence of a rheological coefficient. Combining the RVE method [42] and Fast Fourier Transform (FFT) based computational techniques [43], Sterr et al. [18] extended work by Bertóti et al. [44] on Newtonian fiber suspensions to suspensions with non-Newtonian solvents. They visualized the anisotropic viscosity tensor in the case of a Cross-type matrix fluid and studied the effects of fiber volume fraction and shear rate on the suspension viscosity.

1.2 Contributions

In this article, we combine high fidelity, FFT-based computational methods and a supervised machine learning strategy to discover material models for the effective viscosity of shear-thinning fiber suspensions. To do so, we study the anisotropic and shear rate dependent effective viscosity of fiber suspensions with a Cross-type matrix behavior and a fiber volume fraction of 25%. In section 2 we outline the setup for the FFT-based computational investigations, where we compute the effective material response for 109 different fiber orientation states and a variety of loading states. In terms of computational scope, this constitutes a significant extension to previous FFT-based work on shear-thinning fiber suspensions, in which a single fiber orientation state was considered [18]. Based on the computational data, we visualize the suspension viscosity tensor in three dimensions and formulate an anisotropy criterion applicable in a non-linear setting using a loading direction and shear rate dependent scalar viscosity, see section 3. We find that the anisotropy of the suspension viscosity shows a significantly different shear rate dependence for different fiber orientation states. Also, for all investigated microstructures, we confirm that the anisotropy of the suspension viscosity depends on the degree of non-linearity of the matrix material, which was previously only studied for a transversely isotropic microstructure [18]. In section 4, based on the insights into the shear rate and orientation state dependence of the suspension viscosity, we formulate requirements a model of the suspension viscosity needs to fulfill. According to the formulated requirements we propose four models with different numbers of parameters, as well as different phenomenological and theoretical motivations. Using the ADAM algorithm, we employ supervised machine learning techniques for non-convex optimization to learn the parameters of the model candidates. Overall, three models achieve similar maximum validation errors below 5.15 %, while one model based on superposition and orientation averaging performs unfavorably.

2 A computational study of the effective behavior of shear-thinning fiber suspensions

2.1 Description of fiber orientation states

Since the effective behavior of a fiber suspension depends on the fiber orientation statistics in the suspension, a mathematical description of the orientation state is essential to the study of fiber suspensions. In the following, we use a fiber orientation distribution function [45]

$$\begin{aligned} \rho : S^2 \rightarrow {\mathbb { R}}, \quad {\varvec{ n}}\mapsto \rho ({\varvec{ n}}), \end{aligned}$$

(2.1)

to encode the probability that fibers are oriented in direction ${\varvec{ n}}$ on the 2-sphere $S^2$, and thus describe the orientation state of a fiber suspension. The temporal and spatial evolution of the orientation distribution function $\rho$ is governed by a partial differential equation, the Fokker–Planck equation [46]. However, in component scale molding simulations, computing the evolution of the orientation distribution function $\rho$ using the Fokker-Planck equation requires huge computational effort. Instead, it is common [1] to use the second order fiber orientation tensor [45, 47]

$$\begin{aligned} {\varvec{ N}}= \int _{S^2} {\varvec{ n}}\otimes {\varvec{ n}}\, \rho ({\varvec{ n}})\,\, \!\textrm{d}S({\varvec{ n}}), \end{aligned}$$

(2.2)

as a measure for the fiber orientation state. The tensor ${\varvec{ N}}$ is symmetric, positive semi-definite, and has unit trace, such that

$$\begin{aligned} N_{ii} = \lambda _1 + \lambda _2 + \lambda _3 = 1, \end{aligned}$$

(2.3)

where $\lambda _1$, $\lambda _2$, and $\lambda _3$ denote the eigenvalues of the tensor ${\varvec{ N}}$. By sorting the eigenvalues

$$\begin{aligned} {\lambda _1 \ge \lambda _2 \ge \lambda _3}, \end{aligned}$$

(2.4)

and considering equation (2.3), the bounds for the largest eigenvalue $\lambda _1$ are found as

$$\begin{aligned} 1 \ge \lambda _1 \ge \frac{1}{3}. \end{aligned}$$

(2.5)

Additionally, an upper bound for the eigenvalue $\lambda _2$ follows from positive semi-definiteness of the tensor ${\varvec{ N}}$, and a lower bound may be derived by eliminating $\lambda _3$ from equation (2.4) using equation (2.3), such that

$$\begin{aligned} \min \left( \lambda _{1}, 1 - \lambda _{1}\right) \ge \lambda _2 \ge \frac{1-\lambda _{1}}{2}. \end{aligned}$$

(2.6)

Thus, we may parametrize the tensor ${\varvec{ N}}$ by its two eigenvalues $\lambda _1$ and $\lambda _2$, and the rotation ${\varvec{ Q}}$ in terms of an eigendecomposition

$$\begin{aligned} {\varvec{ N}}= {\varvec{ Q}}\, {\varvec{\textrm{diag}}}(\lambda _1, \lambda _2, \lambda _3) \, {{\varvec{ Q}}}^{\textsf{T}}, \end{aligned}$$

(2.7)

where the ${\varvec{\textrm{diag}}}$ operator constructs a second order tensor in the standard basis of $\mathbb {R}^3$. By objectivity, the results of this article generalize to all rotations ${\varvec{ Q}}$, and for simplicity we choose

$$\begin{aligned} {\varvec{ Q}}= {\varvec{ I}}, \end{aligned}$$

(2.8)

where ${\varvec{ I}}$ is the second order unit tensor. Consequently, any second order fiber orientation tensor ${\varvec{ N}}$ may be encoded by a vector $\underline{\lambda }=(\lambda _1, \lambda _2)^{\textsf{T}}$, and represents a point in the fiber orientation triangle $S_{\textsf{T}}$ defined through equations (2.5) and (2.6), such that

$$\begin{aligned} S_{\textsf{T}}&{=}&\left\{ \underline{\lambda }{=} {(\lambda _1,\lambda _2)}^{\textsf{T}} \quad \Bigg |\quad 1\, {\ge }\, \lambda _1\, {\ge }\, \frac{1}{3} \quad \text {and}\right. \nonumber \\{} & {} \quad \left. \min \left( \lambda _{1}, 1 {-} \lambda _{1}\right) {\ge }\, \lambda _2 \ge \frac{1-\lambda _{1}}{2} \right\} . \end{aligned}$$

(2.9)

Following Köbler et al. [48], we use a CMYK coloring scheme to visualize the fiber orientation state within the fiber orientation triangle $S_{\textsf{T}}$. The isotropic, unidirectional, and planar isotropic orientation states represent the corners of the fiber orientation triangle and are colored cyan, magenta, and yellow, respectively.

2.2 Computational homogenization procedure

In this article, we consider incompressible, shear-thinning fiber suspensions, occupying a rectangular volume $Y \subseteq {\mathbb { R}}^3$. First, we give a short summary of the numerical procedure for the homogenization of shear-thinning fiber suspensions following Sterr et al. [18, §2]. We are interested in computing the effective viscous stress $\bar{\varvec{\tau }}\in \textsf{Sym}_0(3)$ of the suspension in response to an applied, effective shear rate tensor $\bar{{\varvec{ D}}}\in \textsf{Sym}_0(3)$, where $\textsf{Sym}_0(3)$ denotes the vector space of symmetric and traceless second-order tensors. For a pressure field $p: Y \rightarrow \mathbb {R}$, a solenoidal velocity field ${\varvec{ v}}: Y \rightarrow \mathbb {R}^3$ and a local viscous stress field

$$\begin{aligned} \varvec{\tau }= \mathcal {T}(\cdot ,\bar{{\varvec{ D}}}+ \nabla ^{\textsf{s}} {\varvec{ v}}), \end{aligned}$$

(2.10)

with associated stress operator

$$\begin{aligned} \mathcal {T}: Y \times \textsf{Sym}_0(3)&\rightarrow \textsf{Sym}_0(3),\end{aligned}$$

(2.11)

$$\begin{aligned} ({\varvec{ x}}, {\varvec{ D}})&\mapsto {\frac{\partial \Psi }{\partial {\varvec{ D}}}} {({\varvec{ x}},{\varvec{ D}})}, \end{aligned}$$

(2.12)

and dissipation potential ${\Psi : Y \times \textsf{Sym}_0(3) \rightarrow \mathbb {R}}$, the local balance of linear momentum without inertial effects

$$\begin{aligned} {\textrm{div}\ }{\varvec{\tau }} - \nabla p = {\varvec{0}}, \end{aligned}$$

(2.13)

needs to be fulfilled. In the context of suspensions with rigid inclusions, the local viscous stress $\varvec{\tau }$ in equation (2.13) is, constitutively, not well defined inside the rigid inclusions. We address this issue by changing to a dual formulation as follows. With the complementary dissipation potential

$$\begin{aligned} \Phi (\varvec{\tau }) := \sup \big \{\varvec{\tau }\cdot {\varvec{ D}}-\Psi ({\varvec{ D}}) \, | \, {\varvec{ D}}\in \textsf{Sym}_0(3) \}, \end{aligned}$$

(2.14)

arising as the Legendre–Fenchel dual of the dissipation potential $\Psi$, we search for minimizers of the variational problem

$$\begin{aligned} \left\langle {\Phi ( \cdot ,\varvec{\tau }) - \varvec{\tau }\cdot \bar{{\varvec{ D}}}} \right\rangle _Y \longrightarrow \inf . \end{aligned}$$

(2.15)

Here, $\left\langle {\cdot } \right\rangle _Y$ denotes the spatial average

$$\begin{aligned} \left\langle {\cdot } \right\rangle _Y \equiv \frac{1}{|Y|}\int _Y (\cdot )\,\, \!\textrm{d}{\varvec{ x}}\quad \text {with} \quad \ |Y| \equiv \int _Y \!\textrm{d}{\varvec{ x}}, \end{aligned}$$

(2.16)

and the infimum is taken over all stress fields $\varvec{\tau }$ satisfying the equilibrium equation (2.13). Minimizers of the variational problem (2.15) satisfy the Euler–Lagrange equation

$$\begin{aligned} {\mathbb { P}}_{\mathcal {E}}\left[ \frac{\partial \Phi }{\partial \varvec{\tau }} (\varvec{\tau })- \bar{{\varvec{ D}}}\right] = {\varvec{0}}, \end{aligned}$$

(2.17)

where ${\mathbb { P}}_{\mathcal {E}}$ refers to the $L^2$-projector onto the shear stresses satisfying the equilibrium equation (2.13). We refer to Bertóti et al. [44, §2] for a closed form expression of the action of ${\mathbb { P}}_{\mathcal {E}}$ in Fourier space. In case of suspensions with rigid particles the shear rate tensor ${\varvec{ D}}$ and hence the derivative ${\partial \Phi / \partial \varvec{\tau }}$ vanishes inside the particles. Thus, the formulation of the optimization problem (2.15) in terms of the complementary dissipation potential $\Phi$ is advantageous for numerical schemes based on the Euler–Lagrange equation (2.17). If the optimization problem (2.15) is convex, a minimizer can be found with, e.g., gradient descent [18], the Barzilai–Borwein method [49], or Newton-CG [50, 51] approaches. Finally, the effective viscous stress $\bar{\varvec{\tau }}$ can be computed by spatial averaging, such that

$$\begin{aligned} \bar{\varvec{\tau }}= \left\langle {\varvec{\tau }} \right\rangle _Y. \end{aligned}$$

(2.18)

2.3 Computational study setup and material parameters

To study the material response of shear-thinning fiber suspensions with a variety of microstructures, we generated fiber suspension microstructures for 109 points of the fiber orientation triangle $S_{\textsf{T}}$ (2.9), see Figs. 1a and 2, using the sequential addition and migration method [52]. Building upon the investigations in Sterr et al. [18], a commercially available polyamide 6 [53] was chosen as the matrix material, and a Cross-type material law

$$\begin{aligned} \eta (\dot{\gamma }) = \eta _{\infty } + \frac{\eta _0-\eta _{\infty }}{1 + (k\dot{\gamma })^m} , \end{aligned}$$

(2.19)

was fitted to the available material data for shear rates $\dot{\gamma }$ in the interval ${[1.7,16300] \, \text {s}^{-1}}$ at a temperature of ${250^\circ \text {C}}$. The resulting model parameters are collected in Table 1.

Table 1 Parameters of the Cross-type material law (2.19) for a commercially available polyamide 6 [53]

The viscosities $\eta _0$ and $\eta _\infty$ define the material behavior for shear rates $\dot{\gamma }=0$ and $\dot{\gamma }\rightarrow \infty$, respectively, while the parameters k and m control the non-linear transition between the viscosities $\eta _0$ and $\eta _\infty$. The suspension microstructures were discretized on a staggered grid [54] using composite voxels [55] with a general dual mixing rule for the special case of rigid particles [18]. The resulting non-linear system of equations was solved with a Newton-CG approach. To limit the required computational effort, we restricted to microstructures with a fiber volume fraction $c_{\textsf{F}}= 25 \%$, where all fibers have equal length $\ell$ and diameter d. More precisely, we prescribed an aspect ratio $r_{\textsf{a}}= \ell /d$ of 10. The resolutions and sizes of the microstructure volume elements were chosen according to the investigations in Sterr et al. [18], such that the number of voxels per fiber diameter is $v/d=15$ and the edge length of the cubic volume elements is $L = 2.2\ell$.

Fig. 1

Fiber orientation triangle $S_{\textsf{T}}$ in CMYK coloring with 109 evaluation points (a), and material data with Cross-type fit for Ultramid®B3K (b)

For each macroscopic scalar shear rate $\dot{\gamma }$ in the set of studied shear rates $S_{\dot{\gamma }}$, such that

$$\begin{aligned}{} & {} \dot{\gamma }\in S_{\dot{\gamma }}= \left\{ a \cdot 10^b \ \text {s}^{-1}| \ a=1,2,5; \ b = 1,2,3,4\right\} \cup \nonumber \\ {}{} & {} \left\{ 10^5 \, \text {s}^{-1}\right\} , \end{aligned}$$

(2.20)

we investigate the six load cases collected in the matrix $\underline{\underline{\bar{D}}}$ in Mandel notation

$$\begin{aligned} \underline{\underline{\bar{D}}}= \dot{\gamma }\sqrt{\frac{2}{3}} \left[ \begin{array}{rrrrrr} 1 &{} -\frac{1}{2} &{} -\frac{1}{2} &{} 0 &{} 0 &{} 0\\ -\frac{1}{2} &{} 1 &{} -\frac{1}{2} &{} 0 &{} 0 &{} 0\\ -\frac{1}{2} &{} -\frac{1}{2} &{} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \sqrt{\frac{3}{2}} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \sqrt{\frac{3}{2}} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \sqrt{\frac{3}{2}} \end{array}\right] . \end{aligned}$$

(2.21)

Here, the set of studied shear rates $S_{\dot{\gamma }}$ is intended to cover a broad variety of engineering process shear rates, and is motivated by the typical shear rates in compression molding, standard injection molding, as well as thin-wall and micro molding [56, 57]. For shear rates $\dot{\gamma }$, where the matrix behavior is mostly Newtonian and the superposition of material responses is valid, we compute and collect the components of the effective viscosity tensor $\bar{{\mathbb { V}}}$ in a matrix ${\underline{\underline{\bar{V}}}}$ with

$$\begin{aligned} \underline{\underline{\bar{\tau }}}={\underline{\underline{\bar{V}}}}\ \underline{\underline{\bar{D}}}, \quad \text {i.e.,} \quad {\underline{\underline{\bar{V}}}}=\underline{\underline{\bar{\tau }}}\ \underline{\underline{\bar{D}}}^{\dagger }. \end{aligned}$$

(2.22)

Here, $(\cdot )^{\dagger }$ stands for the Moore–Penrose pseudoinverse, and $\underline{\underline{\bar{\tau }}}$ collects the computed effective stresses

$$\begin{aligned} \underline{\underline{\bar{\tau }}}= \left[ \begin{array}{rrrrrr} \bar{\tau }_{11}^{(1)} &{} \bar{\tau }_{11}^{(2)} &{} \bar{\tau }_{11}^{(3)} &{} \bar{\tau }_{11}^{(4)} &{} \bar{\tau }_{11}^{(5)} &{} \bar{\tau }_{11}^{(6)}\\ \bar{\tau }_{22}^{(1)} &{} \bar{\tau }_{22}^{(2)} &{} \bar{\tau }_{22}^{(3)} &{} \bar{\tau }_{22}^{(4)} &{} \bar{\tau }_{22}^{(5)} &{} \bar{\tau }_{22}^{(6)}\\ \bar{\tau }_{33}^{(1)} &{} \bar{\tau }_{33}^{(2)} &{} \bar{\tau }_{33}^{(3)} &{} \bar{\tau }_{33}^{(4)} &{} \bar{\tau }_{33}^{(5)} &{} \bar{\tau }_{33}^{(6)}\\ \sqrt{2}\bar{\tau }_{23}^{(1)} &{} \sqrt{2}\bar{\tau }_{23}^{(2)} &{} \sqrt{2}\bar{\tau }_{23}^{(3)} &{} \sqrt{2}\bar{\tau }_{23}^{(4)} &{} \sqrt{2}\bar{\tau }_{23}^{(5)} &{} \sqrt{2}\bar{\tau }_{23}^{(6)}\\ \sqrt{2}\bar{\tau }_{13}^{(1)} &{} \sqrt{2}\bar{\tau }_{13}^{(2)} &{} \sqrt{2}\bar{\tau }_{13}^{(3)} &{} \sqrt{2}\bar{\tau }_{13}^{(4)} &{} \sqrt{2}\bar{\tau }_{13}^{(5)} &{} \sqrt{2}\bar{\tau }_{13}^{(6)}\\ \sqrt{2}\bar{\tau }_{12}^{(1)} &{} \sqrt{2}\bar{\tau }_{12}^{(2)} &{} \sqrt{2}\bar{\tau }_{12}^{(3)} &{} \sqrt{2}\bar{\tau }_{12}^{(4)} &{} \sqrt{2}\bar{\tau }_{12}^{(5)} &{} \sqrt{2}\bar{\tau }_{12}^{(6)} \end{array}\right] . \end{aligned}$$

(2.23)

Fig. 2

Investigated microstructures for isotropic (a), unidirectional (b), and planar isotropic (c) fiber orientation states

3 Spatial representation and anisotropy of the effective suspension viscosity

With the goal of modeling the effective behavior of shear-thinning fiber suspensions in mind, it is essential to understand the anisotropic effective viscosity of such suspensions, as well as its dependence on the fiber orientation state $\underline{\lambda }$ and the shear rate $\dot{\gamma }$ first. Accordingly, we begin by visualizing the effective viscosity and studying its anisotropy for low shear rates $\dot{\gamma }$ in the following, before studying the effects of non-linear shear-thinning. To reduce the dimensional complexity when studying the effective viscosity, we use a scalar elongational viscosity $\eta _{\textsf{app}}$. Following Sterr et al. [18, §4], we define the viscosity $\eta _{\textsf{app}}$ based on a modified approach by Böhlke and Brüggemann [58], such that

$$\begin{aligned} \eta _{\textsf{app}}(\dot{\gamma }, \underline{\lambda }, {\varvec{ d}}) = \bar{{\mathbb { V}}}(\dot{\gamma }, \underline{\lambda }) \cdot ({\varvec{ d}}\otimes {\varvec{ d}}\otimes {\varvec{ d}}\otimes {\varvec{ d}}), \end{aligned}$$

(3.1)

where ${{\varvec{ d}}\in S^2}$ denotes the direction of elongation, $\underline{\lambda }\in S_{\textsf{T}}$ refers to the fiber orientation state, and $S_{\textsf{T}}$ is the fiber orientation triangle defined in equation (2.9). We use equation (2.22) to approximate the effective viscosity $\bar{{\mathbb { V}}}$ and thus the elongational viscosity $\eta _{\textsf{app}}$ with

$$\begin{aligned} \eta _{\textsf{app}}(\dot{\gamma }, \underline{\lambda }, {\varvec{ d}}) \approx {\underline{a}({\varvec{ d}})}^{\textsf{T}} {\underline{\underline{\bar{V}}}}(\dot{\gamma }, \underline{\lambda }) \ \underline{a}({\varvec{ d}}), \end{aligned}$$

(3.2)

where $\underline{a}({\varvec{ d}})$ denotes the components of ${\varvec{ d}}\otimes {\varvec{ d}}$ in Mandel notation. In addition to the elongational viscosity $\eta _{\textsf{app}}$, the bulk viscosity

$$\begin{aligned} \eta _{\textsf{b}}(\dot{\gamma },\underline{\lambda },{\varvec{ d}}) = {\varvec{ I}}\cdot \bar{{\mathbb { V}}}(\dot{\gamma },\underline{\lambda }) ({\varvec{ d}}\otimes {\varvec{ d}}) = ({\varvec{ d}}\otimes {\varvec{ d}}) \cdot \bar{{\mathbb { V}}}[{\varvec{ I}}], \end{aligned}$$

(3.3)

is required to capture all information contained in the effective viscosity $\bar{{\mathbb { V}}}$ [59, Sec. 4.3] if the effective material is compressible. However, as we consider incompressible material behavior, the bulk viscosity $\eta _{\textsf{b}}$ vanishes, since

$$\begin{aligned} \bar{{\mathbb { V}}}[{\varvec{ I}}] = 0. \end{aligned}$$

(3.4)

Hence, the elongational viscosity $\eta _{\textsf{app}}$ encodes all information contained in the matrix ${\underline{\underline{\bar{V}}}}(\dot{\gamma }, \underline{\lambda })$, and allows us to study the anisotropic flow resistance of the suspension in a complete manner. For the elongational viscosity and related quantities we omit denoting the dependence on the shear rate $\dot{\gamma }$, the fiber orientation state $\underline{\lambda }$, and the direction of elongation ${\varvec{ d}}$ explicitly. Because of the interpolating property of equation (2.22), we may visualize the direction-dependent material behavior for load cases not collected in $\underline{\underline{\bar{D}}}$, and develop intuition for the influence of different fiber orientation states on the elongational viscosity $\eta _{\textsf{app}}$. For a discussion on the applicability of equation (2.22) in the case of non-linear material behavior, we refer to Sterr et al. [18, §2.3, §4]. For the visualization of the elongational viscosity $\eta _{\textsf{app}}$, we restrict to a shear rate $\dot{\gamma }=10 \, \text {s}^{-1}$, where the material behavior is mostly linear and the superposition principle encoded in equation (2.22) holds. The elongational viscosity bodies for the isotropic, the planar isotropic, the transversely isotropic, and the unidirectional fiber orientation states are visualized in Fig. 3 for a shear rate $\dot{\gamma }=10~\, \text {s}^{-1}$. To study the suspension anisotropy at the same shear rate $\dot{\gamma }= 10 \, \text {s}^{-1}$, for each orientation state and over all directions ${\varvec{ d}}$, we compute the range $\Delta \eta _{\textsf{app}}$ and the ratio $r_{\textsf{app}}$

$$\begin{aligned} \Delta \eta _{\textsf{app}}= \max (\eta _{\textsf{app}}) - \min (\eta _{\textsf{app}}), \quad r_{\textsf{app}}= \frac{\max (\eta _{\textsf{app}})}{\min (\eta _{\textsf{app}})}, \end{aligned}$$

(3.5)

and collect the results in Table 2. For the isotropic state, the elongational viscosity $\eta _{\textsf{app}}$ lies between 1513 $\text {Pa} \, \text {s}$ to 1576 $\text {Pa} \, \text {s}$, resulting in a range $\Delta \eta _{\textsf{app}}=63 \, \text {Pa} \, \text {s}$ and a ratio $r_{\textsf{app}}=1.04$. Because there is no principal fiber orientation axis in the isotropic state, the maximum viscosity $\eta _{\textsf{app}}$, the range $\Delta \eta _{\textsf{app}}$, and the ratio $r_{\textsf{app}}$ are lower than in the more strongly oriented states, see Fig. 3a. In contrast, the maxima of the elongational viscosity $\eta _{\textsf{app}}$ occur in the principal fiber orientation axes clearly visible in Fig. 3b–d. For the planar isotropic state, the maximum of the elongational viscosity $\eta _{\textsf{app}}$ occurs in the $x$-$y$ plane with 1947 $\text {Pa} \, \text {s}$, and for the transversely isotropic and unidirectional cases, the maxima occur in the x direction with 2973 $\text {Pa} \, \text {s}$ and 4845 $\text {Pa} \, \text {s}$, respectively. Also, with increasing degree of orientation, the range $\Delta \eta _{\textsf{app}}$ and ratio $r_{\textsf{app}}$ grow from 977 $\text {Pa} \, \text {s}$ and 2.01 in the planar isotropic state, 1810 $\text {Pa} \, \text {s}$ and 2.56 in the transversely isotropic state, and up to 4130 $\text {Pa} \, \text {s}$ and 6.78 in the unidirectional state. The strong dependence of the maximum elongational viscosity, the range $\Delta \eta _{\textsf{app}}$, and the ratio $r_{\textsf{app}}$ on the orientation state highlights the influence of the fibers on the anisotropy and magnitude of the effective viscous material behavior. Furthermore, the location and magnitude of the minimum elongational viscosity $\eta _{\textsf{app}}$ depend on the orientation state as well. In an isotropic volume element, the fibers increase the elongational viscosity $\eta _{\textsf{app}}$ uniformly across orientation space. Consequently, with a magnitude of 1513 $\text {Pa} \, \text {s}$, the minimum of the effective viscosity $\eta _{\textsf{app}}$ in the isotropic state is larger than in the other orientation states. In comparison, the minima of the effective viscosity $\eta _{\textsf{app}}$ are 970 $\text {Pa} \, \text {s}$ in the planar isotropic state, 1163 $\text {Pa} \, \text {s}$ in the transversely isotropic state, and 715 $\text {Pa} \, \text {s}$ in the unidirectional state. Interestingly, the minima of the elongational viscosity $\eta _{\textsf{app}}$ occur in directions where there is the least flow along the main fiber orientation directions. Because of incompressibility, the direction with the least flow in fiber direction is not perpendicular to the principal fiber orientation axis. Rather, it occurs at a specific angle which depends on the orientation state.

Table 2 Range $\Delta \eta _{\textsf{app}}$ (3.5) and ratio $r_{\textsf{app}}$ (3.5) of the elongational viscosity $\eta _{\textsf{app}}$ at a shear rate $\dot{\gamma }= 10 \, \, \text {s}^{-1}$ for isotropic, planar isotropic, transversely isotropic, and unidirectional fiber orientation states

Fig. 3

Elongational viscosity $\eta _{\textsf{app}}$ at a shear rate $\dot{\gamma }= 10 \, 1/\text {s}$ for isotropic (a), planar isotropic (b), transversely isotropic (c), and unidirectional (d) fiber orientation states

Fig. 4

Coefficient of variation $C_{\eta }$ for shear rates  ${\dot{\gamma }\in [10,10^5]\, \text {s}^{-1}}$ (a), and range of the coefficient of variation $\Delta C_{\eta }$ (b) over the fiber orientation triangle $S_{\textsf{T}}$

So far, we investigated the effective viscosity of selected fiber suspensions for a relatively low shear rate ${\dot{\gamma }=10\, \text {s}^{-1}}$ using the elongational viscosity $\eta _{\textsf{app}}$, the range $\Delta \eta _{\textsf{app}}$, and the ratio $r_{\textsf{app}}$. However, the ratio $r_{\textsf{app}}$ or popular anisotropy measures used in crystal elasticity [60,61,62] rely on the existence of load independent stiffness and compliance tensors. To model the effective suspension viscosity, we want to study its load dependence for all shear rates ${\dot{\gamma }\in S_{\dot{\gamma }}}$ in the set $S_{\dot{\gamma }}$, which includes shear rates where the effective material behavior is non-linear. Thus, a way of computing the suspension anisotropy without relying on the interpolative properties of equation (2.22) is necessary and is introduced in the following. A convenient expression for the elongational viscosity $\eta _{\textsf{app}}$ in terms of the investigated load cases collected in the matrix $\underline{\underline{\bar{D}}}$ follows from equation (3.1) with $\bar{{\varvec{ D}}}= \dot{\gamma }/ \sqrt{2} \, {\varvec{ d}}\otimes {\varvec{ d}}$ and $\bar{\varvec{\tau }}= \bar{{\mathbb { V}}}[\bar{{\varvec{ D}}}]$, such that

$$\begin{aligned} \eta _{\textsf{app}}(\dot{\gamma }, \underline{\lambda }, \bar{{\varvec{ D}}}) = 2\frac{\bar{{\varvec{ D}}}\cdot \bar{\varvec{\tau }}}{\bar{{\varvec{ D}}}\cdot \bar{{\varvec{ D}}}}. \end{aligned}$$

(3.6)

We use this expression (3.6) to define a vector $\underline{\eta }$ for all studied shear rates $\dot{\gamma }$

$$\begin{aligned} \underline{\eta }(\dot{\gamma }, \underline{\lambda })&= (\eta _{\textsf{app}}(\dot{\gamma },\underline{\lambda },\bar{{\varvec{ D}}}_1), \eta _{\textsf{app}}(\dot{\gamma },\underline{\lambda },\bar{{\varvec{ D}}}_2), ...,\nonumber \\&\qquad \eta _{\textsf{app}}(\dot{\gamma },\underline{\lambda },\bar{{\varvec{ D}}}_6))^{\textsf{T}}, \end{aligned}$$

(3.7)

which contains the elongational viscosity $\eta _{\textsf{app}}$ for each load case $\bar{{\varvec{ D}}}_{\textsf{i}}$ collected in the columns of the matrix $\underline{\underline{\bar{D}}}$. To measure the average magnitude and the dispersion of the elongational viscosities $\eta _{\textsf{app}}$ collected in the vector $\underline{\eta }$, we compute the mean $\mu _{\eta }$ and the standard deviation $s_{\eta }$

$$\begin{aligned} \mu _{\eta }(\dot{\gamma },\underline{\lambda })= & {} \frac{1}{6} \sum _{i=1}^{6} \eta _{\textsf{app, i}}(\dot{\gamma },\underline{\lambda }), \nonumber \\ s_{\eta }(\dot{\gamma },\underline{\lambda })= & {} \sqrt{\frac{1}{6} \sum _{i=1}^{6} \left( \eta _{\textsf{app, i}}(\dot{\gamma },\underline{\lambda }) - \mu _{\eta }(\dot{\gamma },\underline{\lambda }) \right) ^2}. \end{aligned}$$

(3.8)

The standard deviation $s_{\eta }$ is not a dimensionless quantity and its magnitude is a nominal measure of dispersion. Thus, the standard deviation $s_{\eta }$ is unsuitable to interpret the dispersion of the values collected in the vector $\underline{\eta }$ in relation to their magnitude. Instead, we use the coefficient of variation $C_{\eta }$ defined by the equation

$$\begin{aligned} C_{\eta }(\dot{\gamma }, \underline{\lambda }) = \frac{s_{\eta }(\dot{\gamma }, \underline{\lambda })}{\mu _{\eta }(\dot{\gamma }, \underline{\lambda })}, \quad \end{aligned}$$

(3.9)

to relate the standard deviation $s_{\eta }$ to the mean $\mu _{\eta }$ and thus compute a dimensionless anisotropy measure of the suspension viscosity for a given fiber orientation state.

Also, the coefficient of variation $C_{\eta }$ is a useful quantity to compare the anisotropy of fiber orientation states with elongational viscosities $\eta _{\textsf{app}}$ of varying magnitudes. To study the maximum load dependent change of the anisotropy for a given fiber orientation state, we define the range over all shear rates $\Delta C_{\eta }$

$$\begin{aligned} \Delta C_{\eta }(\underline{\lambda }) = \max _{\dot{\gamma }}(C_{\eta }(\dot{\gamma }, \underline{\lambda })) - \min _{\dot{\gamma }}(C_{\eta }(\dot{\gamma }, \underline{\lambda })). \end{aligned}$$

(3.10)

The development of the coefficient of variation $C_{\eta }$ for selected orientation states over the shear rate $\dot{\gamma }$, and the range $\Delta C_{\eta }$ for all fiber orientation states are shown in Fig. 4. For all investigated shear rates and orientation states, the coefficient of variation $C_{\eta }$ is largest in the unidirectional state, and smallest in the isotropic state, see Fig. 4a. The coefficient of variation $C_{\eta }$ for all other investigated orientation states lies between these bounds. Qualitatively, the coefficient of variation $C_{\eta }$, and hence, the degree of anisotropy at a given shear rate, decreases up to a shear rate $\dot{\gamma }\approx 10^3 \, \text {s}^{-1}$ for all orientation states. This decrease in the coefficient $C_{\eta }$ suggests increased local velocity gradients, and thus stronger shear-thinning in the matrix, during flow along the fiber orientation directions. Quantitatively the range $\Delta C_{\eta }$ depends on the orientation state, and is largest in the unidirectional state, see Fig. 4(b).

In the isotropic state, the coefficient of variation $C_{\eta }$ and its range $\Delta C_{\eta }$ are close to zero for all investigated shear rates, showing that non-linear shear thinning effects occur at equivalent strengths, independent of the load direction. With increasing degree of orientation, the coefficient of variation $C_{\eta }$ and its range $\Delta C_{\eta }$ grow. In the planar isotropic state, the coefficient of variation $C_{\eta }$ varies with a range $\Delta C_{\eta }=0.13$ between $C_{\eta }=0.38$ at a shear rate $\dot{\gamma }=10 \, \text {s}^{-1}$ and $C_{\eta }=0.25$ at a shear rate $\dot{\gamma }=10^3 \, \text {s}^{-1}$. The range $\Delta C_{\eta }$ is largest in the unidirectional state, where the coefficient of variation $C_{\eta }$ varies strongly with a range $\Delta C_{\eta }=0.32$ between $C_{\eta }=0.82$ at a shear rate $\dot{\gamma }=10 \, \text {s}^{-1}$ and $C_{\eta }=0.50$ at a shear rate $\dot{\gamma }=10^3 \, \text {s}^{-1}$. The distinct differences in the coefficient of variation $C_{\eta }$ and the range $\Delta C_{\eta }$ between the studied fiber orientation states highlight the strong influence of the fiber orientation on the magnitude and anisotropy of the effective material behavior. As a consequence of the Cross-type material law (2.19) and increasing velocity gradients in the polymer matrix, the coefficient of variation $C_{\eta }$ increases for shear rates $\dot{\gamma }$ larger than $10^3 \, \text {s}^{-1}$ up to similar values as observed for a shear rate $\dot{\gamma }=10 \, \text {s}^{-1}$. The results discussed in this section thus underline the need to account for the shear rate and load direction dependent shear thinning behavior of the suspension when modeling the suspension viscosity. This is in line with findings in the literature [29, 31, 35, 63], where the effect of the suspended fibers on the matrix shear rate is estimated using fiber orientation statistics. In the next section we will use a different approach, and discuss how the anisotropic shear thinning effect can be characterized with supervised machine learning based on the computational results of the FFT-based homogenization and knowledge of the local Cross-type material law.

4 Modeling the effective suspension viscosity

4.1 Model requirements

With the results presented in the previous section 3 at hand, we wish to model the effective viscosity of shear-thinning fiber suspensions with analytical means and identify the model parameters using supervised machine learning. To do so, we first summarize the key criteria a model of the effective viscous behavior should fulfill. The model should

• (I) be tensorial, i.e., capture shear rate and load direction dependence objectively.

• (II) replicate the local Cross-type material behavior on the macro-scale, i.e., the model should show Newtonian behavior in the shear rate limits $\dot{\gamma }\rightarrow 0 \, \text {s}^{-1}$ and $\dot{\gamma }\rightarrow \infty \, \text {s}^{-1}$, and capture the shear rate and load direction dependent, non-linear transition between the two Newtonian limits. This requirement is based on the investigations in Sterr et al. [18, §4], the results of the anisotropy investigation in the previous section 3, and considerations in literature [29, 31, 35, 63].

• (III) yield an incompressible and orthotropic effective viscosity $\bar{{\mathbb { V}}}$. Because the fourth order fiber orientation tensors of the generated microstructures are orthotropic, see Schneider [52] and Montgomery-Smith et al. [64], the effective viscosity $\bar{{\mathbb { V}}}$ of the suspensions is orthotropic as well.

• (IV) be applicable on the whole fiber orientation triangle $S_{\textsf{T}}$, as defined in equation (2.9).

In accordance with requirements (I) and (II), we restrict our investigations to tensorial models of the type

$$\begin{aligned} \bar{{\mathbb { V}}}({\varvec{ D}}, \underline{a}) = \bar{{\mathbb { V}}}_\infty (\underline{a}) + {\mathbb { T}}_{\textsf{8}}({\varvec{ D}}, \underline{a}) \left[ \bar{{\mathbb { V}}}_0(\underline{a}) - \bar{{\mathbb { V}}}_\infty (\underline{a})\right] , \end{aligned}$$

(4.1)

where $\underline{a}\in \mathbb {R}^m$, $m \in \mathbb {N}$, is the vector of model parameters, ${\mathbb { T}}_{\textsf{8}}: \textsf{Sym}_0(3) \times \mathbb {R}^m \rightarrow (\mathbb {R}^3)^{\otimes 8}$ stands for an eighth order tensor function, and $\bar{{\mathbb { V}}}_0: \mathbb {R}^m \rightarrow \textsf{Sym}_0(3)$ as well as $\bar{{\mathbb { V}}}_\infty : \mathbb {R}^m \rightarrow \textsf{Sym}_0(3)$ denote fourth order tensor functions. The functions $\bar{{\mathbb { V}}}_0$ and $\bar{{\mathbb { V}}}_\infty$ are used to construct the Newtonian viscosity tensors $\bar{{\mathbb { V}}}_0(\underline{a})$ and $\bar{{\mathbb { V}}}_\infty (\underline{a})$ in the shear rate limits $\dot{\gamma }\rightarrow 0 \, \text {s}^{-1}$ and $\dot{\gamma }\rightarrow \infty \, \text {s}^{-1}$, respectively. Equation (4.1) is a tensor-valued generalization of the Cross-type material law (2.19), where the scalar Newtonian viscosities are replaced by the viscosity tensors $\bar{{\mathbb { V}}}_0(\underline{a})$ and $\bar{{\mathbb { V}}}_\infty (\underline{a})$, and the function ${\mathbb { T}}_{\textsf{8}}$ is introduced to model the non-linear transition between the two Newtonian viscosity tensors $\bar{{\mathbb { V}}}_0(\underline{a})$ and $\bar{{\mathbb { V}}}_\infty (\underline{a})$. The function ${\mathbb { T}}_{\textsf{8}}$ varies between the individual models, and encodes the direction dependent non-linearity of the models as stated in requirement (II). In summary, three objects in the Ansatz (4.1) need to be modeled: the Newtonian viscosity tensors $\bar{{\mathbb { V}}}_0(\underline{a})$ and $\bar{{\mathbb { V}}}_\infty (\underline{a})$, as well as the eighth order tensor function ${\mathbb { T}}_{\textsf{8}}$ controlling the anisotropic and non-linear shear rate dependence. In the following sections, we discuss the respective modeling approaches for these three objects.

4.2 Modeling the Newtonian limits of the effective suspension viscosity

To integrate orthotropic symmetry and incompressibility according to requirement (III) into the models, we first consider the vector space $\textsf{V}_0$ of fourth order incompressible tensors with minor and major symmetries

$$\begin{aligned} \textsf{V}_0= & {} \{{\mathbb { X}}\quad |\quad {\mathbb { X}}\in (\mathbb {R}^3)^{\otimes 4}, \quad \text {and} \quad {\mathbb { X}}[{\varvec{ I}}] = 0 \nonumber \\{} & {} \quad \text {and} \quad {\mathbb { X}}^{\mathsf{T_H}}={\mathbb { X}}^{\mathsf{T_L}}={\mathbb { X}}^{\mathsf{T_R}}={\mathbb { X}}\}, \end{aligned}$$

(4.2)

where $(\cdot )^{\mathsf{T_H}}$, $(\cdot )^{\mathsf{T_L}}$, and $(\cdot )^{\mathsf{T_R}}$ stand for major transposition, left transposition, and right transposition, respectively. Second, we then define a basis $\mathcal {B}$ of the space $\textsf{V}_0$

$$\begin{aligned} \underline{\underline{\mathcal {B}}} = \left[ \begin{array}{rrrrr} 0 &{} \frac{-2}{\sqrt{6}} &{} 0 &{} 0 &{} 0\\ \frac{-1}{\sqrt{2}} &{} \frac{1}{\sqrt{6}} &{} 0 &{} 0 &{} 0\\ \frac{1}{\sqrt{2}} &{} \frac{1}{\sqrt{6}} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1\\ \end{array}\right] , \end{aligned}$$

(4.3)

such that the columns of the matrix $\underline{\underline{\mathcal {B}}}$ represent the basis vectors of $\mathcal {B}$ in Mandel notation. Finally, using the basis $\mathcal {B}$, we define a function

$$\begin{aligned} {\mathbb { A}}: \mathbb {R}^6&\rightarrow \textsf{V}_0^+(3),\end{aligned}$$

(4.4)

$$\begin{aligned} \underline{a}&\mapsto \mathcal {P}_{\mathcal {B}}^{+}{\mathbb { M}}(\underline{a}) = \mathcal {P}_{\mathcal {B}}^{+}\left[ \begin{array}{rrrrr} a_1 &{} a_2 &{} 0 &{} 0 &{} 0\\ a_2 &{} a_3 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} a_4 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} a_5 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} a_6\\ \end{array}\right] _{\mathcal {B}}, \end{aligned}$$

(4.5)

which constructs an orthotropic fourth order tensor using the components $a_i$ of the model parameter vector $\underline{a}$, and the non-unique projector $\mathcal {P}_{\mathcal {B}}^{+}$ into the space $\textsf{V}_0^+$ of fourth order tensors that are positive definite on the space spanned by the basis $\mathcal {B}$. Employing eigendecomposition, we define the action of the projector $\mathcal {P}_{\mathcal {B}}^{+}$ as

$$\begin{aligned} ~ \mathcal {P}_{\mathcal {B}}^{+}\left[ {\mathbb { X}}\right] = \mathcal {P}_{\mathcal {B}}^{+}\left[ \sum _{i=0}^{5} \lambda _i \, {\varvec{ p}}_{i} \otimes {\varvec{ p}}_{i}\right] = \sum _{i=0}^{5} \max (\lambda _i, \beta ) \, {\varvec{ p}}_{i} \otimes {\varvec{ p}}_{i}, \end{aligned}$$

(4.6)

where $\lambda _i$ and ${\varvec{ p}}_i$ denote eigenvalue eigentensor pairs of a fourth order tensor ${\mathbb { X}}$ on the space spanned by the basis $\mathcal {B}$, and $\beta \in \mathbb {R}_{>0}$ is a small positive and real constant. The definition of the projection operator $\mathcal {P}_{\mathcal {B}}^{+}$ involves a tunable constant $\beta$, which is required for numerical purposes. In fact, formally setting $\beta$ to zero leads to the projector onto positive semi-definite tensors, i.e., those which may be degenerate. However, positive definiteness on the incompressible subspace $\mathcal {B}$ is preferred over positive semi-definiteness, because of the following physical and numerical reasons. We wish to use the tensor function ${\mathbb { A}}$ to build fourth order tensors ${\mathbb { X}}\in \textsf{V}_0^+$ from six model parameters, i.e., the viscosity tensors $\bar{{\mathbb { V}}}_0(\underline{a})$ and $\bar{{\mathbb { V}}}_\infty (\underline{a})$. Therefore, encoding a vanishing stress response through vanishing eigenvalues would not adhere to the physical model considered in the context of this article.

4.3 Modeling the anisotropic and non-linear shear rate dependence of the effective suspension viscosity

To capture the anisotropic and non-linear viscous behavior in accordance with requirement (II), we incorporate a generalized distance g from zero load

$$\begin{aligned} g : \textsf{Sym}_0(3) \times \mathbb {R}^7&\rightarrow \mathbb {R}, \end{aligned}$$

(4.7)

$$\begin{aligned} ({\varvec{ D}},\underline{a})&\mapsto ({\varvec{ D}}\cdot {\mathbb { A}}(\underline{a})[{\varvec{ D}}])^{a_7}, \end{aligned}$$

(4.8)

into the models, which is similar to the Mahalanobis distance [65] popular in statistics. The generalized distance g depends on the components $a_i$ collected in the model parameter vector $\underline{a}$, as well as the magnitude and direction of the shear rate tensor ${\varvec{ D}}$. Because of these properties, we use the generalized distance g as a model building block to encode the fiber orientation state specific, anisotropic shear rate dependence of the effective suspension viscosity. However, for an exponent ${a_7 < 1}$ the gradient of this generalized distance g is singular whenever ${\varvec{ D}}\cdot {\mathbb { A}}(\underline{a})[{\varvec{ D}}]$ vanishes, posing a problem during gradient based learning of the model parameters $\underline{a}$. This singularity is circumvented by the enforced positive definiteness of the tensors constructed by the function ${\mathbb { A}}$ and non-vanishing load ${\varvec{ D}}$. Here, the constant $\beta$ acts as a lower bound on the eigenvalues of the tensor ${\mathbb { A}}(\underline{a})$, as can be seen from equations (4.4) and (4.6), and restricts the space of possible tensors ${\mathbb { A}}(\underline{a})$ that can be constructed from the model parameters $\underline{a}$. Improper choice of the constant $\beta$, such that $\beta$ is greater than the smallest eigenvalue of the optimal tensor ${\mathbb { A}}(\underline{a})$, could therefore influence the quality of fit. However, because we wish to learn the model parameters $\underline{a}$ from homogenization data, the optimal tensor ${\mathbb { A}}(\underline{a})$ and its smallest eigenvalue are not known a priori. Therefore, the constant $\beta$ should be chosen to be a small number, and we nominally select $\beta = 10^{-6}$ in the unit of the associated eigenvalue $\lambda _i$. To model the anisotropic Cross-type non-linearity using the generalized distance g, we define two non-linear eighth order tensor functions ${\mathbb { T}}_{\textsf{8}}^{(1)}$ and ${\mathbb { T}}_{\textsf{8}}^{(2)}$ through their actions on an orthotropic tensor ${\mathbb { X}}\in \textsf{Sym}_0$. We define the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ through

$$\begin{aligned} {\mathbb { T}}_{\textsf{8}}^{(1)}({\varvec{ D}},\underline{a})\left[ {\mathbb { X}}\right] = \frac{{\mathbb { X}}}{1 + g({\varvec{ D}},\underline{a})}, \quad \underline{a}\in \mathbb {R}^7, \end{aligned}$$

(4.9)

such that the scalar shear rate dependence of the Cross-type model (2.19) is replaced by the generalized distance g (4.7). Thus, the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ scales all the components of the orthotropic tensor ${\mathbb { X}}$ equally, depending on the load ${\varvec{ D}}$ and the model parameter vector $\underline{a}$. Because all components of the tensor ${\mathbb { X}}$ are scaled equally, the anisotropy of the tensor ${\mathbb { X}}$ remains unchanged under the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$. However, the non-linear shear rate dependence encoded in the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ may be anisotropic since the magnitude of the scaling depends on the function g, and hence on a possibly anisotropic tensor ${\mathbb { A}}(\underline{a})$ and the load ${\varvec{ D}}$. Of the seven model parameters collected in the model parameter vector $\underline{a}$, six model parameters control the influence of the direction of the load ${\varvec{ D}}$ on the scaling, and one parameter controls the rate of transition between the Newtonian limits for shear rates ${\dot{\gamma }\rightarrow 0}$ and ${\dot{\gamma }\rightarrow \infty }$.

To allow for greater flexibility in the scaling of the orthotropic tensor ${\mathbb { X}}$, we also define the tensor function ${\mathbb { T}}_{\textsf{8}}^{(2)}$ through

$$\begin{aligned} {\mathbb { T}}_{\textsf{8}}^{(2)}({\varvec{ D}},\underline{a})\left[ {\mathbb { X}}\right] = \left[ \begin{array}{rrrrr} h_1({\varvec{ D}},\underline{a})X_{11} &{} h_2({\varvec{ D}},\underline{a})X_{12} &{} 0 &{} 0 &{} 0\\ h_2({\varvec{ D}},\underline{a})X_{12} &{} h_3({\varvec{ D}},\underline{a})X_{22} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} h_4({\varvec{ D}},\underline{a})X_{33} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} h_5({\varvec{ D}},\underline{a})X_{44} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} h_6({\varvec{ D}},\underline{a})X_{55}\\ \end{array}\right] _{\mathcal {B}}, \quad \underline{a}\in \mathbb {R}^{42}, \end{aligned}$$

(4.10)

such that the six components of the tensor ${\mathbb { X}}$ are scaled individually by a scalar $h_i({\varvec{ D}},\underline{a}), \, i \in \{1,2,3,4,5,6\}$, defined as

$$\begin{aligned} h_i({\varvec{ D}},\underline{a}) = \frac{1}{1 + g({\varvec{ D}}, \underline{f}_i)}, \ \underline{f}_i = (a_{7(i-1)+1}, ..., a_{7i}) \in \mathbb {R}^7. \end{aligned}$$

(4.11)

Like the scaling factor in the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$, the scalars $h_i({\varvec{ D}},\underline{a})$ are each computed from seven model parameters, the shear rate tensor ${\varvec{ D}}$, and the function g. Therefore, the tensor ${\mathbb { X}}$ is not only scaled under the function ${\mathbb { T}}_{\textsf{8}}^{(2)}$, but the anisotropy of the tensor ${\mathbb { X}}$ may also change under the function ${\mathbb { T}}_{\textsf{8}}^{(2)}$. In this sense, the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ is a special case of the function ${\mathbb { T}}_{\textsf{8}}^{(2)}$, where all scalars $h_i({\varvec{ D}},\underline{a})$ are equal. The increased flexibility in the scaling of the tensor ${\mathbb { X}}$ with function ${\mathbb { T}}_{\textsf{8}}^{(2)}$ requires 36 parameters to control the influence of the direction of the load ${\varvec{ D}}$, and six parameters to control the rate of transition between the Newtonian limits for shear rates ${\dot{\gamma }\rightarrow 0}$ and ${\dot{\gamma }\rightarrow \infty }$. This results in a total of 42 parameters for the function ${\mathbb { T}}_{\textsf{8}}^{(2)}$.

4.4 Definitions of effective suspension viscosity models

In the following, we combine the definitions of the previous sections 4.2 and 4.3 with the Ansatz (4.1) to build four models for the effective suspension viscosity. With the symbol $\mathbin {+\hspace{-5.55542pt}+}$ denoting concatenation of vectors the four models presented in Table 3 are considered and described in the following.

Table 3 Number of parameters m, choices for the functions $\bar{{\mathbb { V}}}_0$, $\bar{{\mathbb { V}}}_\infty$, and ${\mathbb { T}}_{\textsf{8}}$, as well as the complete expression for the effective viscosity tensor $\bar{{\mathbb { V}}}({\varvec{ D}},\underline{a})$ for the Models 1, 2, 3, and 4

4.4.1 Model 1

In Model 1, we use the function ${\mathbb { A}}$ (4.4) to construct the Newtonian viscosity tensors $\bar{{\mathbb { V}}}_0(\underline{b})$ and $\bar{{\mathbb { V}}}_\infty (\underline{c})$ from twelve model parameters collected in the vectors $\underline{b}\in \mathbb {R}^6$ and $\underline{c}\in ~\mathbb {R}^6$. Also, we use the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ (4.9) with seven parameters collected in the vector $\underline{d}\in \mathbb {R}^7$ to model the anisotropic and non-linear shear rate dependence of the effective suspension viscosity. Overall, Model 1 has 19 parameters and is the most general considered model that uses the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$.

4.4.2 Model 2

Like in Model 1, we use the function ${\mathbb { A}}$ to construct the Newtonian viscosity tensor $\bar{{\mathbb { V}}}_\infty (\underline{b})$ in the shear rate limit$\dot{\gamma }\rightarrow \infty \, \text {s}^{-1}$ from six model parameters, and the non-linear function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ to model the non-linear transition between the Newtonian limits with seven model parameters. These 13 parameters are collected in the vectors $\underline{c}\in \mathbb {R}^6$ and $\underline{d}\in \mathbb {R}^7$. However, in Model 1, the viscosity tensor $\bar{{\mathbb { V}}}_0(\underline{b})$ in the shear rate limit $\dot{\gamma }\rightarrow 0\, \text {s}^{-1}$ is also constructed with the function ${\mathbb { A}}$ (4.4), using six model parameters. In Model 2, we exploit the fact that the viscosity tensors $\bar{{\mathbb { V}}}_0(\underline{b})$ and $\bar{{\mathbb { V}}}_\infty (\underline{c})$ share the same anisotropy in the shear rate limits $\dot{\gamma }\rightarrow 0 \, \text {s}^{-1}$ and $\dot{\gamma }\rightarrow \infty \, \text {s}^{-1}$, see Fig. 4 and Sterr et al. [18], and express the viscosity tensor $\bar{{\mathbb { V}}}_0(\underline{b})$ as a scalar multiple of the tensor $\bar{{\mathbb { V}}}_\infty (\underline{c})$, such that the condition

$$\begin{aligned} {\mathbb { V}}_0(\underline{b}) = b_1\,{\mathbb { V}}_\infty (\underline{c}), \end{aligned}$$

(4.12)

is satisfied. This relation reduces the number of parameters from 19 in Model 1 to 14 in Model 2. We found that this adaption introduces only small errors, as we discuss in section 4.6 in more detail, and use equation (4.12) in Model 3 and Model 4 as well.

4.4.3 Model 3

In Model 3, like in Model 1 and Model 2, we use the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ to model the non-linear transition between the Newtonian limits with seven model parameters collected in the vector $\underline{d}\in \mathbb {R}^7$. Also, as in Model 2, we use equation (4.12) to relate the viscosity tensors  $\bar{{\mathbb { V}}}_0(\underline{b})$ and $\bar{{\mathbb { V}}}_\infty (\underline{c})$ via a scalar coefficient collected in the vector $\underline{b}\in \mathbb {R}^1$. To further reduce the number of model parameters through physical considerations motivated by superposition and orientation averaging [32, 33, 44], we introduce the equation

$$\begin{aligned} \bar{{\mathbb { V}}}_\infty (\underline{c}) = {\mathbb { P}}_2\left( c_1\,{\mathbb { P}}_2 + c_2\, {\varvec{ I}}\Box _s {\varvec{ N}}+ c_3\, {\mathbb { N}}\right) {\mathbb { P}}_2, \end{aligned}$$

(4.13)

for the viscosity tensor $\bar{{\mathbb { V}}}_\infty (\underline{c})$, where ${\mathbb { P}}_2$ denotes the identity on the space $\textsf{Sym}_0(3)$. The operator $\Box _s$ stands for the symmetrized box product, which, for the second order tensors ${{\varvec{ A}},{\varvec{ B}},{\varvec{ C}}\in \left( \mathbb {R}^3\right) ^{\otimes 2}}$, is defined as

$$\begin{aligned} {\varvec{ A}}\Box _s {\varvec{ B}}= \frac{1}{2}({\varvec{ A}}\Box {\varvec{ B}}+ {\varvec{ B}}\Box {\varvec{ A}}), \quad \textrm{where} ({\varvec{ A}}\Box {\varvec{ B}})\left[ {\varvec{ C}}\right] = {\varvec{ A}}{\varvec{ C}}{\varvec{ B}}. \end{aligned}$$

(4.14)

Overall, this reduces the number of parameters from 14 in Model 2 to 11 in Model 3.

4.4.4 Model 4

In Model 4, in contrast to the Models 1, 2, and 3, we use the function ${\mathbb { T}}_{\textsf{8}}^{(2)}$ instead of the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ to model the non-linear transition between the Newtonian limits. As discussed in the previous section 4.3, this allows for greater flexibility in exchange for more model parameters, making Model 4 the most general of the considered models. Like in Model 2 and Model 3, we use seven parameters collected in the vectors $\underline{b}\in \mathbb {R}^1$ and $\underline{c}\in \mathbb {R}^6$ to model the viscosity tensors $\bar{{\mathbb { V}}}_0(\underline{b})$ and $\bar{{\mathbb { V}}}_\infty (\underline{c})$. In combination with the 42 input parameters of the function ${\mathbb { T}}_{\textsf{8}}^{(2)}$, which we collect in the vector $\underline{d}$, this leads to a total of 49 model parameters for Model 4. Overall, each model parameter controls a distinct effect or quantity of the model. In other words, Model 4 could not be expressed with fewer parameters while maintaining the same type of non-linearity and the same degree of modeling flexibility.

4.5 Supervised learning of model parameters

In the previous sections 4.1 and 4.4, we described the requirements for models of the effective suspension viscosity and presented four model candidates satisfying these requirements. In this section, we discuss the supervised machine learning strategy we use to identify the model parameters. To learn the model parameters from the data obtained with FFT-based computational homogenization, we first construct a loss function ${\mathcal {L}}$ measuring the difference between the model predictions and the FFT-based computational results, and then minimize the loss ${\mathcal {L}}$ using the ADAM [66] optimization algorithm. We consider all fiber orientation states $\underline{\lambda }\in S_{\textsf{T}}^{109}$ in the set $S_{\textsf{T}}^{109}\subset S_{\textsf{T}}$ of 109 points of the discretized fiber orientation triangle shown in Figs. 1a and 4b. For every load case $\bar{{\varvec{ D}}}$, fiber orientation state $\underline{\lambda }$, and parameter vector $\underline{a}$, we define the loss ${\mathcal {L}}$

$$\begin{aligned} {\mathcal {L}}(\bar{{\varvec{ D}}},\underline{\lambda },\underline{a}) = \frac{||\bar{\varvec{\tau }}^{\textsf{FFT}}(\bar{{\varvec{ D}}},\underline{\lambda }) - \bar{\varvec{\tau }}^{\textsf{Model}}(\bar{{\varvec{ D}}},\underline{\lambda },\underline{a})||_2}{||\bar{\varvec{\tau }}^{\textsf{FFT}}(\bar{{\varvec{ D}}},\underline{\lambda })||_2}, \end{aligned}$$

(4.15)

where $||\cdot ||_2$ stands for the Euclidean norm, $\bar{\varvec{\tau }}^{\textsf{model}}: \textsf{Sym}_0(3)\times \mathbb {R}^2\times \mathbb {R}^m\rightarrow \textsf{Sym}_0(3)$ refers to the effective stress predicted by a particular model, and $\bar{\varvec{\tau }}^{\textsf{FFT}}: \textsf{Sym}_0(3)\times \mathbb {R}^2\rightarrow \textsf{Sym}_0(3)$ refers to the effective stress obtained with FFT-based computational homogenization. Similar to section 3, we omit the dependence of the loss ${\mathcal {L}}$ and the derived quantities on various variables for improved readability and compactness. For each model and fiber orientation state $\underline{\lambda }$, we wish to identify the model parameters $\underline{a}$ minimizing the worst case loss ${\mathcal {L}}$ for the set of investigated load cases $\bar{{\varvec{ D}}}_{\dot{\gamma }}$, such that

$$\begin{aligned} \underline{a}(\underline{\lambda }) = \text {argmin}_{\underline{a}\in \mathbb {R}^m} \max _{\varvec{\bar{D}} \in \varvec{\bar{D}}_{\dot{\gamma }}} {\mathcal {L}}(\bar{{\varvec{ D}}},\underline{\lambda },\underline{a}). \end{aligned}$$

(4.16)

Here, the set of investigated load cases $\bar{{\varvec{ D}}}_{\dot{\gamma }}$ is defined via equations (2.20) and  (2.21). However, since the models described in the previous section are not convex in the model parameters $\underline{a}$ and have multiple local minima, the exact minimizer $\underline{a}$ is difficult to determine. We wish to start our investigations with a word of warning: identifying the model parameters from computational multiscale simulations does not qualify as a mathematically well-posed problem [67], for a number of reasons. For a start, there might not be a unique solution, and the outcome of the learning process, i.e., the model parameters, might change drastically for small variations in the data. Also, depending on the optimization algorithm and the optimization hyperparameters, the learned model parameters can vary as well. Accordingly, the model parameters obtained with the supervised learning procedure we present in this article are possibly not the global minimizers of the optimization problem (4.16). However, as we show in the next section 4.6, the presented supervised learning procedure can be employed to successfully identify model parameters which result in model predictions with engineering accuracy. To capitalize on the advances in the field of non-convex optimization and machine learning, we use the Python programming language and the machine learning framework PyTorch [68] with version 1.12 to identify the model parameters $\underline{a}$. When this article was written, more recent PyTorch versions were available that feature Just In Time (JIT) compilation, which could possibly increase the performance of custom code modules. However, for compatibility with existing code, we use version 1.12. For each model and fiber orientation state $\underline{\lambda }$, we randomly initialized 5000 realizations of the parameter vector $\underline{a}$ and then used the field-tested ADAM [66] algorithm to improve the initial guesses, thus generating the set $S_{\textsf{min}}$ of minimizing parameter vectors $\underline{a}$. We selected the ADAM algorithm from the optimization algorithms available in the PyTorch framework, since the ADAM algorithm combines an adaptive learning rate with a classical momentum [69] based approach. This provides advantages over the standard gradient descent method [70, 71], and algorithms relying on adaptive learning rates alone, such as AdaGrad [72], AdaDelta [73] and RMSprop [74]. For a detailed discussion on the convergence properties of the ADAM algorithm and its variants, we refer the reader to an article by Chen et al. [75]. Also, for an overview on a variety of other optimization algorithms in machine learning, we refer the reader to a review by Sun et al. [76]. Conveniently, the ADAM algorithm’s learning rate hyperparameters are approximate bounds of the optimization step size. Exploiting this feature, we use PyTorch’s option to define parameter groups with individually varying learning options for parameters with different magnitudes, such that the step sizes for nominally large parameters are not bounded by the step sizes for nominally small ones. As a viable alternative to first-order optimization techniques, PyTorch also offers the powerful second-order optimization algorithm L-BFGS [77]. However, when this article was written, the PyTorch L-BFGS algorithm did not support multiple learning rates and parameter groups, which we have found to be valuable in accelerating convergence. Therefore, we opted to use the first-order optimization algorithm ADAM. Overall, we use four parameter groups, with one group each for the parameters of the functions $\bar{{\mathbb { V}}}_0$ and $\bar{{\mathbb { V}}}_\infty$, as well as one group each for the parameters associated with the anisotropy and the rate of non-linear transition encoded in the tensor function ${\mathbb { T}}_{\textsf{8}}$, see equations (4.9), (4.10) and (4.11). We distinguish the two parameter groups associated with the tensor function ${\mathbb { T}}_{\textsf{8}}$ with the symbols  $G_8^{\textsf{aniso}}$, which contains six parameters in case of the function ${\mathbb { T}}_{\textsf{8}}^{(1)}$ and 36 parameters in the case of the function ${\mathbb { T}}_{\textsf{8}}^{(2)}$, as well as the group $G_8^{\textsf{expo}}$ containing one and six parameters for the functions ${\mathbb { T}}_{\textsf{8}}^{(1)}$ and ${\mathbb { T}}_{\textsf{8}}^{(2)}$, respectively. Except for Model 1, the learning rates for the respective parameter groups were chosen as shown in Table 4. For Model 1 in particular, the learning rate for the parameters associated with the function $\bar{{\mathbb { V}}}_0$ was chosen as 0.5, because Model 1 does not use the scalar relationship (4.12). We determined the numerical values of the learning rates for each parameter group by trial and error. To improve convergence towards minima as the learning process proceeds [78, 79], we used PyTorch’s ReduceLROnPlateau learning rate scheduler to half the learning rates if the loss ${\mathcal {L}}$ has not improved for 200 epochs. This rule was applied with a cooldown of 400 epochs and all other options were kept standard. For the ADAM algorithm, other than the learning rates, standard hyperparameters were used such that the two momentum coefficients $\beta _1$ and $\beta _2$ are set to $\beta _1=0.9$ and $\beta _2=0.999$, and the stabilization constant $\varepsilon$ is set to $\varepsilon =10^{-8}$. Finally, we consider the learning process to be finished when the loss ${\mathcal {L}}$ has not improved for 2000 epochs.

Table 4 Learning rate hyperparameter by parameter group for use with the ADAM algorithm

4.6 Model accuracy

To compare the accuracy of the presented models, we define error measures and describe a validation procedure in the following. Since finding a global minimum for the problem (4.16) is hard, we restrict to the set of minimizing parameters $S_{\textsf{min}}$, and identify the parameters $\underline{a}^{{\textsf{min}}}\in S_{\textsf{min}}$ minimizing the worst case loss ${\mathcal {L}}$ over the set of investigated load cases $\bar{{\varvec{ D}}}_{\dot{\gamma }}$, such that

$$\begin{aligned} \underline{a}^{{\textsf{min}}}(\underline{\lambda }) = \text {argmin}_{\underline{a}\in S_{\textsf{min}}} \max _{\varvec{\bar{D}} \in \varvec{\bar{D}}_{\dot{\gamma }}} {\mathcal {L}}(\bar{{\varvec{ D}}}, \underline{\lambda },\underline{a}). \end{aligned}$$

(4.17)

The minimizing parameters $\underline{a}^{{\textsf{min}}}$ are only available on the given discretization points $\underline{\lambda }$ where homogenization data is available as well. Yet, in accordance with requirement (IV), we are interested in generalizing a given model for fiber orientation states $\underline{\lambda }$ where no minimizing parameters $\underline{a}^{{\textsf{min}}}$ are available. For this purpose, we follow Köbler et al. [48] and use a convex linear combination to interpolate stresses as follows. Suppose the nodes $\underline{\lambda }_1,\underline{\lambda }_2,$ and $\underline{\lambda }_3$ form a triangle and the minimizing parameters $\underline{a}^{{\textsf{min}}}$ are known in those nodes. Then we compute the effective stresses $\bar{\varvec{\tau }}^{{\textsf{C}}}$ at some point $\underline{\lambda }$

$$\begin{aligned} \bar{\varvec{\tau }}^{{\textsf{C}}}(\bar{{\varvec{ D}}},\underline{\lambda })&= \sum _{i=1}^{3}s_i\,\bar{\varvec{\tau }}^{{\textsf{model}}}(\bar{{\varvec{ D}}},\underline{\lambda }_i,\underline{a}^{{\textsf{min}}}(\underline{\lambda }_i)), \end{aligned}$$

(4.18)

$$\begin{aligned} \underline{\lambda }&= s_1\,\underline{\lambda }_1 + s_2\,\underline{\lambda }_2 + s_3\,\underline{\lambda }_3 , \quad s_i \ge 0, \, i \in {1,2,3}, \,\nonumber \\&\quad \sum _{i=1}^3 s_i = 1, \end{aligned}$$

(4.19)

through interpolation of the model stresses $\bar{\varvec{\tau }}^{{\textsf{model}}}$ at the points $\underline{\lambda }_1,\underline{\lambda }_2,$ and $\underline{\lambda }_3$. In addition to generalizing the models over the entire fiber orientation triangle $S_{\textsf{T}}$, we use equation (4.18) to validate the models against the data obtained with FFT-based computational homogenization. For this purpose, we define the validation error $e_{\textsf{V}}$ similarly to the loss ${\mathcal {L}}$, i.e., we define

$$\begin{aligned} e_{\textsf{V}}(\bar{{\varvec{ D}}}, \underline{\lambda }) = \frac{||\bar{\varvec{\tau }}^{\textsf{FFT}}(\bar{{\varvec{ D}}},\underline{\lambda }) - \bar{\varvec{\tau }}^{\textsf{C}}(\bar{{\varvec{ D}}},\underline{\lambda })||_2}{||\bar{\varvec{\tau }}^{\textsf{FFT}}(\bar{{\varvec{ D}}},\underline{\lambda })||_2}, \end{aligned}$$

(4.20)

for each considered model. Of the 109 triangulation points $\underline{\lambda }$ contained in the set $S_{\textsf{T}}^{109}$ we designate 45 points as the set $S_{\textsf{T}}^{\textsf{F}}\subset S_{\textsf{T}}^{109}$ of fitting points $\underline{\lambda }^{\textsf{F}}$, see Fig. 5. For validation purposes, we designate the centroids of the triangles formed by the fitting points $\underline{\lambda }^{\textsf{F}}$ as validation points, defining the set $S_{\textsf{T}}^{\textsf{V}}\subset S_{\textsf{T}}^{109}$ of 64 validation points $\underline{\lambda }^{\textsf{V}}$. By definition of the interpolation (4.18), the loss ${\mathcal {L}}$ coincides with the validation error $e_{\textsf{V}}$ at the fitting points $\underline{\lambda }^{\textsf{F}}$. To study the quality of fit and the quality of the stress interpolation, we define the largest loss ${\mathcal {L}^{\textsf{max}}}$ and the largest validation error $e_{\textsf{V}}^{{\textsf{max}}}$

$$\begin{aligned} ~&{\mathcal {L}^{\textsf{max}}}= \max _{\underline{\lambda }\in S_{\textsf{T}}^{109}} \max _{\varvec{\bar{D}} \in \varvec{\bar{D}}_{\dot{\gamma }}} {\mathcal {L}}(\bar{{\varvec{ D}}}, \underline{\lambda }, \underline{a}^{{\textsf{min}}}(\underline{\lambda })), \quad \nonumber \\&e_{\textsf{V}}^{{\textsf{max}}}= \max _{\underline{\lambda }\in S_{\textsf{T}}^{109}} \max _{\varvec{\bar{D}} \in \varvec{\bar{D}}_{\dot{\gamma }}} e_{\textsf{V}}(\bar{{\varvec{ D}}}, \underline{\lambda }). \end{aligned}$$

(4.21)

Furthermore, we define the mean validation error $e_{\textsf{V}}^{{\textsf{mean}}}$ and the maximum validation error $e_{\textsf{V}}^{{\bar{\varvec{D}}}}$ over the set of investigated load cases $\bar{{\varvec{ D}}}_{\dot{\gamma }}$

$$\begin{aligned}&e_{\textsf{V}}^{{\textsf{mean}}}= \frac{1}{109}\sum _{\underline{\lambda }\in S_{\textsf{T}}^{109}}\max _{\varvec{\bar{D}} \in \varvec{\bar{D}}_{\dot{\gamma }}} e_{\textsf{V}}(\bar{{\varvec{ D}}},\underline{\lambda }), \quad \nonumber \\ {}&e_{\textsf{V}}^{{\bar{\varvec{D}}}}(\underline{\lambda }) = \max _{\varvec{\bar{D}} \in \varvec{\bar{D}}_{\dot{\gamma }}} e_{\textsf{V}}(\bar{{\varvec{ D}}}, \underline{\lambda }), \end{aligned}$$

(4.22)

that occurred for a given model on the discretized fiber orientation triangle. Before discussing the prediction accuracy of the presented models in detail, we briefly summarize the supervised learning procedure presented in the previous section 4.5, and the validation approach for the stress interpolation (4.18) discussed above. For each model, and in each of the 109 investigated triangulation points $\underline{\lambda }\in S_{\textsf{T}}^{109}$, we conducted 5000 optimization runs for the minimization problem (4.16) and thus obtained the set $S_{\textsf{min}}$ of minimizing parameter vectors $\underline{a}$. From this set $S_{\textsf{min}}$, we identified the single best parameter vector $\underline{a}^{{\textsf{min}}}\in S_{\textsf{min}}$ (4.17), which is associated with the smallest worst case loss of a model in a fixed triangulation point $\underline{\lambda }$. To study whether stress interpolation (4.18) can be used to generalize a model beyond points where the parameters $\underline{a}^{{\textsf{min}}}$ are available, we designated the 45 points $\underline{\lambda }^{\textsf{F}}\in S_{\textsf{T}}^{\textsf{F}}$ as fitting points and the 64 points $\underline{\lambda }^{\textsf{V}}\in S_{\textsf{T}}^{\textsf{V}}$ as validation points. On these points $\underline{\lambda }^{\textsf{F}}$ and $\underline{\lambda }^{\textsf{V}}$, we compute the validation error $e_{\textsf{V}}$ (4.20) using the stress interpolation procedure defined through the equations (4.18) and (4.19), such that only the parameter vectors $\underline{a}^{{\textsf{min}}}$ in the fitting points are used. Finally, to investigate whether a model captures the underlying material behavior appropriately, how stress interpolation affects the prediction quality, and how the prediction quality varies over the fiber orientation triangle $S_{\textsf{T}}$, we are interested in the error measures ${\mathcal {L}^{\textsf{max}}}$, $e_{\textsf{V}}^{{\textsf{max}}}$, $e_{\textsf{V}}^{{\textsf{mean}}}$, and $e_{\textsf{V}}^{{\bar{\varvec{D}}}}$.

Thus, we list the largest Loss ${\mathcal {L}^{\textsf{max}}}$, as well as the validation errors $e_{\textsf{V}}^{{\textsf{max}}}$, and $e_{\textsf{V}}^{{\textsf{mean}}}$ in Table 5, visualize the validation error $e_{\textsf{V}}^{{\bar{\varvec{D}}}}$ over the fiber orientation triangle $S_{\textsf{T}}$ in Fig. 5, and discuss the errors in the following.

Fig. 5

Validation error $e_{\textsf{V}}^{{\bar{\varvec{D}}}}$ over the fiber orientation triangle $S_{\textsf{T}}$ for Models 1 to 4

Table 5 Largest loss ${\mathcal {L}^{\textsf{max}}}$, as well as validation errors $e_{\textsf{V}}^{{\textsf{max}}}$, and $e_{\textsf{V}}^{{\textsf{mean}}}$ for the Models 1 to 4

Model 1 and Model 2 differ only in their modeling approach for the viscosity tensor $\bar{{\mathbb { V}}}_0(\underline{b})$, where the parameter based construction of an orthogonal tensor ${\bar{{\mathbb { V}}}_0(\underline{b}) = {\mathbb { A}}(\underline{b})}$ in Model 1 is replaced by the scalar relationship (4.12) in Model 2. This reduction in dimensionality does not increase the loss ${\mathcal {L}}$, as the largest loss ${\mathcal {L}^{\textsf{max}}}$ for both Model 1 and Model 2 is 5.00%. Also, the largest validation error ${e_{\textsf{V}}^{{\textsf{max}}}=5.15\%}$ and mean validation error ${e_{\textsf{V}}^{{\textsf{mean}}}=2.73\%}$ of Model 2 are only 0.10% and 0.08% larger than the errors ${e_{\textsf{V}}^{{\textsf{max}}}=5.05\%}$ and ${e_{\textsf{V}}^{{\textsf{mean}}}=2.65\%}$ of Model 1. Hence, the scalar relationship defined by equation (4.12) appears to be a valid assumption in the context of the investigated physics and microstructures. The largest loss ${\mathcal {L}^{\textsf{max}}}$ occurred for the orientation state ${\underline{\lambda }= (0.83,0.08)^{\textsf{T}}}$ for both Model 1 and Model 2. In contrast, the largest validation errors $e_{\textsf{V}}^{{\textsf{max}}}$ occurred at orientation states ${\underline{\lambda }= (0.90,0.07)^{\textsf{T}}}$ for Model 1 and ${\underline{\lambda }= (0.59,0.38)^{\textsf{T}}}$ for Model 2. For the chosen discretization of the fiber orientation triangle $S_{\textsf{T}}$, a small additional error is introduced by stress interpolation, as shown by the slight differences between the largest losses ${\mathcal {L}^{\textsf{max}}}$ and the largest validation errors $e_{\textsf{V}}^{{\textsf{max}}}$ for Model 1 and Model 2. Among the investigated models, Model 3 shows the largest loss and the largest validation error with ${{\mathcal {L}^{\textsf{max}}}= 15.36\%}$ and ${e_{\textsf{V}}^{{\textsf{max}}}= 15.36\%}$, occurring at the orientation state ${\underline{\lambda }= (0.69,0.31)^{\textsf{T}}}$. For orientation states towards the lower and left edges of the fiber orientation triangle $S_{\textsf{T}}$, the magnitude of the validation error $e_{\textsf{V}}^{{\bar{\varvec{D}}}}$ for Model 3 is comparable to that of the other models, see Fig. 5. However, a mean validation error ${e_{\textsf{V}}^{{\textsf{mean}}}=7.76\%}$ in combination with the relatively large validation errors $e_{\textsf{V}}^{{\bar{\varvec{D}}}}$ occurring at orientation states towards the upper edge of the fiber orientation triangle $S_{\textsf{T}}$ indicate that equation (4.13) is not a sufficiently accurate approximation over the whole fiber orientation triangle $S_{\textsf{T}}$. For the most general model, Model 4, the largest loss ${\mathcal {L}^{\textsf{max}}}$ and the largest validation error $e_{\textsf{V}}^{{\textsf{max}}}$ are both 5.00% for the orientation state ${\underline{\lambda }= (0.83,0.08)^{\textsf{T}}}$. Hence, the increased anisotropic capability of Model 4 improves the quality of fit and prediction only slightly compared to Models 1 and 2, albeit Model 4 uses more parameters. The mean validation error ${e_{\textsf{V}}^{{\textsf{mean}}}=2.28\%}$ of Model 4 is also only 0.37% and 0.45% lower than for Models 1 and 2. In summary, Model 3 performed the worst among the investigated models and Model 4 performed the best. The orientation averaging incorporated in Model 3 reduced the prediction accuracy, while the anisotropic function ${\mathbb { T}}^{(2)}$ improved the prediction accuracy of Model 4. However, Models 1 and 2 use fewer parameters than Model 4 and show rather similar prediction accuracy. Consequently, the degree of anisotropic non-linearity encoded in Model 1 and Model 2 seems to be sufficient to capture the effective viscous behavior to engineering accuracy in the investigated load cases. In terms of practical implementation, computational efficiency and balanced prediction accuracy we consider Model 2 the best of the investigated models, since it uses a moderate amount of parameters and yields accuracy comparable to Model 4.

5 Conclusions

In this work, we used supervised machine learning and FFT-based computational techniques to discover models for the effective suspension viscosity of fiber suspensions with shear-thinning matrix behavior. We first extended the computational investigations of previous work to a broad variety of fiber orientation states. For all considered orientation states, we studied the anisotropy and shear rate dependence of the suspension viscosity over a wide range of shear rates of engineering interest. Confirming previous observations in the case of a transversely isotropic orientation state, we found that the anisotropy of the suspension viscosity for a particular orientation state varies substantially depending on the load direction and shear rate. Furthermore, the degree of non-linearity of the matrix material in the studied volume elements influences the anisotropy of the suspension viscosity strongly. Based on the observed material behavior, we introduced four requirements a model of the suspension viscosity should satisfy, and formulated four model candidates according to these requirements. Using supervised machine learning techniques for non-convex optimization, we identified the model parameters based on the high-fidelity FFT-based computational results, and found that three of the four presented models achieve validation errors below 5.15 %. One model containing an approximation of the suspension viscosity based on superposition and orientation averaging did not perform favorably when compared with the other presented models.

In future work, the models presented in this article could be employed to enhance the prediction accuracy of engineering process simulations, such as compression and injection molding simulations. In component scale simulations, the presented models could provide substantial reductions in computational cost when compared with multiscale computational approaches, such as FE$^2$ [80,81,82], or combinations of the finite element method with FFT-based methods [83]. Prediction capabilities of the presented approach could be further extended by considering additional physical effects, such as temperature dependence and polymer crystallization in the presented models, and in the FFT-based computational approach. Also, with the procedure presented in this article, models for microstructures with curved fibers, fiber bundles or fibers with higher aspect ratios could be developed to facilitate the development of engineering systems in the context of long fiber reinforced systems. Furthermore, the supervised learning procedure presented in this article could be modified to potentially identify more suitable model parameters, and thus increase the prediction accuracy of the presented models further. For example, the effect of using different optimization algorithms, such as AdamW [84] and NAdam [85], on the model prediction accuracy could be explored. Also, different approaches to determine the optimization hyperparameters, such as gradient-based techniques, Bayesian optimization, and metaheuristic algorithms could be used [86], and their effect on the model prediction accuracy could be studied as well. Additionally, relationships between the model parameters and the model prediction quality could be investigated using visualization techniques for high-dimensional data, such as t-Distributed Stochastic Neighbor Embedding [87] or uniform manifold approximation and projection [88].