Two regression approaches for prediction of large radius air bending

Abstract

The industrial importance of air bending applications with high-strength steels has increased in recent years. However, the limited cold formability of high-strength steels requires the application of punches with large radii. The usage of large radii tooling leads to a change of the loading scheme from traditional 3-point to 4-point bending. Therefore, the conventional formulas used for the prediction of 3-point bending operations fail to deliver accurate results. In the current work, two regression approaches are proposed to achieve an accurate prediction of industrially important bending parameters. The first model is based on phenomenological observations and fitting of well-established formulas. The second model utilizes the circular approximation model as base for the regression prediction. Large radius bending is used mostly for high-strength steels. Therefore, Strenx 700 MC and Strenx 1300 with thicknesses of 4 and 6 mm were used for the investigation. The following bending characteristics have been studied: position of contact points, bend allowance, bending force and springback. The predicted values are compared with the experimental results to assess the prediction accuracy of the proposed methods. Neither the phenomenological, nor the circular model delivers superior overall prediction quality for all output parameters, thus a combination of the two regression models is an attractive option for a better prediction of large radius air bending.

Introduction

Small radius air bending is an established and extensively used forming process within the sheet metal processing industry (Fig. 1a). This process delivers the common and predictable technology, which is known for its flexibility, because it allows producing different bending angles using the same pair of punch and die. If however a part is bent by tooling with a ratio of punch radius to die opening above 1/4, the progress of the bending process is dissimilar to small radius bending, with its own peculiarities. This process is called large radius bending (Fig. 1b) and it is used mostly for bending of high-strength steels, since it imposes less deformation, and materials with limited cold bendability can still be formed. Another problem with high-strength steels is that they exhibit greater and more variable springback, and this issue adds even more complexity to the control and prediction of the forming process.

Fig. 1

Small (a) and large (b) radius air bending

To be able to reduce the post-forming operations, an accurate prediction of any forming process is required. A number of methods can be used for that purpose, but in this work, we focus on regression analysis based on the extensive available bending database. This approach remains a popular technique for the prediction of the various bending characteristics. Narayanasamy and Padmanabhan used the multiple regression analysis for the springback prediction of interstitial free steel [1, 2]. The finite element method in conjunction with orthogonal regression analysis has been implemented by Li et al. [3] for the prediction of U-bending and deep drawing. The regression model for the prediction of the forming limit has been proposed by Yoshida et al. in [4]. Teimouri et al. [5] implemented a regression model for carbon spring steel. Multi-regression modelling of the springback effect on an automotive body in white stamped parts has been done by Bashah et al. [6]. Zhan et al. [7] used the regression prediction for the numerical control of thin-walled tube forming. Initial study of the phenomenological regression approach has been already done by Vorkov et al. [8] in order to predict various bending characteristics.

Naturally, besides the regression modelling the forming community tried to predict the bending characteristics by various means. Kurtaran [9] compared different approaches (artificial neural network, empiric DIN-6935, and response surface models) for prediction of bend allowance. Analytical approach to predict springback and bend allowance have been developed by the research group of T. Altan [10, 11]. De Vin [12] has studied the real curvature of a bend plate and its implication on the adaptive control in air bending. Currently, also less traditional approaches have been used, for instance, Strano et al. [13] used fusion or hierarchical metamodeling for the prediction of bend allowance.

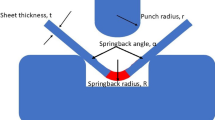
Most of the prediction models for air bending focus on springback prediction (Fig. 2b). Indeed, the springback angle Δβ (Fig. 2b) is probably the most important and the most difficult to control parameter. However, the knowledge of other bending characteristics is also necessary to apply the bending process in industrial applications. For instance, the bend allowance, as the difference between the initial plate length and the sum of bent flange lengths (Fig. 2c), is necessary to obtain the exact bend length of a flat pattern. The bending force is another bending characteristic that should be considered carefully. It informs about the required press-brake capability and the risk of tooling damage. Finally, the position of contact points (Fig. 2a) is important to predict the bending force [14].

Fig. 2

Characteristics of large radius bending: contact points position (a), springback (b), and bend allowance (c)

While there are several existing closed form analytical solutions for air bending, they are not able to predict large radius air bending accurately due to its peculiarities (e.g. multi-breakage effect [15]). Regression analysis provides a flexible and robust way to get a valid prediction of large radius air bending. In this work, we developed prediction models for all-important bending characteristics (contact points, bending force, springback, and bend allowance) by means of two regression approaches.

Experimental investigation

Regression fitting and comparison procedures have been developed on the basis of an extensive experimental investigation which is completely described in [16] and experimental data are presented in the Dataverse scientific repository [17]. Two types of high-strength steels are considered in this work: Strenx 700 MC – a hot-rolled structural steel - and Strenx 1300 – a cold-rolled ultra-high strength structural steel. Table 1 presents the material parameters used for the development of the regression models obtained by the tensile tests.

Table 1 Material and plate parameters of high-strength steels

The experimental investigation was conducted on a press-brake with a capacity of 50 metric tons (Fig. 3). A camera attached to the upper ram of the press-brake was used to film the bending process. For minimization of the telecentric effect, the camera is mounted at a distance of 1.5 m from the forming station. The forming stage was monitored by means of a LabVIEW script: a profile of the plate was extracted from the images and the forming angles were measured afterwards. A force cell, which consists of two Kistler 9031a washers, was used for the measurement of the bending force. The data from the force cell were also logged by a LabVIEW script. The complete description of accuracy and reproducibility of the measurement equipment and methods can be found in [16] with the corresponding data set in [18].

Fig. 3

Press-brake and testing equipment

Four dies with different openings w₀ have been selected for the experimental study: 40 mm, 50 mm, 60 mm, and 80 mm. Punches with a radius R_p of 10 or 20 mm were used for every die, a radius of 30 mm was used for the 60 mm and 80 mm dies, and a radius of 40 mm for the 80 mm die. Figure 4 shows the notation for the plate and tooling dimensions. The width of the bent plates is 60 mm. The experimental investigation used in this work resulted in the dataset with 167 data points split up between both materials [17], Table 2 presents the scheme of experimental plan. Experiments are restricted to configurations that are physically possible (e.g. a punch diameter less than a die opening).

Fig. 4

Tooling and plate dimensions

Table 2 Scheme of experimental plan

Phenomenological approach

This section describes the phenomenological approach for the regression modelling. 167 experiments have been used to calculate models for phenomenological and circular approaches. The model is based on phenomenological observations and conventional analytical formulas, and further compared with the experimental data of the large radius air bending. Extensive analysis and interpretation of the large data set that was generated previously made clear that process parameters exhibit clear tendencies, which should in principle qualify a regression model concept for the quantification of process laws.

All fitting procedures and statistical parameter calculations for both models have been carried out in JMP Pro 13 software. The fitting is done with the polynomial centering, which allows making the regression coefficients more interpretable when interactions are presented in a model. In order to distinguish the parameters obtained by the phenomenological approach, these parameters are expressed with the index p e.g. l_cp, F_p etc.

Contact points position

The position of the contact points between a punch and a plate determines the bending force. This position should be considered carefully to achieve an adequate prediction of the loading scheme during the forming process. The parameter l_c is used as the characteristic value for the contact points position and is defined as the distance between the contact points and the central bend position (Fig. 2a).

As shown in [14, 16], the position of the contact points l_c obeys a linear trend with respect to the bending angle. Figure 5 illustrates this trend. This parameter also shows limited dependency on the material parameters, whereas it strongly depends on the tooling and plate dimensions. Since a linear behavior trend is expected for the contact points, multiple linear regression with the plate and tooling dimensions as the independent variables is expected to deliver the necessary prediction quality.

Fig. 5

Position of the contact points for a die opening of 80 mm and a punch radius of 20 mm. Thickness: 6 mm

After the fitting procedure, the position of the contact points as parameter l_cp (depicted as l_c in Fig. 2a) is given as:

$$ \kern.02em {l}_{cp}=25.933+0.479\ t+0.518\ {R}_p-0,035\ {w}_0-0.217\kern0.2em \beta -0.010\cdotp \left({R}_p-20.419\right)\left(\beta -121.431\right)+0.001\cdotp \left({w}_0-62.395\right)\left(\beta -121.431\right)\kern2em $$

(1)

where t is the plate thickness, R_p the punch radius, w₀ the die opening, and β the bending angle in degrees.

Equation 1 gives a prediction of contact points position with R² = 0.9890 and mean squared error (MSE) of 0.5428. Table 3 lists statistical parameters for each model effect, where only parameters with p-value of less than 0.01 are kept. The LogWorth parameter is calculated as –log₁₀(p-value). This transformation is used in order to adjust p-value for a more interpretable scale. Sign “*” depicts the interaction between considered effects. Figure 6 shows the residuals for the contact points position prediction, and according to the Shapiro-Wilk test (p-value = 0.1404, W = 0.9874) there is not enough evidence that the residuals are not normally distributed.

Table 3 Statistical parameters for each model effect of Eq. 1

Fig. 6

Residuals for the prediction of contact points position by phenomenological regression

Bending force

The loading scheme for large radius bending is defined by the contact points position and the bending angle. The loading scheme determines the value of the bending force, and the correct value of the bending force allows performing the forming process safely and accurately. However, traditionally industry uses a formula that takes into account only the geometrical configuration of tooling and the material strength:

$$ F=K\frac{R_m\cdot {t}^2}{w_0} $$

(2)

where K is a material-based constant, R_m the ultimate strength, t the plate thickness, w₀ the die opening.

Equation 2 does not take into account the change of loading scheme throughout the forming stage due to the presence of the multi-breakage effect [15]. Figure 7 shows the four point bending scheme – a typical representation of large radius bending. We propose a better estimation of the die opening or the effective die opening which takes into account the actual loading scheme. It reduces the initial die opening by considering sliding of a plate into a die and the position of contact points which both affect the resulting bending force. The effective die opening is defined as:

$$ {w}_{ef}=w-{R}_d\sin \frac{180-\beta }{2}-{R}_p\ \mathit{\sin}\frac{l_{cp}}{R_p} $$

(3)

where R_d is the die radius, β the bending angle in degrees, l_cp the position of the contact points, R_p the punch radius and w is calculated according to the following equation (Fig. 8):

$$ w={w}_0+2{R}_d\tan \left(45-\frac{\alpha_d}{4}\right) $$

(4)

where α_d is the die angle.

Fig. 7

Loading scheme of large radius air bending

Fig. 8

Scheme for the determination of the die opening

Taking into account the effective die opening as Eq. 3 and considering that the position of the contact points has a non-linear effect on the value of the bending force, the improved prediction model is expressed, by substitution of Eq. 3 in Eq. 2 and adding the fitting parameters.

The fitting parameters are added according to the following reasoning. Figures 9 and 10 show that the conventional prediction does not coincide with the measured values both in absolute values and in the slope of the curve, thus the fitting parameters k_f1 and k_f3 aim to bring the prediction curve to the correct values and slope. Further, the parameter k_f2 adds additional non-linearity effect to projection of the contact points position to fit the measured values more effectively.

Fig. 9

Bending force for a die opening of 40 mm and a punch radius of 20 mm. Plate: Strenx 1300. Thickness: 4 mm

Fig. 10

Bending force for a die opening of 80 mm and a punch radius of 10 mm. Plate: Strenx 700 MC. Thickness: 6 mm

Finally, the fitting equation is given as:

$$ {F}_p={k}_{f1}\frac{R_m\cdot {t}^2}{w-{R}_d\sin \frac{180-\beta }{2}-{\left({R}_p\ \mathit{\sin}\frac{l_{cp}}{R_p}\right)}^{k_{f2}}}+{k}_{f3} $$

(5)

where k_f1, k_f2, and k_f3 are fitting parameters and l_cp is calculated according to Eq. 1.

Since the fitting model for the bending force is not linear in regression parameters, the non-linear regression fitting was executed with a predefined custom model in a form of Eq. 5. After this procedure, the resulting equations for the bending force calculation can be obtained by inserting the corresponding fitting parameters from Table 4 into Eq. 5. The resulting equation delivers the prediction with R² equal to 0.9669 and MSE equal to 11,447.18. Figure 11 shows the residuals for the bending force prediction, and according to the Shapiro-Wilk test (p-value = 0.1404, W = 0.8571) there is enough evidence that the residuals are not normally distributed.

Table 4 Fitting parameters for phenomenological model of bending force according to Eq. 5

Fig. 11

Residuals for the prediction of bending force by phenomenological regression

Springback

Springback is defined as the recovery of the elastic deformations after the removal of applied external forces. A typical formula for the calculation of the springback value can be written as:

$$ \Delta \beta =\frac{2}{E^{\prime }I}{\int}_0^{L_{tot}} MdL $$

(6)

where M is the internal bending moment, E’ = E / (1-ν²) the plane strain modulus, ν the Poisson ratio, I = bt³/12 the second moment of area about the middle axis, and L the position of the plate along a curvilinear axis.

The difference in the transverse displacement of the bent plate allows to distinguish three regions (Fig. 12a). In the outer regions, the displacement pattern is rather straight, whereas significant curvature is observed in the central region between the two contact points. The evolution of the elasticity modulus due to deformation has a significant effect on the resulting value of springback [19]. Taking into account this evolution, it is reasonable to conclude that the deformation level should dictate the value of the elasticity modulus. Thus, two different values of elasticity modulus E and E_sec are assigned to the regions of limited and significant deformations correspondingly (Fig. 12b).

Fig. 12

a Division of the bent plate into three regions according to the level of deformations; b approximation of the bending moment diagram for large radius bending, with the selected elasticity modulus for every region of the plate; c real moment distribution; d representation of the fitting model

The approximation of bending moment diagram is presented in Fig. 12b. This approximation is oversimplified representation of the real bending moment distribution (Fig. 12c). In order to this approximation able to reflect the real moment distribution, we propose the fitting model that allows adjusting for the real moment distribution as depicted in Fig. 12d. This adjusting is assured by inserting two fitting parameters k_s1 and k_s2 in the regression model. The fitting parameter k_s3 is added to the model in order to give a final overall correction to the prediction.

Finally, the fitting equation for the springback in degrees for a unit of length can be written as:

$$ \Delta {\beta}_p=\frac{12}{t}\left({k}_{s1}\frac{2{l}_c}{E_{\mathrm{sec}}^{\prime }}+{k}_{s2}\frac{s}{E^{\prime }}\right)\frac{180}{\pi }+{k}_{s3} $$

(7)

where E’_sec = E_sec/ (1-ν²) is the secant plain strain modulus, k_s1, k_s2, and k_s3 are the fitting parameters.

Table 5 provides the values of the regression parameters along with 95% confidence interval for them obtained by the fitting the linear model of Eq. 7. The resulting equation delivers the prediction with R² equal to 0.9819 and SME equal to 0.4539. Figure 13 shows the residuals for bend allowance prediction, and according to Shapiro-Wilk test (p-value = 0.0018,W = 0.9719) there is enough evidence that these values are not distributed normally.

Table 5 Fitting parameters and 95% confidence interval for phenomenological model of springback according to Eq. 7

Fig. 13

Residuals for the prediction of springback by phenomenological regression

Bend allowance

In addition to the springback, the bend allowance determines the final shape of a bent part. The bend allowance is the difference between the original length of a plate and the sum of the bent flanges (Fig. 2c), and it is used for the determination of the initial length of a blank.

The bend allowance is a measure of the final shape of the bent plate. Therefore, this bending characteristic is primarily associated with the final or product angle. Moreover, when considered for the same geometrical configuration of the plate and tooling, the bend allowance does not exhibit a notable dependence on the material properties, whereas it strongly depends on the geometrical configuration of the tooling and the plate. Figure 14 illustrates the abovementioned points.

Fig. 14

Bend allowance for a die opening of 80 mm and a punch radius of 20 mm. Thickness: 4 mm

As it can be seen from Fig. 14, the bend allowance approximately obeys an exponential trend. The exponential relation should satisfy the following condition: if product angle equals to 180°, the bend allowance should be equal to zero. This condition is derived from the fact that if there is no plastic deformation in the plate, then the bend allowance correction is not required. As in the case of the contact point position, the fitting coefficient should take into account of the geometrical configuration of the plate and tooling. Therefore, based on the phenomenological observations of the experimental data, we propose the following equation for the bend allowance approximation:

$$ {BA}_p=1-{e}^{\left(180-{\beta}^{\hbox{'}}\right)\cdot {f}_{BA}} $$

(8)

where β’ is the measured product angle in degrees, f_BA the fitting parameter that depends only on geometrical parameters.

After a non-linear fitting procedure of the geometrical parameters, the fitting parameter f_BA can be written as:

$$ {f}_{BA}=0.024185+0.000761\ t+0.000240\ {R}_p $$

(9)

Equation 8 gives a prediction of bend allowance with R² = 0.9522 and mean squared error (MSE) of 0.9021. Table 6 lists the statistical parameters for each model effect of Eq. 9, where only parameters with p-value of less than 0.01 are kept. Figure 15 shows the residuals for bend allowance prediction, and according to Shapiro-Wilk test (p-value <0.001, W = 0.8680) there is enough evidence that these values are not distributed normally.

Table 6 Statistical parameters for each model effect of Eq. 9

Fig. 15

Residuals for the prediction of bend allowance by phenomenological regression

Circular approximation approach

The plate is formed into a complicated shape, the cross section of which can be described by a spline approximation or piecewise function. However, as shown in [20], the representation of the plate as two straight lines and a circle can be used to predict the trends within large radius air bending. The complete description of the circular approximation model can be found in [16].

The circular approximation model provides a convenient calculation tool, but does not give an accurate prediction. Nevertheless, the theoretical trends of the circular approximation for the bending characteristics were verified by an experimental investigation, therefore this approximation can be used as the base for the regression model. The difference between the phenomenological approximation and the circular approximation is that the latter is based on the physical based formulas instead of empirical conclusions. It yields the advantage that the regression coefficients obtained from the circular approximation may be used for materials of different types, while the regression coefficients obtained from the phenomenological approximation are more linked to high-strength steels in particular Strenx 700 MC and Strenx 1300. A complete description of the circular approximation can be found in [10] and schemes of this approximation are presented in Fig. 16.

Fig. 16

Circular approximation: (a) profile description, (b) reactions and their levers

For the circular approximation, the bent plate is modeled to be wrapped around the forming tool, thus the radius R_A of curvature at the mid-plane of the plate is equal to the radius of the punch R_p plus half of the plate thickness t. For the model the friction coefficient μ is used based on the Coulomb friction approximation. The calculation of the unit moment ${\upsigma}_{\mathrm{A}}^{\ast }$ can be done according to [16, 21]. According to the circular approximation model, the bending characteristics are defined as (Fig. 16):

$$ {l}_{cir}=\theta \cdot \left({R}_A-\frac{t}{2}\right) $$

(10)

$$ {F}_{cir}=2{F}_n\cos \kern0.2em \theta \cdot \left(1+\mu \kern0.2em \tan \kern0.2em \theta \right) $$

(11)

$$ \Delta {\beta}_{cir}=\frac{12{\sigma}_A^{\ast }}{t}\left(\frac{2{l}_a}{E_{sec}^{\hbox{'}}}+\frac{l_d}{E^{\hbox{'}}}\right) $$

(12)

$$ {BA}_{cir}=2\left({R}_p+\frac{t}{2}\right)\theta -2\left({R}_p+t\right)\tan \kern0.2em \theta $$

(13)

The idea behind the regression model based on the circular approximation is that these prediction formulas are amended by the fitting parameters as:

$$ {K}_{cr}={A}_{cr}\cdot {K}_{cir}+{B}_{cr} $$

(14)

where K_cris the prediction of a bending characteristic according to the circular regression, K_cir the circular approximation prediction of the same bending characteristic, A_cr and B_cr the fitting parameters. A_cr is dimensionless and B_cr has the same dimension as K_cr.

Table 7 lists the fitting parameters for the regression model based on the circular approximation.

Table 7 Fitting parameters and corresponding confidence intervals for the circular approximation regression (Eq. 14)

Figures 17, 18, 19 and 20 show residuals for the prediction by means of circular regression, and Table 8 summarizes statistical parameters for the circular regression model.

Fig. 17

Residuals for the prediction of contact points position by circular regression

Fig. 18

Residuals for the prediction of bending force by circular regression

Fig. 19

Residuals for the prediction of springback by circular regression

Fig. 20

Residuals for the prediction of bend allowance by circular regression

Table 8 Statistical parameters for circular regression prediction (Eq. 14)

Results and discussion

This section presents the results obtained by the phenomenological and circular approximation approaches. In addition, in this section we discuss the prediction quality of the models by calculating the several comparison parameters, namely the coefficient of determination R², the average absolute error ε_av and the maximal absolute error ε_max. ε_av is calculated as the average difference between the predicted and experimental data taken by absolute value, and ε_max is the maximum value of this difference or the maximum prediction error.

Table 9 lists comparison parameters for both regression approaches. The same dataset is used both for the fitting and assessment of the regression models. All data used in this section can be found in the Dataverse research data repository: experimental data in [17] and regression data in [22].

Table 9 Comparison of the two regression approaches with experimental results

Examples of comparison for contact points position between the regression prediction and experimental data are presented in Figs. 21 and 22. The phenomenological and circular approaches both deliver an accurate prediction of this bending characteristic. This also can be confirmed by very high values of R² in Table 9, which are very close to 1.0. When compared with circular regression, the phenomenological regression delivers better results since both ε_av and ε_max are lower.

Fig. 21

Position of the contact points for a die opening of 60 mm and a punch radius of 30 mm. Plate: Strenx 700 MC. Thickness: 6 mm

Fig. 22

Position of the contact points for a die opening of 60 mm and a punch radius of 10 mm. Plate: Strenx 1300. Thickness: 4 mm

Figures 23 and 24 provide examples of comparison between predicted values and experimental results for the bending force. In this case, the accuracy of the prediction by both models is acceptable, with R² above 0.96. The prediction by means of circular approximation, however, provides better quality, which can be seen by the higher value of the coefficient of determination and lower values of average and maximal absolute errors. It is also important to mention that the conventional prediction of the bending force (Eq. 2) does not reflect its actual behavior during the bending operation. Whereas, both proposed models, as it can be seen from Fig. 24, predict not only the trend of increase of bending force with decrease of the bending angle, but also calculate values that are very close to the measured data.

Fig. 23

Bending force for a die opening of 50 mm and a punch radius of 20 mm. Plate: Strenx 700 MC. Thickness: 6 mm

Fig. 24

Bending force for a die opening of 60 mm and a punch radius of 30 mm. Plate: Strenx 1300 MC. Thickness: 4 mm

Figures 25 and 26 show examples of comparisons between experimental data and regression prediction according to Eq. 7 and Eq. 12. The springback depends not only on change of the loading scheme, but also on the change of the material parameters during the forming. This makes the prediction of the springback the most challenging task among all bending characteristic predictions. Despite these difficulties, both regression approaches provide a valid prediction with R² above 0.95: phenomenological – 0.9815, circular – 0.9669. Even for the phenomenological regression with very high value of R², the value of ε_max is significant and equal to 3°. This high value of the maximal prediction error is for the biggest angle of the bending process of Strenx 700 MC 4 mm with a die of 80 mm and a punch radius of 40 mm. At the later stages of this forming process, the punch already penetrates the bent plate and the process cannot be considered as pure air bending. Apparently, this cannot be taken into account during the construction of the regression model. These cases should be monitored and excluded from the prediction, and probably specialized models should be developed in order to predict the springback in these cases.

Fig. 25

Springback for a die opening of 60 mm and a punch radius of 20 mm. Plate: Strenx 700 MC. Thickness: 4 mm

Fig. 26

Springback for a die opening of 80 mm and a punch radius of 40 mm. Plate: Strenx 1300 MC. Thickness: 6 mm

Figures 27 and 28 present examples of comparison between measured bend allowance and predicted values for Strenx 700 MC and Strenx 1300 correspondingly. In this case, the phenomenological regression provides superior prediction quality, whereas the circular approximation approach turns out to be less accurate. Both models are able to predict the trends of the bend allowance quite accurately. However, the comparison parameters show that the circular approximation model fails to deliver acceptable results, i.e. R² below 0.85 and high values of average and maximal absolute errors. This can be explained by the fact that the original fit function (Eq. 13) based on a simple trigonometric relation from DIN 6935 does not capture the exact behavior of a bent plate after springback, however the phenomenological equation is able to do this effectively.

Fig. 27

Bend allowance for a die opening of 80 mm and a punch radius of 30 mm. Plate: Strenx 700 MC. Thickness: 4 mm

Fig. 28

Bend allowance for a die opening of 60 mm and a punch radius of 20 mm. Plate: Strenx 1300. Thickness: 6 mm

Taking the prediction accuracy for all bending characteristics, neither the phenomenological, nor the circular approximation approach outperforms the other. The positions of the contact points can be predicted accurately by the two approaches, but the phenomenological approach has a small edge over the circular regression due to the lower average absolute error. The bending force also can be predicted by both approaches, however in overall, for this bending characteristic a slightly better prediction is expected by using the circular approach. For the prediction of the springback, the phenomenological regression model provides a prediction that is a bit more accurate. Finally, for the bend allowance, the phenomenological approach delivers much better results, whereas the use of the circular approach is not desirable.

Based on the above results, a hybrid regression approach is recommended for the prediction of the bending characteristics for large radius bending. Contact points position, springback angle and bend allowance should be predicted by the model based on the phenomenological observations, but the bending force should preferably be calculated by means of the circular regression model. This combination of prediction models assures the maximum values of R² for each prediction parameters, which in general expresses the prediction quality.

Conclusions

Based on regression modelling an accurate prediction of large radius bending can be achieved. However, for different bending characteristics different approaches are advisable. The proposed regression approaches were compared with a wide range of experiments and the quality of the regression prediction was assessed by means of a number of parameters: coefficient of determination R², average absolute error ε_av, and maximal absolute error ε_max.

The regression formulas can be used as an accurate approximation tool for the calculation of the industrially relevant bending characteristics within the working space, which is bounded by the experimental investigation. The formulas for the bend allowance and contact points do not depend on the material parameters and they are expected to be valid for any tool combination. For the bending force and springback, only a few bending tests should be performed in order to obtain a solution for a new material, since the physics reflected by the underlying equations, as shown in the current and previous works of authors, are generic for large radius air bending. It is important to note that only a limited number of material characteristics is needed to achieve acceptable results. These parameters are the elastic modulus and ultimate stress, which are usually easy to obtain, and the secant elastic modulus. Moreover, the secant elastic modulus can be substituted by the initial elastic modulus, but the results are expected to be less accurate in this case.