1 Introduction

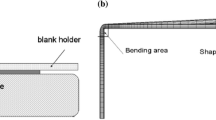
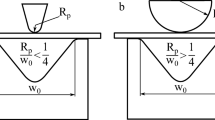
Air bending is one of metal forming processes to produce straight-line bends on metal sheets, by using a die having a pair of shoulders [1]. During the air bending, the sheet metal is placed on the pair of the shoulders that are separated by a certain distance, the die gap. A punch load is applied at the mid-span of the sheet material to render a displacement. At the end of the deformation process, the bend angle is always smaller than the initial load angle after the punch load is removed. This inevitable phenomenon is due to the elastic recovery of the sheet metal, which is called springback.

For materials with high strength, air bending is a preferred method over V-die bending [2,3,4,5]. Also, air bending allows overbending to compensate the springback effect. Generally, the extent of springback radii and the angle of the sheet metal are closely related to the sheet geometry, tool design, and metal properties. It is suggested that the degree of springback increases as a result of an increasing radius of the bend and a decreasing thickness [6, 7]. These parameters are independent from each other and have different impacts on the springback magnitude, which are usually described by the springback radius and angle. The eventual springback magnitude is a synergistic result of these parameters, the understanding of which usually requires a large amount of efforts in experiment design, tests, and measurements. The Taguchi orthogonal array of experiments is commonly used to design experiments with a large number of variables and a relatively small amount of experimental trials [8]. However, parameter optimizations through the Taguchi method are based on minimizing the effects of uncontrollable factors (noise factors), which do not provide numerical correlations between variables and target performance.

Several mathematical methods have been developed to estimate the springback effect. For example, by assuming the workpiece to be a narrow beam, a quantitative method is proposed to predict the residual stress and the springback magnitude [9, 10]. However, this method ignores the presence of the transverse stress during the forming process, which leads to an inaccurate prediction. Another analysis based on the Young’s modulus, yield strength, and thickness of metal sheets presents a chart that provides comparisons between the initial bend radius and final bend radius as a design guidance. Besides, numerical equations are developed to describe the springback magnitude and residual stress distribution as a function of the sheet thickness, punch radius, and mechanical properties of the material, such as stress-strain characteristics [11]. Furthermore, molecular dynamics simulation techniques and finite element modeling (FEM) are utilized to simulate the metal forming process [12,13,14,15,16]. The study shows that the springback is proportional to the bending moment and the bent arc length, which are dependent on the strength, strain hardening, and normal anisotropy. However, these approaches require a lot of data inputs and computational resources due to complexities associated with air bending processes.

Recently, data driven approaches, such as the neural network [17], Gaussian process regression (GPR) [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38], and simple linear regression [39], have been used to model important physical parameters and materials performance in diverse systems, such as magnetocaloric effects in lanthanum manganites [20,21,22, 26], superconducting transition temperature in high-temperature superconductors [18, 19, 35, 37], lattice constants of cubic, orthorhombic, and monoclinic perovskites and half-Heusler alloys [24, 28, 29, 31, 33, 39], optical and electronic properties of oxides [25, 27], thermal properties of nanofluids, lubricant additives, and polymers [23, 34, 36], glass transitions [30], transformation temperature for shape memory alloys [32], and magnetic performance of superconducting solenoids [39]. Particularly, the GPR technique has been found to generate decent prediction performance for small and medium sample sizes. By combining the Taguchi method with statistical methods, researchers are vable to analyze the relationship between multiple manufacturing process parameters and workpiece characteristics [40, 41]. Statistical regression techniques and other soft computing are often categorized as machine learning approaches, which have reasonable tolerances of uncertainties, approximations, and imprecisions [42,43,44,45,46]. Several machine learning approaches have been taken to predict important metal forming and casting behavior. For example, an optimized method combining the artificial neural network and Taguchi method is used to analyze the radial force and strain inhomogeneity in the radial forging process. The results show good agreements between the optimized method and conventional FEM method [47]. Fuzzy logic and support vector regression techniques are also incorporated with the Taguchi method to predict the cutting tool life [48]. For machine learning approaches, the average percent deviation, generalization capability, and runtime are the main characteristics that are used to compare among the models.

GPRs are probabilistic models, which are simple and require relatively short runtime. To authors’ knowledge, this approach has not been used to predict the springback magnitude in air bending. In the current study, we develop the GPR model to predict springback radii and angles of advanced and ultra-high strength sheet steels based on the sheet geometry, tool design, and metal properties. The model manifests accurate and stable performance for the data considered, and thus might be promising as a fast, robust, and low-cost tool for springback magnitude estimations.

2 Methodology

GPRs are nonparametric probabilistic models.Footnote 1 Let \(\left\{ \left( x_{i}, y_{i}\right) ;i=1,2, \ldots , n\right\} \), where \(x_{i} \in {\mathbb {R}}^{d}\) and \(y_{i} \in {\mathbb {R}}\), be the training dataset from a distribution that is unknown. Provided \(x^{new}\)-the input matrix, constructed GPRs make predictions of \(y^{new}\)-the response variable.

Let \(y=x^{T} \beta +\varepsilon \), where \(\varepsilon \sim N\left( 0, \sigma ^{2}\right) \), be the linear regression model. The GPR tries to explain y through incorporating \(l(x_{i})\)-the latent variable, where \(i=1,2, \ldots , n\), from a GP such that \(l(x_{i})\)’s are jointly Gaussian-distributed, and b-basis functions that project x into a p-dimensional feature space. Note that the smoothness of y is captured by \(l(x_{i})\)’s covariance function.

The covariance and mean characterize the GPR. Let \(k\left( x, x^{\prime }\right) ={\text {Cov}}\left[ l(x), l\left( x^{\prime }\right) \right] \) represent the covariance, \(m(x)=E(l(x))\) the mean, and \(y=b(x)^{T} \beta +l(x)\), where \(l(x) \sim GP\left( 0, k\left( x, x^{\prime }\right) \right) \) and \(b(x) \in {\mathbb {R}}^{p}\), the GPR. The parameterization of \(k\left( x, x^{\prime }\right) \) usually is through \(\theta \)-the hyperparameter and thus one could have \(k\left( x, x^{\prime } | \varvec{\theta }\right) \). Different algorithms generally make estimations of \(\beta \), \(\sigma ^{2}\), and \(\theta \) during the process of model training and allow one to specify b and k, as well as parameters’ initial values.

We investigate five kernels-the exponential, squared exponential, Matern 5/2, rational quadratic, and Matern 3/2-specified in Eqs. (1)–(5), respectively, where \(\sigma _{l}\)-the characteristic length scale-defines how far apart \(x's\) could be so that \(y's\) are uncorrelated, \(\sigma _{f}\) is the signal standard deviation, \(r=\sqrt{\left( x_{i}-x_{j}\right) ^{T}\left( x_{i}-x_{j}\right) }\), and \(\alpha >0\) is the scale-mixture parameter. In addition to these five kernels, we also take into consideration their automatic relevance determination (ARD) versions, specified in Eqs. (6)–(10), that use a separate length scale, \(\sigma _{m}\), for each predictor, where \(m=1,2,...,d\) and d is the number of predictors. \(\theta \) under this circumstance is parameterized as \(\theta _{m}=\log \sigma _{m}\) for \(m=1,2,...,d\) and \(\theta _{d+1}=\log \sigma _{f}\).

$$\begin{aligned}&k\left( {x}_{i}, {x}_{j} | {\theta }\right) =\sigma _{f}^{2} \exp \left( -\frac{r}{\sigma _{l}}\right) \end{aligned}$$
(1)
$$\begin{aligned}&k\left( x_{i}, x_{j} | \theta \right) =\sigma _{f}^{2} \exp \left( -\frac{1}{2} \frac{\left( x_{i}-x_{j}\right) ^{T}\left( x_{i}-x_{j}\right) }{\sigma _{l}^{2}}\right) \end{aligned}$$
(2)
$$\begin{aligned}&k\left( {x}_{i}, {x}_{j} | \theta \right) =\sigma _{f}^{2}\left( 1+\frac{\sqrt{5} r}{\sigma _{l}}+\frac{5 r^{2}}{3 \sigma _{l}^{2}}\right) \exp \left( -\frac{\sqrt{5} r}{\sigma _{l}}\right) \end{aligned}$$
(3)
$$\begin{aligned}&k\left( {x}_{i}, {x}_{j} | {\theta }\right) =\sigma _{f}^{2}\left( 1+\frac{r^{2}}{2 \alpha \sigma _{l}^{2}}\right) ^{-\alpha } \end{aligned}$$
(4)
$$\begin{aligned}&k\left( x_{i}, x_{j} | \theta \right) =\sigma _{f}^{2}\left( 1+\frac{\sqrt{3} r}{\sigma _{l}}\right) \exp \left( -\frac{\sqrt{3} r}{\sigma _{l}}\right) \end{aligned}$$
(5)
$$\begin{aligned}&k\left( {x}_{i}, {x}_{j} | {\theta }\right) =\sigma _{f}^{2} \exp \left( -\sqrt{\sum _{m=1}^{d} \frac{\left( x_{i m}-x_{j m}\right) ^{2}}{\sigma _{m}^{2}}}\right) \end{aligned}$$
(6)
$$\begin{aligned}&k\left( x_{i}, x_{j} | \theta \right) =\sigma _{f}^{2} \exp \left( -\frac{1}{2} \sum _{m=1}^{d} \frac{\left( x_{i m}-x_{j m}\right) ^{2}}{\sigma _{m}^{2}}\right) \end{aligned}$$
(7)
$$\begin{aligned}&k\left( x_{i}, x_{j} |\theta \right) =\sigma _{f}^{2}\exp \left( -\sqrt{5\sum _{m=1}^{d} \frac{\left( x_{i m}-x_{j m}\right) ^{2}}{\sigma _{m}^{2}}}\right) \nonumber \\&\left( 1+\sqrt{5\sum _{m=1}^{d} \frac{\left( x_{i m}-x_{j m}\right) ^{2}}{\sigma _{m}^{2}}}+\frac{5}{3} \sum _{m=1}^{d} \frac{\left( x_{i m}-x_{j m}\right) ^{2}}{\sigma _{m}^{2}}\right) \end{aligned}$$
(8)
$$\begin{aligned}&k\left( x_{i}, x_{j} | \theta \right) =\sigma _{f}^{2}\left( 1+\frac{1}{2 \alpha } \sum _{m=1}^{d} \frac{\left( x_{i m}-x_{j m}\right) ^{2}}{\sigma _{m}^{2}}\right) ^{-\alpha } \end{aligned}$$
(9)
$$\begin{aligned}&k\left( x_{i}, x_{j} | \theta \right) =\sigma _{f}^{2}\exp \left( -\sqrt{3\sum _{m=1}^{d} \frac{\left( x_{i m}-x_{j m}\right) ^{2}}{\sigma _{m}^{2}}}\right) \nonumber \\&\qquad \qquad \qquad \quad \left( 1+\sqrt{3\sum _{m=1}^{d} \frac{\left( x_{i m}-x_{j m}\right) ^{2}}{\sigma _{m}^{2}}}\right) \end{aligned}$$
(10)

We investigate four basis functions-the empty, constant, linear, and pure quadratic-specified in Eqs. (11)–(14), respectively, where \({B}=\left( {{b}\left( {x}_{1}\right) },\,{{b}\left( {x}_{2}\right) },\,{\cdots }\, , {{b}\left( {x}_{n}\right) }\right) ^{T}\), \({X}=\left( {x}_{1}, {x}_{2}, {\cdots } , {x}_{n}\right) ^{T}\), and \(X^{2}=\left( \begin{array}{cccc}{x_{11}^{2}} &{} {x_{12}^{2}} &{} {\cdots } &{} {x_{1 d}^{2}} \\ {x_{21}^{2}} &{} {x_{22}^{2}} &{} {\cdots } &{} {x_{2 d}^{2}} \\ {\vdots } &{} {\vdots } &{} {\vdots } &{} {\vdots } \\ {x_{n 1}^{2}} &{} {x_{n 2}^{2}} &{} {\cdots } &{} {x_{n d}^{2}}\end{array}\right) \).

$$\begin{aligned} B= & {} Empty \,Matrix \end{aligned}$$
(11)
$$\begin{aligned} B= & {} I_{n\times 1} \end{aligned}$$
(12)
$$\begin{aligned} B= & {} [1, X] \end{aligned}$$
(13)
$$\begin{aligned} B= & {} \left[ 1, X, X^{2}\right] \end{aligned}$$
(14)

For parameter estimations, we maximize the marginal log likelihood function in Eq. (15), where \(K({X},{X}|{\theta })\) represents the covariance matrix:

\(\left( \begin{array}{cccc}{k\left( x_{1}, x_{1}\right) } &{} {k\left( x_{1}, x_{2}\right) } &{} {\cdots } &{} {k\left( x_{1}, x_{n}\right) } \\ {k\left( x_{2}, x_{1}\right) } &{} {k\left( x_{2}, x_{2}\right) } &{} {\cdots } &{} {k\left( x_{2}, x_{n}\right) } \\ {\vdots } &{} {\vdots } &{} {\vdots } &{} {\vdots } \\ {k\left( x_{n}, x_{1}\right) } &{} {k\left( x_{n}, x_{2}\right) } &{} {\cdots } &{} {k\left( x_{n}, x_{n}\right) }\end{array}\right) \). The algorithm will first compute \(\hat{{\beta }}\left( {\theta }, \sigma ^{2}\right) \), which maximizes the log likelihood with respect to \(\beta \) provided \(\theta \) and \(\sigma ^{2}\). It then gets the \(\beta \)-profiled likelihood,

\(\log \left\{ P\left( {y} | {X}, \widehat{{\beta }}\left( {\theta }, \sigma ^{2}\right) , {\theta }, \sigma ^{2}\right) \right\} \), which will be maximized over \({\theta }\) and \(\sigma ^{2}\) to arrive at their estimates.

$$\begin{aligned} \log P\left( {y}|{X},{\beta },{\theta },\sigma ^{2}\right)= & {} -\frac{1}{2}\{({y}-{B}{\beta })^{T}[K({X}, {X}|{\theta })\nonumber \\&+\sigma ^{2} I_{n}]^{-1}({y}-{B} {\beta })\}-\frac{n}{2}\log 2\pi \nonumber \\&-\frac{1}{2}\log \left| K({X},{X}|{\theta })+\sigma ^{2} {I}_{n}\right| \end{aligned}$$
(15)
Fig. 1
figure 1

The schematic drawing of the experimental setup

Full size image

Model performance will be assessed by the correlation coefficient (CC), mean percentage error (MPE), root mean square error (RMSE), and mean absolute error (MAE) in Eqs. (16)–(19), where n is the number of data points, \(y_{i}^{exp}\) and \(y_{i}^{est}\) are the i-th (\(i=1,2, \ldots , n\)) experimental and estimated value of the target variable, and \(\overline{y^{exp}}\) and \(\overline{y^{est}}\) are their averages. Our analysis is carried out through MATLAB.

$$\begin{aligned} CC= & {} \frac{\sum _{i=1}^{n}\left( y_{i}^{exp}-\overline{y^{exp}}\right) \left( y_{i}^{est}-\overline{y^{est}}\right) }{\sqrt{\sum _{i=1}^{n}\left( y_{i}^{exp}-\overline{y^{exp}}\right) ^{2} \sum _{i=1}^{n}\left( y_{i}^{est}-\overline{y^{est}}\right) ^{2}}}\nonumber \\ \end{aligned}$$
(16)
$$\begin{aligned} MPE= & {} \frac{1}{n}\sum _{i=1}^{n}\frac{y_{i}^{est}-y_{i}^{exp}}{y_{i}^{exp}} \end{aligned}$$
(17)
$$\begin{aligned} RMSE= & {} \sqrt{\frac{1}{n} \sum _{i=1}^{n} (y_{i}^{exp}-y_{i}^{est})^{2}} \end{aligned}$$
(18)
$$\begin{aligned} MAE= & {} \frac{1}{n} \sum _{i=1}^{n} |y_{i}^{exp}-y_{i}^{est}| \end{aligned}$$
(19)
Table 1 Data and predictions
Full size table
Table 2 GPR model performance
Full size table
Fig. 2
figure 2

Predictions and prediction errors calculated as predictions minus experimental values

Full size image

3 Dataset

Details on the experimental setup, tool use, and measurement setup can be found in [17]. Figure 1 illustrates the schematic drawing of the experimental setup. Air bending tests were performed on five types of advanced and ultra-high strength sheet steels, WELDOX700, WELDOX900 and OPTIM960 with different Young’s modulus (E), yield strength (\(\sigma _{y}\)), strength-hardening exponents (n), Poisson’s ratios, and densities. The factors that have a significant impact on the springback are identified as the sheet thickness (t), tool gap (c), punch radius (r), yield strength (\(\sigma _{y}\)), Young’s modulus (E), and punch displacement (e). For these particular materials, the strain-hardening exponents range from 0.0255 to 0.0431, which are small enough to have neglectable effects on springback. Particularly, the strain–stress characteristic of sheet steels is described by the ratio of the yield strength to Young’s modulus (\(\sigma _{y}/E\)). Therefore, a total of 5 descriptors were used in the Taguchi parameter design for air-bending tests. A URSVIKEN OPTIMA 2200t Press Brake was used for air bending tests. The formed workpieces were measured by the Atos-II three-dimensional laser scanning system with the precision of ± 0.005 mm. A total of 25 experimental trials with orthogonally-designed descriptors were carried out. The data in Table 1 from [17] contain a total of 25 experimental trials acquired from the orthogonal array and are utilized in our study to find the correlation between springback magnitude and influencing factors. With the laser scanning system, a 3D datapoint cloud was obtained. The datapoint cloud data were then transferred into the CAD/CAM software for modeling. The two target variables, springback radii (R) and angles (\(\alpha \)) were thus obtained from the CAD model.

4 Result

Among all kernels and basis functions examined, the GPR model is constructed based on the isotropic exponential kernel (Eq. 1) and constant basis function (Eq. 12), with predictors standardized for R-the springback radius. Its parameter estimates are: \(\sigma =1.3210\), \(\beta =273.1362\) \(\sigma _{l}=28.6942\), and \(\sigma _{f}=294.0364\). For \(\alpha \)-the springback angle, the GPR model is built based on the nonisotropic Matern 3/2 kernel (Eq. 10) and empty basis function (Eq. 11), with predictors nonstandardized. Its parameter estimates are: \(\sigma =0.2641\), \(\sigma _{1}=141.6112\), \(\sigma _{2}=239.9583\), \(\sigma _{3}=165.0488\), \(\sigma _{4}=0.0801\), \(\sigma _{5}=208.5101\), and \(\sigma _{f}=180.8414\), where \(\sigma _{1}\), \(\sigma _{2}\), \(\sigma _{3}\), \(\sigma _{4}\), and \(\sigma _{5}\) are associated with the sheet thickness (t (mm)), tool gap (c (mm)), punch radius (r (mm)), ratio of the yield strength to Young’s modulus (\(\sigma _{y}\) (MPa)/E), and punch displacement (e (mm)), respectively.

Detailed numerical predictions of the two target variables are reported in Table 1. Performance summaries are presented in Table 2 and Fig. 2. It is observed that the GPR models produce stable and accurate predictions. The CCs are 99.99%. The MPEs are 0.0048% and − 0.0020% for the training and validation testing sub-samples for R, and the MPEs are − 0.0001% and 0.0029% for the training and validation testing sub-samples for \(\alpha \). The RMSEs are 0.0095 and 0.0335 for the training and validation testing sub-samples for R, and the RMSEs are 0.0122 and 0.0120 for the training and validation testing sub-samples for \(\alpha \). The MAEs are 0.0074 and 0.0175 for the training and validation testing sub-samples for R, and the MAEs are 0.0098 and 0.0106 for the training and validation testing sub-samples for \(\alpha \).

In [17], a back propagation neural network (BPNN) model and a genetic algorithm (GA) BPNN model are developed for the same dataset studied here. These two models both produce good predictions and the GA-BPNN model produces predictions that are better than the BPNN model. In Table 3, we compare performance of the BPNN, GA-BPNN, and GPR models, and find that the GPR models might have potential to further improve accuracy. But this is only based on the five observations and more out-of-sample applications might be needed to further confirm the usefulness of the GPR models to predict springback radii and angles during the air bending of high strength sheet steels. It also has been found that a smaller springback magnitude might be achieved for materials with a decreased ratio of the yield strength to Young’s modulus, an increased thickness, a decreased tool gap, and an increased punch displacement.

Table 3 Model performance comparisons
Full size table

5 Conclusion

We develop the Gaussian process regression models to predict springback radii and angles in air bending of high-strength sheet steel from influencing factors that include the sheet thickness, tool gap, punch radius, yield strength, Young’s modulus, and punch displacement. The models are simple and accurate and stable for the data considered, which might contribute to fast springback magnitude estimations. By combining the optimization results from the Taguchi method and GPR approach, it might be expected that more quantitative data can be extracted from fewer experimental trials at the same time. The approach may apply to a wide variety of metal forming processes to find statistical correlations among process parameters, performance parameters, and final work piece quality. Statistical relationships among materials properties, process parameters, and target properties in rolling, extrusion, die forming, indenting, and forging can be quantitatively interpreted through the GPR and/or other machine learning models.