Identification of material parameters for thin sheets from single biaxial tensile test using a sequential inverse identification strategy

Prates, P. A.; Oliveira, M. C.; Fernandes, J. V.

doi:10.1007/s12289-015-1241-z

Identification of material parameters for thin sheets from single biaxial tensile test using a sequential inverse identification strategy

Original Research
Published: 14 May 2015

Volume 9, pages 547–571, (2016)
Cite this article

Download PDF

Access provided by Autonomous University of Puebla

International Journal of Material Forming Aims and scope Submit manuscript

Identification of material parameters for thin sheets from single biaxial tensile test using a sequential inverse identification strategy

Download PDF

P. A. Prates¹,
M. C. Oliveira¹ &
J. V. Fernandes¹

624 Accesses
18 Citations
Explore all metrics

Abstract

An inverse analysis methodology to simultaneously identify the parameters of various anisotropic yield criteria together with isotropic work-hardening models of metal sheets is outlined. This identification makes use of results of the cruciform biaxial test, i.e., the evolution of the force during the test, for the two axes of the sample, and the major and minor strain distributions along both axes, at a given moment during the test. Based on a study of the sensitivity of the constitutive parameters to the biaxial tensile test results, the inverse identification consists on a procedure that sequentially minimises the gap between experimental and numerical results. Each step of the sequence uses a distinct cost function according to the type of results to be minimised, using a gradient-based optimisation algorithm, the Levenberg-Marquardt method. The inverse methodology allows for the identification of constitutive parameters of complex constitutive models. This sequential identification strategy is compared to a strategy based on a single cost function, involving all parameters and type of results, which has lower performance.

Mechanical design of a heterogeneous test for material parameters identification

Article 21 January 2016

Parameter Identification Applying Full-Field Calibration (FFC) Techniques

Unique Identification of Stiffness Parameters in Hyperelastic Models for Anisotropic, Deformable, Thin Materials Based on a Single Experiment - A Feasibility Study Based on Virtual Full-Field Data

Article Open access 07 February 2024

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

Introduction

The accurate modelling of the plastic behaviour of metal sheets is a fundamental aspect to be considered in numerical simulation of sheet metal forming processes. The non-linear nature of the plastic behaviour of metal sheets makes their characterisation quite complex, depending on factors such as: (i) the constitutive model used to describe the material hardening and anisotropic behaviour; (ii) the experimental tests, comprising the sample geometries and testing conditions and (iii) the strategy for identification of the constitutive parameters. Until now, there is no standard approach for performing the constitutive parameters identification, although several models for describing the yielding [1–9] and hardening [10–16] behaviours, and identification strategies [17–26] have been suggested. The use of deep-drawn components with increasingly elaborate geometries, together with the emergence of new metals and alloys in the sheet metal forming industry, has stimulated the development of sophisticated constitutive models, whose increased flexibility for describing the material plastic behaviour is associated with a larger number of parameters to identify. In contrast, relatively little emphasis has been given to the development of new strategies for constitutive parameters identification, and the classical strategies are predominantly used. In this context, the parameters identification is usually performed using sets of simple mechanical tests that promote linear strain paths and homogeneous deformation in the measuring region, like uniaxial tension, plane strain, shear and biaxial tests. As sheet metal forming processes are carried out under multi-axial strain paths and heterogeneous deformation, the use of these conventional tests is certainly not the most appropriate option to characterise the material plastic behaviour. Therefore, efficient inverse identification procedures are being developed as an alternative to the classical identification strategies. These procedures make use of one mechanical test unlike the classical strategies, for which the number of tests increases with the number of parameters to be identified. In general, this issue does not arise in inverse identifications, provided that the experimental results are sensitive to the parameters to be identified.

The use of optical full-field measurement techniques for analysing heterogeneous strain fields, such as digital image correlation (DIC), has motivated the development of inverse methods for identification of constitutive parameters. These methods are based on the minimisation of the gap between the numerical and experimental results of one mechanical test. A comprehensive overview on this topic can be found in [27]. Approaches for the inverse parameters identification have been conducted using the biaxial tensile testing of cruciform specimens (see e.g., [28–32]). For example, in a recent work by Zhang et al. [32], the parameters identification of Hill’48 [1] and Bron and Besson [5] yield criteria was performed for AA5086 aluminium sheet, using two methods: (i) a classical one, using conventional homogeneous tests, and (ii) an inverse analysis, from only one biaxial tensile test of a cruciform sample. The inverse analysis methodology consists of minimising the gap between the experimental and numerical distributions of the major and minor strains along the diagonal direction of the sample central area, at an instant immediately before rupture, using a SIMPLEX optimisation algorithm. The authors conclude that both methods provide similar yield contours, and so a single biaxial tensile test is adequate to obtain all the material parameters of the yield criterion for the AA5086 sheet. This and other cases have shown the capability to identify parameters of the constitutive laws from tests inducing heterogeneous deformation in the samples, as the biaxial cruciform test adopted in the current work.

It turns out, however, that the evaluation of the performance of inverse methodologies is a sensitive issue. Generally, this assessment is performed using the following procedures. One of them consists on the comparison between experimental and identified results from simple classical tests (e.g., [31, 33, 34]), which are not representative of the whole plastic behaviour, even if in a large number. Also, the direct comparison between the assessed results with those obtained with other identification strategies is used (e.g., [29, 32, 35, 36]). This allows comparing strategies, but does not assess the efficiency of the strategy to represent the mechanical behaviour of the material. In general, none constitutive model and identification strategy allows to perfectly describe the behaviour of a material. Finally, the use of deep-drawing tests for assessing the performance of the identification (e.g., [21, 24, 35, 37, 38]) is sensitive not only to the constitutive parameters but also to process parameters.

The authors of the current work have previously developed an inverse analysis methodology for the simultaneous identification of the parameters of Hill’48 yield criterion and Swift work-hardening law [11], from results of a single biaxial tensile test on a cruciform specimen [30]. The inverse identification procedure consists on determining a solution for the constitutive parameters, according to an algorithm built from a forward analysis study. The algorithm comprises the minimisation of four cost functions in a sequence of six steps, each one referring to the optimisation of distinct parameters. The proposed identification strategy only requires the measurement of the load evolutions during the biaxial tensile test of the cruciform specimen and the evaluations of the major and the minor principal strains along the axes of the specimen, at a given moment of the test. This simplicity, coupled with the wide range of strain paths occurring in the cruciform specimen during the biaxial test, is an advantage over identification strategies previously proposed, related to the use of full-field measurement methods (e.g., [29]). This methodology also proved to be an alternative to classical identification using conventional tests with homogeneous deformation, which is time-consuming, hard to analyse and liable to uncertainties. In this context, it is now established an inverse methodology that allows for the parameters identification of complex plastic constitutive models, from a single biaxial tensile test of a cruciform specimen. Moreover, it also allows the user to decide which constitutive model best describes the material behaviour. The simultaneous identification of the constitutive parameters (yield criteria and isotropic work-hardening laws) is now performed with resource to an optimisation procedure using a gradient-based optimisation algorithm, the Levenberg-Marquardt method [39], and three distinct cost functions in a pre-specified sequence, depending on the type of result that is minimised.

In order to develop the proposed strategy, computer generated results are used. This allows for the proper design of the identification strategy, enabling the direct comparison of the identified constitutive model with that used as input (see e.g., [40]). In contrast, the use of experimental results leads to difficulties in assessing the extent to which the material behaviour is described by the identified constitutive model.

Numerical model

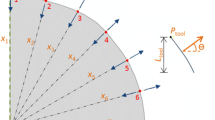
The geometry selected for the cruciform specimen was previously designed and optimised, in order to ensure the occurrence of strain paths that are commonly observed in sheet metal forming processes, i.e., strain paths ranging from uniaxial tension (in the arms region of the specimen) to biaxial tension (in the central region of the specimen) [30]. Fig. 1 shows the geometry and the dimensions of the cruciform specimen in the sheet plane. The 0x and the 0y axes coincide with the rolling direction (RD) and the transverse direction (TD) of the sheet, respectively. The cruciform specimen is submitted to equal displacements in both 0x and 0y directions. The displacements along the 0x and 0y axes are measured at points A and B, respectively. The sheet thickness is equal to 1.0 mm.

Due to geometrical and material (orthotropic) symmetries, the numerical simulation model only considers one eighth of the specimen. The specimen is discretised with tri-linear 8-node hexahedral solid elements associated to a selective reduced integration, with an average in-plane size of 0.5 mm and one layer through-thickness. Numerical simulations were carried out with DD3IMP in-house finite element code, developed and optimised to simulate sheet metal forming processes [41].

Constitutive model

A constitutive model establishes a relationship between the stress and plastic strain states of the deformable body. In case of metal sheets, the full constitutive model is typically defined by: (i) an anisotropic yield function; (ii) a hardening law and (iii) an associated flow rule. The yield function and hardening law allow describing the initial yield surface of the material and its subsequent evolution during plastic deformation. The hypoelastic formulation of the constitutive model assumes that the incremental total strain tensor, dε, can be additively split into elastic and plastic components, dε ^e and dε ^p, respectively:

$$ \mathrm{d}\boldsymbol{\varepsilon } =\mathrm{d}{\boldsymbol{\varepsilon}}^{\mathrm{e}}+\mathrm{d}{\boldsymbol{\varepsilon}}^{\mathrm{p}} $$

(1)

The linear elastic behaviour is considered isotropic and is described by the generalised Hooke’s law, as follows:

$$ \mathrm{d}{\boldsymbol{\varepsilon}}^{\mathrm{e}}=\frac{1+\nu }{E}\mathrm{d}\boldsymbol{\sigma } -\frac{\nu }{E}\mathrm{t}\mathrm{r}\left(d\boldsymbol{\sigma} \right)\mathbf{I} $$

(2)

where ν is the Poisson’s ratio, E is the Young’s modulus and tr(σ) is the trace of the Cauchy stress tensor, σ. The associated flow rule states that the increment of plastic strain tensor dε ^p remains normal to the yield surface, for any arbitrary stress increment driven towards the outside of the yield surface:

$$ \mathrm{d}{\boldsymbol{\varepsilon}}^{\mathrm{p}}=\mathrm{d}\uplambda \frac{\partial f\left(\boldsymbol{\sigma}, {\overline{\varepsilon}}^{\mathrm{p}}\right)}{\partial \boldsymbol{\sigma}} $$

(3)

where dλ is a scalar multiplier that depends on the value of the equivalent stress defined by a given yield criterion function, and $ f\left(\boldsymbol{\sigma}, {\overline{\varepsilon}}^{\mathrm{p}}\right) $ is the yield function, representing herein the plastic potential, expressed as a function of the Cauchy stress tensor, σ, and the equivalent plastic strain, $ {\overline{\varepsilon}}^{\mathrm{p}} $.

In this paper, material parameters identification is performed for the following anisotropic yield functions: (i) Hill’48 [1]; (ii) Barlat’91 - below denoted as Yld’91 [2]; (iii) Karafillis & Boyce - below denoted as KB’93 [3] and (iv) Drucker + L [4]. The last three yield functions contain a number of parameters greater than the Hill’48 criterion, namely the so-called isotropy parameters that provide flexibility to the shape of the yield surface of anisotropic materials. Moreover, these criteria can be converted to Hill’48 criterion for predefined values of its parameters.

Hill’48 yield criterion describes the yield surface for orthotropic materials as follows:

$$ f\left({\sigma}_{ij},{\overline{\varepsilon}}^{\mathrm{p}}\right)=F{\left({\sigma}_{\mathrm{yy}}-{\sigma}_{\mathrm{zz}}\right)}^2+G{\left({\sigma}_{zz}-{\sigma}_{\mathrm{xx}}\right)}^2+H{\left({\sigma}_{\mathrm{xx}}-{\sigma}_{\mathrm{yy}}\right)}^2+2L{\tau}_{\mathrm{yz}}^2+2M{\tau}_{\mathrm{xz}}^2+2N{\tau}_{\mathrm{xy}}^2-{Y}^2\left({\overline{\varepsilon}}^{\mathrm{p}}\right)\le 0 $$

(4)

where σ _xx, σ _yy, σ _zz, τ _xy, τ _xz and τ _yz are the components of the Cauchy stress tensor (σ) in the orthotropic axes system of the metal sheet; F, G, H, L, M and N are the anisotropy parameters to be identified and Y ($ {\overline{\varepsilon}}^{\mathrm{p}} $) is the yield stress, which evolution during deformation is defined by the work-hardening law.

The criteria Yld’91, KB’93 and Drucker + L are described through a stress tensor, s, obtained by a linear transformation of the Cauchy stress tensor, σ:

$$ \mathbf{s}=\mathbf{L}:\boldsymbol{\sigma} $$

(5)

where L is the linear transformation operator proposed by Barlat et al. [2]:

$$ \mathbf{L}=\left[\begin{array}{cccccc}\hfill \left({C}_2+{C}_3\right)/3\hfill & \hfill -{C}_3/3\hfill & \hfill -{C}_2/3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill -{C}_3/3\hfill & \hfill \left({C}_3+{C}_1\right)/3\hfill & \hfill -{C}_1/3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill -{C}_2/3\hfill & \hfill -{C}_1/3\hfill & \hfill \left({C}_1+{C}_2\right)/3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {C}_4\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {C}_5\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {C}_6\hfill \end{array}\right] $$

(6)

in which C _i represents the anisotropy parameters, with i = 1,…,6; C _i is equal to 1 for the isotropy condition.

The Yld’91 yield criterion is an extension to anisotropy of the isotropic yield criterion of Hosford [42]:

$$ f\left({\sigma}_{ij},{\overline{\varepsilon}}^{\mathrm{p}}\right)={\left|{s}_1-{s}_2\right|}^m+{\left|{s}_2-{s}_3\right|}^m+{\left|{s}_3-{s}_1\right|}^m-2{Y}^m\left({\overline{\varepsilon}}^{\mathrm{p}}\right)\le 0 $$

(7)

where s ₁, s ₂ and s ₃ are the principal components of the stress tensor s; m is an isotropy parameter that can assume any positive and real value greater than 1. Hosford [42] proposes values of m depending on the crystallographic structure of the material: m is equal to 6 and 8, for metals with BCC (body centred cubic) and FCC (face centred cubic) structure, respectively. As a more general alternative, m can be optimised in the context of constitutive parameter identification, as in the current work.

Karafillis & Boyce yield criterion describes the anisotropy as follows:

$$ f\left({\sigma}_{ij},{\overline{\varepsilon}}^{\mathrm{p}}\right)=\left(1-a\right){\Phi}_1+a\frac{3^{2k}}{2^{2k-1}+1}{\Phi}_2-2{Y}^{2k}\left({\overline{\varepsilon}}^{\mathrm{p}}\right)\le 0, $$

(8)

where a is an isotropic weighting parameter, ranging between 0 and 1; 2 k is an isotropic exponential parameter, with k integer and positive to ensure the convexity of the yield surface, and Φ₁ and Φ₂ are defined as:

$$ {\Phi}_1={\left({s}_1-{s}_2\right)}^{2k}+{\left({s}_2-{s}_3\right)}^{2k}+{\left({s}_3-{s}_1\right)}^{2k} $$

(9)

$$ {\Phi}_2={s}_1^{2k}+{s}_2^{2k}+{s}_3^{2k} $$

(10)

Any yield surface described by Eq. (8) lies between the lower bound of the Φ₁ function (a = 0) (the lower bound of this function occurs for k = +∞ - Tresca yield surface - and the upper bound for k = 1 - von Mises yield surface) and the upper bound of Φ₂ function (a = 1) (the lower bound of this function occurs for k = 1 - von Mises yield surface - and the upper bound for k = +∞ - outside von Mises yield surface). Karafillis & Boyce proposed to set k fixed and equal to a high enough value (k = 15), which enables approximately describing any surface between the lower bound and the upper bound of Eq. (8), varying only the value of the weighting factor a [3], as in this work.

Drucker + L is an extension of Drucker isotropic criterion [43] to anisotropy:

$$ f\left({\sigma}_{ij},{\overline{\varepsilon}}^{\mathrm{p}}\right)={\left[1/2\mathrm{t}\mathrm{r}\left({\mathbf{s}}^2\right)\right]}^3-c{\left[1/3\mathrm{t}\mathrm{r}\left({\mathbf{s}}^3\right)\right]}^2-27{\left(Y\left({\overline{\varepsilon}}^{\mathrm{p}}\right)/3\right)}^6\le 0 $$

(11)

where tr (s) is the trace of the stress tensor s and c is a weighting isotropy parameter, ranging between −27/8 and 9/4, to ensure the convexity of the yield surface.

It is worth highlighting that Hill’48 criterion is a special case of the yield functions described above, under the following conditions: (i) m = 2, for Yld’91 criterion; (ii) a = 0 and k = 1, for KB’93 criterion and (iii) c = 0, for Drucker + L criterion. In all these cases, the equations that relate the Hill’48 yield parameters with those of Yld’91, KB’93 and Drucker + L yield criteria are [44]:

$$ \left\{\begin{array}{l}F=\left(2{C}_1^2+{C}_1{C}_2+{C}_1{C}_3-{C}_2{C}_3\right)/6\\ {}G=\left(2{C}_2^2+{C}_1{C}_2+{C}_2{C}_3-{C}_1{C}_3\right)/6\\ {}H=\left(2{C}_3^2+{C}_1{C}_3+{C}_2{C}_3-{C}_1{C}_2\right)/6\\ {}L=\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{C}_4^2;M=\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{C}_5^2;N=\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{C}_6^2\end{array}\right. $$

(12)

The Swift [11] and Voce [10] laws are used for identifying the isotropic hardening. They are written, respectively:

$$ Y\left({\overline{\varepsilon}}^{\mathrm{p}}\right)=C{\left({\varepsilon}_0+{\overline{\varepsilon}}^{\mathrm{p}}\right)}^n $$

(13)

$$ Y\left({\overline{\varepsilon}}^{\mathrm{p}}\right)={Y}_0+\left({Y}_{\mathrm{Sat}}-{Y}_0\right)\left[1- \exp \left(-{\mathrm{C}}_{\mathrm{Y}}{\overline{\varepsilon}}^{\mathrm{p}}\right)\right] $$

(14)

where $ {\overline{\varepsilon}}^{\mathrm{p}} $ is the equivalent plastic strain and C, ε ₀ and n are the material parameters of Swift law (Y ₀ = Cε ₀ ⁿ is the initial yield stress) and Y ₀, Y _Sat and C _Y are the material parameters of Voce law. For simplicity, it is assumed that the work-hardening law is represented by the uniaxial tensile curve along the rolling direction, which means that the parameters of the yield criteria must fulfil the following equations:

Hill’48:

$$ G+H=1 $$

(15)

Yld’91:

$$ \frac{1}{2\times {3}^m}\left({\left|2{C}_2+{C}_3\right|}^m+{\left|{C}_3-{C}_2\right|}^m+{\left|{C}_2+2{C}_3\right|}^m\right)=1 $$

(16)

KB’93:

$$ \begin{array}{l}\frac{1-a}{2\times {3}^{2k}}\left[{\left(2{C}_2+{C}_3\right)}^{2k}+{\left({C}_3-{C}_2\right)}^{2k}+{\left(-{C}_2-2{C}_3\right)}^{2k}\right]+\\ {}\frac{a}{2\times \left(1+{2}^{2k-1}\right)}\left[{\left({C}_2+{C}_3\right)}^{2k}+{\left(-{C}_2\right)}^{2k}+{\left(-{C}_3\right)}^{2k}\right]=1\end{array} $$

(17)

Drucker + L:

$$ 3{\left[\frac{1}{8\times {9}^3}{\left[{\left({C}_2+{C}_3\right)}^2+{C_3}^2+{C_2}^2\right]}^3-\frac{c}{9^4}{\left[{\left({C}_2+{C}_3\right)}^3+{\left(-{C}_3\right)}^3+{\left(-{C}_2\right)}^3\right]}^2\right]}^{\frac{1}{3}}=1 $$

(18)

In this study, the anisotropy parameters associated to the out-of-plane shear stress are kept as in isotropy (i.e., L = M = 1.5, for Hill’48 yield criterion and C ₄ = C ₅ = 1, for Yld’91, KB’93 and Drucker + L yield criteria), since the results of the biaxial cruciform test are not sensitive to these parameters [30]. This approach is generally adopted in the constitutive parameters identification of metal sheets.

Inverse parameter identification

A potential approach for solving the problem of constitutive parameters identification consists on performing successive numerical simulations of the physical experiment using the finite element method, for example, and obtaining the set of parameters by minimising the gap between the experimental and the numerical results. This is known as inverse identification strategy, where the gap to minimise is described by a cost function that depends on the variables to be analysed.

The inverse identification strategy developed in this work follows up a previous one, proposed by the authors, which allows identifying the parameters of Hill’48 yield criterion and Swift work-hardening law [30], using the results of a unique test, the cruciform biaxial tensile test. Now, the strategy covers a wider range of constitutive models. Hill’48 and three other criteria that can be converted to Hill’48 criterion for predefined values of its parameters were used, although the procedure can be naturally extended to any other criterion. The Swift and Voce work-hardening laws were used. The simultaneous identification of the constitutive parameters (yield surface and work-hardening laws) is performed with resource to a sequential optimisation procedure using a gradient-based optimisation algorithm, the Levenberg-Marquardt method. In case of plastic material parameter identification, gradient-based optimisation algorithms seem to be more efficient than gradient-free algorithms, since they require far less iterations, and so a small number of numerical simulations [29]. The results of the biaxial cruciform test required for implementing the proposed inverse identification strategy are:

(i)
the evolutions of the load, P, with the specimen boundaries displacement, Δl, during the test, for the axes 0x and 0y; Δl is measured at A and B in Fig. 1.
(ii)
the distributions of the total equivalent strain, $ \overline{\varepsilon} $, along the axes 0x and 0y of the sample (i.e., $ \overline{\varepsilon} $ as a function of the distance, d, to the centre of the sample), for a given boundaries displacement, Δl, preceding and close to the value of the displacement at maximum load; the total equivalent strain is determined using von Mises definition:
$$ \overline{\varepsilon}=2{\left[\left({\varepsilon_1}^2+{\varepsilon_2}^2+{\varepsilon}_1{\varepsilon}_2\right)/3\right]}^{1/2} $$
(19)

where ε ₁ and ε ₂ are respectively the major and the minor principal strains, in the sheet plane. The principal strain axes are parallel to the axes of the specimen (in case of the 0x axis, ε ₁ is equal to ε _xx and ε ₂ is equal to ε _yy, and in case of the 0y axis, ε ₁ is equal to ε _yy and ε ₂ is equal to ε _xx - see Fig. 1).
(iii)
the distributions of the strain path ratio, defined by ρ = ε ₂/ε ₁, along the axes 0x and 0y of the sample (i.e., ρ as a function of the distance, d, to the centre of the sample), for the boundaries displacement, Δl, as stated above in (ii).

The strain variables ε ₁ and ε ₂ can be experimentally determined using DIC technique or even the classical circle grid strain analysis. In order to correctly calculate the differences for a certain value of d and Δl, the numerical and reference variables were obtained for the same value of d and Δl. This is achieved by performing linear interpolations of the results.

A forward analysis previously performed by the authors [30] led to the following conclusions concerning the sensitivity of the cruciform test results to the variation of the constitutive parameters values:
1. (i)
  the load evolution during the test (P vs. Δl), for the 0x and 0y axes, is almost only influenced by the work-hardening law parameters (i.e., the initial yield stress, Y ₀, and the parameters that define the work-hardening: n, in case of Swift law, and R _Sat (=Y _Sat - Y ₀) and C _Y, in case of Voce law) and by an amount, K, that depends on the parameters of the yield criterion (e.g., for the case of Hill’48 criterion this amount, K, is equal to the value of (F + H)^1/2, when G + H = 1 (Eq.(15))). In fact, when altering this amount, the σ ₀/σ ₉₀ ratio (where σ ₀ and σ ₉₀ are the tensile yield stresses along the rolling and transverse direction, respectively) is changed, and consequently the relative level of the load evolutions between the 0x and 0y axes, is also altered. The following equations summarise how to estimate the value of K for all yield criteria studied in this work, assuming that Eqs. (15) to (18) are observed:
  
  Hill’48:
  $$ K={\left(F+H\right)}^{1/2}\left(={\sigma}_0/{\sigma}_{90}\right) $$
  (20)
  
  Yld’91:
  $$ K={\left[\frac{1}{2\times {3}^m}\left({\left|{C}_1-{C}_3\right|}^m+{\left|2{C}_1+{C}_3\right|}^m+{\left|2{C}_3+{C}_1\right|}^m\right)\right]}^{\frac{1}{m}}\left(={\sigma}_0/{\sigma}_{90}\right) $$
  (21)
  
  KB’93:
  $$ K={\left[\frac{1-a}{2\times {3}^{2k}}\left[{\left(-{C}_3-{C}_1\right)}^{2k}+{\left(-{C}_3\right)}^{2k}+{\left(2{C}_3+{C}_1\right)}^{2k}\right]+\frac{a}{2\times \left({2}^{2k-1}+1\right)}\left[{\left(-{C}_3\right)}^{2k}+{\left(-{C}_1\right)}^{2k}+{\left({C}_1+{C}_3\right)}^{2k}\right]\right]}^{\frac{1}{2k}}\left(={\sigma}_0/{\sigma}_{90}\right) $$
  (22)
  
  Drucker + L:
  $$ K=\frac{1}{3}{\left[\frac{1}{8}{\left[{C_3}^2+{\left({C}_1+{C}_3\right)}^2+{C_1}^2\right]}^3-\frac{c}{9}{\left[{\left(-{C}_3\right)}^3+{\left({C}_1+{C}_3\right)}^3+{\left(-{C}_1\right)}^3\right]}^2\right]}^{\frac{1}{3}}\left(={\sigma}_0/{\sigma}_{90}\right) $$
  (23)
2. (ii)
  the total equivalent strain distribution ($ \overline{\varepsilon} $ vs. d), evaluated nearly before the maximum load, is influenced by the anisotropy parameters and by the parameters that define the work-hardening (for example n, in case of Swift law);
3. (iii)
  the strain path ratio distribution (ρ vs. d), evaluated nearly before the maximum load, is almost not influenced by the parameters of the work-hardening law;

A complementary forward study is now performed in order to analyse the sensitivity of the cruciform test results to variations of the value of the isotropy parameter of each criterion, which defines the shape of the yield surface. The illustrative cases shown below concern the Swift work-hardening law (with Y ₀ = 100 MPa; C = 288.54 MPa and n = 0.2) and the values of the parameters of the yield criteria are as in the isotropy condition. The von Mises yield criterion is used as reference. The behaviours under comparison are described by Yld’91 (with m = 6), KB’93 (with a = 0.90, for k = 15) and Drucker + L (c = 2) criteria; it should be noted that: (i) Yld’91 becomes von Mises for m = 2; (ii) KB’93 with k = 15 approaches von Mises criterion when a is close to 0.97; and (iii) Drucker + L becomes von Mises for c = 0. Figure 2a shows the yield surfaces of these materials on the plane (σ_xx - σ_yy) for $ {\overline{\varepsilon}}^p $ = 0 (i.e., at the onset of plastic deformation). The results of the forward analysis are summarised in Fig. 2b, d, showing the effects of varying the isotropy parameters relatively to the von Mises yield criterion. These results concern: P vs. Δl (Fig. 2b); $ \overline{\varepsilon} $ vs. d (Fig. 2c) and ρ vs. d (Fig. 2d), which are equal for 0x and 0y axes (isotropic materials). The results in Fig. 2c, d are plotted for Δl = 3 mm, with d measured from the centre of the cruciform specimen up to a distance corresponding to the minimum value of ρ (see Fig. 2d; this minimum occurs for a d value near 38 mm after which ρ increases approaching zero - not shown in the figure). The choice of this range of d values to be used in the inverse analysis intends to avoid: (i) considering two points with the same strain path (the strain paths that occur for d values between about 20 and 38 mm are repeated between this latter d value and the end of the arms of the specimen) and (ii) measuring the variables $ \overline{\varepsilon} $ and ρ close to the heads of the sample, where the comparison between experimental and numerical results can be influenced by the boundary conditions, if they are not properly reproduced numerically.

The sensitivity of the cruciform test results to the variation of the values of the isotropy parameters in the studied range, can be summarised as follows: (i) the load evolution during the test (P vs. Δl), for the 0x and 0y axes, is almost not influenced by the isotropy parameters; in contrast, (ii) the total equivalent strain ($ \overline{\varepsilon} $ vs. d) and the strain path ratio (ρ vs. d) distributions are influenced by the isotropy parameters, showing noticeably complex changes.

The forward analysis conclusions allowed developing an inverse strategy for parameters identification, with the following assumptions: (i) the experimental results under the cruciform biaxial test, concerning the evolutions of P vs. Δl, $ \overline{\varepsilon} $ vs. d and ρ vs. d are determined in advance and (ii) the elastic properties of the material are known.

The proposed inverse parameters identification strategy is detached in two stages. The first stage consists on the simultaneous identification of Hill’48 and work-hardening law parameters, using the results of P vs. Δl and $ \overline{\varepsilon} $ vs. d. The work-hardening parameters must be separately identified for Swift and Voce laws and the law (Swift or Voce) that best describes the results of the cruciform test may be selected to proceed to the next stage of identification. The second stage allows extending the parameters identification procedure to more complex yield functions (Yld’91, KB’93 and Drucker + L, in the current work), whenever the identification carried out during the first stage proves to be insufficient to describe the experimental results of the cruciform test, namely the ρ vs. d results, not analysed in the first stage.

First stage of the identification strategy

The first stage of the inverse identification strategy consists on the identification of the Hill’48 parameters, concurrently with the Swift law parameters, by one side, and with the Voce law parameters, by other side. This stage is detached in three steps: firstly, an initial set of parameters is chosen (Step 1) and then the Levenberg-Marquardt optimisation algorithm is applied, in the next two steps (Steps 2 and 3). These steps sequentially minimise the gap between the following numerical and experimental results of the test: (i) P vs. Δl results, along the 0x and 0y axes, are minimised in Step 2 for identifying the parameters of the work-hardening law and the (F + H)^1/2 value; and (ii) $ \overline{\varepsilon} $ vs. d results, along the 0x and 0y axes, are minimised in Step 3, for identifying the values of the Hill’48 criterion parameters. The choice of this sequence is derived from the forward analysis, which allowed concluding that the variables analysed in Step 2 (P vs. Δl results) remain quite stable during Step 3. Moreover, it should be noted that the simultaneous minimisation of both P vs. Δl and $ \overline{\varepsilon} $ vs. d results in a unique step could lead to somewhat unbalanced identifications, resulting in a less adequate combination of the parameters of the yield criterion and hardening law, as it was concluded from a comprehensive study in a previous work [30].

Step 1
Initial estimate of the parameters of Hill’48 yield criterion and Swift and/or Voce work-hardening laws. The initial values of Hill'48 parameters can be set equal to the isotropic material, i.e., F = G = H = 0.5 and L = M = N = 1.5, as in the current work; alternatively, the initial estimate of the parameters can be determined, for example, from the Lankford coefficients values at various directions in the sheet plane (r ₀, r ₄₅ and r ₉₀, for example), if available. For the first estimate of the parameters of the work-hardening laws, typical values of the material can be used, as in the current work; the parameters obtained by fitting a tensile curve for any strain path, such as tension along the rolling direction, can also be used. A comprehensive study showed that the accuracy of the final results is not influenced (i.e., the material behaviour is similarly accurately described) by the first estimate, although it can influence the number of iterations.
Step 2
Optimisation of the work-hardening parameters (Y ₀, C and n, in case of Swift law, and Y ₀, Y _Sat and C _Y, in case of Voce law) and of the value of K = (F + H)^1/2, by modifying F or H values, for example. The optimisation is carried out by minimising the gap between the numerical and experimental P vs. Δl results, along the 0x and 0y axes, through the following least-squares cost function:
$$ {F}_1\left(\mathbf{A}\right)=\frac{1}{Q_1}{{\displaystyle \sum_{i=1}^{Q_1}{\delta_{P_i}}^2}}_{0\mathrm{x}}+\frac{1}{Q_2}{{\displaystyle \sum_{i=1}^{Q_2}{\delta_{P_i}}^2}}_{0\mathrm{y}} $$
(24)

where δ _P is defined as the relative difference between the numerical, P ^num(A), and the experimental reference load values, P ^exp, during the test, δ _P = (P ^num(A) − P ^exp)/P ^exp, along the 0x and 0y axes; A is the set of parameters to be optimised, i is the measuring point of load (which corresponds to a certain Δl value) and Q ₁ and Q ₂ are the total number of load measuring points, in the 0x and 0y axes respectively. The total number of load measuring points should be equal for both axes. The condition G + H = 1 can be kept unchanged during this step, as in the current study.
Step 3
Optimisation of the values of F, G, H and N anisotropy parameters of the Hill’48 criterion. This is performed by minimising the gap between the numerical and experimental $ \overline{\varepsilon} $ vs. d results along the 0x and 0y axes, through the following least-squares cost function:
$$ {F}_2\left(\mathbf{B}\right)=\frac{1}{R_1}{{\displaystyle \sum_{i=1}^{R_1}{\delta_{{\overline{\varepsilon}}_i}}^2}}_{0\mathrm{x}}+\frac{1}{R_2}{{\displaystyle \sum_{i=1}^{R_2}{\delta_{{\overline{\varepsilon}}_i}}^2}}_{0\mathrm{y}} $$
(25)

Where $ {\delta}_{\overline{\varepsilon}} $ is defined as the relative difference between the numerical, $ {\overline{\varepsilon}}^{\mathrm{num}}\left(\mathbf{B}\right) $, and the experimental reference von Mises total equivalent strain, $ {\overline{\varepsilon}}^{\exp } $, distributions, $ {\delta}_{\overline{\varepsilon}}=\left({\overline{\varepsilon}}^{\mathrm{num}}\left(\mathbf{B}\right)-{\overline{\varepsilon}}^{\exp}\right)/{\overline{\varepsilon}}^{\exp } $, along the 0x and 0y axes; B is the set of constitutive parameters to be optimised, i is the measuring point of the total equivalent strain (which corresponds to a certain d value) and R ₁ and R ₂ are the total number of total equivalent strain measuring points in the 0x and 0y axes, respectively. The total number of measuring points should be equal for both axes. This step keeps the work-hardening parameters and the K = (F + H)^1/2 value as identified in Step 2 and also, by choice, the condition G + H = 1 unchanged; therefore, only N and one of the parameters, F, H, and G are updated in B.

The optimisation procedure for both F ₁ and F ₂ stops when the relative difference between a given set of parameters and the next one is less than a user predefined tolerance, for each of the constitutive model parameters. It is inappropriate to predefine a tolerance for the minimum values of the cost functions, because it depends on how the selected constitutive model describes the behaviour of the material. Generally the parameters are properly identified after Step 3. However, in some cases, especially for severe anisotropy, it is advisable to repeat Steps 2 and 3, although one cycle is usually sufficient. The need to repeat Steps 2 and 3 can be evaluated by computing the value of the cost function F ₁ after Step 3 and comparing its value with that obtained at the end of Step 2. No updating is needed if the order of magnitude of F ₁ remains unchanged.

Second stage of the identification strategy

The second stage of the inverse identification strategy consists on extending the parameter identification to other yield functions, starting from the solution of the parameters of Hill’48 criterion, as previous identified in the first stage. Yield functions, like Yld’91, KB’93 and Drucker + L criteria, contain more parameters than Hill’48 criterion, making them more flexible to describe the experimental reference results. Typically, such yield functions contain the so-called isotropy parameters, which affect the shape of the yield surface and therefore mainly influence the strain path ratio distribution, along the 0x and 0y axes. It is worth mentioning that, at the end of Step 3 of the first stage, the gap between numerical and experimental P vs. Δl and $ \overline{\varepsilon} $ vs. d results, along the 0x and 0y axes, is minimised. But if the experimental ρ vs. d results, along these axes, are far from those numerically obtained, this indicates that the Hill’48 criterion does not conveniently describes the material behaviour. Therefore, at the end of Step 3, it is required to check if the strain path distributions along both axes are well predicted by the numerical simulation, to decide whether to stop or proceed with the optimisation procedure. In the first case, it is accepted that Hill’48 criterion properly describes the behaviour of the material; in the second case, this behaviour is not adequately described and the optimisation can proceed selecting other criteria that eventually describes it better.

Step 4
Evaluation of the requirement to expand the identification to other yield criteria. This evaluation can be performed using a function, characterising the gap between the numerical and experimental strain path distributions, along the 0x and 0y axes, defined as
$$ {F}_3\left(\mathbf{B}\right)=\frac{1}{S_1}{{\displaystyle \sum_{i=1}^{S_1}\varDelta {\rho_i}^2}}_{0\mathrm{x}}+\frac{1}{S_2}{{\displaystyle \sum_{i=1}^{S_2}\varDelta {\rho_i}^2}}_{0\mathrm{y}} $$
(26)

where Δρ is defined as the difference between the numerical, ρ ^num(B), and the experimental reference strain path ratios, ρ ^exp, i.e., Δρ = ρ ^num(B) − ρ ^exp, along the 0x and 0y axes; B is the set of constitutive parameters determined at the end of Step 3, i is the measuring point of the strain path ratio (which corresponds to a certain d value) and S ₁ and S ₂ are the total number of strain path ratio measuring points, in the 0x and 0y axes, respectively. The total number of measuring points should be equal for both axes.

It is up to the decision maker to choose the degree to which the correspondence between numerical and experimental results is acceptable. If proceeding to the second stage of the identification strategy, the parameters to continue optimisation must be obtained from the set of Hill’48 yield criterion parameters optimised during the first stage, which must be converted into the set of anisotropy parameters of one of the Yld’91, KB’93 or Drucker + L yield criteria, using Eqs. (12) and assuming that the isotropy parameters are as follows: m = 2 for Yld’91; a about 0.97 when fixing k = 15 for KB’93; and c = 0 for Drucker + L. The following step (Step 5) consists on optimising the isotropy parameter of the yield criterion, keeping the anisotropy parameters and the work-hardening law unchanged.
Step 5
Optimisation of the isotropy parameters of the yield criterion (m, a and c, for Yld’91, KB’93 and Drucker + L criteria, respectively). This consists on minimising the numerical and the experimental reference Δρ vs. d results along both 0x and 0y axes, through the least-squares cost function F ₃(C), defined as in Eq. (22), where C represents the isotropy parameter to be optimised. The total number of measuring points should also be equal for both axes. As for F ₁ and F ₂, the optimisation procedure stops when the relative difference between a given value of the parameter and the next one is less than the user predefined tolerance.

It is important to point out that the change of the isotropy parameter, occurring during this optimisation step, modifies the shape of the yield surface and also alters its size. In fact, when changing the isotropy parameter, keeping fixed the anisotropic ones, Eqs. (16), (17) and (18) are no longer observed, i.e., the size of yield surface will change. However, even changing the isotropy parameter, the size of the surface can be maintained, as much as possible, by acting on the anisotropy parameters. This should be done by multiplying all the anisotropy parameters by the same amount, such that the full set of parameters obeys to Eqs. (16), (17) and (18). This allows keeping the parameters of the work-hardening law unchanged during this step.
Step 6
Evaluation of the requirement for cycling. At the end of Step 5 it should be checked if the numerical results concerning the evolutions of the load during the test, for both axes, and the distributions of total equivalent strain along these axes are not changed. This can be done computing the values of the cost functions F ₁ and F ₂, after Step 5 and comparing their values with those obtained at the end of Step 3. No updating is needed if the order of magnitude of both cost functions remains unchanged. Generally, the numerical results concerning the load evolution are not significantly changed, unless the isotropy parameter of the yield criterion is far from the value that takes for the Hill’48 criterion (i.e., m = 2, for Yld’91; a about 0.97, for the k value used (equal to 15), for KB’93, and c = 0, for Drucker + L). If significant changes are observed, then Step 2 (first stage) must be performed again (minimisation of F ₁). Even without the need to minimise F ₁, the numerical $ \overline{\varepsilon} $ vs. d results are sensitive to the transition from Hill’48 to other criteria and, consequently, the cost function F ₂ must be minimised again after Step 5. Thus, generally it is necessary to perform a step similar to Step 3 of the first stage, to optimise the values of C ₁, C ₂, C ₃ and C ₆, i.e., the anisotropy parameters of the criterion. As in Step 3 for the Hill’48 criterion, where the value of K = (F + H)^1/2 is kept fixed, the equivalent condition on the parameters of the other yield criteria, defined by the K value (Eqs. (21), (22) and (23)), is also kept unchanged; also the condition defined by one of the equations (16), (17) and (18), depending on the criterion, can be kept unchanged. Therefore, only C ₆ and one of the parameters C ₁, C ₂, and C ₃ need to be updated. At this point, it is advisable to repeat Step 5 and again check the orders of magnitude of functions F ₁ and F ₂. Usually, it is sufficient to perform only one cycle.

Final remarks

Table 1 summarises the proposed inverse identification strategy, showing the type of results, numerical and experimental, which are compared at each step, as well as the cost functions evaluated at each step. The proposed strategy recommends that the optimisation begins with the Hill’48 criterion, using results concerning the loading curve (P vs. Δl) and the distribution $ \overline{\varepsilon} $ vs. d, along the axes 0x and 0y. The optimisation of the loading curve allows realizing which law is most suitable for describing the work-hardening behaviour of the material, regardless of the criteria, and so to make the choice between Swift and Voce laws. The optimisation of the strain distribution allows understanding to what extent the material behaviour is described by the Hill’48 criterion. Furthermore, the comparison between the numerical and experimental distributions of the strain path ratios, ρ vs. d (not optimised until this moment) makes an important additional contribution in this analysis (the distribution $ \overline{\varepsilon} $ vs. d, can be satisfactory, but the strain path ratios may not be adequately described by Hill’48). In cases where it is deemed appropriate extending the identification to other criteria, the isotropy parameter of the selected yield criterion must be optimised, using the distributions of the strain path ratios, ρ vs. d. The procedure can continue by repeating the steps of the first stage using the selected yield criterion, and restarting with the second or third step. The latter case occurs when the parameters of the work hardening law does not need to be optimised.

Table 1 Inverse analysis algorithm for the sequential identification of constitutive parameters (yield criterion and isotropic work-hardening law)

Full size table

This procedure allows addressing the parameter identification problem using autonomous cost functions for each step, which are evaluated one after the other in a pre-specified sequence, as an alternative to perform the parameter identification by minimising a single cost function comprising all material parameters and results of different types, as commonly performed by other authors (e.g., [21, 23, 24, 29]). As it will be shown in the next chapter, the use of a single cost function can lead to a somewhat inadequate description of the plastic behaviour of the material, namely the work-hardening. The currently proposed strategy also has the advantage that, first of all, it allows perceiving to what extent the Hill’48 criterion describes the material behaviour, whose usage is always desirable because of its simplicity. If the Hill’48 criterion does not conveniently describes the material behaviour, the identification results for this criterion provide an initial solution which enables the extension of the inverse analysis to other criteria.

This inverse identification can be applied directly to any of the above-mentioned criteria or further criteria, without going through Hill’48 criterion. The proposal of starting the identification procedure with Hill’48 criterion has the advantage of providing a solution that can be used as initial estimate for parameter identification of more flexible yield criteria. In this context, it should be noted that it is not possible to know a priori which is the most convenient constitutive model to describe the experimental results.

Finally, it should be mentioned that, when the parameter identification is performed by minimising a unique weighted cost function comprising all material parameters and different types of experimental results, as classically used, the solution is influenced by the pre-selected weights for each portion of the function. In the methodology proposed herein, the question of the relative weight of each type of result is solved by establishing the sequence of steps for identifying the parameters of the constitutive model. This has the advantage of not requiring user defined weighting factors to consider the influence of each type of result in the identification.

Inverse analysis: case studies

To illustrate the above described inverse identification strategy, two case studies are considered in the next sections. In each case, computer generated results of the cruciform tensile test were used as “experimental” results. Computer generated results allows for the suitable comparison between inverse analysis and “experimental” results, concerning the yield surface and the work-hardening functions. As mentioned in the Introduction, the use of real experimental cases leads to difficulties in assessing the extent to which the material behaviour is described by the identified constitutive model. In Case Study 1, the material plastic behaviour follows Drucker + L criterion and Swift work-hardening law, while in Case Study 2, the material follows CB2001 yield criterion [4] and a Voce work-hardening law.

The purpose of both case studies is to show how to identify the set of parameters of Hill’48 (first stage), Yld’91, KB’93 and Drucker + L (second stage) yield criteria, simultaneously with the work-hardening law parameters. The main objective of Case Study 1 is to illustrate in a simple way how to perform the proposed strategy and only the parameters of Swift law are identified. In Case Study 2, the set of parameters is identified for both work-hardening laws, Swift and Voce, in order to illustrate how to decide which is the more suitable hardening law for describing the material behaviour. The minimisation procedure adopted for the cost functions F ₁, F ₂ and F ₃ stops when the relative difference between a given set of parameters and the next one is less than 5%, for each of the constitutive model parameters. It was tested that, using different initial sets of parameters, the proposed strategy converges to similar solutions, i.e., describing the material behaviour as accurately as possible according to the selected constitutive model.

Case study 1

In this case study, the material anisotropic behaviour is described by Drucker + L criterion and the work-hardening behaviour is described by Swift law, which parameters are shown in Table 2 [30]. The elastic properties are: Young’s modulus, E = 210 GPa and Poisson ratio, ν = 0.3. The number of measured points used to evaluate the cost functions F ₁, F ₂ and F ₃, is equal to 100 (Q ₁ = Q ₂ = R ₁ = R ₂ = S ₁ = S ₂ = 100).

Table 2 Constitutive parameters of the reference material of the Case Study 1, described by Drucker + L yield criterion and Swift work-hardening law

Full size table

The identification is carried out for Hill’48 (first stage), Yld’91, KB’93 and Drucker + L (second stage) yield criteria simultaneously with Swift work-hardening law (Voce’s law was not used). Table 3 shows Hill’48 yield criterion (as for isotropy) and Swift isotropic work-hardening parameters used as first estimate for the inverse identifications, as well as the ones resulting from the identified parameters of Hill’48 yield criterion and Swift isotropic work-hardening law, by the proposed inverse identification. The first stage of the identification procedure involved two returns to Step 2, after Step 3. Table 3 also shows the identified parameters of the Yld’91, KB’93 and Drucker + L criteria, together with the Swift law parameters (second stage). The second stage of the identification procedure involved two returns to Step 3, after Step 6, for Yld’91 and Drucker + L criteria, while for KB’93 criterion it involved only one return to Step 3.

Table 3 Cost functions and sequentially identified constitutive parameters (Final), at the end of the stages 1 (Hill’48 yield parameters) and 2 (Yld’91, KB’93 and Drucker + L yield parameters) of the Case Study 1 (Swift law)

Full size table

Figure 3 compares the reference material results (Mat) of the cruciform test with those obtained in the first stage of the sequential strategy (Hill’48 yield criterion and Swift isotropic work-hardening law - Final), for the 0x and 0y axes. The results concerning the initial estimate (Isotropic) are also shown in Fig. 3a, c and e. The results concern P vs. Δl and δ _P vs. Δl (Fig. 3a, b, respectively); $ \overline{\varepsilon} $ vs. d and $ {\delta}_{\overline{\varepsilon}} $ vs. d (Fig. 3c, d, respectively) and ρ vs. d and Δρ vs. d (Fig. 3e, f, respectively). The results in Fig. 3c to f are plotted for Δl ≈ 6 mm, i.e., the Δl value immediately preceding the maximum load. These results concern the distance, d, from the centre of the cruciform specimen up to a distance corresponding to the minimum value of ρ (see Fig. 3e, where the minimum occurs for a d value slightly less than 40 mm; after this d value, ρ increases approaching zero - not shown in the figure). It can be concluded that the proposed inverse identification strategy leads to an accurate description of the load evolution during the test for both axes (absolute relative differences less than 0.12%), although this is not the case for the total equivalent strain distribution (absolute maximum relative differences of about 15%) and the strain path ratio distribution results (absolute maximum relative differences of about 30%). In fact, the values of F ₁, F ₂ and F ₃ are 1.3 × 10⁻⁶, 8.6 × 10⁻³ and 3.2 × 10⁻², respectively (see Table 3).

Figure 4 shows the results corresponding to δ _P vs. Δl (Fig. 4a, b, for the 0x and 0y axes, respectively), $ {\delta}_{\overline{\varepsilon}} $ vs. d (Fig. 4c, d), for the 0x and 0y axes, respectively) and Δρ vs. d (Fig. 4e and f, for the 0x and 0y axes, respectively), allowing the comparison between all criteria studied. These results show that, when compared with the Hill’48 criterion, the accuracy of the load evolution during the test decreases for both axes, in the case of the KB’93 yield criterion, but increases for the Yld’91 and Drucker + L criteria. The accuracy of the total equivalent strain and strain path ratio distribution results are substantially increased for the Yld’91 and Drucker + L yield criteria. For the Drucker + L criterion, the comparison of the identified constitutive parameters (Swift law and criterion) with the material parameters (Table 2) shows quasi-absolute coincidence of results, since the Drucker + L criterion allows for the full description of the material behaviour. The above findings are supported by the values of the cost functions shown in Table 3.

In order to visualise the results of the identification, Fig. 5 shows the equivalent stress - equivalent plastic strain curves (Fig. 5a) and the yield surfaces (Fig. 5b), in the plane (σ_xx, σ_yy), for $ {\overline{\varepsilon}}^{\mathrm{p}} $ = 0.3, close to the maximum value of $ \overline{\varepsilon} $ attained during the cruciform test (see Fig. 3c, for the material (Mat)) and corresponding to the identifications using Hill’48 criterion (first stage), Yld’91, KB’93 and Drucker + L yield criteria (second stage). When comparing the results obtained from the identified sets of parameters with the material results, the following is observed: (i) the equivalent stress - equivalent plastic strain curve obtained from the proposed inverse identification strategy enables an accurate description of the material curve, whatever the yield criteria used; (ii) the Hill’48 criterion does not conveniently describes the material yield surface, unlike the Drucker + L criterion that exactly fits the material yield surface, as would be expected.

Case study 2

In this case study, the mechanical behaviour of the material is described by Voce law and CB2001 yield criterion [4]. The CB2001 criterion is a generalisation of the Drucker’s isotropic criterion to anisotropy, and is written as follows:

$$ f\left({\sigma}_{ij},{\overline{\varepsilon}}^{\mathrm{p}}\right)={J_2}^3-c{J_3}^2-27{\left(Y\left({\overline{\varepsilon}}^{\mathrm{p}}\right)/3\right)}^6\le 0 $$

(27)

where J ₂ and J ₃ are, respectively, the second and third generalised invariants of the Cauchy stress tensor:

$$ \begin{array}{l}{J}_2=\frac{a_1}{6}{\left({\sigma}_{\mathrm{xx}}-{\sigma}_{\mathrm{yy}}\right)}^2+\frac{a_2}{6}{\left({\sigma}_{\mathrm{yy}}-{\sigma}_{\mathrm{zz}}\right)}^2+\frac{a_3}{6}{\left({\sigma}_{\mathrm{xx}}-{\sigma}_{\mathrm{zz}}\right)}^2+{a}_4{\tau}_{\mathrm{xy}}^2+{a}_5{\tau}_{\mathrm{xz}}^2+{a}_6{\tau}_{\mathrm{yz}}^2\\ {}{J}_3=\frac{1}{27}\left({b}_1+{b}_2\right){\sigma}_{\mathrm{xx}}^3+\frac{1}{27}\left({b}_3+{b}_4\right){\sigma}_{\mathrm{yy}}^3+\frac{1}{27}\left[2\left({b}_1+{b}_4\right)-{b}_2-{b}_3\right]{\sigma}_{\mathrm{zz}}^3\\ {}-\frac{1}{9}\left({b}_1{\sigma}_{\mathrm{yy}}+{b}_2{\sigma}_{\mathrm{zz}}\right){\sigma}_{\mathrm{xx}}^2-\frac{1}{9}\left({b}_3{\sigma}_{\mathrm{zz}}+{b}_4{\sigma}_{\mathrm{xx}}\right){\sigma}_{\mathrm{yy}}^2-\frac{1}{9}\left[\left({b}_1-{b}_2+{b}_4\right){\sigma}_{\mathrm{xx}}+\left({b}_1-{b}_3+{b}_4\right){\sigma}_{\mathrm{yy}}\right]{\sigma}_{\mathrm{zz}}^2\\ {}+\frac{2}{9}\left({b}_1+{b}_4\right){\sigma}_{\mathrm{xx}}{\sigma}_{\mathrm{yy}}{\sigma}_{\mathrm{zz}}-\frac{\tau_{\mathrm{xz}}^2}{3}\left[2{b}_9{\sigma}_{\mathrm{yy}}-{b}_8{\sigma}_{\mathrm{zz}}-\left(2{b}_9-{b}_8\right){\sigma}_{\mathrm{xx}}\right]\\ {}-\frac{\tau_{\mathrm{xy}}^2}{3}\left[2{b}_{10}{\sigma}_{\mathrm{zz}}-{b}_5{\sigma}_{\mathrm{yy}}-\left(2{b}_{10}-{b}_5\right){\sigma}_{\mathrm{xx}}\right]-\frac{\tau_{\mathrm{yz}}^2}{3}\left[\left({b}_6+{b}_7\right){\sigma}_{\mathrm{xx}}-{b}_6{\sigma}_{\mathrm{yy}}-{b}_7{\sigma}_{\mathrm{zz}}\right]+2{b}_{11}{\tau}_{\mathrm{xy}}{\tau}_{\mathrm{yz}}{\tau}_{\mathrm{xz}}\end{array} $$

(28)

The coefficients a _k (k = 1 to 6) and b _k (k = 1 to 11) are the anisotropy parameters of the criterion (a _k and b _k are equal to 1 for the isotropy condition) and c is an isotropy parameter.

This yield function holds 18 parameters and so it is more flexible than the criteria used for identification. The material results for Case Study 2 were obtained considering the constitutive parameters, close to ones of aluminium [45], as indicated in Table 4. The elastic properties are: Young’s modulus, E = 68.9 GPa and Poisson ratio, ν = 0.33.

Table 4 Constitutive parameters of the reference material of the Case Study 2, described by CB2001 yield criterion and Voce work-hardening law [45]

Full size table

Firstly, the proposed inverse identification strategy was performed for the following constitutive models: (i) Hill’48 yield criterion and Swift work-hardening law and (ii) Hill’48 yield criterion and Voce work-hardening law. Tables 5 and 6 show the identified parameters (Final) and those used as first estimate (Step 1) of the inverse identifications. For comparison, these tables also include the parameters identified with a single cost function strategy (Single), for those constitutive models. Details of this strategy as well as the discussion of its results will be made at the end of this section.

Table 5 Cost functions and constitutive parameters identified by the sequential (Final) and single cost function (Single) strategies, for Voce law, at the end of both stages 1 (Hill’48 yield parameters) and 2 (Yld’91, KB’93 and Drucker + L yield parameters) of the Case Study 2

Full size table

Table 6 Cost functions and constitutive parameters identified by the sequential (Final) and single cost function (Single) strategies, for Swift law, at the end of both stages 1 (Hill’48 yield parameters) and 2 (Yld’91, KB’93 and Drucker + L yield parameters) of the Case Study 2

Full size table

The constitutive parameters identified during the first stage of the sequential identification strategy involved one return to Step 2 after Step 3, for both work-hardening laws (Voce or Swift). In case of Voce law, a total of 46 simulations were performed (25 in Step 2 + 21 in Step 3); in case of Swift law, a total of 32 simulations were performed (20 in Step 2 + 12 in Step 3). Tables 5 and 6 also show the identified parameters of the Voce and Swift laws, respectively, together with the Yld’91, KB’93 and Drucker + L criteria (second stage), whose identification involved always only one return to Step 3, after Step 6. In case of Voce law, the second stage of the identification procedure required the following additional number of simulations: (i) 10, for Yld’91 (4 in Step 5 + 6 in Step 3); (ii) 5, for KB’93 (2 in Step 5 + 3 in Step 3) and (iii) 20, for Drucker + L (17 in Step 5 + 3 in Step 3). In case of Swift law: (i) 5, for Yld’91 (2 in Step 5 + 3 in Step 3); (ii) 11, for KB’93 (5 in Step 5 + 6 in Step 3) and (iii) 11, for Drucker + L (8 in Step 5 + 3 in Step 3).

Figures 6 and 7 compare the results of the reference material (Mat) of the biaxial cruciform test with those obtained from the parameters identified at the end of the first stage (Step 3) of the proposed inverse strategy (Final), i.e., for the Hill’48 yield criterion, with the Voce and Swift work-hardening laws, respectively. The results presented are P vs. Δl (Figs. 6 and 7a); $ \overline{\varepsilon} $ vs. d (Figs. 6 and 7c) and ρ vs. d (Figs. 6 and 7e), for both axes. The comparison is also performed in the form of the differences: δ _P vs. Δl (Figs. 6 and 7b), $ {\delta}_{\overline{\varepsilon}} $ vs. d (Figs. 6 and 7 d) and Δρ vs. d (Figs. 6 and 7 f), for both axes. The results in Figs. 6 and 7c to f are plotted for Δl = 3.5 mm, equal for both 0x and 0y axes, immediately preceding the maximum load. The results concerning the initial estimate (Isotropic) are also shown in Figs. 6 and 7a, c and e.

To evaluate which work-hardening law (Swift or Voce) best describes the material behaviour, the δ _P vs. Δl results must be analysed. In fact, the parameters of the work hardening law mainly influence the load evolution results [30] and obviously the type of law also influences the load evolution results, as shown in Figs. 6 and 7b, for the Voce and Swift laws, respectively. These results show that Voce law leads to a quasi-uniform distribution of δ _P vs. Δl for both axes (with absolute relative differences less than 0.8%) while the Swift law leads to an uneven distribution (with absolute relative differences that reach about 2%). The quasi-uniform distribution obtained with the Voce law means that the work-hardening behaviour of the material is better described by this law than by the Swift law, as expected (the reference material follows the Voce law).

Nevertheless, the Hill’48 criterion poorly describes the material $ \overline{\varepsilon} $ vs. d and ρ vs. d distributions whatever the hardening law. The average (0x and 0y axes) of the absolute values of $ {\delta}_{\overline{\varepsilon}} $ are equal to 4.84% (Voce) and 5.97% (Swift), and the F ₃ values are equal to 1.6 × 10⁻² (Voce) and 2.2 × 10⁻² (Swift). Thus, the parameters identification performed for Hill’48 criterion with Voce and Swift laws were extended to other three criteria: Yld’91, KB’93 and Drucker + L.

Figures 8 and 9 allows comparing the results of the biaxial cruciform test obtained from the parameters identified with the sequential identification strategy for these three criteria with the ones of the reference materials, for Voce and Swift laws, respectively. The results are shown in the form of the differences: δ _P vs. Δl (Figs. 8 and 9a, b), $ {\delta}_{\overline{\varepsilon}} $ vs. d (Figs. 8 and 9c and d) and Δρ vs. d (Figs. 8 and 9e and f). The results in Figs. 8 and 9a, c and e concern the axis 0x and in Figs. 8 and 9b, d and f concern the 0y axis. Unlike for Case Study 1, in this case it becomes difficult to realize the improvements attained for each of the three yield criteria used in the second stage, Yld’91, KB’93 and Drucker + L, when compared with the Hill’48 criterion (first stage).

For both work-hardening laws, the results show that the accuracy of the load evolution during the test, for both axes, remains globally the same for the three yield criteria used in the second stage, although it could be argued that for the KB’93 there is a slightly increase of accuracy, in case of the Voce law. Regarding the accuracy of the total equivalent strain and strain path ratio distribution results, the KB’93 criterion is the only one that gets worse compared to Hill’48 criterion. The accuracy of the different cases can be better examined from the values of the cost functions in Tables 5 and 6. The small differences between the accuracy of the results are, however, sufficient to highlight the interaction between the work-hardening law and the yield criterion and show that, as expected for this reference material, globally better results are attained with the Voce law, whatever the yield criteria selected. Lastly, it should be mentioned that the Drucker + L criterion together with the Voce law provides slightly better results (lower values of all cost functions: F ₁, F ₂ and F ₃) than other criteria. However, when comparing the results of all criteria, the improvement of accuracy in performing the second stage of the identification is not significant.

In order to visualise the results of the identification, Fig. 10 shows the equivalent stress - equivalent plastic strain curves and the yield surfaces, in the plane (σ _xx, σ _yy), for $ {\overline{\varepsilon}}^{\mathrm{p}} $ = 0.12, close to the maximum value of $ \overline{\varepsilon} $ attained during the cruciform test for the reference material (Mat - see Fig. 6c) and the corresponding identifications using Hill’48, Yld’91, KB’93 and Drucker + L yield criteria, combined with Voce law. When comparing the results of the sets of identified parameters with the reference ones, the following is observed: (i) the equivalent stress - equivalent plastic strain curves obtained from the sequential inverse identification strategy provides an accurate description of the material, whatever the yield criteria used; (ii) the yield surfaces obtained from the sequential identification strategy are quite similar for all yield criteria and close to the reference yield surface.

For this case study, the above results from the sequential inverse identification strategy are compared with the results obtained from a single cost function approach, where the parameter identification is performed, as traditionally, by minimising a unique cost function comprising all material parameters and the weighted results of the test:

$$ F\left(\mathbf{D}\right)={w}_1{F}_1\left(\mathbf{D}\right)+{w}_2{F}_2\left(\mathbf{D}\right)+{w}_3{F}_3\left(\mathbf{D}\right) $$

(29)

where F ₁(D), F ₂(D) and F ₃(D) are the cost functions, whose formulation is equal to Eqs. (20), (21) and (22), respectively, and D is the set of constitutive parameters to be optimised, i.e., the parameters of the work-hardening law and yield criterion; each term in the cost function is weighted by a factor, w _i, in order to eventually consider, the influence of each type of result in the identification. For example, in classic identification, Barlat et al. (2005) argue that the weight of each data type should reflect the relative precision with which this can be determined, i.e., more robust results must have higher weight values than those less robust [46]. Also, the weight factors may also be selected according to the preference of the user to favour the minimisation of a type of result over the other. Otherwise, the accurate choice of such values of w _i requires some sort of optimisation procedure, which is always difficult to accomplish concomitantly with the identification process. The difficulty of making a good choice of w _i usually leads to consider all weight factors equal to 1, as in the current work. Similarly to the sequential methodology, the minimisation procedure here adopted for the cost function F (D) stops when the relative difference between a given set of parameters and the next one is less than 5%, for each of the constitutive model parameters.

This single cost function identification strategy was performed for all yield criteria and the Voce and Swift laws, starting with the same initial estimate used in the sequential identification. Figures 11 and 12 compare the results of the biaxial cruciform test obtained from the parameters identified with the single cost function strategy for all criteria and the Voce and Swift laws, respectively, with those of the reference materials (as in Figs. 8 and 9 for the sequential strategy). Regarding the influence of the type of work-hardening law, whatever the yield criterion used, the single cost function identification approach leads to a less uniform distribution of the δ _P vs. Δl results than the proposed inverse identification, in case of Voce law, although the same kind of non-uniform distributions occurs for the Swift law (compare with Figs. 8 and 9b). Furthermore, the accuracy of the load evolution during the test is much smaller using the single cost function optimisation procedure than in case of the sequential optimisation. This happens without a visible gain of accuracy in the remaining results (total equivalent strain and strain ratio distributions), as we will see in more detail right away.

The values of the cost function, F ₄, which is minimised in the single cost function identification strategy and the identified constitutive parameters are shown in Tables 5 and 6 (“Single” in these tables), for Voce and Swift laws, respectively. These tables also show the values of F ₁, F ₂ and F ₃, for comparison with the sequential identification strategy. The F ₄ cost function shows similar values (same order of magnitude) for both identification procedures, although the single cost function identification approach (Single) tends to present slightly smaller values (only in one case – Swift law and Hill’48 criterion - F ₄ is slightly greater in the single cost function approach); also, both identification strategies lead to values of cost functions F ₂ and F ₃ which are of the same order of magnitude. However, the values of F ₁ obtained from the sequential identification strategy are about one order of magnitude lower than the ones obtained from the single cost function identification approach. This is the main feature distinguishing both identification strategies. The implications of this distinction can be easily visualised when comparing the equivalent stress - equivalent plastic strain curves and the yield surfaces obtained from the sequential inverse identification strategy with those obtained from the single cost function identification approach, as shown in Fig. 13. Figure 13a shows the equivalent stress - equivalent plastic strain curves and Fig. 13b the yield surfaces in the plane (σ _xx, σ _yy), for $ {\overline{\varepsilon}}^{\mathrm{p}} $ = 0.12, close to the maximum value of $ \overline{\varepsilon} $ attained during the cruciform test for the reference material (Mat - see Fig. 6c) and the corresponding identifications using Hill’48, Yld’91, KB’93 and Drucker + L yield criteria, combined with Voce law. When comparing the results from the identified sets of parameters with the reference ones, it can be concluded: (i) the single cost function approach mainly overestimates the entire work-hardening curve; (ii) the yield surfaces obtained from the sequential inverse identification strategy (see Fig. 10) are closer to the reference yield surface than the ones obtained from the single cost function identification approach. The comparison of the total number of iterations and simulations required for both strategies, also presented in Tables 5 and 6, shows that the first stage of the sequential strategy is the one requiring more simulations, which in the worst case can be twice the total number required by the “Single” strategy. It should be noted that, after identifying the Hill’48 parameters, the extension to more complex yield criteria requires a relatively low number of simulations.