Mechanical design of a heterogeneous test for material parameters identification

Abstract

The main goal of this work is to design virtually a heterogeneous test, with appropriate specimen shape and boundary conditions, which leads to an inhomogeneous strain field promoting the mechanical behavior characterization of thin metallic sheets under several strain paths and strain amplitudes. Finite element simulations were carried out with a virtual material, described by an anisotropic yield criterion (Yld2004-18p) associated to a mixed hardening law. The material parameters were derived from a large experimental database of quasi-homogeneous classical tests. A shape and boundary conditions optimization process was developed based on a quantitative indicator rating the strain field information and used as a cost function for guiding the test design. A heterogeneous test showing a butterfly shape was obtained, with strain states ranging from simple shear to plane strain tension. In addition, the designed heterogeneous test was used to determine the material parameters of the aforementioned constitutive model. The reliability of this identified material parameters set was then assessed and compared with the one coming from the experimental database composed by the quasi-homogeneous classical tests.

Introduction

Nowadays, the numerical simulation of sheet metal forming processes has become a mandatory step in the mechanical design of a product. Moreover, in order to improve the quality of the representation of the mechanical behavior of the materials under various strain states, constitutive models have been developed taking into account the initial anisotropy as well as hardening evolution. Such a trend, in particular within a phenomenological approach, leads to an increase of the number of material parameters to be identified. Usually, the material parameters are identified from a set of classical mechanical tests developing quasi-homogeneous strain fields [1–4] and the post-treatment based on analytical expressions for the stress and strain components from raw data [5], though there are limitations to such an analytical approach [6–8].

Concerning simple constitutive models [9–11], which involve a small number of coefficients, these classical tests seem the most suitable option to identify the material parameters. Nonetheless, when constitutive models with a large number of parameters are chosen [12–16], a high number of classical tests must be used in the experimental database, leading to an expensive and time consuming experimental characterization and identification process. The design of non-homogeneous tests allowing multi-stress and strain states combined with full-field measurement (FFM) methods [17, 18] for post-processing appears then as a very promising solution. The development of FFM methods (c.f. an overview in Grédiac [17]), which directly provide displacement or strain field data over the whole surface of the specimen, allowed an evolution relatively to the experimental data considered in the parameters identification strategies. It becomes possible to analyze complex mechanical tests developing heterogeneous strain fields [19–24]. The large amount of information that can be output from a heterogeneous test (load and strain components) leads to a smaller number of experiments (or even a single one) in the experimental database, as well as a rich mechanical information in terms of strain states [24, 25], and therefore the quality of the identified parameters is improved [20, 22]. As a consequence, an increasing number of innovative tests promoting heterogeneous strain fields as well as parameters identification strategies were proposed in the last years [24, 26].

These recent identification strategies were mainly carried out using a Finite Element Model Updating (FEMU) technique [27]. Such a technique corresponds to an automatic methodology based on the coupling of a finite element (FE) code with an optimization method, where the goal is to seek iteratively for a set of material parameters that leads to the smallest difference between the experimental observations and the numerical predictions. Several geometries for the specimen and mechanical tests were used, like a non-standard notched tensile test [21], a flat specimen with a varying cross-section [28], or a biaxial test with a perforated cruciform specimen [20] or not [24]. The strain field was usually captured by Digital image correlation (DIC) and a comparison of the experimental and numerical strain components was performed via a cost objective function, eventually considering also a global signal like the load. The numerical strain field was also compared with the one obtained from a parameters set identified by standard quasi-homogeneous tests and it was observed that a more reliable prediction was achieved by the set of parameters identified with the heterogeneous test [20, 21]. Such a conclusion was also obtained even using a yield criterion involving a large number of parameters like Bron and Besson [24]. The aforementioned works highlighted that by using heterogeneous tests, several parameters can be identified at the same time when the experimental information was rich enough. However, it should be emphasized that the specimen geometry and the boundary conditions were used from previous knowledge of the mechanical tests, without the deliberate volition to enhance neither the strain range nor the strain path information. It should be interesting to investigate the reverse problem, i.e. finding the specimen shape and boundary conditions leading to an optimized strain field well suited for material parameters identification.

Therefore, the purpose of this work was the design of a heterogeneous test, which developed a strain field leading to an enhanced mechanical characterization of sheet metals, allowing the identification of a large number of parameters of complex constitutive models. An optimization approach leading to the design of the specimen shape as well as boundary conditions was developed in order to find a rich heterogeneous strain field. As an input to the finite element simulations, a virtual material represented by the anisotropic Yld2004-18p yield function [12] coupled with mixed hardening was used. The 24 material parameters were identified from a large experimental database of quasi-homogeneous classical tests obtained for a mild steel thin sheet. In addition, a quantitative indicator evaluating the strain field information [29] was considered as a cost function in the optimization approach for guiding the design of the heterogeneous test. A specific combination of specimen shape and boundary conditions was hence determined. Furthermore, a parameters identification strategy was developed by using the heterogeneous test and the material parameters of the complex constitutive model were identified by considering the virtual mild steel as reference data. Finally, the experimental database of the quasi-homogeneous classical tests was predicted using this identified parameters set with the purpose of evaluating the quality of the material parameters determined with the designed test and the non-homogeneous strategy.

Constitutive model

The numerical simulations for designing the heterogeneous test were performed using a virtual DC04 mild steel, described by the non-quadratic Yld2004-18p yield criterion combined with a mixed isotropic-kinematic hardening law. The yield surface is defined by the generic form

$$ F\left(\boldsymbol{\upsigma}, \boldsymbol{\upalpha}, {\overline{\varepsilon}}^{\mathrm{p}}\right)=\overline{\eta}\left(\boldsymbol{\upsigma} -\boldsymbol{\upalpha} \right)-{\sigma}_{\mathrm{Y}}\left({\overline{\varepsilon}}^{\mathrm{p}}\right)=0, $$

(1)

where $\overline{\eta}$ is the equivalent stress which is a function of the tensor η, defined by η = σ − α and α is a backstress tensor that describes the kinematic hardening, σ _y is the yield stress related to the isotropic hardening and ${\overline{\varepsilon}}^{\mathrm{p}}$is the equivalent plastic strain. The isotropic hardening, controlling the size of the yield surface is defined by an exponential law written as [30]

$$ {\sigma}_{\mathrm{Y}}\left({\overline{\varepsilon}}^{\mathrm{p}}\right)={\sigma}_0+\left({\sigma}_{\infty }-{\sigma}_0\right).\left[1- \exp \left(-\updelta .{\overline{\varepsilon}}^{\mathrm{p}}\right)\right]+\upbeta .{\overline{\varepsilon}}^{\mathrm{p}}, $$

(2)

where σ ₀, σ_∞, δ and β are material parameters. The kinematic hardening law is based on the additive contribution of several backstress components such as proposed in [31]. This formulation defines the evolution of the backstress tensor as

$$ \overset{\cdot }{\boldsymbol{\upalpha}}={\displaystyle \sum_{i=1}^3{\overset{\cdot }{\boldsymbol{\upalpha}}}_i}={\displaystyle \sum_{i=1}^3\left(\frac{C_i}{\overline{\eta}}\boldsymbol{\upeta} -{\gamma}_i.{\boldsymbol{\upalpha}}_i\right){\overset{\cdot }{\overline{\varepsilon}}}^{\mathrm{p}}}, $$

(3)

where C _i and γ _i , with i = 1,…, 3, are material parameters related to the kinematic hardening behavior, α _i are the backstress components and ${\dot{\overline{\varepsilon}}}^{\mathrm{p}}$ is the equivalent plastic strain rate. The initial anisotropy is represented by the advanced non-quadratic Yld2004-18p anisotropic yield criterion [12]. This yield function is defined by

$$ \overline{\eta}{\left(\boldsymbol{\upeta} \right)}^a={{\displaystyle \sum_{i=1,j=1}^3\left|{{\tilde{\mathbf{S}}}_i}^{(1)}-{{\tilde{\mathbf{S}}}_j}^{(2)}\right|}}^a=4{\sigma_{\mathrm{Y}}}^a, $$

(4)

where a is the yield criterion exponent. In this equation, ${\tilde{\mathbf{S}}}_i^{(k)}$, k = 1, 2 and i,j = 1 ,…, 3, are the eigenvalues of the tensors ${\tilde{\mathbf{S}}}^{(k)}={\tilde{\mathbf{L}}}^{(k)}:\mathbf{S},\kern1em k=1,2$, where ${\tilde{\mathbf{L}}}^{(k)}$are given by.

by a linear transformation of S, the deviatoric part of the tensor η and using the Voigt notation.

$$ {\tilde{\mathbf{L}}}^{(k)}=\left[\begin{array}{cccccc}\hfill 0\hfill & \hfill \hbox{-} {c}_{12}^{(k)}\hfill & \hfill \hbox{-} {c}_{13}^{(k)}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill \hbox{-} {c}_{21}^{(k)}\hfill & \hfill 0\hfill & \hfill \hbox{-} {c}_{23}^{(1)}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill \hbox{-} {c}_{31}^{(k)}\hfill & \hfill \hbox{-} {c}_{32}^{(k)}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {c}_{44}^{(k)}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {c}_{55}^{(k)}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {c}_{66}^{(k)}\hfill \end{array}\right],\kern1em k=1,2 $$

(5)

In this work, the exponent a is fixed to 6 and coefficients${c}_{44}^{(k)}$and${c}_{55}^{(k)}$, with k = 1, 2, were constants and set equal to 1, leading to a total of 24 material parameters. The material parameters were determined with a conventional approach, using an experimental database composed by: (i) uniaxial tensile and simple shear tests at 0°, 22°, 45°, 77° and 90° from the RD; (ii) hydraulic bulge test and (iii) three shear-Bauschinger tests in RD. For this purpose, the stress-logarithmic strain curves (σ-ε) in uniaxial and biaxial tension, shear stress-strain curves (τ-γ) in shear and transverse strain-longitudinal strain (ε₁₁-ε₂₂) curves for the several uniaxial tensile tests and bulge test were used.

Additionally, in order to ascertain that the strains calculated in the numerical model could be reached before rupture, the macroscopic Cockroft and Latham (CL) fracture criterion was considered. The definition of CL criterion is taken as the one given in [32],

$$ {W}_{CL}={\displaystyle {\int}_0^{{\overline{\varepsilon}}_{\mathrm{f}}^{\mathrm{p}}}\frac{\sigma_I}{\overline{\eta}}\mathrm{d}{\overline{\varepsilon}}^{\mathrm{p}}\le {W}_{CL}^{\mathrm{f}}}, $$

(6)

where σ _I is the maximum principal stress. Rupture is expected to occur when the fracture parameter W _CLreaches the critical value ${W}_{CL}^{\mathrm{f}}$, leading to the determination of the equivalent plastic strain at rupture ${\overline{\varepsilon}}_{\mathrm{f}}^{\mathrm{p}}$. A uniaxial tensile test up to rupture was used through an experimental-numerical approach to calibrate ${W}_{CL}^{\mathrm{f}}$. Within this approach, a numerical modeling was defined considering a mesh density of 3 elements/mm over the specimen surface of the uniaxial tensile test. Deep drawing experiments were conducted with two blank-holder forces, leading either to a full drawn cup or to a premature rupture. Though the simplicity of the rupture criterion, it was shown that these two cases were correctly predicted [33].

The detailed description of the parameters identification process adopted and input material parameters reproducing this DC04 mild steel as well as of the experimental-numerical approach calibrating DC04 rupture behavior can be found in [33].

Heterogeneous test design

The main aim of this work was to design a mechanical test by defining the sample geometry and boundary conditions that gave an optimal strain field for material parameters identification. The different steps of this optimization are described in this section.

Shape and boundary conditions parameterization

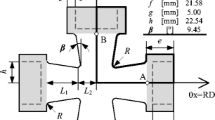
The design of the heterogeneous test must be based on a shape optimization model allowing a free geometry and a loading path evolution. For that, a procedure where the initial specimen shape and loading path can be both subjected to optimization was developed. As a first simplifying assumption, a symmetric model with the specimen geometry defined by curve interpolation and the loading path, imposed by using a rigid tool, was defined, as illustrated in Fig. 1. The free curved boundary was modeled with cubic splines. The specimen shape was governed by 7 control points; their position was defined radially at every 15° (Fig. 1) and could change during the optimization process, so that the specimen shape could be updated. The arrows in Fig. 1 illustrate the variation allowed for the position of the control points; the radial length between the control points and the specimen center x _i , i = 1,…, 7 corresponded to the design variables for the specimen shape.

Fig. 1

Illustration of the sample shape and rigid tool. Control points for the cubic spline definition are highlighted in red. In this work, θ and P _tool were set equal to fixed values, i.e. θ = 90° and P _tool = 90°

For the optimization of the loading path, a rigid tool was used. The shape of this rigid tool was coincident with the specimen shape in each evaluation of the optimization process. This was mandatory, since the specimen geometry was continuously updated during the optimization process and concordance between both shapes was required for a proper contact definition in the model. In this work, it was chosen to fix the tool at P _tool = 90° and, as a result, the orientation of the tool displacement θ must correspond to vertical (90°) displacement due to symmetry conflicts. Only the size of the tool L _tool was considered as a design variable to be optimized. The loading path was applied up to rupture, i.e. until reaching numerically the fracture criterion ${W}_{CL}^{\mathrm{f}}$. In practice, the tool displacement value was just defined large enough to always lead to rupture. Therefore, 8 design variables r were considered in this shape optimization process, namely, 7 radial displacements of the control points and L _tool. The parameter vector r can be written as

$$ \mathbf{r}=\left[{x}_1\kern0.5em {x}_2\kern0.5em {x}_3\kern0.5em {x}_4\kern0.5em {x}_5\kern0.5em {x}_6\kern0.5em {x}_7\kern0.5em {L}_{\mathrm{tool}}\right]. $$

(7)

Cost function

A quantitative indicator able to distinguish, rate and rank mechanical tests was used in the definition of the cost function. This indicator, designated as I _T, quantified the strain state range and deformation heterogeneity as well as the strain level achieved in the test, based on a continuous evaluation of the strain field up to rupture. I _T was formulated as

$$ {I}_{\mathrm{T}}={w}_{\mathrm{r}1}\frac{\mathrm{Mean}\left[Std\left({\varepsilon}_2/{\varepsilon}_1\right)\right]}{w_{\mathrm{a}1}}+{w}_{\mathrm{r}2}\frac{{\left({\varepsilon}_2/{\varepsilon}_1\right)}_{\mathrm{R}}}{w_{\mathrm{a}2}}+{w}_{\mathrm{r}3}\frac{\mathrm{Mean}\left[Std\left({\overline{\varepsilon}}^{\mathrm{P}}\right)\right]}{w_{\mathrm{a}3}}+{w}_{\mathrm{r}4}\frac{{\overline{\varepsilon}}_{\mathrm{Max}}^{\mathrm{P}}}{w_{\mathrm{a}4}}+{w}_{\mathrm{r}5}\frac{A{v}_{{\overline{\varepsilon}}^{\mathrm{P}}}}{w_{\mathrm{a}5}}, $$

(8)

where the different terms are described in Table 1 and w _ri and w _ai , with i = 1, …, 5, are relative and absolute weighting factors. The detailed description as well as applicability of the indicator I _T can be found in [29].

Table 1 Different terms defining the quantitative indicator I _T

The developed shape optimization approach aimed at maximizing the strain field information provided by the heterogeneous test. Therefore, I _T value had to increase during the optimization process. However, as the optimization methods were conceived to proceed to a minimization, the cost function was defined in order that its minimization meant the maximization of I _T. It can be achieved by defining the cost function as

$$ {S}_{\mathrm{cost}}\left(\mathbf{r}\right)=2-{I}_{\mathrm{T}}+Res, $$

(9)

where the difference between 2 and I _T ensured the required condition. Due to its formulation, theoretically, the maximum I _T value that could be reached was unity [29]. Consequently, the value 2 was just set as an upper limit in the cost function definition. A penalty function Res was also introduced in Eq. 9. The aim was to penalize the cost function when abrupt variations for the design variables of consecutive control points occurred during the optimization process. Indeed, these abrupt variations tended to promote either the generation of unrealistic specimen shapes or specimen configurations leading to premature strain localization and rupture.

The optimization constraints were defined based on the admissible range values for each one of the 7 design control points. Thus, it was assumed that the design control point 1 could vary between the lower and upper limits (L _Bound and U _Bound), while the following control points were constrained in function of the previous control point value, as follows:

$$ {L}_{\mathrm{Bound}}\le {x}_1\le {U}_{\mathrm{Bound}} $$

(10)

and

$$ \left(1-{a}_{\mathrm{v}}\right){x}_{k-1}\le {x}_k\le \left(1+{a}_{\mathrm{v}}\right){x}_{k-1}\kern1em ,k=2,\dots, 7 $$

(11)

where a _v. was the parameter value defining the admissible variation; it was set equal to 0.25 in this work. The lower and upper bounds were fixed, respectively, to 10 and 60 mm. The inequalities imposed by Eq. 11 were analyzed in each evaluation of the optimization process and were quantified as

$$ {g}_{\mathrm{U},i}\left(\mathbf{r}\right)={x}_{i+1}-\left(1+{a}_{\mathrm{v}}\right){x}_i $$

(12)

and

$$ {g}_{\mathrm{L},i}\left(\mathbf{r}\right)=\left(1-{a}_{\mathrm{v}}\right){x}_i-{x}_{i+1}, $$

(13)

where i = 1,..., 6. Taking into account the several values obtained in Eqs. 12 and 13, the penalty function Res was defined in order to penalize the cost function when these inequalities were not respected during the optimization. The penalty function Res was calculated by

$$ Res={\displaystyle \sum_{i=1}^6\alpha \left({\left[\mathit{\max}\left({g}_{\mathrm{L},i}\left(\mathbf{r}\right),0\right)\right]}^2+{\left[\mathit{\max}\left({g}_{\mathrm{U},i}\left(\mathbf{r}\right),0\right)\right]}^2\right)}, $$

(14)

where α = 1/(U _Bound -L _Bound)² is a penalty coefficient that defined the importance of the constraints during the optimization process. Note that Eq. (14) led to a quadratic penalization.

In addition, the weighting factors of I _T, initially provided in [29], were adjusted in order to improve the optimization results. An increase of the importance attributed to the terms of the strain level group promoted the global deformation of the specimen and reduced premature strain localization effects. Thus, the set of weighting factors (Eq. 8) was modified and is given in Table 2.

Table 2 Weighing factors used in the I _T formulation

Finite element model

The computational analysis was carried out with ABAQUS finite element code, within the implicit framework, and the most straightforward way to parameterize the numerical model was through a script developed in Python. The script should change the geometry of the model, should define an unstructured mesh and also should vary the size of the rigid tools, in each evaluation. The mesh size had to be defined with 3 elements/mm because it corresponded to the mesh size used to calibrate ${W}_{CL}^{\mathrm{f}}$fracture parameter [33]. Since the loading path was applied up to rupture, ${W}_{CL}^{\mathrm{f}}$ was used as an end condition to stop the numerical simulation of the heterogeneous test design and, therefore, a mesh refinement of the model similar to the one used for the calibration of this fracture parameter was required.

A tridimensional model was created with the script and only one eighth of the sample was defined by considering material and process symmetries. The symmetries in x- and y-directions (Fig. 1) and also along the thickness, allowed for the reduction of the number of design variables and for the saving of calculation time in every evaluation of the optimization process. The specimen was meshed with 3D 8-node linear isoparametric elements with reduced integration (C3D8R) and hourglass control, while the tool was defined as analytical rigid using 3D 4-node rigid elements (R3D4). A tie contact was assumed between tool and specimen boundary in order to apply the loading path. The specimen was defined with an approximated mesh density of 3 elements/mm in the sheet plane and with 2 elements along the thickness by extrusion of the 2D mesh.

Moreover, the entire surface was taken into account for the calculation of the indicator I _T, as recommended in [29], and a rupture zone consisting of a region of 1 × 1.5 mm² was used for determining ${W}_{CL}^{\mathrm{f}}$, as considered for its calibration [33].

Optimization framework

The shape optimization process was performed with an interface program developed within the Matlab environment, which linked the finite element code and the Python script used to update the numerical model and to post-process data from the numerical simulation. The Matlab script also defined the specimen boundary and tool shapes by cubic splines interpolation, calculated the cost function and updated the design variables by using the Nelder-Mead direct search algorithm [34]. Figure 2 illustrates the flow diagram of this optimization process.

Fig. 2

Flow diagram of the shape optimization process developed

The optimization process started with reading the initial values of the design variables in the Matlab script. Then, the script determined the cubic splines defining the specimen outer shape from the 7 control points and the Cartesian coordinates of the boundary were calculated by interpolation. After that, taking into account the position and the size of the tool, the angular range occupied by the tool was calculated, as well as its Cartesian coordinates. These coordinates were written by the Matlab script in text files and were read by the Python script. In the following, the finite element model was generated and the numerical simulation was carried out up to rupture. At the end of the numerical simulation, another Python script was used for post-processing the results, in order to determine the ratio between the minor and major principal strains in the sheet plane (ε₂/ε₁) over the specimen surface and also to read and record the numerical results required for the evaluation of the indicator. The Matlab script then calculated the indicator and the cost function. When the stopping criterion was reached, the optimization process ended and the optimum strain field was found. Alternatively, if the stopping criterion was not reached, the design variables were updated and the process was repeated until achieving the stopping criterion or reaching the maximum number of evaluations. In this work, the stopping criterion was defined with a stagnation value of 10⁻⁴, in terms of the cost function value between two consecutive evaluations. Alternatively, the maximum number of evaluations allowed for this optimization process was 200.

Results and discussion

As the results obtained by the optimization algorithm may depend on the starting guess, three different sets of initial design variables were considered; however, only the best design solution is presented. Table 3 shows (i) the initial and optimal design variables, (ii) the initial and final values of S _cost, Res and I _T and (iii) the number of evaluations performed by the shape optimization process. The initial design variables set of the best design solution corresponded to a circular specimen shape. The analysis of I _T values revealed that an increase of 153 % was reached in the optimization process, meaning that a substantial improvement of the strain field information provided by the designed heterogeneous test was obtained comparatively to the starting guess. Both initial and optimal mechanical test, designed by the optimization process, are shown in Fig. 3.

Table 3 Results obtained in the shape optimization process

Fig. 3

Initial (left) and designed (right) mechanical test. In red, the tool, in blue and green, the areas submitted to horizontal and vertical symmetry conditions respectively

Figure 4 shows the evolution of S _cost. It can be seen that one evaluation led to a S _cost value equal to 2. This is due to the fact that the optimization algorithm tried a design variable set leading to an unfeasible specimen shape and, consequently, to the impossibility of generating the numerical model. As a consequence, calculations were not carried out in this evaluation and I _T = 0. In addition, the evolution of S _cost, with several peaks, pointed out the non-smoothness of the problem and justified the choice of the Nelder-Mead direct search algorithm.

Fig. 4

Evolution of the cost function for the optimization process

Figure 5a shows the distribution of ${\overline{\varepsilon}}^{\mathrm{p}}$at rupture. It can be seen that the designed test achieved a maximum equivalent plastic strain level of about 0.94. However, ${\overline{\varepsilon}}^{\mathrm{p}}$values of about 0.5 were reached in the specimen center. From the ε ₂/ε ₁ distribution at rupture displayed in Fig. 5b, it can be observed that strain states between near shear (ε ₂/ε ₁ = −1) to plane strain tension (ε ₂/ε ₁ = 0) were developed. Note that these results did not consider the area covering compression states (−1.97 ≤ ε ₂/ε ₁ < −1), since it corresponded to a very small deformation level (Fig. 5a). Strain states above plane strain tension, such as equibiaxial tension (ε ₂/ε ₁ = 1), were not developed by the designed test, certainly because it was subjected to a uniaxial loading path, with only one tool. In order to cover biaxial strain states, the use of additional rigid tools in the design optimization approach, leading to a multiaxial loading path should be considered [35]. Moreover, a rather large area in the horizontal arms exhibited a very small equivalent plastic strain (Fig. 5a) whereas the central zone corresponded to a quasi-homogeneous strain state, as illustrated in Figs. 5a and b. These observations pointed out some weakness of the indicator, which should be further enhanced in order to avoid large homogeneous areas.

Fig. 5

Distributions of (a) ${\overline{\varepsilon}}^{\mathrm{p}}$ and (b) ε ₂/ε ₁ for the designed test. Grey zones on ε ₂/ε ₁ contour means that ${\overline{\varepsilon}}^{\mathrm{p}}$ < 10⁻³ and, therefore, were not taken in account. SDV1 and LE-RAPMINMAJ stands for ${\overline{\varepsilon}}^{\mathrm{p}}$ and ε ₂/ε ₁, respectively

Parameters identification using the heterogeneous test

The designed test was used for material parameters identification purposes in order to evaluate its performance. No experiments with this specimen were performed and a virtual reference solution was generated with the virtual material, using the reference parameters set given in Table 4.

Table 4 Material parameters identified from the designed test and the experimental database (reference) and relative gap between these identified and reference parameter sets

A non-homogeneous approach was considered in order to identify the material parameters of the model. A FEMU technique was adopted, using a combination of the finite element code ABAQUS and the optimization software SdL [36]. The communication between these two programs was ensured by a Fortran interface, which compared the reference and numerical results via an objective function, and wrote the updated parameters in the finite element code input file after each evaluation. Moreover, a Python script was also used to read the field data at the end of the numerical simulation. Figure 6 depicts the flow diagram of the identification process developed.

Fig. 6

Scheme of the parameters identification process developed. S _obj stands for the objective function

The objective function S _obj-T(x) was minimized using the Levenberg-Marquardt (L-M) gradient-based algorithm [37, 38]. This algorithm updated the solution by using the information of the derivative of the objective function and its main advantage was the excellent relationship between efficiency and required computational time. The parameters identification process considered a stagnation value of 10⁻¹², in terms of the S _obj-T(x) value between two consecutive evaluations, as the stopping criterion. The derivatives of the objective function were calculated numerically through a forward finite difference scheme with a perturbation value of 5 × 10⁻³ and the maximum number of evaluations was set to 250.

Objective function and reference data

The adopted objective function S _obj(x), given by Eq. 15, consisted of a weighted least-square difference between reference and numerical strain field as well as the resulting tool load. The load was also taken into account, since it led to a better suited solution when strain concentration and localized damage were involved [39].

$$ {S}_{obj}\left(\mathbf{x}\right)={\displaystyle \sum_{i=1}^{n_{im}}\left[{\left(\frac{F_i^{ref}-{F}_i^{num}\left(\mathbf{x}\right)}{F_{\max}^{ref}}\right)}^2+\frac{1}{n_{\mathrm{p}}}{\displaystyle \sum_{j=1}^{n_{\mathrm{p}}}\left[{\left(\frac{\varepsilon_{1,j,i}^{ref}-{\varepsilon}_{1,j,i}^{num}\left(\mathbf{x}\right)}{\varepsilon_{1, \max, i}^{ref}}\right)}^2+{\left(\frac{\varepsilon_{2,j,i}^{ref}-{\varepsilon}_{2,j,i}^{num}\left(\mathbf{x}\right)}{\varepsilon_{2, \max, i}^{ref}}\right)}^2\right]}\right]}, $$

(15)

where the tensor x is the material parameters set to be identified, n _p is the number of points at which the strain components are output (spatial discretization), n _im is the number of strain fields evaluated (time discretization), ${F}_i^{ref}$ and ${F}_i^{num}\left(\mathbf{x}\right)$ are the reference and numerical load values at the strain field i, ${F}_{\max}^{ref}$ is the maximum reference load value for all the strain fields, ${\varepsilon}_{1,j,i}^{ref}$ and ${\varepsilon}_{1,j,i}^{num}\left(\mathbf{x}\right)$ as well as ${\varepsilon}_{2,j,i}^{ref}$ and ${\varepsilon}_{2,j,i}^{num}\left(\mathbf{x}\right)$ are the reference and numerical major and minor principal strain values for the point j at the strain field i, respectively, and, ${\varepsilon}_{1, \max, i}^{ref}$and ${\varepsilon}_{2, \max, i}^{ref}$ the corresponding maximum values. Note that the quadratic difference between the reference and numerical data was weighted by using the maximum reference value of the field data. It allowed defining just one weighting factor for the all field data and it also led to the normalization of different units or scales of the data. The specimen surface was analyzed up to a tool displacement of 10 mm, which corresponded to a maximum equivalent plastic strain of 0.65, by comparing 5 strain fields (n _im = 5). The minor ε₂ and major ε₁ strain fields were evaluated for tool displacements of 0.2, 1, 2, 6 and 10 mm. In the case of the load data, the tool force-displacement curve was considered.

From a preliminary identification process, it was observed some discrepancy in the prediction of the material anisotropy (in tension, in particular at 0° and 22° to RD) when using only one test. Therefore, another test with a similar geometry but a rotation of 90° of the material orientation was also considered for identifying the material parameters. Thus, the objective function S _obj-T(x) was defined as the sum of two terms (n _test = 2), each given by Eq. 15, but corresponding to the designed test without and with a rotation of the material orientation. S _obj-T(x) is given by

$$ {S}_{obj\hbox{-} \mathrm{T}}\left(\mathbf{x}\right)={\displaystyle \sum_{i=1}^{n_{\mathrm{test}}}{S}_{obj,i}\left(\mathbf{x}\right)}. $$

(16)

Numerical model

The numerical model of the designed test was previously generated for the design optimization process with an unstructured mesh. To acquire the strain field data by a similar approach as the one using DIC technique to output the experimental results, a re-meshing of the specimen surface was carried out to create a structured mesh (Fig. 7). It must be emphasized that both meshes present approximately a mesh density of 3 elements/mm and the structured mesh leads to a similar I _T value for the test. Thereby, no influence of the re-meshing was evidenced on the evaluation of the mechanical information from the test. In addition, such as for DIC technique, a region of interest (ROI) for the specimen surface was defined, as can be seen in Fig. 7 (red zone). Only the strain field information coming from the ROI was used for identifying the material parameters. The outer ROI was not considered due to the possible local effects related to the tool contact and also, because, from an experimental point of view, DIC technique may present some difficulty to accurately measure data in this region.

Fig. 7

Structured mesh of the optimized test. The red zone defines the ROI of the sample

Results

Table 4 shows the initial, reference and optimal identified parameters, the initial and final values of the objective function and the number of evaluations carried out by the identification process. The initial values as well as the bounds for the material parameters were set equal to the ones used in the identification of the virtual material [33]. Hence, both identification processes started in similar conditions. The kinematic hardening parameters were considered constant values and equal to the reference ones since the designed test does not involve reverse loading. Then, 18 material parameters, related to the material anisotropy and isotropic hardening behavior, were identified.

Comparing the identified and the reference parameters, it can be seen that these parameters sets are rather different. It results from the fact that multiple solutions can be obtained on the search of parameters of non-linear elastoplastic constitutive models. The relative gap between the identified and reference parameters is also given in Table 4. Concerning the anisotropy coefficients, it can be seen that the identified coefficients of the second linear transformation (${c}_{ij}^{(2)}$) tend to present larger relative variations than the coefficients corresponding to the first linear transformation (${c}_{ij}^{(1)}$). Among these parameters, the coefficients ${c}_{66}^{(k)}$, with k = 1, 2, are the ones that present a larger deviation in relation to the corresponding reference, namely, a relative gap of −22.1 % for ${c}_{66}^{(1)}$ and +57.4 % for ${c}_{66}^{(2)}$. In the case of the isotropic hardening behavior, it can be seen that the initial yield stress (σ₀) value identified is almost identical to the reference one. However, relative gaps of approximately 10 % and 20 % for σ _∞ and δ parameters were calculated while β assumed a deviation of about 75 % to the reference value. Such gaps put in evidence that the optimization algorithm can lead to rather distinct parameters set. Nevertheless, comparing the initial and final objective function values, in the bottom of Table 4, it can be observed that a reduction of 99.6 % was obtained.

Figure 8 depicts the evolution of the objective function value during the identification process. For the first 19 evaluations, individual perturbations of each material parameter were performed in order to calculate numerically the Jacobian of the objective function (sensitivity matrix) and, before 50 evaluations, S _{obj_T} value was significantly decreased. In the following evaluations, a stabilization of S _{obj_T} value was observed till the verification of the stopping criterion after 233 evaluations.

Fig. 8

Evolution of S _{obj_T} during the material parameters identification process

Figure 9 depicts the load-displacement curves obtained for the designed test without and with rotation of the material orientation, using both reference and identified parameter sets. It can be seen that a very good reproduction of the load level was obtained for the test with a rotation of material orientations, whereas a slight over-prediction is noted for the test without rotation.

Fig. 9

Load-displacement curves obtained using the reference and the identified parameters sets for the designed test without (left) and with (right) rotation of the material orientation

Figure 10 shows the major and minor strain distribution for a tool displacement of 10 mm, using both reference and identified parameters set. It can be seen that a good agreement was obtained between the reference and the predicted results. Such a similarity between the identified and the reference strain fields does not reflect the difference in the values of the material parameters (Table 4). Such a result illustrates the non-uniqueness of the material parameters set, that could not be reached even for a rather large number of strain states.

Fig. 10

Major ε₁ and minor ε₂ strain distribution for a displacement d = 10 mm of the designed test (a) without and (b) with rotation of the material orientation

Validation

With the aim of validating the material parameters set identified, the numerical reproduction of the experimental database composed by the several classical tests used to determine the virtual material behavior was carried out. The numerical simulations of the tests were carried out considering tridimensional models with one single 8-node element with linear interpolation and reduced integration (C3D8R). Boundary conditions were applied in order to obtain homogeneous stress and strain states over the element, in uniaxial tension, simple shear and equibiaxial tension (Fig. 11). Concerning the bulge test, such a simplification was checked, since the one element model reproduced the same conditions as in the experiments in the center of the specimen.

Fig. 11

Boundary conditions applied on the numerical model for each classical test. U stands for the displacement

Figures 12 and 13 show the experimental and numerical stress-strain curves for simple shear/uniaxial tension and longitudinal and transverse strains ε₁₁-ε₂₂ curves for uniaxial tension in the five different orientations to RD obtained with the reference and identified parameters sets. Figure 12 also includes the experimental and numerical results for bulge test.

Fig. 12

Experimental and numerical (i) τ-γ curve for simple shear and σ-ε curves for bulge and uniaxial tension to 0°/RD and (ii) ε₁₁- ε₂₂ curves for bulge and uniaxial tension to 0° to RD

Fig. 13

Experimental and numerical (i) τ-γ curves for simple shear and σ-ε curves for uniaxial tension and (ii) ε₁₁- ε₂₂ curves for uniaxial tension

From Fig. 12, it can be observed that a reliable reproduction of the experimental uniaxial tension and simple shear curves was obtained using the identified parameters set. In fact, both identified and reference parameters sets led to similar numerical predictions. In the case of the bulge test, an under-estimation of the hardening evolution was observed using the identified parameters set. Nonetheless, it must be emphasized that the designed test does not cover the equibiaxial stress state. Moreover, identical numerical and experimental ε₁₁-ε₂₂ curves were obtained for both uniaxial and biaxial tension.

Concerning the numerical reproductions of the stress level in uniaxial tension and simple shear as well as ε₁₁-ε₂₂ curves at 22° and 45° to RD, depicted in Figs. 13 (a) and (b), it can be seen that the identified parameters led to almost identical stress-strain curves to the ones obtained with the reference parameters set. However, the numerical ε₁₁-ε₂₂ curves at 22° and 45° using the identified parameters set were not accurately predicted. These curves tended to deviate from the experimental behavior with the increase of deformation. In the case of the uniaxial tension and simple shear curves as well as ε₁₁-ε₂₂ curves at 77° and 90° to RD, shown in Figs. 13 (c) and (d), very reliable predictions were obtained. The experimental and numerical curves using the identified and reference parameters sets were similar.

In order to give also a quantified comparison of the results presented in Figs. 12 and 13, initial yield stresses and plastic anisotropic coefficients were calculated with both parameters sets and are given in Table 5. It can be seen that a close prediction was obtained for the initial yield stress values, with a maximum relative gap of 5 %. A similar trend was noticed for the plastic anisotropic coefficients, except at 22° and 45°, for which the relative gap culminated at 12 % and 29 % respectively.

Table 5 Anisotropic and flow stress values obtained by the reference and identified parameters set

In addition, the normalized projection of the yield surface in the plane (σ_XX/σ_Y(0), σ_YY/σ_Y(0)) is illustrated in Fig. 14 for the identified and reference material parameters set. It can be seen that the one obtained with the identified parameters set was not able to reach the equibiaxial stress point, however, it was close to this experimental value. Nonetheless, it can be seen that a general agreement was verified between the yield projections obtained using the reference and identified parameters set.

Fig. 14

Projection of the Yld2004-18p yield surface in the plane (σ_XX/σ_Y(0), σ_YY/σ_Y(0)) for the reference and identified material parameters sets

From the numerical predictions using the identified parameters set, it appears that quite interesting results can be obtained for material parameters identification considering the designed test. These predictions revealed that this heterogeneous test is able to characterize the mechanical behavior of sheet metals under several strain states and strain amplitudes. Concerning the constitutive model used in this work, the designed test, without and with a rotation of 90° of the material orientation, led to similar numerical predictions to the ones obtained from 5 uniaxial tension and 5 simple shear tests at different orientations to RD as well as 1 bulge test. However, the biaxial stress state was not accurately predicted. Nevertheless, it was pointed out that a heterogeneous test performed in uniaxial loading path can be very effective to identify the material parameters of a complex phenomenological model involving a large number of parameters.

Conclusions

In this work, shape and boundary optimization was applied to design a heterogeneous test aiming at better material parameters identifications involving constitutive models with a large number of parameters.

The main advantage of the developed design optimization process is the resemblance with the experimental reality, because a rigid tool leading to uniaxial loading path is used for applying the displacement in a similar way as universal standard testing machines. The heterogeneous test designed characterizes a strain state range between simple shear to plane strain tension. Such a result suggests that when a uniaxial loading path is applied, the design optimization process tends to search for a specimen shape covering this strain state range.

A non-homogeneous parameters identification approach using the designed test (i) without and (ii) with a rotation of 90° of the material orientation was carried out considering a virtual material identified from conventional quasi-homogeneous tests as a reference material. This virtual material behavior was reproduced using a complex phenomenological model combining Yld2004-18p yield function with mixed hardening. The identified material parameters from this heterogeneous test were used to predict the experimental data of the conventional tests and reliable numerical reproductions were obtained. The quantitative indicator representative of the strain field and used in the cost function exhibited some weakness in taking into account the test heterogeneity and the anisotropy and should be further improved. However, it was shown that the designed test, in two different material orientations, is able to (i) characterize the mechanical behavior of sheet metals under several stress and strain paths, (ii) give identical numerical predictions to the ones obtained from 5 uniaxial tension and 5 simple shear tests at different orientations to RD as well as 1 bulge test and (iii) promote an effective material parameters identification for complex phenomenological models involving a large number of parameters.