Introduction

Nowadays the use of simulative tools takes a significant part in the development process of components and production technologies. In particular process design for automotive bulk forming parts is difficult to be realized efficiently without simulative investigations. Models have to be developed to ensure a precise prediction of the process who takes into consideration the relevant effects. In the special case of forming processes, the prevision of the energy needed or of damage is one of the most relevant objectives. To get to this target, the knowledge of the flow behaviour is an important part. This behaviour can be influenced by different factors: strain, strain-rate and temperature to quote the most important ones. Those factors can be described with a constitutive law which express the flow stress of the material as a function of the considered factors.

The number of constitutive laws usable for forming processes has strongly increased over the last decades. This amount of models can be split into two categories which are the phenomenological models and the physical-based models [1]. Whereas the phenomenological models are based on the observation of the flow of metals in precise conditions, the physical-based models are related to microscopic properties of the material. Most of these models can describe dependencies of the flow stress on plastic strain, strain-rate and temperature. First the work will be focused on the dependency on plastic strain which describes the static behaviour of materials called strain hardening. The method used will be extended to strain-rate and temperature dependencies afterwards to reach the objective which is a reliable predictability of the behaviour of the part during forming processes. A recent review of important laws used in forming simulations has been performed by Lin and Chen [2].

To precisely describe the behaviour the constitutive law has to be adapted to the range of deformation that will occur in reality. In the case of bulk forming local deformations can be extremely large. Most of the models implemented in computational codes are able to describe the flow behaviour within a limited domain of strains [3]. For the description of larger values extrapolation is usually used which makes the results uncertain and often false because the behaviour at low strains is different from the one at high strains. Bonora et al. [4] observed the strong influence of the flow law on the form of the specimen after a Taylor test. More recently, Lemoine et al. [5] used virtual experiments to study the large plastic strain levels based on hydraulic bulge test.

In the present work, experimental data is generated by performing upsetting tests of cylindrical specimens with diameter D and height H. These experimental data are used to characterize the material behaviour.

The contact between the sample and the compressive tool is of huge importance in terms of friction:

In fact the friction at the specimen-tool interface increases the force necessary for a given reduction of height so that fundamental results on the flow behaviour of the material under compressive loading cannot directly be extracted from the results. Moreover friction initiates a triaxial state of stress with a visual consequence: barrelling. The amplitude of the influence of friction on the upsetting force is directly dependent to the materials in contact described with a friction coefficient and to the upsetting ratio D/H [6]. One way to reduce the friction at the specimen-tool interface, is the use of high quality lubricants or special specimen geometries which can provide interesting results for moderate strains [7]. However, the friction is not completely suppressed by any approach and still affects the measured flow curves for large strains [8].

To neglect the influence of friction, different upsetting ratios can be used to extrapolate the results to a frictionless state with D/H=0. Cook and Larke [9] developed a methodology to extrapolate the behaviour on copper cylindrical specimens at room temperature. For high upsetting ratios D/H, the influence of friction becomes more explicit. On the opposite, very low values make the influence of friction near to negligible. Han [10] applied the extrapolation to aluminium alloys.

Based on obtained experimental data, material characterization can be conducted in order to obtain the mechanical parameters of the material to be implemented in a constitutive law. These numerical technics are widely used in the literature. Identification based on Finite Element simulation loops are possible, however the simulation time can be consequent [11]. Kim and Choi [12] used inverse analysis to predict the deformation behavior and interfacial friction under hot working conditions. A minimization of the error function comparing experimental data and finite element simulation was conducted using gradient-based algorithms like the Golden-section search and the Broyden-Fletcher-Goldfarb-Shanno method (BFGS). Guzman et al. [13] identified the constitutive parameters of a Johnson-Cook model with temperature measurements during dynamic upsetting tests.

Finally, in this paper, experimental axial compression test were first performed with an aluminum alloy Al6082 on a SHPB apparatus. Following this step of experimental tests, numerical identification was used to calculate material parameters of three different models (Ludwik model [14], Swift [15] model, and the recent flow stress law developed by El-Magd [16]) using the sequential quadratic programming (SQP) algorithm. Two different strategies were used. The first one is based on a classical sequential quadratic programming. The second one combines SQP with a reduction of the model dimension in order to improve the convergence related to the identification process. In the literature, Harb et al. [17] used a combination between genetic algorithm (GA) and analytical optimization. The number of non-linear parameters used in the optimization is reduced, but this technique is also time-consuming because the number of evaluation of GA is very great.

Two optimization steps are conducted in this paper. Firstly the material parameters of the Ludwik, Swift and El-Magd models are identified with the calculation of the objective function by the quadratic difference between the analysed models and experimental data obtained from upsetting tests. Then we analyse if large scatter can be obtained with different models, even for the same initial flow curve and the same fitting strain range (experimental strain range).

In the second optimization study, a new flow curve is extrapolated for a large strain hardening. The same optimization approach was used to identify the material parameters of the previous models, (El-Magd, Ludwik and Swift), and a comparison between these models in terms of scatter is discussed, for the extrapolated flow curve and for the same fitting strain range (large strain range).

Then, the friction coefficient is identified by an inverse analysis fitting experimental data related to a axial test with a 3D finite element results. Finally, by using all the identified parameters inside the 3D Finite Element model (friction coefficient and material parameters of the laws), numerical replication of the side pressing test was performed for a validation step, showing an excellent correlation between the numerical and experimental values of the forging force for steel 100Cr6. The different steps of the proposed methodology are illustrated in Fig. 1.

Fig. 1
figure 1

different steps of the methodology: experimental tests, parameters optimization and validation

Full size image

Material models

To get the most accurate description of the behaviour a theoretical model derived from the physical processes at an atomic level should be used. However, a solid theoretical approach is not available yet. In consequence semi phenomenological models are an appropriate way to do [7]. Within the present work three models will be studied. The first one, the Ludwik model, is one of the most often used in finite element codes such as Abaqus [18], Ansys [19] or LS-Dyna [20]. This model relates the stress level σ to the plastic strain level ε p .

$$ \sigma ={C}_1+{C}_2{\varepsilon}_p^n $$
(1)

In this expression, C 1, C 2 and n respectively represent the yield stress, the strain hardening modulus and the strain hardening exponent of the material. The Ludwik model is used within the Johnson-Cook model to describe the static behaviour of the material [21].

The Swift model is also often used to model the material behaviour. This model introduces three constants parameters to relate the stress level σ to the plastic strain level εp as follow:

$$ \sigma ={C}_1.\;{\left({C}_2+{\varepsilon}_p\right)}^n $$
(2)

Where C 1, C 2 and n are material constants.

The third model that will be examined was developed by El-Magd [16] and introduces five constants for a more precise description of material flow.

$$ \sigma ={C}_1+{C}_2{\varepsilon}_p+{C}_3{\left[1- \exp \left(-\frac{\varepsilon_p}{C_4}\right)\right]}^n $$
(3))

This model showed good results for aluminium alloy AA6060 (AlMgSi0.5) and steel 42CrMo4 in the investigations of Emde [22]. This model is an extension of the Voce model [23] and combines a linear part with a coupled exponential-potential function. A similar form without the exponent n is already integrated in the finite element code Ansys [19]. The most important advantage of this model is to consider the linear satiation of flow stress at very high plastic deformation. In fact for large strains the law will satiate to a linear curve with a slope C2. In the case of C2 = 0, the flow stress exhibits a maximum value.

Experimental method and materials

Extrapolation methodology

The friction has an important influence on the upsetting force. As a consequence the results obtained from an upsetting test cannot directly be used to gain the flow curve. To limit this issue, the influence of the friction has to be established in order to be able to eliminate it from the measurement results.

A basic and practical way to eliminate the influence of friction is to use different upsetting ratios D/H and to extrapolate the results to the frictionless state corresponding to a very low value of (D/H) = 0 [9]. For high (large) upsetting ratios D/H, the influence of friction was found significant while very low values make the influence of friction near to negligible.

Instead of using extrapolation method, another possibility is to try to physically suppress the friction at the contact surfaces with lubrication. But usable results can only be obtained with specific specimens like the Rastegaev specimen [7]. Nevertheless, this solution was not followed in this work since such specimens do not allow to maintain the near to frictionless state for large strains [8].

To extrapolate the flow stress data obtained from experiments to suppress the influence if friction, different upsetting ratios were used. It should be taken in consideration that there is a minimal value of the D/H ratio that can be realized. In fact if the specimen becomes too slim, buckling will occur. This exhibits a minimal value of the upsetting ratio which mostly admitted to be equal to 0.4–0.5. The considered values of upsetting ratios are 0.4, 0.5, 0.67, 1.0 and 2.0. The diameter is kept constant and the height is varied to fit the different ratios, as illustrated in Fig. 2. All samples were machined with the same cutting conditions from the same piece of steel in order to minimize the variance due to manufacturing.

Fig. 2
figure 2

Different sample geometries for extrapolation to infinite height

Full size image

Materials

Within this paper the steel 100Cr6 will be studied. This steel is a high strength material for bearing applications [24] . The Fig. 3 shows the structure of the material before deformation. This steel has a ferritic structure with chromium carbides evenly distributed over the volume. The measured hardness is 240 HV1. The measures made on the element concentration correspond to the norm for this steel, the DIN EN ISO 683–17, see Table 1. The material is considered as isotropic.

Fig. 3
figure 3

Original state of the steel 1.3505 (scale 10 μm)

Full size image
Table 1 Element composition of the steel 1.3505 in comparison with DIN EN ISO 683-17
Full size table

Assuring isothermal conditions

During plastic deformation a part of the mechanical work is converted into heat [25]. If the process time is short, the heat cannot be conducted quickly enough out of the sample and temperature rises. Since the static part of the flow stress models is used for the current work, isothermal conditions have to be ensured.

In order to find the required time for isothermal case, the dimensionless Fourier number F0 can be used [26]. It gives the time span over which the process is isothermal or adiabatic. It can be calculated as following:

$$ {F}_0=\frac{\alpha t}{L^2} $$
(4)

In this expression α, t and L are the thermal diffusivity, the process time and the characteristic dimension of the sample respectively. For the upsetting test, L is assumed to be the radius of the sample before deformation [27]. As this characteristic dimension increases, the duration of the experiment has to be increased for fully isothermal conditions. It is assumed that the process is isothermal for values of F0 over 10. For the samples used in this paper, duration of 22 s is the minimum according to the 5 mm radius of the samples. This duration leads to a maximal initial strain rate of \( \dot{\varepsilon} \) = 0.027 s−1 for the smallest sample and \( \dot{\varepsilon} \) =0.045 s−1 for the biggest sample. The strain rate used for all samples is \( \dot{\varepsilon} \) =0.01 s−1, which corresponds to the fully isothermal domain. The velocity of the tooling is calculated based on the samples height.

Operating conditions

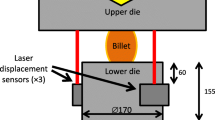
The upsetting test is performed within a compressive testing machine. Both dies are made of carbide with high mechanical properties to avoid permanent deformation during the upsetting test. The contact surfaces of the dies are grinded to a roughness of Rz=0.4 μm (maximum height of the profile). Figure 4 exhibits the experimental setup.

Fig. 4
figure 4

Experimental setup for the upsetting tests on the universal testing machine

Full size image

During the compression of the sample, the forging force is measured using a 600 kN “S-Type” load cell. The deformation is measured using the stroke of the upper die. Since the entire machine deforms during the testing, its stiffness is considered by measuring a load curve without any sample.

Results

As previously explained in section 3.1, a practical way to eliminate the influence of friction is to use different upsetting ratios D/H and to extrapolate the results to the frictionless state corresponding to D/H = 0. The results of the upsetting tests are illustrated in Fig. 5. The total true strain ε and the true stress σ are calculated from the experimental force-displacement diagrams as followed:

Fig. 5
figure 5

Experimental flow curves for different upsetting ratios and extrapolated flow curve for steel 100Cr6

Full size image
$$ \varepsilon = \ln \left(\frac{h}{h_0}\right) $$
(5)
$$ \sigma =\frac{F}{S_0}\cdot \left(1+\frac{h-{h}_0}{h_0}\right) $$
(6)

For both expressions, h represents the actual height of the sample, h0 the initial height of the sample, F the actual force applied to the sample and S0 the initial cross section of the sample. The true plastic strain εp can be calculated from the total true strain ε by subtracting the elastic part assuming a value of 0.2 %.

It is noted that the geometry has a great influence on the flow curve (Fig. 5). At a true plastic strain εp greater than 1 the value of the true flow stress σ is double for the D 10 x H 5 mm sample than for the D 10 x H 25 mm one. On the other side, the difference between sample geometries is negligible for strains below 0.2 except the D 10 x H 5 mm sample. In the case of the D 10 x H 5 mm sample, the influence of friction is strong enough to increase the measured yield strength.

For the samples with initial heights 5, 10, 15, 20 and 25 mm, the heights after upsetting are respectively 1.75, 2.78, 3.63, 4.46 and 5.15 mm.

To perform the extrapolation, the value of true flow stress σ is determined for the different upsetting ratios D/H and different true plastic strains ε p. Then for each true plastic strain εp a curve of true stress σ as a function of the upsetting ratio D/H is made as illustrated in Fig. 6. In the present work, the extrapolation to D/H=0 is obtained with a second order polynomial function. Afterwards the extrapolated point is adjusted by minimizing the first order term. Since the extrapolation is only possible when more than one experimental curve is available, the extrapolated flow curve is only built until εp=1.5 (Fig. 6). To summarize the results of the extrapolation, Fig. 5 illustrates the frictionless flow curves for H → ∞. For the identification of the material parameters, only the extrapolated curve without friction effect is used.

Fig. 6
figure 6

Computation of the frictionless (extrapolated) flow curve for steel 100Cr6

Full size image

Identification of models parameters

Two optimization steps are conducted in this paper. Firstly the modelling parameters of three flow stress laws i.e. Ludwik, Swift and El-Magd are identified. A comparison between these models is conducted. in this study we analyse if large scatter can be obtained with different models, even for the same initial flow curve and the same fitting strain range (experimental strain range). The comparison is performed only up to 1.5 strain

Experimental flow curve identification

The material parameters used in equations (1)-(3) (i.e. C 1, C 2, C 3, C 4 and n) have to be identified up to a range of true stresses and true plastic strains to predict experimental compression test. The three identification problems are formulated as the minimisation of the difference between measured data and analytical results.

$$ \mathrm{minimize}\left\{\begin{array}{c}\hfill J\left(\mathrm{x}\right)={\displaystyle \sum_{i=1}^m\frac{{\left({\sigma}^i\left(\mathrm{x}\right)-{\sigma}^imes\right)}^2}{\sigma^imes}}\hfill \\ {}\hfill \mathrm{Such}\;\mathrm{that}\ {\mathrm{x}}^l\le \mathrm{x}\le {\mathrm{x}}^u\hfill \end{array}\right. $$
(7)

Where J is the objective function, σi(x) and σi mes are respectively the vectors component of calculated and measured stress and m is the number of the measured data. x is the vector of the optimization parameters. Three optimization problem which represent the identification of material parameters of Ludwik,Swift and El Magd model are resolved, the objective functions and the vectors of optimization variables are respectively represented as follows:

$$ \begin{array}{c}\hfill J\left(\mathbf{x}\right)={\displaystyle \sum_{i=1}^m\frac{{\displaystyle {\left(\left({C}_1+{C}_2{\left({\varepsilon}_p^i\right)}^{\;n}\right)-{\sigma}_{mes}^i\right)}^2}}{\sigma_{mes}^i}}\kern0.36em \Rightarrow \kern2.04em x=\left[\begin{array}{ccc}\hfill {C}_1\hfill & \hfill {C}_2\hfill & \hfill n\hfill \end{array}\right]\mathrm{Ludwik}'s\ \mathrm{model}\hfill \\ {}\hfill J\left(\mathbf{x}\right)={\displaystyle \sum_{i=1}^m\frac{{\displaystyle {\left(\left({C}_1.\;{\left({C}_2+{\varepsilon}_p^i\right)}^n\right)-{\sigma}_{mes}^i\right)}^2}}{\sigma_{mes}^i}}\kern1.8em \Rightarrow \kern2.4em x=\left[\begin{array}{ccc}\hfill {C}_1\hfill & \hfill {C}_2\hfill & \hfill n\hfill \end{array}\right]\mathrm{Swift}'s\ \mathrm{model}\hfill \\ {}\hfill J\left(\mathbf{x}\right)={\displaystyle \sum_{i=1}^m\frac{{\left[\left({C}_1+{C}_2{\varepsilon}_p+{C}_3{\left[1- \exp \left(-\frac{\varepsilon_p^i}{C_4}\right)\right]}^n\right)-{\sigma}_{mes}^i\right]}^2}{\sigma_{mes}^i}}\Rightarrow x=\left[\begin{array}{c}\hfill {C}_1\hfill \\ {}\hfill {C}_2\hfill \\ {}\hfill {C}_3\hfill \\ {}\hfill {C}_4\hfill \\ {}\hfill n\hfill \end{array}\right] El-\mathrm{Magd}'s\ \mathrm{model}\hfill \end{array} $$

This vector is bounded by xl and xu which represent lower and upper limits respectively, and which are reported in Table 2, for all models. These bounded values correspond to the maximum range usually accepted for the kind of material considered in this work. It should be noticed that, for the SQP-AO strategy, only the two last variables are bounded by lower and upper limits as the three first variables are analytically calculated.

Table 2 Lower and upper limits of optimization variables
Full size table

Following the approach proposed by Harb et al. in [17], it is observed for example that the El-Magd model can be expressed as follows:

$$ \sigma =\left[\begin{array}{ccc}\hfill 1\hfill & \hfill {\varepsilon}_p\hfill & \hfill {\left(1- \exp \left(-\frac{\varepsilon_p}{C_4}\right)\right)}^n\hfill \end{array}\right]\kern0.5em \left[\begin{array}{c}\hfill {C}_1\hfill \\ {}\hfill {C}_2\hfill \\ {}\hfill {C}_3\hfill \end{array}\right]=N\left({\mathbf{x}}_{nlin}\right)\cdot {\mathbf{x}}_{lin} $$
(8)

xlin represents the linear parameters C1, C2 and C3 while N(xlin) includes the nonlinear parameters xnlin = {C4, n}.

The combination of (7) and (8) yields to a classical least squares problem with C1, C2 and C3. This problem can be analytically solved by calculating the partial derivative of σ(x) with respect to xlin

$$ {\mathbf{x}}_{lin}={\left({N}^TN\right)}^{-1}{N}^T{\sigma}_{mes} $$
(9)

Injecting this analytical solution inside the identification process will lead to running the identification algorithm over a reduced number of two parameters C4 and n. This space reduction can be used with any search strategy in order to minimize J(x). Gradient based approaches including BFGS (Broyden-Fletcher-Goldfarb-Shanno) and SQP (sequential quadratic programming) algorithm are among one of the earlier methods used in a non-linear optimization problem [28, 29]. In this paper, the SQP algorithm was used to solve the identification problem and search of optimal parameters. Results obtained with the reduced space minimization problem are labelled by SQP-AO. Those obtained with standard minimization problem are labelled SQP.

The convergence history during the optimization run is presented in Fig. 7. According to this figure it is obvious that the objective function values decreases during the optimisation iterations (Fig. 7a) and converges at the 11th and 74th iterations for SQP-AO and SQP method respectively. It can be observed in Fig. 7b that the number of function evaluations increases for the global model (SQP). This is due to the reduced number of variables (2 against 5) used by the SQP-AO method.

Fig. 7
figure 7

Convergence histories of SQP and SQPAO algorithms during the optimization run

Full size image

Table 3 presents a summary of the results obtained with the initial and optimal parameters for both optimization strategies (SQP and SQP-AO). The effect of the initial value is analysed, in terms of accuracy of the result and number of function evaluation. In order to compare the two optimization strategies, the initial values were charged and in two cases (1) and (2) the same initial value were imposed. It can be noticed that both optimization strategies give the same optimal parameters and objective function. It is also observed that the SQP-AO gives low number of function evaluation.

Table 3 Optimization results for steel 1.3505, using SQP and SQPAO algorithm – El Magd model
Full size table
Table 4 Optimization results for El Magd, Ludwik, and Swift models - steel 1.3505
Full size table

The same approach was also used to identify the material parameters of the other models such as Ludwik and Swift model. The optimal parameters are summarized in Table 4.

By using these identified parameters, the behaviour laws related to equations (1) (2) and (3) were compared to the experimental curve in Fig. 8. A good correlation can be observed between all models and the experimental flow curve. The relative error between identified models (El-Magd, Ludwik, and Swift) is illustrated in Fig. 9. It is observed that the relative error is less than 4 % except Ludwik model at very low values of true strain φ. It can also be noticed that El-Magd model gives the best value of the objective function, with a relative error under 1 %.

Fig. 8
figure 8

Comparison between identified models (El-Magd, Ludwik and Swift) and experimental curve for steel 100Cr6

Full size image
Fig. 9
figure 9

Error between identified models (El-Magd, Ludwik and Swift) and experimental flow curve for steel 100Cr6

Full size image

Extrapolation to large strains

According to the results obtained in [22, 23] a stress satiation can be extended beyond the limit of εp=1.5, as illustrated in Fig. 10. The strain hardening slope δσ /δεp exhibits clearly an exponential decrease. This point leads to extrapolate the strain hardening with an exponential function (represented on Fig. 10 with square symbol). The true stress values are next approximated according to following integration formula:

Fig. 10
figure 10

Extrapolation of the frictionless flow curve to higher values of true plastic strain

Full size image
$$ f\left({\varepsilon}_p+\varDelta {\varepsilon}_p\right)=f\left({\varepsilon}_p\right)+\varDelta {\varepsilon}_p\cdot f\hbox{'}\left({\varepsilon}_p\right) $$
(10)

The fitting results strongly depend on the strain range chosen for the fitting. Such discrepancies between experimental and fitting flow curve should be reduced.

For the optimization procedure, the same approach was also used to identify the material parameters of the previous models (El-Magd, Ludwik and Swift) for the extrapolated flow curve.

Table 5 presents a summary of the optimization results obtained for the three behaviour law. The optimal parameters of the behaviour laws for the extrapolated flow curve are reported with the final value of the objective function. It can be noticed that the value of the objective function for El-Magd model is very small (J = 13.6) compared to the other values obtained for both Ludwik and Swift models which are 1,883 and 1,514 respectively.

Table 5 Optimization results with extrapolated flow curve for El Magd, Ludwik, and Swift models
Full size table

By using these identified parameters, the behaviour laws related to the three studied models were compared to the experimental extrapolated flow curve in Fig. 11. It can be observed that El-Magd model give a very good correlation over the model and this is for both flow curve i.e. experimental flow curve limited to εp=1.5 and extrapolated one (extended beyond the limit of εp=1.5). For the other models and with the hypotheses of extrapolated flow curve presented in [22, 23] it can be observed that Ludwik and Swift models do not saturate and give a poor correlation compared to El-magd. Figure 12 illustrates the relative error between extrapolated experimental flow curve and the three models, for Swift and Ludwik model the relative error is about 5 % except at low values of true strain φ, it can reach 10 %. Since the Ludwik and Swift model is only based on a potential term, it is not possible to have good results for both hardening and satiated parts of the flow curve. With the El-Magd model, a good correlation over the whole domain of true plastic strain is achieved and the flow curve is modelled with a relative error under 1.5 %.

Fig. 11
figure 11

Comparison between identified models (El-Magd, Ludwik and Swift) and extrapolated flow curve

Full size image
Fig. 12
figure 12

Error between identified models (El-Magd, Ludwik and Swift) and extrapolated flow curve

Full size image

FE simulation: identification of the friction coefficient

Numerical identification of the friction coefficient using axial upsetting tests

In order to identify the friction coefficient, a finite element simulation is conducted with the identified material parameters (cf section 4). A sensitivity study on the friction coefficient is performed comparing the numerical curves (force) with experimental ones obtained from the upsetting tests (cf section (Fig. 4).

The 3D finite element model is created using Abaqus 6.11 [18]. The velocity of the upper tool is calculated so that the global strain rate of the specimen is equal to the one used for the material calibration. Inertial effects are neglected. Accounting for the symmetry of the specimen only one half of the specimen is modelled. The mesh is built using 8-node hexahedral elements with reduced integration, distortion control and hourglass control. 16,250 elements and 18,258 nodes using a global line seed of 0.40 mm are used. The tool is modelled as a rigid body.

The contact between the rigid tool and the sample was modelled with a penalty-controlled surface-to-surface explicit contact. Coulomb’s friction law is used for the calculation. The tangential behaviour on the interface was defined with a penalty friction formulation.

The friction coefficient μ of this model was identified using an inverse analysis method. The identification process was performed by using the quadratic error between experimental and numerical curves for different friction coefficients varying from 0.15 to 0.25. Figure 13 illustrates the sensitivity study. A value of 0.195 gives the best value which minimizes this difference.

Fig. 13
figure 13

Identification of thefriction coefficient for steel 100Cr6

Full size image

Modelling of the side pressing test

In the last paragraphs a flow stress model was picked and calibrated using an extrapolation of flow curves from upsetting tests of cylinders with different upsetting ratios. In order to validate the capabilities of the model and the relevance of the material parameters and friction coefficient identification, another finite element analysis was conducted in order to replicate the side pressing test, with the aim of comparing experimental data to the obtained numerical results as illustrated in Fig. 14.

Fig. 14
figure 14

FE-Model of the side pressing test

Full size image

The experimental protocol used to conduct the comparison was the side pressing test. This experimental configuration is a radial compression of a cylindrical specimen.

The experimental protocol for the radial compression test is similar to the axial test described in Fig. 4. The specimen used for the side pressing is the D 10 × H 20 mm one.

In addition to the axial test which allow conducting the material parameters identification, the new configuration of the radial compression allowed providing new data to validate the FE model,

Validation of the model and discussion

Both mechanical parameters of the constitutive laws and friction coefficient were identified in order to minimize the error between experimental data and numerical simulations using a given configuration of test (axial tests). Mechanical parameters were identified using an optimization algorithm, and friction coefficient was identified using FE simulation

In order to validate the models as well as the friction coefficient, a second configuration of the test was used: five side pressing tests were simulated using the same friction coefficient, and the predicted forces were compared to the experimental ones. On Figure15, the predictions of the cylindrical upsetting tests with the identified friction coefficient and identified mechanical parameters are presented. An excellent correlation was observed between experimental data and numerical simulation. It can be seen in Fig. 15, that the force vs. displacement curves perfectly fit experimental data for the five tested samples.

Fig. 15
figure 15

Comparison between experimental and numerical force for different upsetting ratios for steel 100Cr6

Full size image

This correlation demonstrates the efficiency of the El-Magd law and its capability to model large deformations problems corresponding to forming processes such as forging or stamping. The identified friction coefficient is also validated.

In terms of shape of the sample, Fig. 16 also illustrates a comparison between experimental results and FE simulation. With the identified friction parameter and constitutive law, good correlation was found between experimental and numerical results in terms shape (radial and axial deformation).

Fig. 16
figure 16

Comparison between numerical (left) and experimental (right) deformed geometry for steel 100Cr6

Full size image

Conclusion

In this paper an identification method for an extrapolated flow curve at large strains is proposed for high strength steel. The approach is based on several points:

  • Use of upsetting tests to acquire experimental data for large strains

  • Use of different specimens to extrapolate the behaviour to a “frictionless” state

  • Use of adequate material model and parameter identification procedure

  • Implementation of the identified parameters in a FE code in order to find the appropriate friction coefficient with sensitivity study.

  • Validation of the constitutive law and friction coefficient with finite element simulation by comparison with experimental side pressing test.

In the case of the steel 1.3505 the method was used with a flow stress model adapted for large strains and an identification procedure based on a reduced dimension of the identification problem. The identified parameters were implemented in a FE code in order to find the friction coefficient which minimized the quadratic error between experimental and numerical results of upsetting test.

Side pressing tests were also conducted at an experimental level. Based on this configuration of test, the identified model (El-Magd) with the identified friction coefficient were implemented in a FE code and a numerical replication of the side pressing test was performed. Numerical Results in terms of shape of the sample and force/displacement curves were compared to experimental data showing excellent correlations, even if further improvements of the model could be conducted by including the strain rate dependency and the thermal effects.

Finally, the optimal mechanical parameters being identified with different methods, the study provides efficient methodology for the investigation of bulk metal forming.