Modeling and optimization of spring-back in bending process using multiple regression analysis and neural computation

Abstract

The current work involves both modeling and optimization approaches to achieve minimum spring-back in V-die bending process of heat treated CK67 sheets. Number of 36 experimental tests have been conducted with various levels of sheet orientation, punch tip radius and sheet thickness. Firstly, various predictive models based on statistical analysis, back-propagation neural network (BPNN), counter propagation neural network (CPNN) and radial basis function network (RBFNN) have been developed using experimental observations. Then the accuracy of the developed models has been compared based on values of mean absolute error (MAE), and root mean square error (RMSE). Secondly, the model with lowest values of MAE, and RMSE has been applied as objective function for optimization of process using imperialist competitive algorithm (ICA). After selection of optimal bending parameters, a confirmation test has been conducted to prove the optimal solutions. Results indicated that the radial basis network fulfills precise prediction of process rather than the other developed models. Also, confirmation tests proved that both RBFNN and ICA could predict and optimize the process vigorously.

Introduction

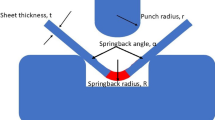
Sheet metal bending process is one of the most widely applied sheet metal forming operations. In this process, lack of dimension precision is a major concern due to the considerable elastic recovery during unloading. This phenomenon is called spring-back. Also, under certain conditions, the final bending angle may be smaller than the original angle. Such a bending angle is referred to as negative spring-back. The amount of spring-back is influenced by various factors, such as tool shape and dimension, contact friction condition, material properties, sheet orientation, and sheet thickness [1–4]. Figure 1 shows the spring-back and negative spring-back with respect to original bending angle.

Fig. 1

Bending process, a before unloading the punch, b spring-back phenomenon, c negative spring-back phenomenon [4]

During the past two decades, a number of researchers have investigated and attempted to obtain a basic understanding of spring-back behavior using numerical and experimental methods. Tekiner [5] examined the effect of bending angle on spring-back of six types of materials with different thicknesses in V-die bending. Moon et al. [6] experimentally showed the effect of combined hot die and cold punch on reduction of spring-back of aluminum sheets. Li et al. [7] showed that the accuracy of spring-back simulation is directly affected by the material-hardening model. In addition, Cho et al. [8] have carried out numerical studies on the effects of some parameters such as punch and die corner radii, punch-die clearance, and coefficient of friction on spring-back in U-die bending process. Gomes et al. [9] simulated material models based on various anisotropic models and compared their results with the experimental outcomes to show the variation of spring-back with the orientation of anisotropic sheet in U-die bending process.

The disadvantage of the previous simulation modeling is that the modeling cannot be done without considering some simplifying assumptions. Artificial neural networks as non-linear modeling technique are suitable for model-based supervision of uncertain systems. A neural network model can be developed by using the experimental data without having to make any simplifying assumption. Instead, it needs sufficient input–output data.

The neural networks have been widely used for mapping input and output parameters of the bending processes. Bozdemir and Golsu [10] predicted the spring-back angle when the input parameters were the sheet material, bending angle, and the ratio of punch tip radius to sheet thickness. Liu et al. [11] developed the prediction model of spring-back in the typical U-shaped bending by using the integrated neural network genetic algorithm. Ruffini and Cao [12] developed a neural network control system for spring-back reduction in a channel section stamping process of aluminum. Pathak et al. [13] proposed a model for prediction of the responses of the sheet metal bending process using an artificial neural network. The model was trained, based on the results of 44 cases analyzed using the finite element technique. Forcellese and Gabriella [14] investigated the effect of the training set size and the number of input parameters on the predictive capability of a neural-network-based control system for spring-back compensation in air bending. Inamdar et al. [15] discussed the development of an artificial neural network which was used to predict the spring-back in an air V-bending process. Viswanathan et al. [16] used a neural network control system along with a stepped binder force trajectory, to control the spring-back angle in a steel channel forming process. Cao et al. [17] demonstrated the exceptional ability of a neural network along with a stepped binder force trajectory to control spring-back angle and maximum principal strain in a simulated channel forming process. Kazan et al. [18] developed a predictive model of spring-back by neural network, based on data obtained from finite element analysis. In the previous paper by the authors [19], finite element method (FEM) was used to study the effects of sheet thickness, sheet orientation and punch tip radius on spring-back in V-die bending process of CK67 steel sheet.

The imperialist competitive algorithm (ICA) is one of the recent meta-heuristic optimization techniques. This novel optimization method was developed based on a socio-politically motivated strategy. The ICA is a multi-agent algorithm in which each agent is a country and can be either a colony or an imperialist. This algorithm proposed by Atashpaz-Gargari et al. [20, 21]. Kaveh and Talatahari [22, 23] improved the ICA by defining two new movement steps and investigated the performance of this algorithm to optimize the design of skeletal structures and engineering optimization problems. Due to novelty of this algorithm, there is not certain publication which used ICA in optimization of manufacturing processes.

Although neural network was used most commonly in modeling of spring-back, but all the developed models were simple networks such as back-propagation network. In present work, various predictive models namely regression analysis, back-propagation network, counter-propagation network and radial basis network are developed to estimate spring-back of CK67 sheet. Then, the accuracy of each model is compared with others to find most accurate model which can predict the bending process precisely. Afterward, the most accurate model is associated with imperialist competitive algorithm to minimize the spring-back in V bending process. Due to novelty of ICA algorithm and generation of various neural models, this work can be introduced as new approach for improvement of bending process.

Principles of spring-back

Figure 1(a) illustrates the stress distribution on the sheet in the bending process before the unloading stage which brings about the spring-back phenomenon.

During the bending process of sheet metals, regardless of stiffness level of material, the regions far from the neutral axis undergo plastic deformation, while it always remains a band around the neutral axis which is still in elastic zone. The material on the punch side is under compressive stresses, whereas the material on the die side is under tensile stresses. As a result of the stress distribution, the material in the compressive zone tries to enlarge and the material in the tension zone tries to shrink owing to the existence of elastic band through the sheet thickness. Consequently, the material in the bending area tries to spring-back and the bended workpiece slightly opens as shown in Fig. 1(b) [4].

Under certain circumstances, however, the final bending angle might be smaller than original one (die angle). Such a phenomenon which is referred to as negative spring-back (Fig. 1c) originates from another similar reason. Thiprakmas and Rojananan [4] examined the occurrence of reversed bending. They discussed material flow analysis and explained theoretical reasons of the occurrence of the negative spring-back phenomenon. The reversed bending phenomenon generated reversed stress distribution compared with the bend zone; therefore, the tensile and compressive stresses were generated on the punch and die side respectively. The difference of material flow characteristics in various angular bending radii caused the different stress distribution and also different amounts of reversed stress in the sheet. Hence, when the generated stresses in the bend zone suppressed the generated stresses in the reversed bending zone, the spring-back phenomenon occurred. In contrast, when the generated stresses in the reversed bending zone suppressed the generated stresses in the bend zone, the negative spring-back phenomenon occurred.

Experimental procedure

To characterize the material properties and orientation, different specimens of 25 × 100 mm CK67 steel sheets were cut at different orientations to the rolling directions (0°, 45°, 90°). Tensile specimens were used to determine the stress–strain curves and the sheet orientation parameters, r-values [24]. Moreover, rectangular specimens (40 × 120 mm) cut from the same sheets were used in the die bending experiments.

During the bending tests, the sheets with thicknesses 0.5, 0.7, and 1 mm were examined. A universal Denison Mayes Group (DMG) testing machine with a capacity of 600 kN was used for the experiments.

The plastic properties of rolled sheets vary in the through-thickness direction, normal orientation, and also vary with orientation in the plane of the sheet, planar orientation. At a given angle, θ, to the rolling direction, the sheet orientation is defined by the plastic strain ratio, r-value [25], which is:

$$ {r_{\theta }}=\frac{\varepsilon_w }{\varepsilon_t } $$

(1)

where ε _w and ε _t are the width and thickness strains of a uniaxial tension specimen cut at an angle, θ, to the rolling direction, respectively. It should be noted that for thin sheets, it is difficult to measure the thickness strain. It is concluded from the constancy of volume that:

$$ {r_{\theta }}=\frac{{-{\varepsilon_w}}}{{\varepsilon_1 +{\varepsilon_w}}} $$

(2)

where, ε ₁ = ln (l/l ₀) and ε _w  = ln (w/w ₀). Thus:

$$ {r_{\theta }}=\frac{{-\ln \left( {{w \left/ {w_0 } \right.}} \right)}}{{\ln \left( {{{{w_0 {l_0}}} \left/ {wl } \right.}} \right)}} $$

(3)

Fig. 2 shows the schematic of the V-die set. It contains a die and a punch with 60^o bend angle. Alternative punches with different tip radiuses 2, 3, 4, and 5 mm were used to investigate the effect of the punch tip radius. The die set was made of St-52 steel. To install the die set on the machine, a shoe set with 130 mm guide pillars was used. The tests were performed at a constant velocity. After placing the blank on the die, the upper shoe, which was attached to the ram of the machine, moved against the lower shoe.

Fig. 2

V-die bending set

The bending process was divided into two stages. In the loading stage the punch moved down until its stroke reached to a specific value, 34.6 mm. In the unloading stage, the punch moved up. The number of 36 experiments was repeated for various bending parameters. An optical profile projector, Baty R14, was used to measure the bend angles. Experimental results are listed in Table 1.

Table 1 Experimental results

Intelligent predictive models

This section is allocated to definition of predictive models which have been used for prediction of spring-back. As mentioned above, intelligent predictive models are back-propagation neural network, counter-propagation neural network and radial basis function network.

Back-propagation neural network (BPNN)

Using of neural network is fashionable in telecommunication, signal processing, pattern recognition, prediction, automated control and economical analysis. BPNN has been adopted in literatures due to its accuracy and fast response. The BP structure consists of an input layer, some hidden layers and an output layer. In this structure neurons are connected to each other by some weighted links. The information from input layer is mapped to output layer through one or more hidden layers. The relationship between input–output of a single node can be written as follow [26]:

$$ {a_k}=f\left( {{W_{ki }}{p_i}+{b_k}} \right) $$

(4)

where a _k is the value of node output, W _ki is the weight connection between inputs and nodes, p _i is the output of pervious nodes in their hidden layer, b _k is the bias value of current layer, and f is transfer function. Generally the transfer functions selected for hidden layers are log-sigmoid, Eq. 5, or hyperbolic tan-sigmoid, Eq. 6. And also for the output layer the linear function is recommended [26].

$$ f(n)=\frac{1}{{1+{e^{-n }}}} $$

(5)

$$ f(n)=\frac{{e^n -{e^{-n }}}}{{e^n +{e^{-n }}}} $$

(6)

A feed forward back-Propagation neural network (BPNN) includes two main stage namely feed forward stage and back-propagation stage. In the first stage (feed forward stage) the network is trained by using of inputs and some weighted links, then outputs are calculated. Hereafter the network’s outputs are compared with real outputs and the errors are evaluated. The second stage (back-propagation stage) inspects the value of mean square error (MSE), Eq. 7. At this stage, if the value of MSE is acceptable, training is stopped and the network reaches to its desired weight vectors. Otherwise, if the MSE is not acceptable, the back-propagation algorithm updates pervious weight matrices and generates new ones until it achieves to eligible MSE.

$$ MSE=\frac{1}{N}\sum\limits_{k=1}^N {{{{\left( {t_k ={a_k}} \right)}}^2}} $$

(7)

where N is the whole number of training samples, t _k is the real target value, and a _k is the output value of the network. A learning rate is an important factor which controls the training schedule to reach in global minimum of MSE consider to the lowest training time.

Counter-propagation neural network (CPNN)

The counter-propagation neural network developed by Nielsen [27] is a combination of a portion of the Kohonen self-organizing map and the output layer. The architecture of the CPNN is the same as that of the BP network. The net consists of three layers: input layer, cluster layer (Kohonen layer) and output layer (Grossberg layer). The training procedure for the CPNN comprises two steps. First, an input vector is presented to the input node. The nodes in the cluster layer then compete (winner-take-all) for the right to learn the input vector. The weights of the network are adjusted automatically during the learning process. Unsupervised learning is used in this step to cluster the input vector as separate distinct clusters of input data. Second, the weight vectors between the cluster and output layers are adjusted using supervised learning to reduce the errors between the CPNN outputs and the corresponding desired target outputs [28].

During the first step, the Euclidean distance between the input and weight vectors is calculated. The winner node is selected based on comparing the input vector X = (x ₁, x ₂, . . ., x _n )^T and the weight vectors v _ij  = (v _1j ,v _2j , . . ., v _nj )^T . The winning node z _J has the weight vector w _Jk  = (w _J1 ,w _J2 , . . ., w _Jp )^T, winner-take-all operation that permits cluster node J to be the most similar to the input vector. The weights of the cluster node J are adjusted. The weight vector of the winner is updated according to the following equation:

$$ v_{iJ}^{new }=v_{iJ}^{old }+\alpha \left( {x_i -v_{iJ}^{old }} \right) $$

(8)

where α denotes the learning rate and x _i represents the ith node of input layer.

After training the weights from the input layer to the cluster layer, the weights from the cluster layer to output layer are trained. Each training pattern inputs the input layer, and the associated target vector is presented to the output layer. The competitive signal is a binary variable, assuming a value of 1 for the winning node and a value of 0 for other nodes of the cluster layer. Each output node k has a calculated input signal w _Jk and target output y _k . The weights between the winning cluster node and the output layer nodes are updated as follows:

$$ w_{Jk}^{new }=w_{Jk}^{old }+\beta \left( {y_k -w_{Jk}^{old }} \right) $$

(9)

where w _Jk denotes the weights from the cluster layer to output layer, and β represents the learning rate. The competitive signal of cluster layer z _j is computed by:

$$ {z_j}=\left\{ {\begin{array}{*{20}c} 1 \hfill & {if\,j=J} \hfill \\ 0 \hfill & {otherwise} \hfill \\\end{array}} \right. $$

(10)

where J is winning node.

And the kth output of CPNN is given by:

$$ {{\widehat{y}}_k}=\sum\limits_{j=1}^m {{w_{jk }}{z_j}} $$

(11)

where m is the number of neurons in hidden layer.

Termination criterion may either be the number of cycles, or mean square error (MSE) which is defined as:

$$ MSE=\frac{1}{2pG}\sum\limits_{t=1}^G {} \sum\limits_{k=1}^p {{{{({{\hat{y}}_k}-{y_k})}}^2_t}} $$

(12)

where G represents the number of training examples or patterns. The CPNN classifies the input vector to most similar cluster nodes, and then outputs the prediction result. The learning speed of CPNN is fast as compared to other neural networks. The CPNN can compress the input patterns to p clusters. The adaptive p cluster nodes determine the accuracy of the network output.

Radial basis function neural network (RBFNN)

RBFNN is alternative supervised learning network architecture to the multilayered perceptrons (MLP). The topology of the RBFNN is similar to the MLP but the characteristics of the hidden neurons are quite different. The RBFNN consists of an input layer, an output layer and a hidden layer. The input layer is made up of source neurons with a linear function that simply feeds the input signals to the hidden layer. The neurons calculate the Euclidean distance between the center and the network input vector, and then pass the result through a non-linear function (Gaussian function/multiquadric/thin plate spline, etc.). It produces a localized response to determine the positions of centers of the radial hidden elements in the input space. The output layer, which supplies the response of the network, is a set of linear combiners which is given by [29]:

$$ f(x)=\sum\limits_{i=1}^N {{w_{ij }}G\left( {\left\| {x-{c_i}} \right\|.b} \right)} $$

(12)

where N is the number of data points available for training, w _ij is the weight associated with each hidden neuron, x is the input variable, c _i is the center points, and b is the bias. The localized response from the hidden element using Gaussian function is given by:

$$ G\left( {\left\| {x - {{c}_{i}}} \right\|.b} \right) = \exp \left( { - \frac{1}{{2\sigma _{i}^{2}}}{{{\left( {\left\| {x - {{c}_{i}}} \right\|.b} \right)}}^{2}}} \right) $$

(13)

where σ _i is the spread of Gaussian function. It represents the range of ||x−c _i || in the input space to which the RBF neuron should respond.

Imperialist competitive algorithm (ICA)

The optimization algorithms mainly are inspired from nature procedures or life of animals. In these algorithms, socio-political and cultural concepts are not considered. Recently, a new optimization methodology namely imperialist competitive algorithm originates the socio-political evolution. ICA has been modeled mathematically by Atashpaz-gargary et al. [21] which is utilizing this historical phenomenon as powerful tool for solving the optimization problems. This algorithm has recently attracted the attention of many researchers for tackling of optimization problems. Briefly, ICA starts with initial solutions which are called initial countries that are similar to chromosome in genetic algorithm and particle in particle swarm optimization algorithm. These countries are divided into two groups. First group is made of imperialist countries and second group is formed with membership of colonies countries. Imperialist countries try to decrease the gaps between colonies and them through applying assimilation strategy. Imperialistic competition beside the assimilation and revolution form the main core of ICA to make it possible to reach the reliable and efficient solutions. Stages of ICA algorithm shown in Fig. 3 are explained as follows:

Fig. 3

The flow chart of ICA algorithm

• First step: Generating initial empires

  In ICA each solution is shown by an array and each array composes the amounts of variables to be optimized. These values are defined with characteristics of each specific problem. In ICA terminology, this array is called “country”. In an N dimensional optimization problem, a country is a 1×N array which is defined by:

  $$ country=\left[ {v_1, {v_2}, \ldots, {v_N}} \right] $$

  (14)

  where v _N is the variable to be optimized. Each variable in a country denotes a socio-political characteristic in that country such as culture, language, business, economical policy and etc. At first, the algorithm generates initial countries randomly in number of population size. Then, the most powerful countries are selected in number of N _imp . Remaining countries will form imperialists based on imperialist’s power. For calculating the power of imperialists, first, the normalized cost of an imperialist is applied based on the following equation:

  $$ \begin{array}{*{20}c} {C_n =\max {c_i}-{c_n}} \hfill & {i=1,2, \ldots, {N_{imp }}} \hfill \\ \end{array}$$

  (15)

  where, c _n is the cost of nth imperialist and C _n is its normalized cost which is equal to the deviation of the maximum total completion time from the nth imperialist cost. Then, the power of each imperialist is calculated according to the following equation:

  $$ \begin{array}{*{20}c} {P_n =\left| {\frac{C_n }{{\sum\limits_{i=1}^{{{N_{imp }}}} {c_i } }}} \right|,} \hfill & {\sum\limits_{i=1}^{{{N_{imp }}}} {P_i =1} } \hfill \\\end{array}$$

  (16)

  By attention to imperialist’s power, the colonies are distributed among the imperialist. In addition, the initial number of colonies of an imperialist is calculated as follows:

  $$ N{C_n}=round\left( {P_n \times {N_{col }}} \right) $$

  (17)

  where, NC _n is the initial number of colonies of nth empire and N _col is the number of all colonies.

• Second step: Assimilation

  Imperialists try to improve all of their colonies. The aim of the assimilation procedure is to assimilate the colonies’ characteristic toward their imperialist such as culture, social structure, language and etc. Each colony moves toward the imperialist by x units. x is a random number with uniform distribution. x∼U (0, β × d), β > 1 where β is a number greater than 1 and d is distance among colony and imperialist which is the vector of movement for colony toward imperialist. The parameter β causes the colony to get closer to imperialist from both sides. To intensify property of this method and to search wider area around current solution the random amount of deviation θ was added to the direction of movement. θ is a number with uniform distribution. θ∼U (−γ, +γ) where γ is a parameter that adjusts the deviation from the original path.

• Third step: Revolution

  This mechanism is similar to mutation process in genetic algorithm for creating diversification in solutions. In each iteration, for every colony a random number which is varying between 0 and 1 is generated, and then this value is compared with probability of revolution (i.e. PR). If random number is lower than PR, the procedure of revolution is performed. For conducting the revolution procedure, at first, the number of variables which should be changed is determined based on revolution ratio (R _R ). In other words, R _R multiplies in number of jobs. After determining the number of elements for revolution, these elements are selected randomly. Then, values of selected elements are changed randomly. The new colony will replace with the previous colony while its cost is improved.

• Fourth step: Exchanging positions of the imperialists of colony

  After assimilation for all colonies and revolution for a percentage of them, the best colony in each empire is compared with its imperialist. If the best colony is better than its imperialist, then the positions of best colony and imperialist are exchanged.

• Fifth step: Total power of an empire

  The total power of an empire is calculated to be used in the imperialistic competition section. It is clear that the power of an empire includes the imperialist power and their colonies. Moreover, obviously the power of imperialist has main effect on total power of an empire while colonies power has lower impact. Hence, the equation of the total cost is defined as follows:

  $$ T{C_n}=cost\left( {imperialis{t_n}} \right)+\xi .mean\left[ {colonies\,of\,empir{e_n}} \right] $$

  (18)

  where TC _n is the total cost of the nth empire and ξ is a positive number which is considered to be less than 1. The total power of the empire will be determined by just the imperialist when the value of ξ is small. The role of the colonies, which determines the total power of an empire, becomes more important as the value of ξ increases.

• Sixth step: Imperialistic competition

  Imperialists try to increase their power by possessing and control the colonies of other empires. To apply this concept in our proposed algorithm, at first the weakest colony of the weakest empire is determined in each iteration. Then, this colony is given to the other empires which depend on their total power. For this purpose we should calculate the possession probability of each empire, first the normalized total cost is calculated as follows:

  $$ \begin{array}{*{20}c} {NT{C_n}=\max \left( {T{C_i}-T{C_n}} \right)} \hfill & {i=1,2, \ldots, {N_{imp }}} \hfill \\\end{array}$$

  (19)

  where NTC _n is the normalized total cost of nth empire and TC _n is the total cost of nth empire. By having the normalized total cost, the possession probability of each empire is calculated as below:

  $$ {P_{emp }}=\left| {\frac{{NT{C_n}}}{{\sum\limits_{i=1}^{{{N_{imp }}}} {NT{C_i}} }}} \right| $$

  (20)

  The roulette wheel method for assigning the mentioned colony has been selected for mentioned colony to empires.

• Seventh step: Elimination of powerless empires

  When an empire loses all of colonies this empire will collapse and is considered as a colony and is assigned to other empires.

• Eighth step: Stopping condition

  The stop condition is based on the problem nature, such as number of decreases as iterations.

Results and discussion

Results of modeling approach

In this work, the modeling of spring-back consists of two stages. In the first stage, the models are developed based on regression analysis, BPNN, CPNN and RBFNN. Then their accuracy will be compared using comparison tools.

Development of mathematical model

In order to create a mathematical model that can forecast the spring-back in V-die bending process, a second order multiple regression model has been employed. The proposed regression model for prediction of spring-back in terms of process parameters can be given by the following equation:

$$ Y={b_0}+\sum\limits_{i=1}^k {b_i {x_{iu }}+\sum\limits_{i=1}^k {{b_{ii }}x_{iu}^2+\sum\limits_{i=1}^k {{b_{ij }}{x_{iu }}{x_{ju }}} } } $$

(21)

where Y is the response (spring-back); b ₀ , b _i , b _ii and b _ij are the coefficients; x _iu is the variable (t, θ, and r); u is the experiment number (1–36); k is the factor number (1–3); $x_{iu}^2$ is the higher order term of variable and x _iu x _ju are the interaction terms. The MINITAB statistical package has been used to analyze the experimental data and response parameters. The significant terms in the model were found by analysis of variances. Among 36 experimental data, 32 of them have been contributed in developing a regression model, and then its adequacy has been checked with 4 remaining data sets. The obtained model to predict the spring-back using regression analysis has been presented by the following equation:

$$ \begin{array}{*{20}c} {\alpha =-24.7+13.3t-0.0437\theta +9.19r+0.0215t\theta -4.06tr+0.0073r\theta } \hfill \\ {+0.941{t^2}+0.000064{\theta^2}-0.607{r^2}} \hfill \\\end{array}$$

(22)

The analysis of variances (ANOVA) has been carried out to evaluate the adequacy of developed mathematical model. The F ratio of predictive model was calculated and compared with the standard tabulated value of the F ratio for a specific confidence interval. Table 2 demonstrates the results of ANOVA for the developed second order model in Eq. 22.

Table 2 ANOVA results for spring-back

According to Table 2, it can be inferred that the above model qualify the adequacy test as the F value of the model is larger as compared to the tabulated F value at 95 % confidence level. Also, according to the values of R ² and $R_{adj}^2$ obtained from ANOVA results, it can be inferred that there is good correlation between process inputs and main outputs. But, the obtained models are complicated as it contains too many terms. So the following models have been modified by neglecting the terms that have an insignificant effect on the spring-back. The terms having P-values more than 0.05 were eliminated, and the model is reanalyzed for the adequacy. The ANOVA results for clarification of significant factors in prediction of spring-back are presented in Table 3.

Table 3 Significant factors based on ANOVA contributed in modeling of spring-back

According to the above explanation, the modified mathematical model for estimation of spring-back is described by:

$$ \alpha =-24.7+13.3t+9.19r-4.06tr+0.0073r\theta +0.941{t^2}-0.607{r^2} $$

(23)

In order to check the accuracy of the mathematical model, the model has been examined with 4 experimental observations. Table 4 shows the comparison between measured and modeled values which were obtained by experiments and mathematical model, respectively.

Table 4 Comparison between measured values with mathematical modeled values

Development of BPNN model

As mentioned above, in present work, feed forward back-propagation neural network has been used as one of the estimators to forecast spring-back in bending process. Here, MATLAB 7.1 Neural Network Toolbox was used to develop BPNN model. So a model with three inputs and one output has been considered. In all 36 obtained data, the values of 30 data were selected stochastically to train the network, and then the trained network was tested with 6 remaining data sets. In order to find the best model mean absolute error is defined as follows:

$$ MAE=\frac{1}{T}\sum\limits_{i=1}^T {\left| {t_i -{a_i}} \right|} $$

(24)

where T is the number of test data, t _i is the target value and a _i is BPNN modeled value.

Since the size of hidden layer(s) is one of the most important factors for generation of accurate model, various architectures based on hidden layers and their neurons have been practiced. In other words in order to find a precise model that gives much more acceptable results, architectures based on one and two hidden layers with various hidden nodes were trained separately. Then, their accuracy were checked based on their values of MAE for test data. It means that a network with lowest MAE predicts the process precisely. Also, the various types of transfer function of log-sigmoid and tan-sigmoid were checked on the model accuracy. For training of the network, the gradient descent method with variable learning rate has been trained and the momentum factor was set 0.5 and the error goal value was 0.01.

By training and testing various topographies with different types of transfer functions, finally a model by 3-12-1 topography with “tansig” transfer functions was selected as the most accurate BPNN estimator. It means that networks with different topographies have been trained and tested and their MAEs were calculated. Then, by comparison of MAE values between practiced networks, results showed that the 3-12-1 network has the lowest value (e.g. 0.2275). Figure 4 indicates an agreement between measured and BPNN predicted values according to test data.

Fig. 4

Comparison between measured values and BPNN predicted values of test data

Development of CPNN model

As mentioned above, like a BP network, development of CP model consists of training and testing. So, among 36 data, number of 30 data used for training and 6 remaining data discarded for testing. In order to develop CPNN model the process inputs are normalized properly before training. For a given MSE (e.g. 0.05) several CPNN trials were practiced. Finally, a network with 3-10-1 structure is considered as a reliable architecture due to its lowest value of MAE (e.g. 0.2311). Numbers of twenty training sets of CPNN model with various structures, various learning rates, and various transfer function have been examined and their MAE value calculated. Finally, a network with 3-10-1 architecture with learning rate (e.g. β = 0.4) and momentum factor (e.g. α = 0.7) respond to lowest value of MAE. Figure 5 demonstrates an agreement between measured and CPNN predicted values according to test data.

Fig. 5

Comparison between measured values and CPNN predicted values of test data

Development of RBFNN model

Such as BP and CP models, finding an accurate RBF model includes testing and training. But, unlike BP and CP models, in RBF model instead of changing neurons of hidden layer(s) or varying of transfer functions, the spread of Gaussian function are changed to achieve acceptable value of MAE. Thirty data sets among 36 existing experimental data were used for training and then the performance of the trained network was checked by the other remaining 6 data sets. The value of MSE for this network was set 0.05, and the spread of the Gaussian function was set equal to 0.6. This value was not selected stochastically; various values of the spread were selected for training of RBF network and then the performance of the network was evaluated by the value of MAE. Results indicated that a RBF network with 15 hidden neurons and spread value of 0.6 can predict the spring-back so accurate due to lowest value of MAE (e.g. 0.2295). Figure 6 shows an agreement between measured values and RBF predicted values according to test data.

Fig. 6

Comparison between measured values and RBFNN predicted values of test data

Comparison of developed models

In order to find the most accurate model to serve as objective function in optimization, comparisons have been fulfilled based on mean absolute error (MAE), and root mean square error (RMSE) as comparison tools. As discussed above, developed models are mathematical model, 3-12-1 BPNN model, 3-10-1 CPNN model, and 3-15-1 RBFNN model. To obtain best estimator, the above developed models have been applied to all 36 experimental data and their MAE and RMSE were calculated. Finally, a model with lowest values of MAE and RMSE is introduced as a most accurate model which can be applied as objective function in optimization of spring-back.

The following equation describes the formulation of RMSE. Moreover the formulation of MAE was expressed in Eq. 24.

$$ RMSE=\sqrt{{\frac{1}{M}\sum\limits_{z=1}^M {{{{\left( {S_z -{Y_z}} \right)}}^2}} }} $$

(25)

where M is the number of all data (in this work M = 36) S _z is the real value of a given output obtained by experiments and Y _z is the value of modeled output by developed models.

Table 5 demonstrates the values of MAE and RMSE for the developed models. It can be inferred from Table 5 that the models which were developed based on artificial intelligence techniques (e.g. BPNN, CPNN, and RBFNN) could predict the process more accurately than the model based on the regression analysis. Also, the intelligent model based on radial basis network has the lowest value of MAE and RMSE. This is due to the fact that, the performance of radial basis network is very powerful in the case of problems with small number of experimental data. Another outperformance of RBFNN compared to other models is its fast performance to modeling of the process. It means that using of RBF model accelerates the speed of network about 50 times faster than models based on BP and CP. So, among the developed models the RBF one is served as objective function to optimize the spring-back in bending process.

Table 5 Values of MAE and RMSE for the developed models according to all data sets

Results of optimization approach

In this work, imperialist competitive algorithm has been used to optimize the spring-back in bending process. After selection of optimum parameters in the case of minimal spring-back, further renewed experiments have been conducted to verify the optimal solutions. The following steps define the procedure of optimization of spring-back in bending process:

Definition of constraints and objective function

According to the results of modeling approach in the previous section, the radial basis network (RBFNN) was selected as objective function due to its accuracy and faster performance compared to other developed models. The objective of this study is to identify the optimal bending conditions to minimize the spring-back. Thus, the objective function H can be expressed as:

$$ H=\left| \alpha \right| $$

(26)

where α is spring-back and the absolute of α should be minimize due to spring-back or negative spring-back. Also, according to the experimental investigation in this study, the limits on the input variables of punch tip radius (r), sheet orientation (θ) and sheet thickness (t) are:$\left( {2<r<5} \right),\,\left( {0 < \theta <90} \right)\,and\,\left( {0.5<t<1} \right).$

Optimization of bending process using ICA

A MATLAB code was developed during this study according to flowchart shown in Fig. 3. Before applying to the present problem, the code was tested on rastrigin optimization function. The formulation of this function for a problem with two variables is expressed as follow:

$$ f\left( {z_1, {z_2}} \right)=20+z_1^2+z_2^2-10\cos \left( {2\pi {z_1}} \right)-10\cos \left( {2\pi {z_2}} \right) $$

(27)

As shown in Fig. 7, a Rastrigin function has a lot of local minima due to existing of cosine in it. But it has the global minimum in z ₁ = z ₂ = 0 and value of function in this point is zero. Table 6 demonstrates the comparisons between real minima of Rastrigin function and the minimum solutions obtained by developed ICA code. It is evidence that ICA algorithm can minimize the Rastrigin function as well.

Fig. 7

Rastrigin function

Table 6 Solutions which minimize the Rastrigin function using ICA code

Such as other evolutionary optimization algorithms, the ICA needs some setup parameters for implementation. These parameters can help the algorithm to find optimal solutions accurately. Table 7 presents the setup parameters which are needed for implementation of ICA.

Table 7 Setup parameters for implementation of ICA

Table 8 demonstrates the optimal solutions which were obtained through optimization of process using ICA. The ICA algorithm warrants finding better answers according to increasing in run times. So, in this work, the algorithm was run 4 times, and it can be inferred from Table 8 that the ICA algorithm developed the answers to lower spring-back when run times increases.

Table 8 Optimal solutions obtained by ICA in the case of minimum spring-back

As discussed above the ICA algorithm warrants finding better when increasing the number of runs. So, the results of 4^th run are better than results of previous runs. Therefore, the best result for minimal spring-back is the result of fourth run in Table 8.

Verification of optimal results

In order to verify the obtained optimal solutions of fourth run as the best result for optimization of process, a renewed experimental test has been conducted. In this test optimal solutions of fourth run which were obtained by ICA have been rounded and used as parameters of bending process. Then, the value of spring-back for this test has been measured. The result of confirmation test is visible in Table 9. According to this table, it can be inferred that both radial basis network and ICA algorithm are appropriate tools for prediction and optimization of process due to equality of measured value of spring-back in confirmation test with predicted value of spring-back using RBFNN-ICA.

Table 9 Result of confirmation test to verify obtained optimal solution using RBF/ICA

Conclusion

In this research, in order to predict the spring-back in V-bending process the models based on regression analysis, back-propagation neural network, counter-propagation neural network and radial basis network were developed by using experimental observations. The process inputs were sheet thickness, sheet orientation and punch tip radius and main output was spring-back. The required training and validation data have been obtained from experimental observation. After development of predictive models, their performances were checked using mean absolute error (MAE) and root mean square error (RMSE). Among the developed models, finally a 3-15-1 radial basis network was selected as the most accurate model, due to its lower values of MAE and RMSE. Also, the speed performance of this model was much higher compared to those of the other models. Thus, the RBF model was served as objective function in minimization of spring-back. Then, a constrained optimization methodology was presented using imperialist competitive algorithm. Through the application of ICA, optimal solutions were obtained in the case of minimal spring-back. Then, confirmation test was carried out to prove optimal results obtained by integration of RBFNN-ICA.

The ability of the prediction and optimization can be extended to consider an increased number of parameters and experimental results. Also, the variability of the experimental results affects the prediction and optimization performances.