On the use of effective limit strains to evaluate the forming severity of sheet metal parts after nonlinear loading

Abstract

The conventional forming limit curve (FLC) is significantly strain path-dependent and therefore is not valid for formability evaluation of sheet metal parts that undergo nonlinear loading paths during the forming process. The stress-based forming limit curve (SFLC) is path-independent for all but very large prestrains and is a promising tool for formability evaluation. The SFLC is an ideal failure criterion for virtual forming simulations but it cannot be easily used on the shop floor as there is no straightforward experimental method to measure stresses in stamped parts. This paper presents a theoretical basis for predicting the effective limit strain curve (ELSC) using the Marciniak and Kuczynski (MK) analysis (Int J Mech Sci 9:609–620, 1967, Int J Mech Sci 15:789–805, 1973). Since the in-plane strain components are sufficient to calculate the effective strain, the ELSC can easily be determined from strains measured in the stamping plant, and therefore it is a better alternative to the SFLC for formability evaluation. This model was validated using experimental data for AISI-1012 steel (Molaei 1999) and AA-2008-T4 aluminum alloys Graf and Hosford (Metall Trans 24A:2503–2512, 1993). Predicted results showed that, similar to SFLC, the ELSC remains practically unchanged for a significant range of prestrain values under various bilinear loading paths, but some strain-path dependence can be observed for significant magnitudes of the effective prestrain (ε _e  ≥ 0.37 for AISI-1012 steel and ε _e  ≥ 0.25 for AA-2008-T4 aluminum).

Introduction

The formability of sheet metal is limited by the occurrence of localized necking, i.e. non-uniform strains within a small region in the plane of the sheet. The forming limits, given in terms of limiting principal strains and determined from observations of localized necking under different loading conditions, are often represented on the so-called forming limit curve (FLC).

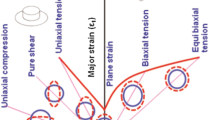
The concept of a forming limit curve (FLC) was first reported by Keeler and Backhofen [13] for drawn sheet metal specimens. They concluded that localized necking in sheet metals occurs for critical combinations of the major and minor strains in the plane of the sheet. Subsequently this concept was extended by Goodwin [4] to sheet specimens stretched in biaxial tension, thereby completing the range of loading paths between uniaxial tension on the left of the FLC and balanced biaxial tension on the right. The FLC was defined such that any combination of principal in-plane strains which lies beneath the curve is safe, whereas combinations of strains that lie above the FLC lead to a risk of localized necking and rupture.

The FLC can be determined experimentally or theoretically. The experimental determination of FLC is relatively costly as it requires specialized equipment, tooling and experienced personnel. It is also time-consuming to conduct formability tests, measure the principal strains and establish where in strain space the onset of necking actually occurs. The experimental determination of FLC requires great care and consistency because it is used to establish the quality of large volumes of production parts. The somewhat subjective determination of experimental FLC leads to variability in FLC data and underscores the need for an objective approach to determine FLC. Consequently, researchers have developed different theoretical models to predict the FLC of sheet metals.

Hill [10] introduced the first criterion for localized necking in sheet metals under plane stress conditions using the bifurcation flow theory. Hill assumed that the onset of failure occurred once a discontinuity appears in the Cauchy stress and the strain rate. Hill then formulated the restrictions on the flow stress and the rate of work hardening in the growth of the localized neck. He developed a method that shows that at the onset of instability the magnitude of plastic work decreases below the minimum value required for uniform deformation along the zero-extension direction.

The MK method, developed by Marciniak and Kuczynski in [16], was the first realistic mathematical model for FLC prediction, and has been the most common theoretical approach for calculating the FLC of sheet materials. The MK method was extended by Hutchinson and Neale [12] using J2 deformation theory. As a result of their work, the entire FLC can be calculated using the MK approach. In recent years it was employed by several researchers, such as Yoshida et al. [29]; Butuc et al. [3]; Nurcheshmeh and Green [20–22] and many others.

It is well known that sheet deformation in many industrial metal forming processes is characterized by nonlinear strain paths and it has been observed by several researchers [1, 3, 5, 7, 14, 15, 24]) that the as-received FLC can translate and distort significantly in strain space due to a nonlinear loading path. This signifies that the as-received FLC is not reliable for assessing the forming severity of parts that were deformed in multi-stage forming operations. Furthermore, since each material point in such a component may follow a different (nonlinear) loading path, each location in the part potentially has a different FLC. It is obviously not possible to experimentally determine the FLC for every nonlinear strain path in a given part, and even if it was, it would be practically unmanageable to accurately carry out an analysis of forming severity. So although 80 % of stamped parts can be reliably evaluated with the as-received FLC, there are nevertheless a number of complex stamped parts and parts formed in multi-stage forming processes where the as-received FLC is not adequate to carry out formability analyses.

Researchers have also proposed that the forming limits of sheet materials are more likely dependent on locally reaching a critical state of stress rather than a critical state of strain. Therefore an increasing number of researchers and engineers have adopted the stress-based forming limit curve (SFLC) to evaluate the forming severity of metal forming operations. Kleemola and Pelkkikangas [14] discussed the limitations of the FLC in the case of copper, brass and steel sheets formed in a deep-drawing operation followed by a flanging operation. They observed significant variability of the FLC after this two-stage forming process and the resulting nonlinear strain paths, and recommended the use of a stress-based forming limit curve (SFLC) as an alternative to the FLC. They also provided experimental data that showed the path independence of the stress-based forming limit curves for these alloys.

Arrieux et al. [1] also pointed out the non-uniqueness of the FLC after nonlinear loading cases and again proposed the use of a stress-based forming limit curve in applications where there is more than one loading stage.

Some researchers [24, 25, 27, 32, 33] showed that the SFLC is path-independent and these investigations indicated that forming severity can be accurately evaluated using the SFLC in combination with a finite element simulation, not only for proportional loading but also in cases where the material has a complex strain history. Although it is difficult to experimentally determine the SFLC, Stoughton showed that it can be easily determined from the as-received FLC, and therefore it is essential to be able to determine the FLC.

In 2005, Yoshida et al. [28] performed biaxial tension tests on aluminum tubes utilizing a tension–internal pressure testing machine to verify the path-independence of stress forming limits. They confirmed that the stress forming limit curve is path-independent. Yoshida et al. [29] subsequently calculated the stress forming limits for a variety of two-stage combined stress paths using the Marciniak and Kuczynski (MK) model [16, 17] based on a phenomenological plasticity theory. In this work they confirmed the experimental observations of Yoshida et al. [28] and concluded that if the path-independence of the SFLC holds, the equivalent plastic strains at the onset of localized necking for a given stress ratio must be identical, irrespective of the strain path. Furthermore, Yoshida et al. also showed that the SFLC will show path-dependence at very high prestrain magnitudes. Nurcheshmeh and Green [20] also reported that the SFLC will remain path-independent up to a large prestrain at different loading paths and the SFLC will show some path-dependence in the vicinity of the plane strain region for very large prestrain magnitudes. In other research, Yoshida and Suzuki [30] showed that the path-dependence of SFLC may be due to the variations in the material’s stress–strain behaviour in different loading stages.

The main obstacle to the widespread implementation of the SFLC is the prohibitive cost and inaccessibility of experimental stress measurements in the metal forming industry. In order to take advantage of the path-independence of the SFLC in a prototype shop or a manufacturing plant, Green [6]) proposed a simple methodology to predict the FLC from the SFLC once the strain path in a given location of a part is known. However press shops continue to measure the strains in stamped parts and to evaluate the measured strains against the conventional as-received FLC [24, 26].

Zeng et al. [31] proposed an effective strain versus material flow direction curve to assess localized necking in sheet metals. They believed that this curve combines the advantages of stress-based FLC for its path-independence and the FLC for its ease of interpretation.

In the present work, a modified MK model was used to predict history-dependent forming limit curves (FLC) and effective limit strain curves (ELSC) for sheets that have undergone various sequences of plane stress loading. Predicted FLC and ELSC were compared with experimental data obtained for AISI-1012 steel and AA-2008-T4 sheets under the same loading conditions [5, 19]. Finally, the path-dependence of ELSCs was evaluated based on different non-proportional loading histories.

Theoretical model

The MK approach assumes that the sheet material has an initial inhomogeneity which can be due to, for instance, a non-uniform distribution of micro-voids or the roughness at the surface of the sheet. Marciniak and Kuczynski [16] modeled this inhomogeneity in a sheet specimen as a geometric defect in the form of a narrow band with a reduced thickness. Figure 1 shows a schematic of the MK model in which the imperfection band is designated as region (b), and region (a) is the area outside the band.

Fig. 1

Schematic of the MK model with a thickness imperfection in the sheet

The initial imperfection factor of the groove,f ₀, is defined as the thickness ratio between the two regions as follows:

$$ {f_0} = \frac{{t_0^b}}{{t_0^a}} $$

(1)

where, subscript ‘0’ denotes the initial state. The definition of the thickness ratio between these two regions has a significant effect on the predicted limit strains. In many analyses this factor is used as an adjusting parameter to correlate theoretical results with experimental data. However in this work the initial thickness ratio between regions (a) and (b) was considered more realistically as a function of the surface roughness of the sheet metal as follows:

$$ {t_b} = {t_a} - 2{R_Z} $$

(2)

where, R _Z is the surface roughness of the sheet metal.

Stachowicz [23] experimentally showed that the surface roughness of sheet metals changes during plastic deformation as follows:

$$ {R_Z} = {R_{{Z0}}} + Cd_0^{{0.5}}{\varepsilon_e^b} $$

(3)

where d ₀ is the initial grain size of the as-received sheet, ε _e is the effective plastic strain, and C is a material constant. By taking Stachowicz’s assumption into account the imperfection factor becomes:

$$ {f_0} = \frac{{t_0^a - 2\left[ {{R_{{Z0}}} + Cd_0^{{0.5}}\varepsilon_e^b} \right]}}{{t_0^a}} $$

(4a)

$$ f = \frac{{t_0^a - 2\left[ {{R_{{Z0}}} + Cd_0^{{0.5}}\varepsilon_e^b} \right]}}{{t_0^a}}\exp \left( {\varepsilon_3^b - \varepsilon_3^a} \right) $$

(4b)

where $\varepsilon_3^a$ and $\varepsilon_3^b$ are the third principal strain increments in areas (a) and (b), respectively.

As shown in Fig. 1, the orientation of the imperfection band is considered randomly on the sheet surface and the angle between the groove axis and the second principal stress is defined as θ. The groove orientation will change as plastic deformation proceeds, and this may affect the limit strains. For better FLC prediction, groove rotation during deformation can be considered in plasticity calculations and its value should be updated at every increment of deformation. Barata et al. [2]) proposed an empirical formula to specify the rotation of the imperfection band, as follows:

$$ \tan \left( {\theta + d\theta } \right) = \tan \left( \theta \right)\frac{{1 + d\varepsilon_1^a}}{{1 + d\varepsilon_2^a}} $$

(5)

where dε ₁ ^a and dε ₂ ^a are the major and minor principal strains in the nominal area of the sheet, respectively.

A constitutive equation was derived in which the yield function can be expressed in the following general form for isotropic hardening:

$$ f = {\left( {\frac{3}{2}{S_{{ij}}}:N:{S_{{ij}}}} \right)^{{1/2}}} - {\sigma_e} $$

(6)

where, S is the deviatoric stress tensor and N is a tensor that describes the anisotropy of the sheet material in terms of the anisotropic constants in Hill’s 1948 yield function [8].

The plastic potential function was implemented in the MK analysis for plane stress conditions as follows:

$$ 2h = \left( {G + H} \right){\sigma_x}^2 + \left( {F + H} \right){\sigma_y}^2 - 2H{\sigma_x}{\sigma_y} + 2N{\sigma_{{xy}}} = {f^2} $$

(7)

where F, G, H and N are anisotropic coefficients. These coefficients can be determined as a function of uniaxial yield stresses [9]:

$$ 2G = \frac{1}{{{{\left( {\sigma_x^Y} \right)}^2}}} - \frac{1}{{{{\left( {\sigma_y^Y} \right)}^2}}} + \frac{1}{{{{\left( {\sigma_B^Y} \right)}^2}}} $$

(8a)

$$ 2{\text{F}} = \frac{1}{{{{\left( {\sigma_y^Y} \right)}^2}}} - \frac{1}{{{{\left( {\sigma_x^Y} \right)}^2}}} + \frac{1}{{{{\left( {\sigma_B^Y} \right)}^2}}} $$

(8b)

$$ 2{\text{H}} = \frac{1}{{{{\left( {\sigma_x^Y} \right)}^2}}} + \frac{1}{{{{\left( {\sigma_y^Y} \right)}^2}}} - \frac{1}{{{{\left( {\sigma_B^Y} \right)}^2}}} $$

(8c)

$$ 2{\text{N}} = \frac{1}{{{{\left( {\tau_{{xy}}^Y} \right)}^2}}} $$

(8d)

where σ _x ^Y, σ _y ^Y are the yield stresses in the x and y directions, respectively, σ _b ^Y is the yield stress in equibiaxial tension and $\tau_{{xy}}^Y$ is the yield stress in simple shear in the xy plane.

The work-equivalent effective strain derived from in Hill’s 1948 yield criterion can be written as follows:

$$ {\varepsilon_e} = \sqrt {{\frac{1}{H}\left[ {\frac{{{r_0}{r_{{90}}}}}{{1 + {r_0} + {r_{{90}}}}}\left( {\frac{{1 + {r_{{90}}}}}{{{r_{{90}}}}}\varepsilon_x^2 + \frac{{1 + {r_0}}}{{{r_0}}}\varepsilon_y^2 + 2{\varepsilon_x}{\varepsilon_y}} \right)} \right]}} $$

(9a)

where r ₀ and r ₉₀ are the plastic anisotropy (Lankford) coefficients in the rolling and transverse directions, respectively.

Strain hardening was described by a power law and includes strain rate sensitivity effect as follows:

$$ {\sigma_e} = k{\left( {{{\mathop{\varepsilon }\limits^{ \bullet } }_e}} \right)^m}{\left( {{\varepsilon_e} + {\varepsilon_0}} \right)^n} $$

(9b)

where ε ₀ is a prior uniform prestrain applied to the sheet, m is the strain-rate sensitivity coefficient, n is the strain-hardening coefficient, σ _e and ε _e are the effective stress and strain, respectively.

The power law used for the second loading stage was then modified according to the prestrain level. The different power law functions in the nominal and weak areas of the sheet for the second loading stage are represented by the following equations, respectively:

$$ \sigma_e^a = k{\left( {{{\mathop{{{\varepsilon_e}}}\limits^{ \bullet } }^a}} \right)^m}{\left( {\varepsilon_e^{{(1)a}} + \varepsilon_e^{{(2)a}} + {\varepsilon_0}} \right)^n} $$

(10a)

$$ \sigma_e^b = k{\left( {{{\mathop{{{\varepsilon_e}}}\limits^{ \bullet } }^b}} \right)^m}{\left( {\varepsilon_e^{{(1)b}} + \varepsilon_e^{{(2)b}} + {\varepsilon_0}} \right)^n} $$

(10b)

where ε _e ^(1)a and ε _e ^(1)b are the effective plastic strains reached after the prestrain in areas (a) and (b), respectively.

The associated flow rule was employed to calculate the plastic strain increments as follows:

$$ d{\varepsilon_{{ij}}} = d\lambda \times grad(h) = d\lambda \times \frac{{\partial h}}{{\partial {\sigma_{{ij}}}}} $$

(11)

where dλ is the plastic multiplier and h is the plastic potential function.

In order to predict the onset of necking, a uniform and proportional biaxial stress was applied to the sheet in the MK model. As plastic deformation proceeds, the major strain in the thinner band becomes increasingly greater than in the rest of the sheet. Consequently, the thickness ratio (t _b /t _a ) decreases until, eventually, a localized neck is formed. Throughout the deformation it was assumed that the strain component in the neck direction in the imperfection band is always the same as the corresponding strain outside the groove:

$$ d\varepsilon_{{tt}}^a = d\varepsilon_{{tt}}^b $$

(12)

Furthermore, the equilibrium of the normal and shearing forces across the imperfection are also maintained throughout the deformation, i.e.:

$$ F_{{nn}}^a = F_{{nn}}^b $$

(13a)

$$ F_{{nt}}^a = F_{{nt}}^b $$

(13b)

where subscripts n and t denote the normal and tangential directions of the groove, respectively, and F is the force per unit width, i.e.:

$$ F_{{nn}}^a = \sigma_{{nn}}^a{t^a} $$

(14a)

$$ F_{{nn}}^b = \sigma_{{nn}}^b{t^b} $$

(14b)

$$ F_{{nt}}^a = \sigma_{{nt}}^a{t^a} $$

(14c)

$$ F_{{nt}}^b = \sigma_{{nt}}^b{t^b} $$

(14d)

By combining Eqs. (1), (9b) and (14a, 14b) the following relation was obtained:

$$ {{{\left[ {\frac{{\sigma_{{nn}}^a}}{{\sigma_e^a}}} \right]}} \left/ {{\left[ {\frac{{\sigma_{{nn}}^b}}{{\sigma_e^b}}} \right]}} \right.} = f{{{\left( {\left[ {{\varepsilon_0} + \varepsilon_e^b} \right] \times {{\mathop{{\varepsilon_e^b}}\limits^{ \bullet } }^m}} \right)}} \left/ {{\left( {\left[ {{\varepsilon_0} + \varepsilon_e^a} \right] \times {{\mathop{{\varepsilon_e^a}}\limits^{ \bullet } }^m}} \right)}} \right.} $$

(15a)

Since the strain rate is defined as $\mathop{{{\varepsilon_e}}}\limits^{ \bullet } = d{e_e}/dt$, it follows that:

$$ {{{\left[ {\frac{{\sigma_{{nn}}^a}}{{\sigma_e^a}}} \right]}} \left/ {{\left[ {\frac{{\sigma_{{nn}}^b}}{{\sigma_e^b}}} \right]}} \right.} = f{\left( {\left[ {{\varepsilon_0} + \varepsilon_e^b} \right]/\left[ {{\varepsilon_0} + \varepsilon_e^a} \right]} \right)^n} \times {\left[ {d\varepsilon_e^b/d\varepsilon_e^a} \right]^m} $$

(15b)

The stress transformation rule leads to the expressions:

$$ \sigma_{{nn}}^a = \sigma_x^a{\cos^2}\left( \theta \right) + \sigma_y^a{\sin^2}\left( \theta \right) $$

(16a)

$$ \sigma_{{nt}}^a = - \left( {\sigma_x^a - \sigma_y^a} \right)\sin \left( \theta \right)\cos \left( \theta \right) = \sigma_x^a\left[ {\left( {\alpha - 1} \right)\sin \left( \theta \right)\cos \left( \theta \right)} \right] $$

(16b)

where α is the ratio of the second true principal stress to the first true principal stress in the nominal area ($\alpha = {{{\sigma_2^a}} \left/ {{\sigma_1^a}} \right.}$) and indicates the stress path.

Considering the yield criterion and associated flow rule, the strain path ρ can be written as:

$$ \rho = \frac{{d{\varepsilon_2}}}{{d{\varepsilon_1}}} = \frac{{\left( {F + H} \right)\alpha - H}}{{1 - H\alpha }} $$

(17)

Expressions similar to Eqs. (16a) and (16b) can be written for region (b), and using Eqs. (12), (13a, 13b), and (15a, 15b) we obtain:

$$ \frac{{\sigma_{{nt}}^b}}{{\sigma_{{nn}}^b}} = \frac{{\sigma_{{nt}}^a}}{{\sigma_{{nn}}^a}} = \frac{{\left( {\alpha - 1} \right)\sin \left( \theta \right)\cos \left( \theta \right)}}{{{{\cos }^2}\left( \theta \right) + \alpha {{\sin }^2}\left( \theta \right)}} $$

(18)

With consideration of the consistency condition, the plastic potential function and the strain transformation rule we have:

$$ \begin{array}{*{20}{c}} \hfill {\frac{{d\varepsilon _{e}^{a}}}{{\sigma _{e}^{a}}}\left\{ {\left[ {\left( {F + H} \right) \times {{\alpha }^{a}} - H} \right]\sigma _{x}^{a}{{{\cos }}^{2}}\theta + \left( {1 - H{{\alpha }^{a}}} \right)\sigma _{x}^{a}{{{\sin }}^{2}}\theta } \right\} = } \\ \hfill {\sigma _{x}^{b}\frac{{d\varepsilon _{e}^{b}}}{{\sigma _{e}^{b}}}\left\{ {\left[ {\left( {F + H} \right) \times {{\alpha }^{b}} - H} \right]{{{\cos }}^{2}}\theta + \left( {1 - H{{\alpha }^{b}}} \right){{{\sin }}^{2}}\theta } \right\}} \\ \end{array} $$

(19)

By combining Eqs. (15a, 15b), (18), and (19), the final governing equation was analytically determined as a function of the ratio of the effective plastic strain inside and outside the imperfection band (η = ε ^b _e /ε ^a _e ). This final differential equation indicates the evolution of the effective plastic strain ratio η as the sheet is deformed.

When the material inhomogeneity is thus modeled as a geometrical thickness variation, the physical problem is thereby simplified to a single dimension. Because of the plane stress assumption, the stress and strain increments inside the neck can be solved directly in terms of the strain increments prescribed outside the neck. Although the strain ratio (dρ = dε ₂/dε ₁) outside the groove remains constant during any deformation stage, it actually decreases inside the groove until it eventually approaches plane strain deformation (${{{d\varepsilon_2^b}} \left/ {{d\varepsilon_1^b}} \right.} = 0$). When this occurs, the principal strains outside the groove are identified as the limit strains for this material under the corresponding deformation mode. The analysis can be repeated for different initial orientations (ϕ _o ) of the groove in the range between 0^o and 45^o and the forming limit can be obtained after minimizing the $\varepsilon_1^a$ vs. ϕ _o curve. While the minimum in-plane limit strain is determined for any specific loading path, the corresponding effective strain in region (a) will denote the effective limit strain for the current loading path. By changing the strain path between ρ = −0.5 and ρ = 1.0 the entire forming limit curve and the corresponding effective limit strain curve can be obtained.

Validation of the MK model

The validation of the proposed MK model was carried out by comparing predicted FLC with the experimental data obtained with two different sheet materials: AISI-1012 low carbon steel [19] and AA-2008-T4 aluminum alloy [5]. Table 1 shows material data including thickness, strain hardening constants, anisotropy coefficients, and surface roughness data for the AISI-1012 steel sheet and Table 2 shows the same data for the AA-2008-T4 aluminum sheet.

Table 1 Material properties of AISI-1012 low carbon steel [19]

Table 2 Average mechanical properties of AA-2008-T4 [5]

The parameters in Stachowicz’s surface roughness equation (C, d ₀ , R _Z0 ) were not available for the AA-2008-T4 aluminum sheet that was used in Graf and Hosford’s investigation [5]. These parameters were therefore calibrated by fitting the theoretical FLC to the experimental as-received FLC. The parameters were optimized one at a time by a series of FLC predictions in which one parameter was varied successively while the other two were held constant. For each case, the value of the variable parameter that gave the best overall fit of the predicted FLC with the experimental as-received FLC was selected as the calibrated value for this parameter. This procedure was repeated for all three parameters and the material constants thus obtained are C = 0.70, d ₀  = 8.00 μm and R _Z0  = 2.5 μm.

Equation (4a) was used to calculate the value of the initial imperfection factor in the MK analysis. It was found that f ₀ = 0.995 for AISI-1012 steel and f ₀ = 0.997 for AA-2008-T4 aluminum.

The experimental FLC work was described by Molaei [19] and Graf and Hosford [5]. As-received FLC were determined by stretching sheet specimens over a hemispherical dome until the onset of necking and by measuring the strains in the necked region. Other FLCs were also obtained by prestraining large sheet specimens, either in uniaxial tension or in equibiaxial tension, and then forming these prestrained specimens over hemispherical domes up to the onset of necking. The reader can refer to the original publications by Molaei [19] and Graf & Hosford [5] for further details on the experimental work.

The FLCs of AISI-1012 steel and AA-2008-T4 aluminum sheets were calculated and compared with the corresponding experimental data [5, 19] determined for both as-received sheets and for samples deformed along nonlinear loading paths. Comparison of the theoretical and experimental FLC for as-received AISI-1012 steel is shown in Fig. 2. This figure shows that the theoretical model predicts the as-received forming limit of this steel with an acceptable level of accuracy.

Fig. 2

Comparison of theoretical and experimental FLC of as-received AISI-1012 steel sheet

The FLCs were also predicted for steel specimens deformed along two types of bilinear loading paths: in the first case, the sheet metal was subjected to 0.08 equibiaxial prestrain, and in the second case to 0.1 uniaxial prestrain. The FLCs of AISI-1012 steel for these two nonlinear loading paths are plotted in Figs. 3 and 4 with the corresponding experimental FLCs. In the case of 0.08 equibiaxial prestrain shown in Fig. 3, experimental data is only available for the left side of the shifted FLC. Figures 3 and 4 indicate that the proposed MK model is capable of predicting the FLCs of this steel sheet subject to non-proportional loading with good accuracy.

Fig. 3

Theoretical and experimental FLC of AISI-1012 with 0.08 equibiaxial prestrain

Fig. 4

Theoretical and experimental FLC of AISI-1012 with 0.10 uniaxial prestrain

The developed MK model was further validated by comparing theoretical FLCs of AA-2008-T4 aluminum sheet with the corresponding experimental data [5]. Figures 5, 6, 7 compare the predicted and experimental FLCs for AA-2008-T4 aluminum sheet metal. As mentioned previously, some of the material constants (C, d ₀ , R _Z0 ) used to calculate the initial imperfection factor (Eq. 4a) of AA-2008-T4 aluminum alloy were not provided by Graf and Hosford [5], therefore these constants were adjusted so that the predicted FLC would be calibrated to the experimental as-received FLC (Fig. 5).

Fig. 5

Comparison of calibrated and experimental FLCs of as-received AA-2008-T4 aluminum sheets

Fig. 6

Theoretical and experimental FLCs of AA-2008-T4 with 0.04 and 0.12 equibiaxial prestrain after calibrating the MK model to the as-received FLC

Fig. 7

Theoretical and experimental FLCs of AA-2008-T4 with 0.05 and 0.12 uniaxial prestrain after calibrating the MK model to the as-received FLC

Figure 6 shows the predicted and experimental FLCs of AA-2008-T4 aluminum sheets after 0.04 and 0.12 equibiaxial prestrain. The comparison between predicted and experimental FLCs after preloading to 0.05 and 0.12 in uniaxial tension is shown in Fig. 7. Both Figs. 6 and 7 show that, even when in Hill’s 1948 quadratic yield function is used, this MK model still predicts the FLCs of this aluminum alloy with an acceptable accuracy. It is expected that the calculation of the FLC using a non-quadratic yield criterion would lead to more accurate predictions for this aluminum sheet.

Effective limit strain curves

Determination of the effective limit strain curve

As seen in the previous section, the FLC is a dynamic curve that can vary significantly due to changes in loading path. However, Yoshida et al. [29] and Zeng et al. [31] showed that, for a given stress ratio, the equivalent plastic strain at the onset of localized necking remains constant irrespective of the strain path. Therefore the present authors propose to employ the effective limit strain curve (ELSC) rather than the conventional FLC to evaluate the severity of industrial forming processes. The ELSC is defined in terms of the effective strain at the onset of necking versus the final strain path just prior to necking. The ELSC can be easily determined from an experimental (or predicted) as-received FLC which consists of a set of in-plane principal strains (ε ₁ , ε ₂ ) that define the forming limit. The effective strain is a function of the principal strains and is calculated assuming a suitable yield function. For instance the effective strain for in Hill’s 1948 yield criterion can be defined using Eq. (9a). The strain path is defined in Eq. (17) as the ratio of the two in-plane principal strains in the final stage of a forming process.

Utilization of the effective limit strain curve

A typical theoretical ELSC is shown in Fig. 8, and similar to the conventional FLC, effective strain data that lie below the ELSC would lead to a safe part and effective strain data that lie on or above this curve would indicate a risk of necking. In order to illustrate how the ELSC can be used, Fig. 8 shows a diagram with an ELSC and three different theoretical loading paths that lead to the same effective limit strain. Path 1 and Path 2 represent two different bilinear loading paths in principal strain space and Path 3 represents a linear loading path in a sheet metal component. Path 1 indicates that a material point in the formed part was first strained in equibiaxial tension (ρ = 1.0) up to an effective plastic strain of 0.23 and then in biaxial tension with a strain ratio ρ = 0.65 up to the onset of necking. Each linear portion of this bilinear strain path is represented in Fig. 8 by a vertical line (i.e. a constant strain ratio), and the horizontal line that links the two vertical segments merely represents a momentary transition between these two linear strain paths. Similarly, loading path 2 describes the strain history at a different location in the part and shows that the sheet material was prestrained first in uniaxial tension (ρ = −0.5) up to an effective strain of ε _e  = 0.12 and secondly in biaxial tension with a strain ratio of ρ = 0.65 up to the onset of necking. Once again, the horizontal line that links the two vertical segments does not represent a deformation, per se, but is simply a convenient way to create a visual link between the two linear strain paths. Loading path 3 represents the strain history of a material point that maintained a constant strain ratio of ρ = 0.65 up to the onset of necking.

Fig. 8

Schematic illustration of the ELSC following different loading paths

The three loading paths in Fig. 8 begin very differently but they reach the same strain ratio in the final stage of the hypothetical forming process. According to the observations of Yoshida et al. [29] and Zeng et al. [31] the onset of plastic instability should occur for the same value of the effective strain for all three strain paths. This signifies that regardless of the previous strain history, the onset of necking only depends on the final strain ratio.

The conceptual effective strain vs. strain ratio diagram shown in Fig. 8 suggests that any arbitrary nonlinear strain path can be represented by a finite series of linear strain paths, each having a different strain ratio. It is thought that in the majority of cases, the actual strain path at a particular location could easily be approximated by a manageable number of linear segments.

Assuming for the moment that the ELSC is invariable, the ELSC appears to be a very user-friendly criterion to evaluate the forming severity of stamped parts. Once the ELSC is established for a given sheet material it can be used to evaluate any forming process with either linear or non-linear loading paths. This failure criterion can be adopted to assess part quality in the press shop by measuring the principal surface strains in areas of concern, as it has been done for decades. Once the principal strains are recorded, simple software on a laptop computer would suffice to calculate the strain ratios and the effective strains at given locations. For parts that exhibit non-proportional strain histories, it would be necessary to produce parts at different intermediary stages throughout the forming process. After measuring the strains in the same material location at each successive stage, it would be possible to construct the multi-linear strain path for that location. By comparing the measured effective strain data with the ELSC, it can be easily verified if the process is safe and robust.

Moreover, this ELSC could be very easily implemented into finite element software to evaluate the results of virtual forming simulations. Indeed, finite element software incrementally computes the strains in each element of a virtual part and therefore the strain ratio and the effective plastic strain in each element can be deduced at every increment of deformation. Consequently, the entire strain path of each element can be tracked and the forming severity of the part can be evaluated by comparing the effective strain vs. strain ratio data for the final strain increment with the ELSC.

The effective limit strain curves of AISI-1012 steel corresponding to all the predicted and experimental FLCs in Figs. 2, 3, and 4 for both as-received and nonlinear loading paths are shown in Fig. 9. It can be seen in this figure that the theoretical ELSCs of this grade of steel lie on a single curve regardless of the type of prestrain. Also, the experimental data for the different loading paths vary within a narrow band around the theoretical ELSCs. The discrepancies between predicted and experimental data may be due to inaccuracies in strain measurements, but are perhaps more likely due to inaccurate estimations of the experimental strain paths. Indeed, it would have been difficult for Molaei [19] to maintain exactly constant strain ratios during each stage of the two-stage loading process. In fact the various strain paths that are typically generated in hemispherical dome tests remain essentially linear throughout most of the test, however, prior to the onset of necking they tend to rotate toward plane strain. Therefore the bilinear strain paths that were assumed in the predictions shown in Fig. 9 are not likely to be exactly the same as those that were followed during Molaei’s experimental work [19].

Fig. 9

Theoretical and experimental ELSCs of AISI-1012 for different loading paths

The predicted and experimental ELSCs of the AA-2008-T4 aluminum alloy in the as-received and prestrained conditions are shown in Fig. 10. It can be seen that most of the experimental data for this alloy lie within a narrow band around, or close to, the theoretical ELSCs. The discrepancies between the theoretical and experimental data may be partly due to the assumption that the strain ratio was constant during each stage of the two-stage loading history, and partly due to the fact that in Hill’s 1948 yield criterion is not adequate to describe the plastic behaviour of aluminum alloys. For this reason, the effect of the anisotropic yield criterion on the prediction of ELSC will be discussed in the next section. It can also be seen from Fig. 10 that all the predicted ELSCs for the AA-2008-T4 aluminum alloy merge into a single curve except for the ELSC data obtained after 0.12 prestrain in equibiaxial tension. This particular prestrain corresponds to an effective prestrain ε _e  = 0.23 which is greater than the plane-strain minimum of the as-received ELSC (ELSC₀ = 0.19 when ρ = 0). This observation will be further discussed in section 4.4.

Fig. 10

Theoretical and experimental ELSCs of AA-2008-T4 for different loading paths

Influence of the yield criterion on the effective limit strain curve

In order to observe the influence of the yield criterion on the prediction of ELSC, three different yield criteria were considered to predict the ELSC of both AISI-1012 steel and AA-2008-T4 aluminum alloys: the von Mises [18] and Hill 1948 [8] quadratic yield criteria and Hosford’s 1979 [11] non-quadratic yield criterion. The ELSCs of AISI-1012 steel predicted with these three yield criteria are compared with the corresponding experimental data in Fig. 11. As it can be seen, all three criteria predict the ELSC of this grade of steel with relatively good accuracy. It can also be seen that the variability in the predicted ELSCs due to the yield criterion is worse at the far left and right ends compared to the centre of the ELSC, and this underscores the importance of using a yield function that accurately describes the planar anisotropy of the sheet material.

Fig. 11

Comparison of the ELSC of AISI-1012 steel predicted with different yield criteria

The ELSC of AA-2008-T4 aluminum sheet was also predicted with the same yield criteria and the comparison of predicted and experimental ELSCs is shown in Fig. 12. This figure shows that the two quadratic yield criteria underestimate the ELSC of this AA-2008-T4 aluminum sheet and that Hosford’s 1979 non-quadratic yield function provides a better prediction than the quadratic yield criteria.

Fig. 12

Comparison of the ELSC of AA-2008-T4 aluminum predicted with different yield criteria

Uniqueness of effective limit strain curves

In this section, the strain path-dependence of the ELSC is investigated. The MK analysis was used to predict the ELSCs of AISI-1012 steel and AA-2008-T4 aluminum sheets after a theoretical prestrain along different loading paths and with different magnitudes of prestrain. ELSCs were predicted for the AISI-1012 steel sheet after prestrains of ε _e  = 0.10, 0.20 and 0.45 in uniaxial tension and also in equibiaxial tension. The ELSCs of the AISI-1012 steel obtained for prestrains in uniaxial tension are shown in Fig. 13, and it can be seen that for prestrains up to a certain magnitude (ε _e  ≤ 0.20) the predicted ELSCs are all identical. However, for a very high value of prestrain (e.g. ε _e  = 0.45) the ELSC shifts upward, especially in the vicinity of plane-strain deformation.

Fig. 13

Comparison of the ELSCs after different levels of prestrain in uniaxial tension with the as-received ELSC of AISI-1012 steel

Figure 14 shows the predicted ELSCs of the steel sheet after effective prestrains of ε _e  = 0.10, 0.20 and 0.45 in equibiaxial tension. Figure 14 indicates that the ELSC is invariable for prestrains in equibiaxial tension up to significant magnitudes (ε _e  ≤ 0.20), however some variability appears for an effective prestrain of ε _e  = 0.45.

Fig. 14

Comparison of the ELSCs after different levels of prestrain in equibiaxial tension with the as-received ELSC of AISI-1012 steel

In order to determine the effect of the prestrain path on the ELSC, the ELSCs for AISI-1012 steel sheet obtained after an effective prestrain ε _e  = 0.45 in uniaxial and in equibiaxial tension are shown together in Fig. 15. It is evident from this figure that the ELSC is essentially the same for both strain histories, and the greatest difference between the ELSCs calculated for bilinear loading paths and the as-received ELSC occurs in the mode of plane strain (ρ = 0).

Fig. 15

Comparison of the ELSCs after an effective prestrain ε _e  = 0.45 in uniaxial and equibiaxial tension with the as-received ELSC of AISI-1012 steel

In an attempt to quantify the variability of the ELSC, the deviations between the ELSCs predicted for bilinear strain paths and the as-received ELSC of AISI-1012 steel were calculated. The percent deviations are shown in Fig. 16 and it can be seen that for lower values of the effective prestrain (ε _e   ≤ 0.20), the differences between the ELSCs are negligible across the entire range of strain paths (−0.5 ≤ ρ ≤ 1.0). However when the effective prestrain reaches ε _e  = 0.45, the deviation between the ELSCs increases to a maximum of 17 %. It is important to notice that the greatest deviation occurs in the mode of plane strain and this difference gradually decreases as the strain path moves away from plane strain until it practically reaches zero at each end of the curve (i.e. for ρ = −0.5 and for ρ = 1.0).

Fig. 16

Deviation in effective limit strain between prestrained and as-received ELSCs for different effective prestrain magnitudes in AISI-1012 steel sheets

Since the maximum deviation of the ELSC occurs in plane strain (i.e. for ELSC₀), the deviation from the as-received ELSC₀ was plotted as a function of the magnitude of the effective prestrain. Figure 17 shows the percent deviation of ELSC₀ from the as-received value as a function of the effective prestrain, and it can be seen that for effective prestrains less than ε _e  = 0.30, the maximum deviation from the as-received ELSC does not exceed 2 %, and for effective prestrains up to ε _e  = 0.41 (i.e. the as-received ELSC₀) the maximum deviation remains less than 10 %. If the maximum allowable deviation from the as-received ELSC₀ is set at 0.02 effective strain (i.e. approximately 5 % deviation from the as-received ELSC₀), which typically corresponds to the experimental error in conventional FLC strain data, then the ELSC of AISI-1012 steel can be considered practically path-independent for effective prestrains up to ε _e  = 0.37 (see Fig. 17).

Fig. 17

Maximum deviation of the effective limit strain between prestrained and as-received ELSCs of AISI-1012 steel for different magnitudes of effective prestrain

A similar analysis was carried out in order to investigate the variability of the ELSC of AA-2008-T4 aluminum. Once again, the MK model was used to predict the ELSCs of the AA-2008-T4 aluminum sheet after bilinear loading paths with prestrains of different magnitudes (ε _e  = 0.10, 0.15, 0.20 and 0.25) in either uniaxial tension or equibiaxial tension.

Figure 18 shows the ELSCs of the AA-2008-T4 aluminum that were predicted for different levels of prestrain in uniaxial tension. For prestrain values up to ε _e  = 0.20, the ELSC of this aluminum alloy remains practically invariable. However, for a prestrain of ε _e  = 0.25, a significant variation in the ELSC can be observed. Similarly, the ELSC was predicted for this aluminum alloy after prestrains of increasing magnitude in equibiaxial tension and the predicted ELSCs are plotted in Fig. 19. Again, no significant change in the ELSC is observed for effective prestrain values up to ε _e  = 0.20.

Fig. 18

Comparison of the ELSCs after different levels of prestrain in uniaxial tension with the as-received ELSC of AA-2008-T4 aluminum

Fig. 19

Comparison of the ELSCs after different levels of prestrain in equibiaxial tension with the as-received ELSC of AA-2008-T4 aluminum

The ELSC of the AA-2008-T4 aluminum sheet predicted for different bilinear loading paths but with the same magnitude of prestrain, ε _e  = 0.25, are plotted in Fig. 20, and it can be seen that the ELSCs for a prestrain in uniaxial and in equibiaxial tension are identical.

Fig. 20

Comparison of the ELSCs after an effective prestrain ε _e  = 0.20 in uniaxial and equibiaxial tension with the as-received ELSC of AA-2008-T4 aluminum

The variability of the ELSC of AA-2008-T4 aluminum alloy with the magnitude of the effective prestrain was also evaluated and plotted in Fig. 21. When the sheet material is prestrained up to an effective strain of ε _e  = 0.15, the variation in the ELSC remains less than 2 % across the entire range of strain ratios (−0.5 < ρ < 1.0). Figure 21 also shows that the deviation of the ELSC relative to the as-received ELSC can reach over 40 % when the magnitude of the prestrain is ε _e  = 0.25, and similar to the AISI-1012 steel, the greatest deviation from the as-received ELSC of AA-2008-T4 occurs in the region of plane-strain deformation. In order to visualize the influence of the prestrain on the ELSC, the maximum deviation from the as-received ELSC (i.e. the deviation of ELSC₀) was plotted as a function of the effective prestrain, and Fig. 22 shows how the percent deviation of ELSC₀ increases with the effective prestrain for this AA-2008-T4 aluminum alloy. Considering Figs. 21 and 22, it appears that the ELSC of AA-2008-T4 is practically invariable until the magnitude of the effective prestrain reaches ε _e  = 0.19 (i.e. the value of the as-received ELSC₀); but beyond this value, the variation of ELSC₀ increases with the magnitude of the prestrain.

Fig. 21

Deviation in effective limit strain between prestrained and as-received ELSCs for different effective prestrain magnitudes in AA-2008-T4 aluminum sheets

Fig. 22

Maximum deviation of the effective limit strain between prestrained and as-received ELSCs of AA-2008-T4 aluminum for different magnitudes of effective prestrain

Based on the predicted ELSCs for AISI-1012 steel in Fig. 15 and the similar results for AA-2008-T4 aluminum sheets in Fig. 20, it appears that the magnitude of the effective strain prior to the final forming stage has an influence on the variability of the ELSC whereas variations in strain history do not. For both sheet materials, the ELSC remains unchanged up to a certain level of effective strain, but begins to shift upward in the vicinity of plane strain for prestrains that exceed this threshold.

It is also important to observe in Figs. 18, 19 and 20 that when the magnitude of the effective prestrain exceeds the as-received ELSC₀, the predicted ELSC becomes perfectly flat in the vicinity of plane strain. Moreover, this flat, horizontal portion of the ELSC lies at the very same level of effective strain as that which was specified in the prior strain history. Therefore, it would seem that the most significant variations in the shape of the ELSC of this AA-2008-T4 aluminum are not so much due to strain path-dependence, but rather to the fact that the effective limit strain can never be less than that which was safely reached prior to the final linear strain path. Therefore the path-dependence should really be evaluated by the deviation from the as-received ELSC outside the flat, horizontal section of the prestrained ELSC. In the case of this AA-2008-T4 aluminum alloy the maximum percent deviation outside the flat section of the ELSC (i.e. for ρ < −0.27 and ρ > 0.34 as seen in Figs. 18, 19, 20) is less than 10 % when an effective prestrain of ε _e  = 0.25 is applied. This level of deviation from the as-received ELSC corresponds in fact with a variation in effective strain of about 0.02, which is typically equivalent to the experimental error in conventional FLC data. Therefore the ELSC of this AA-2008-T4 aluminum can be considered practically path-independent for effective prestrains up to ε _e  = 0.25. In this work, plastic strains were computed assuming isotropic hardening and therefore the conclusions in this paper are based on this assumption. Some unreported work was carried out in which the FLC and ELSC were computed using the combined isotropic and nonlinear kinematic hardening rule; it was found that the differences in FLC due to the hardening rule were relatively small and the ELSC still remained unchanged for a significant range of prestrains. Nevertheless, there is a need for further research to more fully understand the influence of anisotropic hardening on the variability of ELSC when the sheet material is subject to nonlinear loading paths using different alloys.

Finally, it is thought that the region near plane strain between the as-received ELSC and the flat portion of an ELSC obtained after a severe prestrain (Figs. 18, 19, 20) corresponds approximately with the region in stress space where the yield locus lies above the stress forming limit curve (SFLC) after the yield locus has expanded due to severe work hardening. When the effective strain reaches this region of the effective limit strain diagram, the material will remain in an elastic state until the stress reaches the yield locus. But once the stress reaches the yield locus, plastic deformation will immediately lead to strain localization, and necking will take place because the SFLC has already been exceeded.

Conclusions

In this research, forming limit curves and effective limit strain curves of AISI-1012 steel and AA-2008-T4 aluminum sheets were predicted for linear and bilinear loading paths using a modified MK-based model. The developed MK analysis utilizes surface roughness and its evolution during deformation to define a dynamic and realistic non-uniformity factor in the sheet metal. Furthermore, the rotation of the imperfection band was considered in plastic calculations to minimize theoretical limit strains.

It was shown that it is advantageous to represent sheet forming limits in terms of the effective limit strain versus the principal strain ratio, because this failure criterion can easily be used to assess the forming severity of parts that were manufactured by a process that generates complex, multi-linear strain histories. Furthermore, the ELSC can be easily implemented in both process simulation software and in the press shop where the quality of actual parts needs to be closely monitored.

Predictions of the ELSC of AISI-1012 steel and of AA-2008-T4 aluminum sheets using the MK model were compared with calculations of the ELSC using experimental forming limit data that was determined from specimens that were formed along bilinear loading paths [5, 19]. The correlation between predicted and experimental ELSC data was quite good, and the discrepancies are thought to be due to the fact that the actual strain paths generated during the experimental work differed slightly from the bilinear strain paths that were assumed in the calculations.

Furthermore, predictions of the ELSC obtained after a prestrain in uniaxial and equibiaxial tension with a same level of effective prestrain were found to be essentially identical, therefore the ELSC appears to be insensitive to the strain path but dependent on the magnitude of the effective prestrain. Indeed, the ELSC remains invariable until the magnitude of the effective prestrain exceeds a certain threshold. When this threshold is exceeded, however, the ELSC starts to shift up in the vicinity of plane strain deformation (ρ = 0). It was also shown that, when an effective prestrain is applied that is greater in magnitude than the as-received ELSC₀ and that also corresponds with a prior strain history that terminates safely below the ELSC, the minimum of the ELSC will shift up to this same effective prestrain. This shifting of the ELSC in the region of plane strain is primarily a consequence of the fact that the effective limit strain can never be less than the effective prestrain that was safely attained in a previous strain history (i.e. with a different strain ratio).

The forming limit predictions carried out in this study seem to indicate that the variability of the ELSC need only to be considered in the event of very large values of prestrain (ε _e  > 0.37 for AISI-1012 steel, and ε _e  > 0.25 for AA-2008-T4 aluminum) and therefore the ELSC should be suitable for the analysis of forming severity in a majority of metal forming operations. This signifies that the ELSC is a better alternative to the stress-based forming limit curve (SFLC), especially in press-shop applications. However, further experimental work is required to demonstrate the efficiency and reliability of the ELSC in the press shop.