Stress based prediction of formability and failure in incremental sheet forming

Abstract

A strain-based forming limit criterion is widely used in sheet-metal forming industry to predict necking. However, this criterion is usually valid when the strain path is linear throughout the deformation process [1]. Strain path in incremental sheet forming is often found to be severely nonlinear throughout the deformation history. Therefore, the practice of using a strain-based forming limit criterion often leads to erroneous assessments of formability and failure prediction. On the other hands, stress-based forming limit is insensitive against any changes in the strain path and hence it is first used to model the necking limit in incremental sheet forming. The stress-based forming limit is also combined with the fracture limit based on maximum shear stress criterion to show necking and fracture together. A derivation for a general mapping method from strain-based FLC to stress-based FLC using a non-quadratic yield function has been made. Simulation model is evaluated for a single point incremental forming using AA 6022-T43, and checked the accuracy against experiments. By using the path-independent necking and fracture limits, it is able to explain the deformation mechanism successfully in incremental sheet forming. The proposed model has given a good scientific basis for the development of ISF under nonlinear strain path and its usability over conventional sheet forming process as well.

Introduction

With advanced computer hardware and software, it is possible to model sheet metal forming processes. Although the fine-tuning of product manufacturing and performance is empirical, modeling can be an efficient tool to guide and optimize design, to evaluate material attributes, and to predict life time and failure. Moreover, modeling can be used as a research tool for a more fundamental understanding of physical phenomena that can result in the development of improved or new products.

The success of a sheet forming operation can be limited by several phenomena, such as fracture, buckling, and plastic flow localization. For a given forming operation, the sheet may undergo deformation up to a given strain prior to failure by one of the limiting phenomena. The forming limit curve (FLC) or diagram illustrates the major and minor strains expected on the surface of a deforming sheet material at the onset of local necking. This curve is usually plotted on axes representing the major and the minor strains in the plane of the sheet. It can be plotted in either strain or stress space. The characterization of forming limits in sheet metal is a significant challenge in complex processes since the conventional strain-based FLC is sensitive to strain path effects.

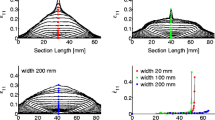
The most promising solution for dealing with strain-path effects in the FLC is to use a stress-based curve, as independently proposed by Kleemola and Pelkkikangas [2], Stoughton [3], and Stoughton and Yoon [1, 4]. These authors have shown that the stress-based FLC is not affected by strain path, and should be applicable without modification to analysis of all forming problems. As can be seen in Fig. 1, the FLCs described in strain space with pre-strains are mapped to a single curve in stress space. This verifies the path independency of the stress-based FLC. Furthermore, Kuwabara et al. [5] measured the stress state at the forming limit in tube expansion with end feed under proportional and non-proportional conditions and directly confirmed that the forming limit as characterized by the state of stress is insensitive to loading history.

Fig. 1

Comparisons of path effects: (a) Strain-based FLC (path effect), (b) Stress-based FLC (no path effect) (taken from Stoughton [3])

In this research, stress-based forming limit combined with a fracture polygon approach based on maximum shear stress criterion [6] which used for deep drawing is employed to explain the mechanism of incremental sheet forming following nonlinear strain path for AA 6022-T4E32. A Barlat’s yield function [7, 8] (called Yld2000-2d) has been used to predict anisotropic behavior of the aluminum sheet. In Haque and Yoon [9], a brief result from the Yld2000-2d has been presented for a cone shape. In this work, in order to provide a theoretical basis, a detail derivation has been made for a general mapping method from strain-based FLC to stress-based FLC using a non-quadratic yield function. Also, the theory has been also applied for a pyramidal shape as well as a cone shape to show a generality of method. Local strain and stress along the rolling direction has been also measured and incorporated in the fracture model. The related experimental data have been presented. Necking and post-necking behavior during incremental sheet forming has been discussed with the proposed stress-based forming limit curve at necking and fracture limit curve at fracture. The proposed model incorporating the limit curve at neck and fracture together gives an advantage to explain the post necking ductility of incremental sheet forming.

Constitutive modelling

Constitutive laws in materials generally consist of a state equation and evolution equations. The state equation describes the relationship between the strain rate $\dot{\varepsilon}$, stress σ, temperature T and state variables x _i , which represent the microstructural state of the material. This can be translated, for instance in a scalar form for uniaxial deformation, as

$$ \dot{\varepsilon}=\dot{\varepsilon}\left(\sigma, T,{x}^k\right) $$

(1)

The evolution equations describe the development of the microstructure through the change of the state variables and can take the form

$$ {\dot{x}}^k={\dot{x}}^k\left(\sigma, T,{x}^k\right) $$

(2)

At the continuum scale, for a multiaxial stress space, plastic deformation is well described with a yield surface, a flow rule and a hardening law. The yield surface in stress space separates stress states producing elastic and elasto-plastic deformation. It is a generalization of the tensile yielding behavior to multiaxial stress states. Plastic anisotropy is the result of the distortion of the yield surface shape due to the material microstructural state. Życzkowski [10] discussed different phenomena attached to the yield surface shape at a macroscopic scale. Regardless of the shape of the yield surface, strain hardening can be isotropic or anisotropic. The former corresponds to an expansion of the yield surface without distortion. Any other form of hardening is anisotropic and leads to different properties in different directions after deformation, even if the material is initially isotropic. Whether the yield surface expands, translates or rotates as plastic deformation proceeds, a shape must be defined to account for the current anisotropic axes.

The material description is fully defined using the following set of equations

$$ \begin{array}{l}\phi \left(\boldsymbol{\upsigma} \right)=\phi \left({\sigma}_{ij}\right)=\overline{\sigma}\kern0.24em \left( yield\kern0.40em condition\right)\hfill \\ {}{\dot{\varepsilon}}_{ij}=\dot{\lambda}\frac{\partial \phi }{\partial {\sigma}_{ij}}\kern0.24em \left( flow\kern0.40em rule\right)\hfill \\ {}\overline{\sigma}=\overline{\sigma}\left(\overline{\varepsilon}\right)\; with\;\overline{\sigma}\;\dot{\overline{\varepsilon}}={\sigma}_{ij}{\dot{\varepsilon}}_{ij}\kern0.24em \left( hardening\kern0.40em function\right)\hfill \end{array} $$

(3)

It is assumed that the effects of temperature and strain rate can be included in the formulation through $\overline{\sigma}$, for instance using $\overline{\sigma}=\overline{\sigma}\left(\overline{\varepsilon},\dot{\overline{\varepsilon}},T\right)$. However, deformations involving creep and grain sliding are not accounted for in this discussion. The problem reduces to define the functions $\overline{\sigma}$ and ϕ.

The yield surface of FCC and BCC metals is usually represented adequately by an even function of the principal values S _k of the stress deviator s suggested by Hosford [11], i.e.,

$$ \phi ={\left|{S}_1-{S}_2\right|}^a+{\left|{S}_2-{S}_3\right|}^a+{\left|{S}_3-{S}_1\right|}^a=2{\overline{\sigma}}^a $$

(4)

The exponent a is connected to the crystal structure of the material, i.e., 6 for BCC and 8 for FCC. This was established as a result of many polycrystal simulations. Therefore, although this model is macroscopic, it contains some information pertaining to the structure of the material.

Yoon et al. [7] introduced two linear transformations operating on the sum of two yield functions in the case of plane stress. The complete form of the linear transformation-based plane stress function was proposed by Barlat et al. [8] called Yld2000-2d. FE implementation of Yld2000-2d can be found in Yoon et al. [12]. More sophisticated yield function (called Yld2004-18p [13]) was developed and implemented especially for highly anisotropic rigid-packaging alloys which have more than four ears shown in Yoon et al. [14]. However, in this study, Yld2000-2d is only used to consider a moderate anisotropy for AA6022-T4E32 (which has only four ears).

Extensions of Eq. 4 based on the case of planar anisotropy are briefly summarized for a plane stress state and a general stress state. Both formulations are based on two linear transformations of the stress deviator. The two linear transformations can be expressed as

$$ \begin{array}{l}{\tilde{\mathbf{s}}}^{\mathbf{\prime}}={\mathbf{C}}^{\mathbf{\prime}}\mathbf{s}={\mathbf{C}}^{\mathbf{\prime}}\mathbf{T}\boldsymbol{\upsigma } ={\mathbf{L}}^{\mathbf{\prime}}\boldsymbol{\upsigma} \\ {}{\tilde{\mathbf{s}}}^{\mathbf{{\prime\prime}}}={\mathbf{C}}^{\mathbf{{\prime\prime}}}\mathbf{s}={\mathbf{C}}^{\mathbf{{\prime\prime}}}\mathbf{T}\boldsymbol{\upsigma } ={\mathbf{L}}^{\mathbf{{\prime\prime}}}\boldsymbol{\upsigma} \end{array} $$

(5)

where T is a matrix that transforms the Cauchy stress tensor σ to its deviator s. ${\tilde{\mathbf{s}}}^{\mathbf{\prime}}$ and ${\tilde{\mathbf{s}}}^{\mathbf{{\prime\prime}}}$ are the linearly transformed stress deviators and C′ and C″ (or L′ and L″) are the matrices containing the anisotropy coefficients.

For plane stress, these two linear transformations reduce to

$$ \left[\begin{array}{c}\hfill {\tilde{s}}_{xx}^{\prime}\hfill \\ {}\hfill {\tilde{s}}_{yy}^{\prime}\hfill \\ {}\hfill {\tilde{s}}_{xy}^{\prime}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill {\alpha}_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {\alpha}_2\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha}_7\hfill \end{array}\right]\left[\begin{array}{c}\hfill {s}_{xx}\hfill \\ {}\hfill {s}_{yy}\hfill \\ {}\hfill {s}_{xy}\hfill \end{array}\right],\;\left[\begin{array}{c}\hfill {\tilde{s}}_{xx}^{{\prime\prime}}\hfill \\ {}\hfill {\tilde{s}}_{yy}^{{\prime\prime}}\hfill \\ {}\hfill {\tilde{s}}_{xy}^{{\prime\prime}}\hfill \end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc}\hfill 4{\alpha}_5-{\alpha}_3\hfill & \hfill 2{\alpha}_6-2{\alpha}_4\hfill & \hfill 0\hfill \\ {}\hfill 2{\alpha}_3-2{\alpha}_5\hfill & \hfill 4{\alpha}_4-{\alpha}_6\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 3{\alpha}_8\hfill \end{array}\right]\left[\begin{array}{c}\hfill {s}_{xx}\hfill \\ {}\hfill {s}_{yy}\hfill \\ {}\hfill {s}_{xy}\hfill \end{array}\right] $$

(6)

Let ${{\tilde{S}}^{\prime}}_i$ and ${\tilde{S}}_j^{{\prime\prime} }$ denote the principal values of the tensors ${\tilde{\mathbf{s}}}^{\mathbf{\prime}}$ and ${\tilde{\mathbf{s}}}^{\mathbf{{\prime\prime}}}$ defined above. The plane stress anisotropic yield function Yld2000-2d is defined as

$$ \phi ={\left|{\tilde{S}}_1^{\prime }-{\tilde{S}}_2^{\prime}\right|}^a+{\left|2{\tilde{S}}_2^{{\prime\prime} }+{\tilde{S}}_1^{{\prime\prime}}\right|}^a+{\left|2{\tilde{S}}_1^{{\prime\prime} }+{\tilde{S}}_2^{{\prime\prime}}\right|}^a=2{\overline{\sigma}}^a $$

(7)

Note that this formulation is isotropic and reduces to Eq. 4 if C′ and C″ are both equal to the identity matrix. It also reduces to the von Mises and Tresca yield functions if a = 2 (or 4) and a = 1 (or ∞), respectively. More details regarding Yld2000-2d can be obtained in Barlat et al. [8].

Strain-based formability

The forming limit curve (FLC) corresponds to the maximum admissible local strains achievable just before necking. This curve is usually plotted on axes representing the major (ε ₁) and the minor (ε ₂) strains in the plane of a sheet.

For materials exhibiting isotropy or planar isotropy (same properties in any direction in the plane of the sheet), the main equilibrium equation of the The Marciniak and Kuczynski (MK) model reduces to the following form:

$$ \left[1-D\right]\left[\frac{h\left({\overline{\varepsilon}}^I\right)}{h\left(\overline{\varepsilon}\right)}\right]\left[\frac{{\overline{\sigma}}_1^I}{{\overline{\sigma}}_1}\right]=1 $$

(8)

where $h\left(\overline{\varepsilon}\right)$ is the hardening law and ${\overline{\sigma}}_1={\sigma}_1/\overline{\sigma}$ is the maximum principal stress normalized by the effective stress. The superscript “I” stands for the imperfection region.

The MK model also suggests the necking direction. In the negative ρ range (ρ = dε ₂/dε ₁) lying between uniaxial tension and plane strain tension (ε ₂ ≤ 0), the necking direction is at an angle with respect to the maximum principal strain. However, in the biaxial stretching range (both ε ₁ and ε ₂ are positive), necking occurs most of the time in a direction perpendicular to the major principal strain, which correspond to the assumption of Eq. 8. Studies of damage based on microscopic observations and probability calculations have shown that the order of magnitude of ‘D’ in Eq. 8 for typical commercial alloys is 0.4 %. In the following discussion the value of 1 − D = 0.996 has been used to quantitatively characterize the imperfection.

Stress-based formability

The discussion above assumed that deformation occurs along linear strain paths, i.e., ρ = dε ₂/dε ₁ is constant. In practice, particularly for multi-step forming, this is not the case. Moreover, it was shown by Stoughton and Yoon [1] that non-linear strain paths have an influence on the FLC. Graf and Hosford [15] showed that the FLC strongly depends on the strain path for steel and aluminum alloy sheets, respectively. The characterization of forming limits in strain space is therefore a practical challenge for complex forming processes due to this sensitivity.

In this section, a general mapping procedure from strain-based FLC to stress-based FLC for a non-quadratic yield function including Yld2000-2d is derived. In order to compute the stress-based FLC, a representation of the forming limit behavior for proportional loading in strain space, i.e., the locus of principal strains, is specified as follows

$$ strain-FLC=\left[\begin{array}{c}\hfill {e}_1^{FLC}\hfill \\ {}\hfill {e}_2^{FLC}\hfill \end{array}\right]={e}_1^{FLC}\left(\rho, {\theta}^{\prime}\right)\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill \rho \hfill \end{array}\right] $$

(9)

where ρ is a parameter in the range ρ = [−1, + 1] that defines the ratio of the principal strains on the FLC and θ′ is the angle between the principal strain axis and the rolling direction of the sheet in the strain space. A serious limitation of the strain-based FLC is that it applies only to cases of proportional loading, and will lead to a false assessment of formability in a multi-stage cup drawing, where the strain-path is highly non-linear. The solution to the latter issue is to use the stress-based FLD, which has been shown to be independent of loading history. This section describes how to derive the stress-based forming limit criterion from the strain-based FLC defined in the above strain-based forming limit criterion.

The minor principal stress, σ ^FLC₂ , is proportional to the major stress by a parameter α = [−1, + 1], i.e., σ ^FLC₂  = ασ ^FLC₁ . Note that with the specified range for the α parameter, the magnitude of the minor principal stress is always less than or equal to the major stress, so that we can use the major principal stress as a normalizing factor in the following derivation without concern about singularities in the calculations. The stress tensor components at the stress state (σ ^FLC₁ , σ ^FLC₂ (=ασ ^FLC₁ ), θ) where θ is the angle between the principal stress axis and the rolling direction of the sheet in the stress space are given by

$$ \left[\begin{array}{c}\hfill {\sigma}_{11}^{FLC}\hfill \\ {}\hfill {\sigma}_{22}^{FLC}\hfill \\ {}\hfill {\sigma}_{12}^{FLC}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\sigma}_1^{FLC}{ \cos}^2\left(\theta \right)+{\sigma}_2^{FLC}{ \sin}^2\left(\theta \right)\hfill \\ {}\hfill {\sigma}_1^{FLC}{ \sin}^2\left(\theta \right)+{\sigma}_2^{FLC}{ \cos}^2\left(\theta \right)\hfill \\ {}\hfill \left({\sigma}_1^{FLC}-{\sigma}_2^{FLC}\right) \sin \left(\theta \right) \cos \left(\theta \right)\hfill \end{array}\right]={\sigma}_1^{FLC}\left[\begin{array}{c}\hfill {\lambda}_{11}\hfill \\ {}\hfill {\lambda}_{22}\hfill \\ {}\hfill {\lambda}_{12}\hfill \end{array}\right] $$

(10)

where

$$ \left[\begin{array}{c}\hfill {\lambda}_{11}\hfill \\ {}\hfill {\lambda}_{22}\hfill \\ {}\hfill {\lambda}_{12}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill { \cos}^2\left(\theta \right)+\alpha { \sin}^2\left(\theta \right)\hfill \\ {}\hfill { \sin}^2\left(\theta \right)+\alpha { \cos}^2\left(\theta \right)\hfill \\ {}\hfill \left(1-\alpha \right) \sin \left(\theta \right) \cos \left(\theta \right)\hfill \end{array}\right] $$

(11-a)

Specifically when θ = 0 (normal anisotropy), Eq. 11-a reduces to

$$ \left[\begin{array}{c}\hfill {\lambda}_{11}\hfill \\ {}\hfill {\lambda}_{22}\hfill \\ {}\hfill {\lambda}_{12}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill \alpha \hfill \\ {}\hfill 0\hfill \end{array}\right] $$

(11-b)

Using Eq.10 with the selected material model, we can define the yield function as a constant σ ^FLC₁ multiplying the yield function,

$$ \overline{\sigma}\left({\sigma}_{11}^{FLC},{\sigma}_{22}^{FLC},{\sigma}_{12}^{FLC}\right)={\sigma}_1^{FLC}\overline{\sigma}\left({\lambda}_{11},{\lambda}_{22},{\lambda}_{12}\right) $$

(12)

The gradient of the plastic potential at this stress state is also uniquely defined in terms of the λ _ij coefficients and the material parameters, independently of the magnitude of σ ^FLC₁ . These equations are described in the next section using Yld2000-2d. Under proportional loading, the plastic strain tensor components are proportional to the gradients of the plastic potential,

$$ \left[\begin{array}{c}\hfill {e}_{11}^{FLC}\hfill \\ {}\hfill {e}_{22}^{FLC}\hfill \\ {}\hfill 2{e}_{12}^{FLC}\hfill \end{array}\right]={\overline{\varepsilon}}_p^{FLC}\left[\begin{array}{c}\hfill {p}_{11}\hfill \\ {}\hfill {p}_{22}\hfill \\ {}\hfill {p}_{12}\hfill \end{array}\right]={\overline{\varepsilon}}_p^{FLC}{\left[\begin{array}{ccc}\hfill \frac{\partial \overline{\sigma}}{\partial {\sigma}_{11}^{FLC}}\hfill & \hfill \frac{\partial \overline{\sigma}}{\partial {\sigma}_{22}^{FLC}}\hfill & \hfill \frac{\partial \overline{\sigma}}{\partial {\sigma}_{12}^{FLC}}\hfill \end{array}\right]}^T $$

(13)

and the principal strains on the forming limit are given by

$$ \left[\begin{array}{c}\hfill {e}_1^{FLC}\hfill \\ {}\hfill \hfill \\ {}\hfill {e}_2^{FLC}\hfill \end{array}\right]=\frac{1}{2}\left[\begin{array}{c}\hfill {e}_{11}^{FLC}+{e}_{22}^{FLC}+\sqrt{{\left({e}_{11}^{FLC}-{e}_{22}^{FLC}\right)}^2+{\left(2{e}_{12}^{FLC}\right)}^2}\hfill \\ {}\hfill \hfill \\ {}\hfill {e}_{11}^{FLC}+{e}_{22}^{FLC}-\sqrt{{\left({e}_{11}^{FLC}-{e}_{22}^{FLC}\right)}^2+{\left(2{e}_{12}^{FLC}\right)}^2}\hfill \end{array}\right] $$

(14)

Substitution of Eq. 13 into Eq. 14 gives,

$$ \left[\begin{array}{c}\hfill {e}_1^{FLC}\hfill \\ {}\hfill \hfill \\ {}\hfill {e}_2^{FLC}\hfill \end{array}\right]=\frac{{\overline{\varepsilon}}_p^{FLC}}{2}\left[\begin{array}{c}\hfill {p}_{11}+{p}_{22}+\sqrt{{\left({p}_{11}-{p}_{22}\right)}^2+{p}_{12}^2}\hfill \\ {}\hfill \hfill \\ {}\hfill {p}_{11}+{p}_{22}-\sqrt{{\left({p}_{11}-{p}_{22}\right)}^2+{p}_{12}^2}\hfill \end{array}\right] $$

(15)

Note that the principal strains at this stress state are oriented at an angle θ′ ≠ θ for anisotropic materials given by

$$ \tan \left(2{\theta}^{\prime}\right)=\frac{2{e}_{12}^{FLC}}{e_{11}^{FLC}-{e}_{22}^{FLC}}=\frac{p_{12}}{p_{11}-{p}_{22}} $$

(16)

meaning that the orientation of the principal strains is in general not parallel to the orientation of the principal stresses for an anisotropic material. From Eq. 15, the ratio of principal strains is defined uniquely in terms of the gradients of the plastic potential,

$$ \rho =\frac{e_2^{FLC}}{e_1^{FLC}}=\frac{p_{11}+{p}_{22}-\sqrt{{\left({p}_{11}-{p}_{22}\right)}^2+{p}_{12}^2}}{p_{11}+{p}_{22}+\sqrt{{\left({p}_{11}-{p}_{22}\right)}^2+{p}_{12}^2}} $$

(17)

Using the values for θ′ and ρ from Eqs. 16 and 17, respectively, the strain tensor components on the forming limit are now fully specified for this stress state,

$$ \left[\begin{array}{c}\hfill {e}_{11}^{FLC}\hfill \\ {}\hfill {e}_{22}^{FLC}\hfill \\ {}\hfill 2{e}_{12}^{FLC}\hfill \end{array}\right]={e}_1^{FLC}\left(\rho, {\theta}^{\prime}\right)\left[\begin{array}{c}\hfill { \cos}^2\left({\theta}^{\prime}\right)+\rho { \sin}^2\left({\theta}^{\prime}\right)\hfill \\ {}\hfill { \sin}^2\left({\theta}^{\prime}\right)+\rho { \cos}^2\left({\theta}^{\prime}\right)\hfill \\ {}\hfill 2\left(1-\rho \right) \sin \left({\theta}^{\prime}\right) \cos \left({\theta}^{\prime}\right)\hfill \end{array}\right] $$

(18)

where e ^FLC₁ (ρ, θ′) is defined by Eq. 9. Adding together the two components of the principal strains from Eq.15 and solving for the effective plastic strain leads to the following equation, whose value can now be calculated explicitly,

$$ {\overline{\varepsilon}}_p^{FLC}=\frac{e_1^{FLC}+{e}_2^{FLC}}{p_{11}+{p}_{22}}=\frac{\left(1+\rho \right){e}_1^{FLC}\left(\rho, {\theta}^{\prime}\right)}{p_{11}+{p}_{22}}=\frac{2{e}_1^{FLC}\left(\rho, {\theta}^{\prime}\right)}{p_{11}+{p}_{22}+\sqrt{{\left({p}_{11}-{p}_{22}\right)}^2+{p}_{12}^2}} $$

(19)

Using the power law (Swift law) and inverting Eq. 12, we can finally calculate the major principal stress,

$$ {\sigma}_1^{FLC}\left(\alpha, \theta \right)=\frac{K{\left({\varepsilon}_o+{\overline{\varepsilon}}_p^{FLC}\right)}^n}{\overline{\sigma}\left({\lambda}_{11},{\lambda}_{22},{\lambda}_{12}\right)} $$

(20)

and then the minor principal stress σ ^FLC₂  = ασ ^FLC₁ . This procedure is followed for all values of α = [−1, + 1], defining the locus of points (σ ^FLC₁ , σ ^FLC₂ ) on the stress-based FLC for major stress at an angle θ to the rolling direction of the sheet. Each point on this curve, characterized by the function σ ^FLC₁ (α, θ), has a corresponding point on the experimental strain-based FLC given by the function e ^FLC₁ (ρ, θ′). The only difference is that the stress-based curves are applicable for arbitrary loading history, while the strain-based curves apply only for proportional loading.

Material characterization

The data from hydraulic bulge test, and uniaxial test at seven different directions (0⁰, 15⁰, 30⁰, 45⁰, 60⁰, 75⁰, 90⁰) are available from Numisheet benchmark data for AA 6022-T4E32 [16]. Due to the lack of the materials taken from the same stock, one additional tensile test has been conducted to measure a local fracture stain along 45^o direction by using Digital Image Correlation (DIC) technique as shown in Fig. 2. A local fracture strain reached around 0.5. It is interested to know that very good part of hardening is observed at the time of fracture without any saturation. Therefore, Swift fits better than Voce law in overall. The hardening curve has been modeled by Swift. Table 1 shows Swift and Yld2000-2d coefficients used in the simulation. The stress ratios input for Yld2000-2d are calculated based on principle of minimum plastic work to fracture.

Fig. 2

Fitting of experimental hardening curve to fracture with Swift and Voce curves

Table 1 Material properties and anisotropic coefficients for AA 6022-T4E32

In Fig. 3a, the results are compared with the experimental data shown in a Progress Report published by US department of Energy [17] which determined the necking limit using the limit-dome test apparatus at the Advanced Materials Processing Laboratory at NWU. It is found that the MK prediction in the right-hand side shows very good correlation with experimental data.

Fig. 3

Representation of predicted forming limit and failure curves for AA 6022-T4E32: (a) Strain space, (b) Stress space

To plot the failure limit, maximum shear stress (MSS) criterion is used, can be expressed as follows:

$$ {\sigma}_{mss}=\frac{1}{2}\left( \max \left({\sigma}_1,{\sigma}_2,{\sigma}_3\right)- \min \left({\sigma}_1,{\sigma}_2,{\sigma}_3\right)\right) $$

(21)

The fracture polygon is drawn with the available maximum shear stress data in uniaxial tension direction in Fig. 3b.

Experiment and finite element analysis of cone and pyramid shapes

Both cone and pyramid shapes (base diameter 140 mm) are formed by a CNC machine with the slope of 45⁰ to the depth of 45 mm tool by using a spherical ball of 12.66 mm diameter. Very low friction co-efficient is selected considering very well lubricated experimental condition. The length and width of the initial finite elements are 2.5 mm × 2.5 mm. The dimension of the initial blank is 200 mm × 200 mm x 1 mm. Tool path is generated with a CAM software. A constant speed of 1000 mm/min is maintained in anticlockwise motion throughout the experiment and downward step size is kept constant with 0.5 mm at the completion of each incremental cycle. The finished part is then put under ASAME target system to measure the strain at non-contact surface. The result is presented in strain space with the experimentally measured (strain-based) forming limit in Fig. 4a, which clearly shows failure for cone and pyramid shapes. However, number of repeated experiments was successfully carried out without any crack or failure. In the initial FEM modelling, the rolling direction is coincided with the global X-direction. The fixed boundary condition was imposed on all edges of the blank and support plate is introduced as a fixed rigid body. High normal force is applied over the blank to provide the stability of the top plate. A ball-shaped tool with a radius of 6.33 mm was modelled as a rigid body and a small amount friction coefficient (surface to surface) of 0.01is imposed between the ball and blank. Experimentally generated tool path has been imported. The time step is selected carefully compatible with the experiment condition and a forming depth is kept 0.5 mm. Implicit FE simulation under the plane stress condition is carried out at 9 through thickness integration points with Yld2000-2d and Swift hardening model by using 4-nodes Belytschko Wong and Chang (BWC) element. In Fig. 4a and c, experimental measurements for major & minor strains and thickness strain contours have been displayed from the automatic strain measurement system for the cone and pyramidal shapes. The compatible comparisons have been made in Fig. 4b and d for the cone and pyramidal shapes. For both the cone and pyramidal shapes, the corresponding principle strain distribution in Fig. 4(b) and (d) shows the results exceeding both the necking and failure limit.

Fig. 4

(a) Thickness strain contour of experimental results for a cone shape with experimentally measured major & minor strains, (b) Thickness strain contour obtained from Yld2000-2d model for a cone shape with the predicted strains at the bottom plane plotted in strain-based necking and fracture limits (c) Thickness strain contour of experimental results for a pyramidal shape with experimentally measured major & minor strains, (d) Thickness strain contour obtained from Yld2000-2d model for a pyramidal shape with the predicted strains at the bottom plane plotted in strain-based necking and fracture limits

The same simulation data are plotted in Fig. 5 based on the stress-based necking and failure space shown in Fig. 3b. There are the differences in stresses between continuous loading and unloading by the tool movement. However, a projection method based on the final stresses only was introduced to compensate the current unloaded stress by projecting it back to the current yield surface or hardening (called the projected stress) using the following equation [6], i.e.,

Fig. 5

Projected FE stress values represented in the stress-based FLC for both cone and pyramid shapes : (a) Upper surface of the cone shape and (b) Lower surface of the cone shape (c) Upper surface of the pyramid shape (d) Lower surface of the pyramid shape

$$ {\sigma}_{ij}^p={\sigma}_{ij}\frac{h\left({\overline{\varepsilon}}_p\right)}{\overline{\sigma}\left({\sigma}_{ij}\right)} $$

(22)

In the reconstruction, the projected stress is based on the effective plastic strain and the set of the final stress components. The projected stress state is determined by the effective plastic strain and yield function. The projected stresses calculated using Eq. 22 are plotted in Fig. 5 for both top and bottom surfaces. Figure 5a & b and c & d include the major and minor stresses at the top and bottom surfaces for the cone and pyramidal shapes, respectively. It is shown that the stress data are within the failure limit under post necking, which is consistent with experimental data. It is because nonlinear path effect has been considered in the stress path combined with path-independent stress-based forming and fracture limits.

Summary

Stress-based forming and fracture limits have been introduced as a new approach to predict necking and failure in incremental sheet forming. The reliability of this new stress-based approach for necking and failure were successfully verified through experimental testing and finite element simulation. An advanced constitutive model of Yld2000-2d was also introduced in the analyses. It is shown that predictions from stress-based necking and failure model are consistent with the experimental observation.