Introduction

Metal forming can be defined as process in which the desired size and shapes are obtained through the plastic deformation of a material. The stresses induced during the process are greater than the yield strength, but less than the fracture strength of the material. Using metal forming process; desired shape, size and finish can be obtained without any significant loss of material. Moreover, strength of the product is improved through improved stress flow lines. Bending is a metal forming process in which straight length is transformed into a curved length. Roller forming is a continuous bending operation in which a long strip of metal (typically coiled steel) is passed through consecutive sets of rollers or roller stands, each performing only an incremental part of the bend, until the desired cross sectional profile is obtained. Roller forming is an ideal process for producing longer parts in large quantities.

The roller bending process usually produces higher dimensional accuracy of the finished products [1]. Although there are many types of roller benders available for the plate and sheet bending industry, the normal practice of plate roller bending still heavily depends upon the experience and the skill of the operator. Working to templates, or by trial and error, yet remains a common practice in industry [2].

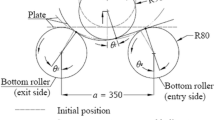
Whole process of 3-roller conical bending, have four stages namely (i) static bending, (ii) Forward rolling, (iii) Backward rolling and (iv) unloading. First stage of static bending is performed by loading the blank between top roller and bottom rollers as shown in Fig. 1 and then pressing the top roller downwards. This process is similar to air bending process but is performed by the rollers instead of punch & die. In the subsequent stages bottom rollers are given rotation in forward and reverse direction to perform the rolling. After the rolling is completed the rolled plate is unloaded during which the plate undergoes springback.

Fig. 1
figure 1

Schematic arrangement of 3-roller conical bending setup

Full size image

Cone frustum bending mechanics is complex to understand as compared to cylindrical shell bending. Knowledge of the machine configuration for continuous bending of cone frustums on roller bending machine, will be important to original equipment manufacturer and small to large scale fabricators. Utilizing such knowledge they can achieve economy, quality and competency in their products. It is also beneficial to simulate the forces acting on rollers, to get the friction coefficient, during the rolling process. Researchers have already worked on machine setting parameters for required geometry consideration [3]. In this paper, work related to development of analytical model for the prediction of bending load and estimate the value of coefficient of friction at roller plate interface for 3-roller conical bending process have been discussed.

A lot of work has been reported by researchers in the area of analytical modeling of bending process and its implication in FEA models. Mathematical models for plane-strain sheet bending have been established by Wang et. al., to predict springback[4]. They incorporated the true (non-linear) strain distribution across the sheet thickness. They showed that the bending moment is greater for materials with higher strength, strain hardening and normal anisotropy.

Hua et. al. have proposed a mathematical model for determining the plate internal bending resistance at the top roll contact for multi-pass four-roll thin-plate bending operations [5].

An analytical model for continuous single-pass four-roll thin plate bending was proposed by Baines et al. considering the equilibrium of the internal and external bending moment at and about the plate-top roll contact[6]. Hua and Lin had given a mathematical model to simulate the mechanics in a steady continuous bending mode for four-roll thin plate bending process considering varying radius of curvature of the plate between the rollers [1].

Hua and Lin also investigated Influence of material strain hardening on the mechanics of steady continuous roll and edge-bending mode in the four-roll plate bending process [8].

Moreira and Ferron had investigated the influence of the plasticity model adopted in sheet metal forming simulations by means of a numerical study of experimental tests [9]. They concluded that the isotropic hardening assumption provides a good fit of experiments for the tests where the sheet is submitted to relatively linear loading paths. Firat had employed two rate-independent anisotropic plasticity models in the deformation modeling of a stamping part [10]. Kim et. al. have developed an analytical model to predict springback and bend allowance simultaneously in air bending, and prepared computer program [11].

Gandhi et. al. had reported the formulation of springback and machine setting parameters for continuous multi-pass bending of cone frustum on 3-roller bending machines with non-compatible (cylindrical) rollers [2, 3, 12]. They analyzed the effect of change of flexural modulus during the deformation on springback prediction.

Sanchez presented an elastic–plastic mathematical model for plane strain flow of sheet metal subjected to strain rate effects during cyclic bending under tension [13]. He also included Bauschinger factors in the model for stress reversal.

Majority of the work done by the researchers is for cylindrical bending processes. Some preliminary investigation related to conical bending as far as bending force is concerned is done by A. H. Gandhi et. al. [2, 3, 12], but none have addressed the problem of bending force prediction in this area to the best of the knowledge of the authors. So here is an attempt made to develop force prediction model for 3-roller conical bending process which will be useful to the researchers to understand the complex mechanics of the process.

Mathematical formulation

It is observed that maximum force is acting on the roller during the static bending in roll bending process [2]. So mathematical model is developed for the static bending case only.

Hua et al. commented that it is difficult to achieve a single mathematical model that takes into account all the complexities of the bending process [5]. Similarly the process of 3-roller conical bending process is also complex. A realistic simplification is thus necessary.

So for formulation of the relations for force prediction and coefficient of friction, following simplifying assumptions have been made:

Assumptions

  • Plate is always having line contact with the roller, along the full length of the roller, which is parallel to roller axis during entire process.

  • The plate to be bend is having some weight but the weight of the plate quite less as compared to the forces that are acting on the plate during the bending. So it can be neglected.

  • The system of forces acting on the roller and at the roller-plate interface is symmetrical about the vertical plane at the midpoint of the line joining the centers of the bottom roller and perpendicular to that line, which can be observed in the Fig. 2.

    Fig. 2
    figure 2

    Schematic of blank and roller arrangement for pre-bending

    Full size image

  • There is no shift of the neutral plane in the bent plate.

  • Frictional force is always tangent to the roller surface.

  • When the bending takes place considerable portion of the plate is left overhanging at the inlet side of the plate as you can see in Fig. 1. Similarly some portion of the blank is left overhanging on the exit side of the plate. The effect on the bend radius of curvature of the plate, in the deformation zone, due to the counter-bending moment produced by the weight of the overhanging plate, before the inlet side roll and after the exit from the roll, is neglected.

  • The deflection of the rolls, during the bending operation, is neglected, i.e. roller is assumed to be rigid.

  • Material is with stable microstructure throughout the deformation process.

  • Deformation occurs under isothermal conditions.

  • Modulus of Elasticity ‘E’ remains constant during the process.

  • Blanks for the cone frustum bending are selected such that ((w/t) > 8) and hence plane strain conditions prevail [4, 7], as cone angle considered being small.

  • While bending conical section along with the bending stress there will be torsional shear stresses along the cross section of the plate. As the cone angle is small and bottom roller inclination will be almost half the cone angle [12], axial forces along the roller axis will be very small. Hence the torsional shear stresses in the plate will also be smaller and they are neglected for the present analysis.

  • Plane section remains plane, before and after the bending.

  • Baushinger effect is neglected.

  • Blank is having uniform/constant radius of curvature for the supported length between two bottom rollers.

  • Thickness of the blank (t) remains constant during and after the bending.

  • Further simplifying assumptions have been made as and when required in the formulation.

Model of bending moment M and top roller load P

Continuing above assumptions, model for the bending force has been derived considering change of span and friction at bottom roller blank interface as below:

First stage of the process is static bending as stated earlier. In this stage bottom rollers are inclined at required angle, the blank is kept between top and bottom rollers and the top roller is give vertically downward movement. This stage is shown in Fig. 2. Cross section at some radius of blank R is shown. Top roller is not shown in the figure but the vertical reaction at the top roller and plate interface, P is shown. As the cross section along the width of the blank at which the bending radius is R is considered, bottom roller inclination angle cannot be seen. For particular bottom roller inclination, bending radius at front end and rear end will have certain values. Thus bottom roller inclination will affect the value of R along the width of the blank. In figure reaction at the top roller i.e. bending load P at the top roller is shown. Top roller is given the displacement U. Normal reaction on the bottom roller by the plate is Q and the frictional resistance to the movement of the blank on the roller will be μQ, tangent to the roller surface as shown in Fig. 2. Other geometrical parameters are also shown in the Fig. 2. For the pre-bending of the blank as shown in Fig. 2, bending moment at point A (i.e. point at an intersection of the line of action of the concentrated load & outer fiber of the blank) can be given by [12, 14]

$$ {M_{{ext}}} = Q\;g $$
(1)

For the reaction on both the rollers, taking moments at point H,

$$ Px\prime - J\prime a\prime = 0 $$
(2)

Where,

$$ P = Q \; \prime + J\prime $$
(3)

From Eqs. 2 & 3, reaction \( Q\prime \) can be derived to the form,

$$ Q \; \prime = P ( 1 - \frac{{x\prime }}{{a\prime }}) $$
(4)

From Fig. 2. \( Q \; \prime = Q\cos \theta + \mu \;Q\sin \theta \)

$$ ∴ Q \; \prime = Q\;(\cos \theta + \mu \sin \theta ) $$
$$ ∴ Q = \frac{{Q \; \prime }}{{(cos\;\theta + \mu \sin \theta )}} = \frac{P}{{\left( {\cos \;\theta + \mu \sin \theta } \right)}}(1 - \frac{{x \prime }}{{a\prime }}) $$
(5)

From Fig. 2,

$$ c = \frac{{x\prime }}{{\cos \gamma }};U\prime = x\prime \tan \gamma; h = c\sin \psi; g = c\cos \psi = x\prime \frac{{\cos \psi }}{{\cos \gamma }} $$
(6)
$$ \sin \psi = \sin (\theta - \gamma ) = \sin \theta \cos \gamma - \cos \theta \sin \gamma ) = \cos \gamma \left( {\sin \theta - \sin \theta \tan \gamma } \right) $$
(7)

Replacing Eqs. 5 & 6 in Eq. 1 & simplifying;

$$ {M_{{ext}}} = P( 1 - x\prime /a\prime )(1/1 + \mu \tan \theta )(x\prime + U\prime \tan \theta ) $$
(8)

In Eq. 8, replacing

$$ a\prime \approx a - {r_1}\sin \theta; U\prime \approx U - {r_1}\left( {1 - \cos \theta } \right);x\prime \approx x - {r_1}\sin \theta $$

From Fig. 2 [12],

$$ {M_{{ext}}} = P( 1 - x - {r_1}\sin \theta )(1/1 + \mu \tan \theta )(x - \tan \theta ({r_1} - U)) $$
(9)

External bending moment due to friction

From Fig. 2, bending moment due to friction (M friction ) at point A (i.e. point at an intersection of the line of action of the concentrated load & outer fiber of the blank) as explained by [12];

$$ {M_{{friction}}} = \mu Qh $$
(10)

Replacing Eqs. 5 and 7 into Eq. 10 & simplifying;

$$ {M_{{friction}}} = \mu P\left( {1 - x\prime /a\prime } \right)\left( {1/\left( {1 + \mu \tan \theta } \right)\left( {x\prime \tan \theta - U\prime } \right)} \right. $$
(11)

In Eq. 11, replacing

$$ \matrix{<!--{*{20}{c}}--> {a\prime \approx a - {r_1}\sin \theta; \;U\prime \approx U - {r_1}\left( {1 - \cos \theta } \right);\;x\prime \approx x - {r_1}\sin \theta; } \hfill \cr {{M_{{friction}}} = \mu P(1 - \frac{{x - {r_1}\sin \theta }}{{a - {r_1}\sin \theta }})\;(\frac{1}{{1 + \mu \tan \theta }})\;(x * \tan \theta - {r_1}\left( {\sin \theta * \tan \theta + \cos \theta - 1} \right) - U)} \hfill \cr } $$
(12)

Bending moment considering friction & varying contact

If the effects of friction & varying contact are considered than the total bending moment can be presented by [12];

$$ {M_{{total}}} = {M_{{ext}}} + {M_{{friction}}} = Qg + \mu Qh $$
(13)

As the system of forces is symmetrical about the central vertical axis passing through the top roller the left hand side of the above equation will be multiplied by 2.

$$ 2{M_{{total}}} = {M_{{ext}}} + {M_{{friction}}} = Qg + \mu Qh $$
(13A)

Replacing Eq. 9 and 12 in Eq. 13A & simplifying;

$$ {M_{{total}}} = P/2\left( {1 - \frac{{x - {r_1}\sin \theta }}{{a - {r_1}\sin \theta }}} \right)\;\left( {\frac{1}{{1 + \mu \tan \theta }}} \right)\;\left[ {x - \tan \theta \left( {{r_1} - U} \right) + \mu \left\{ {x\tan \theta - {r_1}\left( {\sin \theta \tan \theta + \cos \theta - 1} \right) - U} \right\}} \right] $$
(14)

Internal bending moment

To calculate internal bending moment developed in the material due to deformation, consider an element of the plate along the length of the plate. The stress state in the element can be shown by the Fig. 3.

Fig. 3
figure 3

Stress state for elastic–plastic bending of plate

Full size image

Here the plate deformation through the plate thickness, caused by internal bending moment, at the top roll contact, can be divided into regions of a fully elastic zone, sandwiched between two elastoplastic zones as shown in Fig. 3a. This region is shown in Fig. 3b as ‘abc’ and ‘dfe’ are two elastoplastic zones [5]. The region ‘bf’ undergoes elastic deformation. This condition can be simplified by considering elastic region sandwiched between two plastic regions as shown in Fig. 3c. The figure shows stress variation along the thickness of the plate. yep is the thickness of the elastic region from the midplane along the thickness of the plate as shown in Fig. 3c.

For the static bending of the plate the Power law material behaviour is assumed in the plastic region. The bending moment can be split into an elastic contribution and plastic contribution and can be calculated from:

$$ \matrix{<!--{*{20}{c}}--> {{M_{{total}}} = {M_{{elastic}}} + {M_{{elastoplastic}}}} \hfill \cr {\quad \quad = 2\int {_{{elastic}}{\sigma_x}y\;dy} + 2\int {_{{elastoplastic}}{\sigma_x}y\;dy} } \hfill \cr } $$
(15)

As the torsion shear is neglected, the present case can be considered as plane strain deformation. Hill’s non-quadratic yield criteria [15] for plane strain deformation in plastic region for isotropic material is,

$$ {\sigma_x} = (2/\sqrt {3} )\bar{\sigma }\;and\;\bar{\varepsilon } = (2/\sqrt {3} ){\varepsilon_x}, $$

Also,

From this, \( {\sigma_x} = {(2/\sqrt {3} )^{{n + 1}}}K\;\varepsilon_x^n \) [12]

(Where, \( \bar{\sigma } \) is effective stress and \( \bar{\varepsilon } \) is effective strain)

For elastic region \( {\sigma_x} = {\varepsilon_x} * E, \) Considering plane strain bending, E is replaced by E′ and

\( E\prime = \frac{E}{{(1 - {\upsilon^2})}}, \) inserting the values of σ x and E′ in Eq. 15, we get,

$$ {M_{{total}}} = 2\int {_0^{{{y_{{ep}}}}}E\prime {\varepsilon_x}y\;dy} + 2\int {_{{{y_{{ep}}}}}^{{t/2}}{{(2/\sqrt {3} )}^{{n + 1}}}\;K\;\varepsilon_x^ny\;dy} $$
(16)

For the present case to evaluate \( \overline \varepsilon \) in terms of y, pure bending of beam is considered. For the case of pure bending of beams \( \frac{M}{I} = \frac{E}{R} = \frac{\sigma }{y} \)

Where M = bending moment, I = moment of intertia

From this it can be derived that \( {\varepsilon_x} = \frac{\sigma }{E} = \frac{y}{R}, \) inserting the value in Eq. 16 we get,

$$ \matrix{<!--{*{20}{c}}--> {{M_{{elastic}}} = 2\int {_0^{{{y_{{ep}}}}}E\prime \left( \;{y/R} \right)y\;dy} } \hfill \cr {{M_{{elastic}}} = 2\left[ {E\prime /R} \right][{\;y^3}/3]_0^{{{y_{{ep}}}}} } \hfill \cr {\quad \quad = \frac{2}{3}\left[ {E\prime /R} \right]\;y_{{ep}}^3} \hfill \cr } $$
(17)
$$ \matrix{<!--{*{20}{c}}--> {{M_{{elastoplastic}}} = 2\;\int {_{{{y_{{ep}}}}}^{{t/2}}{{(2/\sqrt {3} )}^{{n + 1}}}} \;K\;\varepsilon_x^ny\;dy} \hfill \cr {\quad \quad \quad = 2\;{{(2/\sqrt {3} )}^{{n + 1}}}\;K\int {_{{{y_{{ep}}}}}^{{t/2}}{{(y/R)}^n}y\;dy} } \hfill \cr { = 2\;{{(2/\sqrt {3} )}^{{n + 1}}}K{{\left( {1/R} \right)}^n}\left[ {{y^{{n + 2}}}/n + 2} \right]_{{{y_{{ep}}}}}^{{t/2}}} \hfill \cr = 2{(2/\sqrt {3} )^{{n + 1}}}K{\left( {1/R} \right)^n}\left[ {1/n + 2} \right]\left[ {{{\left( {t/2} \right)}^{{n + 2}}} - y_{{ep}}^{{n + 2}}} \right] \hfill \cr } $$
(18)
$$ \begin{gathered} {M_{{Total}}} = \frac{2}{3}\frac{{E\prime }}{R}y_{{ep}}^3 + {(2/\sqrt {3} )^{{n + 1}}}K{[\frac{1}{R}]^n}\left[ {\frac{1}{{n + 2}}} \right]\frac{{{t^{{n + 2}}}}}{{{2^{{n + 1}}}}} - 2{(2/\sqrt {3} )^{{n + 1}}}K\;{[\frac{1}{R}]^n}\left[ {\frac{1}{{n + 2}}} \right]y_{{ep}}^{{n + 2}} \hfill \cr \end{gathered} $$
(19)
$$ {M_{{Total}}} = \frac{2}{3} \frac{{E'}}{R} y_{{ep}}^3 + {( \frac{2}{{\sqrt {3} }} )^{{n + 1}}}K {[\frac{1}{R}]^n}\left[ {\frac{1}{{n + 2}}} \right]\frac{{{t^{{n + 2}}}}}{{{2^{{n + 1}}}}} - 2{( \frac{2}{{\sqrt {3} }} )^{{n + 1}}}K {[\frac{1}{R}]^n}\left[ {\frac{1}{{n + 2}}} \right]y_{{ep}}^{{n + 2}} $$
(20)

The strain ε along the axis passing through the mid-plane of the sheet along the length is determined by the relation given by Nepershin [16],

$$ \varepsilon = {\varepsilon_0} + \chi \;y $$
(21)

Where, ε0 is the strain of the strip mid-line & χ is curvature of the bend plate between the bottom rollers.

For an elsatoplastic model of the strip with stress σ less than the yield strength σs, the dependence of σ on ε is determined by the Hooke’s law

$$ \sigma = E\;\varepsilon, \left| \varepsilon \right| < \frac{1}{{E * }} = \varepsilon *, $$
(22)

where ε* is strain at yield point and E* is the ratio of modulus of elasticity to σs.

From above Eqs. 21 and 22, elastoplatic boundaries y 1 and y 2 in the extension and compression regions can be found out for \( \varepsilon = \pm \varepsilon * \)& the thickness \( {t_e} = {y_1} - {y_2} \) of the elastic layer;

$$ \matrix{<!--{*{20}{c}}--> {{y_1} = \frac{1}{\chi }(\frac{1}{{E * }} - {\varepsilon_0}),\;{y_2} = \frac{1}{\chi }\left( {\frac{1}{{E * }} + {\varepsilon_0}} \right),\;{t_e} = \frac{2}{{E * \chi }}} \hfill \cr {\therefore {y_{{ep}}} = {t_e}/2 = 1/E * \chi } \hfill \cr }, $$
(23)

Expression for bending load P

Equating Eqs. 14 & 20, and rearranging,

$$\begin{array}{*{20}{c}} {{M_{{Total}}} = \frac{2}{3}\frac{{E\prime }}{R}y_{{ep}}^3 + {{(2/\sqrt {3} )}^{{n + 1}}}K\;{{[\frac{1}{R}]}^n}\left[ {\frac{1}{{n + 2}}} \right]\frac{{{t^{{n + 2}}}}}{{{2^{{n + 1}}}}} - 2{{(2/\sqrt {3} )}^{{n + 1}}}K\;{{[\frac{1}{R}]}^n}\left[ {\frac{1}{{n + 2}}} \right]y_{{ep}}^{{n + 2}}} \hfill \\ { = P/2\left( {1 - \frac{{x - {r_1}\sin \theta }}{{a - {r_1}\sin \theta }}} \right)\left( {\frac{1}{{1 + \mu \tan \theta }}} \right)\left[ {x - \tan \theta \left( {{r_1} - U} \right) + \mu \left\{ {x\tan \theta - {r_1}\left( {\sin \theta \tan \theta + \cos \theta - 1} \right) - U} \right\}} \right]} \hfill \\ {P = \frac{{\frac{4}{3}\frac{{E\prime }}{R}y_{{ep}}^3 + {F^{{n + 1}}}K{{\left[ {1/R} \right]}^n}\left[ {1/n + 2} \right]\frac{{{t^{{n + 2}}}}}{2} - 4{F^{{n + 1}}}K{{\left[ {1/R} \right]}^n}\left[ {1/n + 2} \right]y_{{ep}}^{{n + 2}}}}{{\left( {1 - \frac{{x - {r_1}\sin \theta }}{{a - {r_1}\sin \theta }}} \right)\left( {\frac{1}{{1 + \mu \tan \theta }}} \right)\left[ {x - \tan \theta \left( {{r_1} - U} \right) + \mu \left\{ {x\tan \theta - {r_1}\left( {\sin \theta \tan \theta + \cos \theta - 1} \right) - U} \right\}} \right]}}} \hfill \\ \end{array} $$
(24)

Assuming constant radius of curvature, χ = 1/R and Substituting \( {y_{{ep}}} = \frac{1}{{E * \chi }} = \frac{R}{{E * }} \) from Eq. 23, in Eq. 24,

$$ \matrix{<!--{*{20}{c}}--> {P = \frac{{\frac{4}{3}\frac{{E\prime }}{R}{{[\frac{R}{{E * }}]}^3} + {{(2/\sqrt {3} )}^{{n + 1}}}K{{\left[ {1/R} \right]}^n}\left[ {1/n + 2} \right]\frac{{{t^{{n + 2}}}}}{{{2^n}}} - 4{{(2/\sqrt {3} )}^{{n + 1}}}K{{\left[ {1/R} \right]}^n}\left[ {1/n + 2} \right]{{[\frac{R}{{E * }}]}^{{n + 2}}}}}{{\left( {1 - \frac{{x - {r_1}\sin \theta }}{{a - {r_1}\sin \theta }}} \right)\left( {\frac{1}{{\cos \theta + \mu \sin \theta }}} \right)(x - tan\theta \left( {{r_1} - U} \right) + \mu (x * tan\theta - {r_1}\left( {sin\theta * tan\theta + cos\theta - 1} \right) - U))}}} \cr {P = \frac{{\frac{4}{3}\frac{{E\prime }}{{E{ *^3}}}{R^2} + {{(2/\sqrt {3} )}^{{n + 1}}}K{{\left[ {1/R} \right]}^n}\left[ {1/n + 2} \right]\frac{{{t^{{n + 2}}}}}{{{2^n}}} - 4{{(2/\sqrt {3} )}^{{n + 1}}}K\frac{{{R^2}}}{{\left( {n + 2} \right)E{ *^{{n + 2}}}}}}}{{\left( {1 - \frac{{x - {r_1}\sin \theta }}{{a - {r_1}\sin \theta }}} \right)\left( {\frac{1}{{\cos \theta + \mu \sin \theta }}} \right)(x - tan\theta \left( {{r_1} - U} \right) + \mu (x * tan\theta - {r_1}\left( {sin\theta * tan\theta + cos\theta - 1} \right) - U))}}} \cr } $$

Substitute value of E*

$$ P = \frac{{\frac{4}{3}\frac{{{R^2}}}{{{E^2}(1 - {\upsilon^2})}}\sigma_y^3 + {{(2/\sqrt {3} )}^{{n + 1}}}K{{\left[ {1/R} \right]}^n}\left[ {1/n + 2} \right]\frac{{{t^{{n + 2}}}}}{{{2^n}}} - 4{{(2/\sqrt {3} )}^{{n + 1}}}K\frac{{{R^2}}}{{\left( {n + 2} \right){E^{{n + 2}}}}}\sigma_y^{{n + 2}}}}{{\left( {1 - \frac{{x - {r_1}\sin \theta }}{{a - {r_1}\sin \theta }}} \right)\left( {\frac{1}{{\cos \theta + \mu \sin \theta }}} \right)(x - tan\theta \left( {{r_1} - U} \right) + \mu (x*tan\theta - {r_1}\left( {sin\theta * tan\theta + cos\theta - 1} \right) - U))}} $$
(25)

In Eq. 25, there is no term which directly represents the bottom roller inclination. But bottom roller inclination is indirectly incorporated as bottom roller inclination can be considered by bending radius at front end and rear end. When bottom rollers are inclined in the horizontal plane bending radius at front end will be smaller while it will have higher value at rear end as can be seen in Fig. 1. So from the value of bottom roller inclination bending radius at front end and rear end can be calculated and vice versa. The relation between rolling radius and bottom roller inclination is given in Equation 26 [12]. If bottom roller inclination is zero than both the radius will be same, with no top roller inclination, this condition can be called as cylindrical bending.

$$ \beta = {\tan^{{ - 1}}}\left[ {\left( {\frac{{{A_R} - {A_F}}}{2}} \right)\;\left( {\frac{1}{{\cos \alpha }}} \right)\;\left( {\frac{{\sin \varphi /2}}{{{R_R} - {R_F}}}} \right)} \right] $$
(26)

Where,

β:

bottom roller inclination

AF, AR :

Center distance between bottom rollers at front and rear end respectively

α:

top roller inclination, in the present case it is zero

φ:

Cone angle

RF, RR :

Bending radius at the front end and rear end respectively

To get the value of P i.e. top roller load, from the above equation 25 along with the material properties and geometrical parameters of the machine setting, the value of coefficient of friction μ at roller plate interface is required. Value of angle θ can be calculated from the geometrical configurations of the machine setting.

To study the effect of various parameters, variation of bending load P has been plotted for different parameters, keeping all other parameters constant.

Analytical results

Based on the Eq. 25, derived earlier, study of effect of various parameters on bending load has been carried out. The ranges of the parameters taken are as follows:

  • Range of n = 0.1 to 1 in steps of 0.1 (Typical range for any metal plates)

  • Range of variation of μ = 0.05 to 2 in steps of 0.05 (Typical range for any roller-blank material combinations)

  • Plate thickness t = 6, 8, 10, 12, 14. (Based on the availability of the plates in the market)

  • Range of variation of σy = 200 to 1,200 in steps of 10 (Typical range for any metal plates)

  • Range of variation of K = 500 to 1,500 in steps of 10 (Typical range for any metal plates)

To get the values of P for different bottom roller inclinations, values of bending radius at various bottom roller inclinations are taken. For designation of radius of curvature following nomenclatures have been adopted:

C1R:

Case 1 when cylindrical bending is being done at radius 696 mm.

C2RL:

Case 2 when conical bending is being done and the radius at larger end is 780 mm.

C3RL:

Case 3 when conical bending is being done and the radius at larger end is 869 mm.

C4RL:

Case 4 when conical bending is being done and the radius at larger end is 963 mm.

C5RL:

Case 5 when conical bending is being done and the radius at larger end is 1,060 mm.

Here the radius at larger end is considered. It can also be done using radius at smaller end.

The values of radius of curvature have been selected from previously published literature, (A. H. Gandhi, 2010)

  • Top roller inclination is zero.

  • β is bottom roller inclination.

Effect of plate thickness on bending force

To study the effect of plate thickness on bending load for different values of coefficient of friction, graphs for variation of bending load with respect to (w.r.t.) coefficient of friction for different thickness, taking bending radius as constant are plotted as shown in Fig. 4.

Fig. 4
figure 4

Variation of Bending load P, w.r.t. μ, for different thickness, at same radius of curvature

Full size image

From the Fig. 4 above it can be observed that:

Bending force increases as the thickness increases which is very common observation.

The rate of increase of bending load w.r.t. μ, increases as the thickness increases for the same radius of curvature. It indicates that for the same radius of curvature the bending load is more sensitive to the coefficient of friction μ.

Effect of coefficient of friction on bending load

To study the effect of variation of friction coefficient of friction on the bending force, plot for variation of bending load w.r.t. coefficient of friction μ for each thickness as shown below:

From Fig. 5 above it can be observed that:

Fig. 5
figure 5

Variation of Bending load P, w.r.t. to μ, for different radius of curvature for the same thickness

Full size image

As thickness increases bending force required increases as can be seen from the above graphs. As bend radius R increases, i.e. as we move from front end to rear end in Fig. 1, bending moment required will be less. Hence the bending force required will also reduce as the bend radius increase. The same can be observed in the graphs in Fig. 5. As the radius of curvature R increases from 696 mm to 1,060 mm for all the thicknesses, the bending load decreases.

As μ increases for the same thickness plate, rate of increase of bending force increases with increase in bending radius. Again it indicates that for the same thickness plate bending force is more sensitive to the coefficient of friction μ. It is because as the friction between the roller and plate is increased the roller will hold the plate firmly which will increase the required bending force.

Effect of dimensionless ratio, yield stress by strength coefficient (σy/K)

To study the effect of limiting yield stress σy and the strength coefficient K on the bending force, dimension less ratio σy/K is taken as a parameter. First plot of bending load v/s σy with the ratio σy/K as one parameter is plotted as shown in figure:

From the Fig. 6 following observations can be made:

Fig. 6
figure 6

Variation of Bending load P, w.r.t. σy, for different values of dimensionless ratio σy/K for same thickness

Full size image

It can be observed that for the same plate thickness as the ratio of σy/K increases from 0.4 to 0.8 the slope of the bending load curve with respect to σy, decreases. Also the curvature of the bending load curve increases as the ratio increases for the same thickness of plate as can be observed in the figure.

For σy/K = 0.4, bending load varies linearly w.r.t. σy, irrespective of the plate thickness. It indicates that bending load is directly proportional to σy, if the ratio σy/K is kept 0.4.

As the thickness increases the curvature of the bending load curve w.r.t. σy increases for the values of σy/K more than 0.4. It indicates that as the ratio σy/K increases from 0.4 bending force non-linearly varies w.r.t. σy.

To study the effect of strength coefficient K on the bending load, plot of bending load v/s K is plotted with σy/K as one parameter as shown in figure:

From the Fig. 7 following observations can be made:

Fig. 7
figure 7

Variation of Bending load P, w.r.t. K, for different values of dimensionless ratio σy/K for same thickness. Bottom roller inclination β = 1.860. Bottom roller inclination β = 5.560

Full size image

For the same thickness as the ratio σy/K increases, the curvature of the bending load curve w.r.t. K increases. For the values of σy/K = 0.8 it almost becomes linear. It indicates that for the higher values of the ratio σy/K, the non-linearity in bending force variation w.r.t. K decreases.

For lesser value of K, bending force is same irrespective of the ratio σy/K, for the same thickness. It indicates that for lesser values of K, the ratio σy/K do not affect the bending force for the same thickness.

As the thickness increases the bending ratio curves w.r.t. K, comes closer. The slope of the linear curve at the ratio σy/K = 0.8 increases, as the thickness of the plate increases. It indicates that for higher plate thickness the bending force is more sensitive to the strength coefficient K, for higher values of the ratio σy/K.

Effect of bottom roller inclination β on bending load

Bottom roller inclination can be varied be varying the center distance between the roller bearings as explained earlier. As the bottom roller inclination β is increased the difference between bend radius at smaller end and larger end increases. In order to study the effect of β on bending load, variation of bending load has been plotted for different values of β as below for thickness t = 14 mm:

It can be observed from the Fig. 8 that as the bottom roller inclination increases the difference in the bending load at smaller end and larger end of the rollers increases.

Fig. 8
figure 8

Variation of Bending load P, w.r.t. to μ, for different bottom roller inclination and constant thickness

Full size image

If bottom roller inclination β is smaller there will be less difference in the radii at the roller ends, which in turn suggest that there will be less difference in the reaction forces on the roller. If β is larger there will be large difference in the radii at the roller ends and the force at the smaller end will be much larger that the force at the larger end as can be seen from Fig. 8.

Conclusions

Analytical model for prediction of bending force have been developed by equating external bending moment and plate internal bending moment. Plots for variation of bending forces have been plotted using various parameters involved in the bending process and their effects on the bending forces have been studied. Following conclusions can be made from the observations:

The bending force increases as the thickness increases which is obvious fact that it will require higher force for bending the thicker plate. Also the sensitivity of the bending force to coefficient of friction, increases as the radius of the bend increases, as it has been observed in Figs. 4 & 5.

For the same thickness, bending force is linearly proportional to μ for the same bending radius as shown in Fig. 5. It is also observed that as the bend radius increases, required bending force decreases for same value of coefficient of friction. It suggests that bend with larger radius can be produced with less efforts.

For a particular combination of the material and other geometrical parameters the roller-plate interface friction coefficient can be evaluated if the experimental value of the required bending force is available for that combination from the developed analytical model.

For lower values of the dimensionless ratio σy/K, bending force is linearly proportional to σy. But as this dimensionless ratio increases the bending force varies non-linearly with respect to σy.

It is also observed that for the higher values of the ratio σy/K, the non-linearity in bending force variation w.r.t. K decreases. It is also observed that for higher plate thickness the bending force is more sensitive to the strength coefficient K, for higher values of the ratio σy/K.

If bottom roller inclination β is smaller there will be less difference in the radii at the roller ends, which in turn suggest that there will be less difference in the reaction forces on the roller. If β is larger there will be large difference in the radii at the roller ends and the force at the smaller end will be much larger that the force at the larger end as can be seen from Fig. 8.

In the present analysis shear forces were neglected while deriving the internal bending moment considering plane strain bending. Shear forces can be included by using proper material and bending model to increase the accuracy of the bending load prediction.

It was assumed during the external moment calculation that the bend radius of the plate is constant throughout the length of the plate. In actual practice it is not the case. The curvature of the plate varies along the length. So there are scopes of further modifications of the developed model by considering different functions for the varying radius of curvature.

In the present case instantaneous radius of the bent plate is considered to avoid the complexity of the transient analysis of the problem. Only static case is considered in the derivation of the prediction model. The prediction model can be further enhanced by doing the transient analysis through FEM and/or any other theoretical method as suggested by the reviewer.