Forces and coefficient of friction during cylindrical three roller bending

Abstract

Three roller bending process is one of the processes of forming cylindrical shells, for manufacturing drums, pressure vessels, windmill towers, etc. During the bending process, forces on the rollers must not exceed their bending capacity. Along with operational and material parameters, the forces exerted during bending and power consumption are affected by the coefficient of friction at the roller-plate interface. It is difficult to determine the coefficient of friction practically during three roller bending process. An attempt is made to determine the forces and friction coefficient at each roller–plate interface, through derived mathematical model, using experimental results. The variation of coefficient of friction under the higher loading conditions was also determined as a case study. With the present mathematical formulation along with the coefficient of friction, the forces at each roller–plate interface could be determined more precisely. The determination of forces and friction coefficient helps in deciding operational and design parameters of the bending machine, respectively.

1 Introduction

Cylindrical shells for the large components, such as the drums, pressure vessels, and many others, can be formed by plastically deforming the plate to the required dimension using three roller bending process. The process includes two rollers at the bottom positioned at fixed span between them and a top roller with its centre at the mid of the span. For bending, the plate is placed between the bottom and the top rollers. After resting, the plate on the bottom roller, the top roller is moved against the plate to the required displacement. This completes the static bending. After static bending, the bottom rollers are rotated in the same direction at the constant rotational speed. Due to friction at the roller–plate interface, the plate gets driven across the rollers. The bottom rollers are rotated till the required length of the plate passes through the roller. As plate passes through rollers, it gets deformed continuously due to bending. Hence, this stage is termed as dynamic bending. In dynamic bending, required length of the plate is deformed to obtain cylindrical shell.

Curvature variation of the plate across the rollers during three roller cylindrical bending was discussed by Yang and Shima [1]. A model was reported [2, 3] for three roller bending to predict the position of the top roller, for the required curvature. In this reported model, the radius of curvature was assumed to be constant throughout bending operation, to simplify the model. In fact, the radius of the plate varies as plate moves through roller in actual bending operation, the effect of which was not accounted in this reported model. Chudasama and Raval [4, 5] reported a model for prediction of the static and dynamic forces, during three roller bending. The model was derived by comparing the internal bending moment and the external bending moment. Internal bending moment was derived through the power law material constitutive equation, while the external bending moment was derived considering similar assumption of constant bend radius to simplify mathematical calculation, leading to equal forces at bottom rollers, unlike in an actual condition. It was found from the reported model that the bending forces increases with increase in the thickness [4]. Assuming the coefficient of friction at each roller-plate interface as constant, finite-element analyses (FEA) were also reported in the literatures for three roller bending [6,7,8,9]. Kagzi and Raval [8, 9] through reported simulation explained the change in curvature of the plate as well as studied static and dynamic forces during three roller bending. They reported that the forces [8, 9] and power [9] increase with increase in thickness of the plate. They [8] explained the effect of directions of the frictional forces acting on the rollers, on the resultant static as well as dynamic bending forces. However, in the reported simulations [6,7,8,9], the effect of the forces on coefficient of friction was not addressed, rather coefficient of friction between each roller–plate interface was assumed to be constant.

In the reported analytical as well as FEA models, the coefficient of friction (CF) was assumed to be constant for all the contacts between the plate and the rollers. The analytical models [3,4,5] were reported under the assumption that the plate is having constant curvature when it is loaded under static as well as dynamic bending. Under this assumption, the radius of curvature was taken as the radius of the circle, which is tangent to the three rollers, as shown in Fig. 1. Therefore, unlike the real condition, with this assumption, the contact angles obtained at both the bottom rollers are equal. This results in the dynamic forces being calculated at both the bottom rollers to be equal. Moreover, in reported literatures [3,4,5,6,7,8,9], assume the value of coefficient of friction at roller–plate interfaces, unlike the real condition where the CF depends on the forces at the interface.

Fig. 1

Illustrative diagram of pyramid type three roller bending process

It is very difficult to practically determine CF at each roller–plate interface during bending operation. Therefore, it is felt necessary to evaluate CF indirectly through mathematical formulation. With the reported model, the forces as well as CF at each roller–plate interface could be evaluated precisely, during bending operation. The result obtained can be used for the determination of forces and power for bending of plate on similar setup. The reported methodology can be applied on the other types of bending process such as asymmetrical three roller bending. In the present study, different geometries of the plate are considered at the entry and at the exit sides. The modified plate geometry is shown in Fig. 1. With this variation in plate geometry, the shifting of contact point at the bottom rollers as well as the top rollers could be obtained for the dynamic bending. Therefore, the contact angle at each roller-plate contact and corresponding coefficient of friction (CF) can be precisely evaluated, unlike the reported work where CF at each roller is considered as constant. Thus, the work represents more realistic approach as compared to assumption of constant bend radius made in the reported literatures. The CF is considered to be the ratio of the tangential force to the normal force at the point of contact, as per Amonton–Coulomb model of friction (Eq. 1).

$$\mu = \frac{{F_{\text{tangential}} }}{{F_{\text{normal}} }}.$$

(1)

From the mechanics of forces and equilibrium conditions, the model was developed to calculate the CF, iteratively. Experiments of cylindrical bending were performed for different thicknesses. Using the experimental results and the developed model, the CF at each roller–plate interface were evaluated. The experimentation performed for the cylindrical bending is discussed in the following section. Later, the mathematical model including mechanics of forces and bending moment is discussed followed by the discussion of simultaneous effect of the force and power on CF as a case study.

2 Experimentation

2.1 Description of experimentation

The schematic diagram (Fig. 1) shows the dimensions for the span of the bottom rollers and the top roller displacement during the experimentation carried out for the cylindrical bending. The span and the top roller displacement was kept as the same for all experiments. The cylindrical bending performed on the three roller bending machine is shown in Fig. 2a. The span between the bottoms rollers was maintained with the help of spacers placed between the bearing blocks of the roller, as shown in Fig. 2a.

Fig. 2

a Plate being bent during bending operation. b Schematic diagram of arrangements for measuring force and power

Plate was placed between the rollers and the top roller was given the required displacement manually against the plate, for static bending. For performing dynamic bending, the bottom rollers were rotated in same direction at fixed rotational speed with the help of electric motor attached to the shaft of the bottom rollers, as shown in Fig. 2b. The load-cells were placed vertically on the bearing blocks at the front and the rear ends of the top roller (Fig. 2a, b), for the measurement of bending force. The vertical movement of the top roller was measured with the help of the scale on the top roller as well as LVDT placed at the bottom of the plate. The top roller was kept free to rotate with the motion of the plate. Both the bottom rollers were connected with the independent motors to drive the rollers individually at the constant rotation. Each motor, at the entry and the exit side, was connected with power meter, to measure the power consumed at the entry side (p_e) and that at the exit side (p_x) individually, during the dynamic bending operation. The schematic diagram for the forces and power measurement is shown in Fig. 2b.

The bending was carried out for the plates of same grade of structural steel (IS2062FE440 W [10]) with different thicknesses (t = 8, 10, 12 mm). The strength of the plates was determined by performing the tensile test. Three specimens from plate of each thickness were cut along the rolling direction of the plate and tested as per standard [11]. The mean values of the properties were taken into consideration in the present study. The plate materials are of same grade but from the different batch. Therefore, plate material shows some variation in properties with respect to thickness. Table 1 represents the mean values of material properties for each thickness. Here, σ_y, K, and n are the yield strength, strength coefficient, and strain-hardening exponent, respectively. It can be seen that the deviation in material properties (σ_y, K, and n) is less than seven percentage of its mean value.

Table 1 Material properties of the plate used for the experimentation

For cylindrical bending, the blank must be of rectangular shape of required width and length corresponding to the perimeter of cylinder to be formed. As the bending forces were to be measured, only the part of the cylinder is sufficient to be deformed, instead of the complete cylinder. Therefore, the length of plates of each thickness was kept as 1200 mm. Limiting the length of the plates had reduced the cost of the blanks used for experimentations. To maintain the plane strain condition, the width of the plate must be sufficiently higher than the thickness of a plate [12]. In the present study, the width of the plate of each thickness was kept as 300 mm. The plate before cylindrical bending (t = 8 mm) with the above-mentioned dimensions is shown in Fig. 3a. The deformed plates of each thickness obtained after the bending operation are as shown in Fig. 3b. The force and power measurement during bending of these plates of different thickness is discussed in the following section.

Fig. 3

a Initial geometry of the plate of thickness 8 mm. b Deformed geometry of each plate after bending

2.2 Responses measured during experimentation

As discussed earlier, during bending operation, power at each roller was measured with the help of power meter connected to motor. Power consumed at the bottom rollers on the entry and the exit side (p_e and p_x, respectively) measured during dynamic bending process, for the different plate thickness, is as shown in Fig. 4. The power consumed by the bottom rollers increases with the increase in the thickness of the plate. In addition, the power at the entry side is higher than the power at the exit side. It was observed that the power p_x is on average 86% of the power p_e, as the bottom roller at entry side drives the top roller and partly the plate across the rollers. The bottom roller at the exit side consumes the remaining fraction of the total power to drive plate out of the machine.

Fig. 4

Forces and power measured during experimentation for different thickness

As the load-cells are placed vertically at front and rear end (Fig. 2a, b) of the top roller, they measure the vertical components of the force exerted at their respective sides. Therefore, the summation of the forces measured by these front and rear load-cells is taken as the total vertical component of force (V_t). The vertical force (V_t) measured during the experimentation is as shown in Fig. 4. The bending resistance increases with the thickness of plate; therefore, the vertical force also increases with thickness of the plate. The measured data are used for evaluating CF by means of the model described in following section.

3 Bending mechanics

3.1 The contact angles at the entry and the exit side

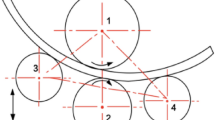
The angle made by the normal at the point of contact (between roller and plate) with the vertical is termed as the contact angle. In the present work, θ_e and θ_x are considered as the contact angles made by two different plate geometries at entry and exit sides, respectively. The curvature of plate is almost zero at the entry side. Hence, the contact point at the bottom roller towards the entry side was considered to be the point of contact made by the bottom roller at the entry and the line tangent to the top roller and the bottom roller at the entry side. Similarly, the contact point at exit is the point of contact made by the bottom roller at the exit with the circle tangent to the top roller, the bottom roller at the exit, and the line (considered earlier) tangent to the top roller and the bottom roller at the entry side. The contact point at the entry and the exit side is as shown in Fig. 1. The contact angles θ_e and θ_x are fixed by the geometry of the plate, while contact angle θ_t is calculated iteratively as discussed in successive sections. Thus, in present case, shifting of the contact point under the dynamic bending condition at the bottom rollers as well as the top roller is taken into account. The shift of contact point occurring at the rollers and contact angles (θ_t, θ_e, and θ_x) during bending is as shown in Figs. 1 and 5.

Fig. 5

Mechanics of forces acting on the rollers

3.2 Equilibrium of forces

Two forces are acting on each roller, the normal force at the contact and the tangential force, due to the friction. The resultant of these two forces can be divided into the horizontal component (H) and vertical component (V), as shown in Fig. 5. Equations (2–7) show the expression for horizontal and vertical components of the resultant forces. Where, normal forces acting on the bottom roller at the entry side, the bottom roller at the exit side, and the top roller are designated as J, Q, and P, respectively:

$$H_{e} = J\left( {\sin \theta_{\text{e}} + \mu_{\text{e}} \cdot \cos \theta_{\text{e}} } \right)$$

(2)

$$V_{\text{e}} = J\left( {\cos \theta_{\text{e}} - \mu_{\text{e}} \cdot \sin \theta_{\text{e}} } \right)$$

(3)

$$H_{\text{x}} = - Q\left( {\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} } \right)$$

(4)

$$V_{\text{x}} = Q\left( {\cos \theta_{\text{x}} + \mu_{\text{x}} \cdot \sin \theta_{\text{x}} } \right)$$

(5)

$$H_{\text{t}} = - P\left( {\sin \theta_{\text{t}} - \mu_{\text{t}} \cdot \cos \theta_{\text{t}} } \right)$$

(6)

$$V_{\text{t}} = - P\left( {\cos \theta_{\text{t}} + \mu_{\text{t}} \cdot \sin \theta_{\text{t}} } \right).$$

(7)

As the contact point at top roller shifts towards the entry side, the horizontal component can be equated as shown in the following equation:

$$H_{\text{e}} + H_{\text{x}} + H_{\text{t}} = 0.$$

(8)

Substituting Eqs. (2) and (4) in Eq. (8), it gives:

$$Q = J\left( {\frac{{\sin \theta_{\text{e}} + \mu_{\text{e}} \cdot \cos \theta_{\text{e}} }}{{\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} }}} \right) - \frac{{H_{\text{t}} }}{{\left( {\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} } \right)}}.$$

(9)

Along with the vertical bending force V _t , there also exists the vertical force due to weight of the roller and plate. Thus, the weight of top roller and plate first get overcome and then bending force is exerted on the top roller. Let the weight the plate be W, then equating vertical components of forces will give the following equation:

$$V_{\text{e}} + V_{\text{x}} = - V_{\text{t}} + W = V.$$

(10)

Using Eqs. (3) and (5), the left-hand side of the Eq. (10) gives:

$$V = J\left( {\cos \theta_{\text{e}} - \mu_{\text{e}} \cdot \sin \theta_{\text{e}} } \right) + Q\left( {\cos \theta_{\text{x}} + \mu_{\text{x}} \cdot \sin \theta_{\text{x}} } \right).$$

(11)

From Eqs. (9) and (11), it yields

$$V = J\left( {\cos \theta_{\text{e}} - \mu_{\text{e}} \cdot \sin \theta_{\text{e}} } \right) + \left( {J\left( {\frac{{\sin \theta_{\text{e}} + \mu_{\text{e}} \cdot \cos \theta_{\text{e}} }}{{\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} }}} \right) - \frac{{H_{t} }}{{\left( {\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} } \right)}}} \right) \cdot \left( {\cos \theta_{\text{x}} + \mu_{\text{x}} \cdot \sin \theta_{\text{x}} } \right).$$

(12)

The above equation (Eq. 12) can be simplified as shown in the following equation:

$$V = V_{\text{e}} + V_{\text{x}} = \frac{{JC_{\text{b}} }}{{\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} }} - H_{\text{t}} \left( {\frac{{\cos \theta_{\text{x}} + \mu_{\text{x}} \cdot \sin \theta_{\text{x}} }}{{\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} }}} \right) ,$$

(13)

where $C_{\text{b}} = \left( {1 + \mu_{\text{e}} \mu_{\text{x}} } \right) \cdot \sin \left( {\theta_{\text{e}} + \theta_{\text{x}} } \right) + \left( {\mu_{\text{e}} - \mu_{\text{x}} } \right) \cdot \cos \left( {\theta_{\text{e}} + \theta_{\text{x}} } \right).$

From Eqs. (10) and (13), one can obtain the following equation:

$$J = \frac{1}{{C_{\text{b}} }}\left( {C_{\text{e}} + W\left( {\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} } \right)} \right) ,$$

(14)

where

$$C_{\text{e}} = \left( {V_{\text{t}} \left( {\sin \theta_{\text{x}} - \mu_{\text{x}} \cdot \cos \theta_{\text{x}} } \right) + H_{\text{t}} \left( {\cos \theta_{\text{x}} + \mu_{\text{x}} \cdot \sin \theta_{\text{x}} } \right)} \right).$$

(15)

Considering Eqs. (6) and (7), Eq. (15) can be further simplified as follows:

$$C_{\text{e}} = P \cdot \left( {\left( {1 - \mu_{\text{t}} \mu_{\text{x}} } \right) \cdot \sin \left( {\theta_{\text{t}} + \theta_{\text{x}} } \right) - \left( {\mu_{\text{t}} + \mu_{\text{x}} } \right) \cdot \cos \left( {\theta_{\text{t}} + \theta_{\text{x}} } \right)} \right).$$

(16)

Thus, the normal force on the bottom roller on the entry side (J) can be derived as a function of contact angles, CF, and top roller force (P). Similarly, the equation of normal force for the bottom roller at the exit (Q) can be obtained, as shown in the following equation:

$$Q = \frac{1}{{C_{\text{b}} }}\left( {C_{\text{x}} + W\left( {\sin \theta_{\text{e}} + \mu_{\text{e}} \cdot \cos \theta_{\text{e}} } \right)} \right) ,$$

(17)

where

$$C_{\text{x}} = P \cdot \left( {\left( {1 - \mu_{\text{e}} \mu_{\text{t}} } \right) \cdot \sin \left( {\theta_{\text{e}} - \theta_{\text{t}} } \right) + \left( {\mu_{\text{e}} + \mu_{\text{t}} } \right) \cdot \cos \left( {\theta_{\text{e}} - \theta_{\text{t}} } \right)} \right).$$

(18)

While, following the algorithm discussed in successive section, the value of normal load (Q) at the exit side obtained from Eq. (17) must be same as that of Eq. (9). This provides check in iterative calculation. Load (W) being very small as compared to P, for the simplicity, it is neglected in present evaluation.

3.3 Evaluation of bending moment

The moment of the forces at the bottom rollers, about the contact point of the top roller, can be obtained from the product of the components of the forces and their corresponding perpendicular distance from the contact point. Top roller displacement (U) is considered from the reference point, on the bottom side of the plate at the mid of the span, as shown in Fig. 6. This is because the bottom surface of plate initially rests on the bottom rollers making contact angle equal to zero degree at each roller. At this position, the U is zero. The horizontal and the vertical distances of the contact points from their centre of the rollers are shown in Fig. 6, where a is the span of the bottom rollers. From Fig. 6, following Eqs. (19–24) can be derived as follows:

$$y_{\text{e}} = r_{\text{b}} \cdot \left( {1 - \cos \theta_{\text{e}} } \right)$$

(19)

$$x_{\text{e}} = r_{\text{b}} \cdot \sin \theta_{\text{e}}$$

(20)

$$y_{\text{x}} = r_{\text{b}} \cdot \left( {1 - \cos \theta_{\text{x}} } \right)$$

(21)

$$x_{\text{x}} = r_{\text{b}} \cdot \sin \theta_{\text{x}}$$

(22)

$$y_{\text{t}} = r_{\text{t}} \cdot \left( {1 - \cos \theta_{\text{t}} } \right) + t$$

(23)

$$x_{\text{t}} = r_{\text{t}} \cdot \sin \theta_{\text{t}} .$$

(24)

Fig. 6

Horizontal and vertical distances of point of contacts from centre

The perpendicular distance, of the top roller contact from the corresponding force component (horizontal or vertical), is equivalent to the corresponding perpendicular distance of its point of action from the contact point at the top roller. The perpendicular distance of the horizontal forces of the bottom rollers from the point of contact of the top roller is given by the following equation:

$$u_{\text{e}} = U - \left( {y_{\text{t}} + y_{\text{e}} } \right)\,{\text{and}}\,u_{\text{x}} = U - \left( {y_{\text{t}} + y_{\text{x}} } \right).$$

(25)

Similarly, the perpendicular distance of the vertical forces at the bottom rollers from the point of contact of the top roller is given by the following equation:

$$a_{\text{e}} = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0pt} 2} - \left( {x_{\text{t}} + x_{\text{e}} } \right)\,{\text{and}}\,a_{\text{x}} = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0pt} 2} - \left( {x_{\text{x}} - x_{\text{t}} } \right).$$

(26)

Thus, the bending moment of the resultant force at the bottom roller on the entry side about the contact point of the top roller can be written as shown in Eq. (27). Similarly, for the bottom roller at the exit, the bending moment is given by Eq. (28).

$$M_{\text{e}} = H_{\text{e}} \cdot u_{\text{e}} + V_{\text{e}} \cdot a_{\text{e}}$$

(27)

$$M_{{_{\text{x}} }} = H_{\text{x}} \cdot u_{{_{\text{x}} }} + V_{\text{x}} \cdot a_{\text{x}} .$$

(28)

The bending moment of the forces at the bottom rollers about the contact point of top roller must be equal (Yang and Shima [1]), and hence, at the contact point of the top roller, Eq. (29) must satisfy:

$$M_{\text{x}} = M_{\text{e}} .$$

(29)

In the present calculation, to have a top roller contact point at which the bending moment at the entry and that at the exit are equal (Eq. 29), the contact angle θ_t is varied iteratively.

3.4 Relation between the measured power and coefficient of friction (CF)

During bending, the motor at the entry side consumes power (p_e), which is required to drive the shafts of the top, the respective bottom roller due to their inertia, and the fraction of power (x) for driving the plate (Eq. 30a). Similarly, the motor at the exit side consumes power (p_x) to drive the respective bottom roller shaft due to inertia and remaining fraction of power (1 − x) to drive the plate (Eq. 30b). The total power measured (p_e + p_x) during the bending of the plate (Eq. 30c) must be the summation of the power required to drive the shaft of the top roller (p_t), the bottom rollers (p_e-shaft and p_x-shaft) due to inertia, and the power consumed in bending and driving plate across the rollers (p_pl). To measure the CF at the roller–plate interface, it is required to have p_t and p_pl. The power consumed for rotating the shaft of the bottom rollers (p_e-shaft and p_x-shaft) was obtained by measuring the power consumed in just rotating the shaft of the bottom rollers under the ideal condition without the plate. Thus, the power required for driving the top roller and the plate is given by Eq. (31):

$$p_{\text{e}} = p_{\text{t}} + x \cdot p_{\text{pl}} + p_{\text{e - shaft}}$$

(30a)

$$p_{\text{x}} = \left( {1 - x} \right)p_{\text{pl}} + p_{\text{x - shaft}}$$

(30b)

$$p_{\text{e}} + p_{\text{x}} = p_{\text{t}} + p_{\text{pl}} + p_{\text{e - shaft}} + p_{\text{x - shaft}}$$

(30c)

$$\left( {p_{\text{e}} - p_{\text{e - shaft}} } \right) + \left( {p_{\text{x}} - p_{\text{x - shaft}} } \right) = p_{\text{t}} + p_{\text{pl}} .$$

(31)

Here, the subscripts e, x, and t refer to the bottom roller at the entry side, the bottom roller at the exit side, and the top roller, respectively. The top roller is the idle roller supported on the bearings and is driven by the motion of plate. Hence, the power required to drive the top roller (p_t) is the product of its moment of inertia (I_t) and its angular acceleration. Angular acceleration (Λ) at the top roller can be considered as an average of the angular acceleration of the bottom rollers (Eq. 32), assuming no slip condition between the rollers and plate. An average no-load power of the bottom rollers (p_n(av)) is the average of p_e-shaft and p_x-shaft. From same dimensions and material of the bottom rollers, their mass moment of inertia (I_b) obtained would be equal. Thus, the power (p_t) required to drive the top roller could be obtained from the following equation:

$$\varLambda = \left( {\frac{{p_{\text{n(av)}} }}{{I_{\text{b}} }}} \right) = \left( {\frac{{p_{\text{t}} }}{{I_{\text{t}} }}} \right)_{\text{t}} .$$

(32)

The top roller power (p_t) was thus calculated to be 62.833 W. The rotational speed of the bottom rollers (N _b ) was kept as 6.5 RPM. Assuming no slip condition at the roller–plate interface, the tangential velocity of the top roller was considered to be same as that of the bottom rollers. Therefore, if r_b and r_t are the radius of the bottom rollers and the top roller, respectively, then Eq. (33) holds true:

$$N_{\text{t}} \cdot r_{\text{t}} = N_{\text{b}} \cdot r_{\text{b}} .$$

(33)

With the normal force at top roller be P and its CF be μ_t, the power at top roller can be defined as shown in the following equation:

$$p_{\text{t}} = \frac{{2\pi N_{\text{b}} }}{60} \cdot r_{\text{b}} \cdot \left( {\mu_{\text{t}} \cdot P} \right).$$

(34)

Rearranging terms for CF of top roller (μ_t), Eq. (34) can be written as follows:

$$\mu_{\text{t}} = \frac{60}{{2\pi N_{\text{b}} }} \cdot \frac{{p_{\text{t}} }}{{r_{\text{b}} \cdot P}}.$$

(35)

Similarly, let μ_e and μ_x be the CF at the bottom roller at the entry and at the exit, respectively, and then, the power measured at the entry and the exit side can be expressed as shown in Eqs. (36) and (37), respectively:

$$p_{\text{e}} = \frac{{2\pi N_{\text{b}} }}{60} \cdot r_{\text{b}} \cdot (\mu_{\text{e}} \cdot J) + p_{\text{e - shaft}} + p_{\text{t}}$$

(36)

$$p_{\text{x}} = \frac{{2\pi N_{\text{b}} }}{60} \cdot r_{\text{b}} \cdot (\mu_{\text{x}} \cdot Q) + p_{\text{x - shaft}} .$$

(37)

From Eqs. (36) and (37), ratio of the power can be defined as shown in the following equation:

$$\frac{{p_{\text{e}} - p_{\text{e - shaft}} }}{{p_{\text{x}} - p_{\text{x - shaft}} }} = \frac{{\mu_{\text{e}} \cdot J + \mu_{\text{t}} \cdot P}}{{\mu_{\text{x}} \cdot Q}}.$$

(38)

Rearranging Eq. (38) for CF of the bottom roller on exit side, it yields,

$$\mu_{\text{x}} = \frac{{\mu_{\text{e}} \cdot J + \mu_{\text{t}} \cdot P}}{{\frac{{p_{\text{e}} - p_{\text{e - shaft}} }}{{p_{\text{x}} - p_{\text{x - shaft}} }} \cdot Q}}.$$

(39)

Equation (39) is utilised for the determination of CF at interface of bottom rollers iteratively (as described in successive section).

3.5 Algorithm for finding CF

Following the algorithm as mentioned below, the coefficient of friction and normal forces at each roller was iteratively evaluated.

• 1. From the experiment of the cylindrical bending, the values of V_t, p_e, and p_x can be obtained.

• 2. The value of p_t can be obtained from Eq. (32).

• 3. Assuming θ_t to be 1°, the value of P and µ_t can be found by solving Eqs. (7) and (35).

• 4. Assuming µ_e and µ_x as 0.1, the value of J, Q, p_e, and p_x can be evaluated from Eqs. (14, 18, 36, and 37).

• 5. New value of µ_x is found out from Eq. (39).

• 6. Steps 3 and 4 are repeated with same µ_e and new µ_x obtained from step 4, till the constant value of µ_x up to three decimal places is obtained.

• 7. If the power p_e obtained in final iteration is found to be less than the experimental value, µ_e is increased by ∆µ_e.

• 8. Steps 3–6 are repeated, till the constant value of µ_e up to three decimal places is obtained.

• 9. The bending moments about top roller contact point are compared (Eq. 29). If found to be unequal, the value of θ_t is increased by ∆θ_t.

• 10. Steps 2–8 are repeated till the Eq. (29) is satisfied within two decimal places.

• 11. On agreement of step (9), the last iteration provides the values of normal forces and CF at each roller–plate interface.

The flow chart of the algorithm is shown in Appendix. The validation of this model is discussed in the following section.

3.6 Validation of the present model

In the present model, the bending moment obtained is based on the magnitude and direction of externally exerted forces and their corresponding perpendicular distance from the point of application of bending moment. Therefore, the bending moment obtained from the present model is termed as external bending moment (M_external). From Eqs. (2, 3, 27, and 29), the equation of M_external can be written as follows:

$$M_{\text{external}} = M_{\text{e}} = M_{\text{x}} = J \cdot \left( {\sin \theta_{{_{\text{e}} }} + \mu_{\text{e}} \cdot \cos \theta_{\text{e}} } \right) \cdot u_{{_{\text{e}} }} + J \cdot \left( {\cos \theta_{\text{e}} - \mu_{\text{e}} \cdot \sin \theta_{\text{e}} } \right) \cdot a_{\text{e}} .$$

(40)

From Eqs. (14) and (40), the equation of M_external can be written as follows:

$$M_{\text{external}} = \frac{{V_{\text{t}} '}}{{\left( {\cos \theta_{\text{t}} + \mu_{\text{t}} \cdot \sin \theta_{\text{t}} } \right)}} \cdot \left( \begin{aligned} \left( {\frac{{\left( {1 - \mu_{\text{t}} \mu_{\text{x}} } \right) \cdot \sin \left( {\theta_{\text{t}} + \theta_{\text{x}} } \right) - \left( {\mu_{\text{t}} + \mu_{\text{x}} } \right) \cdot \cos \left( {\theta_{\text{t}} + \theta_{\text{x}} } \right)}}{{\left( {1 + \mu_{\text{e}} \mu_{\text{x}} } \right) \cdot \sin \left( {\theta_{\text{e}} + \theta_{\text{x}} } \right) - \left( {\mu_{\text{e}} - \mu_{\text{x}} } \right) \cdot \cos \left( {\theta_{\text{e}} + \theta_{\text{x}} } \right)}}} \right) \cdot \hfill \\ \left( {\left( {\sin \theta_{\text{e}} + \mu_{\text{e}} \cdot \cos \theta_{e} } \right) \cdot u_{\text{e}} + \left( {\cos \theta_{\text{e}} - \mu_{\text{e}} \cdot \sin \theta_{\text{e}} } \right) \cdot a_{\text{e}} } \right) \hfill \\ \end{aligned} \right).$$

(41)

Thus, the external bending moment is expressed as a product vertical force at top roller (V_t’) and function of CF and contact angles at the rollers. The CF and contact angles at the roller were obtained as discussed in successive section. The reported formulation of internal bending moment (M_internal) [7] derived using the power law material constitutive equation, is as shown in Eq. (42). Here, K, n, and R are the strength coefficient, the strain hardening exponent and the loaded radius respectively. Loaded radius (R) is considered to be the radius of the circle which is tangent to all three rollers (Fig. 1) and ν is the Poisson’s ratio taken as 0.3. The material properties (K and n) were obtained by performing the tensile testing. The material properties for the plate of each thickness are described in Table 1. Thus, the internal bending moment was calculated using the following equation:

$$M_{\text{internal}} = \frac{2}{3} \cdot \frac{{E' \cdot y_{\text{ep}}^{3} }}{R} + 2K \cdot \left( {\frac{2}{\sqrt 3 }} \right)^{n + 1} \cdot \frac{1}{{\left( {n + 2} \right) \cdot R^{n} }} \cdot \left[ {\left( {\frac{t}{2}} \right)^{n + 2} - y_{\text{ep}}^{n + 2} } \right] ,$$

(42)

where $y_{\text{ep}} = \frac{{R\sigma_{\text{y}} }}{E'},\,E' = \frac{E}{{1 - \nu^{2} }}.$

As reported in the literatures [3,4,5, 13] to predict the bending forces, under equilibrium condition, the M_internal (obtained based on the material properties and amount of bending) can be equated with the M_external (based on the mechanics of the forces and CF). Therefore, under the equilibrium condition at an instant during dynamic bending, M_internal can be equated with M_external, as shown in Eq. (43). The M_internal shown in Eq. (42) is for the unit width; therefore, the total internal bending moment can be written as described in Eq. (43), where w_p is the width of the plate. Equations (41–43) yield the Eq. (44), for the vertical component of top roller force (V_t’):

$$M_{\text{internal}} \cdot w_{\text{p}} = M_{\text{e}} = M_{\text{x}} = M_{\text{external}}$$

(43)

$$V_{t} ' = \frac{{M_{\text{internal}} \cdot w_{\text{p}} \cdot \left( {\cos \theta_{\text{t}} + \mu_{\text{t}} \cdot \sin \theta_{\text{t}} } \right)}}{{\left( \begin{aligned} \left( {\frac{{\left( {1 - \mu_{\text{t}} \mu_{\text{x}} } \right) \cdot \sin \left( {\theta_{\text{t}} + \theta_{\text{x}} } \right) - \left( {\mu_{\text{t}} + \mu_{\text{x}} } \right) \cdot \cos \left( {\theta_{\text{t}} + \theta_{\text{x}} } \right)}}{{\left( {1 + \mu_{\text{e}} \mu_{\text{x}} } \right) \cdot \sin \left( {\theta_{\text{e}} + \theta_{\text{x}} } \right) - \left( {\mu_{\text{e}} - \mu_{\text{x}} } \right) \cdot \cos \left( {\theta_{\text{e}} + \theta_{\text{x}} } \right)}}} \right) \cdot \hfill \\ \left( {\left( {\sin \theta_{\text{e}} + \mu_{\text{e}} \cdot \cos \theta_{\text{e}} } \right) \cdot u_{\text{e}} + \left( {\cos \theta_{\text{e}} - \mu_{\text{e}} \cdot \sin \theta_{e} } \right) \cdot a_{\text{e}} } \right) \hfill \\ \end{aligned} \right)}}.$$

(44)

From Eq. (44), the calculated vertical component of the top roller force (V_t’) is compared, with the vertical component of force (V_t) measured at the top roller during experimentation, as shown in Table 2. The difference in the experimental and calculated values of the vertical component of top roller force is within 13%. Hence, the present mathematical model (described in Sect. 3), is considered to be validated.

Table 2 Comparison of vertical force for the validation of model

4 Result and discussion

4.1 Result of CF at the each roller–plate interface

Following the algorithm of the present model discussed in Sect. 3.5, CF at each roller were evaluated. The normal force calculated at the each roller is as shown in Fig. 7. It is seen that the normal forces at the bottom rollers and at the top roller increase with the increase in the thickness of the plate, which is in line with the reported literature [4, 5, 8]. It is found that the bottom roller on the entry side bears higher force than that on the exit side. Moreover, the difference in the normal force on the entry and the exit rollers is very less at smaller thickness. This difference increases with the thickness of the plate. It was observed that the value of Q is about 88% of J for 8 mm thickness which reduces to about 82% for thickness of 12 mm.

Fig. 7

Forces on the rollers versus thickness of the plate

The plot of the CF versus the thickness of the plate and the normal force (P) is shown in Figs. 8a and b, respectively. It is seen that the increase in the plate thickness results in reduction in CF of the top roller. The plot of CF versus normal force is shown in Fig. 8b. It is seen that the curve of the CF at exit side is above the curve of CF at the entry side.

Fig. 8

a CF versus plate thickness each roller. b CF versus normal force at each roller

4.2 Case study

For studying the simultaneous effect of the power (p_e and p_x) and the vertical force (V_t) on the coefficient of friction, the curves shown in Fig. 4 were extrapolated using the second-order polynomial equation, for the thickness of plate arbitrarily taken up to 35 mm. This was done to know the variation of CF under the higher loading condition. The fitted curves along with their polynomial equation, for vertical top roller force (V_t) and power of bottom rollers (p_e and p_x) are shown in Fig. 9a, b, respectively. Thus, for each thickness, the value of V_t, p_x, and p _e was calculated through this fitted polynomial equation and was taken as an input parameter for the evaluation of CF using present model described in Sect. 3. Following algorithm described in Sect. 3.5, the values of the normal forces and the CF were evaluated. The effect of normal forces on CF at the top and the bottom rollers is plotted, as shown in Fig. 10. It is seen (from Fig. 10) that with increase in normal force, the CF at the bottom rollers increases approximately linearly till the normal force of around 2Ton, and then onwards, it varies non-linearly. At higher normal force, the CF at the entry side almost remains constant. On the exit side, the CF varies almost linearly at higher normal force.

Fig. 9

a Function used for extrapolation of V_t for higher thickness. b Function used for extrapolation of p_e and p_x for higher thickness

Fig. 10

CF versus respective normal force at the top and bottom rollers

4.3 Discussion of the result

The bottom roller at the entry side needs to drive the plate during dynamic bending from the infinite to the minimum loaded radius at the top roller contact point. In addition, the bending occurs mainly in between the bottom roller at the entry side and the top roller. The springback occurs in between the top roller and the bottom roller on the exit side. Thus, the force exerted on the bottom roller on the exit side is mainly due to the springback of the plate. Therefore, the force on the bottom roller at the entry side is higher than that at the exit side, as shown in Fig. 7. For the same span and the top roller displacement or the loaded radius, as the thickness of plate increases springback decreases [2, 9] for cylindrical bending. Hence, relatively, the ratio of the force of the entry to the exit side decreases with increase in the thickness of the plate. Smaller springback results in the smaller opening of the blank and hence less reactive force on the roller at the exit. This may result in decrease in the ratio of normal force at exit to that of entry side.

Top roller is the idle shaft rested on the bearing and driven by the plate itself. Hence, the power required to drive the top roller is constant which depends upon mass moment of inertia of the roller. Therefore, as the thickness of the plate increases, the normal force on the top roller increases, and as power required to drive the top roller is constant, the CF at the top roller contact decreases, as shown in Fig. 8a, b. The plot of CF versus normal force is shown in Fig. 8b. It is seen that the curve of the CF at exit side is above the curve of CF at the entry side. This shows that the CF at the exit is higher than that at the entry side for the same normal force. This may be due to the larger contact angle of plate with roller at the exit side. This requires the larger CF to drive the plate across the roller without slippage. Moreover, for the thickness of 8 mm, the CF at entry is higher than that at the exit and reverse is the case of 12 mm (Fig. 8a). This is due the higher ratio of the normal force on the bottom roller at the exit to that at the entry (which is 0.88) for 8 mm thickness of plate, as compared to that for 12 mm plate thickness (which is 0.82). In addition, the angle of contact at the exit roller is higher than entry side. The combine effect of contact angle and reduced normal force results in the behaviour of CF at the bottom rollers, as shown in Fig. 8a. The CF at the bottom rollers increases with thickness as well as normal force.

This variation of CF with respect to normal force (Fig. 10) can be tribologically explained as reported by Bharat Bhushan [14]. The rotation of the bottom rollers can be considered to be tractive rolling, providing enough force required driving the plate during bending. The CF at the low normal load is less due to presence of oxide film, which effectively separates two metals [14]. This oxide film acts as a solid lubricant. With increase in normal force, this film breaks resulting in intimate metallic contact, which is responsible for high friction [14]. Therefore, CF at bottom roller increases with increase in the normal load. Thus, CF increases with load at low force because of oxide film breakdown and remains at a constant for larger normal force, as reported in the literature [14]. The CF at the top roller decreases with increase in the normal force. As top roller being non-powered idle roller supported on the bearings at either end, its rotation can be considered to be the free rolling condition driven with the motion of the plate. Therefore, CF required to rotate the top roller is very small [14]. As explained earlier, the power required to rotate the roller is constant based on its moment of inertia. Therefore, CF required to rotate the shaft decreases with the normal load. The curve so obtained can be used to know the value of CF at different normal force at the each roller–plate interface, for the considered top roller displacement and roller configuration. As seen in the experimental results, the normal force on the entry side is found to be higher than that at the exit side. Moreover, from the geometry, the contact angle at the exit is also higher than that of entry. This results in CF to be higher at the bottom roller at the exit side as compared to entry side.

5 Conclusion

A mathematical model is derived to calculate dynamic forces at the bottom rollers and the CF at each roller–plate interface during three roller bending. For the contact angles at the bottom rollers, different plate geometries were considered at the entry and the exit side. An experimentation of cylindrical bending was performed for three plates of different thickness and their corresponding values of the top roller force and the power was determined. Using the model available in the literature and experimental results, the present model was validated. From the results of dynamic forces evaluated from the present model, it was found that the dynamic force exerted on the bottom roller at the entry side is more than the forces exerted on bottom roller at the exit side. The difference in the bending force at the bottom rollers increases with increase in the thickness of the plate.

From the results of CF, evaluated with the help of present model, it was found that the CF at the bottom rollers was higher than that of the top roller. The CF at the bottom roller and plate interface increases with the thickness of the plate and the normal forces, while the CF at the top roller and plate interface decreases with the increase in the normal force and plate thickness. When the loading condition is varied by extrapolating the experimental results, it was found that the CF at the bottom rollers increases with the normal force linearly followed by the nonlinear increase in curve. Under the higher loading condition, the CF at the entry side almost remains constant, while that at the exit side, the curve of CF increases with low slope. The curve so obtained (Fig. 10) can be used to determine the CF at the roller–plate interface, which is required to drive the plate at particular loading condition for considered roller configuration. The model developed is more realistic as compared to the reported model due to the fact that different radius is considered before and after the contact point of the plate and the top roller. The reported model determined CF indirectly during bending operation which is otherwise very difficult to obtain practically. However, the reported methodology requires load on the top roller and power consumed for the determination of CF. The plot of CF obtained can used for the future estimation CF for corresponding roller configuration. The reported methodology can also be applied for determination of CF for the configuration other than symmetrical three roller bending.

Appendix

Flow chart for the algorithm is described in Sect. 5.3.