Introduction

The dynamics of the triple contact line motion has been considered within the context of the problems of fluid mechanics using various formulations (De Gennes 1985). Both the intrinsic properties of the system (surface tension, viscosity etc.) (Bratukhin et al. 2007; Chen et al. 2015; Gaponenko and Shevtsova 2016) and the external forces (vibrations, heating etc.) (Brandenbourger et al. 2017; Goldobin et al. 2014; Smorodin et al. 2017) play an important role in this phenomenon. The study of the sessile droplet behavior in an electric field (electrowetting, EW) is one of these problems (Mugele and Baret 2005). Electrowetting-on-dielectric (EWOD) is a special but equally important case. In our time, EWOD has found wide appication in various fields, such as electronic display technology (Hayes and Feenstra 2003; Roques-Carmes et al. 2004), variable-focus liquid lenses (Kuiper and Hendriks 2004; Li and Jiang 2014a), digital (droplet) microfluidic devices for bioanalysis (lab-on-a-chip) (Hua et al. 2010; Li et al. 2014b), etc.

The YoungLippmann equation, which is generally used in many EWOD studies (see Fig. 1) (Berge 1993; Chen and Bonaccurso 2014; Chevalliot et al. 2012; Mugele and Baret 2005; Quilliet and Berge 2001; Zhao and Wang 2013) is written as:

$$\begin{array}{@{}rcl@{}} \begin{array}{cccccc}\cos\vartheta & = \cos {\vartheta_{0}} + {E_{w}}, \qquad \cos{\vartheta_{0}}&=\sigma_{ic}^{-1}\left( {{\sigma_{ip}} -{\sigma_{cp}}} \right) \\ &{E_{w}}= 0.5C{V^{2}}\sigma_{ic}^{-1}, &C=\varepsilon{\varepsilon_{0}}{d^{-1}}, \end{array} \end{array} $$
(1)

where E w is the EW number (it represents the ratio of the electrostatic energy to the liquid surrounding fluid interfacial energy), C is capacitance per unit area, V is the value of the applied DC voltage, 𝜗 0 is the contact angle without the applied voltage the equilibrium contact angle, which is defined by well-known Youngs equation, σ is the interfacial tension between the drop of conducting fluid (c) and the isolating (surrounding) fluid (i)and the dielectric plate (p), d is the thickness of the dielectric film, ε 0and ε are the vacuum and the dielectric layer permittivity, respectively. Although Young-Lippmann Eq. 1 is the fundamental equation of EWOD, different hypothesis were used to provide the framework for its derivation (Mugele and Baret 2005; Quilliet and Berge 2001).

Fig. 1
figure 1

Typical schematic configurations of EWOD-devices. 1 – electrode, 2 – dielectric layer

Full size image

However, the obtained experimental results proved to be very much different from the theoretical predictions of the YoungLippmann equation (1). Thus, it might be expected that the contact angle would be zero just after some critical voltage value (complete wetting and the contact angle is tend to zero), but in fact the experimental value of the contact angle is always finite (Mugele and Baret 2005; Zhao and Wang 2013; Chevalliot et al. 2012). The mechanism of the contact angle saturation is not clearly understood and is still the question under discussion (Mugele and Baret 2005).

In our previuos paper (Alabuzhev and Kashina 2016), we proposed another effective boundary condition of EWOD on the basis of Hockings equation (Hocking 1987):

$$ \frac{{\partial {\zeta^{*}}}}{{\partial {t^{*}}}} = \pm {{\Lambda}^{*}}\left( {\frac{{\partial {\zeta^{*}}}}{{\partial {z^{*}}}} + {A^{*}}\cos \left( {2{\omega^{*}}{t^{*}}} \right)} \right), $$
(2)

where ζ ∗ is the deviation of the drop interface from the equilibrium position, z ∗is the axial coordinate, Λ∗is a phenomenological constant (the so-called wetting parameter or Hocking parameter), having the dimension of velocity, A ∗ is the effective amplitude, ω ∗ is the AC frequency. Note that the conditions of a fixed contact line and constant contact angle are particular cases of the boundary conditions Λ∗ = 0and \({{\Lambda }^{*}} = \infty \), respectively. Consequently, this coefficient describes the interaction of the contact line with the substrate. Thus Hocking’s condition (Hocking 1987) specifies the energy dissipation due to the fluid motion near the contact line, but the fluid is assumed to be inviscid.

Another important problem is the non-uniform wetting of the surface along which the contact line moves (Savva and Kalliadasis 2013; 2014). Heterogeneous substrates can cause different effects (Brunet et al. 2007), for example, hysteresis of the contact angle (Fayzrakhmanova and Straube 2009),(Fayzrakhmanova et al. 2011). Note, that in the majority of the relevant studies the mechanical (acoustical) vibrations or gravity are considered to be a driving force (Savva and Kalliadasis 2014). However, the heterogeneity of the substrate surface can initiate effects, which were observed in the experiment described in Mampallil et al. (2013). Here, the azimuthal oscillations of the oblate droplet were initiated by periodic excitation of the contact line by the applied AC voltage. Various mode shapes can be excited one by one by tuning the frequency of the AC voltage.

This study is intended as an extension to work (Alabuzhev and Kashina 2016). We consider the behavior of a oblate drop between two heterogeneous plates under the applied AC-voltage. In order to describe the motion of the contact line the modified boundary condition (2) is used with Hocking parameter as a function of space variables. In the next paper we will compare the obtained results with the experimental data (Mampallil et al. 2013). As it has been mentioned above, the observed effects can be provoked both by the nonuniformity of the field and heterogeneity of the substrate. Note, that the natural oscillations of a cylindrical droplet of inviscid liquid surrounded by another liquid and bounded in the axial direction by the solid planes are studied in Alabuzhev and Lyubimov (2007).

Problem Formulation

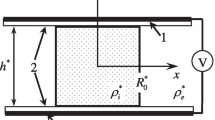
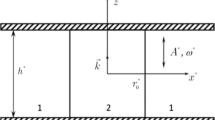
The problem formulation largely coincides with what we considered in papers (Alabuzhev 2016) and (Alabuzhev and Kashina 2016). Here we focus our attention on the dynamic behavior of an incompressible liquid drop of density ρ i∗sandwiched between two parallel solid surfaces (separated by a distance h ∗) and surrounded by another liquid of density ρ e∗(here and in the following, quantities with subscript i refer to the drop, and those with subscript e to the surrounding liquid) (see Fig. 2). The equilibrium shape of the drop is a circular cylinder of radius R0∗ by the height h ∗. The contact angle 𝜗 0 the lateral surface of the drop and the solid surface is equal to π/2. The external nonuniform alternating electric field acts as an external force that initiates the contact line motion.

Fig. 2
figure 2

Problem geometry (1 – electrode, 2 – dielectric layer)

Full size image

Let the surface of the drop be described by the equation \({r^{*}} = R_{0}^{*} + {\zeta ^{*}}\left ({\alpha ,{z^{*}},{t^{*}}} \right )\) in the cylindrical coordinates r ∗, α, z ∗and the axis of cylinder symmetry be parallel to the z-axis. The azimuthal angle α is measured from the x-axis. Assuming a potential liquid motion, we introduce the velocity potential \({\vec v^{*}} = \vec \nabla {\varphi ^{*}}\). Taking the length R0∗, the height h ∗, the density ρ e∗ + ρ i∗, the time \({\sigma ^{- 1/2}}\sqrt {\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )R_{0}^{*3}}\), the velocity potential \({A^{*}}\sqrt \sigma {\left ({\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )R_{0}^{*3}} \right )^{- 1/2}}\), the pressure \({A^{*}}\sigma {\left ({R_{0}^{*}} \right )^{- 2}}\) and the deviation of the surface A ∗as characteristic quantities, we pass to dimensionless variables and obtain the following linear problem

$$\begin{array}{@{}rcl@{}} {p_{j}} &=& - {\rho_{j}}{\varphi_{j}}_{t}, {\Delta} {\varphi_{j}} = 0, j = i,e, \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} {\Delta} &=& \frac{1}{r}\frac{\partial} {{\partial r}}\left( {r\frac{\partial} {{\partial r}}} \right) + \frac{1}{{{r^{2}}}}\frac{{{\partial^{2}}}}{{\partial {\alpha^{2}}}} + {b^{2}}\frac{{{\partial^{2}}}}{{\partial {z^{2}}}}, \\ r &=& 1: \left[\varphi_{r}\right] = 0, {\zeta_{t}} = {\varphi_{r}}, \left[ p \right] = \zeta + {\zeta_{\alpha \alpha} } + {b^{2}}{\zeta_{zz}}, \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} z &=& \pm \frac{1}{2}: {\varphi_{z}} = 0, \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} r &=& 1, z = \pm \frac{1}{2}\!:\! {\zeta_{t}} = \mp \lambda \left( \alpha \right)\left( {{\zeta_{z}} + af\left( \alpha \right)\cos \left( {2\omega t} \right)} \right)\!, \end{array} $$
(6)

where p is the fluid pressure, \(f\left (\alpha \right )\) is the function of the nonuniform electric field, \(\lambda \left (\alpha \right )\) describes the heterogeneity condition for plates, the square brackets denote the jump in the quantity at the interface between the external liquid and the drop. The boundary-value problem (3)–(6) involves six parameters:

the aspect ratio – b = R 0 h − 1,

the dimensionless densities – \({\rho _{i}} = \rho _{i}^{*}{\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )^{- 1}}\) and \({\rho _{e}} = \rho _{e}^{*}{\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )^{- 1}}\),

the wetting parameter – λ =Λ∗ b σ − 1/2 \(\sqrt {\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )R_{0}^{*}}\),

the AC frequency – ω = ω ∗ σ − 1/2 \(\sqrt {\left (\rho _{e}^{*} + \rho _{i}^{*} \right )R_{0}^{*3}} \)

the AC amplitude – a = 0.5A ∗ C σ − 3/2 \(\sqrt {\left (\rho _{e}^{*} + \rho _{i}^{*} \right )R_{0}^{*3}}\).

Forced Oscillations

The functions \(f\left (\alpha \right )\) and \(\lambda \left (\alpha \right )\) are represented as a Fourier series in eigenfunctions of the Laplace operator. Let us consider a particular case of nonuniform electric field and heterogeneous plates: \(f\left (\alpha \right ) = \left | {\sin \left ({{k_{a}}\cos \left (\alpha \right )} \right )} \right |\) and \(\lambda \left (\alpha \right ) = {\lambda _{0}}\left | {\sin \left ({{k_{\lambda }} \cos \left (\alpha \right )} \right )} \right |\), where k a and k λ are the wavenumbers. Note, that we used such function \(f\left (\alpha \right )\) in Alabuzhev and Kashina (2016). The solutions for the velocity potential φ and the surface deviation ζ are written as

$$\begin{array}{@{}rcl@{}} {\varphi_{i}}\left( {r,\alpha,z,t} \right) &=& Re \left( i2\omega \sum\limits_{m,k = 0}^{\infty} {F_{mk}\left( r,\alpha, z\right) {e^{i2\omega t}}} \right), \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} {\varphi_{e}}\left( {r,\alpha,z,t} \right) &=& Re \left( i2\omega \sum\limits_{m,k = 0}^{\infty} { G_{mk}\left( r,\alpha, z\right) {e^{i2\omega t}}}\right), \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} \zeta \left( {z,t} \right) &=& Re\! \left( \! {\left( {\sum\limits_{m,k = 0}^{\infty} {{c_{mk}}{Z_{k}}\!\left( z \right){A_{m}}\left( \alpha \right)}} \right. \!+ {d_{0}}\sin \left( {\frac{z}{b}} \right) +} \right. \hfill \\ &&\left. {\left. { + \sum\limits_{m = 1}^{\infty} {{d_{m}}\sinh\! \left( {\frac{{\sqrt {4{m^{2}} - 1}} }{b}z} \right)\!{A_{m}}\left( \alpha \right)}} \right)\!{e^{i2\omega t}}} \right) \hfill\!, \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} F_{mk}(r,\alpha, z)&=&{a_{mk}}R_{mk}^{i}\left( r \right) Z_{n}\left( z\right) A_{m}\left( \alpha\right), \\ G_{mk}(r,\alpha, z)&=&{b_{mk}} R_{mk}^{e}\left( r \right) Z_{n}\left( z\right)A_{m}\left( \alpha\right), \\ R_{mk}^{i}(r)&=&I_{m}({\left( {2k + 1} \right)\pi b r}), R_{mk}^{e}(r)=K_{m}({\left( {2k + 1} \right)\pi b r}), \\ Z_{n}\left( z\right)&=&\sin {\left( {\left( {2k + 1} \right)\pi z} \right)}, A_{m}\left( \alpha\right) = \cos \left( {2m\alpha} \right), \end{array} $$

where F m k (r,α,z) and G m k (r,α,z) are eigenfunctions of Laplace operator, I m and K m are the modified Bessel functions of m-th order. Substituting solutions (10)(12) into (3)(6), we obtain the expressions for the unknown amplitudes a m k , b m k , c m k and d m .

The dependence of the amplitude of the surface oscillations and the contact angle at the upper plate on the frequency of the driving force is given in Fig. 3 for different values of the Hocking parameter and wavenumbers. It can be seen from the presented Fig. 3a-c that there are no antiresonances, i.e. the amplitude of the contact line goes to zero. Such resonances were observed in the case of homogeneous substrate both under the mechanical vibrations (Alabuzhev 2016; Lyubimov et al. 2006) and in the electric field (Alabuzhev and Kashina 2016): at certain values of ω the drop motion is independent of the wetting parameter and the contact line remains motionless at any λ. Thus, the antiresonances vanish due to the heterogeneity of the substrate, and not because of the nonuniformity of the AC field. The values of these frequencies are independent of λ and depend on the parameters of the drop (aspect ratio b, density ρ i etc.).

Fig. 3
figure 3

Deviation of the contact line (a-c) and the contact angle at the upper plate (d-f) vs frequency. (a = 3.2,b = 1,ρ i = 0.7), λ 0 = 0.1– solid line, λ 0 = 1– dotted, λ 0 = 10– dashed. a, d – k λ = 0.1, k a = 1, b, e – k λ = 1, k a = 0.1, c, f – k λ = 1, k a = 1

Full size image

Figure 4 shows the amplitude dependence for different values of the aspect ratio b. The amplitude decreases with increasing aspect ratio b and vibration frequency ω. One of the reasons for such a behavior is quite obvious: a larger drop is more difficult to move (the length of the contact line increases with increasing value of the parameter b). Apparently, the other reason is related to the fact that dissipation at high-frequency oscillations is more intensive than at low-frequency oscillations.

Fig. 4
figure 4

Deviation of the contact line (a) and the contact angle at the upper plate (b) vs the frequency. (a = 3.2,λ 0 = 1,ρ i = 0.7), b = 0.5– solid line, b = 1– dotted, b = 2– dashed

Full size image

For the main eigenfrequencies with the azimuthal numbers m = 2,3,... there exists a certain range of the capillary parameter λ in which the real parts of these frequencies vanish (Alabuzhev and Lyubimov 2007). This implies that at such values of the the problem parameter the resonance effect is absent. The axisymmetric eigenmode frequency can also vanish in a certain range of the capillary parameter λ, depending on the value of the geometrical parameter b. For b < π − 1 and a certain characteristic value of λ, the frequency vanishes and the increment becomes negative, which corresponds to the occurrence of the Rayleigh instability. As the value of b increases, the length of this range decreases. However, in contrast to the azimuthal modes, the length of this range decreases with increasing parameter b.

The wavenumber k λ plays the role of an effective wetting coefficient λ. The smaller the parameter λ, the greater the interaction between the contact line and the substrate and the smaller the amplitude of the oscillations (see Fig. 3c). Consequently, the long-wave heterogeneity of the substrate leads to a decrease in the oscillation amplitude. The deviation of the contact angle is less than 0.5π(see Fig. 3d, f), i.e. complete wetting does not occur. The wavenumber k a plays the role of the effective vibrations amplitude: the amplitude of the oscillations increases with increasing wavenumber k a (see Fig. 3a, b). Thus parameter k a (i.e. nonuniform field) has a considerable effect on the variation of the contact angle. An increase in the wavenumber k λ contributes to a decrease in the oscillation amplitude and, consequently, in the deviation of the contact angle, but for large values of λ 0this effect becomes insignificant.

Figure 5 shows the variation in the shape of the contact line during the oscillation period T = π. It can be seen that the drop extends along the surface inhomogeneity. Note that in the case of non-uniform field and homogeneous surfaces, the axisymmetric oscillations are the main oscillation modes.

Fig. 5
figure 5

The shape of the contact line at upper plate at oscillation perod T = π/ω(a = 3.2,λ 0 = 1,ρ i = 0.7,b = 1,ω = 1), t = 0. – solid line, t = 0.125T– dotted, t = 0.25T– dashed,t = 0.375T– dot-dashed

Full size image

The deviation of the contact angle as a function of the square root of the amplitude a (i.e. proportional to AC potential V) is given in Fig. 6 for different values of the Hocking’s parameter λ and AC frequency ω. The responses obtained qualitatively agree with the experimental data. However, the maximum deviation of the contact angle tends to 0.5π, i.e. 𝜗 → 0 or 𝜗 → π whereas the contact angle found in experiments is finite.

Fig. 6
figure 6

Deviation of the contact angle at the upper plate vs the square root of the amplitude (b = 1, ρ i = 0.7), λ 0 = 0.1solid line, λ 0 = 1dotted, λ 0 = 10dashed. a-c ω = 2, d-f ω = 2.5. a, d k λ = 0.1, k a = 1, b, e k λ = 1, k a = 0.1, c, f k λ = 1, k a = 1

Full size image

Conclusions

The behavior of the cylindrical drop between two solid plates has been considered taking into account the dynamics of the contact angle under the action of the nonuniform electric field \(\left | {\sin \left ({{k_{a}}x} \right )} \right |\). The solid plates have heterogeneous surfaces described by the function \(\lambda \left (\alpha \right ) = {\lambda _{0}}\left | {\sin \left ({{k_{\lambda }} \cos \left (\alpha \right )} \right )} \right |\). The main purpose of this paper is to develop a method for studying the drop forced oscillation of the oblate drop on heterogeneous substrates and determining of contact angle. The investigation of the forced oscillations has shown that the wavenumber k λ plays the role of the effective wetting parameter, k a is the effective amplitude.

The nonuniform electric field excites various azimuthal modes of forced oscillations. In our case, the oscillation amplitude for each mode is determined by the coefficient of expansion of the external force into a Fourier series. These expansion coefficients depend not only on the amplitude a but also on the wave number k a . However, the greatest contribution to the drop dynamics is made by the mode, whose frequency is close to the vibration frequency 2ω, i.e. azimuthal oscillations of the drop are exited by periodic motion of the contact line via AC field. In the case of homogeneous substrates there are “antiresonant” frequencies, i.e. such external frequencies, at which the contact line does not move and the contact angle does not change.

In the case of heterogeneous surface the energy produced by the excited oscillation mode is transferred to other modes. For example, if the ac field is uniform, then the external field excites axisymmetrical mode of drop oscillations. Energy from this mode is redistributed to other azimuthal modes due to heterogeneous surfaces. For small values of the parameter λ 0, at which the energy of the interaction between the contact line and the plate is strong, the oscillations amplitude is small. In the opposite case, the amplitude of the surface forced oscillations is large and tends to infinity in the limit \({\lambda _{0}} \to \infty \). The “antiresonant” frequencies are absent both in the uniform and nonuniform electric fields for such surfaces.