1 Introduction

In a service system which is composed of the service agents and many potential customers, the queue is very common and it controls and allocates the service ability for customers. When the service ability of the agent is uncomfortable with the number of customers, such as too idle or too tense, adjustment may occur and the service agent should change its service rate or suggest other service scheme to increase its efficiency of the service, for example, establishing the high–low rate transferring policy, or some gates/thresholds to control the entrance of customers.

Working vacation policy is a high–low rate transferring policy and also a class of semi-vacation policy that was introduced by Servi and Finn [7] in 2002, where a customer is served at a lower rate during a vacation period. Such a vacation is different from the classical vacation queueing models. In the classical vacation queueing models, the server doesn’t take the original work and possibly deals with the other tasks. Such policy may make the loss or dissatisfaction of the customers. For the working vacation policy, the server also can work in the lower rate. So, the working vacation is more reasonable and general than the classical vacation.

For working vacation models, Servi and Finn [7] studied an M/M/1 queue with working vacations, and obtained the probability generating function of the queue length and the LST of the waiting time, and applied results to performance analysis of gateway router in fiber communication networks. Subsequently, Kim et al.[3], Wu and Takagi [11] generalized results in [7] to an M/G/1 queue with working vacations. Baba [1] extended this study to a GI/M/1 queue with working vacation by the matrix-analysis method. Liu et al. [8] obtain the concise expressions for the queue length and waiting time for the M/M/1 queue with multiple working vacation and verify the stochastic decomposition structures of the queue length and waiting time. Li and Tian [4, 5] obtained the expressions for the queue length and waiting time for two types of GI/Geo/1 queue with working vacations and verified the stochastic decomposition structures of the queue length and waiting time. Tian and Zhang [10], Zhang et al.[12] gave the threshold policy analysis for multi-server queue and M/G/1 queue with general vacations. For general queueing analysis, including the vacation policy, the readers are recommended to Gross and Harris [2] and Tian and Zhang [9].

In recent papers on the working vacations, the authors only concentrate on the vacation queues with exhaustive service and the server only takes the vacation when the system is empty. In this paper, we will consider the M/M/1 queue with the threshold policy and working vacations. Such model is different from the other models with working vacations. The server begins or ends to take the vacation at the certain point, i.e.the threshold. Such policy is also called by the non-exhaustive service. Meanwhile, the server also works in the vacation period at the lower rate rather than stoping working completely. The motivation for studying this kind of models can be presented both in practical aspect and theoretical aspect. Firstly, such model can be seen as the service system with high and low speed periods controlled by thresholds. When the number of customers or signals under one certain threshold in the system, the server can work slowly. Such policy will enable the cost of system to reduce. Such a model also is more practical than the classical threshold queue with vacation where the server can not work during the vacation period. Many practical problems present this character. In banks, when the number of customers or work is under some value, some counters will be closed to do other work. Under this case, the bank needs to consider what will happen based on the performance indices of the bank, such as the queue length or waiting time. So this kind of models has important practical background. In theoretical view, this kind of models will be more general than those M/M/1 queues considered before and the classical threshold queues with vacations are also the special examples of this kind of models.

The rest of this paper is organized as follows. In Sect. 2, we study the M/M/1 queue with \(m\)-policy, where the quasi birth and death process, the distribution of the queue length is presented. Section. 2.3 turns to the M/M/1 queue with \((m,N)\)-policy. In Sect. 4, some numerical examples are presented to verify the validity of the model and the cost function is also established in M/M/1 queue with \(m\)-policy. Section. 5 concludes the results.

2 M/M/1 queue with \(m\)-policy

2.1 Model formulation and quasi birth and death process (QBD)

Consider a classical M/M/1 queue with an arrival rate \(\lambda \) and service rate \(\mu _b\). At the instant of a service completion, the server begins a vacation of random length at the instant when the queue length is below \(m\) and vacation duration \(V\) follows an exponential distribution with parameter \(\theta \). During a vacation, the original customers or arriving customers in a vacation period can be served at a mean rate of \(\mu _v\). When a vacation ends, if the number of customers in the queue is less than \(m\), another vacation is taken; Otherwise, the server switches service rate from \(\mu _v\) to \(\mu _b\). This service discipline is a \(m\)-threshold policy with working vacation. Evidently, this model is a non-exhaustive service queue and the server can begin to take the vacation when there are customers in the system. Many service systems are the special cases of this model and when \(m=1\), this model becomes the general M/M/1 queue with multiple working vacations which was considered by Servi and Finn [7] and Liu et al. [8].

We assume that inter-arrival times, service times, and working vacation times are mutually independent. In addition, the service discipline is first in first out(FIFO).

Let \(Q_1(t)\) be the number of customers in the system at time \(t\) and let

$$\begin{aligned} J_1(t)=\left\{ \begin{array}{ll} 0,&{} \hbox {the system is in a working vacation period at time } t,\\ 1,&{} \hbox {the system is in a regular busy period at time } t. \end{array}\right. \end{aligned}$$

then \(\{ Q_1(t), J_1(t)\}\) is a QBD with the state space

$$\begin{aligned} \Omega = {\Big \{(k,0):0\le k\le {m-1}\Big \}}\bigcup \Big \{(k,j): k \ge m, \quad j=0 ,1 \Big \}. \end{aligned}$$

Evidently, when the number of customers is less than \(m\), the server only stays in vacation period.

Using the lexicographical sequence for the states, the infinitesimal generator can be written as

$$\begin{aligned} \mathbf{Q_1 }= \left[ {{\begin{array}{*{20}c} -\lambda &{}\quad {C_0 } &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad \\ {B_1 } &{}\quad {A_1 } &{}\quad {C_1 } &{}\quad &{}\quad &{}\quad &{}\quad \\ &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad &{}\quad \\ &{}\quad &{}\quad {B_{m-1} } &{}\quad {A_{m-1} } &{}\quad {C_{m-1}} &{}\quad &{}\quad &{}\quad \\ &{}\quad &{}\quad &{}\quad {B_m} &{}\quad {A} &{}\quad {C} &{}\quad &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad B &{}\quad {A} &{}\quad C &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots \\ \end{array} }} \right] , \end{aligned}$$

where

$$\begin{aligned} B_k&= \mu _v, 1\le k\le m-1,B_m=(\mu _v,\mu _b)^T;\\ C_k&= \lambda ,0\le k \le m-2, \quad C_{m-1}=(\lambda ,0);\quad A_k=-(\lambda +\mu _v),1\le k\le m-1;\\ C&= \left[ \begin{array}{cc} \lambda &{} 0\\ 0 &{} \lambda \\ \end{array}\right] ,\quad B=\left[ \begin{array}{cc} \mu _v &{} 0\\ 0 &{} \mu _b \\ \end{array}\right] ,\quad A=\left[ \begin{array}{cc} -(\lambda +\theta +\mu _v)&{}\theta \\ 0&{}-(\lambda +\mu _b) \end{array}\right] . \end{aligned}$$

To analyze this QBD process, it is necessary to solve for the minimal non-negative solution of the matrix quadratic equation

$$\begin{aligned} R{} ^2B + RA + C = 0. \end{aligned}$$
(1)

and this solution is called the rate matrix and denoted by \(R\). Obviously, we have

Lemma 1

If \(\rho = \lambda (\mu _b)^{ - 1} < 1\), the matrix equation (1) has the minimal non-negative solution

$$\begin{aligned} R=\left[ {{\begin{array}{*{20}c} {r\;} &{} {\dfrac{\theta \;r}{\mu _b (1 - r)}} \\ 0 &{} \qquad \rho \\ \end{array} }} \right] , \end{aligned}$$
(2)

where

$$\begin{aligned} r= \dfrac{1}{2\mu _v}\left( \lambda + \theta + \mu _v - \sqrt{(\lambda + \theta + \mu _v )^{^{\,2}} - 4\lambda \mu _v } \right) \end{aligned}$$

and \(0 < r <1\).

Proof

Because the matrices \(A\), \(B\), \(C\) of (1) are all upper triangular, we can assume that \(R\) has the same structure as

$$\begin{aligned} R=\left[ {{\begin{array}{*{20}c} {r_{11} \;} &{} {r_{12} } \\ 0 &{} {r_{22} } \\ \end{array} }} \right] . \end{aligned}$$

Substituting \(R^2\) and \(R\) into (1) gives the following set of equations:

$$\begin{aligned} \left\{ \begin{array}{l} \mu _v r_{11}^2 - (\lambda \,\; + {} \theta + \mu _v)\,r_{11} + \lambda = 0, \\ \mu _br_{22}^2 - (\lambda \,\; + {} \mu _b )\,r_{22} + \lambda = 0,\\ \mu _b \;r_{12}(r_{11} + r_{22} ) + {} \theta \;r_{11} - (\lambda + \mu _b)r_{12} = 0. \end{array}\right. \end{aligned}$$
(3)

To obtain the minimal non-negative solution of (1), taking \(r_{22} = \rho \) (the other root is \(r_{22} = 1\)) in the second equation and \(r_{11} = r\) (the other root is greater than 1) in the first equation of (3). Using the elementary method (discriminant of quadratic equation), we can prove that \(0<r<1\). Substituting \(r\) and \(\rho \) into the last equation of (3), we get the expression for \(r_{12}\). Thus, we can have the results in Lemma 1.

Lemma 2

\(r\) satisfies the following relationship

$$\begin{aligned} \lambda + {} \theta + \mu _v(1 - r) = \mu _v + \dfrac{\theta }{1 - r} = \dfrac{\lambda }{r}. \end{aligned}$$
(4)

Proof

From the Lemma 1, \(r\) satisfies the first equation of (3). Dividing two ends of this equation by \(r\), we give

$$\begin{aligned} r \mu _v-(\lambda + {} \theta + \mu _v)+ \dfrac{\lambda }{r}=0. \end{aligned}$$

Hence, we have

$$\begin{aligned} \lambda + {} \theta + \mu _v(1 - r) =\dfrac{\lambda }{r}. \end{aligned}$$

Transferring \(\lambda \) from left to right of the above relation, dividing two ends of this equation by \(1-r\), we get the other equation of (4)

$$\begin{aligned} \mu _v + \dfrac{\theta }{1 - r} = \dfrac{\lambda }{r}. \end{aligned}$$

Theorem 1

The QBD process \(\{Q_1(t),J_1(t)\}\) is positive recurrent if and only if \(\rho < 1\).

Proof

Based on Theorem 3.1.1 of Neuts [6], the QBD process \(\{Q_1(t),J_1(t)\}\) is positive recurrent if and only if the spectral radius SP \((R)\) of the rate matrix \(R\) is less than 1, and set of equations

$$\begin{aligned} (x_{00},x_{10},\cdots , x_{m-1,0},x_{m0},x_{m1})B[R] = 0 \end{aligned}$$
(5)

has positive solution, where

$$\begin{aligned} B[R] = \left[ {{\begin{array}{*{20}c} -\lambda &{}\quad {C_0 } &{}\quad &{}\quad &{}\quad &{}\quad \\ {B_1 } &{}\quad {A_1 } &{}\quad {C_1 } &{}\quad &{}\quad &{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \\ &{}\quad &{}\quad &{}\quad {B_{m-1} } &{}\quad {A_{m-1} } &{}\quad {C_{m-1}} \\ &{}\quad &{}\quad &{}\quad &{}\quad {B_m} &{}\quad {RB+A} \\ \end{array} }} \right] , \end{aligned}$$

where

$$\begin{aligned} RB+A=\left[ \begin{array}{cc} -\dfrac{\lambda }{r} &{}\qquad \dfrac{\lambda }{r}-\mu _v \\ 0 &{} \qquad -\mu _b \\ \end{array}\right] . \end{aligned}$$

With (4), we can easily verify \(B[R]\) is an infinitesimal generator. Substituting \(B[R]\) into the above relation, we obtain the set of equations

$$\begin{aligned} \left\{ \begin{array}{l} -\lambda x _{00}+\mu _v x _{10} =0;\\ \lambda x _{k-1,0}-(\lambda + \mu _v)x _{k0}+\mu _vx_{k+1,0}=0, \quad 1\le k\le m-2 ;\\ \lambda x _{m-2,0}-(\lambda + \mu _v)x _{m-1,0}+\mu _vx_{m,0}+\mu _bx_{m1}=0 , \quad k=m-1;\\ \lambda x_{m-1,0}-\dfrac{\lambda }{r}x_{m0}=0;\\ \left( \dfrac{\lambda }{r}-\mu _v\right) x_{m0}-\mu _bx_{m1}=0.\\ \end{array}\right. \end{aligned}$$
(6)

From the first and second equations in (6), we easily get

$$\begin{aligned} x_{k0}=x_{00}\bigg (\dfrac{\lambda }{\mu _v}\bigg )^k, \quad 0\le k\le m-1. \end{aligned}$$

Then, from the other equations and (4),

$$\begin{aligned} \left\{ {\begin{array}{ll} x_{m0}=rx_{m-1,0}=x_{00}r\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1};\\ x_{m1}=\dfrac{1}{\mu _b}\bigg (\dfrac{\lambda }{r}-\mu _v\bigg )x_{m0} =x_{00}\left( \dfrac{\lambda }{\mu _v}\right) ^{m-1}\dfrac{\theta r}{\mu _b(1-r)},\\ \end{array}} \right. \end{aligned}$$
(7)

where \(x_{00}\) is a random real number, so Eq. (5) has positive solution. Thus, the QBD process \(\{Q_1(t),J_1(t)\}\) is positive recurrent if and only if SP \((R)=\mathrm{max }(r,\rho )<1\).

2.2 Queue length distribution

If \(\rho < 1\), let \((Q_1,J_1)\) be the stationary limit of the QBD process \(\{Q_1(t),J_1(t)\}\). Introduce

$$\begin{aligned} \begin{array}{l} \pi {} _k=\pi {} _{k0},\quad 0\le k\le m-1;\quad \pi _k = (\pi _{k0}, \pi _{k1} ),\quad k\ge m \\ \pi {} _{kj} = P\{Q = k,J = j\} = \mathop {\lim }\limits _{t \rightarrow \infty } P\{Q(t) = k, J(t) = j\},\quad (k,j) \in \Omega . \end{array} \end{aligned}$$

Theorem 2

If \(\rho < 1\), the stationary probability distribution of \((Q_1,J_1)\) is

$$\begin{aligned} \left\{ {\begin{array}{ll} \pi _{k0} = K \bigg (\dfrac{\lambda }{\mu _v}\bigg )^k, \quad 0\le k \le m-1, \\ \pi _{k0}=K\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1}r^{k-m+1}, \quad k\ge m;\\ \pi _{k1}=K\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1}\dfrac{\theta r}{\mu _b(1-r)} \displaystyle \sum _{j=0}^{k-m}r^j\rho ^{k-m-j} , \quad k\ge m,\\ \end{array}} \right. \end{aligned}$$
(8)

where

$$\begin{aligned} K=\left[ \displaystyle \sum _{k=0}^{m-1}\left( \dfrac{\lambda }{\mu _v}\right) ^{k} +\left( \dfrac{\lambda }{\mu _v}\right) ^{m-1}\dfrac{r}{1-r}+ \left( \dfrac{\lambda }{\mu _v}\right) ^{m-1}\dfrac{\theta r}{\mu _b(1-r)} \dfrac{1}{1-r}\dfrac{1}{1-\rho }\right] ^{-1}. \end{aligned}$$

Proof

With the matrix-geometric solution method(see in [8]), we have

$$\begin{aligned} \pi _k = (\pi _{k0} ,\pi _{k1} ) = (\pi _{m0} ,\pi _{m1} )R^{k - m}, \quad k \ge m. \end{aligned}$$
(9)

and \((\pi _{00} ,\pi _{10} ,\ldots ,\pi _{m-1,0},\pi _{m0},\pi _{m1})\) satisfies the set of equations

$$\begin{aligned} (\pi _{00},\pi _{10},\ldots , \pi _{m-1,0},\pi _{m0},\pi _{m1})B[R] = 0. \end{aligned}$$
(10)

We have obtained the expressions for \(\pi _{k0},0\le k\le m\) and \(\pi _{m1}\) in Theorem 1. Thus, for \(k\ge m\), note that

$$\begin{aligned} R^k = \left[ {\begin{array}{c@{\quad }c} r^k&{} \dfrac{\theta {} r}{\mu _b (1 - r)}\sum \limits _{j = 0}^{k - 1} {r^j\rho ^{k - 1 - j }} \\ 0&{}\rho ^k \\ \end{array}} \right] , \qquad k \ge 1. \end{aligned}$$

With (7), substituting \((\pi _{m0} ,\pi _{m1})\) and \(R^{k-m}\) into (9), we obtain (8). Finally, the constant factor \(K\) can be determined by the normalization condition.

Further, we can obtain the distribution for the number of customers \(Q_1\)

$$\begin{aligned} P\{Q_1=k\}&= \pi _{k0}=K\bigg (\dfrac{\lambda }{\mu _v}\bigg )^k,\quad 0\le k\le m-1;\\ P\{Q_1=k\}&= \pi _{k0}+\pi _{k1}=K\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1} \bigg [r^{k-m+1}+\dfrac{\theta r}{\mu _b(1-r)}\displaystyle \sum _{j=0}^{k-m}r^j\rho ^{k-m-j} \bigg ],\\&k\ge m.\\ \end{aligned}$$

After some computation, the generating function of \(Q_1\) is as follows

$$\begin{aligned} Q_1(z)&= K\dfrac{1\!-\!(\rho _0z)^m}{1\!-\!\rho _0 z} \!+\!K{\rho _0}^{m-1}z^m\bigg [\dfrac{r}{1\!-\!rz}\!+\!\dfrac{\theta r}{\mu _b(1\!-\!r)}\dfrac{1}{1\!-\!rz}\dfrac{1}{1-\rho z}\bigg ],\quad \rho _0\!=\!\dfrac{\lambda }{\mu _v} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} E(Q_1)&=K\dfrac{1-\rho _0^{m}}{1-\rho _0} \bigg [\dfrac{\rho _0}{1-\rho _0}-m\dfrac{ \rho _0^{m}}{1-\rho _0^{m}} \bigg ]+K\rho _0^{m-1}\dfrac{r}{1-r}\bigg [m +\dfrac{r}{1-r}\bigg ]\\&\quad +K\rho _0\dfrac{\theta r}{\mu _b(1-r)}\dfrac{1}{1-r}\dfrac{1}{1-\rho }\bigg [m+\dfrac{r}{1-r} +\dfrac{\rho }{1-\rho }\bigg ].\\ \end{aligned} \end{aligned}$$

Meanwhile, we can easily obtain the state probabilities of a server in steady-state.

$$\begin{aligned} \begin{aligned} P_v=P\{J_1=0\}&=\displaystyle \sum _{k=0}^{\infty }\pi _{k0} =K\bigg [\dfrac{1- \rho _0^{m}}{1-\rho _0}+ \rho _0^{m-1}\dfrac{r}{1-r}\bigg ], \\ P_b=P\{J_1=1\}&=\displaystyle \sum _{k=m}^{\infty }\pi _{k1}=K \rho _0^{m-1}\dfrac{\theta r}{\mu _b(1-r)} \dfrac{1}{1-r}\dfrac{1}{1-\rho }. \end{aligned} \end{aligned}$$
(11)

Remark 1

Many models studied before are the special examples of the model we consider above.

When \(m=1\), i.e., the server only begins the vacation when the system becomes empty, we can obtain the results of M/M/1 queue with working vacations (see Liu et al. [8]).

When \(\mu _v=0\), i.e., the server does’t take service during the vacation period, our model becomes the classical M/M/1 queue with vacations and \(m\)-policy. Meanwhile, if \(\theta =0,\mu _v=\mu _b\), the model becomes the classical M/M/1 queue without vacation.

2.3 Conditional queue length and sojourn time

Note the expressions for \(Q_1^{(m)}\) and \(S^{(m)}\) below:

$$\begin{aligned} Q_1^{(m)}&= \{Q_1-m|Q_1\ge m, J=1\};\\ S_{m}^b&= \{S|Q_1\ge m, J=1\}. \\ \end{aligned}$$

\(Q_1^{(m)}\) represents the number of customers in the system except for \(m\) customers, and \(S_{m}^b\) represents the sojourn time when the server is in the normal working level.

Firstly, we discuss the conditional number of waiting customers.

Theorem 3

If \(\rho < 1\) and \(\mu _b>\mu _v\), the conditional stationary queue length \(Q_1^{(m)}\) can be decomposed into the sum of three independent random variables: \(Q_1^{(m)}=Q_0+Q_{1d}\), where \(Q_0\) is the stationary queue length of a classical M/M/1 queue without vacation, and follows a geometric distribution with parameter \(1-\rho \); Additional queue length \(Q_{1d} \) follows geometric distribution with parameter \(1-r \).

Proof

Conditional probability that the server is busy and there are more than or equal to \(m\) customers in the system

$$\begin{aligned} P\{Q_1\ge m,J=1\}=P\{J=1\}=\sum _{k=m}^{\infty }\pi _{k1} =K \rho _0^{m-1}\dfrac{\theta r}{\mu _b(1-r)} \dfrac{1}{1-r}\dfrac{1}{1-\rho }. \end{aligned}$$

So, for \(k\ge 0\)

$$\begin{aligned} \begin{array}{ll} P\{Q_1^{(m)}=k\}&{}=P\{Q_1=k+m|Q_1\ge m,J=1\}=\dfrac{\pi _{k+m,1}}{P\{Q\ge m,J=1\}} \\ &{}=(1-\rho )(1-r)\sum _{j=0}^{k}r^j\rho ^{k-j},\quad k\ge 0. \\ \end{array} \end{aligned}$$

Thus, we easily obtain the probability generating function of \(Q_1^{(m)}\) as follows

$$\begin{aligned} Q_1^{(m)}(z)=\sum ^\infty _{k=0}z^k P\{Q_1^{(m)}=k\} =\dfrac{1-\rho }{1-\rho z}\dfrac{1-r}{1-r z}=Q_0(z)Q_{1d}(z). \end{aligned}$$

With the conditional stochastic decomposition structure in Theorem 3, we can easily get the expected number of customers when the server is in the normal busy period.

$$\begin{aligned} \begin{array}{ll} E(Q_1^{(m)})=\dfrac{\rho }{1-\rho }+E(Q_{1d})=\dfrac{\rho }{1-\rho }+\dfrac{r}{1-r}.\\ \end{array} \end{aligned}$$

Now, we analyze the conditional sojourn time of each customer when the server is busy and there are more than or equal to \(m\) customers in the system as we denote above.

Lemma 3

  1. (i)

    The LST of the conditional sojourn time when the server is busy is given in

    $$\begin{aligned} S_m^{*b}(s) =\bigg (1-\dfrac{s}{\lambda }\bigg )^m\dfrac{\mu -\lambda }{\mu -\lambda + s}\dfrac{\lambda (1-r)}{\lambda (1-r)+rs} \end{aligned}$$
    (12)
  2. (ii)

    The conditional expected sojourn time when the server is busy can be expressed by

    $$\begin{aligned} E(S_m^{b})=\dfrac{E(Q_1^{(m)})+m}{\lambda }. \end{aligned}$$
    (13)

Proof

From the memoryless of exponential distribution and the Little-formula, if a customer departs when the server is busy and there are more than or equal to \(m\) customers in the system, the remaining customers should be those who arrive during his sojourn time, that means

$$\begin{aligned} S_m^{*b}(\lambda (1-z))=z^mQ_1^{(m)}(z) \end{aligned}$$

then, we have

$$\begin{aligned} S_m^{*b}(s)=\bigg (1-\dfrac{s}{\lambda }\bigg )^mQ_1^{(m)}\bigg (1-\dfrac{s}{\lambda }\bigg ) =\bigg (1-\dfrac{s}{\lambda }\bigg )^m\dfrac{\mu -\lambda }{\mu -\lambda + s}\dfrac{\lambda (1-r)}{\lambda (1-r)+rs} \end{aligned}$$

Further, from the expression for \(Q_1^{(m)}\), the relation that \(Q_1^{(m)}+m=\{Q_1|Q_1\ge m, J=1\}\) exists, then from the Little law, the conditional expected sojourn time satisfies

$$\begin{aligned} E(Q_1^{(m)})+m=\lambda S_m^{*b}. \end{aligned}$$

So the conditional expected sojourn time is given as Eq. (13).

Similarly, denote \(Q_1^{v}\) and \(S_m^{v}\) as the conditional queue length and sojourn time when the server is in the vacation period, i.e.,

$$\begin{aligned} \begin{array}{ll} Q_1^{v}=\{Q_1|J=0\};\qquad S_m^{v}=\{S|J=0\}. \\ \end{array} \end{aligned}$$

Firstly, we can compute the probability generating function of \(Q_1^{v}\) as follows

$$\begin{aligned} \begin{array}{ll} Q_1^{v}(z)=\displaystyle \sum ^\infty _{k=0}z^k P\{Q_1^{v}=k\}=\sum ^\infty _{k=0}z^k\dfrac{\pi _{k0}}{P\{J=0\}} =\dfrac{\dfrac{1-(\rho _0z)^m}{1-\rho _0 z} +{(\rho _0z)}^{m-1}\dfrac{rz}{1-rz}}{\dfrac{1- \rho _0^{m}}{1-\rho _0}+ \rho _0^{m-1}\dfrac{r}{1-r}} \end{array} \end{aligned}$$

Then, the expected number of customers when the server is in the vacation period is given by

$$\begin{aligned} \begin{array}{ll} E(Q_1^{v})=\dfrac{\dfrac{1-\rho _0^{m}}{1-\rho _0} \dfrac{\rho _0}{1-\rho _0}+\rho _0^{m-1}\dfrac{r}{1-r}\bigg [m +\dfrac{r}{1-r}\bigg ]}{\dfrac{1- \rho _0^{m}}{1-\rho _0}+ \rho _0^{m-1}\dfrac{r}{1-r}}.\\ \end{array} \end{aligned}$$

Lemma 4

  1. (i)

    The LST of the conditional sojourn time under the vacation period is given in

    $$\begin{aligned} S_m^{*v}(s) =\dfrac{\dfrac{1-\bigg (\rho _0-\dfrac{s}{\mu _v}\bigg )^m}{1-\bigg (\rho _0-\dfrac{s}{\mu _v}\bigg )} +\bigg (\rho _0-\dfrac{s}{\mu _v}\bigg )^{m-1}\dfrac{r(\lambda -s)}{\lambda -r(\lambda -s)}}{\dfrac{1- \rho _0^{m}}{1-\rho _0}+ \rho _0^{m-1}\dfrac{r}{1-r}} \end{aligned}$$
    (14)
  2. (ii)

    The conditional expected sojourn time under the vacation period can be expressed by

    $$\begin{aligned} E(S_m^{v})=\dfrac{E(Q_1^{v})}{\lambda }. \end{aligned}$$
    (15)

Proof

From the memoryless of exponential distribution and the Little-formula, if a customer departs when the server is in vacation period, the remaining customers should be those who arrive during his sojourn time, which means

$$\begin{aligned} S_m^{*v}(\lambda (1-z))=Q_1^{v}(z) \end{aligned}$$

then, we have

$$\begin{aligned} S_m^{*v}(s)=Q_1^{v}\bigg (1-\dfrac{s}{\lambda }\bigg ) \end{aligned}$$

from which, the Eq. (14) is obtained. Further, the conditional expected sojourn time satisfies

$$\begin{aligned} E(Q_1^{v})=\lambda E(S_m^{v}). \end{aligned}$$

Then the conditional expected sojourn time is given as Eq. (15).

Theorem 4

For an arbitrary customer who arrives to the system, the Laplace transform and mean of his sojourn time should be

$$\begin{aligned} \begin{aligned} S_m^*(s)&=P_vS_m{*v}(s)+P_bS_m^{*b}(s)=Q_1\bigg (1-\dfrac{s}{\lambda }\bigg ),\\ E(S_m)&=P_vE(S_m^{v})+P_bE(S_m^{b})=E(Q_1)/\lambda , \end{aligned} \end{aligned}$$
(16)

where \(S_m^{*v}(s),S_m^{*b}(s),E(S_m^{v}),E(S_m^{b})\) are given in Eqs. (12)–(15), respectively.

3 M/M/1 queue with \((m,N)\)-policy

3.1 QBD model

Consider a classical M/M/1 queue with arrival rate \(\lambda \) and service rate \(\mu _b\) (see Gross and Harris [3]). After a service, the server begins a vacation of random length at the instant when the queue length is below \(m\) and vacation duration \(V\) follows an exponential distribution with parameter \(\theta \). During a vacation, the original customers or arriving customers in a vacation period can be served at a mean rate of \(\mu _v\). When a vacation ends, if the number of customers in the queue is less than \(N\) , another vacation is taken; Otherwise, the server switches service rate from \(\mu _v\) to \(\mu _b\), and a regular busy period starts. This service discipline is a two-threshold policy with working vacation. Evidently, this model is an non-exhaustive service queue and the server can begin to take the vacation when there are customers in system. Many service systems are the special cases of this model and when \(m=N\), this model becomes the M/M/1 queue with \(m\)-policy in Sect. 2.

Let \(Q_2(t)\) be the number of customers in system at time \(t\) and let

$$\begin{aligned} J_2(t)=\left\{ \begin{array}{ll} 0,&{} \hbox {the system is in a working vacation period at time } t,\\ 1,&{} \hbox {the system is in a regular busy period at time } t. \end{array}\right. \end{aligned}$$

then \(\{ Q_2(t), J_2(t)\}\) is a QBD with the state space

$$\begin{aligned} \Omega = {\Big \{(k,0):0\le k\le {m-1}\Big \}}\bigcup \Big \{(k,j):k \ge m, \quad j=0 ,1 \Big \}. \end{aligned}$$

Using the lexicographical sequence for the states, the infinitesimal generator can be written as

$$\begin{aligned} Q_2 = \left[ {{\begin{array}{*{20}c} -\lambda &{}\quad {C_0 } &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad \\ {B_1 } &{}\quad {A_1 } &{}\quad {C_1 } &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad &{}\quad &{}\quad &{}\quad \\ &{}\quad &{}\quad &{}\quad {B_{m-1} } &{}\quad {A_{m-1} } &{}\quad {C_{m-1}} &{}\quad &{}\quad &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad {B_m}&{}\quad {A_m} &{}\quad {C} &{}\quad &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad &{}\quad &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad {B_{N-1}} &{}\quad {A_{N-1}}&{}\quad C &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad {B_{N}} &{}\quad {A}&{}\quad {C} &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad B &{}\quad {A} &{}\quad C &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad \ddots \ddots &{}\quad \ddots \\ \end{array} }} \right] , \end{aligned}$$

where

$$\begin{aligned} B_k&= \mu _v, 1\le k\le m-1,B_m=(\mu _v,\mu _b)^T;\\ C_k&= \lambda ,0\le k \le m-2, C_{m-1}=(\lambda ,0); A_k=-(\lambda +\mu _v),1\le k\le m-1;\\ B_k&= \left[ \begin{array}{cc} \mu _v &{} 0\\ 0 &{} \mu _b \\ \end{array}\right] ,m+1\le k\le N-1; \\ A_k&= \left[ \begin{array}{cc} -(\lambda +\mu _v)&{}0\\ 0&{}-(\lambda +\mu _b) \end{array}\right] , m\le k\le N-1.\\ C&= \left[ \begin{array}{cc} \lambda &{} 0\\ 0 &{} \lambda \\ \end{array}\right] , B=\left[ \begin{array}{cc} \mu _v &{} 0\\ 0 &{} \mu _b \\ \end{array}\right] A=\left[ \begin{array}{cc} -(\lambda +\theta +\mu _v)&{}\theta \\ 0&{}-(\lambda +\mu _b) \end{array}\right] . \end{aligned}$$

To analyze this QBD process, it is necessary to solve for the minimal non-negative solution of the matrix quadratic equation

$$\begin{aligned} R{} ^2B + RA + C = 0. \end{aligned}$$
(17)

Because that \(B,A\) and \(C\), \(R\) has the same expression (2) with that in M/M/1 queue with \(m\)-policy, we have

Theorem 5

The QBD process \(\{Q_2(t),J_2(t)\}\) is positive recurrent if and only if \(\rho < 1\).

Proof

Based on the theorem 3.1.1 of Neuts [6], the QBD process \(\{Q_2(t),J_2(t)\}\) is positive recurrent if and only if the spectral radius SP \((R)\) of the rate matrix \(R\) is less than 1, and set of equations

$$\begin{aligned} (x_0,x_{10},\ldots , x_{m-1,0},x_{m0},x_{m1},\ldots ,x_{N0},x_{N1})B[R] = 0 \end{aligned}$$
(18)

has positive solution, where

$$\begin{aligned} B[R] = \left[ {{\begin{array}{*{20}c} -\lambda &{}\quad {C_0 } &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\\ {B_1 } &{}\quad {A_1 } &{}\quad {C_1 } &{}\quad &{}\quad &{}\quad &{}\quad &{}\\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad &{}\quad &{}\\ &{}\quad &{}\quad &{}\quad {B_{m-1} } &{}\quad {A_{m-1} } &{}\quad {C_{m-1}} &{}\quad &{}\\ &{}\quad &{}\quad &{}\quad &{}\quad {B_m}&{}\quad {A_m} &{}\quad {C} &{}\\ &{}\quad &{}\quad &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad &{}\\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad {B_{N-1}} &{}\quad {A_{N-1}}&{}\quad C \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad {B_{N}} &{}\quad RB+A&{}\\ \end{array} }} \right] \end{aligned}$$

and

$$\begin{aligned} RB+A=\left[ \begin{array}{cc} -\dfrac{\lambda }{r} &{}\qquad \dfrac{\lambda }{r}-\mu _v \\ 0 &{} \qquad -\mu _b \\ \end{array}\right] . \end{aligned}$$

With (4), we can easily verify \(B[R]\) is an infinitesimal generator, that (18) has positive solution. Thus, the QBD process \(\{Q_2(t),J_2(t)\}\) is positive recurrent if and only if SP\((R)=\mathrm{max }(r,\rho )<1\).

3.2 Queue length distribution

If \(\rho < 1\), let \((Q_2,J_2)\) be the stationary limit of the QBD process \(\{Q_2(t),J_2(t)\}\). Let

$$\begin{aligned} \pi _k&= \pi {} _{k0},\quad 0\le k\le m-1; \pi _k = (\pi _{k0}, \pi _{k1} ),\quad k\ge m \\ \pi _{kj}&= P\{Q_v = k,J = j\} = \mathop {\lim }\limits _{t \rightarrow \infty } P\{Q_v(t) = k, J(t) = j\},\quad (k,j) \in \Omega . \end{aligned}$$

For convenience, let

$$\begin{aligned} \begin{aligned} \psi (k)&=1+(1-r)\displaystyle \sum _{j=1}^{N-1-k}{\left( \dfrac{\mu _v}{\lambda }\right) }^j, \quad 1\le k \le N-1;\\ \psi (N)&=r. \end{aligned} \end{aligned}$$
(19)

Theorem 6

If \(\rho < 1\), the stationary probability distribution of \((Q_2,J_2)\) is

$$\begin{aligned} \left\{ {\begin{array}{ll} \pi _{k0} = K (\dfrac{\lambda }{\mu _v})^k, \quad 0\le k \le m-1,\\ \pi _{k0} =K\dfrac{\psi (k)}{\psi (m-1)}\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1} , \quad m\le k\le N;\\ \pi _{k0}=K\beta _{N0}r^{k-N}, \quad k\ge N;\\ \pi _{k1}=K\dfrac{1}{\psi (m-1)}\dfrac{\theta r}{\mu _b(1-r)} \bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1}\dfrac{1-\rho ^{k-m+1}}{1-\rho }, \quad m\le k\le N;\\ \pi _{k1}=K\beta _{N0}\dfrac{\theta r}{\mu _b(1-r)}\displaystyle \sum _{j=0}^{k-N-1}r^j\rho ^{k-N-1-j} +K\beta _{N1}\rho ^{k-N}, \quad k\ge N+1.\\ \end{array}} \right. \end{aligned}$$
(20)

where

$$\begin{aligned} \begin{array}{ll} \beta _{N0}=\dfrac{r}{\psi (m-1)}\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1};\\ \beta _{N1}=\dfrac{1}{\psi (m-1)}\dfrac{\theta r}{\mu _b(1-r)} \bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1}\dfrac{1-\rho ^{N-m+1}}{1-\rho }.\\ \end{array} \end{aligned}$$

And, \(K\) can be achieved by the normalization condition.

Proof

With the matrix-geometric solution method, we have

$$\begin{aligned} \pi _k = (\pi _{k0} ,\pi _{k1} ) = (\pi _{N0} ,\pi _{N1} )R^{k - N}, \quad k \ge N. \end{aligned}$$
(21)

and \((\pi _{00} ,\pi _{10} ,\ldots ,\pi _{m-1,0},\pi _{m0},\pi _{m1},\ldots ,\pi _{N0},\pi _{N1})\) satisfies the set of equations

$$\begin{aligned} (\pi _{00},\pi _{10},\ldots , \pi _{m-1,0},\pi _{m0},\pi _{m1},\ldots ,\pi _{N0},\pi _{N1})B[R] = 0 \end{aligned}$$
(22)

Substituting \(B[R]\) into the above relation, we obtain the set of equations

$$\begin{aligned} \left\{ \begin{array}{l} -\lambda \pi _{00}+\mu _v \pi _{10} =0 ,\\ \lambda \pi _{k-1,0}-(\lambda + \mu _v)\pi _{k0}+\mu _v\pi _{k+1,0}=0, \quad 1\le k\le m-2 ;\\ \lambda \pi _{m-2,0}-(\lambda + \mu _v)\pi _{m-1,0}+\mu _v\pi _{m,0}+\mu _b\pi _{m1}=0 , \quad k=m-1;\\ -(\lambda +\mu _b)\pi _{m1}+\mu _v\pi _{m+1,1}=0, \qquad k=m; \\ \lambda \pi _{k-1,1}-(\lambda +\mu _b)\pi _{k1}+\mu _b\pi _{k+1,1}=0, \quad m+1\le k\le N-1;\\ \lambda \pi _{k-1,0}-(\lambda + \mu _v)\pi _{k0}+\mu _v\pi _{k+1,0}=0 , \quad m\le k\le N-1;\\ \lambda \pi _{N-1,0}-\dfrac{\lambda }{r}\pi _{N0}=0;\\ \lambda \pi _{N-1,1}+(\dfrac{\lambda }{r}-\mu _v)\pi _{N0}-\mu _b\pi _{N1}=0.\\ \end{array}\right. \end{aligned}$$
(23)

Assume that every equation in (23) can be expressed by (23–1) to (23–8), respectively. Taking \(\pi _{00}=K\), from (23–1) to (23–2), we get

$$\begin{aligned} \pi _{k0}=K\bigg (\dfrac{\lambda }{\mu _v}\bigg )^k, \quad 1\le k\le m-1 \end{aligned}$$

from (23–6),

$$\begin{aligned} \pi _{k0}=\sum _{j=0}^{k-m}{\left( \dfrac{\lambda }{\mu _v}\right) }^k\pi _{m0} -\sum _{j=1}^{k-m}{\left( \dfrac{\lambda }{\mu _v}\right) }^k\pi _{m-1,0}; \quad m\le k\le N; \end{aligned}$$

and from (23–7) and the above equation, we get

$$\begin{aligned} \begin{aligned} \pi _{m0}&=\dfrac{1+(1-r)\sum _{j=1}^{N-m-1}\bigg (\dfrac{\mu _v}{\lambda }\bigg )^j}{ 1+(1-r)\sum _{j=1}^{N-m}\bigg (\dfrac{\mu _v}{\lambda }\bigg )^j}\pi _{m-1,0}=\dfrac{\psi (m)}{\psi (m-1)}\pi _{m-1,0},\\ \pi _{k0}&=\dfrac{1+(1-r)\sum _{j=1}^{N-k-1}\bigg (\dfrac{\mu _v}{\lambda }\bigg )^j}{ 1+(1-r)\sum _{j=1}^{N-m}\bigg (\dfrac{\mu _v}{\lambda }\bigg )^j}\pi _{m-1,0}=\dfrac{\psi (k)}{\psi (m-1)}\pi _{m-1,0};\quad m\le k\le N \end{aligned} \end{aligned}$$
(24)

From (23–4), (23–5) and (23–8), we can verify step by step

$$\begin{aligned} \begin{aligned} \pi _{m1}&=\dfrac{\theta r}{\mu _b(1-r)}\dfrac{1}{\psi (m-1)}\pi _{m-1,0},\\ \pi _{k1}&=\displaystyle \sum ^{k-m}_{k=0}\left( \dfrac{\lambda }{\mu _b}\right) ^k\dfrac{\theta r}{\mu _b(1-r)}\dfrac{1}{\psi (m-1)}\pi _{m-1,0}, \quad m\le k\le N; \end{aligned} \end{aligned}$$
(25)

Substituting \(\pi _{m-1,0}\) and we can get the results for \(1\le k\le N\).

For \(k\ge N\), note that

$$\begin{aligned} R^k = \left[ {\begin{array}{cc} r^k&{} \dfrac{\theta {} r}{\mu _b (1 - r)}\sum \limits _{j = 0}^{k - 1} {r^j\rho ^{k - 1 - j }} \\ 0&{}\rho ^k \\ \end{array}} \right] , \qquad k \ge 1. \end{aligned}$$

Substituting \((\pi _{N0} ,\pi _{N1})\) and \(R^{k-N}\) into (21) , then with (23) and (24), we obtain (20). Finally, the constant factor \(K\) can be determined by the normalization condition.

Further, we can obtain the distribution of the number of customers \(Q_2\):

$$\begin{aligned} P\{Q_2=k\}&= \pi _{k0}=K\bigg (\dfrac{\lambda }{\mu _v}\bigg )^k,\quad 0\le k\le m-1;\\ P\{Q_2=k\}&= \pi _{k0}+\pi _{k1}=K\dfrac{1}{\psi (m-1)}\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1}\\&\times \bigg [\psi (k) +\dfrac{\theta r}{\mu _b(1-r)}\dfrac{1-\rho ^{k-m+1}}{1-\rho }\bigg ],\\&\qquad m\le k\le N-1;\\ P\{Q_2=k\}&= \pi _{k0}+\pi _{k1}\\&= K\bigg [\beta _{N0}r^{k-N}+\beta _{N0}\dfrac{\theta r}{\mu _b(1-r)}\displaystyle \sum _{j=0}^{k-N-1}r^j\rho ^{k-N-1-j} +\beta _{N1}\rho ^{k-N}\bigg ],\\&\qquad k\ge N. \end{aligned}$$

Meanwhile, we can easily obtain the state probabilities of a server in steady-state.

$$\begin{aligned} \begin{aligned} P\{J_2=0\}&=\displaystyle \sum _{k=0}^{\infty }\pi _{k0}\\&=K{\left[ \displaystyle \sum _{k=0}^{m-1}\bigg (\dfrac{\lambda }{\mu _v}\bigg )^k +\displaystyle \sum _{k=m}^{N-1}\dfrac{\psi (k)}{\psi (m-1)} \bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1}+ \displaystyle \sum _{k=N}^{+\infty }\beta _{N0}r^{k-N}\right] }\\&=K\left[ \dfrac{1-\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m}}{1-\dfrac{\lambda }{\mu _v}}+\dfrac{1}{\psi (m-1)}\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1} \displaystyle \sum _{k=m}^{N-1}\psi (k)+\dfrac{\beta _{N0}}{1-r}\right] \\ P\{J_2=1\}&=\displaystyle \sum _{k=m}^{\infty }\pi _{k1}= K\dfrac{1}{\psi (m-1)}\bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1} \dfrac{\theta r}{\mu _b(1-r)} \displaystyle \sum _{k=m}^{N}\dfrac{1-\rho ^{k-m+1}}{1-\rho }\\&\quad +K\displaystyle \sum _{k=N+1}^{+\infty } \bigg (\beta _{N0}\dfrac{\theta r}{\mu _b(1-r)}\displaystyle \sum _{j=0}^{k-N-1}r^j\rho ^{k-N-1-j} +\beta _{N1}\rho ^{k-N}\bigg ) \\&=K\dfrac{1}{\psi (m-1)} \bigg (\dfrac{\lambda }{\mu _v}\bigg )^{m-1}\dfrac{\theta r}{\mu _b(1-r)} \dfrac{(N-m)(1-\rho )-\rho (1-\rho ^{N-m})}{{1-\rho }^2}\\&\quad +K\bigg [\beta _{N0}\dfrac{\theta r}{\mu _b(1-r)}\dfrac{1}{1-r}\dfrac{1}{1-\rho }+\beta _{N1} \dfrac{\rho }{1-\rho }\bigg ]. \end{aligned} \end{aligned}$$
(26)

3.3 Conditional queue length and sojourn time

Now, we give conditional stochastic decomposition structures of the stationary length of waiting customers when the server is busy and there are more than or equal to \(N\) customers in the system, denoted by \(Q_2^{N}\).

We can have the expression for \(Q_2^{N}\) below

$$\begin{aligned} Q_2^{N}=\{Q_2-N|Q_2\ge N, J=1\}; \end{aligned}$$

Firstly, we discuss the conditional number of waiting customers.

Theorem 7

If \(\rho < 1\) and \(\mu _b>\mu _v\), the conditional stationary queue length \(Q_2^{N}\) can be decomposed into the sum of two independent random variables: \(Q_2^{N}=Q_0+Q_{2d}\), where \(Q_0\) is the stationary queue length of a classical M/M/1 queue without vacation, follows a geometric distribution with parameter \(1-\rho \); Additional queue length \(Q_{2d} \) has a modified geometric distribution

$$\begin{aligned} \begin{array}{l} P\{Q_{2d}=0\}=\dfrac{\beta _{N1}}{\delta },\\ P\{Q_{2d}=k\}=\left( 1-\dfrac{\beta _{N1}}{\delta }\right) (1-r)r^k,\qquad \quad k\ge 1. \end{array} \end{aligned}$$
(27)

where

$$\begin{aligned} \delta =\beta _{N1}+\beta _{N0}\dfrac{\theta r}{\mu _b(1-r)^2}. \end{aligned}$$

Proof

Conditional probability that the server is busy and there are more than or equal to \(N\) customers in the system

$$\begin{aligned}&P\{Q_2\ge N,J=1\}=\displaystyle \sum _{k=N}^{\infty }\pi _{k1} \\&\quad =K\left[ \beta _{N0}\dfrac{\theta r}{\mu _b(1-r)}\displaystyle \sum _{k=N+1}^{+\infty }\displaystyle \sum _{j=0}^{k-N-1}r^j\rho ^{k-N-1-j} \beta _{N1}\sum _{k=N}^{+\infty }\rho ^{k-N}\right] \\&\quad =K\left[ \beta _{N1}\dfrac{1}{1-\rho }+\beta _{N0}\dfrac{\theta r}{\mu _b(1-r)^2} \dfrac{1}{1-\rho }\right] =K\dfrac{1}{1-\rho }\delta . \end{aligned}$$

So, for \(k\ge 0\)

$$\begin{aligned} P\{Q_2^{N}=k\}&= P\{Q=k+N|Q\ge N,J=1\}=\dfrac{\pi _{k+N,1}}{P\{Q_2\ge N,J=1\}} \\&= \dfrac{1-\rho }{\delta }\bigg [\beta _{N1}\rho ^{k}+\beta _{N0}\dfrac{\theta r}{\mu _b(1-r)}\displaystyle \sum _{j=0}^{k-1}r^j\rho ^{k-1-j}\bigg ] \end{aligned}$$

And, the probability generating function of \(Q^{N}\) is as follows

$$\begin{aligned} Q_2^{N}(z)&= \displaystyle \sum ^\infty _{k=0}z^k P\{Q_2^{N}=k\}\\&= \dfrac{1-\rho }{\delta }\displaystyle \sum ^\infty _{k=0}z^k{\left[ \beta _{N1}\rho ^{k}+\beta _{N0}\dfrac{\theta r}{\mu _b(1-r)}\sum _{j=0}^{k-1}r^j\rho ^{k-1-j}\right] }\\&= \dfrac{1-\rho }{\delta }{\left[ \beta _{N1}\dfrac{1}{1-\rho z}+\beta _{N0}\dfrac{\theta {} r}{\mu _b (1 - r)}\dfrac{z}{1-r z}\dfrac{1}{1-\rho z}\right] }\\&= \dfrac{1-\rho }{1-\rho z}\dfrac{1}{\delta }\Bigg [\beta _{N1}+\beta _{N0}\dfrac{\theta {} r}{\mu _b (1 - r)^2}\dfrac{(1-r)z}{1-r z}\Bigg ]\\&= \dfrac{1-\rho }{1-\rho z}Q_d(z)=Q_0(z)Q_{2d}(z). \end{aligned}$$

From the equation \(Q_{2d}(z)\), we can get the result.

Equation (27) indicates that the additional delay \(Q_{2d}\) can be written as the mixture of two random variables: \(Q_{2d}=q_0X_0+q_1X_1\), where \(q_0=\dfrac{\beta _{N1}}{\delta },\, q_1=\dfrac{\beta _{N0}}{\delta }\dfrac{\theta {} r}{\mu _b (1 - r)^2}\), and \(X_0\equiv 0,\, X_1\) follows a geometric distribution with parameter \((1-r)\) on the set \(\{1,2,\ldots \}\).

With the conditional stochastic decomposition structure in Theorem 7, we can easily get means

$$\begin{aligned} \begin{array}{ll} E(Q_{2d})=\dfrac{\beta _{N0}}{\delta }\dfrac{\theta {} r}{\mu _b (1 - r)^3},\qquad \\ E(Q_2^{N})=\dfrac{\rho }{1-\rho }+E(Q_{2d})=\dfrac{\rho }{1-\rho }+\dfrac{\beta _{N0}}{\delta }\dfrac{\theta {} r}{\mu _b (1 - r)^3}.\\ \end{array} \end{aligned}$$

Denote the conditional sojourn time by \(E(S_2^{N})\), we have

$$\begin{aligned} E(S_2^{N})= \dfrac{E(Q_1^{N})+N}{\lambda }. \end{aligned}$$

Similar to analysis in Sect. 3, the LSTs of the conditional sojourn times when the server is busy and vacation can be computed by

$$\begin{aligned} S^{*b}_{mN}(s)=\displaystyle \sum _{k=m}^{\infty } \dfrac{\pi _{k1}}{P\{J=1\}} \bigg (1-\dfrac{s}{\lambda }\bigg )^k;\qquad S^{*v}_{mN}(s)=\displaystyle \sum _{k=0}^{\infty } \dfrac{\pi _{k0}}{P\{J=0\}} \bigg (1-\dfrac{s}{\lambda }\bigg )^k. \end{aligned}$$

The LST of the sojourn time of an arbitrary customer can be concluded that

$$\begin{aligned} S^*_{mN}(s)={P\{J=1\}}S^{*b}_{mN}(s)+{P\{J=0\}}S^{*v}_{mN}(s) =\displaystyle \sum _{k=0}^{\infty }{P\{Q_2=k\}} \bigg (1-\dfrac{s}{\lambda }\bigg )^k, \end{aligned}$$

4 Performance analysis

In the above analysis, we obtain some performance measures, such as the mean queue length, server’s state probability and conditional waiting time in the steady state. The working vacation policy enables the system to operate flexibly and the queue length and waiting time may decrease. Thus, our model should be reasonable to analyze the practical problems. For example, consider an ATM networks, where cell arrivals in a switched virtual channel(SVC) form a poisson process with parameter \(\lambda \), cell transmission time is an exponential distributed random variable with rate \(\mu _b\). When there are less than certain value \(m\) cells, we set a period of working vacation, during which arriving cells can be transmitted at a lower rate \(\mu _v\)(\(\mu _v<\mu _b\)) immediately in order to save the operating cost. The policy of working vacation takes over cell transmission and save switching cost together, therefore, our model is fitter for practical situation than others.

In Table 1, in a SVC, some special performance measures are presented when \(\rho =0.67\) and \(\theta =0.25\) in two cases, where \(E(Q_{11})(E(Q_{12})), P_1\{J_1=1\}(P_2\{J_1=1\}), E(S_1)(E(S_2))\) represent the mean number of cells, the state probability of the SVC in the normal period and the processing time with the lower transmission rate \(\mu _v=0.25 (\mu _v=0.5)\), respectively. Evidently, with the increase of \(m\), the state probability of the SVC in the normal period decreases, but the expected mean number and processing time of cells may not have the decreasing/increasing property. With the increase of the value of \(m\), the expected mean number and processing time of cells may increase first, when \(m\) increases to one value, the the expected mean number or processing time of cells begins to decrease. This may be caused by the fact that the SVC also can provide low transmission below \(m\) level. When the threshold value \(m\) is small(\(m>1\)), the transfers of two periods should be more frequent to induce more crowd of the cells than that in no threshold case(\(m=1\)). But when the threshold is increased to one proper value(\(m>1\)), more cells will be transmitted by the slow rate during the vacation period and certainly the expected mean number and processing time of cells will also decrease. This also demonstrates that the connection of the threshold policy and working vacation will increase the efficiency of the system.

Table 1 Numerical results when \(\rho =0.67\) and \(\theta =0.25\)
Full size table

For the model, the different systems may have the different parameters in the practical problems. Certainly, the change of parameters, such as the lower service rate and vacation rate in the system, also may influence the performance measures in the model. So, we present numerical examples in some situations to explain that our model represents some practical problems reasonably well.

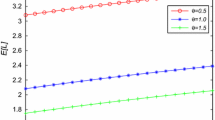
According to the expression for \(E(Q_1)\), we show the effect of \(\mu _v\) on the queue length when two parameters of the system are fixed in two situations (see Fig. 1). Evidently, along with the increase of the \(\mu _v\), i.e., the service rate in the vacation period, the number of the customers in steady state decreases. And, we also find that the vacation rate and arrival rate have small and large effect on the queue length, respectively. Meanwhile, we only show the trend of the certain range of \(\mu _v\), and if the value of \(\mu _v\) is too small or approaches \(\mu _b\), it is not worth to take service in the vacation period. Meanwhile, with the increase of \(\theta \), the expected queue length also decreases (see Fig. 2). Such change trends are consistent with the practical situations which can be simulated by the model we consider.

Fig. 1
figure 1

The Curve of expected queue length with the change of \(\mu _v\)

Full size image
Fig. 2
figure 2

The Curve of expected queue length with the change of \(\theta \)

Full size image

In this model, we set a threshold \(m\) and \(N\), and under the thresholds, the server will work at the lower rate \(\mu _v\). Thus, the system is a model with two service periods: the higher speed and lower speed periods. Such policy will decrease the service cost, but with the lower service rate, the waiting time and the queue length will increase to make the cost of system rise correspondingly. Thus, we must consider the vacation service rate to minimize the system cost.

The cost of the system is considered. Assume \(c_w\) represent the unit time cost of every waiting customer, and \(c_1\) and \(c_2\) are the service costs every unit time during the normal working level and vacation period, respectively. Thus, we can establish the cost function \(Z(m,\mu _v)\) per time:

$$\begin{aligned} Min: Z(m,\mu _v)=c_wE(Q_1)+c_1\mu _{b}P\{J_1=1\}+c_2\mu _vP\{J_1=0\} \end{aligned}$$

where \(E(Q_1),P\{J_1=1\}\) and \(P\{J_1=0\}\) have been obtained in sections above.

The optimal \(m^*\) and \(\mu _v^*\) to minimize \(Z(m,\mu _v)\) should be found. First, we consider the optimal \(m\). When \(\mu _v\) is constant, \(m^*\) satisfies

$$\begin{aligned} Z(m^*)\le Z(m^*+1),\quad Z(m^*)\le Z(m^*-1). \end{aligned}$$

By the Boundary analysis method(BAM), the minimal \(m^*\) can be given step by step. The basic steps can be showed as follows: Take \(m=k(k\ge 1)\), if \(Z(k)\le Z(k+1),Z(k)\le Z(k-1)\), the optimal threshold \(m^*=k\), and we obtain the minimal threshold; otherwise, take \(m=k+1\), continue the same process.

In theory, we should obtain the optimal threshold in this process, but in Fig. 3, we obverse that with the increase of the value \(m\), the system cost may always decrease so that no optimal threshold can be found, but the decreasing trend becomes not evident when \(m\) increases to one certain value. This can be explained in practice and if there are not leavings/balkings of the customers and once they arrive at the system, they will be waiting until their service completion, and the service agent controls the whole service process. Under this condition, the larger the threshold is, the smaller the cost is, but when the threshold achieves one certain value, most customers will be served by the slow rate and the effect of the normal service cost \(c_1\) on the system cost will decrease. This also will cause the unwillingness and leaving/balking of the customers. And we will consider this phenomenon in our further research.

Fig. 3
figure 3

The Curve of system costs with the change of \(m\)

Full size image

If \(m\) is given, the optimal vacation service rate \(\mu _v^*\) can also be found in special situations. In Fig. 4, the system costs when \(c_w=8,c_1=20,c_2=10\), are presented and from the trend of the curve, the optimal vacation service rate \(\mu _v^*\) exists \((0<\mu _v^*<0.6)\).

Fig. 4
figure 4

The Curve of system costs with the change of \(\mu _v\)

Full size image

5 Conclusion

In this paper, we consider the M/M/1 queue with two threshold-policies and working vacations. In fact, we establish the system with lower and higher speed operation periods. Many performance measures, including the state probability of the server and corresponding expected conditional queue length and sojourn time are obtained. With those results, we can further optimize for the \((m,N)\) and the engineers can set up the reasonable thresholds to make the cost of the system lowest or profit highest. But there are some works which the paper cannot give more analysis, for example, the practical sojourn time or its distribution. The service process in two threshold-policy system is so complex that we can not conduct the specific waiting time analysis. This may be the weakness of the model, but we give the sojourn time analysis under two threshold policies which also can give some guides for the practice and further research.

This paper only consider the system indices for the M/M/1 queue with two threshold-policies and working vacations. As we stated in Sect. 4, the larger threshold may induce the customers to leave/balk for other service agents. In further research, we may consider whether the customers’behavior can be analyzed because the behavior may be complex under some information levels if one or two-threshold policy is established under working vacations.