M/M/1 Vacation Queue with Multiple Thresholds: A Fluid Analysis

Abstract

We propose an analytical method for an M/M/1 vacation queue with workload dependent service rates. We obtain the distribution of the workload in the system, and consider a power-saving and performance trade-off problem. Numerical experiments reveal that square root service rate function has lower cost than that of linear and quadratic service functions under certain scenarios.

1 Introduction

Cloud computing is supported by data centers with a large number of servers and a huge amount of energy consumption. This calls for energy saving mechanisms in data centers while keeping service level high. A natural approach to this problem is to adjust the processing rate of data centers according to the workload level in the system so as to balance the energy consumption and performance. This can be realized by turning the servers on and off (ON-OFF policy) in data centers  [3], frequency scaling or dynamic voltage and frequency scaling (DVFS)  [5].

In this paper, we model power-saving in data centers by a single server queueing system with vacation and workload-dependent service rate. We are able to obtain the probability distribution and relevant statistics of the workload in the system. This allows us to consider the energy-performance trade-off problem and to investigate optimal service rate function as well as vacation policy.

As related work, Yajima and Phung-Duc  [5] consider an M/M/1 system where the service rate is proportional to the number of jobs in the system and analyze the response time distribution. Marin et al.  [2] consider an M/M/1 system with SRPT scheduling policy and K speeds. In these papers, the service rate depends on the number of jobs in the system. In contrast, in our present paper, we consider the workload in the system instead of the number of jobs. As a closely related work, Sakuma et al.  [4] consider the same model and analyzed it using renewal theory and level-crossing approach. Yazici and Akar [6] analyzed the MAP/PH/1 queue with workload-dependent behavior.

Fig. 1.

The modulating CTMC of the fluid model, and the corresponding drift rates.

In this paper, we approach the problem using fluid queues. We numerically solve the exact distribution of the workload, and analytically compute relevant statistics. One of the advantages of our approach is that it could easily be extended to analyze models with MAP arrivals and PH-type service times, which is the main difference between our work and [4]. The remainder of the paper is organized as follows. In Sect. 2, we describe our model in detail. Section 3 shows some numerical results while concluding remarks are presented in Sect. 4.

2 System Model

We consider an infinite-capacity vacation queue with Poisson arrivals, whose intensity is $\lambda$, and exponentially distributed job sizes with mean $1/\mu$. The service rate depends on the instantaneous workload, x, through a piecewise-constant function, i.e. the rate is $r_i$ when $B_{i-1}<x<=B_{i}$ where $B_0=0,\ B_K=\infty$ and $i\in \{1,\ldots ,K\}$. The server enters vacation when the workload hits 0, and returns from vacation when the workload reaches $B_V$. Without loss of generality, we assume $B_V\in \{B_1,\ldots ,B_{K-1}\}$. We model the workload as a fluid and thus, the system can be described as a multi-regime feedback fluid queue  [1] due to the piecewise dependence of the service rate to the workload. The modulating continuous-time Markov chain (CTMC) is given in Fig. 1, along with the associated drift rates for each state. Notice that transition rates also depend on the workload, hence producing a multi-regime fluid model.

To obtain the numerical results, we employed the methodology described in  [1]. One important detail worth mentioning is that the drift rate in the vacation regime is 0, and this needs special treatment. In general, the pdf of the regimes with 0 drifts can be expressed as a linear combination of the pdf’s of the remaining states; see equations (20)–(22) in [1] and the explanations therein. Furthermore, Vacation state does not exist beyond $x>B_V$.

After the distribution of the fluid in each state is obtained, the Arrival and Vacation Arrival states are censored out, as the linear increases in these two states represent the abrupt increases in the workload due to job arrivals and in reality, the system does not spend any time in either of these states.

To study the effect of the rate function and the vacation threshold, $B_V$, we consider a cost function as follows  [2]:

$$\begin{aligned} C = \left( \sum _{i=1}^{K} p_i r_i^2\right) + p_0 c_0 + c_h E[V] + c_s \lambda V(0), \end{aligned}$$

(1)

where $p_i$ is the probability that the server works at speed $r_i$, $p_0$ is the probability that the server is on vacation, $c_0$ is the power consumption when the server is on vacation, $c_h$ is the weight placed on the mean workload, i.e., performance, E[V] is the mean workload, $c_s$ is the switching cost, and V(0) is the probability that the workload is 0. Here, the product $\lambda V(0)$ is equal to the reciprocal of the mean cycle time from the beginning of one vacation to the next [4], and hence represents switching frequency of the server from OFF to ON.

Following the definitions in [1], the pdf of the workload is of the form

$$\begin{aligned} f^{(i)}(x) = a_0^{(i)} L_0^{(i)} + a_-^{(i)} \exp {(A_-^{(i)}(x-B_{i-1}))} L_-^{(i)} + a_+^{(i)} \exp {(-A_+^{(i)}(B_i-x))} L_+^{(i)},\\ B_{i-1}<x<B_i,\ i\in \{1,\ldots ,K\}, \end{aligned}$$

(2)

where $A_-^{(i)}$ and $A_+^{(i)}$ are blocks of a matrix obtained through a similarity transform on $A^{(i)}=Q^{(i)}(R^{(i)})^{-1}$, $Q^{(i)}$ and $R^{(i)}$ being the infinitesimal generator of the CTMC and the diagonal drift matrix, respectively, for each regime, $L_0^{(i)}$, $L_-^{(i)}$, and $L_+^{(i)}$ are blocks of the inverse of the aforementioned similarity transform matrix, and $\left[ a_0^{(i)},\,a_-^{(i)},\,a_+^{(i)}\right]$ are coefficients obtained through a set of boundary conditions  [1]. Hence, the required statistics can be obtained as

$$\begin{aligned} p_i = \int _{B_{i-1}}^{B_i}{f_S^{(i)}(x)\,dx},\quad \text {and}\quad E[V] = \sum \limits _{i=1}^{K} \int _{B_{i-1}}^{B_i}{x\,f_S^{(i)}(x)\,dx}, \end{aligned}$$

(3)

where $f_S(x)$ is the pdf of the workload in Service state after Arrival and Vacation Arrival states are censored out. Considering that the pdf expression in (2) contain matrix exponentials only, it is clear that the integrals in (3) can be evaluated analytically (We omit the exact expressions due to space limitation.).

3 Numerical Results

We obtained numerical results with $\lambda =1$, $\mu =1$, $B_i=(i/4),\,i\in \{1,\ldots ,40\}$ via implementation in Matlab. The parameters $c_0,\ c_h,\ c_s$, and $B_V$ are varied. The service rate functions we experimented with are $r^{sr}_i = \sqrt{ B_{i-1} } + 1,\ r^{lin}_i = B_{i-1} + 1,\ r^{sq}_i = (B_{i-1})^2 + 1,$ representing square root, linear, and square dependence, respectively, on the threshold values. We first give pdf plots of the workload in Fig. 2 for $B_V\in \{2,4,6\}$ and $r_i=r^{lin}_i$. This illustrates the dynamics of the workload and the effect of the selection of vacation threshold, $B_V$.

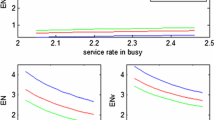
Next, we compare the mentioned rate functions under various operating scenarios with respect to $c_0,\ c_h,\ c_s$, and $B_V$. We plot in Fig. 3 normalized service cost (C values for $c_0 = c_h = c_s = 0$), $p_0$, normalized E[V], and $\lambda V(0)$, with $r_i=r^{lin}_i$. As $B_V$ is increased, all but $\lambda V(0)$ increase monotonically. Hence, we conclude that $c_s$ is the critical component of the cost against other coefficients. In Fig. 4, we plot the cost for $c_s\in \{10,30,50\}$ with $r_i=r^{lin}_i$. We observe that the cost function turns out to be convex in this scenario, and there exist optimum $B_V$ values for each $c_s$ value, which are marked with asterisks on the plots. Finally, we compare the rate functions with $c_0=c_h=1,\ c_s=30$ in Fig. 5. Again, we observe a similar dynamic with respect to $B_V$.

Fig. 2.

Workload pdf with $B_V\in \{2,4,6\}$, and $r_i=r^{lin}_i$.

Fig. 3.

Cost components against $B_V$. Service cost and E[V] are normalized, with maximum values of 5.8137 and 4.0301, respectively.

Fig. 4.

Costs for different values of $c_s$ with $r_i=r^{lin}_i$, $c_0=c_h=1$.

Fig. 5.

Costs for different rate functions, $c_0=c_h=1,\ c_s=30$.

4 Conclusion

In this study, we model the M/M/1 vacation queue for the purpose of performance analysis and optimization of cloud data centers. The main mathematical tool we use for our model is multi-regime fluid queues. We observe that the cost is sensitive to the selection of several parameters, as well as the rate function. We quantitatively demonstrate the behavior of the cost function with respect to vacation threshold. It is clear that further analysis is necessary to determine realistic values for the cost coefficients. Hence, future studies will comprise extensive experimentation with regards to the cost parameters, and improvement of the model by considering finite buffer systems and more complicated inter-arrival time and job size distributions.