A novel two-stage stochastic programming model to design an integrated disaster relief supply chain network-a case study

Abstract

When a disaster strikes, there is always a demand for life-supporting commodities, whose slow and ineffective delivery can result in huge human and financial losses. Warehouse location and the storage of necessary relief commodities (RCs) before a disaster, and the proper distribution of RCs among affected people following a disaster can improve performance and reduce latency when responding to a given disaster. Hence, many researchers have focused on these fields while overlooking some crucial actual conditions as a result of the complexity of the problem. Consequently, this study develops a location-inventory-distribution problem in disaster relief supply chain (DRSC) considering the gradual injection of the limited pre-disaster budgets, the time value of money, and various evaluation criteria for locating warehouses. In this regard, a novel multi-objective two-stage scenario-based stochastic programming model under a pre-disaster multi-period planning time horizon (PTH) is presented. In each period, pre-disaster warehouse location and inventory management are addressed in the first stage, and the post-disaster distribution of the stocked RCs is planned in the second stage. Utilizing new priority-weighted service utility and balance measures, the model strives to optimize deprivation cost, demand coverage, and fair service. The maximization of warehouses’ utility is done according to various criteria and using a data envelopment analysis (DEA) model integrated with the model. The applicability and performance of the model are validated via a real-world case study followed by various tests and sensitivity analyses. The outcomes show that the model significantly improves logistics and deprivation costs, satisfied demands, fair service, and warehouses’ utility.

1 Introduction

Disasters have always significantly and extensively impacted and threatened human lives worldwide. However, humans are still unable to predict accurately and prevent disasters. On the one hand, the increase in the number of catastrophes and the expansion of their destructive range, and on the other hand, population growth in different areas of the world have increased material losses and human casualties caused by such incidents. The Emergency Events Database EM-DAT reports 399 natural disasters worldwide in 2023, which resulted in 86,473 fatalities, affected 93.1 million people, and caused $202.7 billion in economic damage (EM-DAT, http://www.emdat.be).

The losses caused by disasters cannot be compensated in various aspects, especially the human aspect; however, with preventive measures and proper planning to provide necessary preparations for coping with such incidents, these losses can be reduced as much as possible. In this regard, pre-disaster warehouse location and inventory management, as well as relief distribution planning are vital and critical tactics to improve relief performance, as they directly and significantly affect demand coverage, relief time, victims’ satisfaction, and relevant costs (Khalili-Damghani et al. 2022). Moreover, any incorrect measures in these areas result in a dramatic increase in human and financial losses. For instance, during Hurricane Katrina in 2005, inefficient storage of crucial RCs considerably delayed relief operations. The RCs that had been pre-positioned were far less than what was needed and were stocked too far from the impacted areas (Pradhananga et al. 2016). According to this experience, RCs were overstocked in 2006. Nonetheless, no massive hurricanes occurred in 2006, resulting in the loss of 279 truckloads of food valued at about $43 million (Hu et al. 2019). When the Bam earthquake struck Iran in 2003, a high percentage of stored RCs were lost, as some warehouses were located in inappropriate and unsafe locations that were entirely or heavily damaged by the earthquake. In the early days following the earthquakes in Haiti and Chile in 2010, some victims plundered RCs due to the inequitable distribution policy (Hu et al. 2016). Thus, owing to the high unpredictability of the time, place, and magnitude of a disaster and the restricted prior information on post-disaster demands and donations, relief organizations (ROs) encounter enormous challenges when deciding where to locate warehouses and how to manage inventories at pre-disaster (preparedness phase) and how to distribute RCs at post-disaster (response phase). Consequently, numerous researches have recently been carried out in these areas. The following provides a concise review of some of the studies, which have determined locations for stockpiling RCs, scheduled the procurement and storage of required RCs in the preparedness phase, and adjusted the distribution strategy of RCs in the response phase.

Rezaei-Malek et al. (2016a) minimized human suffering by maximizing a new function calculated based on the priorities of RCs and affected areas, and the utility of delivery time and the fraction of the covered demand.

Li et al. (2018) proposed a cooperative maximal covering location model in which RCs were given priority.

Sanci and Daskin (2019) integrated location, storage, damaged routes restoration, distribution, and routing decisions under backlogged shortages.

Wang and Nie (2019) presented two mathematical models considering traffic congestion and a criticality weight for each RC.

To provide more service to the demand point less resistant to an earthquake, Wang et al. (2020) introduced a seismic resilience index calculated using fault tree analysis, analytic hierarchy process, fuzzy set theory, and neural network methods.

Unlike Abazari et al. (2021), who accounted for perishability when planning post-disaster distributions, Rezaei-Malek et al. (2016b), Tavana et al. (2018), Akbarpour et al. (2020), and Sheikholeslami and Zarrinpoor (2023) looked into the inventory management of perishable RCs prior to the disaster. They made the supposition that if the supply’s remaining lifespan is less than a certain threshold, it can be sold (sale mechanism; Rezaei-Malek et al., Tavana et al., and Sheikholeslami and Zarrinpoor) or sold back to the suppliers (buyback mechanism; Akbarpour et al.) at pre-disaster. Unlike Akbarpour et al., the others also made decisions about the lifespan of purchased commodities. Tavana et al. modeled the post-disaster distribution of RCs as a multi-echelon multi-depot vehicle routing model. Akbarpour et al. also located mobile pharmacies at each post-disaster period using a cooperative coverage mechanism. Additionally, in order to provide required medicines at each pre-disaster period, they presented a multi-sourcing mechanism based on option and buyback contracts with the pre-positioning policy applied only to critical medicines, considerable and time-dependent lead time and safety inventories. Abazari et al. took account of various vehicles and determined the needed number of each vehicle and the type of vehicle of each transportation. They presumed that a commodity would decay if its travel time exceeded a certain amount in the response phase. Managing the transfer of injured people to hospitals and health centers, the transfer of affected people to shelters, transport fleet, human resources were other primary concerns of Sheikholeslami and Zarrinpoor.

In addition to Akbarpour et al., the following studies also paid attention to procuring RCs in both the response and preparedness phases. Condeixa et al. (2017), and Che et al. (2024) considered RCs donated in the post-disaster phase. Haghi et al. (2017) also planned transferring injured people to hospitals and health centers. In the response phase, Aslan and Çelik (2019) addressed decisions on transportation, repairing damaged roads, and the arrival times of RCs at demand points, in addition to how to distribute RCs and the re-procurement of RCs. They attempted to minimize total response time by considering three approaches based on efficacy, equity, and robustness. Hu and Dong (2019) took into consideration physical inventory, as well as price discounts based on delivery time and order quantity, as supplier selection criteria. Additionally, they assumed that the RO would pay a fine to suppliers for utilizing their physical inventory in the response phase to compensate for the risk of losing their regular customers. Cotes and Cantillo (2019) optimized human suffering by minimizing the total social cost.¹ Boostani et al. (2020) took into account the ecological effects of the packaging of RCs and CO₂ emissions in the shipments of the proposed network and strived to minimize these effects. Nezhadroshan et al. (2021) considered the possibility of secondary disasters occurring after a primary one and also decided on the transportation mode of some network shipments at post-disaster. Moreover, their model maximized the resilience level of each relief facility. Ghasemi et al. (2022a) designed a humanitarian relief network to manage the blood supply chain in disaster situations. In addition to Haghi et al., Cotes and Cantillo, Hu and Dong, Akbarpour et al., Boostani et al., Wang et al., Nezhadroshan et al., and Ghasemi et al., Torabi et al. (2018), and Aghajani et al. (2023) also utilized a multi-sourcing mechanism to procure RCs. Torabi et al. (2018) integrated a multi-sourcing mechanism with a quantity flexibility contract and accounted for monetary donations in the post-disaster budget. Aghajani et al. (2023) introduced a procurement-warehousing-distribution model under supply disruption. In the pre-disaster, the model set up a number of multi-period quantity flexibility contracts with primary suppliers, a number of dynamic option contracts with backup suppliers, and a multi-period warehousing contract with a third party providing warehousing service. The model also adjusted the required storage spaces in the post-disaster.

The following papers employed robust optimization methods to develop the problem under uncertainty. Rezaei-Malek et al. (2016b), Haghi et al., Nezhadroshan et al., and Ghasemi et al. developed a two-stage robust stochastic programming model according to the approaches proposed by Mulvey et al. (1995), and Yu and Li (2000). Condeixa et al. proposed a two-stage stochastic mean-conditional value-at-risk (CVaR) model. A fuzzy value-at-risk programming model with credibility constraints was developed by Bai et al. (2018). Elçi and Noyan (2018) presented a two-stage chance-constrained stochastic mean-CVaR model. In this study, lost shortages are only possible in scenarios where the sum of the probabilities of their occurrence does not exceed a predetermined threshold. A min–max robust model was presented by Aslan and Çelik, and Akbarpour et al.. Chen (2020) developed a risk-averse Ψ-expander robust model and showed that this model outperforms stochastic models in terms of shortage cost. Erbeyoğlu and Bilge (2020) also optimized the locations and sizes of distribution centers at post-disaster and formulated a two-stage robust stochastic model. They assigned each demand point to the nearest distribution center that could cover it within a service coverage window. Furthermore, they assumed a minimum fulfilled demand for each distribution center within each service coverage window that must be met by the warehouses that could cover it. Li et al. (2020) proposed a three-stage scenario-based mixed stochastic-robust programming model. They considered secondary disasters, which could result in a significant improvement in the covered demand. In addition, they also planned victims’ accommodation. Wang et al. (2021) prioritized RCs and modeled their problem as a two-stage distributionally robust programming model based on the worst-case mean-CVaR criterion. They demonstrated that the suggested model outperforms its stochastic equivalent in terms of objective value and solution stability. A risk-averse two-stage stochastic programming model that takes into account a CVaR constraint was presented by Noyan et al. (2022). Zhang et al. (2022) presented a distributionally robust programming model that performs better than its stochastic equivalent. A two-stage distributionally robust programming model was developed by Che et al. (2024). Zhang et al. (2024) introduced a robust programming model considering secondary disasters.

Ghasemi and Khalili-Damghani (2021), Ghasemi et al. (2022b), and Khalili-Damghani et al. (2022) developed a simulation–optimization approach in their studies. They utilized the simulation approach in order to estimate some of the model’s parameters. Ghasemi and Khalili-Damghan, and Khalili-Damghani et al., respectively, proposed a robust programming model and a stochastic programming model to determine the optimal locations and inventory levels of distribution and storage centers, and how to distribute RCs in the designed network in the response phase. Khalili-Damghani et al. considered higher priority in coverage for the affected area that has a larger population; thus, equity in the distribution of RCs was disregarded. Ghasemi et al. determined the optimal locations and capacities of shelters and warehouses, homeless people, injured people, corpses, relief staff, vehicles, and RCs flows, and the best routes for the evacuation of victims at post-disaster. They minimized the total probability of unsuccessful evacuation in routes and the maximum number of unsatisfied demands for relief staff, in addition to the total cost.

Table 1 summarizes the above-mentioned body of research and highlights the critical distinctions between these studies and the present paper and some of the gaps observed in the problem under study.

Table 1 A comparison of the features of the proposed model with the most relevant studies in the DRSC literature

Interviews conducted with certain of administrative managers in Mashhad’s² ROs and studies undertaken stimulated us to develop an integrated location-inventory-distribution problem in a three-level network, including supply sources, warehouses, and affected areas under a pre-disaster multi-period PTH, which is formulated as a multi-objective two-stage scenario-based stochastic programming model. In each period, the first stage involves determining the optimal location, storage capacity, and retrofitting level of warehouses and the number of RCs purchased for each warehouse in the pre-disaster, and the second stage decides how to give out RCs among the disaster victims in the post-disaster. The followings are the significant contributions of our research that have not yet been addressed in the DRSC literature and highlight the major gaps observed in the problem under study:

• Despite the large number of researches conducted in DRSC, actual conditions have been overlooked in many inquiries as a result of the complexity of the problem (Kunz et al. 2017; Besiou and Van Wassenhove 2020). In particular, limited budgets for pre-disaster planning have been only considered in a few studies. Moreover, in all these studies, at the beginning of the pre-disaster PTH, the total budgets are immediately accessible, i.e., the total budgets are injected into the project at once and instantaneously (instantaneous budget injection). As a result, the optimal decisions taken to location warehouses and manage inventories prior to the disaster have been implemented immediately, simultaneously, and at once at the beginning of the project.

In practice, owing to the RO’s financial restrictions, the total pre-disaster budgets can only be gradually made available over time (gradual budget injection); therefore, decisions taken can only be implemented sequentially over the pre-disaster PTH, not all at once, immediately, and simultaneously. Hence, limited budgets gradually injected into the project over the pre-disaster PTH are considered in the present study. Accordingly, the pre-disaster PTH is divided into several periods, and as a consequence, integrated location, inventory management, and distribution problems are modeled dynamically (time-dependent) and optimized by a multi-period optimization approach. Notably, considering a dynamic and multi-period pre-disaster operational environment, in addition to information updates and greater flexibility of planning, results in considering the inter-temporal effects of operations and improving the coordination of decisions (Holguín-Veras et al. 2013). However, only the studies conducted by Rezaei-Malek et al. (2016b), Tavana et al. (2018), Akbarpour et al. (2020), and Sheikholeslami and Zarrinpoor (2023) took into account the preparedness phase as a dynamic and multi-period environment due to the inventory management of perishable RCs. Furthermore, in all these researches, warehouses have been established simultaneously prior to the disaster; as a result, unlike inventory management and distribution problems, the location problem has been modeled as a static one (time-independent). However, in actual conditions, the simultaneous establishment of the necessary warehouses before the disaster cannot be possible due to various reasons, such as shortage of financial resources, and lack of human resources.

• The DRSC’s principal goal is to lessen human suffering and mortality to the greatest extent. In addition to efficiency, among the most critical factors that must be considered in DRSC models, efficacy, equity, and happiness/distress play a key role. Noteworthy, a handful of researches simultaneously optimized these factors.

Logistics costs are included in efficiency. However, measures such as coverage, travel distance, response time, security, reliability, or a mix of them, can be used to gauge efficacy (Gutjahr and Nolz 2016). Notably, efficacy is far more crucial than efficiency in DRSCs since human concerns precede financial ones (Balcik and Beamon 2008).

Victims’ expectation that no privileges or priority for particular groups of people necessitates fair service. In particular, the equity concept, which encompasses balance and equitability, is typically used to describe fair service (Karsu and Morton 2015; Gutjahr and Nolz 2016). The balance concept implies serving groups of individuals distinct in terms of their claims, needs, and preferences, as opposed to the equitability concept, which alludes to serving indistinguishable groups of people (Karsu and Morton 2015). Due to various factors like population and calamity severity, different affected areas have varied demand quantity and priority (Gralla et al. 2014; Nagurney et al. 2015). Hence, the balance concept should be employed to define fair service to prevent a potential societal catastrophe (Rezaei-Malek and Tavakkoli-Moghaddam 2014). It is worth noting that so little researchers paid attention to the balance concept.

In addition, reducing victims’ difficulty, pain, affliction, deprivation, social disruptions, and unpleasant emotions is one of the DRSC’s most significant and crucial goals, described by the distress criterion. Indeed, distress alludes to social and psychological expenses, which have been addressed in a tiny minority of studies (Karsu and Morton 2015). In this regard, Holguín-Veras et al. (2013) introduced the notion of deprivation cost to measure the suffering of victims deprived of vital RCs and estimated it as a non-decreasing convex function of deprivation time.

Considering the above materials, the current study, in addition to optimizing the efficiency, strives to optimize the efficacy, balance and distress of the considered DRSC network by developing a novel objective function, which is formulated as a weighted sum of new efficacy-distress and balance measures. Specifically, this objective function indicates the desire to service the affected areas with the greatest possible number of RCs and the lowest possible deprivation cost in the fairest possible manner.

Aiming to maximize the efficacy of the DRSC network, Noham and Tzur (2018) utilized the ratio of fulfilled demand to travel time. This research, inspired by Noham and Tzur, and Holguín-Veras et al. (2016), introduces the new efficacy-distress measure, which is called priority-weighted service utility and is estimated as the ratio of the fraction of fulfilled demand to deprivation cost multiplied by the priority of the affected area.

In order to distribute RCs equitably among affected areas, Tzeng et al. (2007) adopted the minimal amount of the fraction of the total satisfied demand among all affected areas as a balance measure since the amount of demand varies depending on the affected area. Therefore, inspired by Tzeng et al., in the present paper, in order to create equity in service in terms of the number of distributed RCs and deprivation cost, the proposed balance measure is presented as the minimum amount of the total priority-weighted service utility among all affected areas.

• In the DRSC literature, the developed location-inventory-distribution problems have only considered criteria such as storage capacity, travel time, cost, and disruption risk in order to locate required warehouses. While in the real world, in addition to these criteria, it is necessary to consider other evaluation criteria, although this can result in an increase in the complexity of the problem. Accordingly, in addition to criteria such as storage capacity, establishment cost, procurement cost, deprivation cost, and disruption risk, other criteria are also considered in this study, and the proposed model attempts to establish warehouses that are of higher utility based on these criteria. Moreover, considering the specific features and benefits of DEA models,³ the maximization of warehouses’ utility is formulated in the proposed model according to a proposed DEA model (This model is introduced in Appendix 5.1.) based on the DEA model introduced by Sun et al. (2013). In Sun et al.’s model, the utility of alternatives can only be evaluated by minimizing the summation of the weighted coordinate distances between a virtual ideal alternative and all alternatives. In this study, in addition to minimizing the summation of these weighted coordinate distances, the maximum weighted coordinate distances between the virtual ideal alternative and all alternatives are also minimized. Interestingly, the concepts of only two DEA models have been integrated with mathematical programming models in a few studies conducted in fields other than DRSC so far (e.g., Klimberg and Ratick 2008; Afsharian 2021). It is also worth noting that Sun et al.’s model or its developed and generalized models have not been integrated with any mathematical programming model to date.

• Financial parameters change during a time horizon affected by inflation, and accordingly the decision-making policies also change. Furthermore, the RO, like other organizations, puts its budgets in banks or investment institutions and projects with a certain interest rate, and as a result, the earned profits lead to an increase in its budgets. Hence, for the first time in the DRSC literature, this study pays attention to the time value of money by investing budgets and the variability of financial parameters affected by inflation during the pre-disaster PTH.

• The applicability and validity of the proposed model are demonstrated by implementing a real case study for a plausible earthquake in Khorasan Razavi Province.

The rest of the study is structured as follows: The problem under study, the proposed mathematical programming model, and the model solution method are described in Section 2. Section 3 presents a real-world case study with the performance evaluation of the model. Finally, concluding statements, critical managerial insights, and recommendations for future studies are expressed in Section 4.

2 Proposed model

The considered problem, the proposed mathematical programming model, and the model solution method are described in detail in Sections 2.1, 2.2, and 3, respectively.

2.1 Problem description

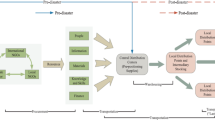
In this research, a specific disaster is taken into account that its occurrence time is unknown and may occur at any time of the considered pre-disaster PTH. Thus, the RO seeks to stockpile the required RCs prior to the disaster. Consequently, the RO would decide on the optimal location of warehouses, their storage capacity and retrofitting level and the number of RCs purchased for each warehouse at pre-disaster, and how to distribute RCs among affected areas (demand points) at post-disaster over a pre-disaster multi-period PTH. The general outline of the intended DRSC network is presented in Fig. 1. Moreover, in respect of interviews conducted with some administrative managers in Mashhad’s ROs and studies undertaken, the proposed assumptions are as follows:

• RCs are packaged in specific numbers in packages, and each relief package (RP) is allocated to an affected person.

• The pre-disaster PTH is considered a multi-period with the same length for each period due to the gradual injection of the budgets. The post-disaster PTH is defined as a single-period horizon lasting 72 h due to the necessity of prompt and efficient emergency response in the first 72 h following a disaster to save and rescue victims.

• There are different disaster scenarios.

• Demand points do not have the same response priority; therefore, a preference score is assigned to each demand point.

• Parameters that are affected by the disaster are demand, usable warehouse stock, and travel time. Therefore, it is not easy to estimate their exact amount. Accordingly, they are considered scenario-dependent parameters.

• The RO, like other organizations, faces financial restrictions. Therefore, it can only devote limited budgets for establishment and procurement operations during the pre-disaster phase. These budgets are not entirely accessible at the start of the pre-disaster PTH. Instead, they become gradually available to the RO over time. Moreover, these budgets are deposited in a bank at a specific variable interest rate so they can be withdrawn at any time.

• Each warehouse can be established at most once during the pre-disaster PTH. Once established, the warehouses are kept open until the end of the PTH.

• Items donated by the public are usually distributed a few days after the disaster since they require some logistical operations before they can be distributed (such as collecting, sorting, amalgamating, and repackaging). Therefore, they are not considered for usage within the first 72 h after the disaster.

• Cost parameters change during the preparedness phase as affected by the inflation phenomenon. Hence, they are considered time-dependent parameters.

• The deprivation cost function given by Holguín-Veras et al. (2016), which is an incremental convex function of deprivation time, is utilized to estimate deprivation cost, while deprivation time is equated to travel time.

• The risk of disruption in the transportation network is taken into account in travel time.

• A disaster can disrupt the capability of warehouses by damaging them. Therefore, the risk of disruption in warehouses is taken into account by considering the amount of warehouse inventory that remains usable after the disaster.

• In addition to criteria such as storage capacity, establishment cost, procurement cost, deprivation cost, and disruption risk, other criteria are also used in order to specify the proper locations of warehouses. Candidate warehouses are evaluated based on these criteria by a proposed DEA model according to the DEA model introduced by Sun et al. (2013), which is integrated with the proposed mathematical programming model. Subsequently, these criteria are divided into two categories of input and output criteria.

Fig. 1

General outline of the proposed DRSC

In the following, the mathematical programming model of the problem is formulated.

2.2 Mathematical formulation

In this section, the considered problem is formulated as a multi-period multi-objective two-stage scenario-based stochastic model, whose notations are listed in Table 2, and whose objective functions and constraints are as follows:

2.2.1 Model M1

Table 2 Sets, indices, parameters, and decision variables used in the model

$$\begin{aligned} \text{Min }{Z}_{1} =&\; \beta_{1}\Big(\sum\nolimits_{i\in I}\sum\nolimits_{l\in L}\sum\nolimits_{r\in R}\sum\nolimits_{t\in T}{x}_{ilrt}\\&\quad\;\Big\{\sum\nolimits_{n\in N}{\vartheta }_{n}\left({E}_{ni}-{E}_{nIDEAL}\right)\\&\quad\;\;+\sum\nolimits_{m\in M}{\tau }_{m}\left({O}_{mIDEAL}-{O}_{mi}\right)\Big\}\Big)\\& + \beta_{2}\Big(\underset{i\in I}{\text{max }}\Big\{\sum\nolimits_{l\in L}\sum\nolimits_{r\in R}\sum\nolimits_{t\in T}{x}_{ilrt}\\&\quad\;\Big\{\sum\nolimits_{n\in N}{\vartheta }_{n}\left({E}_{ni}-{E}_{nIDEAL}\right)\\&\quad\;\;+\sum\nolimits_{m\in M}{\tau }_{m} ({O}_{mIDEAL}-{O}_{mi})\Big\}\Big\}\Big) \end{aligned}$$

(1)

$$\begin{aligned} \text{Max }{Z}_{2} =&\; {\gamma }_{1}(\sum_{i\in I}\sum_{j\in J;{d}_{js}\ne 0}\sum_{s\in S}\sum_{t\in T}{p}_{s}{w}_{j}\frac{\frac{{y}_{ijst}}{{d}_{js}}}{F\left({t}_{ijs}\right)})\\& +{\gamma }_{2}(\sum_{s\in S}\sum_{t\in T}{p}_{s}\underset{j\in J;{d}_{\mathit{js}}\ne 0}{\text{min}}\{\sum_{i\in I}{w}_{j}\frac{\frac{{y}_{ijst}}{{d}_{js}}}{F\left({t}_{ijs}\right)}\}) \end{aligned}$$

(2)

$$\begin{aligned} \text{Min }{Z}_{3} =&\; \sum_{i\in I}\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{{f}_{ilrt}x}_{ilrt}\\& +\sum_{i\in I}\sum_{t\in T}{pc}_{it}{q}_{it} \end{aligned}$$

(3)

Subject to:

$$\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}\le 1, \forall i\in I$$

(4)

$$\sum_{i\in I}\sum_{l\in L}\sum_{r\in R}{{f}_{ilrt}x}_{ilrt}+{\acute{a}}_{t}={a}_{t}+{\acute{a}}_{t-1}\left(1+{ir}_{t-1}\right), \forall t\in T;{a}_{0}=0$$

(5)

$$\sum_{i\in I}{pc}_{it}{q}_{it}+{\acute{b}}_{t}={b}_{t}+{\acute{b}}_{t-1}\left(1+{ir}_{t-1}\right), \forall t\in T;{b}_{0}=0$$

(6)

$$\sum_{m\in M}{\tau }_{m}{O}_{mi}\le \sum_{n\in N}{\vartheta }_{n}{E}_{ni}, \forall i\in I$$

(7)

$$\sum_{n\in N}{\vartheta }_{n}{E}_{nIDEAL}=1$$

(8)

$$\sum_{m\in M}{\tau }_{m}{O}_{mIDEAL}=1$$

(9)

$$\sum_{i\in I}{y}_{ijst}\le {d}_{js}, \forall j\in J;s\in S;t\in T$$

(10)

$$\sum_{j\in J}{y}_{ijst}\le \sum_{l\in L}\sum_{r\in R}\sum_{\acute{t}\in T;\acute{t}\le t}{x}_{ilr\acute{t}}{\rho }_{irs}{q}_{i\acute{t}}, \forall i\in I;s\in S;t\in T$$

(11)

$$\sum_{t\in T}{q}_{it}\le \sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{{c}_{l}x}_{ilrt},\forall i\in I$$

(12)

$${q}_{it}\le \sum\nolimits_{\acute{t}\in T;\acute{t}\le t}\sum\nolimits_{l\in L}\sum\nolimits_{r\in r}{{c}_{l}x}_{ilr\acute{t}}, \forall i\in I;t\in T$$

(13)

$$\sum\nolimits_{i\in I}\sum\nolimits_{t\in T}{q}_{it}\le \theta (\sum\nolimits_{j\in J}\sum\nolimits_{s\in S}{p}_{s}{d}_{js})$$

(14)

$${\tau }_{m},{\vartheta }_{n}\ge \varepsilon , \forall n\in N;m\in M$$

(15)

$${x}_{ilrt}\in \{0, 1\},\forall i\in I;l\in L;r\in R;t\in T$$

(16)

$${{y}_{ijst},q}_{it}\ge 0\text{ and}\; \text{Integer}, \forall i\in I;j\in J;s\in S;t\in T$$

(17)

$${\acute{a}}_{t}, {\acute{b}}_{t}, {\tau }_{m},{\vartheta }_{n}\ge 0, \forall t\in T;n\in N;m\in M$$

(18)

The objective function (1) minimizes the weighted sum of the sum of utility scores of the established warehouses and the maximum values of these scores based on the considered criteria. It should be noted that the utility score of each warehouse is calculated based on its weighted coordinate distance from the virtual ideal warehouse; hence the less, the better. In fact, this objective function maximizes warehouses’ utility. To optimize the balance, distress, and efficacy of the network, a new efficacy-distress measure called priority-weighted service utility and a new balance measure are introduced, which are respectively estimated as the ratio of the fraction of satisfied demand to deprivation cost multiplied by the priority of the demand point and the minimum amount of the total priority-weighted service utility among demand points. Inspired by Lin et al. (2012), who introduced an objective function formulated as the sum of the efficiency and imbalance of the designed network, the objective function (2) is also formulated as the weighted sum of the efficacy-distress and balance of the network. This objective function indicates the desire to service demand points with the highest possible number of RPs and the least possible deprivation cost in the fairest possible manner (in terms of the number of distributed RPs and deprivation cost). The first expression considers the efficacy and distress measures and maximizes the expected value of the total priority-weighted utility of service to demand points. The maximization of this expression leads to the minimization of deprivation costs and the maximization of satisfied demands. The second expression considers the balance measure and focuses on maximizing the equity in service by maximizing the expected value of the minimum amount of the total priority-weighted service utility among demand points. The objective function (3) minimizes the total logistics cost, which includes the costs of establishing warehouses and procuring RPs.

According to constraint (4), each warehouse can be established at most in one period, one storage level, and one retrofitting level. Constraints (5) and (6) show the constraints of the establishment budget and procurement budget in each period, respectively. Constraint (7) determines that the weighted sum of output criteria is less than or equal to the weighted sum of input criteria. Indeed, this constraint states that the efficiency score (the ratio of the weighted summation of output criteria to the weighted summation of input criteria) of each warehouse is less than or equal to one. Constraints (8) and (9) consider both the weighted summation of the input criteria of the virtual ideal warehouse and the weighted summation of the output criteria of the virtual ideal warehouse as equal to one. Constraint (10) shows that the number of RPs sent to the demand point cannot exceed its demand. Constraint (11) confirms that dispatched RPs from the warehouse cannot exceed the number of RPs that remain usable at post-disaster. Constraint (12) indicates the maximum storage capacity in the warehous over the PTH. According to constraint (13), if the warehouse has not been established up to period t, no RPs can be stored in it at period t. Constraint (14) represents the maximum storage capacity in the network over the PTH. Constraint (15) prevents from being zero the weights of input and output criteria. Constraints (16) to (18) indicate the domains of decision variables applied in the model.

The approach required to solve the above model is elaborated in the following section.

2.3 Solution method

The proposed model M1 is a multi-objective non-linear model; therefore, the following procedure is suggested to solve the model efficiently:

Step 1: Linearization of the model

Let ${h}_{i}$, and ${k}_{ij}$ be non-negative continuous variables, ${v}_{j}$ be a binary variable, and ${\alpha }_{i}$, and ${\gamma }_{ij}$ be parameters. The following equations are non-linear, which can be linearized using auxiliary variables ${u}_{ij}$, and $\omega$, as well as the large enough positive constant G as follows (Asghari et al. 2022):

$$\begin{aligned} & {\mathrm{Max }}\;Z \underset{\mathit{ }i\in I}{=\text{min}}\{{\alpha }_{i}{h}_{i}\}\rightarrow{\mathrm{Max }}\;Z=\omega,\\&\quad\;\; {\mathrm{Subject \;to }}:{\alpha }_{i}{h}_{i}\ge \omega, \forall i\in I \end{aligned}$$

(19)

$$\begin{aligned} & {\mathrm{Min}} \;Z\underset{\mathit{ }i\in I}{=\text{max}}\{{\alpha }_{i}{h}_{i}\} \rightarrow{\mathrm{Min}} \;Z=\omega,\\&\quad\;\, {\mathrm{Subject \;to}}:{\alpha }_{i}{h}_{i}\le \omega, \forall i\in I \end{aligned}$$

(20)

$$\begin{aligned} & \text{Min} \;Z=\sum_{i\in I}\sum_{j\in J}{\gamma }_{ij}{h}_{i}{v}_{j}{\rightarrow}\text{Min} \;Z=\sum_{i\in I}\sum_{j\in J}{\gamma }_{ij}{u}_{ij},\\&\quad\;\; {\mathrm{Subject \;to}}:{u}_{ij}\le G{v}_{j},\\&\quad\;\; {u}_{ij}\le {h}_{i}, {u}_{ij}\ge {h}_{i}+G\left({v}_{j}-1\right), \forall i\in I;j\in J \end{aligned}$$

(21)

$$\begin{aligned} & {k}_{ij}\le{\gamma }_{ij}{h}_{i}{v}_{j},\, \forall i\in I, j\in J{\mathbf{\rightarrow}}{k}_{ij}\le {\gamma }_{ij}{h}_{i}+G\left(1-{v}_{j}\right),\\&\qquad {k}_{ij}\le G{v}_{j}, \forall i\in I;j\in J \end{aligned}$$

(22)

The objective functions (1) and (2), and constraint (11) are non-linear, which can be linearized using the above-mentioned procedures as follows:

Step 1.1: Linearization of the objective function (1)

Accordingly Eqs. (20) and (21), the objective function (1) can be transformed into a linear format utilizing the following auxiliary variables:

$$\begin{aligned} \delta =&\; \underset{i\in I}{\text{max }}\{\sum_{l\in L}\sum_{r\in R}\sum_{t\in T }{x}_{ilrt} \{\sum_{n\in N}{\vartheta }_{n}\left({E}_{ni} - {E}_{nIDEAL}\right) \\& + \sum_{m\in M}{\tau }_{m}({O}_{mIDEAL}-{O}_{mi})\}\} \end{aligned}$$

(23)

$$\begin{aligned} & {\acute{x}}_{i}=\sum_{n\in N}{\vartheta }_{n}\left({E}_{ni}-{E}_{nIDEAL}\right)+\sum_{m\in M}{\tau }_{m}\left({O}_{mIDEAL}-{O}_{mi}\right),\\&\quad {\mathrm{if \;warehouse}} \;i \;{\mathrm{is \;established}}; 0,{\mathrm{otherwise}}, \forall i\in I \end{aligned}$$

(24)

Now, using the above variables, the objective function (1) is linearized by replacing it with the objective function (25), and adding constraints (26) to (30) to the model M1.

$$\text{Min }{Z}_{1}={\beta }_{1}\sum_{i\in I}{\acute{x}}_{i}+{\beta }_{2}\delta$$

(25)

$${\acute{x}}_{i}\le \overline{G }(\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}) \forall i\in I$$

(26)

$$\begin{aligned} & {\acute{x}}_{i}\le \sum_{n\in N}{\vartheta }_{n}\left({E}_{ni}-{E}_{nIDEAL}\right)\\&\;\; +\sum_{m\in M}{\tau }_{m}\left({O}_{mIDEAL}-{O}_{mi}\right), \forall i\in I \end{aligned}$$

(27)

$$\begin{aligned} & {\acute{x}}_{i}\ge \sum_{n\in N}{\vartheta }_{n}\left({E}_{ni}-{E}_{nIDEAL}\right)\\&\quad +\sum_{m\in M}{\tau }_{m}\left({O}_{mIDEAL}-{O}_{mi}\right)\\&\quad +\overline{G }\left(\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}-1\right), \forall i\in I \end{aligned}$$

(28)

$${\acute{x}}_{i}\ge 0, \forall i\in I$$

(29)

$${\acute{x}}_{i}\le \delta , \forall i\in I$$

(30)

The parameter $\overline{G }$ is a large enough positive constant. Constraints (26) to (29) calculate the utility scores of established warehouses. Constraint (30) ensures that the auxiliary variable $\delta$ is the maximum value among the utility scores of established warehouses.

Step 1.2: Linearization of the objective function (2)

Accordingly Eq. (19), the objective function (2) can be linearized using the following auxiliary variable.

$${\sigma }_{st}=\underset{j\in J;{d}_{\mathit{js}}\ne 0}{\text{min}}\{\sum_{i\in I}{w}_{j}\frac{\frac{{y}_{ijst}}{{d}_{js}}}{F\left({t}_{ijs}\right)}\}$$

(31)

Considering Eq. (31), the linearized form of the objective function (2) is formulated by substituting the objective function (32) for it, and adding constraint (33) to the model M1.

$$\begin{aligned} \text{Min }{Z}_{2}=&\;{\gamma }_{1}(\sum_{i\in I}\sum_{j\in J;{d}_{js}\ne 0}\sum_{s\in S}\sum_{t\in T}{p}_{s}{w}_{j}\frac{\frac{{y}_{ijst}}{{d}_{js}}}{F\left({t}_{ijs}\right)})\\& +{\gamma }_{2}(\sum_{s\in S}\sum_{t\in T}{p}_{s}{\sigma }_{st}) \end{aligned}$$

(32)

$$\sum_{i\in I}{w}_{j}\frac{\frac{{y}_{ijst}}{{d}_{js}}}{F\left({t}_{ijs}\right)}\ge {\sigma }_{st}, \forall j\in J;{d}_{js}\ne 0;s\in S;t\in T$$

(33)

Constraint (33) guarantees that the auxiliary variable ${\sigma }_{st}$ is the minimum value among the total priority-weighted service utilities of demand points.

Step 1.3: Linearization of the constraint (11)

Accordingly Eq. (22), the linear equivalent of constraint (11) is formulated as the following constraints:

$$\begin{aligned} & \sum_{j\in J}{y}_{ijst}\le \sum_{\acute{t}\in T;\acute{t}\le t}{{ \rho }_{irs}q}_{i\acute{t}}+\overline{\overline{G}}\left(1-\sum_{l\in L}\sum_{\acute{t}\in T;\acute{t}\le t}{x}_{ilr\acute{t}}\right),\\&\qquad \forall i\in I;r\in R;s\in S;t\in T \end{aligned}$$

(34)

$$\sum_{j\in J}{y}_{ijst}\le \overline{\overline{G}}\left(\sum_{l\in L}\sum_{r\in R}\sum_{\acute{t}\in T;\acute{t}\le t}{x}_{ilr\acute{t}}\right), \forall i\in I;s\in S;t\in T$$

(35)

The parameter $\overline{\overline{G}}$ is a large enough positive constant. Constraint (35) ensures that no RPs are sent to demand points from a warehouse that has not yet been established.

Step 2: Transforming the multi-objective model into a single-objective model

In this study, the model M1 is transformed into a single-objective model using the fuzzy multi-objective programming model presented by Lin (2004) called the weighted max–min model. The weighted max–min model presents the following procedure to solve multi-objective models efficiently:

Step 2.1: Calculating the minimum and maximum values of each objective function

Generally, the multi-objective programming model can be defined as follows:

$$\mathrm{Min}\;Z_1,\;Z_2,\;\dots, Z_n$$

(36)

$$\mathrm{Max}\;W_1,\;W_2,\;\dots, W_m$$

(37)

Subject to:

$$x\in X$$

(38)

The minimum value of each objective function (${W}_{j}^{-}$ and ${Z}_{i}^{-}$) and the maximum value of each objective function (${W}_{j}^{+}$ and ${Z}_{i}^{+}$) can be obtained as follows:

$${Z}_{i}^{+}=\text{ Max}\;{Z}_{i},\mathrm{ Subject \;to}: x \in X, \forall i\in \left\{1, 2, ... ,n\right\}$$

(39)

$${Z}_{i}^{-}=\text{ Min}\;{Z}_{i},\mathrm{ Subject\; to}: x\in X,\forall i\in \left\{1, 2, ... ,n\right\}$$

(40)

$${W}_{j}^{+}=\text{ Max}\;{W}_{j},\mathrm{ Subject \;to}: x \in X, \forall j\in \left\{1, 2, ... ,m\right\}$$

(41)

$${W}_{j}^{-} =\text{ Min}\;{W}_{j},\mathrm{ Subject \;to}: x \in X, \forall j\in \left\{1, 2, ... ,m\right\}$$

(42)

Step 2.2: Defining the membership function of each objective function

The values of the objective functions can be shown as fuzzy numbers; accordingly, the values of their membership function change linearly between zero and one. Such linear membership functions are defined below and illustrated in Fig. 2.

$$\mu_{z_i}=\left\{\begin{array}{ll}1&Z_i^-\leq Z_i\\(Z_i^+-Z_i)/(Z_i^+-Z_i^-)&Z_i^-\leq Z_i\leq Z_i^+,\forall i\in\{1,\;2,\;\dots,\;n\}\\0&Z_i^+\geq Z_i\end{array}\right.$$

(43)

$$\mu_{w_j}=\left\{\begin{array}{ll}1&W_i^+\leq W_i\\(W_j-W_j^-)/(W_j^+-W_j^-)&W_i^-\leq W_i\leq W_i^+,\forall j\in\{1,\;2,\;\dots,\;n\}\\0&W_j^-\leq W_j\end{array}\right.$$

(44)

Fig. 2

Membership functions of objective functions

Step 2.3: Formulating a corresponding single-objective programming model

The above multi-objective programming model is transferred into the below single-objective programming model, with the aim of maximizing the minimum membership functions of the objective functions and taking the weight of the objective functions into account.

$$\mathrm{Max}\;\overline Z=\lambda$$

(45)

Subject to:

$$\alpha_j\lambda\leq\mu_{Z_i},\forall i\in\{1,\;2,\;\dots\;,\;n\}$$

(46)

$$\alpha_j\lambda\leq\mu_{W_j},\forall j\in\{1,\;2,\;\dots\;,\;m\}$$

(47)

$$x\in X$$

(48)

where ${\alpha }_{i}$, and ${\alpha }_{j}$ represent the weights of the objective functions.

Now, according to the weighted max–min model and the proposed linearization approach, the proposed programming model is transferred into the below single-objective linear programming model.

$$\mathrm{Max}\;\overline Z=\lambda$$

(49)

Subject to:

$$\alpha_1\lambda\leq(Z_1^+-Z_1)/(Z_1^+-Z_1^-)$$

(50)

$$\alpha_2\lambda\leq(Z_2-Z_2^-)/(Z_2^+-Z_2^-)$$

(51)

$$\alpha_3\lambda\leq(Z_3^+-Z_3)/(Z_3^+-Z_3^-)$$

(52)

Equations (4) to (10), (12) to (18), (26) to (30), and (33) to (35)

It is worth noting that due to the special nature of the first objective function and the model structure, the maximum value of the first objective function (${Z}_{1}^{+}$) becomes an unlimited value by solving the linear counterpart of the model M1 and maximizing only the first objective function. Therefore, to obtain a finite value for ${Z}_{1}^{+}$, the model is solved by maximizing only the first objective function and replacing constraint (30) with the following constraints.

$$\delta \le {\acute{x}}_{i}+\acute{G}{O}_{i},\forall i\in I$$

(53)

$$\sum\nolimits_{i\in I}{O}_{i}=\left|I\right|-1$$

(54)

$${O}_{i}\in \{0, 1\},\forall i\in I$$

(55)

The auxiliary variable ${O}_{i}$ will be equal to zero, if the variable ${x}_{i}$ has the highest value. The parameter $\breve{G}$ is a large enough positive constant.

3 Model implementation and results analysis

In order to demonstrate the model’s applicability and validity, the results of the computational tests are reported in this section. Moreover, the models are solved via IBM ILOG CPLEX 12.10 software running on a laptop with an Intel Core i5-3210 M 2.5 GHz CPU and 4 GB of RAM. In the following, a real case study followed by various sensitivity analyses and tests is introduced.

3.1 Case study

Iran is known as one of the world’s most earthquake-prone countries as numerous major faults pass through it, and in recent decades, it has suffered many destructive earthquakes, resulting in many casualties and huge financial losses. Figure 3 depicts earthquakes with a magnitude greater than four that occurred in Iran from 1900 to 2020 (IIEES, http://www.iiees.ac.ir).

Fig. 3

Seismicity map of Iran from 1900 to 2020

Iran’s second most populous province is Razavi Khorasan, with a population of over 6.5 million (Statistical Center of Iran, http://www.amar.org.ir). This province is one of Iran’s most earthquake-prone areas due to the existence of numerous active faults in it, and as evidenced by its historical earthquakes, financial and human losses caused by earthquakes have been high (Pourkermani and Arian 1998). According to studies, 71% of its area is located in a zone with moderate to high earthquake risk (Jahad Dneshgahi of Mashhad 2010; see Fig. 4 (Akbari et al. 2011)). Moreover, more than 5500 large and small faults have been identified in it so far that 60% of its area, 75% of its cities, and 35% of its villages are within the boundaries of these faults (Hayati et al. 2017). Meanwhile, only 42% of ordinary houses.

Fig. 4

Seismic hazard zonation map of Khorasan Razavi Province

in it have metal frames and reinforced concrete, and 58% of houses have used other materials that would be seriously damaged by earthquakes (Statistical Center of Iran, http://www.amar.org.ir). Thus, it can be stated that the occurrence of an earthquake in it may cause enormous and irreparable human and financial losses. Hence, this case study considers the possibility of an earthquake in it. The data and information are acquired from reliable and trustworthy sources provided based on its actual conditions and via interviews with certain of its disaster management specialists,⁴ as well as from case studies conducted in Iran. Notably, due to confidentiality considerations, some data and references cannot be disclosed. The considered assumptions and data are as follows:

• Due to the presence of critical industrial, social, cultural, and religious centers, and high population density in Mashhad, Neyshabour, Sabzevar, Torbat-e-Hydariyeh, and Torbat-e-Jam cities, these cities are particularly susceptible in Razavi Khorasan Province. Moreover, according to Fig. 4 and the history of seismicity, they have always witnessed very destructive and terrible earthquakes throughout history. It also is noteworthy that Iran’s second most populous city is Mashhad, with a population of over 3 million people (Statistical Center of Iran, http://www.amar.org.ir). This city is Iran’s most significant religious tourism hub, which is visited by over 20 million tourists each year, which results in an increase in its population density. Thus, the mentioned cities are selected as demand points, shown in Fig. 5.

• Ten candidate warehouses are selected in Razavi Khorasan Province according to eight criteria (i.e., population density, distance from incompatible applications (i.e., gas stations, gas transmission lines, and high pressure lines), distance from faults, slope, distance from roads, height of buildings, distance from compatible applications (i.e., green spaces, healthcare centers, police departments, and fire departments), and proximity to affected areas) as proposed by Kharaghani (2020). Noteworthy, the fuzzy AHP method and ARC GIS software are employed to evaluate locations based on the above-mentioned criteria. Figure 5 displays candidate locations for warehouses.

• Warehouses can be established at three storage capacity levels and two retrofitting levels. At most 30000, 48000, and 72000 RPs can be stored in the storage capacity levels 1, 2, and 3, respectively.

• The pre-disaster PTH is three years, which is divided into three one-year periods.

• RCs packaged in packages include drinking water and food with long expiration dates and shelf life. Food is stockedin the form of meals-ready-to-eat (MREs). MRE is a type of individual operational ration that will simply be referred to as ration. The ration includes a variety of food items for breakfast, lunch, and dinner, and an MRE provides about 1.3 of the human body’s daily need for calories. A person’s daily need for water and food is three liters and two MREs, respectively (Sphere 2018). Here, a three-day period are considered to meet demands. Hence, each RP contains nine liters of drinking water and six MREs. By conducting local research in the locations of candidate warehouses, the costs of procuring each RP for each warehouse are estimated in Table 2.

• Razavi Khorasan Province is surrounded by four main active faults, namely Kashafrud, Neyshabour, Sabzevar, and Torbat-e-Jam, the movement of each of which would result in a severe earthquake (see Fig. 6 (Kazemi et al. 2013)). Consequently, four disaster scenarios are suggested: 1) scenario 1: earthquake caused by Sabzevar fault, 2) scenario 2: earthquake caused by Neyshabour fault, 3) scenario 3: earthquake caused by Kashafrud fault, and 4) scenario 4: earthquake caused by Torbat-e-Jam fault. According to experts’ opinions, the relative probabilities of the scenarios are estimated based on the length of the faults (Bozorgi-Amiri and Khorsi 2016) as 0.45, 0.3, 0.1, and 0.15, respectively.

Fig. 5

Map of Razavi Khorasan Province, locations of demand points, and candidate warehouses

Table 3 Costs of procuring a RP (10⁴ tomans)

Fig. 6

Active fault map of Razavi Khorasan Province

• In order to estimate the construction cost per square meter of each warehouse, the seismic resistance of its land is first evaluated using step-wise weight assessment ratio analysis (SWARA) and simple additive weighting (SAW) methods. In particular, horizontal acceleration of faults, soil erosion, slope, proximity to faults, and soil liquefaction are considered as effective criteria of the proposed method. The values of these criteria for each warehouse are attained from the reports prepared by the Roads and Urban Development Office of Khorasan Razavi Province, which can be accessed only with the organization’s permission. It is worth noting that the lower the land’s seismic resistance, the stronger the building is required, which leads to the higher construction cost. Finally, the establishment cost of each warehouse is estimated by considering its seismic resistance, capacity, and retrofitting level, and construction cost per square meter, and inflation rate in its city, which is shown in Table 3.

• The percentage of possible earthquake damage to each warehouse under retrofitting level 1 is estimated using DEA

• Numbers inside parentheses in each cell from left to right represent the establishment cost at periods 1, 2, and 3, respectively. model with the common set of weights (DEA-CSW model) for which eight criteria are considered as follows: 1) network of passages per capita, 2) number of fire stations, 3) horizontal acceleration of faults, 4) soil erosion, 5) slope, 6) proximity to faults, 7) soil liquefaction, and 8) traffic service level (traffic volume/traffic capacity). The values of these criteria for each warehouse are collected from the studies conducted by the Roads and Urban Development Office of Khorasan Razavi Province, which can be accessed only with authorization from the organization. It is worth mentioning that the possible damage percentage in each scenario accounts for a percentage of the inefficiency score obtained from the DEA-CSW model. Finally, the estimated damage percentage is considered as the percentage of stockpiled RPs that are unusable following the disaster (see Table 4). Moreover, 100% of RPs are usable under retrofitting level 2.

  Table 4 Establishment costs (million tomans)

• The priorities of the demand points are determined based on ten various criteria (i.e., distance from active faults, landslide, structural behavior of buildings and infrastructure, electricity, gas, water and sewage networks, transportation network, medical emergency services, fire stations, demographic characteristics (i.e., age, gender, income level, and health status), rescue capability, and mortality ratio) as proposed by Nateghi (2001), and Tofighi et al. (2016). The values of the mentioned criteria for each demand point are obtained from the statistical yearbook of Razavi Khorasan Province (Country’s program and budget organization 2019), and the reports prepared by the Roads and Urban Development Office of Khorasan Razavi Province, which can be accessed only with the organization’s permission. The normalized inefficiency scores obtained from the DEA-CSW model are considered as the priorities of the demand points. The values of these estimated priorities are presented in Table 5.

  Table 5 Percentages of stocked RPs that remain unusable at post-disaster (%)

• The number of affected people in each demand point is estimated by multiplying its population size by its predicted damage percentage calculated regarding sixteen criteria as proposed by Baghban et al. (2019), and Gholami et al. (2015) and utilizing the DEA-CSW model. In particular, the considered criteria are as follows: 1) health per capita, 2) green space per capita, 3) network of passages per capita, 4) number of fire stations, 5) development stage, 6) percentage of low-durability buildings, 7) number of buildings older than thirty years, 8) population density, 9) horizontal acceleration of faults, 10) soil erosion, 11) slope, 12) proximity to faults, 13) soil liquefaction, 14) area of hazardous applications (such as gas station, high-pressure power station, etc.), 15) traffic service level (traffic volume/traffic capacity), and 16) percentage of buildings with more than three floors. The values of these criteria for each demand point are acquired from the statistical yearbook of Razavi Khorasan Province (Country’s program and budget organization 2019), Statistical Center of Iran (http://www.amar.org.ir), and the studies conducted in Roads and Urban Development Office of Khorasan Razavi Province, which can be accessed only with the authorization from the organization. According to the historical data, the characteristics of the faults (such as horizontal acceleration, distance of central point, and magnitude, etc.), and experts’ opinions, the predicted damage percentage in each scenario is estimated by a percentage of the inefficiency score obtained from the DEA-CSW model. Accordingly, the values of demands are reported in Table 5.

• Input criteria: ease of access to transport networks⁵ (I₁), ease of access to supply resources of RPs⁶ (I₂), and difficulty of traversing on routes leading to the warehouse (I₃), and output criteria: security of the warehouse and its routes⁷ (O₁), geographical and climatic conditions (O₂), ease of access to essential infrastructure such as water, electricity, gas, etc. (O₃), and quality of supply resources of RPs (based on production capacity, flexibility, delivery time, disruption risk, economic stability, etc.) (O₄) are considered. Also, the values of these input and output criteria for each warehouse are determined in the range of [1, 0], presented in Table 6.

  Table 6 Demand values (10³ RPs( along with the priorities of the demand points

• For each period, Table 7 shows the available budgets for establishing the warehouses and procuring the RPs.

  Table 7 Scores obtained from the evaluation of warehouses based on the input and output criteria

• Following an earthquake, there may be disruptions in the transportation network due to damage to routes and traffic congestion; as a result, travel times may rise compared to normal conditions. Hence, in each scenario, the post-disaster travel time is calculated by multiplying the normal travel time by the coefficient of disruption in the transport route. The measurement tool on Google Maps is used to determine normal travel times from the warehouses to the centers of the demand points. Also, the coefficient of disruption in the transport route is estimated based on the vulnerability of its network of passages and cities. In each scenario, the vulnerability of the network of passages of the transport route is estimated using the vulnerability rating of the network of passages, created by specialists. Also, the vulnerability of each city was calculated when estimating the values of demands. Post-earthquake travel times are provided in Table 8.

  Table 8 Establishment and procurement budgets (million tomans)

• Numbers inside parentheses in each cell from left to right represent travel times under scenarios 1, 2, 3, and 4, respectively.

• Throughout the pre-disaster PTH, the budgets are deposited in a bank at an annual effective interest rate of 10%, 12%, and 15% in periods 1, 2, and 3, respectively.

• The annual inflation rate in each period and city is set according to historical data.

• Considering the higher priorities and ranges of the first expressions of the objective functions (1) and (2) than their second expressions, ${\beta }_{1}$, ${\beta }_{2}$, ${\lambda }_{1}$, and ${\lambda }_{2}$ are set as Table 9.

  Table 9 Post-earthquake travel times between warehouses and demand points (in hours)

• The rest of the information is presented in Table 9.

Now, in order to obtain the optimal solution of the model M1 according to this case study, the model is coded in IBM ILOG CPLEX 12.10 software, which contains 1184 constraints (including 608 equality constraints) and 1447 variables (including 180 binary variables and 630 integer variables). IBM ILOG CPLEX 12.10 software finds the optimal solution of the model by applying 21 cuts in 1663 iterations and 1.59 s. Figure 7 depicts the optimal solution obtained. For example, in period 2, warehouses 1 and 6 are established at retrofitting level 2 and storage capacity levels 1 and 2 respectively, while warehouses 7 and 10 have been established at retrofitting level 1 and storage capacity levels 1 and 3, respectively, in period 1. The inventory of warehouse 10 in period 2 includes 30,000 RPs, of which 29,000 packages and 10,000 packages are stored from period 1 and period 2, respectively. In case of the disaster in period 2, 33,198, 72,000, 69,120, and 22,421 RPs are dispatched from warehouse 7 to demand point 4 under scenarios 1, 2, 3, and 4, respectively.

Fig. 7

Optimal solution of the model M1 according to the considered case study

In the following, the effects of some of the formulated assumptions, adopted approaches, and parameters on the performance of the model are examined.

3.2 Evaluating the performance efficiency of the proposed programming model

This section is divided into six main subsections that assess the efficiency and effectiveness of the model by conducting several sensitivity analyses on some of the critical assumptions, approaches, and parameters. It is worth noting that in these analyses, which are described below, in addition to the optimal values of the first, second, and third objective functions (Z₁, Z₂, and Z₃), the following indicators are also paid attention:

• Total expected weighted satisfied demands $({I}_{1})=\sum_{i\in I}\sum_{j\in J;{d}_{js}\ne 0}\sum_{s\in S}\sum_{t\in T}{p}_{s}{w}_{j}{y}_{ijst};$

• Total expected weighted unit deprivation cost ${(I}_{2})=\sum_{s\in S}\sum_{t\in T}{p}_{s}\frac{\sum_{i\in I}\sum_{j\in J;{d}_{js}\ne 0}{w}_{j}F\left({t}_{ijs}\right){y}_{ijst}}{\sum_{i\in I}\sum_{j\in J}{y}_{ijst}};$

• Total expected weighted service utility $\left({I}_{3}\right)=\sum_{i\in I}\sum_{j\in J;{d}_{js}\ne 0}\sum_{s\in S}\sum_{t\in T}{p}_{s}{w}_{j}\frac{\frac{{y}_{ijst}}{{d}_{js}}}{F\left({t}_{ijs}\right)};$

• Total expected weighted equity in service $({I}_{4})=\sum_{s\in S}\sum_{t\in T}{p}_{s}\underset{j\in J;{d}_{\mathit{js}}\ne 0}{\text{min}}\{\sum_{i\in I}{w}_{j}\frac{\frac{{y}_{ijst}}{{d}_{js}}}{F\left({t}_{ijs}\right)}\}.$

3.2.1 Assessing the performance efficiency of the proposed procedure to establish the most desirable warehouses according to a set of criteria

In this section, the following three evaluations are carried out to measure the performance efficiency of the proposed approach in line with establishing the most desirable warehouses based on a set of criteria. The results of these evaluations are shown in Fig. 8.

• Evaluating the performance efficiency of the proposed DEA model: The performance efficiency of the proposed DEA model is evaluated by comparing it with the DEA models used in studies done by Klimberg and Ratick (2008), and Afsharian (2021) by maximizing warehouses’ utility based on these DEA models (The proposed model based on each of the DEA models used in these two studies (models M2 and M3) is provided in Appendixes 5.2. and 5.2.).

• Evaluating the effect of integrating the DEA model with the mathematical programming model: The problem under study aims to establish the most favorable warehouses according to a set of criteria; hence, to achieve this purpose, the DEA model has been incorporated into the model M1. Now, it is assumed that the DEA model is not integrated with the model M1 (model M4). In this case, warehouses are first evaluated according to the considered criteria using the DEA model (Its formulation is provided in Appendix 5.1.). The DEA model calculates the efficiency scores of the warehouses (${ES}_{i}$). Then, ${ES}_{i}$ is considered as an input parameter for the model M1, since the most favorable warehouses must be established. Consequently, the objective function (1) is reformulated as follows:

  $$\text{Min }{Z}_{1} = \sum_{i\in I}\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{ES}_i {x}_{ilrt}$$

  (56)

  Like the objective function (1), the objective function (51) also strives to establish the most desirable warehouses.

• Evaluating the performance of the second expression of the first objective function (the maximum utility scores of established warehouses based on a set of criteria): As mentioned earlier, the proposed DEA model is formulated by taking inspiration from the DEA model presented by Sun et al. (2013). Yet unlike the model by Sun et al., in addition to minimizing the summation of the weighted coordinate distances between the virtual ideal warehouse and all established warehouses, the proposed DEA model also minimizes the maximum weighted coordinate distances between the virtual ideal warehouse and all established warehouses. In this regard, this expression is omitted from the objective function (1) (model M5) to assess the performance of the second expression of the objective function (1). Consequently, the objective function (1) is reformulated as follows:

  $$\begin{aligned} \text{Min }{Z}_{1} =&\, \sum_{i\in I}\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}\Bigg\{\sum_{n\in N}{\vartheta }_{n}\left({E}_{ni}-{E}_{nIDEAL}\right)\\&+\sum_{m\in M}{\tau }_{m}\left({O}_{mIDEAL}-{O}_{mi}\right)\Bigg\} \end{aligned}$$

  (57)

Fig. 8

Effects of utilizing the model M1 instead of the models M2, M3, M4, and M5

As seen in Fig. 8, the proposed approach provides more favorable and fairer service to affected people, which results in lower supply risk, higher service efficacy, and less human suffering. Thus, the second objective function, which has a higher priority for the RO, has been realized to a greater extent. Noteworthy, as expected, the results show that the higher the value of the second objective function, the more the weighted satisfied demands, the lower the deprivation costs, and the more favorable and fairer the service. Besides, the proposed approach makes the total logistics cost more affordable, given the lower value of its third objective function. Subsequently, it can be stated that the proposed approach for establishing the most desirable warehouses based on the input and output criteria has a better performance.

3.2.2 Investigating the effects of some other of the considered assumptions and approaches

In this section, the following evaluations are carried out to investigate the effects of some of the critical and fundamental assumptions and approaches considered in the problem under discussion.

• Investigating the effects of taking bank interest into account: In this study, the time value of money is considered by investing the budgets with a specific interest rate. Figure 9 shows the effects of taking into account the time value of money in the proposed programming model by eliminating the interest rate (model M6). Consequently, constraints (5) and (6) are reformulated as follows:

Fig. 9

Percentages of changes caused by considering the time value of money

$$\sum_{i\in I}\sum_{l\in L}\sum_{r\in R}{{f}_{ilrt}x}_{ilrt}+{\acute{a}}_{t}={a}_{t}+{\acute{a}}_{t-1}, \forall t\in T;{a}_{0}= 0$$

(58)

$$\sum_{i\in I}{pc}_{it}{q}_{it}+{\acute{b}}_{t}={b}_{t}+{\acute{b}}_{t-1}, \forall t\in T;{b}_{0}=0$$

(59)

Taking bank interest into account increases the budgets. Hence, the RO is able to provide more RPs and establish more desirable warehouses, which results in more weighted satisfied demands, lower deprivation costs, and more favorable and equitable service and, as a result, more fulfillment of the first and second objective functions and a better optimal value for them. Noteworthy, due to the procurement of more RPs, the establishment of more desirable yet expensive warehouses, and the improvement of the establishment schedule, the total logistics cost has increased. Therefore, as expected, taking the assumed time value into account leads to a better performance from the model, which is also closer to reality.

• Evaluating the performance of the multi-period optimization approach: Holguín-Veras et al. (2013) asserted that the inter-temporal effects of DRSC activities cannot be considered in single-period optimization. Therefore, in this paper, it is claimed that integrating the main decisions, such as location, procurement, and distribution, in a multi-period horizon may improve coordination in the DRSC. Solving a single-period problem iteratively, taking into account the decisions made in previous periods (model M7) proves this claim. This approach is conducted for each period t beginning from the first period onward. As displayed in Fig. 10, in the proposed model M1, the decisions are taken in such a way that they lead to establishing more and more desirable warehouses, an increase in weighted satisfied demands, service utility, equity in service, and the total logistics cost, and a decrease in the deprivation costs. Accordingly, the first and second objective functions have been realized in better values. Therefore, since servicing the affected areas with the greatest possible number of RPs and the lowest possible deprivation costs in the fairest possible manner, as well as establishing the most favorable warehouses are the most important objectives of the problem, the multi-period optimization approach outperforms the single-period optimization approach.

• Investigating the effects of gradual budgets injection into the system: To examine the performance of the proposed approach for injecting budgets into the system (gradual budgets injection approach), it is first assumed that the total budget planned for the establishment of warehouses and the total budget planned for the procurement of RPs are fully available at the beginning of the pre-disaster PTH (instantaneous budgets injection approach (model M8)). Subsequently, the amounts of these budgets for each period are considered as follows:

  $${a}_{1}=\text{ A}, {a}_{2} = 0,{a}_{3} = 0,{b}_{1} =\text{ B}, {b}_{2}= 0,{b}_{3}= 0$$

  (60)

Fig. 10

Results obtained from the multi-period optimization model compared to the single-period optimization model

Now, the model M1 is solved according to these budget values, the results of which are presented in Table 10.

Table 10 Rest of the required information

It is impossible to implement the decisions presented in Table 10 in due time, since, at the beginning of the pre-disaster PTH, the establishment and procurement budgets are not fully available; rather, at the beginning of each period, a part of the budgets is injected into the project. Thus, to schedule for establishing the selected warehouses, procure the determined amounts of RPs, and set the optimal strategy for distributing RPs among the demand points, the model M1 is solved according to the solutions presented in Table 10 and the actual amounts of the budgets of the periods. Given the increasing establishment and procurement costs over time, it is not possible to establish all of the selected warehouses and procure all of the determined RPs; as a result, the model is not solved. If storage capacity, retrofitting and inventory levels of the warehouses are changed, then the model can be solved. Hence, in order to achieve to the best solution close to the solution presented in Table 10, the model M1 is solved by assuming that warehouses 2, 4, 6, 8, and 9 are not established (model M9). The obtained results show that warehouses 1, 3, 5, 7, and 10 are respectively established at storage capacity levels 2, 3, 1, 3, and 3, and retrofitting levels 2, 1, 2, 1, and 1. In Fig. 11, the model M9 is compared with the model M1. According to Fig. 11, it can be concluded that the proposed gradual budget injection approach involves better performance as it leads to the establishment of more desirable warehouses, a more efficient response to affected people, and lower supply risk. Noteworthy, the model M1 plans procurement policy more cost-effectively (a decrease of about 0.8%) while procuring more RPs (an increase of about 5.3%). However, the total logistics cost has increased due to an increase of approximately 6.8% in the total establishment cost.

• Evaluating the performance of the second objective function: As mentioned earlier, one of the objectives of the proposed problem is to service affected people with the highest possible amount of RPs and the lowest possible deprivation cost in the fairest possible way. Hence, to further realize the objective and, at the same time, reduce computational complexities, new service utility and balance measures have been introduced, on the basis of which the objective has been formulated as a single objective function. In the literature, in order to achieve this objective, the following objective functions have been utilized. The functions (56) and (57), respectively, maximize satisfied demands and the minimum fraction of fulfilled demand among all of the demand points. The functions (58) and (59), respectively, minimize deprivation costs and the maximum fraction of deprivation cost among all of the demand points. The functions (57) and (59), respectively, represent the fair service in terms of the amount of distributed RPs and deprivation cost considering the balance concept. Now, in order to investigate the efficiency and efficacy of the objective function (2), it is assumed that the mentioned objective is formulated by the functions (56) to (59); as a result, the model is transferred into the following model:

Fig. 11

Impacts of employing the model M1 instead of the model M9

Model 10:

$$\mathrm{Min}\;Z_1,\;Z_3$$

(61)

$$\mathrm{Min}\;Z_{21}={\textstyle\sum_{i\in I}}{\textstyle\sum_{j\in J;d_{js}\neq0}}{\textstyle\sum_{s\in S}}{\textstyle\sum_{t\in T}}p_sw_jy_{ijst}$$

(62)

$$\mathrm{Min}\;Z_{22}={\textstyle\sum_{s\in S}}{\textstyle\sum_{t\in T}}p_s\underset{j\in J;d_{js}\neq0}{min}\{{\textstyle\sum_{i\in I}}w_j\frac{y_{ijst}}{d_{js}}\}$$

(63)

$$\mathrm{Min}\;Z_{23}={\textstyle\sum_{i\in I}}{\textstyle\sum_{j\in J;d_{js}\neq0}}{\textstyle\sum_{s\in S}}{\textstyle\sum_{t\in T}}\;p_sw_j\;F(t_{ijs})y_{ijst}$$

(64)

$$\mathrm{Min}\;Z_{24}={\textstyle\sum_{s\in S}}{\textstyle\sum_{t\in T}}p_s\underset{j\in J;d_{js}\neq0}{max}\{{\textstyle\sum_{i\in I}}w_jF(t_{ijs})\frac{y_{ijst}}{y_{js}}\}$$

(65)

Subject to: Constrains (4) to (18)

Fig. 12 displays some of the outcomes of running the model M10. The findings reveal considerable changes in the problem decisions, resulting in feeble relief performance. Thus, the function objective (2) outperforms the objective functions (56) to (59).

• Two-stage scenario-based stochastic optimization vs. deterministic optimization: To investigate whether it is worthwhile to use the two-stage scenario-based stochastic optimization approach instead of a deterministic optimization approach, we remove the scenarios of the model M1 and treat all the uncertain parameters as certain parameters, thereby replacing them with their expected values across all scenarios (the deterministic counterpart of the model M1 (model M11)). Now, in order to evaluate the performance of the model M11, the decision variables of stage 1 are fixed in the model M1 according to the optimal solution of the model M11. Then, the optimal values of the decision variables of stage 2 are determined. The model M11 establishes warehouses 5, 6, 7, and 10 at storage capacity levels 1, 3, 3, and 3, retrofitting levels 1, 2, 1, and 2, and periods 1, 3, 1, and 2, respectively, leading to a reduction of about 9.6% in the total logistics cost. Although the model M11 is more cost-effective, it is not more efficient and effective in response to the disaster, as it significantly reduces weighted satisfied demands, service utility, and fair service and increases the deprivation costs, resulting in less fulfillment of the second objective function and, consequently, a lower optimal value for it (see Fig. 13). Therefore, we can conclude that the two-stage scenario-based stochastic optimization can result in more effective and efficient relief.

Fig. 12

Results of the model M1 vs. the model M10

Fig. 13

Outcomes of the model M1 compared to the model M11

3.2.3 Robustness analysis

Expected value of perfect information (EVPI) is a performance measure that represents the value of access to accurate information about the future. It somehow expresses the acceptable cost of access to more accurate information. EVPI is calculated as follows:

$$\text{WSS}\hspace{0.17em}=\sum_{s\in S}{p}_{s }{Z}_{s}$$

(66)

$$\begin{aligned} \mathrm{EVPI}\:=&\:\mathrm{RP}-\mathrm{WSS}\;(\mathrm{for}\;\mathrm{minimization}\;\mathrm{problems})\;\mathrm{or}\\&\,\mathrm{WSS}-\mathrm{RP}\;(\mathrm{for}\;\mathrm{maximization}\;\mathrm{problems}) \end{aligned}$$

(67)

${Z}_{s}$, and RP represent the optimal solution value of the deterministic (single-scenario) problem associated with scenario s and the optimal solution value of the original problem, respectively (Birge and Louveaux 1997).

Table 11 presents the values of EVPI for the proposed model. As shown in Table 11, the values of WSS are very close to their corresponding values of RP; as a result, the values of EVPI are very small. The values of EVPI mean that an increase of 120.95, 0.005, 0.009, 0.005, and 96.95, and a decrease of 0.007, and 0.024 in the optimal values of I₁, I₂, I₃, Z₁, Z₃, I₄, and Z₂, respectively, can be incurred owing to the presence of uncertainty. Therefore, unlike the total expected weighted equity in service and Z₂, the other metrics tend to go down with more disaster information which can be achieved in the preparedness phase. Notably, the total expected weighted satisfied demands and service utility can be decreased by 120.95 and 0.009, respectively, if disaster scenarios can be foreseen. Table 12

Table 11 Selected warehouses, their storage capacity and retrofitting level, and the number of RPs purchased for each of them at each period using the model M8

Table 12 Results obtained from the robustness analysis

Regarding the above-mentioned results, it can be concluded that the planning of the model M1 is very close to that of the deterministic programming model associated with each scenario. In this case, collecting complete and accurate information about the stochastic parameters would not be more attractive than solving the model M1, since randomness plays a vital role in the proposed problem. In conclusion, it can be stated that using the proposed two-stage scenario-based stochastic optimization approach in the location, procurement, and distribution decisions can result in appropriate relief.

3.2.4 Sensitivity analyses on the parameters ${{\varvec{a}}}_{{\varvec{t}}},\boldsymbol{ }{{\varvec{b}}}_{{\varvec{t}}}$, and ir _t

In order to demonstrate the effects of varying the parameters of the model, sensitivity analyses are conducted on the parameters ${a}_{t}, {b}_{t}$, and ir_t. These parameters are opted as any variation in their corresponding values can have remarkable effects and their corresponding values may vary abruptly throughout the pre-disaster PTH. Some outcomes of these sensitivity analyses are illustrated in Fig. 14. An increase in the budgets results in the establishment of more or/and more desirable warehouses, the improvement of establishment scheduling and storage and retrofitting levels, more pre-procured RPs and, subsequently an increase in weighted satisfied demands, service utility, equity in service, and the total logistics cost, and a decrease in the deprivation costs. Thus, an increase in the budgets leads to an increase in the optimal values of the second and third objective functions. Moreover, by raising ir_t, the profits allocated to the budgets increase, so the budgets grow. Hence, the RO can establish more or/and more desirable warehouses, improve establishment scheduling and storage and retrofitting levels, provide more RPs before the disaster, resulting in lower supply risk, and higher efficiency, efficacy and equity, and as a consequence, more realization of the second objective function and an increase in total logistics cost.

Fig. 14

Effects of varying the parameters ${a}_{t}, {b}_{t}$, and ir_t on the model

4 Conclusion

Natural and manmade disasters kill thousands of people and displace millions every year. Therefore, to decrease the damages caused by disasters, proper planning is essential in dealing with these events before their occurrence. Consequently, this study aimed to present a logistical model for making strategic decisions (the location, storage.

capacity, retrofitting level, and inventory level of warehouses at pre-disaster) and tactical decisions (the distribution of required supplies at post-disaster) simultaneously. In this regard, a multi-period multi-objective two-stage scenario-based stochastic programming model was presented to minimize the total social cost and maximize fulfilled demands, fair service, and warehouses’ utility. The maximization of warehouses’ utility was formulated in the proposed mathematical programming model according to various criteria and using a proposed DEA model. Moreover, the maximization of fulfilled demands and fair service and the minimization of deprivation costs were simultaneously calculated using a new objective function based on the fraction of satisfied demand, the deprivation cost function, and the priority of the demand point. In this study, several pre-disaster periods, the gradual injection of limited establishment and procurement budgets, the time value of money, various criteria for evaluating warehouses, the risks of disruption in warehouses and transportation networks, and various storage capacities and retrofitting levels for each warehouse were taken into account. It is worth noting that location, procurement, and distribution problems under discussion were modeled dynamically (time-dependent) due to the assumed financial constraints. Finally, a real case study of the plausible earthquake in Khorasan Razavi Province, along with several sensitivity analyses and tests, was implemented to demonstrate the applicability and performance of the proposed programming model. The findings revealed that integrating the DEA model with the mathematical programming model, optimizing efficacy, equity and distress measures using the second objective function, considering the time value of money, and applying proposed multi-period optimization, two-stage scenario-based stochastic optimization and gradual budgets injection approaches can significantly improve the efficiency, efficacy, equity, and distress of the designed DRSC network.

4.1 Managerial insights

The current research contributes to the DRSC literature by presenting a novel efficient optimization approach for warehouse location and the storage of RCs prior to a disaster, and the distribution of pre-positioned RCs among demand points following a disaster under a dynamic uncertain multi-criteria environment and budgetary constraints. Moreover, the findings show that the proposed programming model has the following significant administrative implications and benefits for ROs:

• ROs have occasionally struggled or failed to implement their disaster management policies in reality. One of the major causes contributing to this is a lack of preemptive readiness. Hence, the current study aims to reduce this gap. The proposed model simplifies strategic and tactical decisions for relief managers by merging inventory-related decisions and warehouse location before the calamity with relief distribution after it. The structure of the DRSC network will be more stable due to this design approach and affected people will be able to get RCs sooner.

• Pre-disaster budgets and their investment have a considerable impact on disaster response performance. As a result, financial planning and management can promote service effectiveness.

• The proposed model strives to simultaneously optimize demand coverage, deprivation cost, and fair service, which can assist ROs to plan an efficient DRSC network from various facets. Moreover, formulating these objectives as the second objective function can result in more fulfillment of them.

• In light of pre-disaster financial limitations, ROs can only allocate limited budgets that will gradually become available over time. This necessitates multi-period decision-making. In this regard, employing the multi-period optimization approach can enhance the responsiveness of DRSC.

• In order to improve the performance of the location-inventory-distribution model, the mathematical programming model should be combined with the DEA model, resulting in accounting for patterns of locations simultaneously for warehouses and the associated relative efficiencies of warehouses at each location. Solving for the DEA efficiency measure, simultaneously with other location modeling objectives, provides a promising rich approach to multi objective location problems. The ability to use location models to test trade-offs between spatial efficiency and facility efficiency provides a promising new rich approach for multi-objective location analysis.

• In view of the intricate and unpredictable nature of catastrophes, some key parameters face a high level of uncertainty. Hence, it is appropriate to consider these parameters as scenario-based stochastic parameters, as overlooking these uncertainties and assuming them as deterministic parameters results in an inefficient DRSC network.

• In addition to the fact that victims expect that there must be no privileges or priority for certain groups of people, fair service can prevent some risky cases (such as plunder), maintain the stability of a DRSC network, and deliver RCs in a timely way, thereby improving the performance of an DRSC network. Consequently, it is essential to pay attention to equity in service when designing a DRSC network.

4.2 Future studies

This study, like other studies, was not without limitations. The lack of sufficient cooperation of some ROs and researchers in accessing some information, and the non-existence of an official database for some of the required data, which resulted in the experts’ estimations were asked to help, were among the most critical limitations of the current research. Moreover, there were certain of limitations in the modelling assumptions made. For instance, post-disaster public donation was neglected, as the post-disaster PTH included the first 72 h after the disaster, which is insufficient to distribute items donated by the public. Due to the reduction of the complexity of the problem, the current research assumed the same priority for different RCs and modeled different RCs as RPs. Although, in practice, the priorities of different RCs are different, and the pre-disaster procurement of different RCs based on their priority can significantly improve service to victims. Thus, the assumption that different RCs have the same priority is another restriction. Finally, since no research can be fully comprehensive and complete and not all dimensions can be examined in a single study, this research had other limitations, based on which the following points are suggested in order to extend the problem in question in the future:

• The random and unpredictable nature of the crisis necessitates crisis management within an uncertain environment. As a result, many of the examined papers used a scenario-based stochastic optimization approach, while other uncertain optimization approaches were overlooked. Besides, given the researchers’ identification of disadvantages in the scenario-based stochastic optimization approach, presenting an uncertainty-set based robust optimization approach for the problem under examination can be helpful for real-world applications

• To provide excellent levels of service, processes in a DRSC should be analyzed in general, rather than in detail. As a result, decentralized and hierarchical decisions can better achieve the goals of a DRSC. For this purpose, the use of multi-level programming can be beneficial. Nevertheless, very few studies have focused on multi-level optimization problems to date. Therefore, modeling the problem under study in the form of a multi-level optimization model can provide a more realistic relief network; it also allows for the observation of how decisions made in each part of the network can influence or be influenced by decisions made in other areas.

• Certain vital RCs are perishable; as a result, the lack of attention to their corruption can lead to considerable financial and human losses. Subsequently, it is necessary to consider the perishability of RCs in the proposed problem and provide an efficient inventory management strategy.

• To decrease the expenses of procuring RCs and the risk of supplying RCs after a disaster, it is necessary to select appropriate suppliers and provide solutions to deal with the risk of supply disruption caused by disruptive suppliers. Moreover, the procurement of RCs using a strategy based on placing contracts with supply sources can decrease the expenses of procurement and warehousing due to fewer pre-positioned items in inventory and lower supply risk. Hence, the responsiveness and cost efficiency of the proposed DRSC can be enhanced by integrating the problem under discussion with a supplier selection problem, in which a new and realistic strategy is used based on placing contracts with suppliers; solutions would also be offered to deal with the risk of supplier disruption.

• Pre- and post-disaster relief operations often involve several ROs working simultaneously. Hence, a collaborative DRSC network consisting of several ROs should be designed to make the required decisions on the ways in which RCs are procured, pre-positioned, and distributed pre- and post-disaster. Moreover, each of these ROs has limitations and purposes; as a result, game theory is a powerful tool to address the interactions among them. Thus, considering joint pre- and pot-disaster interactions and operations between several ROs and modeling them by a proper uncertain game theory method would make for an interesting study.

• To solve the proposed model on a large scale, presenting an exact solution method or a heuristic/meta-heuristic algorithm or a solution method based on deep leaning method is recommended.

• The generated solutions must be robust to the variability of input parameters, remain valid, and be either feasible or able to be transformed into feasible solutions at a reasonable cost. Therefore, in order to achieve more robust solutions for the problem under consideration, developing the proposed model utilizing risk measures (e.g., VaR, CVaR, Worst-case mean-CVAR, Entropic VaR, Worst-case mean-quantile-deviation, Semideviation, Maximum regret, and Mean absolute semideviation) and robust scenario-based stochastic optimization techniques (e.g., approaches presented by Mulvey et al. (1995) and Aghezzaf et al. (2010), and p-robust method) is an interesting research avenue.

• In light of the importance and yet lack of behavioral research in humanitarian relief operations (Sankaranarayanan et al. 2018), considering human behaviors and factors (e.g., public sympathy with victims, which can lead to financial and non-financial donations, and victims’ word of mouth and impatience when facing shortages, which can result in leaving distribution centers or plundering RCs, impacting relief operation.) is another intriguing possible direction for further studies.

Appendix

1.1 Appendix A. Proposed DEA model

The proposed DEA model, whose notations are listed in Table 13, is formulated as follows:

Table 13 Sets, indices, parameters, and decision variables used in the proposed DEA model

$$\begin {aligned}\mathrm{Min}\;Z=&\;\beta\Big\{\sum_{i\in I}\Big(\sum_{n\in N}\vartheta_n\left(E_{ni}-E_{nIDEAL}\right)\\&+\sum_{m\in M}\tau_m\left(O_{mIDEAL}-O_{mi}\right)\Big)\Big\}\\&+\left(1-\beta\right)\Big(\underset{i\in I}{\text{max}}\Big\{\sum_{n\in N}\vartheta_n\left(E_{ni}-E_{nIDEAL}\right)\\&+\sum_{m\in M}\tau_m\left(O_{mIDEAL}-O_{mi}\right)\Big\}\Big)\end {aligned}$$

(A.1)

Subject to:

$$\sum_{m\in M}{\tau }_{m}{O}_{mi}\le \sum_{n\in N}{\vartheta }_{n}{E}_{ni}, \forall i\in I$$

(A.2)

$$\sum_{n\in N}{\vartheta }_{n}{E}_{nIDEAL}=1$$

(A.3)

$$\sum_{m\in M}{\tau }_{m}{O}_{mIDEAL}=1$$

(A.4)

$${\vartheta }_{n},{\tau }_{m}\ge \varepsilon$$

(A.5)

The objective function (A.1) minimizes the weighted sum of the summation of the weighted coordinate distances between the virtual ideal alternative and all alternatives and the maximum weighted coordinate distances between the virtual ideal alternative and all alternatives. Constraint (A.2) ensures that the weighted sum of output criteria is less than or equal to the weighted sum of input criteria. Constraints (A.3) and (A.4) take into account the weighted summation of the input criteria of the virtual ideal alternative and the weighted sum of the output criteria of the virtual ideal alternative as equal to one, respectively. Finally, constraint (A.5) specifies the eligible domains of decision variables.

The efficiency score of the alternative i is calculated as follows:

$${ES}_{i}=\frac{\sum_{m\in M}{\tau }_{m}^{*}{O}_{mi}}{\sum_{n\in N}{\vartheta }_{n}^{*}{E}_{ni}}, \quad \forall i\in I$$

(D.6)

${\vartheta }_{n}^{*}$, and ${\tau }_{m}^{*}$ represent the optimal value of the weight assigned to the n^th input criterion and the m^th output criterion, respectively, which are obtained by solving the DEA model presented above. Notably, since the efficiency score of each alternative is calculated as the ratio of the weighted sum of its outputs to the weighted sum of its inputs; hence the more, the better.

1.2 Appendix B. Proposed model integrated with the Klimberg and Ratick’s model

The proposed programming model based on the DEA model employed in the research conducted by Klimberg and Ratick (2008) is formulated as follows.

1.2.1 Model M2

$$\mathrm{Min}\;Z_1={\textstyle\sum_{i\in I}}(1-U_i)$$

(B.1)

$$\mathrm{Max}\;Z_2$$

$$\mathrm{Min}\;Z_3$$

Subject to:

Eqs. (4) to (6), (10) to (14), and (16) to (18)

$$\sum_{n\in N}{\vartheta }_{ni}{E}_{ni}=\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}, \forall i\in I$$

(B.2)

$$\sum_{m\in M}{\tau }_{mi}{O}_{mi}+{u}_{i}=\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}, \forall i\in I$$

(B.3)

$$\sum_{m\in M}{\tau }_{mi}{O}_{m\acute{i}}-\sum_{n\in N}{\vartheta }_{ni}{E}_{n\acute{i}}\le 0, \forall i,\acute{i}\in I;i\ne \acute{i}$$

(B.4)

$${\tau }_{mi}{O}_{mi}\le \sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}, \forall i\in I;m\in M$$

(B.5)

$${\vartheta }_{ni}\ge \varepsilon (\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt} ), \forall i\in I;n\in N$$

(B.6)

$${\tau }_{mi}\ge \varepsilon (\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}), \forall i\in I;m\in M$$

(B.7)

where variables ${u}_{i}$, ${\tau }_{mi}$, and ${\vartheta }_{ni}$ indicate the level of inefficiency of warehouse i, the weight allocated to the m^th output criterion for warehouse i, and the weight allocated to the n^th input criterion for warehouse i, respectively. The objective function (B.1) maximizes the summation of the efficiencies of warehouses. Constraint (B.2) considers the weighted sum of the input criteria of an established and unestablished warehouse to be equal to one and zero, respectively. Constraint (B.3) indicates the level of inefficiency of a warehouse. Constraint (B.4) determines that the weighted sum of output criteria is less than or equal to the weighted sum of input criteria. Constraint (B.5) requires the weighted output criteria to be less than or equal to one. Constraints (B.6) and (B.7) express the range of the variables.

1.3 Appendix C. Proposed model integrated with the Afsharian’s model

According to the DEA model used in the research conducted by Afsharian (2021), the proposed programming model is formulated as follows.

1.3.1 Model M3

$$\mathrm{Max}\;Z_1=\sum_{m\in M}\sum_{i\in I}\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}x_{ilrt}\tau_mO_{mi}$$

(C.1)

$$\mathrm{Max}\;Z_2$$

$$\mathrm{Min}\;Z_3$$

Subject to:

Eqs. (4) to (7), and (10) to (18)

$$\sum_{n\in N}\sum_{i\in I}\sum_{l\in L}\sum_{r\in R}\sum_{t\in T}{x}_{ilrt}{\vartheta }_{n}{E}_{ni}=1, \forall i\in I$$

(C.2)

The objective function (C.1) maximizes the weighted sum of the output criteria of warehouses. Constraint (C.2) considers the weighted sum of the input criteria of an established warehouse as equal to one.