A stochastic bi-objective simulation–optimization model for cascade disaster location-allocation-distribution problems

Abstract

Cascade disasters can destroy urban infrastructures, kill thousands of people, and permanently displace millions of people. The paramount goal of disaster relief programs is to save lives, reduce financial loss, and accelerate the relief process. This study proposes a bi-level two-echelon mathematical model to minimize pre-disaster costs and maximize post-disaster relief coverage area. The model uses a geographic information system (GIS) to classify the disaster area and determine the optimal number and location of distribution centers while minimizing the relief supplies’ inventory costs. A simulation model is used to estimate the demand for relief supplies. Initially, vulnerable urban infrastructures are identified, and then the interaction among them is investigated for cascade disasters. The aims of this study are threefold: (1) to identify vulnerable urban infrastructures in cascade disasters, (2) to prioritize urban areas based on the severity of cascade disasters using a GIS, and (3) to develop a bi-objective multi-echelon multi-supplies mathematical model for location, allocation, and distribution of relief supplies under uncertainty. The model is solved with an epsilon-constraint method for small and medium-scale problems and the invasive weed optimization algorithm for large-scale problems. A case study is presented to demonstrate the applicability and efficacy of the proposed method. The results confirm the difficulty of relief operations during the night as the cost of night-time relief operations is higher than daytime. In addition, the results show the coverage area increases as the demand surges. Therefore, establishing more distribution centers will increase operating costs and expand coverage are.

1 Introduction

Cascading disasters are high-impact events that progress over time and produce subsequent unanticipated disasters intensified by physical and social infrastructure breakdown. Cascading effects can destroy transportation and communications systems and have irreparable effects on the and infrastructure. Cascading disasters’ side effects can sometimes be more severe and destructive than the primary disaster (Gong et al., 2020; Tang et al., 2019). For example, Japan was hit by a tsunami that damaged a nuclear power plant (Ohnishi, 2012; Yamashita & Shigemura, 2013). This cascading disaster killed thousands, or a flood in central Europe in 2002 led to the emission of toxic and dangerous gases from a nuclear power plant (Pescaroli & Alexander, 2015).

One of the main strategies in increasing disaster relief operations’ efficiency and reducing delays and shortages is the pre-positioning of distribution centers and establishing these centers to distribute relief supplies (Ghasemi et al., 2019a, b; Goodarzian et al., 2020). Determining the location of distribution centers and deciding on the inventory stored in these centers, allocating distribution centers to the affected areas, and mapping the flow between distribution centers and demand points are essential measures in the pre-disaster preparedness phase (Barzinpour & Esmaeili, 2014; Goodarzian et al., 2021). The planners must identify suitable and safe locations for establishing distribution centers during the preparedness phase (Baser & Behnam, 2020; Du et al., 2020). Uncertainty in demand for relief supplies during the occurrence of a disaster has always been a significant problem in disaster relief (Baharmand et al., 2019). Shortage of relief supplies can directly impact efficiency during cascade disasters (Zhang et al., 2019). The severity of the destruction directly correlates with the needed supplies’ quantity (Hasani & Mokhtari, 2018). The number of vulnerable infrastructures in large cities often complicates forecasting demand and relief operations (Sarma et al., 2020). Disaster relief operations can be managed more efficiently if vulnerable urban infrastructures can be identified and carefully studied before a cascade disaster (Oh et al., 2010).

This study presents a bi-level stochastic model for locating distribution centers, allocating them to the demand points, and managing the flow of relief supplies in the event of cascade disasters, including earthquakes, floods, and radiological incidents. The objectives of this study are to minimize pre-disaster costs and maximize post-disaster coverage area. The aims of this study are threefold. The first aim is to identify vulnerable urban infrastructures in cascade disasters such as floods, earthquakes, and radiological incidents. The second aim is to prioritize urban areas based on the severity of cascade disasters using a geographic information system (GIS). And the third aim is to develop a bi-objective multi-echelon multi-supplies mathematical model for location, allocation, and distribution of relief supplies under uncertainty. The remainder of this paper is organized as follows. Section 2 presents the literature review. The problem is described and formulated in Sect. 3. Section 4 presents the simulation model. The mathematical model and solution methods are described in Sects. 5 and 6. We present a case study in Sect. 7 to demonstrate the applicability and efficacy of the proposed method. Section 8 concludes with our conclusions and future research directions.

2 Literature review

Yang et al. (2021) presented a dynamic multi-objective mathematical model for the pre-disaster supply chain management by considering the time-variant penalty function for the lost times in the relief operation. Their primary objective was to locate the relief supplies and minimize the supply chain costs using a robust optimization model to handle uncertain demand. They accomplished this objective by transforming their non-deterministic model into a deterministic chance-constrained model. Zhan et al. (2021) proposed a mathematical model for disaster logistics management problems with unbalanced demand and supply for relief supplies. Their model handled the demand–supply imbalance in disaster relief supply chains, located the distribution centers, and delivered the necessary needs to the affected areas. Arslan et al. (2021) used a cycle-canceling algorithm and a branch-price-and-cut method to address refugee camp location analysis in disasters and minimize the camps’ reopening costs and routing. The results showed that as the number of refugees increases in the camps, the supply chain costs rise exponentially.

Yu (2020) presented a multi-objective mathematical model for locating facilities in the disaster preparedness phase by considering max-flow and shortest path concepts. This model aims to maximize the minimum reachability guarantee and minimize location costs while road destruction is considered an uncertain parameter. Velasquez et al. (2020) presented a robust two-stage model for disaster management in the southeast United States. The location of distribution centers and the pre-positioned amount of relief supplies were determined in the first stage. The distribution of relief supplies to the affected areas was designated in the second stage. The first stage was related to the pre-disaster phase, and the second stage was associated with the post-disaster phase. The main objective of the model is to minimize the pre-disaster and post-disaster costs. They solved this model with the column-and-constraint generation algorithm. Erbeyoğlu and Bilge (2020) presented a two-echelon mixed-integer linear model for locating and determining warehouses’ inventory levels in the pre-disaster phase. Minimizing the costs of transporting, locating, and determining the inventory levels were the model’s objectives. The model was solved with the Benders decomposition approach considering service adequacy and fairness.

Ghasemi et al., (2019a, b) presented a multi-objective stochastic model for distribution management and evacuation planning during earthquake disasters. Simulation was used to estimate uncertain demand, and the non-dominated sorting genetic algorithm II (NSGA-II) was utilized to solve the problem. Doodman et al. (2019) presented a multi-objective two-stage stochastic model for pre and post-disaster planning. Equity and fairness were considered in the proposed model, in addition to improving the costs of relief. Their main idea was to consider lateral transshipment under uncertainty and the possibility of failure of distribution centers. The relief costs were minimized in the first level of the model, and the victim’s satisfaction was considered in the second level of the model. Doan and Shaw (2019) investigated resource allocation when several disasters coincide. Risk analysis of the accessibility to the relief resources is done according to limited resources. The objective is to reduce the risk of a shortage of resources and minimize the risk of buying additional resources.

Cao et al. (2018) presented a multi-objective model for the distribution of relief supplies in the event of a disaster. Considering the sustainability of disaster and calculating the beneficiary perspective on sustainability are among their contributions. Minimizing deviation on perceived satisfaction for distribution centers is the most important objective in their proposed relief chain. Finally, the genetic algorithm was used to solve the model. Feng and Xiang-Yang (2018) developed the concepts of relief in cascade disasters using case-based reasoning. The results indicated that the proposed approach anticipated and addressed the possible escalations of secondary disasters. The case study was a Typhoon in China, which included winds and heavy rains that could cause landslides, water supply failure, and power outage. Haghi et al. (2017) presented a robust multi-objective model for managing the pre and post-disaster distribution of relief supplies. The considered uncertainty included demand and transportation costs. Considering the failure of distribution centers was one of their most important contributions. Their most important objective was to minimize the preparedness phase’s costs and increase the disaster victims’ satisfaction. The NSGA-II and multi-objective genetic simulated annealing (MOGASA) algorithms were used to solve the problem.

Berariu et al. (2015) examined the effect of cascade disasters on disaster relief operations. They identified vulnerable urban infrastructures, considered transportation, electricity, and healthcare infrastructures, and investigated the disaster’s cascading effect using system dynamics. Oh et al. (2010) examined the effect of natural disasters on vulnerable urban infrastructures and industries. They examined the impact of disasters on education, agriculture, and banking by studying water, gas, electricity, and transportation infrastructures (Table 1).

Table 1 Previous studies

3 Problem description

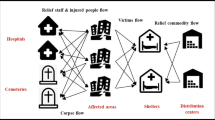
Disaster relief logistics management is the timely delivery of sufficient relief supplies to pre-positioned areas. The efficient distribution of relief supplies requires that distribution centers be established in appropriate and pre-positioned locations. This study presents a two-echelon mathematical model, including distribution centers and affected areas (demand points). This research aims to maximize the covered areas and minimize the costs of establishing distribution centers and transportation costs in the preparedness phase, while more populated areas are a priority. In addition to the distribution centers’ location, the supplies’ quantity transported from the distribution centers to the affected areas, the supplies’ quantity stored in the distribution centers, the allocation of distribution centers to the affected areas, and the shortage of relief supplies are examined. The demand for relief supplies has been considered uncertain. The distribution functions of demand for relief supplies are estimated by simulation based on the severity of each area’s destruction and population. The considered relief supplies include food, tents, water, medicine, and blankets that do not require special maintenance equipment. The distribution function of demand for relief supplies is the simulation model output, which enters the mathematical model as a parameter. Figure 1 shows a view of the proposed disaster relief chain.

Fig. 1

Relief chain configuration

Figure 1 shows the location-allocation and distribution of relief supplies in two echelons includes distribution centers and demand points. Different colors are used to indicate the severity of destruction in different geographical areas determined by the GIS. The ARC-GIS software and RADIUS model are used to divide the considered area into different sections. This software provides a powerful platform for damage estimation functions. The Japan International Cooperation Agency (JICA) database is utilized in the GIS to retrieve the population of the area, the number of buildings, the type of structure, and the type of soil, among others.

Figure 2 presents the proposed framework. The first step is to identify the urban infrastructures affected by the disaster. ARC-GIS and the RADIUS model are used to determine the destruction severity of the vulnerable urban areas. Next, the interactions among the infrastructures are examined using the simulation model and Enterprise Dynamic (ED) software. The simulation model provides an estimate of the demand for relief supplies. The distribution functions of the estimated relief supplies are used in the mathematical model as uncertain parameters. The chance-constrained programming approach is used to convert uncertain results into precise outputs. The proposed model is then solved by an exact model and GAMS software for small and medium-scale problems and by a multi-objective invasive weed model and MATLAB software for large-scale problems.

Fig. 2

Proposed framework

4 Simulation model

This section presents the simulation model used to estimate the demand for relief supplies.

4.1 Infrastructure vulnerability analysis

Five types of flows have been used in designing the interaction among the urban infrastructures according to Table 2 (Abhijeet et al., 2011; Baloye & Palamuleni, 2017; McCormak et al., 1997):

• a. Population flow representing shelters, hospitals, and healthcare infrastructures.

• b. Cash flow representing agricultural and economic infrastructures.

• c. Material flow representing transportation infrastructures, bridges, and supply chains.

• d. Energy flow representing infrastructures of water, gas, electricity, and dams.

• e. Information flow representing communication infrastructures.

Table 2 Vulnerable urban flows and infrastructures

The interaction of the three phenomena of earthquake, flood, and radiological incidents are depicted in Fig. 3. This figure shows earthquakes can lead to “transportation infrastructure destroyed.” This is followed by “destroyed supply chain” and “global production loss,” which lead to demand for relief supplies such as “water, food, medicine, blanket, and tent.” Earthquakes can also lead to “building damage,” in which case relief supplies such as “water, food, medicine, blanket and tent” are needed. If an earthquake causes “dam failure,” there will be demand for “water,” and if it causes “gas supply destruction,” there will be demand for “water and blanket.” If an earthquake causes “fire,” a “temporary shelter” needs to be established, which in turn leads to the demand for supplies such as “water, food, medicine, and blanket.”

Fig. 3

Interaction of vulnerable urban infrastructures in the event of a cascade disaster

When an earthquake occurs, a “flood” may occur due to changes in the underground layers and heavy rainfall, and even dam destruction. The flood can cause “sewer destruction” and “water supply destruction,” which lead to demand for “water.” After a flood, a “shortage of healthcare resources” may occur, which increases the demand for “medicine” and “hospital destruction,” which also increases the demand for “medicine, tent, and blanket.”

Earthquakes can damage “nuclear facilities.” In addition to earthquakes, floods can damage nuclear power plants by causing damage to the power generator. “Nuclear power plant incident” leads to exposure to “radiations,” which can have “long-term effects on agriculture and fishing” and “food exports,” which increases the demand for “food.” Nuclear radiations also cause “harm to people,” leading to demand “water, food, medicine, blankets, and tents.” In addition, if the nuclear effects intensify, there may be “fires,” which lead to demand for “water, food, medicine, and blankets” after the establishment of temporary shelters.

4.2 Infrastructures interaction simulation

ED software is very powerful in simulating discrete event systems. The atoms in the ED software can cover all simulation processes. One of this software’s successful applications is given in Shahabi et al. (2019) and Rooeinfar et al. (2019).

Figure 4 depicts a view of the infrastructure interaction simulation structure in the event of cascading disasters in the ED software. Thirty-four atoms are used to simulate the proposed structure in the simulation software. This includes 32 servers, a source, and a sink. In simulating the proposed structure, each earthquake synapse is considered an entity. The disaster starts with an earthquake, and an earthquake will cause a flood. Flood and earthquake will simultaneously affect nuclear facilities. Therefore, the earthquake is considered a source atom, and flood and “nuclear power plant” are considered servers. There are also five atoms related to relief supplies, including blankets, water, food, tents, and medicine. These atoms count the amount of demand for relief supplies from each scenario. In this study, one blanket, 2 L of water, 2 kg of food, 0.125 tents, and 0.2 kg of medicine are considered per person daily. The simulation method considered in this study is a separate run. The simulation’s warm-up period is 10,000 h, the observation time (simulation time) is 100,000 h, and the number of replications is five in this study. The warm-up period is before the simulation starts collecting results (Grassmann, 2014; Law, 2020). The measurement performance function includes AvgContent (cs) and Output (cs). The AvgContent (cs) index represents the interaction between the simulation infrastructures, and Output (cs) index represents the demand for relief supplies and system output. The separate run simulation conduct conducts and collects data on concurrent simulations.

Fig. 4

Structure of simulation model

The time interval between synapses (inter-arrival time) in the simulation is considered equal to the negative exponential function with parameter 20. The entry time for the first entity (synapse) until the start of the simulation time is zero. The number of entities (number of products) is also considered unlimited. Also, in the server atom (flood) case, considering that it has one input channel and eight output channels, the batch value is equal to 8, and the batch rule is “1 in B out”. The input channel to this server has been “earthquake.” The output channels include “power generator failure,” “sewer destruction,” “water supply destruction,” “shortage of healthcare resources,” “hospital destruction transportation,” “destroyed infrastructure,” “damage of communication network,” and “building damage.”

4DScript codes are used to calculate the interaction among the infrastructures. For example, the calculation of 4DScript codes for gas supply destruction atom is based on Eq. (1) (Goda et al., 2016):

$$ R_{m} \left( {PGV} \right) = R\left( {PGV} \right) \cdot C_{p} \cdot C_{g} \cdot C_{l} $$

(1)

where $R_{m} \left( {PGV} \right) = {\rm{~damage}}~{\rm{ratio}}~\left( {{\rm{points}}/{\rm{km}}} \right)$, PGV: Peak Ground Velocity (kine = cm/sec), R(PGV) = 3.11*$10^{{ - 3}}$*$\left( {PGV - 15} \right)^{{1.3}}$, $C_{p} = {\rm{pipeline~material~coefficient}}~$. $C_{g} = {\rm{ground~condition~coefficient}}$, $C_{l} =$ liquefaction coefficient,

The values of the parameters in this equation vary based on the pipelines’ material and are determined based on Table 3.

Table 3 The values of the parameters based on the material of gas pipelines

As mentioned, Eq. (1) shows the extent of earthquake damage to the gas infrastructure based on peak ground velocity (PGV). The reason for using the PGV index to show the extent of damage to gas pipelines is that it has a relatively high correlation relative to peak ground acceleration (PGA). Figure 5 shows the damage function estimate for welded gas pipelines in Iran. In this figure, the vulnerability of natural gas pipelines exposed to seismic wave propagation is assessed and evaluated (Komak Panah & Hafezi Moghadas, 1993).

Fig. 5

Probability of damage to pipelines based on peak ground velocity

5 Mathematical modeling

Indices

$r = 1,2, \ldots ,R$ Urban sub-regions.

$c = 1,2, \ldots ,C$ Relief supplies.

$a = 1,2, \ldots ,A$ The horizontal axis of the map.

$b = 1,2, \ldots ,B$ The vertical axis of the map.

$e = 1,2, \ldots ,E$ The severity of the disaster (failure) is shown in different colors.

$i = 1,2, \ldots ,I$ Distribution centers.

$s = 1,2, \ldots ,S$ Scenario.

Parameters

$p_{{e\left( {a,b} \right)s}}$ 1 if the coordinates $\left( {a,b} \right)$ in the scenario s are under the severity e, otherwise it is 0.

$a_{{r\left( {a,b} \right)s}}$ 1 if the coordinates $\left( {a,b} \right)$ in scenario s belong to sub-region r, otherwise it is 0.

$g_{{ir\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}}$ 1 if the distribution center i in (a, b) ∈ r is allowed to serve $\left( {a',b'} \right)$ ∈ r in scenario s, otherwise it is 0 $g_{{ir\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} = a_{{r\left( {a,b} \right)s}} \cdot a_{{r\left( {a',b'} \right)s}}$ $\forall i,r,\left( {a,b} \right) \in r,\left( {a^{\prime},b^{\prime}} \right) \in r,s$

$c_{{i\left( {a,b} \right)s}}$ The setup cost of the distribution center i located in coordinates $\left( {a,b} \right)$ in the scenario s.

$L_{{\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)}}$ The distance between the coordinates $\left( {a,b} \right)$ and the coordinates $\left( {a',b'} \right)$.

$tc_{{cs}}$ Transportation cost of relief supplies c per distance unit in scenario s.

$cs_{{c\left( {a,b} \right)s}}$ Shortage cost of relief supplies c in coordinates $\left( {a,b} \right)$ in scenario s.

$v_{c}$ The volume of relief supplies c.

$cap_{{is}}$ The capacity of the distribution center i in scenario s.

$h_{{ic\left( {a,b} \right)s}}$ Holding cost of relief supplies c in the distribution center i placed in the coordinates $\left( {a,b} \right)$ in the scenario s.

$Pop_{{\left( {a,b} \right)}}$ Population size in coordinates $\left( {a,b} \right)$.

$D'_{{ces}}$ Coefficient of demand of relief supplies c is at the severity level e in the scenario s.

$D_{{c\left( {a,b} \right)s}}$ Demand for relief supplies c in coordinates $\left( {a,b} \right)$ in the scenario s $D_{{c,\left( {a,b} \right)s}} = Pop_{{\left( {a,b} \right)}} .\left( {\mathop \sum \limits_{e} a_{{r\left( {a,b} \right)s}} .D'_{{ces}} } \right)$ $\forall \left( {a,b} \right),c,s$

$p_{s}$ Probability of occurrence of scenario s.

Decision variables

$x_{{i\left( {a,b} \right)s}}$ 1 if the coordinates $\left( {a,b} \right)$ in the scenario s are covered by the distribution center i, otherwise it is 0.

$y_{{i\left( {a,b} \right)s}}$ 1 if the distribution center i is established in the coordinates $\left( {a,b} \right)$ in the scenario s, otherwise it is 0.

$z_{{ic\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}}$ The relief supplies quantity c transported from the distribution center i located in the coordinates $\left( {a,b} \right)$ in the scenario s to the demand point in the coordinates $~\left( {a',b'} \right)$.

$I_{{ic\left( {a,b} \right)s}}$ The relief supplies quantity c stored in the distribution center i located in coordinates $\left( {a,b} \right)$ in the scenario s.

$sh_{{c\left( {a,b} \right)s}}$ Shortage of relief supplies c in demand point in coordinates $\left( {a,b} \right)$ in the scenario s

$$ Max~F_{1} = \mathop \sum \limits_{{\left( {a,b} \right)}} \mathop \sum \limits_{i} \mathop \sum \limits_{s} p_{s} \left( {Pop_{{\left( {a,b} \right)}} x_{{i\left( {a,b} \right)s}} } \right) $$

(2)

$$ \begin{gathered} Min~F_{2} = \mathop \sum \limits_{s} p_{s} \left[ {\mathop \sum \limits_{{\left( {a,b} \right)}} \mathop \sum \limits_{i} c_{{i\left( {a,b} \right)s}} y_{{i\left( {a,b} \right)s}} + \mathop \sum \limits_{i} \mathop \sum \limits_{{\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)}} \mathop \sum \limits_{c} tc_{{cs}} ~ \cdot L_{{\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)}} \cdot z_{{ic\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} } \right. \hfill \\ \left. { + \mathop \sum \limits_{i} \mathop \sum \limits_{{\left( {a,b} \right)}} \mathop \sum \limits_{c} \left( {h_{{ic\left( {a,b} \right)s}} I_{{ic\left( {a,b} \right)s}} + cs_{{c\left( {a,b} \right)s}} ~ \cdot sh_{{c\left( {a,b} \right)s}} } \right)} \right] \hfill \\ \end{gathered} $$

(3)

$$ I_{{ic\left( {a,b} \right)s}} \le \mathop \sum \limits_{e} D_{{c\left( {a,b} \right)s}} \cdot y_{{i\left( {a,b} \right)s}} \quad \forall c,i,s,\left( {a,b} \right) $$

(4)

$$ \mathop \sum \limits_{c} I_{{ic\left( {a,b} \right)s}} \cdot v_{c} \le cap_{{is}} \cdot y_{{i\left( {a,b} \right)s}} \quad \forall \left( {a,b} \right),i,s $$

(5)

$$ \mathop \sum \limits_{{\left( {a,b} \right)}} g_{{ir\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} .z_{{ic,\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} \le I_{{ic\left( {a,b} \right)s}} \quad \forall r,i,c,s,\left( {a,b} \right) \in r $$

(6)

$$ x_{{i\left( {a^{\prime},b^{\prime}} \right)s}} \le \mathop \sum \limits_{{\left( {a,b} \right) \in r}} g_{{ir\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} .y_{{i\left( {a,b} \right)s}} ,\;\forall r,i,s,\forall \left( {a^{\prime},b^{\prime}} \right) \in r $$

(7)

$$ \mathop \sum \limits_{i} y_{{i\left( {a,b} \right)s}} \le 1\quad \forall ~\left( {a,b} \right),i,s $$

(8)

$$ sh_{{c\left( {a',b'} \right)s}} = D_{{c\left( {a',b'} \right)s}} - \mathop \sum \limits_{i} \mathop \sum \limits_{{\left( {a,b} \right)}}^{~} g_{{ir\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} .z_{{ic\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} \quad \forall \left( {a^{\prime},b^{\prime}} \right),s $$

(9)

$$ \mathop \sum \limits_{{\left( {a,b} \right)}} g_{{ir\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} .y_{{i\left( {a,b} \right)s}} .z_{{ic\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} \ge D_{{c\left( {a',b'} \right)s}} .x_{{i\left( {a',b'} \right)s}} \quad \forall r,c,i,s,\left( {a',b'} \right) \in r $$

(10)

$$ sh_{{c\left( {a,b} \right)s}} ,z_{{ic\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} ,I_{{ic\left( {a,b} \right)s}} \ge 0 $$

(11)

$$ x_{{i\left( {a^{~} ,b^{~} } \right)s}} ,y_{{i\left( {a,b} \right)s}} = 0~\;or\;1~\quad \forall i,s,\left( {a^{~} ,b^{~} } \right) $$

(12)

The objective function (2) maximizes the coverage of each area. According to this objective function, the area that has a larger population is given priority in coverage. The objective function (3) minimizes the setup cost of distribution centers, transportation costs, holding costs, and shortage costs. Constraint (4) states that only established distribution centers can store relief supplies, and the amount of storage will be less than the total demand. Constraint (5) expresses the volume capacity limit of relief supplies in distribution centers. Constraint (6) states that the supplies’ quantity transported from distribution centers to demand centers must be less than the supplies’ quantity stored in that center. Constraint (7) guarantees that if a distribution center is established in coordinates $\left( {{\rm{a}},{\rm{b}}} \right)$ then it can cover the demand area $\left( {{\rm{a}}',{\rm{b}}'} \right)$. Constraint (8) indicates that at most, one distribution center should be established in each location. Constraint (9) indicates the amount of shortage of relief supplies in each scenario. This amount is equal to the difference between the amount of demand and the supply of relief supplies. Constraint (10) guarantees that if a demand area is covered, its demand must be met by allocated centers. Constraints (11) and (12) express the type of decision variables. Given that the Constraint (10) is nonlinear, the integer variable γ_{c(a,b),(a′,b′)} is defined as the Constraint (13). Therefore, to linearize the model, Constraints (13)–(18) must replace Constraint (10).

$$ \gamma _{{c\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)is}} = y_{{i\left( {a,b} \right)s}} .z_{{ic\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} \quad \forall \left( {a^{~} ,b^{~} } \right),\left( {a^{\prime},b^{\prime}} \right),i,c,s $$

(13)

$$ \mathop \sum \limits_{{\left( {a,b} \right)}} g_{{ir\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} .\gamma _{{c\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)is}} \ge D_{{c\left( {a',b'} \right)s}} .x_{{i\left( {a',b'} \right)s}} \quad \forall \left( {a^{\prime},b^{\prime}} \right),i,c,r,s $$

(14)

$$ \gamma _{{c,\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)is}} \le z_{{ic\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} \quad \forall \left( {a^{~} ,b^{~} } \right),\left( {a^{\prime},b^{\prime}} \right),i,c,s $$

(15)

$$ \gamma _{{c,\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)is}} \le M.y_{{i\left( {a,b} \right)s}} \quad \forall \left( {a^{~} ,b^{~} } \right),\left( {a^{\prime},b^{\prime}} \right),i,c,s $$

(16)

$$ \gamma _{{c\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)is}} \ge z_{{ic\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)s}} - M\left( {1 - y_{{i\left( {a,b} \right)s}} } \right)\quad \forall \left( {a^{~} ,b^{~} } \right),\left( {a^{\prime},b^{\prime}} \right),i,c,s $$

(17)

$$ \gamma _{{c,\left( {a,b} \right),\left( {a^{\prime},b^{\prime}} \right)is}} = {\rm{Integer}}\quad \forall \left( {a^{~} ,b^{~} } \right),\left( {a^{\prime},b^{\prime}} \right),i,c,s $$

(18)

6 Solution methods

In this section, the proposed stochastic model is first converted to a deterministic model using the chance-constrained programming approach. The proposed model is then solved in small and medium scale using the epsilon-constraint method and on a large scale (case study) using the multi-objective invasive weed optimization algorithm approach. Figure 6 shows the interaction between the inputs and outputs in the simulation algorithm. The proposed simulation–optimization method operates by inputting the three phenomena of the earthquake, flood, and radiological incidents into the mathematical model. The simulation inputs include the population flow, cash flow, material flow, and energy flow categories. The population flow inputs include data on the shelters, buildings, hospitals, and the healthcare system, and the cash flow inputs include the global production loss data and the agriculture system. The material flow inputs include transportation system data, and the energy flow inputs include gas supply system, electricity supply chain, water supply system, and dam system data. The simulation model’s output comprises the demand distribution functions for the relief supplies, including food, medicine, blankets, tents, and water. The distribution function of demand for relief supplies is the output of the simulation model. The input of the mathematical model includes parameters such as cost, distance, capacity, the population of affected areas, and demand for relief commodities. The output of the mathematical model is the data on the location and allocation of distribution centers, the number of relief commodities used and stored, and the shortage amount.

Fig. 6

Interaction between the inputs and outputs in the simulation and optimization algorithm

6.1 Stochastic chance-constrained programming

The stochastic mathematical models must first be converted to deterministic models to be solved. There are several methods for converting stochastic models to deterministic models. One of the most popular and widely used methods is stochastic chance-constrained programming, first introduced by Charnes and Cooper (1959). In stochastic models, at least one of the parameters is uncertain (Elçi & Noyan, 2018). The minimization model is assumed with the parameters $d_{{ij}}$, $a_{{kj}}$ and $f_{i}$. The symbol $\sim$ indicates the uncertainty of the parameter. The probability of occurrence of a constraint is defined by Eq. (19):

$$ p\left( {\mathop \sum \limits_{{j = 1}}^{n} d_{{ij}} y_{j} \ge e_{i}^{\sim } } \right) \ge \alpha _{i} \quad i = 1,2, \ldots ,m $$

(19)

Therefore, the model is rewritten as Eqs. (20)–(23):

$$ \min f_{k} = E\left( {\mathop \sum \limits_{{j = 1}}^{n} a_{{kj}}^{\sim } y_{j} \ge e_{i}^{\sim } } \right)\quad k = 1, \ldots ,K;\;i = 1,2, \ldots ,m $$

(20)

$$ p\left( {\mathop \sum \limits_{{j = 1}}^{n} d_{{ij}}^{\sim } y_{j} \ge e_{i}^{\sim } } \right) \ge \alpha _{i} \quad i = 1,2, \ldots ,m $$

(21)

$$ y = \left( {y_{1} , \ldots ,y_{n} } \right) $$

(22)

$$ y \ge 0 $$

(23)

A summary of the results of chance-constrained programming for minimization and maximization problems is in the form of Eqs. (24)–(26). For more information on this algorithm, see Reza-Pour and Khalili-Damghani (2017).

$$ E\left( {\mathop \sum \limits_{{j = 1}}^{n} a_{{kj}}^{*} y_{j} - f_{k}^{ - } } \right) - \varphi ^{{ - 1}} (\alpha _{k} )\sqrt {Var} \left( {\mathop \sum \limits_{{j = 1}}^{n} a_{{kj}}^{*} y_{j} - f_{k}^{ - } } \right) \ge 0\quad k = 1, \ldots ,K $$

(24)

So that $f_{k}^{ - } = \min \mathop \sum \limits_{{j = 1}}^{n} a_{{kj}}^{*} y_{j}$.

$$ E\left( {\mathop \sum \limits_{{j = 1}}^{n} a_{{kj}}^{*} y_{j} - f_{k}^{ + } } \right) + \varphi ^{{ - 1}} (\alpha _{k} )\sqrt {Var} \left( {\mathop \sum \limits_{{j = 1}}^{n} a_{{kj}}^{*} y_{j} - f_{k}^{ + } } \right) \le 0\quad k = 1, \ldots ,K $$

(25)

So that $f_{k}^{ + } = \max a_{{kj}}^{*} y_{j}$

$$ E\left( {\mathop \sum \limits_{{j = 1}}^{n} d_{{ij}}^{\sim } y_{j} - e_{i}^{\sim } } \right) - \varphi ^{{ - 1}} (1 - \alpha _{i} )\sqrt {Var} \left( {\mathop \sum \limits_{{j = 1}}^{n} d_{{ij}}^{\sim } y_{j} - e_{i}^{\sim } } \right) \ge 0\quad i = 1,2, \ldots ,m $$

(26)

Based on Constraints (24)–(26), the multi-objective chance-constrained model is defined as Eqs. (27)–(29) at the ${\alpha }\;\% ~$ level for Constraints (4), (9), and (10), respectively:

$$ I_{{ic(a,b)s}} \le \left( {\mathop \sum \limits_{e} E(D_{{c(a,b)s}} ) + \varphi ^{{ - 1}} \left( {1 - \alpha _{i} } \right).\sqrt {\rm{var} \left( {D_{{c(a,b)s}} } \right)} } \right).y_{{i(a,b)s}} \quad \forall c,i,s,\left( {a,b} \right) $$

(27)

$$ sh_{{c(a',b')s}} = E\left( {D_{{c(a',b')s}} } \right) + \varphi ^{{ - 1}} \left( {1 - \alpha _{i} } \right).\sqrt {\rm{var} \left( {D_{{c(a',b')s}} } \right)} - \sum\limits_{i} {\sum\limits_{{\left( {a,b} \right)}} {g_{{ir\left( {a,b} \right),\left( {a^{'} ,b^{'} } \right)s}} .z_{{ic\left( {a,b} \right),(a^{'} ,b^{'} )s}} } } \quad \forall \left( {a^{\prime},b^{\prime}} \right),s $$

(28)

$$ \mathop \sum \limits_{{(a,b)}} g_{{ir\left( {a,b} \right),(a^{'} ,b^{'} )s}} .z_{{ic\left( {a,b} \right),(a^{'} ,b^{'} )s}} \ge \left( {E\left( {D_{{c(a',b')s}} } \right) + \varphi ^{{ - 1}} \left( {1 - \alpha _{i} } \right).\sqrt {\rm{var} \left( {D_{{c(a',b')s}} } \right)} } \right).x_{{i(a',b')s}} \quad \forall r,c,i,s,\left( {a',b'} \right) \in r $$

(29)

6.2 Epsilon-constraint method

The Epsilon-constraint method is one of the most popular and widely used approaches for solving multi-objective problems on a small and medium scale. In this method, one of the objective functions is selected as the main function, and the problem is solved each time according to one of the functions (Tavana et al., 2018). The interval between the two optimal values of the secondary functions is divided into a predetermined number, and each time the problem is solved for each of the values ${{\varepsilon }}_{2} ,~ \ldots ,~{{\varepsilon }}_{n}$. Finally, Pareto solutions are obtained. The mathematical model of this approach is as Eq. (30) (Rath & Gutjahr, 2014):

$$ \begin{gathered} \min f_{1} \left( x \right) \hfill \\ x \in X \hfill \\ f_{2} \left( x \right) \le \varepsilon _{2} \hfill \\ ~~ \vdots \hfill \\ f_{n} \left( x \right) \le \varepsilon _{n} \hfill \\ \end{gathered} $$

(30)

6.3 Multi-objective invasive weed optimization algorithm

The invasive weed optimization algorithm was first introduced by Mehrabian and Lucas (2006). Weeds are plants whose invasive growth is a significant threat to crops. Weeds are very stable and adaptable to environmental changes. This algorithm mimics the adaptability and randomness of weed populations (Maghsoudlou et al., 2016). The convergence to Pareto optimal front and the proper spread of the solutions after producing several generations in evolutionary algorithms have caused this algorithm to solve multi-objective problems. This algorithm’s steps are as follows (Goli et al., 2019). In the first step, the initial population (a certain number of seeds) are produced and scattered. In the second step, the scattered seeds are grown and become plants, and then, depending on their fitness and competence, they themselves produce seeds. In the third step, the offspring seeds are scattered and grow around their parent. Finally, the second and third steps are repeated to the extent that the population does not exceed a certain limit (available range), otherwise more competent plants will remain, and the rest will be destroyed. The steps of the multi-objective invasive weed optimization algorithm are as follows:

• 1. Initialization In this step, each solution is represented by the length r (representing urban areas) and l (representing distribution centers). The first string of numbers contains r non-repetitive random natural numbers from the set 1 to r. The second string consists of l random numbers that indicate the locations of the distribution centers. It is important to note that the second string’s numbers are always incremental and non-repetitive, and the last number in this string is always equal to r. The following figure shows the multi-objective invasive weed algorithm’s coding structure for a network with nine areas and two distribution centers.

As shown in Fig. 7, in the first string, the sequence of numbers is between 1 and 9. Cells 4 and 9 in the second string are first identified as the distribution centers’ locations. Areas 4 and 7, located inside cells 4 and 9, are then identified as distribution centers in the first string. Because the allocation of distribution centers is not specified, the remaining areas are allocated to the distribution center on their right side. For example, areas 1, 2, and 3 are allocated to distribution center 4. One of the advantages of this method is that the probability of infeasible solution is minimized, and there is no need to check the next weed for feasibility after each production.

• 2. Propagation of seeds based on fitness value (reproduction) All weeds produced should be evaluated and ranked based on their fitness values. The higher the weed’s fitness is, the more seeds it produces. Here, two points are randomly selected for reproduction, according to Fig. 8, then the corresponding cells are moved.

Fig. 7

Coding structure of invasive weed

Fig. 8

Representation of weed reproduction

Constraint handling strategy Some constraints are satisfied by the definitions in the initialization and reproduction sections. A penalty strategy is used to satisfy other constraints. For example, the calculation of violation for Constraints (5) and (6) is as Eqs. (31) and (32). The calculated violation is added to the objective functions and makes them worse. Index j is the number of objective functions.

$$ A_{j} = O_{{rcs(a,b)}}^{5} = \max _{{\forall rcs(a,b)}} \left\{ {0,\mathop \sum \limits_{{(a,b)}} g_{{ir\left( {a,b} \right),(a^{'} ,b^{'} )s}} .z_{{ic,\left( {a,b} \right),(a^{'} ,b^{'} )s}} - I_{{ic(a,b)s}} } \right\}\quad \forall j = 1,2 $$

(31)

$$ B_{j} = O_{{(a,b)s}}^{7} = \max _{{\forall (a,b)s}} \left\{ {0,\mathop \sum \limits_{c} I_{{ic(a,b)s}} .v_{c} - cap_{{is}} .y_{{i\left( {a,b} \right)s}} } \right\}\quad \forall j = 1,2 $$

(32)

The calculated total violation is equal to the sum of the violations, according to Eq. (33).

$$ Violation_{j} = \left( {A_{j} + B_{j} } \right)*iteration $$

(33)

The main idea on constraint handling is inspired by the perishable product supply chain model proposed by Khalili et al. (2015). The violation value in Eq. (33) is a dynamic value dependent on the iteration value. Accordingly, the higher the iteration, the greater the violation value will be. Consequently, Eq. (33) represents the value of the ultimate objective functions for penalized chromosomes. As the algorithm iteration continues, the violated chromosome is penalized harder. Given that the amount of violation defined is dynamic and varies based on the number of iterations, the objective function’s final value is, according to Eq. (34).

$$ f_{j} = f_{j} + penalty_{{}} *Violation_{j} \quad \forall j = 1,2 $$

(34)

• 3. Calculating the number of seeds a plant-based can produce seeds on the plant’s competence, according to Eq. (35).

$$ \sigma _{{iter}} = \frac{{(iter_{{\max }} - iter)^{n} }}{{(iter_{{\max }} )^{n} }}\left( {\sigma _{{initial}} - \sigma _{{final}} } \right) + \sigma _{{final}} $$

(35)

where $\sigma _{{initial}}$ The initial value of the standard deviation, $\sigma _{{final}}$ The final value of the standard deviation, $\sigma _{{iter}}$ The value of standard deviation in the current step, $iter_{{\max }}$ Maximum number of iterations, $n$ Nonlinear modulation index, $ter$ The current iteration number of the algorithm.

• 4. Competitive exclusion When the maximum number of seeds in the colony (P-max) is reached, each seed can produce seeds according to the mechanism expressed in the reproduction section. When all the seeds have found their location in the search space, they will adapt to their parents (the colony of seeds). Then the seeds with the least competence are removed to reach the most acceptable population in the colony. This mechanism allows the plants with less competence to reproduce, and if the competence of the offspring is suitable in the colony, they will survive.

• 5. Go to step 2 and continue until the stopping criterion is met

6.3.1 Stopping criterion

In this study, the algorithm stops if one of the following conditions are met:

• Stopping after a certain number of iterations (Max Iteration), or

• Stopping if, after a certain number of iterations, no improvement will be applied to the values of the objective function.

The results of parameter tuning of the proposed algorithm using the Taguchi approach are as follows: (Table 4).

Table 4 Parameter tuning

6.4 Metrics to evaluate algorithm efficiency

The Mean Ideal Distance (MID) and Spacing Metric (SM) are used to assess the accuracy of the proposed multi-objective invasive weed algorithm. These metrics have been used in many studies to measure the performance of multi-objective algorithms.

• Spacing Metric (SM) This metric calculates the standard deviation of the distance between the solutions and the Pareto points. This metric is defined as Eq. (36) (Zitzler, 1999):

$$ SM = \frac{{\mathop \sum \nolimits_{{i = 1}}^{{n - 1}} \left| {d_{i} - \mathop d\limits^{ - } } \right|}}{{\left( {n - 1} \right)\mathop d\limits^{ - } }} $$

(36)

where n is the number of Pareto points, $d_{i}$ is the Euclidean distance between the two adjacent Pareto points, and $\overline{{d~}}$ is the mean Euclidean distance of the solution points. The closer this value is to zero, the closer the Pareto points are, and the better the performance of the algorithm.

• Mean ideal distance (MID) Calculates the convergence rate of Pareto points to the ideal point (0.0). This metric is defined as Eq. (37) (Zitzler & Thiele, 1998):

$$ MID = \frac{{\sum\nolimits_{i}^{n} {\sqrt {\left( {\frac{{f_{{1i}} - f_{1}^{{best}} }}{{f_{{1,total}}^{{\max }} - f_{{1,total}}^{{\min }} }}} \right)^{2} + \left( {\frac{{f_{{2i}} - f_{2}^{{best}} }}{{f_{{2,total}}^{{\max }} - f_{{2,total}}^{{\min }} }}} \right)^{2} } } }}{n} $$

(37)

where $f_{{ji}} ~$ is the value of jth objective function for ith Pareto front. $f_{{j,total}}^{{\max }} ~$ and $f_{{j,total}}^{{\min }} ~$ are respectively the highest and lowest values of j-th objective function among Pareto points. So the lower the MID value, the better the performance of the algorithm will be.

Table 5 shows the values of the objective functions, solution time, percentage error, and MID and SM values for the two Epsilon-constraint and multi-objective invasive weed optimization methods for small and medium-scale problems. According to this table, the first 5 Pareto points are for small-scale problems and the second 5 Pareto points are for medium-scale problems. As the problem’s scale increases, the objective functions’ values increase in both methods, but the calculated percentage error for each of the ten problems is less than 1 percent. The solving time for the epsilon-constraint method has exponentially increased, while for multi-objective invasive weed optimization, it has increased at a much slower and more reasonable speed. Comparing the two approaches’ performance evaluation metrics suggests that the average SM for the two Epsilon-constraint and multi-objective invasive weed optimization methods is 0.399 and 0.402, respectively. The average MID for Epsilon-constraint and multi-objective invasive weed optimization methods is 6.47 and 6.50, respectively. These reasons confirm the accuracy and validity of the proposed algorithm for solving large-scale problems.

Table 5 The results of the calculation for small and medium-size test problems

7 Case study

This study was conducted for the Iranian Red Crescent Society (IRCS) in Tehran, the capital of Iran. The city has around 9 million residents, and 15 million live in the city’s larger metropolitan area. District 1 in Tehran has ten regions and 26 urban areas. This district is 60 square kilometers without its surroundings and 210 square kilometers with its surroundings (Akbari et al., 2021). The existence of 29 embassies, schools, organizations, and various government agencies and corporate headquarters in this district has made it one of Tehran’s sensitive and strategic districts. The area with four faults of Mosha, north Tehran, south Ray and floating has been selected as the case study in this research.

Table 6 shows the earthquake, flood, and radiological incidents scenarios considered in the case study. Different studies have considered different scenarios for disaster relief operations. In this study, the approaches used by Khojasteh and Macit (2017) for defining the earthquake scenario, Schroeder et al. (2016) for defining the flood scenario, and Caunhye et al. (2015) and Hrdina et al. (2009) for defining the radiological scenario have been used. Therefore, the earthquake scenario is defined based on four faults, two types of occurrence time (day and night), and earthquake severity. The magnitude of the earthquake is defined from 6 to 10 Richter with an accuracy of 0.1 (41 scenarios). The flood severity is divided into five categories used by Schroeder et al. (2016). Finally, three scenarios have been defined concerning radiological incidents. The total number of scenarios is 4920 (4 × 2 × 41 × 5 × 3 = 4920).

Table 6 Case study scenarios

Figure 9 present the demarcation of radiation zones. With a radiation rate of over 10 rem/hr, the inner zone causes the most financial and human losses due to its proximity to the disaster location. Intermediate zone with radiation rate between 1 rem/hr to 10 rem/hr causes less financial and human losses. Finally, the outer zone, which is farthest from the disaster location, has the least damage than the other two zones. Therefore, a 7-Richter earthquake in the morning at the Mosha fault is analyzed in this section with the flood severity of the “severe” and the radiological incident of the “inner zone.”

Fig. 9

Demarcation of radiation zones

Figure 10 presents the output of the Arc GIS software and the Radius model. As shown in this figure, District 1 is divided into ten regions and 64 sub-regions (pixels). According to software forecasts, the red sections are critical sub-regions where more than 400 buildings have been destroyed. Similarly, the yellow sections are the sub-regions with 250 to 400 buildings destroyed, and the green sections are the sub-regions where between 100 to 250 buildings are destroyed. Eventually, the blue sub-regions, which are safer than the rest of the areas, have less than 100 buildings destroyed. White sub-regions are areas where no information is available.

Fig. 10

Damage estimation output for urban district

Given that the divided sections are discrete, the location is discrete, and the coordinates of the sub-region centers are considered the coordinates of that pixel. The entire district is divided into several regions, and it is assumed that each established distribution center can only cover its region. This assumption will prevent unnecessary travel between regions. According to the output of the GIS software, 20 pixels are marked in red, 12 pixels in yellow, 6 pixels in green, and 19 pixels in blue.

Table 7 shows the parameters related to relief supplies. The coefficient of demand for relief supplies, the volume of each relief supply, the cost of transportation per distance unit, and the penalty for the shortage of relief supplies are presented in this table. Table 8 shows the cost of establishing distribution centers in each sub-region.

Table 7 Parameters related to relief supplies

Table 8 The cost of establishing distribution centers based on each sub-region

It should be noted that ARC GIS also calculates the distance between the areas, and the number of distribution centers is 15. Also, the capacity of the distribution centers considered in this scenario is 20,000 ${\rm{m}}^{3}$ for all areas. Figure 11 shows the results of estimating the distribution functions of relief supplies by simulation. The simulation results are for the scenario with a 7-Richter earthquake in the morning for the Masha fault, moderate flood, and radiological incidents with an intermediate zone. As can be seen, the distribution of water, food, medicine, blankets, and tents are normal, with a correlation coefficient of 0.975, 0.990, 0.910, 0.950, and 0.960, respectively. The Anderson–Darling test was used and defined as follows:

Fig. 11

Simulation results

H0

The data follow a normal distribution.

H1

The data do not follow the normal distribution..

This figure shows that the AD statistics for water, food, medicine, blankets, and tents are 0.359, 0.403, 0.232,0.311, and 0.287, respectively. Also, the calculated p-values are 0.467, 0.473, 0.294, 0.397, and 0.355, respectively. By comparing the values of AD and p-value, we can conclude the null hypothesis is not rejected. Therefore, the distribution function for all relief commodities follows a normal distribution function.

Figure 12 is used to validate the proposed simulation model by comparing it with the real system. The JICA data and simulation software have been used for this comparison. The model is implemented 100 times with a simulation time of 1000,000 h. Figure 12 compares the performance of the simulation model with the real system with a confidence interval of 0.95. The vertical axis shows the estimated amount of supplies in the two states. Taking into account the normality and 95% confidence interval and the hypothesis test of ${\rm{H}}_{0} :\mu = \mu _{0}$ against ${\rm{H}}_{1} :\mu \ne \mu _{0}$, it can be concluded that the proposed model is an accurate example of the performance of the real system. The value of $\mu _{0}$ represents the expected value of the estimated parameters. The Maan Whitney nonparametric test for the null and two-sided research hypotheses was used and defined as follows:

Fig. 12

A 95% confidence interval for results obtained by simulation and real system

H0

The two populations are equal.

H1

The two populations are not equal.

The calculated p-values are 0.267, 0.365, 0.317, 0.408, and, 0.228 respectively. According to the results presented in Fig. 12, we do not reject H0 because sig (p-value) > 0.05. As a result, we do not have sufficient evidence to conclude that the two populations are not equal.

Figure 13 shows a set of 20 Pareto points obtained from solving the case study. The vertical axis shows the second objective function’s values, and the horizontal axis shows the values of the first objective function. The mean Pareto points for the first objective function is 280,227.85, and for the second objective function, it is 135,482,902.20. Figure 14 shows the location of 16 distribution centers (D1–D16) in different sub-regions (locations 7, 8, 10, 12, 18, 26, 27, 28, 31, 32, 36, 40, 54, 56, 58, and 61).

Fig. 13

Pareto solutions

Fig. 14

Location of distribution centers

Table 9 shows the allocation of affected areas to distribution centers. For example, D1 has been established in Region 1, covering sub-regions 5, 6, 16, 17, and 18. Also, in Region 2, two distribution centers, D2 and D3, have been established. The D2 distribution center covers sub-regions 1, 2, 7, 19, and 20, and the D3 distribution center covers sub-regions 8, 9, and 21.

Table 9 Allocation of affected areas to distribution centers

Table 10 shows the number of distribution centers established in each region, the injured coverage percentage, and the relief supplies quantity stored in each region. The total number of established distribution centers is 16. The injured coverage is 100% for all regions except for Region 9. As for the stored relief supplies quantity, 517,280 L of water, 4520 kg of medicine, 338,705 kg of food, 32,850 blankets, and 8220 tents are stored in Region 1. The total amount of relief supplies needed for relief operations in Region 1 is 58602600 L of water, 72,058 kg of medicine, 4,538,504 kg of food, 755,953 blankets, and 2,015,544 tents.

Table 10 Computational results

7.1 Sensitivity analysis

Sensitivity analysis is performed to confirm the model’s robustness and validity by changing various parameters in the model and examining these changes’ effects on the variables and the objective functions (Maghfiroh & Hanaoka, 2020).

7.1.1 Sensitivity analysis of the simulation model

In this section, various scenarios are used to study the changes in average demand for relief supplies. Table 11 shows the results. The scenarios related to flood and radiological incidents are constant (severe and inner, respectively). Meanwhile, earthquake scenarios are variable for three different types of the severity of occurrence (6, 7, and 8 Richter), the two faults of Mosha and north Tehran, and two morning and night states. Table 11 shows the average supplies required for a 6-Richter earthquake are less than those of a 7-Richter quake, and the supplies needed for a 7-Richter earthquake are less than those of an 8-Richter earthquake. For example, the amount of food required during the day for the Mosha fault is 2,826,412 kg for a 6-Richter earthquake, 4,538,504 kg for a 7-Richter earthquake, and 9,569,608 for an 8-Richter earthquake. It should be noted that the estimated amount of supplies for the night state in this fault is more than the day state. For example, the number of tents required for a 7-Richter earthquake for the north Tehran fault is 125,460 during the day and is 192,752 during the night. This shows the difficulty of relief operations during the night compared to the day. Also, due to the larger extent of the Mosha fault and more buildings and infrastructures than north Tehran, the estimated amount of relief supplies is more than the north Tehran fault.

Table 11 The estimated average relief supplies based on the severity of the earthquake (Mosha fault and north Tehran fault)

Table 12 examines the average demand for relief supplies in terms of changes in radiological incidents’ severity. In this table, the scenarios related to the flood are constant and equal to “severe.” A 7-Richter scenario for the two south Ray and floating faults in both day and night states has been investigated for the earthquake. This is while the scenario of radiological incidents varies in three states: “inner, intermediate, and outer.” As can be seen, the change in radiological incidents scenarios greatly affects the demand for relief supplies. For example, in the morning state at south Ray fault, in the outer zone, the required number of tents was 38,995, while in the intermediate zone, the number of tents was 83,410, and in the inner zone, it was 16,4555. Therefore, the closer we get to a radiological incidents zone, the more the demand increases. At night, the need for relief supplies usually is higher than in the day. Because the floating fault is wider than the south Ray fault and the more urban infrastructures exist in this fault, the estimated amount of relief supplies is more than the south Ray fault.

Table 12 Average relief supplies estimated based on the severity of radiological incidents (South Ray fault and floating fault)

7.1.2 Sensitivity analysis of the mathematical model

Figure 15 shows the effect of increasing earthquake severity on relief costs. As can be seen, the scenarios related to floods and radiological incidents are considered as constant in this table. The flood severity is moderate, and the area under study during radiological incidents is in the inner zone. Four faults in day and night situations are considered for the severity of the earthquake from 3 to 10 Richter. According to this table, increasing the severity of the quake will increase the relief costs exponentially. For example, the estimated cost for a 4-Richter earthquake in the morning for the North Tehran fault is $ 388,731, for an 8- Richter earthquake for the same fault is $ 6435,197, and for a 10- Richter earthquake is $ 82,269,440. Due to the larger size of the Mosha fault, its relief costs are much higher than other faults and increase at a higher rate. The cost of relief operations during the night for all faults is higher than during the day. For example, the cost of relief operations for a 9- Richter earthquake in the Mosha fault during the day is $ 35,618,523 and during the night is $ 58,617,510.

Fig. 15

The effect of increasing earthquake severity on relief costs

Figure 16 shows the effects of changes in demand on the coverage of affected areas. The severity of the flood is severe, and the area under study during radiological incidents is in the intermediate zone. It should be noted that the data considered is for a 7-Richter earthquake. As can be seen, with the increase in demand, the value of the first objective function (coverage amount) has increased, while the coverage rate has remained almost constant. For example, with the increase in demand from 30 to 50 percent, the coverage increases from 468,250 units to 736,482 units for the North Tehran fault and the morning state. This shows the accuracy of the model behavior.

Fig. 16

Effects of changes in demand on the coverage of affected areas

Figure 17 shows the effect of increasing the demand for relief supplies on the number of established distribution centers in a 7-Richter earthquake scenario during the night for different faults. The severity of the flood is catastrophic, and the radiological incident area is the inner zone. As can be seen, as the demand increases and more distribution centers are needed to meet demand. The largest number of established centers is in Mosha and floating faults. The reason is that these two faults are larger than the others. With the increase in demand for relief supplies from − 50 to 50 percent, the number of distribution centers established in the Mosha fault has increased from 6 to 33 centers. With the increase in demand for relief supplies from − 50 to 50 percent for north Tehran, south Ray, and floating faults, the number of established distribution centers has increased from 5, 4, and 5 centers to 30, 22, and 29 centers. Establishing more distribution centers will increase costs and expand coverage.

Fig. 17

The effect of increasing the demand for relief supplies on the number of established distribution centers

8 Conclusion

This study presents a bi-objective mathematical model for the location, allocation, and distribution of relief supplies in the event of cascade disasters. Disasters considered include earthquakes, floods, and radiological incidents. The objectives of this study are to minimize pre-disaster costs and maximize post-disaster coverage area. The proposed stochastic model is scenario-based, and the scenarios are defined based on the severity of the occurrence of cascade disasters. The distribution functions of demand for relief supplies are estimated using a simulation model. The simulation model presented based on the interaction of vulnerable urban infrastructures has estimated the required water, food, medicine, blankets, and tents. The distribution functions of water, food, medicine, blankets, and tents are normal, with correlation coefficients of 0.975, 0.990, 0.910, 0.950, and 0.960. The simulation results have been compared with the real system results at a 95% confidence interval to validate the model. The results support the accuracy of the estimated values. One of this study’s contributions is to determine the severity of damage in different geographical areas specified by the GIS system. The output of the RADIUS model indicates that more than 400 buildings in 20 sub-regions have been destroyed as predicted. Also, 250–400 buildings in 12 sub-regions, 250–100 buildings in 6 sub-regions, and less than 100 buildings in 19 sub-regions have been destroyed.

The proposed mathematical model has been solved on a small and medium scale by the epsilon-constraint method and GAMS software. A multi-objective invasive weed optimization algorithm and MATLAB software are used for the case study. The performance evaluation of the two approaches shows that the average SM for the two epsilon-constraint and multi-objective invasive weed optimization methods is 0.399 and 0.402, respectively. The average MID for epsilon-constraint and Multi-objective invasive weed optimization methods is 6.47 and 6.50, respectively. Therefore, according to MID and SM’s values, the average solution time and percentage error of less than 1% validate the results. In the case study, the mean Pareto point for the first objective function is 280,227.85 dollars, and for the second objective function, it is 135,482,902.20 dollars. Then, distribution centers have been allocated to the affected areas. For example, two distribution centers, D6 and d7, have been established in area 4. Pixels 4, 14, 15, and 27 are allocated to center D6, and pixels 13, 25, and 26 are allocated to center D7. Sixteen distribution centers have been established for district 1 of Tehran, so the water, medicine, food, tents, and blankets required for these centers are 58,602,600 cubic meters in volume, 72,058 kg, 4,538,504 kg, 755,953, and 2,015,544, respectively. The sensitivity analysis results show that as the severity of earthquakes, floods, and proximity to the radiological incidents increases, the demand for supplies also increases. Also, the estimated amount of relief supplies for the night state is more than the daytime state, and for Mosha fault is more than other faults due to its larger size. Also, with the increase in the severity of the earthquake, relief costs increase exponentially, while the coverage increases at the same rate. Increasing demand will also lead to the establishment of more distribution centers and, consequently, an increase in relief costs.

The results from this study were used by the IRCS. The sensitivity analysis indicated that the Mosha fault possesses the most devastating destruction in a probable earthquake occurrence. This information helps the government agencies and relief organizations to prepare in advance given the high probability of mild to severe quakes in the region. The model proposed in this study is generic, structured, and easy to use. It can be adopted by disaster relief efforts and agencies, blood transfusion services, emergency management establishments, hospitals and health services agencies, fire and rescue departments, and utility companies. The ability to divide the affected area into different pixels and consider the maximal coverage of the disaster-stricken areas can help relief and emergency management organizations to divide the resources and responsibilities effectively. Policymakers and emergency organizations can use this information to identify the vulnerable urban infrastructure and prepare the health, energy, and public work agencies for the worst. Although the proposed model can effectively help cities and governments prepare for disasters, it has several limitations. The mathematical model proposed here does not imply a deterministic approach to emergency preparedness and management. While the proposed method helps policymakers and emergency organizations prepare for imminent disasters, it should be adopted and implemented with care. The effectiveness of any mathematical model depends on the assumptions and good data. As with any quantitative model, policymakers, managers, and decision-makers must be aware of the following limitations of the model:

• The availability of accurate data is always a problem in developing countries. For example, there was no official database for several cost elements, including transportation costs. We had to use unofficial estimates and expert opinions in these situations.

• Similarly, we had limited access to traffic data, and the mathematical and simulation models in this study assumed traffic-free conditions.

• Furthermore, due to the unavailability of geographical information on volcanic activities and data, volcanic eruptions are not considered cascade effects in the simulation.

Finally, we provide the following suggestions for future research. Researchers could consider:

• Other objectives such as maximizing the equity in distribution planning and minimizing response time in the model,

• Sustainability in the disaster relief supply chain by considering a wide range of environmental, social, and economic factors,

• Vehicle routing in the model to avoid the disaster-damaged roads and regions, and

• Using other approaches such as robust optimization instead of chance-constrained programming for solving uncertain problems.