1 Introduction

Rivers and canals have played a vital role in the development of human civilization. Big cities have been mainly developed in the vicinity of rivers. Rivers are used to transport goods and passengers to downstream and upstream as well as access to free waters such as seas and oceans. Furthermore, the supply of required water for drinking, agriculture, industry, and other purposes is feasible from the water flowing in rivers and artificial canals. The stability of the general form of the bed and banks of an erodible river is a function of eight different variables such as slope, width, velocity, discharge, roughness, concentration, and sediment dimensions [1]. In general, secondary circulations and the redirection of river currents occurring in straight and meandered rivers increase the boundary shear stress. Therefore, the stability of banks and the erodible bed of rivers and canals is extremely important. In recent years, various techniques have been proposed for protecting banks and the erodible bed of rivers and canals, for example Iowa vanes, submerged vanes, deflectors, bank barbs, spur dikes, and rock weirs are some structures employed to protect beds and banks. Generally, a protective structure must satisfy the following criteria.

  • Maintenance of the ratio of the width to the stable depth of the channel.

  • Maintenance of the channel stability according to the amount of shear stress for the movement of the largest sediment particles.

  • Reduction of velocity adjacent to banks, shear stress or flow strength.

  • Maintenance of the stability of the protective structure during the flood.

  • Maintenance of the passageway of fish in all parts of the stream.

  • Providing or increasing the passageway of ferry boats.

  • Improving aquatic habitats.

  • Compatibility with the nature of the channel.

  • Reduction of construction costs compared to traditional structures.

  • Reduction of maintenance costs.

  • Prevention from sedimentation, erosion and reduction of scouring in the vicinity of piers and other structures [2].

Therefore, cross-vane structures are one of the best options for protecting the stability of rivers and canals against erosion. Due to the importance of cross-vane structures, many experimental studies have focused on the scour pattern in the vicinity of this type of structures. For instance, Scurlock et al [3] installed several rock weirs at the bend location of an open channel to evaluate the flow pattern near the inner and outer walls of the channel. They proposed a series of formulae for approximating the ratio of the maximum velocity of the inner and outer walls. Pagliara et al [4] established an experimental study to find the scour pattern around J-shaped cross-vane structures located on straight channels in the clear-water condition. They analyzed the experimental results to exhibit that by increasing the Froude number the location of the maximum scour depth is shifted towards the downstream. They also stated that the scour hole width is about 0.7–0.9 the channel width. Besides, Pagliara and Kurdistani [5] experimentally measured scour hole dimensions at the downstream of cross-vane structures with I and U shapes installed in a rectangular channel. By changing the hydraulic and geometric conditions of the flow, they calculated the scour dimensions in the clear-water condition and then conducted a dimensional analysis to evaluate the influence of the effective parameters. It is worth mentioning that they presented several equations for calculating the depth, length and width of the scour hole. Pagliara et al [6] experimentally measured scour values at the downstream of W-shaped cross-vane structures located in a rectangular channel in the clear-water condition. The analysis of the experimental results exhibited that the tailwater depth plays a critical role in forecasting the scour parameters. After that, Pagliara et al [7] experimentally utilized log-vanes for controlling the scour occurring in the straight path of rivers in the clear-water condition. By changing the position of log-vanes, they managed to assess the scour pattern in the vicinity of such structures. It should be noted that in this paper the maximum dimensions of the formed dunes are measured. Mahmoudi Kurdistani and Pagliara [8] conducted an experimental study to compare the scour pattern at the downstream of log-Vanes and log-Deflectors. They performed the experiments in a straight rectangular channel for unified sediments in the clear-water condition. The analysis of the experimental results proved that the position angle of such structures plays an important role in the formation of the scour hole. Pagliara et al [9] experimentally evaluated the influence of the layout of log-Deflectors on the scour pattern around this type of barrier. They exhibited that the position angle of log-Deflectors and the tailwater depth are the most important parameters affecting the scour pattern. Also, Pagliara and Kurdistani [10] evaluated the parameters affecting scour hole dimensions in the vicinity of log-Deflectors. They defined two types of bed morphology for these protective structures.

In contrast, artificial intelligence techniques have great ability in estimating and simulating various linear and non-linear phenomena. These numerical models have considerable flexibility and are utilized as efficient tools for saving the research time and conducting experimental studies. In recent years, such techniques are used for simulating the scour around different structures such as abutments [11, 12] and submerged vanes as well as other scour controller structures [13,14,15,16,17,18].

Reviewing the previous studies indicates that the prevention of the bed of rivers and canals is extremely important and the detection of the effective factors is essential for providing an optimal scheme. On the other hand, artificial intelligence techniques are powerful tools for modeling the scour phenomenon at the downstream of hydraulic structures. Moreover, the scour depth at the downstream of cross-vane structures has not been simulated by artificial intelligence models so far and in this study, for the first time, it is done using a modern approach entitled “outlier robust extreme learning machine (ORELM)”. In other words, first, the input parameters are introduced for simulating the scour depth. After that, the most optimal activation function of the numerical model is selected. Then, eleven ORELM models are defined using the input parameters and the suitable model along with the most effective input parameters are identified through the conduction of a sensitivity analysis. The results of the ORELM suitable model are compared with those of the extreme learning machine. Subsequently, an uncertainty analysis and a partial derivative sensitivity analysis are performed.

2 Method

2.1 Extreme learning machine (ELM)

Extreme Learning Machine (ELM) introduced by Huang et al [19, 20] is an educational algorithm for the single layer feed-forward neural network (SLFFNN). Consider a dataset consisting of N arbitrary training samples in the form of \( \left\{ {(x_{i} ,y_{i} )} \right\}_{i = 1}^{N} \). In this dataset, \( x_{i} \in R^{n} \) is the matrix of the problem inputs and \( y_{i} \in R \) is the output of the interested problem. Given L neurons in the hidden layer and defining g(x) as the activation function, the mathematical structure of ELM is defined for nonlinear mapping between the input matrix and the output of the problem as follows:

$$ y_{j} = \sum\limits_{i = 1}^{L} {\beta_{i} g({\mathbf{w}}_{i} \cdot {\mathbf{x}}_{j} + b_{i} )} ,\quad j = 1,2, \ldots ,N $$
(1)

where, \( {\mathbf{w}}_{i} = (w_{i1} ,w_{i2} , \ldots ,w_{in} ) \) is the matrix of the input weight connecting the ith hidden layer neuron to input neurons. This matrix is randomly initialized. bi is known as the bias of the ith neuron in the hidden layer. The matrix βi represents the output weight matrix connecting the ith hidden layer neuron to the output neuron. In the above relationship, \( {\mathbf{w}}_{i} .{\mathbf{x}}_{j} \) is known as the inner product of two matrices: the matrix of input weights (w) and the matrix of problem inputs (x). The output node in the mathematical form of ELM is linearly defined. The matrix form of the above relationship which includes N different equations is expressed as follows:

$$ {\mathbf{H}}\beta = {\mathbf{y}} $$
(2)

where, \( y = [y_{1} , \ldots ,y_{N} ]^{T} \), \( \beta = [\beta_{1} , \ldots ,\beta_{N} ]^{T} \) and H is defined as follows:

$$ {\mathbf{H}}({\mathbf{w}}_{{\mathbf{1}}} ,{\mathbf{w}}_{{\mathbf{2}}} , \ldots ,{\mathbf{w}}_{{\mathbf{L}}} \text{,}{\mathbf{x}}_{{\mathbf{1}}} ,{\mathbf{x}}_{{\mathbf{2}}} , \ldots ,{\mathbf{x}}_{{\mathbf{L}}} , \ldots ,b_{ 1} ,b_{ 2} , \ldots ,b_{L} {\mathbf{)}} = \left( {\begin{array}{*{20}l} {g\text{(}{\mathbf{w}}_{{\mathbf{1}}} \cdot {\mathbf{x}}_{{\mathbf{1}}} + b_{1} \text{)}} \hfill & \cdots \hfill & {g\text{(}{\mathbf{w}}_{{\mathbf{L}}} \cdot {\mathbf{x}}_{{\mathbf{1}}} + b_{1} \text{)}} \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {g\text{(}{\mathbf{w}}_{{\mathbf{1}}} \cdot {\mathbf{x}}_{{\mathbf{N}}} + b_{1} \text{)}} \hfill & \cdots \hfill & {g\text{(}{\mathbf{w}}_{{\mathbf{1}}} \cdot {\mathbf{x}}_{{\mathbf{N}}} + b_{L} \text{)}} \hfill \\ \end{array} } \right) $$
(3)

where, H is the output matrix of the hidden layer. It is seen from equation (2) that in the structure defined for ELM, all parameters except the output weight matrix (β) are constant. Thus, the main purpose of finding an equivalent precise model is to solve the linear equation provided in equation (2) to obtain the matrix .β Given that the matrix H is a non-square matrix, the solution of equation (2) may be unlike a linear problem. To solve this problem, the minimization of the loss function value is utilized in the optimal least square solution process, i.e., \( \hbox{min} \left\| {{\mathbf{y}} - {\mathbf{H}}\beta } \right\| \). Thus, the optimal result obtained from the minimization of l2-norm is as follows:

$$ \hat{\beta } = {\mathbf{H}}^{ + } {\mathbf{y}} $$
(4)

where, H+ is the Moore-Penrose generalized inverse [21] of H. Given that the number of samples taken into account as training samples is greater than the number of nodes considered in the hidden layer (L<N), equation (4) can be rewritten as follows:

$$ \hat{\beta } = ({\mathbf{H}}^{T} {\mathbf{H}}\text{)}^{{\text{ - 1}}} {\mathbf{H}}^{T} {\mathbf{y}}{\mathbf{.}} $$
(5)

2.2 Outlier robust ELM (ORELM)

In modeling by artificial intelligence (AI) based models, there are always outliers and because of the fact that in many cases such samples often refer to the nature of the problem, there is no way to remove them. Thus, it comprises a percent of the total learning error (e). In order to deal with such data, the existence of outliers is defined by sparsity. Zhang and Luo [22] knowing that the use of the l0-norm reflects sparsity better than the l2-norm, to calculate the output weight (β), instead of using the l0-norm, considered the learning error (e) so that to be sparse.

$$ \mathop {\hbox{min} }\limits_{\beta } \,C\left\| {\mathbf{e}} \right\|\,_{0} + \left\| \beta \right\|_{2}^{2} \,\,\,\,\,\,\text{subject}\,\text{to}\,\,{\mathbf{y}} - {\mathbf{H}}\beta = {\mathbf{e}} $$
(6)

The above relationship is a non-convex programming problem. According to the analysis of the robust principal component and compressive sensing, the term of sparse is obtained using the l0-norm. Displacement of the l0-norm by the l1-norm (equation (6)) not only leads to the convex minimization, but it also guarantees sparse characteristics. Therefore, the convex relaxation of equation (6) is calculated as follows:

$$ \mathop {\hbox{min} }\limits_{\beta } \,\left\| {\mathbf{e}} \right\|\,_{1} + \frac{1}{C}\left\| \beta \right\|_{2}^{2} \,\,\,\,\,\,\text{subject}\,\text{to}\,\,{\mathbf{y}} - {\mathbf{H}}\beta = {\mathbf{e}} $$
(7)

The above relationship is a constrained convex optimization convex which completely fits the proper range of the Augmented Lagrangian (AL) multiplier approach. Thus, the AL function is presented as follows:

$$ L_{\mu } ({\mathbf{e}},\beta ,\lambda ) = \left\| {\mathbf{e}} \right\|_{1} + \frac{1}{C}\left\| \beta \right\|_{2}^{2} + \lambda^{2} ({\mathbf{y}} - {\mathbf{H}}\beta - {\mathbf{e}}) + \frac{\mu }{2}\left\| {{\mathbf{y}} - {\mathbf{H}}\beta - {\mathbf{e}}} \right\|_{2}^{2} $$
(8)

where, \( \mu = = 2N/\left\| {\mathbf{y}} \right\|_{1} \) [23] denotes the penalty parameters and \( \lambda \in R^{n} \) is the Lagrangian multiplier vector. The optimal solution (e, β) and λ as Lagrangian multiplier are achieved through the iterative minimization of the AL function as follows:

$$ \left\{ \begin{aligned} ({\mathbf{e}}_{k + 1} ,\beta_{k + 1} ) = \arg \,\,\mathop {\hbox{min} }\limits_{{{\mathbf{e}},\beta }} L_{\mu } ({\mathbf{e}},\beta ,\lambda )\,\,\,\,\,\,\,\,\,\,\,\,(\text{a}) \hfill \\ \lambda_{k + 1} = \lambda_{k} + \mu ({\mathbf{y}} - {\mathbf{H}}\beta_{k + 1} - {\mathbf{e}}_{k + 1} )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(\text{b}) \hfill \\ \end{aligned} \right\}. $$
(9)

2.3 Goodness of fit

In the current study, in order to assess the accuracy of the introduced numerical models, the correlation coefficient (R), variance accounted for (VAF), Root Mean Square Error (RMSE), and the Nash-Sutcliffe efficiency coefficient (NSC) are employed as follows:

$$ R = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - \overline{F} } \right)\left( {O_{i} - \overline{O} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - \overline{F} } \right)^{2} \sum\nolimits_{i = 1}^{n} {\left( {O_{i} - \overline{O} } \right)^{2} } } } }} $$
(10)
$$ \text{VAF} = \left( {\text{1} - \frac{{\text{var}\left( {F_{i} - O_{i} } \right)}}{{\text{var}\left( {F_{i} } \right)}}} \right) \times \text{100} $$
(11)
$$ RMSE = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - O_{i} } \right)^{2} } } $$
(12)
$$ {\text{NSC}} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left( {O_{i} - F_{i} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {O_{i} - \overline{O} } \right)^{2} } }} $$
(15)

where, Oi is observational values, \( F_{i} \)is values predicted by numerical models, \( \overline{O} \) is the average of observational values and n is the number of observational values. In the next sections, the activation functions are studied. After that, the suitable model and the most effective input parameters are identified. Furthermore, the ORELM suitable model is compared with the ELM suitable model. In addition, an uncertainty analysis and a partial derivative sensitivity analysis (PDSA) are conducted for the suitable model.

2.4 Experimental models

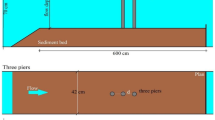
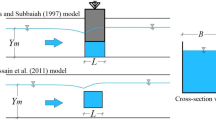
To verify the results of the numerical models, the experimental vakues measured by Pagliara et al [6], Pagliara and Kurdistani [7] and Pagliara et al [8] are employed. The experimental models of cross-vane structures are with the shapes of J and W in a rectangular horizontal channel with the length, height and width (B) of 20 m, 0.75 m and 0.8 m, respectively. Also, the scour depth was measured in the vicinity of cross-vane structures with the shapes of I and U in a flume with the length, width and height of 7 m, 0.342 m and 0.63 m, respectively. They managed to measure the scour depth (Zm) at the downstream of a stone trap with the height of hst and the width of \( b \) for densimetric Froude numbers equal to Fd. Besides, the flow depth difference between the downstream and the upstream of the stone trap is Δy. The schematic layout of the mentioned experimental model is shown in figure 1.

Figure 1
figure 1

Schematic layout of experimental models of stone cross-vane structures (a) J-shaped, (b) I-shaped, (c) U-shaped and (d) W-shaped (Pagliara et al [6]; Pagliara and Kurdistani [7] and Pagliara et al [8]).

Full size image

Pagliara et al [6], Pagliara and Kurdistani [7] and Pagliara et al [8] in their experimental studies stated that the parameters affecting the scour at the downstream of stone traps are: scour depth (Zm), height of the stone trap \( \left( {h_{st} } \right) \), width of the stone trap (b), width of the main channel (B), the flow depth different between the downstream and the upstream of the stone trap (Δy), flow rate (Q), viscosity of sediment and water (ρs, ρ), gravitational acceleration (g) and the average diameter of sediments (d50). Thus, equation (16) is written as follows:

$$ f\left( {Zm,h_{st} ,b,B,\Delta y,Q,\rho_{s} ,\rho ,g,d_{50} } \right) = 0 $$
(16)

Pagliara et al (2013) by means of the dimensional analysis indicated that the scour at the downstream of the stone trap is a function of the following dimensionless parameters:

$$ {{Zm} \mathord{\left/ {\vphantom {{Zm} {h_{st} = f\left( {{b \mathord{\left/ {\vphantom {b B}} \right. \kern-0pt} B},F_{d} ,{{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} {h_{st} }}} \right. \kern-0pt} {h_{st} }}} \right)}}} \right. \kern-0pt} {h_{st} = f\left( {{b \mathord{\left/ {\vphantom {b B}} \right. \kern-0pt} B},F_{d} ,{{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} {h_{st} }}} \right. \kern-0pt} {h_{st} }}} \right)}} $$
(17)

Moreover,\( \varphi \)represents the shape factor of cross-vane structures with the shapes of J, I, U and W. It is worth noticing that the structure shape factor \( \left( \phi \right) \) is assumed to be 0, 1, 2, and 3 for J, I, U, and W cross-vane structures, respectively. Thus, equation (17) is rewritten as follows:

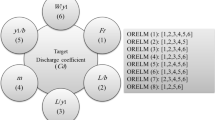
$$ {{Zm} \mathord{\left/ {\vphantom {{Zm} {h_{st} = f\left( {{b \mathord{\left/ {\vphantom {b B}} \right. \kern-0pt} B},F_{d} ,{{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} {h_{st} ,\phi }}} \right. \kern-0pt} {h_{st} ,\phi }}} \right)}}} \right. \kern-0pt} {h_{st} = f\left( {{b \mathord{\left/ {\vphantom {b B}} \right. \kern-0pt} B},F_{d} ,{{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} {h_{st} ,\phi }}} \right. \kern-0pt} {h_{st} ,\phi }}} \right)}} $$
(18)

where, Fd is the densimetric Froude number. Thus, in this study, the parameters belonging to equation (18) are taken into account as the input parameters. In other words, using different combinations, 11 numerical models are introduced for identifying the effective parameter. In figure 2, the combinations of the dimensionless parameters of equation (18) are illustrated.

Figure 2
figure 2

Combinations of input parameters.

Full size image

To identify the best ORELM model and the most influencing input parameters, a sensitivity analysis is implemented for the ORELM models. This means that eleven ORELM models using the input parameters are defined to carry out the sensitivity analysis. For instance, ORELM 1 simulates the target function by using all input parameters and then effect of each input is removed. Thus, ORELM 2 to ORELM 5 models are developed. Lastly, all possible combinations consisting of two input parameters are defined (ORELM 6 to ORELM 11). The best ORELM model owns the lowest error and the highest correlation with experimental measurements. Moreover, the performance of ORELM model decreases significantly as the most effective input parameter is ignored.

3 Result and discussion

3.1 Activation function

First, the activation functions are evaluated for the artificial intelligence model. As discussed, the ORELM model has five activation functions entitled “sigmoid, sine, hardlimit, triangle basis and radial basis”. In this section, all activation functions are assessed and then the superior one is introduced. In figure 3, the results of different statistical indices for the activation functions are illustrated. Also, the corresponding scatter plots to the activation functions are shown in figure 4. Additionally, for this activation function, the value of RMSE in the test mode is calculated 0.572. In contrast, the values of VAF and NSC for the sine activation function in the test mode are also obtained 93.558 and 0.930, respectively. However, the value of VAF for the triangle basis in the test mode is calculated 86.640. Thus, based on the results of the activation functions, sigmoid simulates the scour values with higher accuracy. Therefore, this function is chosen for the remaining modeling steps.

Figure 3
figure 3

Results of statistical indices for different activation functions.

Full size image
Figure 4
figure 4

Scatter plots for sigmoid activation function.

Full size image

3.2 Sensitivity analysis

In this section, the analysis of the results obtained by the ORELM numerical models is carried out. As discussed above, 11 different ORELM models are developed in this study for identifying the suitable model and also the most effective input parameter. In figure 5, the results of all statistical indices for ORELM1 to ORELM11 are shown. ORELM1 estimates the scour values in terms of all input parameters (b/B, Fd, Δy/hst, φ). For ORELM1, the values of R and VAF in the test mode are obtained 0.954 and 91.049, respectively. For this model, the values of RMSE and NSC in the training mode are calculated 0.502 and 0.921, respectively. Moreover, ORELM2 simulated the objective function values in terms of the parameters b/B, Fd, Δy/hst. For ORELM2, the value RMSE in the training mode is 0.498, respectively. In contrast, the values of R, NSC and VAF for the ORELM2 model in the test mode are calculated 0.956, 0.908 and 91.378, respectively. It should be noted that among the all ORELM models, ORELM2 has the lowest error and the highest correlation with the experimental values. Furthermore, ORELM3 models the scour values in terms of the parameters b/B, Fd, φ. For this artificial intelligence model, the values of RMSE and NSC in the test mode are estimated to be equal to 1.149 and −0.517, respectively. Also, ORELM4 models the objective values by the input parameters including b/B, Δy/hst, φ. For ORELM4, the values of VAF and R in the training mode are calculated 81.951 and 0.905, respectively, whereas ORELM5 estimates the scour values using Fd, Δy/hst, φ. For ORELM5, the values of RMSE and NSC in the test mode are obtained 6.10E−01 and 0.887, respectively. Furthermore, ORELM6 simulates the values of the objective function by means of the parameters + b/B, Fd. The values of R and VAF for ORELM6 in the test mode are equal to 0.621, 1.063 and 38.536, respectively. In contrast, ORELM7 simulates the scour values near cross-vane structures by the parameters b/B, Δy/hst. For the training mode, ORELM7 estimates the values of VAF and NSC equal to 77.529 and 0.709, respectively. In addition, ORELM8 calculates the scour values by the dimensionless parameters b/B, φ. The values of RMSE and VAF for this model in the training mode are computed 1.453, 0.913 and 38.471, respectively. ORELM9 calculates the objective function values by the dimensionless parameters Fd, Δy/hst. For this artificial intelligence model, the values of NSC, VAF and RMSE in the test mode are obtained 0.842, 86.432 and 0.723, respectively. ORELM10 simulates the scour values by the dimensionless parameters Fd, φ. For ORELM10, the values of NSC and R in the test mode are estimated −0.753 and 0.603, respectively. Based on the simulation results, ORELM10 has the lowest accuracy among all the artificial intelligence models, while the values of RMSE and R for ORELM11 in the test mode are calculated 0.958 and 0.865, respectively. Furthermore, the scatter plots for all ORELM models are depicted in figure6.

Figure 5
figure 5

Results of statistical indices for ORELM models.

Full size image
Figure 6
figure 6

Comparison of scour values simulated by ORELM 2.

Full size image

Thus, according to the results of the numerical models, ORELM2 is detected as the suitable model. This model estimates the objective function values by the dimensionless parameters \( {b \mathord{\left/ {\vphantom {b B}} \right. \kern-0pt} B},F_{d} ,{{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} {h_{st} }}} \right. \kern-0pt} {h_{st} }} \). It should be noted that the dimensionless parameters b/B, Δy/hst are identified as the most important input parameters.

3.3 Comparison with ELM

In this section, the results of the ORELM2 model as the suitable model are compared with the ELM model. The scatter plots of both models in the test and training modes are shown in figure7. Based on the obtained results, the ORELM artificial intelligence model has a better performance than the ELM model. For instance, the VAF values for ORELM and ELM in the training mode are equal to 92.776 and 91.106, respectively. Furthermore, the values of R, RMSE and NSC for the ELM model in the test mode are obtained 0.938, 0.498 and 0.934, respectively. The ORELM and ELM models are considered as a single layer feed forward neural network (SLFFNN) while the ORELM model overcomes the outlier problems in the ELM model. For instance, the ELM model does not show a good performance in small target function, whereas the ORELM model has an acceptable performance for all scour depth values. Regarding the simulation results, in the training mode, the level of correlation (R index) of the ORELM model is enhanced, with roughly 6% and 2% improvement in the training and testing mode. Moreover, the level of error (RMSE) for the ORELM model in training condition is approximately 7.5% less than the ELM model. Therefore, the ORELM model has better performance in comparison with the ELM model. Table 1 shows the computed statistical indices for the ORELM and ELM models. Indeed, the ELM and ORELM models are considered as a single layer feed forward neural network (SLFFNN) that the ORELM overcomes the outlier problem of the ELM model. For instance, as it can be seen from figure 7, the ELM does not have a reasonable performance in target function ranging from 0 to 4 while the ORELM model owns a better performance for all scour depth values.

Figure 7
figure 7

Scatter plots for ORELM and ELM.

Full size image
Table 1 Computed statistical indices for the ORELM and ELM models.
Full size table

3.4 Uncertainty analysis

In this section, the uncertainty analysis is conducted for the ORELM and ELM models. The uncertainty analysis is to assess the error predicted by numerical models and evaluate the performance of the models. Generally, the value of the error calculated by numerical models (ej) is introduced as the difference between computed values (Pj) and observed values (Tj) (ej = Pj − Tj). Also, the average of the predicted error is calculated as \( \bar{e} = \sum\nolimits_{j = 1}^{n} {e_{j} } \), while the value of the standard deviation of calculated error values are defined as \( S_{e} = \sqrt {\sum\nolimits_{j = 1}^{n} {\left( {e_{j} - \bar{e}} \right)^{2} /n - 1} } \). It is worth mentioning that the negative sign of \( \bar{e} \) indicates the underestimated performance of the numerical model. However, the positive sign of \( \bar{e} \) indicated the overestimated performance of that model. Additionally, using the parameters \( \bar{e} \) and \( S_{e} \), a confidence bound is created by the Wilson score method around value predicted from an error without continuity correction. Then, using \( \pm 1.64S_{e} \) approximately leads to 95% confidence bound which is shown by 95%PEI. The uncertainty analysis parameters are listed in table 2. In this table, width of the uncertainty band is shown by WUB. Based on the uncertainty analysis results, the ORELM model has an overestimated performance, while the ELM model has an underestimated performance. It should be noted that the values of WUB for ORELM and ELM are equal to −0.0669 and −0.0707, respectively. Furthermore, the width of uncertainty band for the ORELM models is narrower than the ELM model, with almost 5.5% narrower.

Table 2 Uncertainty analysis parameters for ORELM and ELM models.
Full size table

3.5 Partial derivative sensitivity analysis (PDSA)

In this section, the partial derivative sensitivity analysis (PDSA) is performed for the suitable model (ORELM2) and the input parameters are evaluated. Generally, the partial derivative sensitivity analysis (PDSA) is one of the most important methods for identifying the change pattern of input parameters (Azimi et al [24]). It is worth noting that the positive partial derivative sensitivity analysis means that the objective function (scour) is increasing, while the negative sign means that the output value is decreasing. In this analysis, the relative derivative of each input parameter is calculated according to the objective function. In other words, the relative derivative of f(x) is calculated for each input variable and it is shown in figure 8. As discussed above, ORELM2 simulates the scour values in terms of b/B, Fd, Δy/hst. For example, by increasing values of the input parameters Fd, Δy/hst, the value of PSDA decreases. Furthermore, for Fd, Δy/hst, the positive values of PSDA are obtained, while most of the PSDA values calculated for the input parameter b/B are positive.

Figure 8
figure 8

Results of PSDA for suitable model.

Full size image

4 Conclusion

Rivers have played a vital role in the development of human civilization. Thus, due to the scouring threat, the protection of their bed and banks are critically important and there are several methods to do this. One of these methods is the utilization of cross-vane structures which are not only natural structures consistent with the surrounding environment, but also are highly efficient in protecting the river bed. In this paper, for the first time, the scour depth at the downstream of cross-vane structures with the shapes of J, I, U and W were simulated using a modern artificial intelligence model entitled “outlier robust extreme learning machine (ORELM)”. At the beginning, the experimental data were divided into two groups including training and test. All the activation functions of the numerical model were evaluated and sigmoid function was selected as the most optimal function. After that, all the parameters affecting the scour hole depth were detected and 11 ORELM models were developed using them. Through the conduction of a sensitivity analysis, the suitable model and the most effective input parameters were introduced. The ORELM suitable model estimated the objective function values with reasonable accuracy. For example, the values of RMSE, SI and NSC in the test mode were approximated 0.561, 0.212 and 0.908, respectively. Moreover, the ratio of the structure length to the channel width (b/B) and the ratio of the difference between the flow depth at the downstream and the upstream of the structure to the structure height (Δy/hst) were identified as the most effective parameters. The results of the ORELM model were compared with ELM and it was concluded that the ORELM model is more accurate. By conducting an uncertainty analysis, the performance of the suitable model was determined and the partial derivative sensitivity analysis exhibited that by increasing the values of the input parameters Fd, Δy/hst, the PSDA value decreases. It is worth mentioning that the applied experimental values came from the precise and reliable laboratory environment. Additionally, the current study is not just to provide a practical solution but it can facilitate future experimental and numerical studies. In other words, companies and engineers are still seeking for conducting more expensive and time consuming laboratory and three-dimensional numerical simulations and the current study can easily reduce such hefty expenditures.