Introduction

The water flow around hydraulic constructions like piers, abutments, and weirs causes the scouring phenomena. The development of a vacuum at the interface of the two media (sediment and fluid) due to the velocity gradient is the cause of this phenomenon. Scouring occurs in the region of bridges, abutments, downstream of the Ogee spillways, and submerged spillways, among other structures. These structures have a high chance of being destroyed if the scour hole size is increased. The restoration and rehabilitation of numerous buildings, particularly bridge piers damaged by scouring, cost a lot of money every year. As a result, assessing and predicting the proportions and pattern of scouring around bridge piers are critical, and numerous studies have been conducted in this area (Harasti et al. 2021; Link et al. 2019).

It should be mentioned that many studies on the scour pattern around complex piers and pier groups have also been conducted. Coleman (2005) undertook an experiment to measure the scour around the intricate piers. They developed a method for calculating the minimum and maximum local scouring in the area of complex piers. Melville et al. (2007) have provided an analytical method for calculating the diameters of scour holes around complex piers. They validated their model’s conclusions with experimental data, demonstrating that this strategy is accurate enough. In the following paper, Ataie‐Ashtiani et al. (2010) tested the scour depth under the vicinity of complex piers in clear-water conditions. They discovered that when the pile cap was undercut, the maximum scour depth occurred. In an experimental investigation, Amini et al. (2012) investigated the scour pattern around pier groups in clear water in shallow waters. Moreno et al. (2016) carried out an experiment to quantify the scour around the complex piers in clear-water flow conditions. They discovered that when a portion of the pile cap is buried in the sediments, the maximum scour depth occurs. F. Liang et al. (2017) also investigated the scour hole depth surrounding the single, twin, and pier groups experimentally. They claimed that the scour pattern around single piers differs significantly from that surrounding pier groupings. Amini Baghbadorani et al. (2017) used empirical relationships to examine experimental values gathered in the area of pier groups in earlier investigations. They devised an equation to compute the scour depth around the pier groups, claiming that the equation’s accuracy was around 10% higher than that of prior research. The scouring pattern around the pier groups and complex piers was studied by Amini Baghbadorani et al. (2018). They demonstrated that the scour pattern changes around pier groups and complex piers, and they established distinct equations for calculating scouring for these two types of structures. The effects of inclination angle on the scour pattern in the vicinity of two types of pier groups were investigated by Bozkuş et al. (2018). They evaluated the findings and gave some empirical equations for determining scour around pier groups.

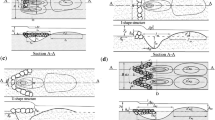
Various investigations on the scouring pattern around twin and three piers have also been conducted. Ataie-Ashtiani and Aslani-Kordkandi (2012) measured the scouring pattern around twin bridge piers. They discovered that between the two bridge piers, the bed shear stress was higher than in other regions. In addition, in an experimental investigation, Das et al. (2016) looked at the scour values around the twin piers with circular, square, and triangular cross sections. They claimed that the scour hole length near the triangular twin piers was shorter than that near the circular and square piers. Wang, et al. (2016a, b) also conducted an experiment to determine the scour depth at the circular twin pier. They discovered that the scour depth around the downstream pier was lower than the scour depth around the upstream pier by examining the testing findings. In an experimental investigation, Wang, et al. (2016a, b) looked at the scouring values around three piers of the same distance. They conducted the tests in clear water and found that the scour depth around the upstream pier was the same as that around the single pier.

Nowadays, artificial intelligence techniques have been widely used for many engineering applications (Bazrafshan et al. 2022; Ehteram et al. 2020; Latif 2021a, 2021b; Latif et al. 2020; Latif et al., 2021a, 2021b; Latif, Birima, et al. 2021a, b; Latif and Ahmed 2021; Najah et al. 2021; Parsaie and Haghiabi 2017; Parsaie et al. 2021). Also, artificial intelligence techniques have been used for scour around bridge piers prediction, for example, Etemad-Shahidi et al. (2015) used the M5 model tree to simulate the scour depth around the bridge piers. They discovered that the M5 model tree outperformed the empirical relationships after assessing the modeling findings. Muzzammil et al. (2015) used the Gene Expression Programming (GEP) model to estimate the scour hole size in cohesive sediments around bridge piers. They compared the results of their numerical model to the experimental findings and found that the GEP model outperformed the nonlinear regression model in terms of accuracy. Azimi et al. (2017) created a hybrid model for simulating scour depth in the vicinity of pier groups utilizing Adaptive Neuro-Fuzzy Inference System (ANFIS), Singular Decomposition Value (SVD), and Differential Evolution (DE) methods. They demonstrated that the hybrid model was accurate enough. Using the Extreme Learning Machine (ELM) model, Ebtehaj et al. (2018) projected scour depth at the pier groups. They also compared their findings to those of artificial neural networks (ANN) and support vector machines (SVM), finding that the ELM model was more accurate.

Artificial neural networks (ANNs) are believed to be very popular and practical approaches based on the results of earlier studies and their acceptable performance in tackling nonlinear problems that are difficult to solve using traditional analytical and numerical methods. Although this strategy has demonstrated accurate results in multiple trials, it also has several drawbacks, the most significant of which is the slow training speed. The slow learning speed of ANN models is caused by the slowness of gradient algorithms and the repeated setting of ANN parameters throughout the training phase. By transforming a nonlinear problem into a linear problem, the extreme learning machine (ELM) method has solved the problem of high-speed modeling in a single-layer feed-forward neural network (SLFFNN) (Huang et al. 2004). Furthermore, this strategy is highly generalizable (N. Y. Liang et al. 2006). Although ELM models have numerous advantages, they tend to outlier data throughout the training phase, reducing the model’s accuracy and validity (Horata et al. 2013). Zhang and Luo (2015) proposed outlier robust ELM (ORELM) approaches to address this issue.

Artificial intelligence techniques, such as ELM and its expanded forms (i.e., ORELM), are, on the other hand, frequently employed by researchers and engineers. Artificial intelligence technologies, on the other hand, have not been used to simulate and estimate scouring in the region of twin and three piers. As a result, a new ORELM approach is used to model the scour depth around the twin and three piers in this study. The optimal number of hidden neurons is chosen utilizing the trial-and-error method to attain this goal. For modeling the scour depth, the optimum activation function is also introduced. It should be mentioned that the k-fold cross-validation approach with k = 4 is utilized to check the numerical model’s results. In addition, the input parameters are used to create four different ORELM models. The superior model and effective parameters are chosen using sensitivity analysis. Error analysis and uncertainty analysis are also implemented in ORELM models. The superior model is then given a realistic and straightforward relationship. A partial derivative sensitivity analysis is performed for this equation.

Material and methods

Experimental model

The experimental data of Wang, et al. (2016a, b) and Wang, et al. (2016a, b) were used in this investigation to develop the soft computing model. A rectangular flume with length, width, and height of 12, 0.42, and 0.7 m is included in the experimental model. Two piers with a diameter of 6 cm were built in the twin pier type. It should be mentioned that the sediment layer had an initial depth of 15 cm and a length of 6 m, and twin piers were positioned in the sediment layer at a distance of d. The distance between the piers was assumed to be between 0 and 15 times the pier diameter in the three piers model. Figure 1 depicts a schematic representation of Wang, et al. (2016a, b) and Wang, et al. (2016a, b) experimental models.

Fig. 1
figure 1

Schematic representation of Wang et al. (2016a) and Wang et al. (2016b) experimental models (2016b)

Full size image

Scour around piers

The scour depth in the vicinity of the pier groups (ds) is a function of the mean diameter of the sediment particles (d50), the number of piers parallel to the flow direction (m), the diameter of the bridge piers (D), the center-to-center distance between bridge piers in the direction parallel to the flow (d), the center-to-center distance between bridge piers in the direction perpendicular to the flow (Sn), flow depth (h), average flow:

$$ds=f({d}_{50},m,n,D,d,{S}_{n},h,U,{U}_{c}$$
(1)

where U is the mean vertical velocity of the approaching flow, and Uc is the incipient velocity of sediment motion. Wang, et al. (2016a, b) and Wang, et al. (2016a, b) used a distance of \(d\) to measure the scour around the piers. The values of d50, m, n, d, Sn, and Uc in their investigation were nearly constant. When the dimensionless parameters are considered, Eq. 1 is rewritten as follows:

$$ds/h=f(D/h,d/h,{F}_{r}$$
(2)

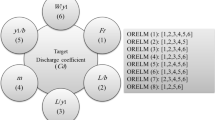
Fr is the Froude number in this case. As a result, the parameters of Eq. 2 are used as input parameters in numerical models in this work. Figure 2 depicts the input parameter combinations for several models. In addition, Table 1 shows the range of experimental values used in this investigation.

Fig. 2
figure 2

ORELM model development using a combination of input parameters

Full size image
Table 1 Experimental values range utilized in this study
Full size table

ELM

Huang et al. 2004) developed ELM, which is an SLFFNN training method. In actuality, SLFFNN is a linear system in which the input weights for hidden neurons and hidden layer biases are chosen at random, but the weights between hidden nodes are calculated analytically. This technique outperforms traditional learning algorithms in terms of performance and learning speed (Huang et al. 2004). Because, unlike traditional methods that necessitate the adjustment of numerous parameters, this method does not necessitate extensive human interaction to attain optimal values (Ebtehaj et al. 2016). The following is a representation of a standard single-layer neural network with N random data (xi, ti), N hidden neurons, and the active function g(x):

$${x}_{i}={\left[{x}_{i1},{x}_{i2},...,{x}_{in}\right]}^{T}\in {R}^{n}$$
(3)
$${x}_{i}={\left[{x}_{i1},{x}_{i2},...,{x}_{in}\right]}^{T}\in {R}^{n}$$
(4)
$${t}_{i}={\left[{t}_{i1},{t}_{i2},...,{t}_{in}\right]}^{T}\in {R}^{m}$$
(5)
$$\sum\limits_{i=1}^N\beta_ig(w_ix_j+b_i)=o_j,j=1,2,...,N$$
(6)

in which, wi = [wi1, wi2, … win]T is the weight vector connecting the hidden neurons to the input neurons; βi = [βi1, βi2, …, βin]T represents the weight vector connecting the hidden neurons to the output neurons; bi is the biases of the hidden neurons; wixj indicates the internal multiplication of wi and xj. The standard SLFFNN network with the N hidden neurons and the activation function g(x) can estimate N data with a zero error \(({\sum }_{j=1}^{N}\Vert {o}_{j}-{t}_{j}\Vert =0)\), in which.

$$\sum\limits_{i=1}^{N}{\beta }_{i}g({w}_{i}{x}_{j}+{b}_{i})={t}_{j},j=\mathrm{1,2},....,N$$
(7)

The above equations can be rewritten as follows:

$$H\beta =T$$
(8)
$$H({w}_{1},...,{w}_{N},{b}_{1},...,{b}_{N},{x}_{1},...,{x}_{N})={\left[\begin{array}{ccc}g({w}_{1}.{x}_{N}+{b}_{1})& \dots & g({w}_{N}.{x}_{1}+{b}_{N}\\ \vdots & \vdots & \vdots \\ g({w}_{1}.{x}_{N}+{b}_{1}& \cdots & g({w}_{N}.{x}_{N}+{b}_{N}\end{array}\right]}_{N*N}$$
(9)
$$\beta ={\left[\begin{array}{c}{\beta }_{1}^{T}\\ \vdots \\ {\beta }_{N}^{T}\end{array}\right]}_{N*m}$$
(10)
$$T={\left[\begin{array}{c}{t}_{1}^{T}\\ \vdots \\ {t}_{N}^{T}\end{array}\right]}_{N*m}$$
(11)

The matrix H is called the output matrix of the hidden layers of the neural network. The ith column of the matrix H represents ith vector of the output of the hidden neurons (considering x1, x2, …, xN as input).

The determination of the input weights (wi) and the hidden layer biases (bi) are equivalent to finding a solution for β least square of the linear system Hβ = T.

$$\Vert H({w}_{1},...,{w}_{N},{b}_{1},...,{b}_{N})\beta -T\Vert ={\mathit{min}}_{\beta }\Vert H({w}_{1},...,{w}_{N},{b}_{1},...,{b}_{N})\beta -T\Vert$$
(12)

The least average solution for the least square of the linear system is

$$\beta ={H}^{+}T.$$
(13)

ORELM

In addition to the general form of ELM, the following cases should be considered in the ORELM technique (Zhang and Luo 2015):

C, a new adjustment parameter, is introduced. The ratio of the training error to the output weight norm is this parameter. This parameter can be used to concurrently minimize the training error and the output weight norm; in other words, it can be used to increase the model’s generalizability performance when compared to the ELM model, which is represented by the equation:

$${\mathit{min}}_{\beta }C{\Vert T-H\beta \Vert }_{2}^{2}+{\Vert \beta \Vert }_{2}^{2}.$$
(14)

The scattering can be better reflected using ℓ0-norm instead of ℓ2-norm. Hence, the output weight β is considered with a smaller ℓ2-norm, so that the training error e is reduced; that is:

$${\mathit{min}}_\beta C{\Arrowvert e\Arrowvert}_0+{\Arrowvert\beta\Arrowvert}_2^2subject\;to\;T-H\beta=e.$$
(15)

A non-convergent programming problem is the one shown above. Refreshing the issue with a tractable form relaxation convex without losing the dispersion index is a simple technique to solve it. The dispersion feature is ensured by replacing the ℓ1-norm with the ℓ0-norm, resulting in maximum convergence. As a result, the equation looks like this:

$${{\mathit{min}}_\beta\Arrowvert e\Arrowvert}_1+\frac1C{\Arrowvert\beta\Arrowvert}_2^2subject\;to\;T-H\beta=e$$
(16)

where, the augmented Lagrangian function is defined as follows:

$${L}_{\mu }(e,\beta ,\lambda )={\Vert e\Vert }_{1}+\frac{1}{C}{\Vert \beta \Vert }_{2}^{2}+{\lambda }^{T}(T-H\beta -e)+\frac{\mu }{2}{\Vert T-H\beta -e\Vert }_{2}^{2}$$
(17)

where μ is the error parameter and λ * Rn is the augmented Lagrangian vector. According to Yang and Zhang (2011), the value of μ should be assumed to be μ = 2 N/||T||. The ideal response (e, β) and the coefficient λ are computed in the augmented Lagrange multiplier (ALM) by repeating to minimize the completed Lagrangian function. In summary, the repeat design of ALM, according to (λk, μ), is as follows:

$$\left\{\begin{array}{c}(e_{k+1},\beta_{k+1})=\mathit{arg}\mathit\;\underset{e,\beta}{min}L_\mu(e,\beta,\lambda_k)\\\lambda_{k+1}=\lambda_k+\mu\left(T-H\beta_{k+1}-e_{k+1}\right).\end{array}\right.$$
(18)

These equations can be rewritten as follows:

$$\left\{\begin{array}{l}\beta_{k+1}=arg\mathit\;\underset\beta{min}L_\mu(e_k,\beta,\lambda_k)\\\beta_{k+1}=arg\mathit\;\underset\beta{min}L_\mu(e_k,\beta,\lambda_k)\\\lambda_{k+1}=\lambda_k+\mu(T-H\beta_{k+1}-e_{k+1})\end{array}\right.$$
(19)

Goodness of fit

The statistical indices of determination coefficients (R2), variance accounted for (VAF), root mean square error (RMSE), scatter index (SI), mean absolute error (MAE), mean absolute relative error (MARE), and Nash–Sutcliffe efficiency coefficient (NSC) are used in this study to evaluate the accuracy of numerical models:

$${R}^{2}=\frac{{\left(n{\sum }_{i=1}^{n}{P}_{i}{O}_{i}-{\sum }_{i=1}^{n}{P}_{i}{\sum }_{i=1}^{n}{O}_{i}\right)}^{2}}{\left(n{\sum }_{i=1}^{n}{\left({P}_{i}\right)}^{2}-{\sum }_{i=1}^{n}{\left({P}_{i}\right)}^{2}\right)\left(n{\sum }_{i=1}^{n}{\left({O}_{i}\right)}^{2}-{\sum }_{i=1}^{n}{\left({O}_{i}\right)}^{2}\right)}$$
(20)
$$VAF=\left(1-\frac{var\left({P}_{i}-{O}_{i}\right)}{var\left({P}_{i}\right)}\right)\times 100$$
(21)
$$RMSE=\sqrt{\frac1n\sum\limits_{i=1}^n\left(P_i-O_i\right)^2}$$
(22)
$$SI=\frac{RMSE}{\overline{O}}$$
(23)
$$MAE=\frac{{\sum }_{i=1}^{n}\left|{P}_{i}-{O}_{i}\right|}{n}$$
(24)
$$MARE=\frac{1}{n}\sum\limits_{i=1}^{n}\frac{\left|{P}_{i}-{O}_{i}\right|}{{O}_{i}}$$
(25)
$${\text{NSC}}=1-\frac{{\sum }_{i=1}^{n}{\left({O}_{i}-{P}_{i}\right)}^{2}}{{\sum }_{i=1}^{n}{\left({O}_{i}-\overline{O}\right)}^{2}}$$
(26)

where Oi denotes the observed values, Pi denotes the numerical models’ simulated values, Ō is the average of observational values, and n denotes the number of observational values.

Because the statistical indices offered do not allow for simultaneous comparison of the models’ mean and variance, the Akaike information criterion (AIC) is used to compare the predicted discharge coefficient to the experimental value (Ebtehaj et al. 2016):

$$AIC=n.\mathit{log}\left[\frac{1}{n}{\sum\limits_{i=1}^{n}\left({R}_{\left(Observed\right)i}-{R}_{\left(\mathit{Pr}edicted\right)i}\right)}^{2}\right]+2k$$
(27)

The number of estimated parameters employed in the numerical model is given by k. The ACI parameter is used as a benchmark for determining how well a statistical model adapts. It is also used to choose a model, and it describes the numerical model’s complexity and accuracy at the same time.

Results and discussion

Number of hidden layer neurons

First, the number of hidden layer neurons is examined. Figure 3 depicts the relationship between the number of hidden layer neurons and numerous statistical indices. Two criteria must be considered when determining the ideal number of hidden layer neurons. (1.) The AIC value is the smallest, and (2.) the MARE value is less than 0.15. The number of hidden layer neurons was first estimated to be two, then increased to thirty. The numerical model considers the number of ideal hidden layer neurons to be 17 based on these two criteria. For example, when NHN equals 15, the numerical model’s MARE and AIC values were calculated to be 0.150 and − 41.807, respectively. Furthermore, the VAF, RMSE, and NSC values for these hidden neuron layers were estimated to be 99.758, 0.018, and 0.968, respectively.

Fig. 3
figure 3

The number of hidden neuron layers varies according to different statistical parameters

Full size image

The scatter plot and comparison of observed and simulated values for NHN = 17 are shown in Fig. 4. R2, MAE, and SI are computed as 0.968, 0.014, and 0.096, respectively, for a model with NHN = 17. As a result, the best number of this parameter was determined to be 17 based on the number of hidden layer neurons.

Fig. 4
figure 4

Scatter plot with simulated and observed scouring values for NHN = 17

Full size image

Activation function selection

The correctness of the numerical model’s numerous activation functions is assessed in this section. Sig, sin, radbas, tribas, and hardlim are the five activation functions in the ELM model. Figure 5 depicts the findings of statistical indicators. The VAF, SI, and RMSE values for the sig activation function are 96.758, 0.096, and 0.018, respectively. Meanwhile, for the sin activation function, the MAE and SI indices are 0.016 and 0.011, respectively. The RMSE, NSC, and VAF indices for the radbas activation function are 0.039, 0.909, and 85.803 correspondingly. The values of SI, MAE, and RMSE for the tribas activation function, on the other hand, are 0.199, 0.030, and 0.038, respectively. The VAF and SI values for the hardlim function are estimated to be 0.831 and 0.578, respectively, based on the findings of the activation functions. The error indices of activation functions tested during the development of ELM model are given in Table 2.

Fig. 5
figure 5

Results of statistical indices for various activation functions

Full size image
Table 2 Error indices of tested activation functions of ELM model
Full size table

Figure 6 also shows scatter plots and outcomes of scouring simulations using various activation functions. The R2 values for the activation functions sig, sin, and radbas, for example, are 0.968, 0.964, and 0.946, respectively. Furthermore, the amount of R2 for tribas and hardlim functions was estimated to be 0.948 and 0.024, respectively. As a result, the sig function is identified as the superior activation function based on the findings of the activation functions.

Fig. 6
figure 6

Scatter plot and comparison of observed and simulated scouring values

Full size image

k-fold cross-validation

The data is separated into k subgroups in this type of validation. One subset is utilized for validation, and the other k − 1 subsets are used for training. This process is repeated, with all data being utilized twice for training and validation. Finally, as a final estimate, the average result of k times validation is chosen. For k = 4, Fig. 7 depicts the k-fold cross-validation procedure. Figure 8 depicts the scatter plots for the four validation stages of the k-fold cross-validation approach. The R2 values for k = 1 and k = 2 in the test mode are 0.949 and 0.952, respectively. The R2 values for k = 3 and k = 4 are calculated to be 0.953 and 0.950, respectively.

Fig. 7
figure 7

Schematic of k-fold cross-validation method for k = 4

Full size image
Fig. 8
figure 8

Scatter plot for k = 4 in the k-fold cross-validation method

Full size image

Performance of ORELM models

The findings of the ORELM 1 to ORELM 4 models are presented in this part to simulate the scour depth around twin and three piers. Figure 9 depicts the findings of various statistical indices for these models. For all input parameters (D/h, d/h, and Fr), the ORELM model calculates the scour depths. The VAF and RMSE statistical indices have been calculated to be 95.249 and 0.033, respectively, for this model, while this model’s scatter index is 0.146.

Fig. 9
figure 9

Results of statistical indices for different ORELM models

Full size image

Three ORELM 2 to ORELM 4 models, on the other hand, estimate the values of the objective function using the three input parameters. The ORELM 2 model, for example, is a function of D/h and d/h. The statistical indices of MAE, SI, and RMSE for this model are 0.099, 0.549, and 0.125, respectively.

ORELM3’s SI, VAF, and NSC values are also predicted to be 0.245, 84.316, and 0.814, respectively. The effect of the d/h has been removed from this model. In other words, the model uses D/h and Froude numbers to estimate the values of the goal function.

Furthermore, because the ORELM4 model is a function of d/h and Fr, the effect of the D/h parameter is neglected. MAE, VAF, and RMSE for ORELM4 are calculated to be 0.056, 75.284, and 0.076, respectively. The NSC for this model is equivalent to 0.671.

Figures 10 and 11 provide a comparison of simulated and observed scouring values, as well as error distribution diagrams for ORELM models. The R2 coefficient for the ORELM model is 0.953. Furthermore, the ORELM1 model simulates nearly half of the scouring values with an inaccuracy of less than 10%. It is worth noting that around a third of the ORELM1 model’s outputs have an inaccuracy of more than 15%. The R2 score for the ORELM2 model is 0.326. Approximately 81% of the outcomes for this model have a margin of error greater than 15%. It should be noted that around 8% of the scouring values simulated by ORELM2 have an inaccuracy of 10 to 15%. Furthermore, the R2 value for the ORELM3 model is predicted to be 0.843, and around 32% of the findings have an error of less than 10%. In comparison, around 68% of the values estimated using the ORELM4 model have an error greater than 15%, and 9% of the findings have an error between 10 and 15%. The R2 value for ORELM is approximately 0.753.

Fig. 10
figure 10

Comparison of observed and simulated scour depths by different ORELM models

Full size image
Fig. 11
figure 11

Error distribution for different ORELM models

Full size image

As a result of the modeling results, the ORELM1 model is determined to be the superior model. In terms of D/h, d/h, and Fr, this model calculates the scour depths in the vicinity of twin and three piers. The parameters of the Froude number (Fr) and the ratio of the pier diameter to the flow depth (D/h) were also found as the most effective input parameters after an analysis of the simulation results.

Uncertainty analysis

The uncertainty analysis of ORELM models is performed in this section to evaluate the projected error by numerical models and to assess their performance. In general, the numerical model’s predicted error is equal to the numerical model’s simulated values (Pi) minus the observational values. (Oi) (ei = Pi − Oi). Also, the average of the predicted error is calculated as \(\overline{e}={\sum }_{i=1}^{n}{e}_{i}\). In addition, the standard deviation of the predicted error values is \({S}_{e}=\sqrt{{\sum }_{i=1}^{n}{\left({e}_{i}-\overline{e}\right)}^{2}/n-1}\). It should be noted that the negative and positive values of ē indicate that the numerical model has an underestimated and overestimated performance, respectively. Also, using parameters of ē and Se, a confidence band is plotted around the predicted error values by Wilson score’s method without continuity correction, then, using ± 1.64Se approximately 95% band, which shown with 95% PEI. Table 3 shows the parameters for the improved model’s uncertainty analysis. The WUB represents the breadth of the uncertainty band in this table. The ORELM1, ORELM2, and ORELM4 models have underestimated performance, while the ORELM3 model has overestimated performance, according to the results of the uncertainty analysis. In addition, the 95% PEI value used by the ORELM1 model to estimate scour depth is between − 0.005 and 0.004. In the meantime, the ORELM2 uncertainty band is around − 0.017 wide. Furthermore, the value of Se for the ORELM3 and ORELM4 models is predicted to be 0.06 and 0.076, respectively.

Table 3 Uncertainty analysis parameters for different ORELM models
Full size table

As a result of the modeling results analysis, the ORELM1 model is chosen as the superior model for estimating scour depth in the region of the twin and three piers. A relationship is constructed for this model as follows:

$$\frac{{d}_{S}}{h}=\left|{\left[\frac{1}{\left(1+\mathit{exp}\left(InW\times InV+BHN\right)\right)}\right]}^{T}\times OutW\right|.$$
(28)

The input weights matrix is InW, the input variables matrix is InV, the bias-layer neuron matrix is BHN, and the output weights matrix is OutW. Furthermore, the best values for these matrices are listed below:

$$InV=\left[\begin{array}{c}D/h\\ d/h\\ Fr\end{array}\right]BHN=\left[\begin{array}{c}\text{0.047}\\ \mathrm{-0.028}\\ 0.223\\ -0.720\\ 0.234\\ 0.655\\ -0.116\\ -0.178\\ -0.068\\ -0.879\\ -0.873\\ -0.066\\ 0.602\\ 0.101\\ -0.833\\ 0.857\\ -0.657\end{array}\right]InW=\left[\begin{array}{ccc}\text{-0.774}& \text{-0.789}& \text{0.918}\\ \text{0.386}& \text{-0.807}& \text{-0.297}\\ \text{0.983}& \text{0.573}& \text{-0.657}\\ \text{0.065}& \text{-0.876}& \mathrm{-0.551}\\ \text{-0.640}& \mathrm{0.665}& \text{0.757}\\ \mathrm{-0.480}& \text{-0.246}& \mathrm{0.455}\\ \text{-0.407}& \mathrm{-0.354}& \text{-0.048}\\ \mathrm{-0.37}{0}& \text{0.876}& \mathrm{-0.495}\\ \text{-0.141}& \mathrm{0.335}& \text{0.335}\\ \mathrm{-0.844}& \text{-0.999}& \mathrm{0.214}\\ \text{0.277}& \mathrm{0.513}& \text{0.463}\\ \mathrm{0.630}& \text{-0.818}& \mathrm{0.931}\\ \text{-0.361}& \mathrm{-0.040}& \text{0.699}\\ \mathrm{0.368}& \text{0.777}& \mathrm{0.807}\\ \text{0.478}& \mathrm{0.939}& \text{0.848}\\ \mathrm{-0.249}& \text{0.595}& \mathrm{-0.209}\\ \text{-0.401}& \mathrm{-0.155}& \text{0.746}\end{array}\right]OutW=\left[\begin{array}{c}\text{73.924}\\ \mathrm{214.041}\\ \text{84.575}\\ \mathrm{-219.899}\\ \text{105.166}\\ \mathrm{-52.979}\\ \text{180.606}\\ \mathrm{35.214}\\ \text{-48.781}\\ \mathrm{-71.814}\\ \text{107.885}\\ \mathrm{-75.918}\\ \text{81.121}\\ \mathrm{-1}\text{94.716}\\ \mathrm{92.059}\\ \text{-216.919}\\ \mathrm{-57.742}\end{array}\right]$$
(29)

Partial derivative sensitivity analysis (PDSA)

The partial derivative sensitivity analysis (PDSA) is applied to the superior model (ORELM1) in this section, and the input parameters are evaluated. In general, one of the most essential methods for determining the pattern of fluctuation of input parameters is partial derivative sensitivity analysis (PDSA) (Azimi et al., 2017). Furthermore, a positive partial derivative sensitivity analysis indicates that the objective function (scour) is increasing; on the other hand, a negative value indicates that the output value is decreasing. The ratio of the objective function is used to derive the relative derivative of each input parameter in this study. In other words, for each input variable, the relative derivative f(x) is determined (Fig. 12). The value of PDSA, for example, diminishes as D/h increases. For d/h greater than 4, however, the scour depth increases, and the d/h (as the input parameter) increases. Furthermore, with increasing Fr, the PDSA pattern displays a declining trend.

Fig. 12
figure 12

The results of PDSA for the ORELM superior model

Full size image

Conclusion

The scour depth around twin and three piers were simulated using a new outlier robust extreme learning machine (ORELM) in this work. k-fold cross-validation for k = 4 was performed to validate the simulation findings. The ideal number of hidden layer neurons and activation function was chosen at first. In other words, the sigmoid function and several ideal neurons of 17 were introduced as optimal activation. Following that, four ORELM models were created utilizing the input parameters. Analyzing the modeling results revealed the superior model and the most effective input parameters. The superior model simulated the scouring values with acceptable accuracy. The optimal values for all input parameters were estimated using this model, and the most effective input parameters were Fr and D/h. For ORELM1 (superior model), the RMSE, MAE, and VAF values were calculated to be 0.033, 0.025, and 95.249, respectively. Furthermore, the error distribution revealed that approximately 18% of the ORELM model’s outputs had an error of between 10 and 15%. In addition, an uncertainty analysis was done on all ORELM models, and the ORELM1 model underperformed. It should be mentioned that for the ORELM1 model, a simple equation was presented for engineers to employ in their practical work. Finally, a PDSA was used to solve this problem.