1 Introduction

It is well known that correctly designed compliant coatings are able to reduce the growth rates of unstable Tollmien–Schlichting waves (TSWs). This has been demonstrated theoretically in, for example, Carpenter & Garrad (1985) and confirmed experimentally by Gaster (1987). Accordingly transition in low-disturbance environments can potentially be postponed, extending the laminar boundary-layer region to yield a valuable reduction to skin-friction drag in marine applications. However, compliant walls support hydro-elastic instabilities such as divergence and travelling-wave flutter (TWF) that can trigger premature transition; for details of these instabilities, see, for example, Gad-el Hak et al (1984), Gad-el Hak (1986), Carpenter & Garrad (1986), Lucey & Carpenter (1992, 1995). Additionally, theoretical and experimental investigations of Blasius flow over rigid (Butler & Farrel 1992; Åkervik et al 2008) and compliant surfaces (Zengl & Rist 2012; Huang & Johnson 2008), but also of Poiseuille flow with compliant walls (Hœpffner et al 2010) have demonstrated the potential for by-pass transition through the transient amplification of linear disturbances that extract energy from the mean flow. The purpose of this paper is therefore to elucidate both the time-asymptotic and transient behaviour of compliant panels in boundary-layer flow.

The multi-mode interactions of compliant walls with boundary-layer flows mean that their design needs to maximize TSW suppression but keep the wall free from hydro-elastic instabilities that can create an alternative route to transition. Optimisations using this strategy have predicted extensions to the transition length by a factor of 4.5 and 5.7 respectively for plate-spring and monolithic viscoelastic-slab types of compliant coatings (Carpenter 1993; Dixon et al 1994; Carpenter et al 2000). However, these optimizations have also suggested that a series of short compliant sections or panels (see Davies & Carpenter (1997) for the corresponding problem of a Poiseuille mean flow), with their structural properties tailored to the local Reynolds number, offer the possibility of massively enhanced transition delay. To date, all optimizations of performance have been based upon a classical local stability analysis of modes and transient effects have not been addressed. Thus, the interaction of finite compliant panels with a boundary-layer flow warrants attention.

In this paper, we develop a hybrid of computational and theoretical models to study the global stability of laminar boundary-layer flow interacting with a compliant panel mounted in an otherwise rigid flat plate aligned with the oncoming flow. However, the methods developed could readily be used to analyse interactions between Falkner-Skan type boundary-layer profiles when a non-zero pressure gradient determines the mean flow. The approach builds from the global stability analysis of Pitman & Lucey (2009); Burke et al (2014) for external and channel potential flow and Pitman & Lucey (2010) for Poiseuille flow interacting with a flexible panel. In the present development, we extend the velocity-vorticity formulation of the flow equations and combine it with a generalized Helmholtz decomposition (Wu & Thompson 1973; Kempka et al 1995) to investigate the global asymptotic and transient behavior of the FSI system. Local spatial stability analysis is also conducted to validate the global analysis, but also to reveal the spatial manifestations of the predicted temporal instabilities. Throughout, we solve a generalized eigenvalue problem to determine all of the fluid and structural branches in the spectrum of eigen-frequencies of the assembled FSI system. We are therefore able to reveal the interaction between different mode types and identify the conditions for temporal instability. In particular we identify, for the first time, modal interactions between each of TSWs and TWF with structural modes of the finite compliant panel that can lead to globally unstable behavior of the FSI system.

Being able to extract a very significant part of the global frequency spectrum and the respective eigenmodes, we then follow Ehrenstein & Gallaire (2005) and express the time evolution of transient disturbances as the linear superposition of the converged two-dimensional temporal modes. We can then track the spatio-temporal evolution of the most amplified initial disturbance as a means to assess whether transient growth is a potentially significant route to by-pass transition in flow over a compliant panel. However, the main goal of the present paper is to demonstrate that global instability can occur in Blasius boundary-layer flow over a finite complaint panel. While we do consider the modification of panel properties as means to understand the instability mechanisms, this paper does not offer a comprehensive parametric investigation of the FSI system with respect to the control or suppression of the new phenomena presented.

Finally, we remark that while the study has been framed in the context of compliant walls for transition postponement, the present work is of a fundamental nature with broad applications from engineered to naturally occurring biomechanical systems such as the interaction of blood flow with spatially dependent compliance in the walls of the small vessels.

2 Methods

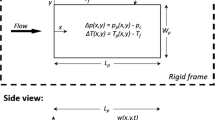
Figure 1 shows the FSI system studied. A Blasius boundary layer progresses over a rigid-wall section of length \(L^{\ast }_{\mathrm {w1}}\) onto a compliant panel of length \(L^{\ast }_{\mathrm {c}}\) comprising a spring-backed flexible plate (that may include a dashpot-type damping) with which it interacts, and finally over a rigid-wall section of length \(L^{\ast }_{\mathrm {w2}}\). Here and hereafter, ∗ denotes a dimensional quantity. At entry and exit to the domain the Reynolds number (based upon free-stream flow speed \(U^{\ast }_{\mathrm {\infty }}\), fluid density \(\rho ^{\ast }_{\mathrm {l}}\) and dynamic viscosity \(\mu ^{\ast }_{\mathrm {l}}\), and boundary-layer displacement thickness δ ∗) are respectively R e s and R e o; \(\omega ^{\ast }_{\mathrm {s}}\) and \(\omega ^{\ast }_{\mathrm {o}}\) are the radian frequencies of perturbation waves that satisfy the Orr-Sommerfeld equation that serve as entry and exit conditions to the system domain.

Figure 1
figure 1

Schematic of the system studied with nomenclature.

Full size image

2.1 Mean flow field

The displacement thickness \(\delta ^{\ast }_{\mathrm {s}}\) at the entrance \(x^{\ast }_{\mathrm {s}}\) (from the origin of the boundary later) of the flow domain modelled provides the characteristic length scale and the undisturbed-flow velocity, \(U^{\ast }_{\infty }\) gives the characteristic speed (hence the characteristic time is \(\delta ^{\ast }_{\mathrm {s}}/U^{\ast }_{{\infty }}\)). The local Reynolds number, R e x at streamwise location x in the system is related to the entry Reynolds number, R e s through R e x =γ(x R e s)1/2 where \(Re_{\mathrm {s}} = {\rho ^{\ast }_{\mathrm {l}} U^{\ast }_{\infty } \delta ^{\ast }_{\mathrm {s}} / {\mu ^{\ast }_{\mathrm {l}}} }\) and γ=1.7208 for the Blasius boundary later. The mean-flow velocity components are given by, \(U_{x} = f^{\prime }\) and \(U_{z} = \gamma / (2(x Re_{\mathrm {s}} )^{1/2}) [ H f^{\prime } - f ]\), where prime denotes differentiation with respect to the dependent variable H=z/(γ(x/R e s)1/2) and f(H) satisfies the Blasius equation

$$ 2f^{\prime\prime\prime} + \gamma^{2} f f^{\prime\prime}=0, $$
(1)

subject to the boundary conditions \(f(0)= f^{\prime }(0) = 0\) and \(f^{\prime }\rightarrow 1\) as \(H\rightarrow \infty \).

2.2 Perturbation fields

Starting from the two-dimensional (2D) velocity-vorticity disturbance formulation of the Navier–Stokes equations, e.g. Davies & Carpenter (2001) and retaining only the linear velocity and vorticity terms, the evolution of perturbations to the mean flow is governed by

$$ \frac{\partial\omega_{y}}{\partial t} +\frac{\partial{\Omega}_{y}}{\partial x}u_{x} +\frac{\partial{\Omega}_{y}}{\partial z}u_{z} +U_{x}\frac{\partial \omega_{y}}{\partial x} +U_{z}\frac{\partial \omega_{y}}{\partial z} =\frac{1}{Re_{\mathrm{s}}}\left( \frac{\partial^{2}\omega_{y}}{\partial x^{2}} +\frac{\partial^{2}\omega_{y}}{\partial z^{2}}\right) $$
(2)

where mean-flow variables appear in capitals, while perturbations to the mean flow quantities are in lower case; u x and u z are the horizontal and vertical components of the velocity disturbance, while Ω y and ω y are respectively the mean-flow and the disturbance vorticity in the direction perpendicular to the x- and z-axes.

Instead of solving the vector Poisson equation, we make use of the Helmholtz decomposition (Wu & Thompson 1973; Kempka et al 1995) and express the disturbance flow field as the sum of its rotational and irrotational parts; thus the perturbation velocity is written as

$$\begin{array}{@{}rcl@{}} \mathbf{u}(\mathbf{x}) &=& {\int}_{R\neq R_{\text{bf}}} \boldsymbol{\nabla} G(\mathbf{x},{\mathbf{x}^{\prime\prime}}) \! \times \! \omega_{y}({\mathbf{x}^{\prime\prime}}){\mathbf{e}_{\mathbf{y}}} \ \mathrm{d}R({\mathbf{x}^{\prime\prime}}) + {\int}_{R_{\text{bf}}} \boldsymbol{\nabla} G(\mathbf{x},{\mathbf{x}^{\prime\prime}}) \! \times \! \omega_{y}({\mathbf{x}^{\prime\prime}}){\mathbf{e}_{\mathbf{y}}} \ \mathrm{d}R({\mathbf{x}^{\prime\prime}}) \\ && - {\int}_{S} \sigma({\mathbf{x}^{\prime\prime}})\boldsymbol{\nabla} G(\mathbf{x},{\mathbf{x}^{\prime\prime}}) \ \mathrm{d}S({\mathbf{x}^{\prime\prime}}) \end{array} $$
(3)

where \(G = -(1 / (2\pi ) ) \ln { \vert \mathbf {x}-\mathbf {x}^{\prime \prime } \vert } \) is the 2D infinite domain Green’s function and σ the strength of the source–sink sheet applied to the flow boundary. In the above integral expressions, the double prime indicates a dummy variable, while R and S respectively denote integration in the fluid domain and on the boundary surface. The rotational part is divided into boundary-flow field, R bf, and domain-flow field, R≠R bf, contributions in order to apply the tangential and normal boundary conditions at the boundary cells and surfaces.

Following Ehrenstein & Gallaire (2005), we make use of the Robin boundary conditions at the entrance x s and exit x o of the fluid domain

$$ \frac{\partial \omega_{y}}{\partial x}=i \alpha \omega_{y},\quad \frac{\partial u_{z}}{\partial x}=i \alpha u_{z} $$
(4)

but the complex wavenumber α is taken as the solution of the Orr-Sommerfeld equation at the entrance and at the exit of the fluid domain for cyclic frequencies ω s and ω o=(R e o/R e s)ω s, respectively.

The boundary conditions u x (x,0,t)=u z (x,0,t)=0 are applied at the rigid-wall portions. On the compliant-panel section, the velocity and stress components are continuous between fluid and solid. Thus, the linearised boundary conditions for the velocity are

$$ u_{x}(x,0,t)+\eta(x,t)\frac{\partial U_{x}}{\partial z}(x,0,t)=0, u_{z}(x,0,t)=\frac{\partial \eta}{\partial t}(x,t), x_{\text{cs}}\le x \le x_{\text{co}} $$
(5)

The pressure perturbation (non-dimensionalized using the free-stream dynamic pressure) that drives the compliant-panel motion is obtained by integrating the linearized z-momentum equation of the Navier–Stokes equations between the fluid–solid interface and infinity and enforcing that the pressure perturbation vanishes at infinity; thus

$$\begin{array}{@{}rcl@{}} p(x,0,t) &=& {\int}_{0}^{L_{\mathrm{H}}} \left( \frac{\partial u_{z}}{\partial t} + \frac{\partial U_{z}}{\partial x}u_{x} + \frac{\partial U_{z}}{\partial z}u_{z} + U_{x}\frac{\partial u_{z}}{\partial x} + U_{z}\frac{\partial u_{z}}{\partial z} \right)\gamma \sqrt{\frac{x}{Re_{\mathrm{s}}}} \ \mathrm{d}H \\ && + {\int}_{0}^{L_{\mathrm{H}}} \frac{1}{Re_{\mathrm{s}}} \frac{\partial \omega_{y}}{\partial x} \gamma \sqrt{\frac{x}{Re_{\mathrm{s}}}} \ \mathrm{d}H \end{array} $$
(6)

where L H is the total height of the computational domain, made large enough to ensure that

$$ \omega_{y}(x,L_{\mathrm{H}},t)=0, \quad u_{z}(x,L_{\mathrm{H}},t)=0 $$
(7)

For the compliant-panel dynamics, we use the one-dimensional beam equation with additional terms to account for a dashpot-type structural damping and a uniformly distributed spring foundation, giving

$$ -p(x,0,t) = M\frac{\partial^{2} \eta}{\partial t^{2}} + D\frac{\partial \eta}{\partial t} + B\frac{\partial^{4} \eta}{\partial x^{4}} + K \eta, $$
(8)

where the non-dimensional coefficients of inertia, damping, flexural rigidity, and spring-foundation stiffness respectively are defined by

$$ M=\frac{\rho^{\ast}_{\mathrm{m}} h^{\ast}_{\mathrm{m}}}{\rho^{\ast}_{\mathrm{l}} \delta^{\ast}_{\mathrm{s}}}, \quad D=\frac{D^{\ast}}{\rho^{\ast}_{\mathrm{l}} U^{\ast}_{\infty}}, \quad B=\frac{B^{\ast}}{\rho^{\ast}_{\mathrm{l}} {U^{\ast}_{\infty}}^{2} {\delta^{\ast}_{\mathrm{s}}}^{3}}, \quad K=\frac{K^{\ast}\delta^{\ast}_{\mathrm{s}}}{\rho^{\ast}_{\mathrm{l}} {U^{\ast}_{\infty}}^{2}}, $$
(9)

η(x,t) is the non-dimensional plate vertical displacement, and p(x,0,t) is the pressure perturbation from equation (6). Hinged boundary conditions are applied at the leading and trailing edges of the compliant panel, hence

$$ \eta(x_{\text{cs}},t)=\eta(x_{\text{co}},t)=0,\quad \frac{\partial^{2} \eta}{\partial x^{2}}(x_{\text{cs}},t)=\frac{\partial^{2} \eta}{\partial x^{2}}(x_{\text{co}},t)=0. $$
(10)

2.3 Eigenvalue formulation

We proceed by applying the decomposition,

$$\begin{array}{@{}rcl@{}} \hspace*{3pc}\lbrace \omega_{y}, \sigma, u_{x}, u_{z} \rbrace (x,z,t) = \lbrace \hat{\omega}, \hat{\sigma}, \hat{u_{x}}, \hat{u_{z}} \rbrace (x,z) \exp{(\lambda t)}, \\ p(x,0,t)=\hat{p}(x,0) \exp{(\lambda t)}, \quad \eta(x,t)=\hat{\eta}(x) \exp{(\lambda t)} \end{array} $$
(11)

where λ=−iω, together with the complex conjugate part of the eigen-decomposition, to the linear system of Eqs. (2), (3) and (8), taking into account the boundary conditions (4)–(7) and (10), to transform it to the generalized eigenvalue system

$$ \left[ C_{2} \right] \lbrace \hat{X} \rbrace = \lambda \left[ C_{1} \right] \lbrace \hat{X} \rbrace,\quad \lbrace \hat{X} \rbrace = \lbrace \hat{\omega}, \hat{\sigma}, \hat{\eta}, \hat{\phi} \rbrace^{T}, $$
(12)

with \( \hat {\phi }=\lambda \hat {\eta }\), from which the eigenvalues λ and eigenvectors \(\lbrace \hat {X} \rbrace \) can be extracted. If the real part of an eigenvalue λ is positive, instability in time occurs, whereas a negative real part indicates that disturbances decay with time. It is noted that the system equation (12) is smaller than that which would ensue if the corresponding Poisson equation were solved, since in the present method \(\hat {\sigma }\) is evaluated only on the boundary.

2.4 Transient-analysis formulation

In order to investigate the transient behavior of the FSI system we adopt standard methods, for example see Schmidt (2007) and Coppola & de Luca (2010), but defining the energy norm for the present FSI system to be

$$\begin{array}{@{}rcl@{}} \hspace*{3pc}E(t) &=& \frac{1}{2} {\int}_{0}^{L_{\mathrm{H}}} {{\int}_{0}^{L}} \left( \vert u_{x} \vert^{2} + \vert u_{z} \vert^{2} \right) \mathrm{d}x \ \mathrm{d}H \\ && +\frac{1}{2} {\int}_{0}^{L_{\mathrm{c}}} \left( M \dot{\eta}^{2} + B \left( \frac{\partial^{2} \eta}{\partial x^{2}} \right)^{2} + K\eta^{2} \right) \ \mathrm{d}x, \end{array} $$
(13)

where the flow kinetic energy is evaluated by the first integral on the right-hand side and the kinetic and potential energy of the compliant panel captured by the second integral. We look for initial disturbances which maximize the energy at time t, i.e.

$$ G(t)=\max_{\mathbf{X}_{0} \neq 0} \frac{\Vert \mathbf{X}(t){\Vert^{2}_{E}}}{\Vert \mathbf{X}_{0} {\Vert^{2}_{E}}}. $$
(14)

Following, for example, Ehrenstein & Gallaire (2005) and Åkervik et al (2008) we consider a linear superposition of the two-dimensional temporal modes as

$$ \mathbf{X}(x,H,t)={\sum}_{j=1}^{Num} k_{j}(t)\hat{\mathbf{X}}_{j}(x,H) $$
(15)

and taking into account that they must satisfy the initial-value form of the system (12), the maximum energy growth becomes

$$ G(t)=\Vert \mathbf{F} \: e^{\mathbf{P} t} \: \mathbf{F}^{-1} {\Vert^{2}_{2}} $$
(16)

where R=F T F the Cholesky decomposition of the Gramian matrix R, corresponding to the energy norm of Eq. (13). The largest growth at time t is then given by the largest singular value of F e Pt F −1 and the initial condition that provides it is given by F −1 z , with z being the right singular vector.

2.5 Solution methods

A second-order finite-difference method is used for the discretisation in the x-direction and a Chebyshev pseudo-spectral method is exploited in the z-direction. The flow domain is discretized into M=M w1+M c +M w2 cells in the streamwise direction, where M w1, M c and M w2, are respectively the number of fluid cells over the upstream rigid-wall, the compliant-panel and the downstream rigid-wall sections, while N+1 points are deployed in the z-direction with a linear transformation used to map the collocation points from the interval [1,0] onto [0,L H].

The Helmholtz decomposition, Eq. (3), is approximated by zero-order vortex sheets in the fluid and boundary domains and zero-order source sheets at the boundary surfaces. Finally, the ARPACK library (Lehoucq et al 1998) has been used to extract a significant part of the spectrum of Eq. (12), namely 3000 eigenvalues and their respective eigenvectors, using a relatively large Krylov subspace of 9000 vectors.

3 Results

We focus on the global stability of system modes arising from each of the well-known travelling-wave flutter (TWF) and Tollmien–Schlichting Waves (TSWs) that have been predicted to occur in Blasius boundary-layer flow over complaint walls using a local analysis. Accordingly, we choose the wall parameters such a way that the critical velocity for the onset of the divergence instability in potential flow over a finite compliant wall (Pitman & Lucey 2009) is well above the free-stream velocity \(U^{\prime }_{{\infty }} = 10\) m/s used herein. Throughout the results, the fluid is water with density 1000 kg/m 3 and dynamic viscosity 1.37×10−3 Ns/m 2 and the Reynolds number at the entrance to the computational domain, R e s, is set to 3000 for the eigen-analysis, and to 1000 for the transient analysis. The frequency at the inlet of the domain was set as ω s=0.07755.

Three types of compliant panels are used herein, namely wall-1, wall-2 and wall-3 with the values of their physical properties listed in table 1. Also included in table 1 are the corresponding non-dimensional parameters. Wall-1 is typical of the Kramer-type wall studied in Carpenter & Garrad (1985) that was shown to be capable of transition postponement, while wall-2 is chosen so that the frequencies of its in vacuo structural modes, when the panel has length 0.05 m, are close to those of the range of unstable TSWs in the boundary layer. Wall-3 is of a similar type to wall-1 but it has been made stiffer so that the FSI system is free of the TWF instability and the structural eigenfrequencies are beyond the range of those of unstable TSWs. For all walls, the effect of structural damping, D ∗, in the range 0 to 10 4 Ns/m 3 was studied, in order to assess its as a means to control system instabilities or transient growth.

Table 1 Physical properties and non-dimensional parameters of the systems studied.
Full size table

A number of tests have been conducted to validate the present modeling and its implementation. Validations of predicted eigenvalues and their corresponding eigen-vectors using the present modeling have been undertaken using appropriate comparisons with local-stability analysis in the literature, for example Carpenter & Morris (1990). Our local-stability results have then been used to construct the spatial amplification of convectively unstable TSWs over a compliant panel in order to create benchmarks against which the spatial amplification computed using the present methods have been compared; for example see Tsigklifis & Lucey (2013).

Equally, we have conducted convergence tests in order to verify the integrity of the new results presented herein. Thus, figure 2 shows the full eigenvalue spectrum using the wall-1 data for three levels of discretisation. The horizontal axis (ω r ) gives the oscillatory part of each mode, while the vertical axis (ω i ) gives its temporal growth(+ ve)/decay(−ve) rate. Five mode types are identified in this figure: M 1 is the TSW branch that for these system properties is seen to be stable, M 2 is the Orr-mode branch, M 3 is the continuous spectrum of the Orr-Sommerfeld equation, M 4 are modes associated with the Orr-Sommerfeld entry boundary conditions, and M 5 is the TWF branch that is seen to be unstable over a range of oscillation frequencies. In this study, we focus on the TSW and TWF branches for which mesh-independence is seen to have been achieved in figure 2. Finally, we have varied both the length of the regions upstream and downstream of the compliant panel and the inlet and outlet conditions of the flow to ensure that the resonance type of behaviours that we report below are not artifacts of the finite computational domain.

Figure 2
figure 2

Eigenvalue spectrum from global-stability analysis for wall-1 data for different levels of discretisation. (The meanings of the mode-branch labels M 1-M 5 are provided in the text.)

Full size image

3.1 Stability analysis

Herein, we present the predictions of the system eigen-analysis that are applicable after all transients from the initiation of system disturbances have either been wholly attenuated or convected away from the region of the compliant panel. The main focus is upon the findings of the global-stability analysis arising from the decomposition of Eq. (11) that leads to the eigen-problem of Eq. (12). However, we also perform local analyses wherein all perturbations are proportional to \(\exp {[\mathrm {i}}(\alpha x - \omega t )]\) in which α=α r +iα i is the complex wavenumber that arises from solving the system equations for a given complex frequency ω. Clearly, this type of analysis uses the assumption of a compliant panel that is infinitely long within a boundary layer of fixed displacement thickness determined by the value of the local Reynolds number, at the mid-chord of the panel, and its formulation only permits spatial growth (α i <0) or decay (α i >0) of system disturbances.

3.1.1 Travelling-wave flutter (TWF) branch

Using local analyses, TWF on a compliant wall of infinite extent has been shown to be a convective instability e.g. Carpenter & Garrad (1986), Carpenter & Morris (1990), Dixon et al (1994) and Lucey & Carpenter (1995). For the definition of convective and absolute instabilities, see Huerre & Monkewitz (1985, 1990) or Lucey (1998) and Lucey & Peake (2003) for the application of these concepts when ideal flow interacts with a flexible panel. Unstable TWF waves grow spatially in the downstream direction from a source of applied excitation. The instability arises from the action of the fluid flow on what are essentially structural waves, their growth caused by irreversible transfer of energy from the flow to the flexible wall that occurs when a critical layer exists within the boundary layer. In the wave-classification system of Benjamin (1963), they are denoted Class B because their activation energy (energy relative to the quiescent system state) is positive and are therefore shown to be attenuated by the action of structural damping.

For a finite panel with wall-1 data, figure 2 (see branch M 5) shows that TWF can become a global, temporally amplifying, instability that would lead to the destabilisation of the compliant panel at all spatial locations and without a continuing applied source of excitation. To understand the global destabilisation mechanism, we present in figure 3 the time-evolution of the panel deflection for the most unstable TWF-branch eigenvalue in figure 2. First, it is clearly seen that the amplitude of the mode grows with time t (non-dimensionalised using displacement thickness and free-stream flow speed). Second, it is also seen to be spatially amplified by comparing deflection amplitudes near the compliant-panel leading edge (x=1040 where the coordinate of location is non-dimensionalised using the displacement thickness) with those near its trailing edge (x=1130). Third, the global mode is a combination of two types of wave, the expected downstream-travelling TWF (as predicted by a local stability analysis) and an upstream travelling wave. It is this combination of waves on a flexible wall with fixed ends that leads to the temporal growth found for the global mode.

Figure 3
figure 3

Temporal evolution of the panel deflection for the globally most unstable mode on the TWF-branch (M 5) in figure 2.

Full size image

We now consider the effect of compliant-panel properties on the globally unstable TWF mode. Figure 4(a) and (b) respectively shows how the global eigenvalues depend upon structural damping, with coefficient D, and stiffening the wall by increasing the value of the spring-foundation coefficient, K. The former shows that the inclusion of sufficient structural damping stabilises the TWF-branch. This might be expected since TWF occurs essentially through the destabilization of what is a wall flexural wave (that exists in vacuo) and it has been categorised as a Class B wave. Stiffening the compliant panel also exercises a stabilising effect as evidenced by figure 4(b). Again, this could have been anticipated on the basis of local-stability analyses, given that in the limit of infinite stiffness the wall is rigid and therefore unable to support the flexural waves that are the source of TWF; in fact, when the compliant coating is sufficiently stiff that the speed of its structural waves exceeds that of the external flow the critical layer ceases to exist.

Figure 4
figure 4

Effect of variation to structural (a) damping and (b) stiffness on the globally unstable TWF-branch modes for wall-1 data which has the base values D=0 and K=0.473 used in figure 2.

Full size image

Finally, we show how the foregoing globally unstable TWF mode might manifest itself in a local-stability analysis. Figure 5(a) and (b) respectively shows the spatial eigen-spectrum of a local analysis conducted at the frequency of the most unstable mode on the TWF-branch and the least stable mode on the TSW-branch in figure 4(a) for various levels of structural damping; in these figures the wavenumber (α r ) of the mode appears on the horizontal axis while its spatial amplification(−ve)/decay(+ ve) rate (α i ) appears on the vertical axis. In figure 5(a), the local-stability analysis reveals an expected downstream propagating (positive α r ) TWF mode (labelled) but it also features an unstable structural mode labelled S that evidences upstream spatial growth. Thus, the global mode that contained two wave types in figure 3 may be considered to be the combined effect of the two unstable modes predicted by the local analysis. However, a local analysis alone would not be sufficient to show that these combine to yield a global instability on a panel of finite extent. Figure 5(a) also shows that structural-damping levels sufficient to eliminate the globally unstable TWF branch (see figure 4(a)) do not eliminate TWF that continues to exist as a convectively unstable mode albeit with a reduced spatial-growth rate. In practical applications of compliant panels for transition delay, this is less dangerous than a temporally unstable mode, because only very long panels would provide sufficient streamwise extent for the wave to grow to levels that might provide an alternative route to transition as found in Lucey & Carpenter (1995). The effect of structural damping on the globally stable TSW-branch is seen in figure 4(a) to be negligible. However, in the local stability analysis of figure 5(b), the spatial growth rate of the convectively unstable TSW mode is seen to be slightly increased by the inclusion of damping. Nevertheless, the compliant panel still has a stabilizing effect on TSWs as compared with a rigid wall.

Figure 5
figure 5

Local stability analysis of (a) the most unstable TWF mode and (b) the least stable TSW mode in the global stability analysis of figure 4(a) including the effects of structural damping.

Full size image

3.1.2 Tollmien–Schlichting wave (TSW) branch

Local stability analyses of laminar boundary-layer flow over a compliant coating, for example Carpenter & Garrad (1985, 1986) and Carpenter (1990), show that TSWs continue to be convective instabilities and are Class A instabilities in the energy classification of Benjamin (1963). Since their activation energy is negative, the latter predicts that the effect of structural damping is destabilising because it removes energy from the system. In the results of section 3.1.1, the choice of wall-1 properties rendered the system globally stable for the TSW-branch of modes.

Throughout this sub-section we use the properties of wall-2 (listed in table 1) to show that TSWs can combine with structural modes of the finite panel to generate global instability. Figure 6(a) shows one part of the full eigenvalue spectrum for three levels of discretisation wherein it is seen that for a fairly narrow range of mode frequencies, ω r , the temporal growth rate, ω i , is positive. We note that only the finest level of discretisation correctly captures the system behavior. Compared to the growth rates for the TWF-branch, for example see figure 2(a), the present rates are very low, being one order of magnitude smaller. However, as a temporal instability, it will come to dominate the system behavior with the passage of sufficient time.

Figure 6
figure 6

Eigenvalue spectrum from the global stability analysis using wall-2 data focusing on the TSW branch: (a) the effect of discretisation for compliant-panel non-dimensional (based upon displacement thickness) length L c=121.7 and (b) the effect of panel length on the global instability of TSW branch for Mesh 240 × 75; the broken lines connecting the discrete eigenvalues (symbols) are sketched in to highlight how growth/decay varies with increasing oscillation frequency for each panel-length case.

Full size image

The mechanism for global instability arises through the interaction of the fluid-based TSW mode and a mode of the wall structure as evidenced by figure 6(b) that shows the eigenvalue spectrum for different (non-dimensional) wall lengths. The very short panel, L c=24.3 yields a globally stable system whereas L c=48.7 is unstable over a very narrow range of oscillation frequencies. Further increases to the panel length, lead to a reduction of growth rate as the system parameters move away from those creating exact resonance.

We now show how structural damping in the panel can be used to suppress global instability of the TSW-branch modes. Figure 7(a) shows the eigenvalue spectrum of the TSW-branch when L c=121.7, for different levels of (non-dimensional) damping coefficient D. As the level of damping is increased (from zero), the eigenvalues of the unstable modes move downwards into the negative ω i plane thereby stabilizing the mode. Although local analyses, for example Carpenter & Garrad (1985), Dixon et al (1994), Lucey & Carpenter (1995) and Carpenter et al (2000), show that structural damping is spatially destabilising for TSWs in an infinite domain, in keeping with its Class A categorisation, it is its effect upon the structural mode that combines with the TSW to create the global temporal instability that results in the overall stabilization of the global mode.

Figure 7
figure 7

Effect of structural damping on (a) the global stability of the TSW-branch mode for L c =121.7 in figure 6(b), and (b) the corresponding local stability analysis of TSW.

Full size image

Figure 7(b) shows the corresponding results from a local analysis conducted at the frequency of the globally most unstable TSW-branch mode. The TSW mode appears as spatially amplifying in the downstream direction. Structural damping is destabilizing in that increases the growth rate. However, it is seen that even with damping present the compliant panel continues to exercise a stabilizing effect on the TSW as compared with its growth rate over an equivalent rigid wall. Also evident is a structural mode, labelled S, which is spatially amplifying in the upstream direction. It is relatively insensitive to damping at the relatively low (when compared to its counterpart in the TWF-branch local analysis) oscillation frequency of the global mode. It is this structural mode that combines, through a resonance mechanism, with the fluid-based TSW mode to create the globally unstable mode seen, for the two lower levels of damping used, in figure 7(a).

3.2 Transient growth

We now briefly assess whether transient growth would be a significant effect in the destabilisation of the finite compliant panels considered in this paper. We consider two types of panel, namely the potentially transition-delaying compliant coating represented by the wall-1 data in table 1 that was found to be susceptible to a global instability of the TWF branch in section 3.1.1, and a stiffer coating represented by wall-3 data in table 1 that is free from global instability. The relatively low Reynolds number, R e s=1000, is used herein.

Figure 8 shows the maximum energy growth G(t) as a function of time for the compliant properties of wall-1 and wall-3 for different levels of structural damping, and for the rigid wall case. First, it is seen that a compliant panel free from global instability (wall-3) advects marginally lower maximum energy downstream than the rigid wall. However, it is seen that the compliant panel with wall-1 properties supports very significant levels of transient growth. In the absence of structural damping, the panel experiences global instability and thus its energy time series asymptotes to infinity. When structural damping at D=0.5 is used to suppress the global instability, as described in section 3.1.1, the maximum energy advected downstream is finite but at a much higher level than that of a rigid wall. The inclusion of a higher level of damping, D=1.0, marginally reduces the peak energy level but increases the temporal width of the energy footprint. Accordingly, transient growth needs to be considered as a factor in the design of compliant panels for transition postponement even if their properties have been tailored to obviate the existence of global instabilities.

Figure 8
figure 8

Maximum growth of fluid–structure system energy G(t), as a function of time for two compliant panels with and without structural damping, D.

Full size image

4 Conclusions

We have formulated a fluid–structure interaction model for a Blasius boundary-layer flow fully coupled with the dynamics of a compliant panel with fixed leading and trailing edges embedded in an otherwise rigid wall. The resulting spatio-temporal analysis is permitted by the hybrid of computational and theoretical modelling used in our novel approach. While we have studied viscous developing flow in the absence of a pressure gradient, our methods could equally be used for the stability analysis of boundary-layer flow developing in a non-zero pressure gradient.

It has been shown that global instability of the linear FSI system can occur through two distinct mechanisms namely, (i) in the wall-based travelling-wave flutter (TWF) eigenvalue branch when its modes interact with a structural mode, and (ii) in the fluid-based Tollmien–Schlichting wave (TSW) eigenvalue branch when its modes interact with a structural mode. The former features higher temporal growth rates than the latter and can be suppressed by stiffening the compliant wall. The latter is strongly dependent upon the length of the finite panel – evidencing a resonant-type behavior with structural modes of the panel – while the former is insensitive to the panel length. Both types of global instability can be suppressed by the use structural damping but would leave the TWF and TSWs modes as convectively unstable for the compliant panel properties used herein.

These types of global instabilities have not been found before in stability studies of this FSI system. First, we remark that most studies of the system have used a local stability analysis that assumes, a priori, that TWF and TSWs over a compliant wall are convective instabilities and necessarily ignore the effects of finite panel length. Corresponding local analyses presented in the present paper show that there also exist separate upstream spatially amplifying modes in tandem with each of the TWF and TSWs predicted. It is the combination of structural and TWF/TSW modes appearing in the local analysis that combine in the present global analysis to yield temporal instability of the FSI system. Second, it might have been expected that these temporal instabilities would appear in the numerical simulations of Davies & Carpenter (1997) for the analogous system of Poiseuille flow over a compliant insert. However, the TSW-branch phenomenon was not seen because the global instability has a very low growth rate and the numerical simulations were not run for long enough for it to become apparent (Davies 2013). That the TWF-branch of global instability did not appear may be due to the forcing frequency (as the entry condition to the numerical domain) being too low in Davies & Carpenter (1997) given that it was chosen to illustrate the development of TSWs over finite compliant panels. The advantage, over numerical simulation, of the modelling developed in the present paper, is that it readily permits investigation and assessment of the full frequency spectrum of system modes.

Finally, the illustrative results of the non-modal analysis developed in this paper suggest that finite compliant panels capable of attenuating TSWs and which are free from global instability of the TWF branch with the inclusion of the necessary amount of structural damping, generate levels of transient growth that significantly exceed (by a factor of 5 for the compliant panels assessed in this paper) that which would occur for boundary-layer disturbances over a rigid or very stiff compliant wall. This could yield an alternative route to transition that would need to be considered in the design of compliant panels for transition postponement.