Global Stability Analysis of Blasius Boundary-Layer Flow over a Compliant Panel Accounting for Axial and Vertical Displacements

Abstract

A state-space method is deployed in order to investigate the global stability of the Blasius base flow over a finite compliant panel embedded between rigid upstream and downstream wall sections accounting both for axial and vertical structural displacements. It is shown that global temporal instability can occur through the resonance between the Travelling-Wave Flutter (TWF) or Tollmien-Schlichting Wave (TSW) instability and the structural modes due to the vertical motion of the compliant section, while the axial structural modes remain stable in time. Local spatial stability of the least stable global temporal TSW mode reveals that a downstream amplified axial structural mode coexists with the downstream amplified TSW mode and it is stabilized by increasing the panel stiffness and destabilized as the Reynolds number decreases.

1 Introduction

In the design of finite compliant panels for applications such as the control of boundary-layer transition, global/absolute instabilities in the fluid-structure interaction system (FSI) must be avoided if laminar flow is to be maintained (Carpenter et al. 2001). Global stability analysis of the Blasius flow over a finite spring-backed compliant panel, embedded between rigid upstream and downstream wall sections, that accounts only for vertical displacements (Tsigklifis and Lucey 2015), has revealed that global temporal instability occurs when resonance/coalescence takes place between the flow-based Tollmien-Schlichting Wave (TSW) or the wall-based Travelling-Wave Flutter (TWF) instability and the structural modes of the one-degree-of-freedom wall.

Local temporal stability and asymptotic analysis of the Couette flow past a flexible surface (Shankar and Kumaran 2002) have shown that if tangential (axial) wall motion is introduced in a spring-backed membrane wall, a new instability associated with the tangential motion appears in the high Reynolds number limit; this is due to energy transfer arising from the interaction of the fluctuating (fluid) shear stress and the axial motion of the wall at the fluid-solid interface. However, less is known about the character of this new instability—whether it is convective or absolute—and its interaction with the structural modes and the TSW or TWF instabilities in a FSI system of finite length. We therefore extend our global stability analysis of the Blasius flow over a finite spring-backed compliant panel (Tsigklifis and Lucey 2015) to account for both vertical and axial displacements of the compliant panel in order to investigate whether axial motion can induce global temporal instability in a finite system through multi-modal interactions.

Fig. 1

Schematic of the system studied

2 System Modelling

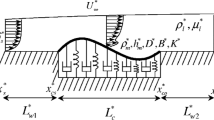
We solve the two-dimensional Navier-Stokes equations written in velocity-vorticity form and linearised for perturbations about the mean Blasius boundary-layer flow. The flow field is characterized by the Reynolds number, $Re_\mathrm{s}=\rho ^*_\mathrm{l} U^*_\mathrm{\infty } \delta ^*_\mathrm{s} / \mu ^*_\mathrm{l}$, which is defined through the displacement thickness $\delta ^*_\mathrm{s}$ at a distance $x^*_\mathrm{s}$ from the origin of the boundary layer, that is the location of the entrance of the flow domain modelled, and the undisturbed-flow velocity, $U^*_\mathrm{\infty }$ ( $\rho ^*_\mathrm{l}$ and $\mu ^*_\mathrm{l}$ are the fluid density and dynamic viscosity, respectively), Fig. 1. The flow solution is developed using a combination of vortex and source boundary—element sheets on a uniform Chebyshev Gauss-Lobatto computational grid; see (Tsigklifis and Lucey 2015). The dynamics of a plate-spring compliant wall that admits both vertical and horizontal deformations are couched in finite-difference form. Flow and wall dynamics are coupled by the kinematic boundary conditions and matching the fluid and solid shear stresses and pressure at the interface, i.e.,

$$\begin{aligned} u_x(x,0,t)+\eta _z\dfrac{\partial U_x}{\partial z}(x,0)=\dfrac{\partial \eta _x}{\partial t}, u_z(x,0,t)=\dfrac{\partial \eta _z}{\partial t} \end{aligned}$$

(1)

$$\begin{aligned} -p(x,0,t)+ \dfrac{2}{Re_\mathrm{s}} \dfrac{\partial u_z}{\partial z}(x,0,t) = M\dfrac{\partial ^2 \eta _z}{\partial t^2} + D_\mathrm{z}\dfrac{\partial \eta _z}{\partial t}+ \nonumber \\ + B\dfrac{\partial ^4 \eta _z}{\partial x^4} - T\dfrac{\partial ^2 \eta _z}{\partial x^2} + \dfrac{2}{Re_\mathrm{s}} \left( \dfrac{\partial U_x}{\partial z}(x,0) + \dfrac{\partial U_z}{\partial x}(x,0) \right) \dfrac{\partial \eta _z}{\partial x} + K \eta _z \end{aligned}$$

(2)

$$\begin{aligned} \dfrac{1}{Re_\mathrm{s}} \left( \dfrac{\partial u_x}{\partial z}(x,0,t) + \dfrac{\partial u_z}{\partial x}(x,0,t) \right) = M\dfrac{\partial ^2 \eta _x}{\partial t^2} + D_\mathrm{x}\dfrac{\partial \eta _x}{\partial t} -A\dfrac{\partial ^2 \eta _x}{\partial x^2} \end{aligned}$$

(3)

where, $\eta _x(x,t)$, $\eta _z(x,t)$, $u_x(x,z,t)$, $u_z(x,z,t)$,and p(x, 0, t) are respectively the non-dimensional plate axial and vertical displacements, disturbance velocities in the directions streamwise and normal to the flow and pressure disturbances at the wall, while $U_x(x,z)$, $U_z(x,z)$ are the streamwise and normal velocity components of the Blasius base flow. In the above expressions, the non-dimensional coefficients of inertia, damping in the streamwise and normal direction, flexural rigidity, spring-foundation stiffness, streamwise tension force per unit span and bending stiffness, are defined by $M=\rho ^*_\mathrm{m} h^*_\mathrm{m} / ( \rho ^*_\mathrm{l} \delta ^*_\mathrm{s} )$, $D_\mathrm{x}= D_\mathrm{x}^*/ ( \rho ^*_\mathrm{l} U^*_\infty )$, $D_\mathrm{z}= D_\mathrm{z}^*/ ( \rho ^*_\mathrm{l} U^*_\infty )$, $B=B^*/ ( \rho ^*_\mathrm{l} {U^*_\infty }^2 {\delta ^*_\mathrm{s}}^3 )$, $K=K^*\delta ^*_\mathrm{s} / ( \rho ^*_\mathrm{l} {U^*_\infty }^2 )$, $T=T^*/ ( \rho ^*_\mathrm{l} {U^*_\infty }^2 {\delta ^*_\mathrm{s}} )$ and $A=E^*h^*_\mathrm{m} / ( \rho ^*_\mathrm{l} {U^*_\infty }^2 {\delta ^*_\mathrm{s}} )$, respectively, with $B^*=E^*{h^*_\mathrm{m}}^3 / [ 12(1-v^2) ]$ where $E^*$, $\rho ^*_\mathrm{m}$, $h^*_\mathrm{m}$ and v are respectively the material elastic modulus, density, thickness of the plate and Poisson ratio. Finally, hinged boundary conditions are applied at the leading and trailing edges of the compliant panel.

The Fluid-Structure Interaction (FSI) system is written (see Tsigklifis and Lucey 2015) as a generalized eigenvalue problem

$$\begin{aligned} \left[ C_2 \right] \lbrace \hat{X} \rbrace = -i \omega \left[ C_1 \right] \lbrace \hat{X} \rbrace , \lbrace \hat{X} \rbrace = \lbrace \hat{\omega }, \hat{\sigma }, \hat{\eta }_x,\hat{\eta }_z, \hat{\phi }_x, \hat{\phi }_z \rbrace ^T, \end{aligned}$$

(4)

with $\hat{\phi }_x=-i \omega \hat{\eta }_x$ and $\hat{\phi }_z=-i \omega \hat{\eta }_z$. $\hat{\omega }$ and $\hat{\sigma }$ are respectively the strengths of the spanwise vorticity in the domain and of the source-sink on the boundary. If the imaginary part of an extracted eigenvalue $\omega =\omega _R + \omega _I \mathrm{i}$ is positive, instability in time occurs, whereas a negative real part indicates that disturbances decay with time. Finally, spatial local stability analysis is also conducted based on the companion matrix method (Bridges and Morris 1984), in order to validate the global numerical scheme but also to reveal the spatial characteristics of the different instability branches.

3 Results and Discussion

Investigations have considered Reynolds numbers at the entrance of the computational domain in the range $700\le Re_s \le 5000$. Figure 2 shows a typical spectrum of eigenmodes from the global-stability analysis with different levels of discretisation (to show convergence) that also includes corresponding results for a one-degree-of-freedom (vertical) compliant-wall model; $\omega _R$ and $\omega _I$ are respectively the oscillatory and amplification(+ve)/decay($-$ve) parts of the temporal eigenvalue. The additional axial structural mode is seen to be globally stable. Neither does it modify the strong TWF-resonance global instability found in our previous work (Tsigklifis and Lucey 2015), nor generate a globally unstable interaction with the TSW mode branch.

Fig. 2

Eigenvalue spectrum from global temporal stability analysis of the FSI system for $Re_s=3000$ for different levels of discretisation and comparison with the model accounting only for the vertical motion

Results of the local spatial stability analysis of the least stable global temporal TSW mode in Fig. 2 are shown in Fig. 3b; $\alpha _R$ and $\alpha _I$ are respectively the wavenumber and spatial amplification($-$ve)/decay(+ve) parts of the eigenvalue. This features the expected convectively unstable TSW (that also exists for a one-degree-of-freedom compliant-wall model) and a downstream-directed convectively unstable axial structural mode. The results in Fig. 3c and d respectively show that the latter is stabilised by increasing the elastic modulus of the plate material but is destabilised when the Reynolds number is decreased so as to increase viscous effects. These effects suggest that the instability is due to energy transfer from the mean flow to the wall caused by the interaction of fluid shear stress and axial wall motion and that the instability aligns with the corresponding phenomenon elucidated in (Shankar and Kumaran 2002) for Couette flow. The absence of an upstream directed unstable axial structural mode precludes a resonant interaction with the TSW mode to create global instability. This is in contrast to Fig. 3a wherein resonance takes place between the TWF instability and the upstream-directed unstable vertical structural mode; this mechanism is largely unaffected by the presence of the axial structural modes.

Fig. 3

Results of local spatial stability analysis. a The most unstable TWF vertical-mode resonance in Fig. 2 and b the least stable TSW mode shown with a blue arrow in Fig. 2 for different numbers of Chebyshev Gauss-Lobatto points. Effect of c the elastic modulus, $E^*$ and d the Reynolds number, $Re_s$, on the TSW and the axial structural modes, respectively

4 Conclusions

A hybrid of computational and theoretical modelling has been developed to study the global stability of the Blasius base flow over a finite compliant panel embedded between rigid upstream and downstream wall sections, accounting both for axial and vertical structural displacements. It has been demonstrated that global instability of the linear FSI system occurs due to the resonance between the vertical structural and TWF or TSW modes, while the axial structural modes are asymptotically stable in time. However, the local spatial stability of the least stable in time TSW mode shows that, besides the convectively unstable TSW, there exists a downstream-directed convectively unstable axial structural mode which is stabilized by the increase of the structural stiffness and destabilized as the Reynolds number decreases.