1 Introduction

Recently, numerous micro/nanofluidic devices such as micro-electro-mechanical systems (MEMS) and lab-on-a-chip (LOC) have been extensively used in several applications (for example, practical separation, medical diagnostics, energy harvesting, drug delivery and biochemical progress [1,2,3,4]). Fluid flow through a micro/nanochannel has entered a new phase in fluid dynamics, with applications in various micro/nanolevel transport phenomena, especially in biomedical and thermal systems [5,6,7,8]. Electro-osmotic flow (EOF) is a crucial mechanism for transporting electrolyte solution through micro/nanoscale domains in electrokinetic theory. Due to an applied electric field, a fluid transport occurs on the unbalanced free ions inside the electric double layer (EDL), which typically forms at the fluid–solid interface and this flow is basically called EOF [9, 10]. Many interesting investigations have been published on the EOF of Newtonian and non-Newtonian fluids with respect to various geometrical configurations [11,12,13,14,15].

Understanding the impact of an applied magnetic field on electrokinetic flows, which often deal with microfluidic systems containing aqueous electrolytes, is a necessary prerequisite for understanding MEMS and their fabrication [16, 17]. A few driving forces mainly used for pumping of fluids in a microfluidic channel are pressure-driven micropump, electro-osmotic pump, electromagnetohydrodynamic (EMHD) pump, etc. Among the many existing driving mechanisms, EMHD-actuated micropumps play a unique role in the transport of liquid through microfluidic channels [18, 19]. The EMHD pumping mechanism is actuated through the Lorentz force generated because of the combined effect of externally applied magnetic forces and electric fields. Over the last decade, many numerical and theoretical investigations on electromagnetic effects in various narrow fluidic domains have been reported [20,21,22].

The well-known causes for the irreversibilities within any thermal/mechanical system are heat transfer effect, magnetic/electric field, viscous dissipation, fluid friction, etc. These irreversibilities reduce the performance of the thermal system. Therefore, it is important to analyse the entropy characteristics and minimise the irreversibility losses. In any thermofluidic system, the amount of irreversibility generated can be characterised and calculated by employing the entropy generation function [23]. In microfluidic devices, minimising the entropy can offer a more reliable environment for moving charged fluids. The principle of reducing entropy production supports appropriate designs and parameter estimation for EOF systems. For the past few decades, researchers have focussed on the efficient design of micro/nanofluidic systems to improve the system performance in energy utilisation. There are important research findings that have been conducted on entropy generation with different Newtonian and non-Newtonian fluids with respect to various geometric aspects [24,25,26,27,28,29,30,31,32,33]. Xie and Jian [34] theoretically scrutinised the two-layer electro-osmotic and magnetohydrodynamic flow of two immiscible fluids in a straight microchannel. Mondal et al [35] analysed entropy generation and thermal characteristics of EMHD flow by taking Newtonian fluid with Navier-slip boundary condition at the wall of a vertical microchannel. Recently, many researchers have examined thermal energy transport and entropy generation in the literature under the influence of electro-osmotic and electromagnetic force in a microscale/nanoscale environment [36,37,38,39,40,41,42]. These studies are mostly linked to numerous EMHD numerical and analytical studies. As previously said, all these works are primarily explored using the viscous medium as a flow domain for investigating the promising potential of Newtonian fluids.

Micro/nanofluidic systems have many engineering and industrial applications, especially in transporting biofluids such as blood, plasma, sperm, serum, saliva, etc. [43,44,45] Recently, non-Newtonian fluid models have become more important in designing and manufacturing small-scale devices in electrokinetic theory. Stokes [46] introduced the concept of polar effects in continuous theory and later established the couple stress fluid (CSF) model, a non-Newtonian model. The standard Cauchy stress that distinguishes Newtonian models is defined in this model. The model’s complex rheological behaviour involves fourth-order derivative terms in the momentum transport equation. This model illustrates the full effects of couple stresses (i.e., stresses caused by the spin of microelements). Recent research on the CSF model has gained much attention in describing the rheological behaviour of the flow dynamics with respect to different geometrical environments without considering any imposed electric field [47,48,49] and including applied electric field effects [50,51,52,53]. The electromagnetic interaction force with couple stress effects is taken into account to examine the thermal transport and entropy production rate of the system in our study, which has been sparsely reported in the literature.

Based on the above investigations, it is intended to analyse hydrodynamic, thermal transport and irreversibility analysis of EMHD flow of CSF through a micro/nanofluidic channel. The analytical solutions for EMHD flow velocity and energy transport in the flow domain are presented with suitable boundary conditions. The results of the present study (velocity and temperature profiles) are validated with the existing results. The dependence of EMHD flow velocity, energy distribution and entropy generation on couple stress parameter, Hartmann number and other active parameters present in this investigation will be illustrated graphically. The influence of a couple stress parameter on EMHD flow velocity, temperature profile and entropy distribution is the prime concern of this work. Moreover, the present investigation reveals that the magnitude of dimensionless temperature and entropy generation have the same trend with couple stress parameter.

2 Present geometric and model description

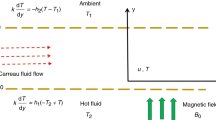
In this article, we choose the flow domain as a micro/nanofluidic channel of length L,  width W and height 2H filled with a non-Newtonian (couple stress fluid) electrolyte solution as represented in figure 1. The width and height of the microchannel are very much smaller than its length, i.e. \(2H<W\ll L\). A uniform zeta potential \(\left( \zeta \right) \) is considered at the channel walls. The imposed axial and transverse/lateral electric field strength \({\textbf {E}}=\left( {E_x}, {E_y}, 0\right) \) is considered along with the axial (flow) and transverse directions, respectively. The applied constant and uniform magnetic field \({\textbf {B}}=\left( 0,0,{B_0}\right) \) is considered along the normal direction of the flow. Furthermore, we have assumed a uniform surface zeta potential and magnetic field, which does not affect the electric potential distribution throughout the cross-section of the microchannel [19]. Constant and uniform heat flux \(q''_w\) is applied at the walls of the microchannel. Moreover, it is assumed that the fluid flow is driven by the combined electromagnetic force in the desired direction of a micro/nanochannel.

Fig. 1
figure 1

Schematic representation of the present model for the combination of electric, pressure and magnetic driven flow through a horizontal microchannel.

Full size image

2.1 Details of the theoretical solution of a steady EMHD flow and potential distribution inside the channel confinement

We now begin this section with details of the electric potential distribution in the channel. The well-known Poisson equation in the field of electrokinetic theory describes the net ionic/electric charge density inside the EDL and its mathematical representation is given by [21, 22]

$$\begin{aligned} \dfrac{{\mathrm {d}^{2}}{\psi }'}{\mathrm{d}{{{z}'}^{2}}}=-\frac{{\rho }_{e}}{\varepsilon }, \end{aligned}$$
(1)

where \({\psi }'\) is the electric potential, \(\rho _e\) is the net charge density and \(\varepsilon \) is the dielectric constant of the electrolyte solution.

For a symmetric electrolyte solution, the ionic charge density can be represented using Boltzmann distribution [10], i.e. \(\displaystyle {{\rho }_{e}}\left( {{z}'} \right) =-2 {{n}_{0}} {{z}_{0}} {e} \sinh \left( {{z}_{0} {e} {\psi }'}/{{k}_{\mathrm {B}} {T}_{ab}}\right) .\) We consider that the electric potential is much smaller than the thermal potential, i.e., \(\displaystyle {{z}_{0} {e} {\psi }'}\le {{k}_{\mathrm {B}} {T}_{ab}}.\) Therefore, the modified form of eq. (1) by applying Debye–Hückel linear approximation \(\displaystyle \left( \sinh \left( {{z}_{0} e {\psi }'}/{{k}_{\mathrm {B}} {T}_{ab}}\right) \approx {{z}_{0} e {\psi }'}\right. \)\(\left. /{{k}_{\mathrm {B}} {T}_{ab}} \right) \) takes the following form:

$$\begin{aligned} \dfrac{{\mathrm {d}^{2}}{\psi }'}{\mathrm {d}{{{z}'}^{2}}}={\kappa }^{2} {\psi '}, \end{aligned}$$
(2)

where \({{n}_{0}}\) is the ion bulk concentration of the solution, e is the free electron charge, \({{z}_{0}}\) is the valence, \({{k}_{\mathrm {B}}}\) is the Boltzmann constant, \({{T}_{ab}}\) is the absolute temperature and \(\kappa ={{( {2{{n}_{0}}{{e}^{2}}{{z}_{0}}^{2}}/{\varepsilon {{k}_{\mathrm {B}}}{{T}_{ab}}})}^{{}^{1/2}}}\) is the inverse of Debye length or Debye–Hückel parameter.

The suitable boundary conditions for the distribution of electrical potential in the EDL are considered in the following way:

$$\begin{aligned} {{\left. \frac{\mathrm {d}{\psi }'}{\mathrm {d}{z}'} \right| }_{{z}'=0}}=0 \,\, and \,\, {{\left. \,{\psi }' \right| }_{{z}'=H}}=\zeta . \end{aligned}$$
(3)

Therefore, the net ionic charge density \({{\rho }_{e}}\) in the microchannel can be evaluated using eqs (1)–(3)

$$\begin{aligned} {{\rho }_{e}}\left( {{z}'} \right) =-\varepsilon {{\kappa }^{2}}\zeta \, {\cosh \left( \kappa {z}' \right) }/{\cosh \left( \kappa {H}\right) }. \end{aligned}$$
(4)

The existence of an applied magnetic field may alter the ionic distribution. However, the electric potential will then be redistributed throughout the channel. Due to the small amount of electromagnetic induction, the effect of the magnetic field on the EDLs can be ignored [19].

After obtaining the electrical potential inside a micro/nanochannel, we would like to present the mathematical approach for EMHD flow field. The following equations govern the transport equations for the EMHD flow of CSF in the flow domain [52, 53]:

Continuity equation

$$\begin{aligned} \nabla \cdot {\textbf {q}}=0 \end{aligned}$$
(5)

and momentum equation

$$\begin{aligned}&\rho \left[ \frac{\partial {\textbf {q}}}{\partial t'}+\left( {\textbf {q}}\cdot \nabla \right) {\textbf {q}} \right] \nonumber \\&\quad =\frac{1}{2}\left( \nabla \times (\rho {\textbf {c}})\right) -\nabla {\textbf {P}}-\mu \left( \nabla \times \nabla \times {\textbf {q}}\right) \nonumber \\&\qquad -\eta \left( \nabla \times \nabla \times \nabla \times \nabla \times {\textbf {q}}\right) \nonumber \\&\qquad +\left( \lambda +2\mu \right) \nabla \left( \nabla \cdot {\textbf {q}}\right) +\mathbf {F}, \end{aligned}$$
(6)

where \({\textbf {q}}\) is the velocity field, \(\rho \) is the fluid density, \((\lambda ,\mu )\) are the viscosity coefficients, \({\textbf {c}}\) is the body couple per unit mass, \({\textbf {P}}\) is the pressure, \(\eta \) is the couple stress viscosity coefficient and \({\textbf {F}}\) is the body force term which consists of both electrical force and Lorentz force and can be represented as \({\textbf {F}}={{\rho }_{e}}\,{\textbf {E}}+{\textbf {J}} \times {\textbf {B}}\). Here, \({\textbf {J}} =\sigma \,\left( {\textbf {E}}+{\textbf {q}}\times {\textbf {B}}\right) \) is the current density vector and \(\sigma \) is the electrical conductivity of the fluid.

A few additional assumptions are specified now for the present investigation apart from the above-mentioned assumptions:

  • The flow is regarded to be thermally fully developed, laminar, steady and incompressible, while the CSF model describes the non-Newtonian characteristics.

  • The physical dimensions of the microchannel \(2H<W\ll L\) show that the microchannel’s height and width are smaller than the microchannel’s length. This turns the study into the unidirectional flow. Therefore, the transient EMHD flow velocity in the flow domain can be expressed as \({\textbf {q}}=\left( {u}'({z}'),0,0\right) \).

  • We exclude the entire couple stress tensor analysis and the body couple term components from this study.

  • A low magnetic Reynolds number is considered, which is one of the important assumptions in the magnetohydrodynamic analysis (\(\displaystyle \text {Re}_{m}=\sigma _{e} \mu _{e} u_{\mathrm {ref}}/l_{\mathrm {ref}}\)) where \(u_{\mathrm {ref}}\) is the reference velocity scale, \(l_{\mathrm {ref}}\) is the reference length scale and \(\mu _{e}\) is the magnetic permeability. The order of \(\text {Re}_{m}\) is about \(10^{-5}\) \(\displaystyle \left( \text {Re}_{m} \ll 1\right) \) in a typical micro/nanochannel flow. Hence, the induced magnetic field eventually becomes independent of the flow velocity.

The modified form of momentum conservation eq. (6) using the above assumptions and eq. (4) becomes

$$\begin{aligned}&-\frac{\mathrm {\mathrm {d}}p}{\mathrm {d}{x}'}+\mu \,\frac{{{\mathrm {d}}^{2}}{u}'}{\mathrm {d} {{{{z}'}}^{2}}}-\eta \frac{{{\mathrm {d} }^{4}}{u}'}{\mathrm {d} {{{{z}'}}^{4}}}-{{\kappa }^{2}}\,\varepsilon {{E}_{x}}\zeta \, \nonumber \\&\times \frac{\cosh \left( \kappa {z}' \right) }{\cosh \left( \kappa H \right) }+\sigma {{E}_{y}}{{B}_{0}}-\,{{\sigma }_{e}}{{B}^2_{0}}{u}'=0. \end{aligned}$$
(7)

The detailed derivation of the body force term is presented in the Appendix. The physically relevant boundary conditions for steady EMHD flow pattern in the flow domain are given by

$$\begin{aligned} {{\left. {u}'\left( {z}'\right) \right| }_{{z}'=\pm 1}}=0\quad and \quad \, {{\left. \frac{{{\mathrm {d} }^{2}}{u}'}{\mathrm {d} {{{{z}'}}^{2}}} \right| }_{{z}'=\pm 1}}=0. \end{aligned}$$
(8)

To reduce the physical quantities appearing in eq. (7), we consider the following non-dimensional variables and suitable parameters in this analysis:

$$\begin{aligned}&z=\frac{{{z}'}}{H},\,u=\frac{{{u}'}}{{{U}_{HS}}},\,\textit{K} =\kappa H,\,S=\frac{{{E}_{y}}H}{{{U}_{HS}}}\,\sqrt{\frac{\sigma }{\mu }} \nonumber \\&\quad and \nonumber \\&Ha={{B}_{0}}\,H\,\sqrt{\frac{\sigma }{\mu }}, \end{aligned}$$
(9)

where \(\displaystyle {{U}_{HS}}={-\varepsilon {{E}_{x}}\,\zeta }/{\mu }\;\) is the reference electro-osmotic velocity, K is the electrokinetic width of the EDL, S is the dimensionless transverse electric field parameter and Ha is the Hartmann number.

Applying the above non-dimensional quantities to eqs (7) and (8), we get the non-dimensional form of momentum transport and boundary conditions as follows:

$$\begin{aligned}&\Omega +\frac{{{\mathrm {d} }^{2}}u}{\mathrm {d} {{z}^{2}}}-\frac{1}{{{\gamma }^{2}}}\,\frac{{{\mathrm {d} }^{4}}u}{\mathrm {d} {{z}^{4}}}-{{K}^{2}}\,\frac{\cosh \left( Kz \right) }{\cosh \left( K \right) }\, \nonumber \\&\quad +S\,Ha-\,H{{a}^{2}}\,u=0, \end{aligned}$$
(10)
$$\begin{aligned}&{{\left. u \right| }_{z=\pm 1}}=0 \quad and \quad {{\left. \frac{{{\mathrm {d} }^{2}}u}{\mathrm {d} {{z}^{2}}} \right| }_{z=\pm 1}}=0, \end{aligned}$$
(11)

where

$$\begin{aligned}\displaystyle \Omega =\frac{\Delta P{{H}^{2}}}{\mu \,{{U}_{HS}}}\end{aligned}$$

is the dimensionless pressure gradient parameter,

$$\begin{aligned}\displaystyle \gamma =\sqrt{\frac{\mu \,{{H}^{2}}}{\eta }}\quad \text {is the couple stress parameter.} \end{aligned}$$

Therefore, the EMHD flow velocity in the flow domain can be obtained using the aforementioned boundary conditions represented in eq. (11) and is given by

$$\begin{aligned} u\left( z \right)= & {} {{C}_{1}}\,\cosh \left( {{\alpha }_{1}}z \right) +{{C}_{2}}\,\cosh \left( {{\alpha }_{2}}z \right) \nonumber \\&+{{C}_{3}}\,\cosh \left( Kz \right) +{{C}_{4}}, \end{aligned}$$
(12)

where

$$\begin{aligned}&\displaystyle {{\alpha }_{1}}=\pm \sqrt{\frac{{{\gamma }^{2}}-\sqrt{{{\gamma }^{4}}-4\,{{\gamma }^{2}}H{{a}^{2}}}}{2}},\\&\displaystyle {{\alpha }_{2}}=\pm \sqrt{\frac{{{\gamma }^{2}}+\sqrt{{{\gamma }^{4}}-4\,{{\gamma }^{2}}H{{a}^{2}}}}{2}},\\&\displaystyle {{C}_{1}}=\frac{{{\delta }_{2}}-{{\delta }_{1}}\,{{\alpha }_{2}^{2}}}{\left( {{\alpha }^{2}_{2}}-{{\alpha }_{1}^{2}} \right) \,\cosh \left( {{\alpha }_{1}} \right) },\\&\displaystyle {{C}_{2}}=\frac{{{\delta }_{1}}\,{{\alpha }_{1}^{2}}-{{\delta }_{2}}}{\left( {{\alpha }_{2}^{2}}-{{\alpha }_{1}^{2}} \right) \,\cosh \left( {{\alpha }_{2}} \right) },\\&\displaystyle {{C}_{4}}=\frac{\Omega +S\,Ha}{H{{a}^{2}}},\\&\displaystyle {{C}_{3}}=\frac{{{\gamma }^{2}}\,{{K}^{2}}}{\left( {{K}^{4}}-{{\gamma }^{2}}\,{{K}^{2}}+{{\gamma }^{2}}\,H{{a}^{2}} \right) \,\left( \cosh \left( K \right) \right) },\\&\displaystyle {{\delta }_{1}}={{C}_{3}}\,\cosh \left( K \right) +{{C}_{4}},\\&\displaystyle {{\delta }_{2}}={{C}_{3}}{{K}^{2}}\,\cosh \left( K \right) .\end{aligned}$$

2.2 Exact solution of the energy distribution in the channel

The governing equation for thermal energy transfer in the flow domain for the present analysis can be represented as follows:

$$\begin{aligned} \rho \,{{c}_{p}}\,\left( \frac{\partial {T}'}{\partial t}+{\textbf {q}}\cdot \nabla {T}' \right) ={{k}_{f}}\,{{\nabla }^{2}}{T}'+\mu \,\Phi +\frac{J\cdot J}{\sigma _{e}}, \end{aligned}$$
(13)

where \({T}'\) is the local temperature of the fluid, \({{c}_{p}}\) is the specific heat at constant pressure, \({{k}_{f}}\) is the thermal conductivity of the fluid, \(\sigma _{e}\) is the liquid electrical resistivity, J is the rate of volumetric heat generation due to Joule heating and \(\Phi \) is the viscous dissipation.

We assume that the EMHD flow is steady, thermally fully developed with constant properties within the microchannel. The unsteady energy equation turns into the following form [22, 42]:

$$\begin{aligned}&\rho \,{{c}_{p}}\,{u}'\,\frac{\partial {T}'}{\partial {x}'}={{k}_{f}}\left( \frac{{{\partial }^{2}}{T}'}{\partial {{{{z}'}}^{2}}}+\frac{{{\partial }^{2}}{T}'}{\partial {{{{x}'}}^{2}}} \right) \nonumber \\&\quad +\mu \,{{\left( \frac{\mathrm {d}{u}'}{\mathrm {d}{z}'} \right) }^{2}}+\eta \,{{\left( \frac{{{\mathrm {d}}^{2}}{u}'}{\mathrm {d}{{{{z}'}}^{2}}} \right) }^{2}} \nonumber \\&\quad +\sigma ( {{E}_{x}}^{2}+{{E}_{y}}^{2} )+\sigma ( {{B}^2_{0}}{{{{u}'}}^{2}}-2{{E}_{y}}{{B}_{0}}\,{u}' ). \end{aligned}$$
(14)

The penultimate term in the right-hand side of eq. (14) arises due to the combined electro and magnetic effects.

For the thermally fully developed flow, we have

$$\begin{aligned} \displaystyle \frac{\partial {T}'}{\partial {x}'}=\frac{\partial {{{{T}_w'}}}}{\partial {x}'}=\frac{\partial {{{{T}_m'}}}}{\partial {x}'}=\mathrm {constant} \end{aligned}$$

and

$$\begin{aligned} \displaystyle \frac{{{\partial }^{2}}{T}'}{\partial {{{{x}'}}^{2}}}=0. \end{aligned}$$

Here, \(\displaystyle {{{T}_w'}_{}}\) and \(\displaystyle {{{T}_m'}_{}}\) are the wall and the bulk mean temperatures, respectively.

The modified temperature distribution equation can be written as

$$\begin{aligned}&\rho \,{{c}_{p}}\,{u}'\,\frac{\partial {T}'_{m}}{\partial {x}'}\nonumber \\&={{k}_{f}} \left( \frac{{{\mathrm {d} }^{2}}{T}'}{\mathrm {d} {{{{z}'}}^{2}}} \right) +\mu \,{{\left( \frac{\mathrm {d}{u}'}{\mathrm {d}{z}'} \right) }^{2}}+\eta \,{{\left( \frac{{{\mathrm {d}}^{2}}{u}'}{\mathrm {d}{{{{z}'}}^{2}}} \right) }^{2}}\nonumber \\&\quad +\sigma ( {{E}^2_{x}}+{{E}^2_{y}}+{{B}^2_{0}}\,{{{{u}'}}^{2}}-2{{E}_{y}}{{B}_{0}}{u}' ). \end{aligned}$$
(15)

To solve eq. (15), we adopt the following thermal boundary conditions:

$$\begin{aligned} {{\left. \,\,{T}' \right| }_{{z}'=H}}={{{{T}_w'}}} \quad and \quad \, {{\left. \frac{\mathrm {d}{T}'}{\mathrm {d}{z}'} \right| }_{{z}'=0}}=0. \end{aligned}$$
(16)

An overall thermal energy balance for an elemental control volume can written as

$$\begin{aligned}&2\,\rho \,{{c}_{p}}\,H\,{{{u}_m'}}\,\mathrm {d}{{{T}_m'}}\nonumber \\&\quad =2\,{{q''_{w}}}\, \mathrm {d}{x}'+2\sigma \,( {{E}_{x}}^{2}+{{E}_{y}}^{2} )\,H\,\mathrm {d}{x}'\nonumber \\&\quad +\sigma \int _{-H}^{H}{( {{B}_{0}}^{2}\,{{{{u}'}}^{2}}-2\,{{E}_{y}}\,{{B}_{0}}\,{u}' )\mathrm {d}{z}'\,\mathrm {d}{x}'}\nonumber \\&\quad +\mu \,\int _{-H}^{H}{{{\left( \frac{\mathrm {d}{u}'}{\mathrm {d}{x}'} \right) }^{2}}}\mathrm {d}{z}'\,\mathrm {d}{x}', \end{aligned}$$
(17)

where

$$\begin{aligned} \displaystyle {{{u}_m'}}=\frac{1}{2\,H}\int _{-H}^{H}{{u}'\,\mathrm {d}{z}'} \end{aligned}$$

is the axial mean velocity. The constant average temperature gradient \( {\mathrm {d}{{{{T}_m'}}}}/{\mathrm {d}{x}'}\) can be represented from eq. (17) as

$$\begin{aligned} \frac{\mathrm {d}{{{{T}_m'}}}}{\mathrm {d}{x}'}=\frac{1}{\rho \,{{c}_{p}}}\,M=\ constant, \end{aligned}$$
(18)

where

$$\begin{aligned}&M=\frac{1}{2\,H\,{u}'}\left[ 2\,{{q''_{w}}}+2\sigma \left( {{E}_{x}}+{{E}_{y}} \right) \,H\right. \\&\quad \left. +\sigma \,{{B}_{0}}^{2}A+\mu \,B \right] -2\,\sigma \,{{E}_{y}}\,{{B}_{0}} \end{aligned}$$

and the coefficients

$$\begin{aligned}&A=\int _{-H}^{H}{{{{{u}'}}^{2}}}\mathrm {d}{z}' \\&\quad \mathrm {and}\\&B=\int _{-H}^{H}{{{\left( \frac{\mathrm {d}{u}'}{\mathrm {d}{z}'} \right) }^{2}}\mathrm {d}{z}'}. \end{aligned}$$

Introducing the following non-dimensional variables:

$$\begin{aligned}&T =\frac{{T}'-{{{{T}_w'}}}}{{{{q}''_{w}}\,H}/{{{k}_{f}}}\;},Br=\frac{\mu \,{{U}_{HS}^{2}}}{{{q}''_{w}}\,H}, \nonumber \\&{{S}_{x}}=\frac{\sigma {{E}^2_{x}}\,H}{{{q}''_{w}}}\,\, and \,\, {{S}_{y}}=\frac{\sigma {{E}^2_{y}}\,H}{{{q}''_{w}}}, \end{aligned}$$
(19)

where \({{S}_{x}}\) and \({{S}_{y}}\) are the Joule heat parameters and Br is the Brinkman number. The dimensionless temperature distribution within the channel can be obtained from eq. (17) using the aforementioned non-dimensional variables and it is represented as follows:

$$\begin{aligned}&\frac{{{\mathrm {d}}^{2}}T }{\mathrm {d}{{z}^{2}}}=-Br\,{{\left( \frac{\mathrm {d}u}{\mathrm {d}z} \right) }^{2}}-\frac{Br}{{{\gamma }^{2}}}\,{{\left( \frac{{{\mathrm {d}}^{2}}u}{\mathrm {d}{{z}^{2}}} \right) }^{2}} \nonumber \\&\quad -Br\,H{{a}^{2}}{{u}^{2}}-( {{S}_{x}}+{{S}_{y}} ) \nonumber \\&\quad +\left[ 2 Ha Br S+\left( \frac{2+2( {{S}_{x}}+{{S}_{y}} )+\beta }{{{\beta }_{1}}} \right) \right] u, \end{aligned}$$
(20)

where

$$\begin{aligned}{{\beta }_{1}}=\int _{-1}^{1}{u\,\mathrm {d}z}, \quad {{\beta }_{2}}=\int _{-1}^{1}{{{u}^{2}}\,\mathrm {d}z},\quad {{\beta }_{3}}=\int _{-1}^{1}{{{\left( \frac{\mathrm {d}u}{\mathrm {d}z} \right) }^{2}}\,\mathrm {d}z}\end{aligned}$$

and

$$\begin{aligned}\beta =-2Br\,Ha\,S\,{{\beta }_{1}}+H{{a}^{2}}\,Br\,{{\beta }_{2}}+Br\,{{\beta }_{3}}. \end{aligned}$$

The corresponding boundary conditions for solving the above modified temperature distribution are given by

$$\begin{aligned} {{\left. T \right| }_{z=1}}=0 \quad and \quad {{\left. \frac{\mathrm {d} T }{\mathrm {d}z} \right| }_{z=0}}=0. \end{aligned}$$
(21)

Therefore, the solution of dimensionless temperature distribution eq. (20) using the boundary conditions mentioned in eq. (21) is given by

$$\begin{aligned} T\left( z \right) =f\left( z \right) -{{\left. f\left( z \right) \right| }_{z=1}}, \end{aligned}$$
(22)

where the function \(f\left( z \right) \) is evaluated using the MATHEMATICA software and we do not include \(f\left( z \right) \) expression in this investigation.

The Nusselt number Nu is one of the most important dimensionless heat transfer parameters which can be calculated as follows:

$$\begin{aligned} Nu=\frac{{{q}''_{w}}\,H}{{{k}_{f}}\left( {{{{T}_w'}}}-{{{{T}_m'}}}\right) }, \end{aligned}$$
(23)

where

$$\begin{aligned} {{{T}'}_{m}}=\frac{\int _{-1}^{1}{{T}'\!\left( {{z}'} \right) \,{u}'\left( {{z}'} \right) \,\mathrm {d}{z}'}}{\int _{-1}^{1}{{u}'\!\left( {{z}'} \right) \,\mathrm {d}{z}'}} \end{aligned}$$

is the mixed-mean temperature of the fluid. Using the dimensionless temperature profile (eq. (22)), we obtain the non-dimensional form of \({{{T}_m'}}\) as

$$\begin{aligned} {{T }_{m}}=\frac{\int _{-1}^{1}{T\left( z \right) \,u\left( z \right) \,\mathrm {d}z}}{\int _{-1}^{1}{u\left( z \right) \,\mathrm {d}z}}={{k}_{f}}\frac{\left( {{{{T}_m'}}}-{{{{T}_w'}}} \right) }{{{q}''_{w}}\,H}. \end{aligned}$$
(24)

The dimensionless expression for the Nusselt number can be obtained using eqs (23) and (24) and it is defined as follows:

$$\begin{aligned} Nu=-\frac{1}{{{T}_{m}}}. \end{aligned}$$
(25)

2.3 Entropy generation analysis

We next focus on getting the entropy production rate inside the channel after obtaining the EMHD flow velocity and temperature profile in the flow domain. Based on the aforementioned steady-state EMHD velocity and temperature transport, the dimensional representation of the volumetric entropy generation within the system for the present analysis is given by [22, 37]

$$\begin{aligned}&{{\langle {S}'\rangle }}=\frac{{{k}_{f}}}{{{{{T}'}}^{2}}}\,{{\left( \frac{\partial {T}'}{\partial {z}'} \right) }^{2}}\nonumber \\&\quad +\frac{{{\sigma }_{e}}}{\left| {{T}'} \right| }\,( {{E}_{x}^{2}}+{{E}_{y}^{2}})+\frac{{{\sigma }_{e}}}{\left| {{T}'} \right| }\,( 2{{E}_{y}}{{B}_{0}}\,{u}' )\nonumber \\&\quad +\frac{{{\sigma }_{e}}}{\left| {{T}'} \right| }\,( {{B}_{0}}^{2}\,{{{{u}'}}^{2}} ) +\left[ \frac{\mu }{\left| {{T}'} \right| }\, {{\left( \frac{\mathrm {d}{u}'}{\mathrm {d}{z}'} \right) }^{2}}+\frac{\eta }{\left| {{T}'} \right| }\,{{\left( \frac{{{\mathrm {d}}^{2}}{u}'}{\mathrm {d}{{{{z}'}}^{2}}} \right) }^{2}} \right] , \nonumber \\ \end{aligned}$$
(26)

where \({\langle {S}'\rangle }\) is the dimensional entropy generation. The first term on the R.H.S. represents the irreversibility emerging from heat transfer in the fluid; the second and third terms represent the irreversibility generation from the Joule heating effect and electrical and magnetic field interaction. The fourth term brings up the irreversibility from the applied magnetic field, while the final term represents the irreversibility associated with the viscous dissipation effect.

The non-dimensional representation of entropy generation rate can be obtained by using the characteristic entropy transfer rate \(( {{{k}_{f}}}/{{{H}^{2}}} )\).

$$\begin{aligned}&{\langle {S}\rangle }=\frac{1}{{{\left( T +{{T}_{0}} \right) }^{2}}}\,{{\left( \frac{\mathrm {d}T }{\mathrm {d}z} \right) }^{2}}+\frac{1}{\left| T +{{T}_{0}} \right| }( {{S}_{x}}+{{S}_{y}} )\nonumber \\&\quad +\frac{1}{\left| T +{{T}_{0}} \right| }\left( 2\,Br\,Ha\,S\,u \right) +\frac{1}{\left| T +{{T}_{0}} \right| }( Br\,H{{a}^{2}}\,{{u}^{2}} ) \nonumber \\&\quad +\frac{1}{\left| T +{{T}_{0}} \right| }\left[ Br\,{{\left( \frac{\mathrm {d}u}{\mathrm {d}z} \right) }^{2}}+\frac{Br}{{{\gamma }^{2}}}\,{{\left( \frac{{{\mathrm {d}}^{2}}u}{\mathrm {d}{{z}^{2}}} \right) }^{2}} \right] , \end{aligned}$$
(27)

where

$$\begin{aligned} {{T}_{0}}=\frac{{{{{T}_w'}}}\,{{k}_{f}}}{{{q}''_{w}}\,H} \end{aligned}$$

is a constant. Another important parameter that can determine the irreversibility distribution in the channel is the Bejan number and it is defined as follows:

$$\begin{aligned} Be=\frac{\frac{1}{{{\left( T +{{T}_{0}} \right) }^{2}}}\,{{\left( \frac{\mathrm {d} T }{\mathrm {d}z} \right) }^{2}}}{{\langle {S}\rangle }}. \end{aligned}$$
(28)

3 Model validation

Before proceeding with the significance of base parameters (couple stress parameter \(\left( \gamma \right) \), Hartmann number \(\left( Ha\right) \), transverse electric field parameter \(\left( S\right) \), Brinkman number \(\left( Br\right) \)) on EMHD flow velocity, temperature and entropy generation, it is essential to compare/validate our present model results with the existing/reported results in the literature. It is worth mentioning that Chakraborty et al [21] reported the thermal analysis of electromagnetic flow of Newtonian fluid through a narrow fluidic channel. Figure 2 shows a comparison of the present analytical EMHD flow velocity and the existing results of Chakraborty et al [21]. A large value of couple stress parameter, say \(\gamma =50,\) is considered in this study for comparing our results and it signifies the nature of the Newtonian viscous fluid. Further, other parameters for the same are considered as follows: \(K=4,\,Ha=1\) and \(\Omega =1\). A perfect agreement is identified in figure 2a between the current steady EMHD flow velocity and the electromagnetic flow velocity reported by Chakraborty et al [21]. Moreover, verifying the exact solution of the temperature calculated in this study is essential. To validate our energy transport distribution in the microfluidic channel, we compare the present temperature profile (see figure 2b) for \(K=20,\,Ha=1,\,Br=0.01\) and \(\Omega =1\)with Jian [22]. It is apparent from figure 2b that the temperature profiles of the current study and the analytical temperature obtained by Jian [22] demonstrate a strong agreement.

Fig. 2
figure 2

The validation of the present model. (a) Comparison of the current theoretical EMHD flow velocity with Chakraborty et al [21] and (b) comparison of the current analytical temperature distribution with Jian [22].

Full size image

4 Results and discussion

4.1 Parametric selection

After verifying the present model results with the reported results, we next focus on fixing the ranges of the essential parameter values. The most important selective parameters which govern the transport characteristics for EMHD flow velocity, temperature and irreversibility in the microchannel are as follows: couple stress parameter \(\left( \gamma \right) \), Brinkman number \(\left( Br\right) \), Hartmann number \(\left( Ha\right) \), Nusselt number \(\left( Nu\right) \), transverse electric field parameter \(\left( S\right) \) and Bejan number \(\left( Be\right) \). In the present investigation, to achieve \(O\!\left( Ha\right) \sim 0\)–10 [20,21,22], we consider that the viscosity of the fluid is \(\mu \sim {{10}^{-3}}\)–\(1.5\times {{10}^{-3}}\) \(\text {Pa s}\), the order of half-height of the channel is \(H\sim 10\)–500 \(\mu \text {m}\), electrical conductivity is \(\sigma \sim 2.2\times {{10}^{-4}}\)–\({{10}^{4}}\) \(\text {S}/\text {m}\) and the range of magnitude of the applied magnetic field is \({{B}_{0}}\sim 0.01\)–6 \(\text {T}\). In addition, the lateral electric field has the order \(O( {{E}_{y}})\sim 0\)–30 \(\text {V}/\text {m}\) and the reference electro-osmotic velocity has the order \(O\left( {{U}_{HS}} \right) \sim 100\) \(\mu \)\(\text {m}/\text {s}\). Therefore, the range of parameter \(O\left( S \right) \sim 0-6\times {{10}^{3}}\) [20,21,22] can be achieved. The range of the couple stress parameter \(\gamma \sim 0.5\)–10 [48, 52, 53] and the range of Brinkman number \(Br\sim 0\)–0.1 [21, 22] are considered in this research. Other dimensionless parameters obtained in this study are determined by analysing widely available literature [21, 22]. Unless otherwise mentioned, \(K=20,\,\Omega =1\) and \(S_{x}+S_{y}=1\).

The practical/experimental range of appropriate dimensionless flow-driven parameters has been mentioned. The following sections will explain how these parameters affect flow velocity, temperature and entropy generation distributions.

4.2 Effect of couple stress parameter on EMHD flow velocity

The impact of \(\gamma \) on the dimensionless EMHD flow velocity in the channel at two different values of Ha (\(Ha=0.5\) and 10) is depicted in figure 3. When \(H =0.5\), an augmentation in flow velocity with \(\gamma \) in the channel confinement is observed (see figure 3a). This is due to the important effect of a combined applied electromagnetic force, as the non-Newtonian parameter \(\gamma \) in the flow domain always attempts to oppose the fluid flow moment. However, when \(Ha=10\), first the EMHD flow velocity grows towards the channel’s wall/boundary and gradually decreases towards the microchannel’s centre (see figure 3b). It can be elucidated that, in the case of large Ha the opposing/retarding force term (\(-\,\sigma {{B}^2_{0}}{u}'\)) plays a dominant role in declining the flow velocity near the channel’s centre line compared to the driving/aiding force (\(\sigma {{E}_{y}}{{B}_{0}}\)) which is present in eq. (7).

Fig. 3
figure 3

The variation of non-dimensional EMHD flow velocity for diverse values of \(\gamma \) when (a) \(Ha=0.5\) and (b) \(Ha=10\) \(\left( K=20, S=1, \Omega =1\right) \).

Full size image

4.3 Effect of Hartmann number on temperature distribution

Figure 4 elucidates the impact of Ha on the non-dimensional temperature distribution. The variations of temperature profile with small \(\left( Ha\le 1\right) \) and large \(\left( Ha>1\right) \) values of Ha are described in the absence \(\left( S=0\right) \) and the presence \(\left( S=10\right) \) of a transverse electric field in figures 4a–4b and figures 4c–4d, respectively. The case of \(S=0\) describes the only nature of the axial electric field, which is applied along the axial/flow direction of the channel by the imposed electric current. For \(S=0\), the variations in the temperature distribution with increasing values of Ha, i.e., smaller \(Ha\le 1\) and higher \(Ha>1\) are decreasing as depicted in figures 4a and 4c. The reason for decreasing temperature distribution in the flow domain is that the augmenting magnitude of Ha reduces the flow velocity, especially in the absence of an imposed electric field, which can in turn lower the convective energy transport in the channel. Therefore, the diffusive energy transport can be increased because of the constant temperature at the wall. Also, the magnitude of \(\left( {{T}'_{w}}-{T}'\right) \) decreases consistently, resulting in a decrease in the fluid’s local temperature. Thus, the dimensionless temperature decreases with increasing values of Ha for \(S=0.\) However, when \(S=10\), the thermal distribution increases for smaller values of Ha and then decreases for grater values of Ha, as shown in figures 4b and 4d. When \(S=10\), the supporting and opposing forces coexist in the flow domain. For \(Ha\le 1\), the convective energy transfer is more dominant than the thermal diffusion, resulting in the increase of \(\left( {T}'_{w}-{T}' \right) \). Subsequently, this leads to the enhancement in the temperature in the case of smaller values of Ha as depicted in figure 4b. Further, it can be identified from figure 4d that the thermal energy decelerates for higher values of Ha. This is mainly because the influence of supporting/driving magnetic force succeeds over the effect of opposing/retarding magnetic force.

Fig. 4
figure 4

The variation of temperature profile for diverse values of Ha when (a) \(S=0\), (b) \(S=10, \) (c) \(S=0\) and (d) \(S=10\) \(\left( K=20, Br=0.01, \gamma =10, \Omega =1\right) \).

Full size image

4.4 Effect of couple stress parameter and Brinkman parameter on temperature distribution

We are now very much interested in showing the impact of \(\gamma \) and Br on fluid temperature in figure 5. It should be emphasised here that, in this analysis, \(\gamma =\sqrt{{\mu {{H}^{2}}}/{\eta }}\) represents the relative measure of viscous force to the viscoelasticity/couple stress effect. From figure 5a, it can be seen that the nature of temperature distribution is decreasing with \(\gamma \). The evidence for this behaviour may be due to the enhancement of couple stress effect among fluid particles in the flow region that decreases the fluid temperature, especially in the middle portion. Also, the temperature profiles are parabolic in nature in the channel. Figure 5b depicts the impact of Br on dimensionless temperature. One can easily understand from this figure that the temperature increases with increasing values of Br. This is because of viscous dissipation, which can be an energy source to enhance the temperature in the channel.

Fig. 5
figure 5

The variation of temperature profile for diverse values of (a) \(\gamma \) and (b) Br \(\left( K=20, S=1, Ha=1, \Omega =1\right) \).

Full size image

4.5 Effect of Hartmann number on Nusselt number

To understand more details about the heat transfer characteristics in the microparallel channel, the profiles of Nu vs. Br for diverse values of Ha are shown in figure 6. It is interesting to mention here that the Nusselt number variations show a decreasing behaviour for the corresponding magnitude of Br. It is clearly understood from figures 6a and 6b that the Nusselt number increases with increasing values of Ha,  i.e., both smaller and higher values of Ha. It is mainly because the effect of an imposed magnetic field is stronger than the applied transverse electric field. Consequently, the temperature difference \(\left( {T}'_{w}-{{T}'_{m}} \right) \) decreases because of significant viscous heating near the boundary of the channel. Therefore, the magnitude of \(T_{m}\) reduces consistently, which enhances Nu.

4.6 Effect of couple stress parameter and transverse electric field parameter on Nusselt number

Further, the impact of \(\gamma \) and S on Nu vs. Br is depicted in figures 7a and 7b, respectively. From figure 7a, one can clearly understand that Nu first increases up to the particular range of Br,  i.e., about 0.04 and then decreases continuously further from the value of \(Br=0.06\) onwards, for increasing values of \(\gamma \). Figure 7b illustrates the Nu profiles with Br for diverse values of S. It is noticed from figure 7b that Nu declines with increasing values of S. This is because the transverse electric field parameter usually enhances the fluid flow in the channel. Subsequently, the EMHD flow velocity in the domain increases, which causes the reduction effect on thermal transport. Eventually, the temperature profiles in the flow domain decrease.

4.7 Effect of Hartmann number on entropy generation

Figure 8 shows the variations of dimensionless entropy generation for diverse values of Ha, including lower and higher values of Hartmann number. It can be seen from figures 8a and 8b that the pattern of entropy generation variation is opposite for smaller and larger values of Ha. It is essential to note that increasing the magnitude of the magnetic field parameter can reduce entropy. Also, the entropy production augments with respect to Ha from the centre to the channel walls, reaching its maximum value at the wall, as seen in the above figure. This is because most of the changes in temperature profiles occur at the wall.

Fig. 6
figure 6

The variation of Nu for diverse values of Ha (a) \(Ha \le 1\) and (b) \(Ha>1\) \((K=20, Br=0.01, \gamma =10, \Omega =1, S=1)\).

Full size image
Fig. 7
figure 7

The variation of Nu for diverse values of (a) \(\gamma \) and (b) S \(\left( K=20, Ha=1, \Omega =1\right) \).

Full size image
Fig. 8
figure 8

The variation of entropy generation for diverse values of Ha (a) \(Ha\le 1\) and (b) \(Ha>1\) \(\left( K=20, Br=0.01, \gamma =10, \Omega =1, S=1\right) \).

Full size image

4.8 Effect of couple stress parameter and Brinkman parameter on entropy generation

The effects of parameters \(\gamma \) and Br on entropy generation are presented in figures 9a and 9b, respectively. From figure 9a, it is clear that the entropy profiles first decrease near the centre and then increase rapidly towards the wall of the channel. Finally, the entropy generation is minimum in the core region of the channel. However, the entropy generation grows consistently from the centre of the channel to the wall concerning Br values, as shown in figure 9b. From this plot, it can be observed that the entropy generation is minimum and remains constant near the middle of the channel. This may be due to the effect of significant retarding magnetic force which is more than the driving magnetic force. This influences the strong viscous dissipation effect. Thus, an increase in Br leads to an increase in entropy generation. Overall, from these figures, it can be seen that Br produces a marked enhancement in entropy production rate as compared to \(\gamma \). This indicates that \(\gamma \) can be used to optimise the entropy production in the channel.

Fig. 9
figure 9

The variation of entropy generation for diverse values of (a) \(\gamma \) and (b) Br \(\left( K=20, Ha=1, \Omega =1, S=1\right) \).

Full size image
Fig. 10
figure 10

The variation of Be for diverse values of (a) \(\gamma \) and (b) Br \(\left( K=20, Ha=1, \Omega =1, S=1\right) \).

Full size image

4.9 Effect of couple stress parameter and Brinkman parameter on Bejan number

Finally, the distributions of Be for diverse values of \(\gamma \) and Br are depicted in figures 10a and 10b, respectively. It is obvious from figure 10a that the Bejan number is decreasing consistently for increasing values of \(\gamma \). It happens because the viscous resistance of the fluid flow, which shows the significance of \(\gamma \) in the flow domain and eventually, the magnitude of the entropy generation decreases in the presence of electromagnetic force. Moreover, the Bejan number grows gradually from the middle portion of the channel to the wall. It can be seen from figure 10b that the Bejan number profiles are first increasing from the centre line of the channel and then decreasing near the channel boundary with respect to the Br values. Further, figures 10a and 10b show that the Bejan number is zero for both active parameters \(\gamma \) and Br at the centre of the channel.

5 Conclusion

The heat transfer and irreversibility analysis of EMHD flow of couple stress fluid in a microparallel channel are analysed. The EMHD flow velocity and temperature distribution in the channel are first obtained theoretically to analyse entropy generation characteristics. The exact solutions of flow velocity and temperature are validated with reported data in the literature. The impacts of flow parameters/governing parameters on temperature, Nusselt number, entropy generation and Bejan number are demonstrated graphically. The present study establishes the importance of couple stress parameter on the fluid medium, along with the electromagnetic influence. The impact of couple stress parameter on EMHD flow velocity, heat transfer and entropy generation is one of the prime concerns in this analysis. It is identified that in the absence of an applied transverse electric field, the magnetic field attempts to reduce the fluid flow and finally diminishes the magnitude of dimensionless temperature with the Hartmann number. However, in the presence of an applied transverse electric field, the magnitude of non-dimensional temperature profile first increases for low values of Hartmann number. It then decreases for higher values of Hartmann number. It is noticed that the Nusselt number shows the increasing trend consistently with Hartmann number. It is observed that the magnitude of temperature, Nusselt number and entropy generation have the same trend with an increase in couple stress parameter. This study further reveals that the irreversibility rate highly depends on the velocity and temperature distribution in the channel.