1 Introduction

Photonics science is one of the active areas of research. The literature includes numerous mathematical models that are used to investigate the propagation mechanisms of pulses across the globe. The essence of these models depends on the class of pulses which is known as soliton. For communication, pure glass strands are utilised in optical fibre technology to transmit light waves. Optical fibres give improved bandwidth along with a reduction in the power attenuation due to light signals that makes it more efficient than the electrical transmission mediums. Optical fibres behave different from other electrical mediums such that response of copper to current is linear while response of glass to light is nonlinear [1]. One interesting example is the Fokas–Lenells (FL) equation, which appears in the field of nonlinear optical fibres.

The perturbed Fokas–Lenells model (p-FLM) [3] is discussed here in the following form:

$$\begin{aligned}&iF_{t}+d_{1}F_{xx}+d_{2}F_{xt}+\mid \! F\!\mid ^{2}(d_{3}F+id_{4} F_{x})\nonumber \\&\quad -i\big [\alpha F_{x} +\beta (\mid \! F\!\mid ^{2n}\!\!F)_{x} + \gamma (\mid \! F\! \mid ^{2n})_{x}F\big ]= 0,\nonumber \\&i = \sqrt{-1}, \end{aligned}$$
(1)

where F(t, x) describes wave function, x and t are independent variables representing the spatial and temporal components respectively. Dispersion of group velocity and spatiotemporal dispersion are represented by the constants \(d_{1}\) and \(d_{2}\) respectively, while self-phase modulation is represented by \(d_{3}\). The constant \(d_{4}\) is due to the nonlinear dispersion, \(\alpha \) exhibits the effect of intermodal dispersion, \(\beta \) displays the self-steepening effect while the constant \(\gamma \) is due to the effect of nonlinear dispersion with full non-linearity. Equation (1) is a completely integratable, integrable generalisation of the nonlinear Schrödinger (NLS) equation. Equation (1) regulates the nonlinear pulse propagation of optical fibres in monomode and is the first negative member of the integrable hierarchy linked to the derivative NLS equation [4]. Within such a model, in addition to group velocity dispersion (GVD), one considers intermodal dispersion as well as nonlinear dispersion, thus treating it with a taste of additional dispersive impact. A plethora of analytical techniques for analysing FLE has been added.

Differential equations (DEs) are widely used to examine the various aspects of the sciences. Travelling wave structures of nonlinear partial differential equations (PDEs) always remain essential to understand the nature of the physical phenomenon. A lot of techniques and their applications are available in the literature for exact solutions of various forms of DEs. Exact solutions of nonlinear DEs are imperative to explore the actual process with accuracy. That is one of the reasons why solving DEs is a growing area of investigation among researchers. Some of them are given in [5,6,7,8,9,10,11,12] and reference therein.

Knowing the soliton dynamics will lead to substantial technical and industrial improvements. A lot of extensive studies are also dedicated to the nonlinear NLS equation family, since it is the governing equation that defines the propagation of the soliton in many branches of science, e.g. nonlinear optics. FLM has been investigated by many researchers from different perspectives. Zhang et al [13] reported exact solutions by constructing the Darboux transformation. In [14], the modified extended direct algebraic approach is applied to eq. (1) to get different classes of solutions that contain soliton solutions, solitary wave solutions and elliptic function solutions. Exact combined solitary wave solutions of FLM by using envelope function ansatz are computed in [15]. Biswas et al [16] computed singular soliton solutions to the model.

Mathematical analysis of the solutions for qualitative variance in a family of differential equations, i.e. bifurcation analysis, is one of the widely accepted methods for analysing dynamic systems. Physically, a sudden qualitative change in the system characterises a bifurcation for a gentle difference in parameter values, often called bifurcation parameters. An essential part of investigating differential equations is the exploration of the dynamic behaviour of nonlinear periodic waves and the investigation of chaos by any means. These areas are considered to be handy tools to see the insight of any physical phenomena that are governed by a differential equation. Some interesting and latest work in this field can be seen in [17,18,19,20] and references therein. In recent years, the study of differential equations employing bifurcation analysis is a hot topic of research. To the best of our knowledge, any study related to the dynamics of nonlinear periodic travelling waves for the p-FLM equation is not done before. Therefore, an in-depth study of eq. (1) for these dimensions is worthwhile and is presented here.

In this paper, we shall use one of the finest and elegant approaches in the literature, i.e. the extended \(({G{'}}/{G})\)-method. This technique is based on the idea that the travelling wave solutions of nonlinear differential equations are expressed by polynomials in \(({G{'}}/{G})\), where G satisfies the ordinary linear differential equation in second order. This method helps one to describe the hyperbolic, trigonometric and logical functions of moving wave solutions which make it different from other approaches.

The paper is organised as follows: description of the extended method of \(({G{'}}/{G^{2}})\)-expansion and its application to the model under consideration is given in §2. Section 3 is reserved for the analysis of bifurcation, while §4 deals with quasiperiodic and chaotic behaviours. Section 5 gives conclusion.

2 Travelling wave structures

2.1 The extended \(({G{'}}/{G^{2}})\)-expansion method

Assume the PDE, written as

$$\begin{aligned} P(F,F_{t},F_{x},F_{tt},F_{xx},...)=0, \end{aligned}$$
(2)

where F is a dependent variable and (t, x) are independent variables. After applying the complex transformation

Step 1

$$\begin{aligned} F(t,x)=L(\xi )\text {e}^{ik\xi },~~~\xi =x-st \end{aligned}$$
(3)

eq. (2) converts into the following form:

$$\begin{aligned} P(L,L{'},L{''},...)=0, \end{aligned}$$
(4)

where \(L{'}={\text {d}L}/{\text {d}\xi }\), \(L{''}={\text {d}^{2}L}/{\text {d}\xi ^{2}}\) and so on.

Step 2

Let us assume eq. (4) has the following solution:

$$\begin{aligned} L(\xi )=a_{0}+\sum _{i=1}^{m} \bigg [a_{i}\bigg (\frac{G{'}}{G^{2}}\bigg )+b_{i} \bigg (\frac{G{'}}{G^{2}}\bigg )^{-1}\bigg ], \end{aligned}$$
(5)

where

$$\begin{aligned} \bigg (\frac{G{'}}{G^{2}}\bigg )^{\prime }=c_{1}+c_{2}\bigg (\frac{G{'}}{G^{2}}\bigg )^{2}, \end{aligned}$$
(6)

while the constants \(c_{1}\) and \(c_{2}\) are real.

The general solutions of eq. (6) for the parameters \(c_{1}\) and \(c_{2}\) are presented as follows:

  • \(c_{1}c_{2}>0\)

    $$\begin{aligned}&\bigg (\frac{G{'}}{G^{2}}\bigg )\nonumber \\&\quad =\pm \sqrt{\frac{c_{1}}{c_{2}}}\bigg [ \frac{r_{1}\cos (\sqrt{c_{1}c_{2}}\xi )+r_{2}\sin (\sqrt{c_{1}c_{2}}\xi )}{r_{2}\cos (\sqrt{c_{1}c_{2}}\xi )-r_{1}\sin (\sqrt{c_{1}c_{2}}\xi )}\bigg ]. \nonumber \\ \end{aligned}$$
    (7)

  • \(c_{1}c_{2}<0\)

    $$\begin{aligned}&\bigg (\frac{G{'}}{G^{2}}\bigg ){'}= - \frac{\sqrt{\mid \! c_{1}c_{2}\!\mid }}{c_{2}} \bigg [ \frac{r_{1}\sinh (2\sqrt{\mid \! c_{1}c_{2}\!\mid }\xi )+r_{1}\cosh (2\sqrt{\mid \! c_{1}c_{2}\!\mid }\xi )+r_{2}}{r_{1}\sinh (2\sqrt{\mid \! c_{1}c_{2}\!\mid }\xi )+r_{1}\cosh (2\sqrt{\mid \! c_{1}c_{2}\!\mid }\xi )-r_{2}}\bigg ]. \end{aligned}$$

  • \(c_{1}=0, c_{2}\ne 0\)

    $$\begin{aligned} \bigg (\frac{G{'}}{G^{2}}\bigg )^{'}=-\bigg [ \frac{r_{1}}{c_{2}(r_{1} \xi +r_{2})}\bigg ]. \end{aligned}$$
    (8)

Step 3

After plugging eq. (5) in eq. (4) and comparing the coefficients of \(({G{'}}/{G^{2}})\) for different values, we obtain a set of algebraic equations. This system of algebraic equations can be solved by using Mathematica/ Maple and solutions of eq. (4) with the aid of (7) and (8) can be computed.

2.2 Application to eq. (1)

In this section, authors will compute travelling wave solutions of eq. (1). Replacing the complex envelope (3) in eq. (1) and splitting it into real and imaginary parts, we obtain the following equations:

$$\begin{aligned}&k^{2}L +d_{1}L{''}-d_{1}k^{2}L-d_{2}sL{''}+d_{2}sk^{2}L\nonumber \\&+d_{3}L^{3} -d_{4}kL^{3}+k\alpha L +\beta kL^{2n+1}=0, \end{aligned}$$
(9)
$$\begin{aligned}&-sL{'}+2d_{1}kL{'}+d_{1}k^{2}L-2d_{2}skL{'}+d_{4}L^{2}L{'} \nonumber \\&-\alpha L{'}-\beta (2n+1)L^{2n}L{'}-2nL^{2n}L{'}=0. \end{aligned}$$
(10)

After comparing, it is perceived that eqs (9) and (10) have the same solutions with the following restrictions [3]:

$$\begin{aligned} d_{4}=3 \beta -2 \mu ,\ \alpha =-s+2d_{1}k-2skd_{2},\ n=1.\nonumber \\ \end{aligned}$$
(11)

It can be verified that restrictions (11) convert eqs (9) and (10) into the following single equation:

$$\begin{aligned}&(d_{1}-d_{2}s)L{''}+k^{2}(d_{1}-d_{2}s)L\nonumber \\&\quad +(d_{3}-2\beta k+2k)L^{3}=0. \end{aligned}$$
(12)

2.2.1 Application to eq. (1)

In this section, we shall determine eq. (1)’s travelling wave solution, which needs solving only eq. (12). After combining the derivative terms of the highest order with the nonlinear terms that appear in eq. (12), we get \(m=1\) and so solution (5) takes the following form:

$$\begin{aligned} L(\xi )=a_{0}+a_{1}\bigg (\frac{G{'}}{G^{2}}\bigg )+b_{1}\bigg (\frac{G{'}}{G^{2}}\bigg )^{-1}. \end{aligned}$$
(13)

After substituting (13) in eq. (12) and comparing the coefficients of like powers of \(({G{'}}/{G^{2}})\), we obtain a system of the following algebraic equations.

$$\begin{aligned} \bigg (\frac{G{'}}{G^{2}}\bigg )^{-3}&:2(d_{1}-d_{2}s)b_{1}c_{1}^2 +b_{1}^{3}(d_{3}-2\beta k+2k)\\&\qquad =0, \\ \bigg (\frac{G{'}}{G^{2}}\bigg )^{-2}&:3(d_{3}-2\beta k+2k)a_{0}b_{1}^2=0, \\ \bigg (\frac{G{'}}{G^{2}}\bigg )^{-1}&:2(d_{1}-d_{2}s)b_{1}c_{1}c_{2}\\&+b_{1}(d_{1}-d_{2}s)k^{2}+3(d_{3}-2\beta k+2k)a_{0}^2b_{1}\\&\quad +3(d_{3}-2\beta k+2k)a_{1}b_{1}^2=0, \\ \bigg (\frac{G{'}}{G^{2}}\bigg )^{0}&:(d_{1}-d_{2}s)k^{2}a_{0}+(d_{3}-2\beta k+2k)a_{0}^3\\&+6(d_{3} -2\beta k+2k)a_{0}a_{1}b_{1}=0, \\ \bigg (\frac{G{'}}{G^{2}}\bigg )^{1}&:2(d_{1}-d_{2}s)a_{1}c_{1}c_{2}\\&+Ba_{1} +3(d_{3}-2\beta k+2k)a_{0}^2a_{1}\\ {}&+3(d_{3}-2\beta k+2k)a_{1}^2b_{1}=0, \\ \bigg (\frac{G{'}}{G^{2}}\bigg )^{2}&:3(d_{3}-2\beta k+2k)a_{0}a_{1}^2=0, \\ \bigg (\frac{G{'}}{G^{2}}\bigg )^{3}&:2(d_{1}-d_{2}s)a_{1}c_{2}^2+(d_{3}-2\beta k+2k)a_{1}^3\\&\qquad =0. \end{aligned}$$

With the help of Mathematica, the above algebraic equations are solved to get different sets of non-trivial solutions.

Set 1

$$\begin{aligned} a_{0} =\pm \sqrt{\frac{-(d_{1}-d_{2}s)k^{2}}{(d_{3}-2\beta k+2k)}},~~ a_{1} =0,~~ b_{1} =0. \end{aligned}$$
(14)

Set 2

$$\begin{aligned}&a_{0} =0,~~ a_{1} =\pm \sqrt{\frac{-2(d_{1}-d_{2}s)}{(d_{3}-2\beta k+2k)}}c_{2},\nonumber \\&b_{1} =0,~~~c_{1} =\frac{-k^{2}}{2c_{2}}. \end{aligned}$$
(15)

Set 3

$$\begin{aligned}&a_{0} =0,~~ a_{1} =0,~~ b_{1} =\pm \frac{\sqrt{(d_{1}-d_{2}s)}k^{2}}{\sqrt{2(d_{3}-2\beta k+2k)}c_{2}},~~~\nonumber \\&c_{1} =\frac{-k^{2}}{2c_{2}}. \end{aligned}$$
(16)

Set 4

$$\begin{aligned}&a_{0} =0,~~ a_{1} =\pm \sqrt{\frac{-2(d_{1}-d_{2}s)}{(d_{3}-2\beta k+2k)}}c_{2},~~ \nonumber \\&b_{1} =\pm \frac{\sqrt{(d_{1}-d_{2}s)}k^{2}}{2\sqrt{2(d_{1}-d_{2}s)(d_{3}-2\beta k+2k)}c_{2}},\nonumber \\&c_{1} =\frac{k^{2}}{4c_{2}}. \end{aligned}$$
(17)

Set 5

$$\begin{aligned}&a_{0} =0,~~ a_{1} =\pm \sqrt{\frac{-2(d_{1}-d_{2}s)}{(d_{3}-2\beta k+2k)}}c_{2},~~\nonumber \\&b_{1} =\pm \frac{\sqrt{(d_{1}-d_{2}s)}k^{2}}{4\sqrt{2(d_{1}-d_{2}s)(d_{3}-2\beta k+2k)} c_{2}},\nonumber \\&c_{1} =\frac{-k^{2}}{8c_{2}}. \end{aligned}$$
(18)

It is important to mention here that the above computed sets have different significances. Set 1 leads to the simplest solution, and hence may not contribute anything towards the physical importance of the considered model. Sets 2 and 3 give non-trivial solutions but they are not as general as claimed in (13). Sets 4 and 5 are different from the other solutions as they are non-trivial and more general than the other sets and thus are more meaningful in terms of the physical description of eq. (1).

2.2.2 Set 1

Using (14) with the help of eq. (13) and transformation (3) leads to the following solution of eq. (1):

$$\begin{aligned} F_{1\pm }(t,x)=\pm \sqrt{\frac{-(d_{1}-d_{2}s)k^{2}}{(d_{3}-2\beta k+2k)}}\text {e}^{ik(x-st)}. \end{aligned}$$

Working on the same lines, different solution sets of the following travelling structure are given.

2.2.3 Set 2

2.2.3.1 \(c_{1}c_{2}<0\)

$$\begin{aligned}&F_{2\pm }(t,x)=\pm \sqrt{\frac{-2| c_{1}c_{2}\mid (d_{1}-d_{2}s)}{(d_{3}-2\beta k+2k)}} \nonumber \\&\qquad \qquad \quad \quad \times \bigg [ \frac{r_{1}\sinh (2\sqrt{| c_{1}c_{2}|}(x-st))+r_{1}\cosh (2\sqrt{| c_{1}c_{2}|}(x-st))+r_{2}}{r_{1}\sinh (2\sqrt{| c_{1}c_{2}|}(x-st))+r_{1}\cosh (2\sqrt{| c_{1}c_{2}|}(x-st))-r_{2}}\bigg ]\text {e}^{ik(x-st)}. \end{aligned}$$
(19)

2.2.4 Set 3

2.2.4.1 \(c_{1}c_{2}<0\)

$$\begin{aligned}&F_{3\pm }(t,x)=\pm \frac{\sqrt{(d_{1}-d_{2}s)}k^{2}}{\sqrt{2| c_{1}c_{2}|(d_{3}-2\beta k+2k)}} \nonumber \\&\times \bigg [ \frac{r_{1}\sinh (2\sqrt{| c_{1}c_{2}|}(x-st))+r_{1}\cosh (2\sqrt{|c_{1}c_{2}|}(x-st))+r_{2}}{r_{1}\sinh (2\sqrt{| c_{1}c_{2}|}(x-st))+r_{1}\cosh (2\sqrt{| c_{1}c_{2}|}(x-st))-r_{2}}\bigg ]^{-1}\text {e}^{ik(x-st)}. \end{aligned}$$
(20)

2.2.5 Set 4

2.2.5.1 \(c_{1}c_{2}>0\)

$$\begin{aligned} F_{4\pm }(t,x)&=\pm \sqrt{\frac{-2c_{1}c_{2}(d_{1}-d_{2}s)}{(d_{3}-2\beta k+2k)}}\bigg [ \frac{r_{1}\cos (\sqrt{c_{1}c_{2}}(x-st))+r_{2}\sin (\sqrt{c_{1}c_{2}}(x-st))}{r_{2}\cos (\sqrt{c_{1}c_{2}}(x-st))-r_{1}\sin (\sqrt{c_{1}c_{2}}(x-st))}\bigg ]\text {e}^{ik(x-st)} \nonumber \\&\quad \pm \frac{\sqrt{(d_{1}-d_{2}s)}k^{2}}{2\sqrt{2c_{1}c_{2}(d_{3}-2\beta k+2k)}}\bigg [ \frac{r_{1}\cos (\sqrt{c_{1}c_{2}}(x-st))+r_{2}\sin (\sqrt{c_{1}c_{2}}(x-st))}{r_{2}\cos (\sqrt{c_{1}c_{2}}(x-st))-r_{1}\sin (\sqrt{c_{1}c_{2}}(x-st))}\bigg ]^{-1}\text {e}^{ik(x-st)}. \end{aligned}$$
(21)

2.2.6 Set 5

2.2.6.1 \(c_{1}c_{2}<0\)

$$\begin{aligned} F_{5}(t,x)&=\pm \sqrt{\frac{-2| c_{1}c_{2}|(d_{1}-d_{2}s)}{(d_{3}-2\beta k+2k)}} \nonumber \\&\quad \times \bigg [ \frac{r_{1}\sinh (2\sqrt{| c_{1}c_{2}|}(x-st)) +r_{1}\cosh (2\sqrt{|c_{1}c_{2}|}(x-st))+r_{2}}{r_{1} \sinh (2\sqrt{| c_{1}c_{2}|}(x-st))+r_{1}\cosh (2\sqrt{| c_{1}c_{2}|} (x-st))-r_{2}}\bigg ]\text {e}^{ik(x-st)}\nonumber \\&\quad \pm \frac{\sqrt{(d_{1}-d_{2}s)}k^{2}}{4\sqrt{2| c_{1}c_{2}|(d_{3} -2\beta k+2k)}}\nonumber \\&\quad \times \bigg [ \frac{r_{1}\sinh (2\sqrt{| c_{1}c_{2}|}(x-st))+r_{1}\cosh (2\sqrt{|c_{1}c_{2}|}(x-st))+r_{2}}{r_{1}\sinh (2\sqrt{| c_{1}c_{2}|}(x-st))+r_{1}\cosh (2\sqrt{| c_{1}c_{2}|}(x-st))-r_{2}}\bigg ]^{-1}\text {e}^{ik(x-st)}. \end{aligned}$$
(22)

2.3 Physical Interpretation

Figures 1–3 describe travelling wave solutions of p-FLM. In figure 1 there is a bright travelling wave structure displaying frequency peaks of a complex-valued function F at \(\xi =5\) and \(-5\) and a break in between these two values. In figure 2 there is a dark travelling wave structure displaying frequency dips of a complex-valued function F between \(\xi =-2.5\) and 2.5 and a smooth curve for the rest of the domain. In figure 3 there are peakon-type travelling wave structures whose peaks posses discontinuous first derivative. These types of travelling wave structures are of extreme importance owing to their efficiency and of course flexibility in the long-distance optical communication.

2.3.1 Remarks

After performing some analysis, the sufficient conditions for the obtained travelling wave solutions can be described by the following proposition.

PROPOSITION

If \(F_{i\pm }(t,x),~~i=1,2,\ldots ,5,\) are the travelling wave solutions of eq. (1) computed by using the extended \(({G{'}}/{G^{2}})\)-expansion approach, then the constraint conditions for the existence are

$$\begin{aligned} \frac{-(d_{1}-d_{2}s)}{(d_{3}-2\beta k+2k)}>0~~ \mathrm{and}~~(d_{3}-2\beta k+2k)\ne 0. \end{aligned}$$

3 Phase portraits and nonlinear periodic waves

In this section, bifurcation method is used for a detailed analysis of eq. (1). For this, some notations and definitions are taken from literature and presented here. Equation (12) can be written using the Galilean transformation as a system of nonlinear dynamic equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\text {d} L}{\text {d} \xi }=Y, &{} \\ \displaystyle \frac{\text {d} Y}{\text {d} \xi }=-k^{2}L-\frac{(d_{3}-2\beta k+2k)}{(d_{1}-d_{2}s)}L^{3}. \end{array}\right. } \end{aligned}$$
(23)
  1. (1)

    Level curves \(C_{h}(L,y)\) are defined as

    $$\begin{aligned} C_{h}=\{ (L,Y) \in R \times R: H(L,Y)=h \}, \end{aligned}$$

    where H(L, Y) is a Hamiltonian function and for system (23) it can be written as

    $$\begin{aligned} H(L,Y)= & {} \frac{Y^{2}}{2}+\frac{k^{2}L^{2}}{2}\nonumber \\&+\frac{(d_{3}-2\beta k+2k)L^{4}}{4(d_{1}-d_{2}s)}=h, \end{aligned}$$
    (24)

    where h represents the energy levels. From (24), it can be verified that

    $$\begin{aligned} \frac{\partial L}{\partial \xi }=\frac{\partial H}{\partial Y}\quad \text {and}\quad \frac{\partial Y}{\partial \xi }=-\frac{\partial H}{\partial L}. \end{aligned}$$
    (25)

    Equation (25) confirms the conservation of the planar Hamiltonian system (23) which guarantees that phase orbits defined by the vector fields of (23) posses all travelling wave solutions of eq. (1) (for details, see [7] and references therein). In phase portraits at each energy level there is an orbit, where

    $$\begin{aligned} Y=\pm \sqrt{2h-k^{2}L^{2}-\frac{(d_{3}-2\beta k+2k)L^{4}}{2(d_{1}-d_{2}s)}}. \nonumber \\ \end{aligned}$$
    (26)
  2. (2)

    Equilibrium point \(E_{i}=(L_{e}, Y_{e})\) is called

    1. (a)

      saddle point if \(J<0\),

    2. (b)

      centre point for \(J>0\) and \(T_{1}=0\),

    3. (c)

      a node if \(J>0\) and \(T^{2}_{1}-4J>0\),

    4. (d)

      zero point when \(J=0\) and Poincaré index of \((L_{e}, Y_{e})\) is zero, where J and \(T_{1}\) represent the determinant and trace of the Jacobian matrix for system (23). System  (23) contains three equilibrium points:

      $$\begin{aligned}&E_{1}=(0,0),~ E_{2}\!=\!\bigg (\sqrt{\frac{-(d_{1}-d_{2}s)k^{2}}{(d_{3}\!-\!2\beta k+2k)}},0\bigg ) \end{aligned}$$

      and

      $$\begin{aligned}&E_{3}=\bigg (-\sqrt{\frac{-(d_{1}-d_{2}s)k^{2}}{(d_{3}-2\beta k+2k)}},0\bigg ). \end{aligned}$$
Fig. 1
figure 1

\(\mid \!F_{2}\!\mid \) for \(k\!=\!1,\beta \!=\!1, d_{1}\!=\!-2, d_{2}\!=\!0.5, d_{3}\!=\!1, s=-2\).

Full size image
Fig. 2
figure 2

\(\mid \! F_{3}\! \mid \) for \(k\!=\!1,\beta \!=\!1, d_{1}\!=\!-2, d_{2}\!=\!0.5, d_{3}\!=\!1, s=-2\).

Full size image
Fig. 3
figure 3

\(\mid F_{4} \mid \) for \(k\!=\!1,\beta \!=\!1, d_{1}\!=\!-2, d_{2}\!=\!0.5, d_{3}\!=\!1, s=-2\).

Full size image

3.1 \({[(d_{1}-d_{2}s)}/{(d_{3}-2\beta k+2k)]}<0\)

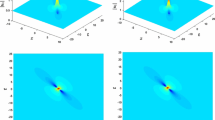
System (23) for this case contains three equilibrium points \( E_{1}, E_{2}\) and \( E_{3}\). At \( E_{1}\) we get \( J(E_{1})>0\) and \(T_{1}(M(Q_{1}))=0\), and thus \( E_{1}\) by definition is a centre point. For both \( E_{2}\) and \(E_{3}\) the values of the corresponding Jacobian is greater than zero with Poincarè index zero. Thus, the above analysis suggests that \( E_{2}, E_{3}\) are cusp points as can be seen in figure 6a. It is noted that phase portrait of the system of nonlinear ODEs (23) as shown in figure 4a contains a family of NPO(1,0) which envelops the centre \(E_{1}\). It is noted that two nonlinear heteroclinic orbit NHTO (1,0) carries \( E_{1}\) and passes through the cusp points \( E_{2}\) and \(E_{3}\). For this case, system (23) contains a nonlinear periodic wave which is drawn in figure 4b.

3.2 \({[(d_{1}-d_{2}s)}/{(d_{3}-2\beta k+2k)}]>0\)

Here, planer dynamical system (23) has only one equilibrium point which is \( E_{1}\) and is presented in figure 5a. For \( E_{1}\), determinant and trace of the Jacobian matrix for system  (23) remain the same as in the previous case, presented in figure 5b. It can be observed from figure 6b that it contains a family of nonlinear periodic orbit NPO(1,0) which envelops \(E_{1}\). Nonlinear periodic wave is computed by using Range–Kutta method of order 4.

Fig. 4
figure 4

For \(k\!=\!0.5,\beta \!=\!2, d_{1}\!=\!1, d_{2}\!=\!1, d_{3}\!=\!1, s\!=\!2,\) nonlinear dynamical system are depicted.

Full size image
Fig. 5
figure 5

For \(k\!=\!0.5,\beta \!=\!2, d_{1}\!=\!3, d_{2}\!=\!1, d_{3}\!=\!1, s\!=\!2\) nonlinear dynamical system are depicted.

Full size image

4 Quasiperiodic and chaotic dynamics

In this section, we shall examine the quasiperiodic and chaotic behaviour of the perturbed system that follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\text {d} L}{\text {d} \xi }=Y, &{} \\ \displaystyle \frac{\text {d} Y}{\text {d} \xi }=-k^{2}L-\frac{(d_{3}-2\beta k+2k)}{(d_{1}-d_{2}s)}L^{3}+g_{0}\cos {(\zeta t)}, \end{array}\right. } \end{aligned}$$
(27)

where \(\zeta \) is the frequency and \(g_{0}\) is the perturbation intensity. The difference between systems (23) and (27) is the addition of the superficial periodic force into system (27). The existence of seven parameters, viz. \(k, \beta , d_{1}, d_{2}, d_{3},g_{0} \) and \(\zeta \) along with perturbation terms makes the study of periodic and chaotic behaviour of p-FLM a difficult task. In order to tackle our problem, we shall use different tools such as phase portrait method, time series analysis and Poincaré section. To investigate the problem from different aspects, we analyse the influence of parameters by assuming two different cases. For the first case we keep \(k, \beta , d_{1}, d_{2}, d_{3}, g_{0}\) constant and discuss the effect of frequency while for the second case we investigate by assuming \(\zeta \) and \(g_{0}\) as constants and varying the other parameters.

In figure 6, two-dimensional phase portrait, time series graph and Poincaré section are presented for \(k=0.5,\beta =2, d_{1}=3, d_{2}=1, d_{3}=1, s=2, g_{0}=-2\) and \(\zeta =0.31\). It is noticed that system (27) is a quasiperiodic system for \(\zeta =0.31\), while a pattern can be seen in Poincaré section which negates the chaotic properties at given values of parameters. In figure 7, the two-dimensional phase portrait is represented, along with the time series graph and Poincaré section for \(\zeta =6.3\), keeping the other parameters the same as in figure 6. It is observed that system (27) represents quasiperiodic properties for \(\zeta =6.3\). The points on Poincaré section carries a specific shape for these values which nullify the existence of chaotic structure for these specific values of parameters.

Fig. 6
figure 6

Nonlinear dynamical systems are depicted for \(k=0.5,\beta =2, d_{1}=3, d_{2}=1, d_{3}=1, s=2, g_{0}=-2\) and \(\zeta =0.31.\)

Full size image
Fig. 7
figure 7

Nonlinear dynamical systems are depicted for \(k=0.5,\beta =2, d_{1}=3, d_{2}=1, d_{3}=1, s=2, g_{0}=-2\) and \(\zeta =6.3.\)

Full size image
Fig. 8
figure 8

Nonlinear dynamical systems are depicted for \(k=2.5, \beta =1, d_{1}=2, d_{2}=1, d_{3}=1.5, s=1, g_{0}=-2\) and \(\zeta =0.31\).

Full size image
Fig. 9
figure 9

Nonlinear dynamical systems are depicted for \(k=0.5, \beta =1, d_{1}=1.5, d_{2}=1, d_{3}=0.75, s=0.5,\) \(g_{0}=-2\) and \(\zeta =0.31.\)

Full size image
Fig. 10
figure 10

2D Graphics of sensitive analysis for \(k=0.5, \beta =1, d_{1}=1.5, d_{2}=1, d_{3}=0.75, s=0.5,\) \(g_{0}=-2\) and \(\zeta =0.31.\)

Full size image
Fig. 11
figure 11

2D Graphics of sensitive analysis for \(k=0.5, \beta =1, d_{1}=1.5, d_{2}=1, d_{3}=0.75, s=0.5,\) \(g_{0}=-2\) and \(\zeta =0.31.\)

Full size image
Fig. 12
figure 12

2D Graphics of sensitive analysis for \(k=0.5, \beta =1, d_{1}=1.5, d_{2}=1, d_{3}=0.75, s=0.5,\) \(g_{0}=-2\) and \(\zeta =0.31.\)

Full size image

In figure 8, we plotted the two-dimensional phase portrait, time series graph and Poincaré section for \(\zeta =6.3\) by taking the other parameters the same as in figure 6. It is perceived that perturbed dynamical structure (27) carries quasiperiodic behaviour for \(\zeta =6.3\). The points on Poincaré section represents a particular pattern for these values which nullify the existence of chaotic structure for these specific values of parameters. In figure 8, we present the two-dimensional phase portrait, time series graph and Poincaré section for \(k=2.5, \beta =1, d_{1}=2, d_{2}=1, d_{3}=1.5, s=1, g_{0}=-2\) and \(\zeta =0.31\). It is noticed that perturbed dynamical system (27) depicts quasiperiodic properties, whereas the Poincaré section shows a particular behaviour that balances the presence of chaotic properties for the considered values of parameters. In figure 9, we presented the two-dimensional phase portrait, time series graph and Poincaré section for \(k=0.5, \beta =1, d_{1}=1.5, d_{2}=1, d_{3}=0.75, s=0.5\), keeping the other parameters the same as in figure 8. It is observed that perturbed dynamical system (27) displays quasiperiodic–chaotic properties. The points on Poincaré section are scattered and do not admit any specific shape. This is due to the quasiperiodic–chaotic properties of perturbed dynamical system (27).

4.1 Sensitivity analysis

Here we are inclined to investigate the sensitivity for the solution of the perturbed dynamical system (27). For this purpose, we have considered three different initial conditions: \((L,Y)= (0.01,0.01)\) in red solid line, \((L,Y)= (0.02,0.02)\) in dashed blue curve and \((L,Y)= (0.5,0.5)\) in dotted dashed green curve while the values of other parameters are the same as in figure 9. The comparison of the solutions at different initial conditions are displayed in figures 10–12. The quasiperiodic chaotic properties of the perturbed dynamical system (27) makes the system desensitised with the tested initial condition for some specific values of parameters.

5 Conclusion

The current study discussed the chirped soliton solutions of the FL equation in the presence of Hamiltonian perturbation terms. The complex envelope travelling-wave hypothesis is invoked to reduce the governing model to an ODE. The resultant ODE is a first-order nonlinear ODE with six-degree terms. Hence, it is handled analytically using the auxiliary equation method with two structures. As a result, different types of chirped soliton solutions including bright, dark, kink and singular solitons are derived. Additionally, a set of combo optical soliton solutions are obtained as well. The associated chirp is also induced for each of these optical solitons. The graphical representations for some of the obtained chirped solitons are also exhibited by selecting suitable values of parameters.

Travelling wave solutions of p-FLM have been computed via the extended \(({G{'}}/{G^{2}})\)-method and the constraint conditions for the existence of these solutions are reported. We have studied the qualitative behaviour of the periodic nonlinear waves using the theory of the planer dynamical system. It is observed that the governing model only contains the nonlinear periodic wave. Also, bifurcation theory is utilised and two different phase portraits are presented. Each phase portrait is labelled for orbits. The effect of physical parameters: dispersion of group velocity (\(d_{1}\)), spatio-temporal (\(d_{2}\)), self-phase modulation (\(d_{3}\)), nonlinear dispersion (\(d_{4}\)), intermodal dispersion (\(\alpha \)), self-steepening (\(\beta \)) nonlinear dispersion with full non-linearity (\(\gamma \)), frequency of the travelling wave (s), strength of the perturbation \(g_{0}\) and frequency of the perturbed term (\(\zeta \)) have been analysed on the quasiperiodic and chaotic properties of the dynamical structure with perturbation (27). The results reported are confirmed by the Poincaré section and later by sensitive analysis. It is noticed that when group velocity is decreased from 2 to 1.5, self-phase modulation is reduced from 1.5 to 0.75 and the frequency of the travelling wave is considered 0.5 instead of 1 by keeping the other parameters the same as in figure 8 a chaotic behavior is observed.