1 Introduction

The Shynaray-IIA equation is a well-known nonlinear partial differential equation (PDE) that presents a challenging problem due to its complex behavior and wide-ranging implications across various scientific fields, such as engineering, mathematics, environmental science and many more. In the field of applied mathematics, the quest for exact solutions to the Shynaray-IIA Equation (S-IIAE) is noteworthy due to its importance in defining the basic characteristics of nonlinear systems (Dong et al. 2022). Over the last ten years, there has been an increasing interest in the study of nonlinear partial differential equations in both applied mathematics (Akinyemi 2023) and pure mathematics (Liu et al. 2022). The application of computer technology has greatly facilitated the exploration process (Zhang and Shi 2022), offering mathematicians more opportunities in the applied sciences. The advent of nonlinear models, which are commonly found in domains like engineering and mathematical physics, has grown in importance and calls for careful analysis and understanding. The increasing significance of nonlinear partial differential equations (PDEs) in modern scientific research can be seen by the intersection of exact mathematical formulations, computer technology advancements, and their practical applications (Nayyer et al. 2022). Academics have become interested in researching soliton solutions within nonlinear partial differential equations (NLPDEs) using new mathematical analysis techniques. There has been a shift in attention in this discipline towards the dynamical modelling of these complex equations, aiming to discover exact solutions through the application of scientific methods. Furthermore, there is an increasing interest in using computer programmers to enhance the efficiency of complex mathematical calculations. Various fields of research and engineering, including quantum physics, nonlinear optics, electrical and computer engineering, and hydrodynamic and plasma dynamics, heavily depend on these equations (Kumar et al. 2022, 2020; Khan et al. 2022; Osman 2019).

The search for travelling wave solutions demonstrates the importance of accurately modelling physical circumstances. The fundamental importance of solitons stems from their stable, self-contained, and perpetual wave properties, which enable them to preserve their distinctiveness when transitioning between different mediums. The phenomena discussed here arise from the interplay between dispersion and nonlinearity, offering a profound comprehension of the fundamental physical dynamics. These findings are particularly significant for studying travelling waves and solitary solutions in NLPDEs. Optical solitons, which exhibit characteristics similar to particles, have been effectively utilized in telecommunications. They have been created and utilized in waveguides such fibers and lasers (Osman et al. 2019; Alquran and Jarrah 2019; Jaradat et al. 2017, 2015; Alquran et al. 2018). The study of optical solitons in nonlinear materials is one field that is currently receiving a lot of attention from researchers. All-optical switch’s function and high-speed data transmission over optical fibers are made possible by optical solitons, which are persistent bundles of waves (Zhang and Shi 2022; Kumar and Prakash 2022). Their outstanding capacity to maintain their strength and structural integrity over long distances is essential to ensuring the uninterrupted flow of signals. Consequently, this improves modern telecommunication systems’ efficiency and reliability considerably (Tao et al 2022; Debnath and Debnath 2005). The primary objective of exploring this field of study is to gain a deeper understanding of the behavior shown by solitons in order to ultimately improve their usefulness in practical applications. By doing this, researchers hope to significantly advance communication technology and improve the ways in which we share and communicate information. Currently, the application of various methods to obtain exact solutions for partial differential equations (PDEs) and nonlinear evolution equations (NLEEs) is very advantageous. Such as the tanh method (Wazwaz 2006), the extended auxiliary equation method (Seadawy 2017; Akram et al. 2021; Rizvi et al. 2020), the variational method (Seadawy 2011), the modified and extended simple equation method (Ali and Seadawy 2017; Arshad et al. 2017; Arnous et al. 2017), the direct algebraic method (Seadawy and El-Rashidy 2013), generalized exponential rational function method (Younas et al. 2021), extended F-expansion method (Bhrawy et al. 2013; Ebadi et al. 2013), \({G \mathord{\left/ {\vphantom {G {G^{\prime } }}} \right. \kern-0pt} {G^{\prime } }}\)–expansion method (Iqbal et al. 2021), sine–Gordon expansion method (Ali et al. 2020), modified sub-equation method (Akinyemi et al 2023), Darboux method (Mani Ranjan et al. 2023), homogeneous balance (Jafari et al. 2014), and so on.

Current academic research is mostly centered around a diverse range of nonlinear partial differential equations (PDEs) and the corresponding dynamic systems that govern them. The presence of sophisticated symbolic software has significantly enhanced researchers’ understanding of dynamic systems, enabling comprehensive investigation (He et al. 2023; Zhu et al. 2023). Exploring bifurcation, investigating chaotic behaviors, and conducting sensitivity analysis are just a few of the numerous methodologies employed in the study of dynamic systems. Academic interest in these realms of dynamic systems has recently increased significantly. The increasing interest is demonstrated by the attention given to widely recognized partial differential equations (PDEs). Xu et al. (2023) examined the application of a bifurcation extended hybrid controller architecture in a delayed chemostat model. Luo et al. (2023) studied the perturbed non-linear Schrödinger equation with Kerr law non-linearity. They also performed sensitivity analysis and examined bifurcations and chaotic dynamics. In addition, they identified multiple novel optical solitons. Du et al. (2023) conducted a study on the novel extended Vakhnenko-Parkes equation, exploring numerous solitons, bifurcations, and high-order breathers. Han et al. (2023) conducted a study on the bifurcation, sensitivity analysis, and accurate travelling wave solutions of the stochastic fractional Hirota-Maccari system. Li et al. (2023) examined the coupled Kundu-Mukherjee-Naskar equation to analyze its chaotic pattern, bifurcation, sensitivity, and travelling wave solution. Hosseini et al. (2023) examined this generalized Schrödinger equation to analyze its bifurcation, chaotic dynamics, sensitivity, and soliton solutions. Jhangeer et al. (2021) examined the quasi-periodic, chaotic, and travelling wave structures of the modified Gardner equation.

Our work takes advantage of the enhanced generalized Riccati equation mapping method to address this mathematical problem. The focus of our study is the Galilean transformation, a fundamental concept in classical mechanics that enables us to reduce complex partial differential equations (PDEs) into simpler ordinary differential equations (ODEs). Including a re-spatial derivative component that emphasizes temporal variations simplifies the mathematical examination and resolution of ordinary differential equations (ODEs). Studying relative motion across different inertial frames is crucial. We initiate our research by doing a thorough bifurcation analysis, utilizing the standard planar dynamical systems model to determine the system’s intricate properties. By employing the Runge–Kutta method, we enhance the effectiveness of this analysis, ensuring that our solutions remain stable and unaltered even when there are minor modifications to the initial conditions. This rigorous approach guarantees the replies’ reliability by allowing us to assess their stability in the face of minor disturbances. In addition, we investigate the realm of disorder in disrupted dynamic systems, utilizing several techniques to identify chaotic patterns in both visual depictions and temporal data sequences. By providing insights into the intricate exchanges between the many parameters that make up the Shynaray-IIA equation, this approach has shown to be a useful tool for solving nonlinear PDEs exactly. The mathematical form of the Shynaray-IIA equation can be expressed as

$$\begin{aligned} & iw_{t} + w_{xt} - i\left( {vw} \right)_{x} = 0, \\ & ir_{t} - r_{xt} - i\left( {vr} \right)_{x} = 0, \\ & v_{x} - \frac{{n^{2} }}{m}\left( {rw} \right)_{t} = 0. \\ \end{aligned}$$
(1)

The unknown variables denoted as, \(w(x,t)\), \(r(x,t)\) and \(v(x,t)\), are dependent on the independent variables x and t. It is important to note that m and n are constants. The equation possesses integrable characteristics through the application of the inverse scattering transform. Various properties, including geometrical and gauge equivalence as well as integrable motion along apace curves, have been thoroughly investigated. Recently, an improved Sardar sub-equation method and a new direct algebraic method have been presented to investigate solitary wave solutions in the Shynaray-IIA equation, phenomena such as tidal waves and tsunamis are characterized by distinctive features (Faridi et al. 2024; Khan et al. 2024). Our primary objective is to contribute to existing knowledge by presenting new exact solutions for the Shynaray-IIA equation including rational, exponential, hyperbolic trigonometric and trigonometric based on the enhanced generalized Riccati equation mapping technique. By doing so, we hope to advance the understanding of the equation’s dynamics and open new avenues for its application across scientific domains.

The organization of this paper is outlined as follows: Sect. 1 offers a concise introduction; Sect. 2 details the methodology employed in the scheme; Sect. 3 delves into bifurcation analysis, chaotic behavior, and sensitivity analysis; Sect. 4 discusses the application of the IMREMM; Sect. 5 presents the graphical representation of the solution; and Sect. 6 concludes the study.

2 Methodology of the proposed improved techniques

Examine the nonlinear partial differential equation

$$F\left( {u,u_{t} ,u_{x} ,u_{xx} , \ldots } \right) = 0.$$
(2)

where \(u=u(x,t)\) is an unknown function that depends on \(x\) and \(t.\) At the moment, a specific wave transformation has been introduced

$$U = U\left( \Omega \right), \;\Omega = x - ct.$$
(3)

By utilizing the transformation from Eq. (3) to Eq. (2) with \(c\ne 0\), the nonlinear partial differential equation (NPDE) is reduced and transformed into a nonlinear ordinary differential equation (ODE) with an integral order

$$N\left( {U^{\prime},U^{\prime\prime},U^{\prime\prime\prime}, \ldots } \right).$$
(4)

We have solved the above non-linear ODE by using IGREMM, the techniques have the following standard form:

$$U\left( \Omega \right) = a_{0} + \mathop \sum \limits_{j = 1}^{N} a_{j} Q^{j} \left( \Omega \right) \quad a_{N} \ne 0,$$
(5)

where \({a}_{j}\) \((j=\text{0,1},\text{2,3},\dots .N)\).

The value of \(N\) is found by balancing the highest order derivative term and the highest order nonlinear term in Eq. (4). Thus, the highest degree of \(\frac{{d^{r} U}}{{d\Omega^{r} }}\) is identified as:

$$O\left( {\frac{{d^{r} U}}{{d\Omega^{r} }}} \right) = n + r, r = 1,2,3, \ldots$$
(6)
$$O\left( {U^{q} \frac{{d^{r} U}}{{d\Omega^{r} }}} \right) = \left( {q + 1} \right)n + r, q = 0, 1,2, \ldots { }r = 1,2,3, \ldots$$
(7)

2.1 The enhanced generalized Riccati equation mapping method

The \(Q\left( \Omega \right)\) in Eq. (5) is the solution of

$$Q^{\prime}\left( \Omega \right) = \beta_{2} Q^{2} \left( \Omega \right) + \beta_{1} Q\left( \Omega \right) + \beta_{0} ,$$
(8)

where \(\beta_{i} , i = 0,1,2{ }\) are constants and they need to be determined later. The following set of solutions is obtained with the integration constant\(\text{C}\):

  • 1 For \(\beta_{0} = \beta_{1} = 0\) and \(\beta_{2} \ne 0,\) the rational solutions will be of the form:

    $$Q_{1}^{ \pm } \left( \Omega \right) = \pm \frac{1}{{\beta_{2} \left( {\Omega + C} \right)}}.$$
    (9)

  • 2 For \(\beta_{0} = 0\), the solution of the exponential type is simply obtained as:

    $$Q_{2} \left( \Omega \right) = - \frac{{\beta_{1} \phi }}{{\beta_{1} (e^{{ - \beta_{1} \left( {\Omega + C} \right)}} + \varphi ) }},$$
    (10)
    $$Q_{3} \left( \Omega \right) = - \frac{{\beta_{1} e^{{\beta_{1} \left( {\Omega + C} \right)}} }}{{\beta_{2} (e^{{\beta_{1} \left( {\Omega + C} \right)}} + \varphi ) }}.$$
    (11)

  • 3 For \(\rho = \beta_{1}^{2} - 4\beta_{0} \beta_{1} > 0\), \(\beta_{1} \beta_{2} \ne 0\) or \(\beta_{0} \beta_{2} \ne 0\), and \({\text{p}}\) and \({\text{q}}\) are nonzero real constants, the solutions presented in the form of trigonometric hyperbolic functions are given below:

    $$Q_{4} \left( \Omega \right) = - \frac{\sqrt \rho }{{2\beta_{2} }}\tanh \left( {\frac{\sqrt \rho }{2}\left( {\Omega + C} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (12)
    $$Q_{5} \left( \Omega \right) = - \frac{\sqrt \rho }{{2\beta_{2} }}\coth \left( {\frac{\sqrt \rho }{2}\left( {\Omega + C} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (13)
    $$Q_{6}^{ \pm } \left( \Omega \right) = - \frac{\sqrt \rho }{{2\beta_{2} }}(\tanh \left( {\sqrt \rho \left( {\Omega + C} \right)} \right) \pm isech\left( {\sqrt \rho \left( {\Omega + C} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (14)
    $$Q_{7}^{ \pm } \left( \Omega \right) = - \frac{\sqrt \rho }{{2\beta_{2} }}\left( {\coth \left( {\sqrt \rho \left( {\Omega + C} \right)} \right) \pm csch\left( {\sqrt \rho \left( {\Omega + C} \right)} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (15)
    $$Q_{8} \left( \Omega \right) = - \frac{\sqrt \rho }{{4\beta_{2} }}(\tanh \left( {\frac{\sqrt \rho }{4}\left( {\Omega + C} \right)} \right) + coth\left( { \frac{\sqrt \rho }{4}\left( {\Omega + C} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (16)
    $$Q_{9}^{ \pm } \left( \Omega \right) = \frac{{ \pm \sqrt {\rho \left( {p^{2} + q^{2} } \right)} - p\sqrt \rho \cosh \left( {\sqrt \rho \left( {\Omega + C} \right)} \right)}}{{2\beta_{2} \left( {p sinh\left( {\sqrt \rho \left( {\Omega + C} \right)} \right) + q} \right)}} - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (17)
    $$Q_{10} \left( \Omega \right) = \frac{{2\beta_{0} \cosh \left( { \frac{\sqrt \rho }{2}\left( {\Omega + C} \right)} \right)}}{{\sqrt \rho sinh\left( {\frac{\sqrt \rho }{2}\left( {\Omega + C} \right)} \right) - \beta_{1} cosh\left( {\frac{\sqrt \rho }{2}\left( {\Omega + C} \right)} \right)}},$$
    (18)
    $${\text{Q}}_{11} \left( \Omega \right) = \frac{{2{\upbeta }_{0} \sinh \left( {{ }\frac{{\sqrt {\uprho } }}{2}\left( {\Omega + {\text{C}}} \right)} \right)}}{{\sqrt {\uprho } \cosh \left( {\frac{{\sqrt {\uprho } }}{2}\left( {\Omega + {\text{C}}} \right)} \right) - {\upbeta }_{1} \sinh \left( {\frac{{\sqrt {\uprho } }}{2}\left( {\Omega + {\text{C}}} \right)} \right)}},$$
    (19)
    $$Q_{12}^{ \pm } \left( \Omega \right) = \frac{{2\beta_{0} \cosh \left( { \sqrt \rho \left( {\Omega + C} \right)} \right)}}{{\sqrt \rho \sinh \left( {\sqrt \rho \left( {\Omega + C} \right)} \right) - \beta_{1} \cosh \left( {\sqrt \rho \left( {\Omega + C} \right)} \right) \pm i\sqrt \rho }},$$
    (20)
    $$Q_{13}^{ \pm } \left( \Omega \right) = \frac{{2\beta_{0} sinh\left( { \sqrt \rho \left( {\Omega + C} \right)} \right)}}{{\sqrt \rho cosh\left( {\sqrt \rho \left( {\Omega + C} \right)} \right) - \beta_{1} \sinh \left( {\sqrt \rho \left( {\Omega + C} \right)} \right) \pm \sqrt \rho }},$$
    (21)
    $$Q_{14} \left( \Omega \right) = \frac{{2\beta_{0} \sinh \left( {\frac{\sqrt \rho }{4}\left( {\Omega + C} \right)} \right)\cosh \left( {\frac{\sqrt \rho }{4}\left( {\Omega + C} \right)} \right)}}{{2\sqrt \rho \cosh^{2} \left( {\frac{\sqrt \rho }{4}\left( {\Omega + C} \right)} \right) - 2\beta_{1} \sinh \left( {\frac{\sqrt \rho }{4}\sqrt \rho \left( {\Omega + C} \right)} \right)\cosh \left( {\frac{\sqrt \rho }{4}\left( {\Omega + C} \right)} \right) - \sqrt \rho }}.$$
    (22)

  • 4 For \(\rho = \beta_{1}^{2} - 4\beta_{0} \beta_{2} < 0, \beta_{1} \beta_{2} \ne 0\) or \(\beta_{0} \beta_{2} \ne 0\), the solutions of the trigonometric form are demonstrated as follows:

    $$Q_{15} \left( \Omega \right) = \frac{{\sqrt { - \rho } }}{{2\beta_{2} }}\tan \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (23)
    $$Q_{16} \left( \Omega \right) = - \frac{{\sqrt { - \rho } }}{{2\beta_{2} }}\cot \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (24)
    $$Q_{17}^{ \pm } \left( \Omega \right) = \frac{{\sqrt { - \rho } }}{{2\beta_{2} }} \left( {\tan \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right) \pm \sec \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (25)
    $$Q_{18}^{ \pm } \left( \Omega \right) = - \frac{{\sqrt { - \rho } }}{{2\beta_{2} }}\left( {\cot \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right) \pm \csc \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (26)
    $$Q_{19} \left( \Omega \right) = \frac{{\sqrt { - \rho } }}{{4\beta_{2} }}\left( {\tan \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right) - cot\left( {\frac{{\sqrt { - \rho } }}{4}\left( {\Omega + C} \right)} \right)} \right) - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (27)
    $$Q_{20}^{ \pm } \left( \Omega \right) = \frac{{ \pm \sqrt { - \rho \left( {p^{2} - q^{2} } \right)} - p\sqrt { - \rho } \cos \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right)}}{{2\beta_{2} \left( {psin(\sqrt { - \rho } \left( {\Omega + C} \right) + q} \right)}} - \frac{{\beta_{1} }}{{2\beta_{2} }},$$
    (28)
    $$Q_{21} \left( \Omega \right) = - \frac{{2\beta_{0} \cos \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right)}}{{\sqrt { - \rho } \sin \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right) + \beta_{1} \cos \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right)}},$$
    (29)
    $$Q_{22} \left( \Omega \right) = \frac{{2\beta_{0} \sin \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right)}}{{\sqrt { - \rho } \cos \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right) - \beta_{1} \sin \left( {\frac{{\sqrt { - \rho } }}{2}\left( {\Omega + C} \right)} \right)}},$$
    (30)
    $$Q_{23}^{ \pm } \left( \Omega \right) = - \frac{{2\beta_{0} \cos \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right) }}{{\beta_{1} cos\left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right) + \sqrt { - \rho } sin\left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right) \pm \sqrt { - \rho } }},$$
    (31)
    $$Q_{24}^{ \pm } \left( \Omega \right) = \frac{{2\beta_{0} \sin \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right)}}{{\beta_{1} \sin \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right) - \sqrt { - \rho } \cos \left( {\sqrt { - \rho } \left( {\Omega + C} \right)} \right) \pm \sqrt { - \rho } }},$$
    (32)
    $$Q_{25} \left( \Omega \right) = \frac{{4\beta_{0} \sin \left( {\frac{{\sqrt { - \rho } }}{4}\left( {\Omega + C} \right)} \right)\cos \left( {\frac{{\sqrt { - \rho } }}{4}\left( {\Omega + C} \right)} \right)}}{{2\sqrt { - \rho } \cos^{2} \left( {\frac{{\sqrt { - \rho } }}{4}\left( {\Omega + C} \right)} \right) - 2\beta_{1} \sin \left( {\frac{{\sqrt { - \rho } }}{4}\left( {\Omega + C} \right)} \right)\cos \left( {\frac{{\sqrt { - \rho } }}{4}\left( {\Omega + C} \right)} \right) - \sqrt { - \rho } }}.$$
    (33)

We substitute the Equations represented by Eq. (5 and 8) into Eq. (4), equating the coefficients of each power of \(Q^{i} \left( {\Omega } \right)\) to zero. The resulting system of algebraic equations was then solved with the help of Maple. We obtained the constants (coefficients) by solving, and we used these to solve Eq. (4) and get different kinds of solutions, as explained by Eqs. (9–33). We were to obtain a variety of exact solutions for NPDEs using this method.

2.2 Solution of the Shynaray IIA equation

In this subsection, we provide the exact solutions for the S-IIAE (1) model using IGREMM:

$$\begin{aligned} & iw_{t} + w_{xt} - i\left( {vw} \right)_{x} = 0, \\ & ir_{t} - r_{xt} - i\left( {vr} \right)_{x} = 0, \\ & v_{x} - \frac{{n^{2} }}{m}\left( {rw} \right)_{t} = 0. \\ \end{aligned}$$

If \(r = \varepsilon \overline{w} \left( {\varepsilon = \pm 1} \right)\), then S-IIAE has the following form

$$\begin{aligned} & iw_{t} + w_{xt} - i\left( {vw} \right)_{x} = 0, \\ & v_{x} - \frac{{n^{2} \varepsilon }}{m}\left( {\left| w \right|^{2} } \right)_{t} = 0. \\ \end{aligned}$$
(34)

Equation (34) can be reduced to the following ordinary differential equation (ODE) by applying the wave transformation to the given equation, where \(m, n\) and \(\varepsilon\) are constants.

$$\begin{aligned} & w\left( {x,t} \right) = U\left( \Omega \right)e^{{i\xi \left( {x,t} \right)}} , \quad v\left( {x,t} \right) = G\left( \Omega \right), \\ & \xi \left( {x,t} \right) = - \delta x + \omega t + \theta , \quad \Omega = x - ct, \\ \end{aligned}$$
(35)

Let \(v, \theta , \omega\) and \(\delta\) denote the frequency, phase constant, wave number, and velocity of the soliton respectively. By inserting Eq. (35) into the first part of the system (34) and separating the real and imaginary parts, the real part takes the following form:

$$\begin{aligned} & cU^{\prime\prime}\left( \Omega \right) + \omega \left( {1 - \delta } \right)U\left( \Omega \right) + \delta G\left( \Omega \right)U\left( \Omega \right) + i\left( {\omega - c\left( {1 - \delta } \right)} \right)U^{\prime}\left( \Omega \right) - G\left( \Omega \right)U^{\prime}\left( \Omega \right) - G^{\prime}\left( \Omega \right)U\left( \Omega \right) = 0, \\ & G^{\prime}\left( \Omega \right) + \frac{{2c \in n^{2} }}{m}U\left( \Omega \right)U^{\prime}\left( \Omega \right) = 0. \\ \end{aligned}$$
(36)

Equation (36), once integrated, gives the following expression

$$G\left( \Omega \right) = - \frac{{c\varepsilon n^{2} }}{m}U^{2} \left( \Omega \right).$$
(37)

Inserting Eq. (37) into the first part of Eq. (36) and separating the real and imaginary parts yields:

$$cU^{\prime\prime}\left( \Omega \right) + \omega \left( {1 - \delta } \right)U\left( \Omega \right) - \frac{{\delta c\varepsilon n^{2} }}{m}U^{3} \left( \Omega \right) = 0.$$
(38)

where the imaginary part is represented by

$$\left( {\omega - c\left( {1 - \delta } \right)} \right)U^{\prime}\left( \Omega \right) + \frac{{3c\varepsilon n^{2} }}{m}U^{\prime\prime}\left( \Omega \right)U^{\prime}\left( \Omega \right) = 0.$$
(39)

We determine \(N=1\) by applying the hbp, by balancing the highest order nonlinear term and the highest order derivative term. After substituting this determined value of N into Eq. (5), the solution is obtained in its simplified form as

$$U\left( \eta \right) = a_{0} + a_{1} Q\left( \Omega \right).$$
(40)

3 Investigating the realms of bifurcation analysis, chaotic behavior, and sensitivity analysis in relation to the governing equation

This section delivers an in-depth exploration of bifurcation analysis, chaotic behavior, and sensitivity analysis as they apply to the governing equation.

3.1 Bifurcation analysis

In this subsection, we closely examine the parameter-driven representation via bifurcation theory. By applying the Galilean transformation to Eq. (38), we transform it into the ensuing dynamical system, setting the stage for the implementation of bifurcation concepts.

$$\left\{ \begin{aligned} & \frac{{dU}}{{d\Omega }} = \Phi , \\ & \frac{{d\Phi }}{{d\Omega }} = \Re _{1} U^{3} \left( \Omega \right) - \Re _{2} U\left( \Omega \right), \\ \end{aligned} \right.$$
(41)

where, \({\mathfrak{R}}_{1}=\frac{\delta \epsilon {n}^{2}}{m}\) and \(\Re_{2} = \frac{{\omega \left( {1 - \delta } \right)}}{c}\). The system’s Hamiltonian, as defined in Eq. (41), is presented as follows

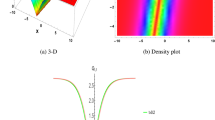
$$H\left( {U,\Phi } \right) = 0.5\Phi^{2} + 0.5\Re_{2} U^{2} - 0.25\Re_{1} U^{4} = \hbar ,$$
(42)

Here, \(\hslash\) is Hamiltonian constant. The system (41) has its equilibrium points at \(\in_{1} = \left( {0, 0} \right), \in_{2} = \left( {\frac{{\sqrt {\Re_{1} \Re_{2} } }}{{\Re_{1} }}, 0} \right), {\text{and}} \in_{2} = \left( {\frac{{ - \sqrt {\Re_{1} \Re_{2} } }}{{\Re_{1} }}, 0} \right).\) The determinant of the Jacobian matrix for system (41) is \(D\left( {U, \Phi } \right) = - 3\Re_{1} U^{2} + \Re_{2} .\) Furthermore, it is established that (U,Φ) represents a saddle point, center point, or cuspid point, corresponding to when D(U,Φ) is less than zero, greater than zero, and equal to zero, respectively. The possible results from modifying the relevant parameter are outlined below. Case 1: \({\mathfrak{R}}_{1}>0\) and \({\mathfrak{R}}_{2}>0\), Case 2: \({\mathfrak{R}}_{1}<0\) and\({\mathfrak{R}}_{2}>0\), Case 3: \({\mathfrak{R}}_{1}<0\) and \({\mathfrak{R}}_{2}<0\) and Case 4: \({\mathfrak{R}}_{1}>0\) and \({\mathfrak{R}}_{2}<0.\) When parameters align with case 1 criteria, three equilibrium points emerge (0, 0), (− 2.8983, 0), and (2.8983, 0). The point (0, 0) is a center point as shown in Fig. 1a, and the remaining are saddle points. For case 2, the sole equilibrium point at (0, 0) serves as a center, illustrated in Fig. 1b. Case 3’s adherence to specific parameters reveals three equilibrium points: (0, 0), (− 0.9165, 0), and (0.9165, 0), with (0, 0) being a saddle point and the others center points, as seen in Fig. 1c. Finally, under case 4 conditions, there’s a singular equilibrium point at (0, 0), acting as a saddle, depicted in Fig. 1d.

Fig. 1
figure 1

Phase diagrams illustrating the bifurcations of the proposed system under diverse conditions for \({\mathfrak{R}}_{1}\) and \({\mathfrak{R}}_{2}\), contingent upon varying parameter values

Full size image

3.2 Chaotic analysis

In this subsection, we introduce the perturbed term into the dynamical system described by Eq. (41) to observe the chaotic trajectories it produces. The system, incorporating the perturbed term, is expressed as follows:

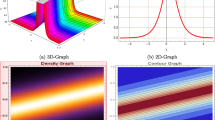
$$\left\{ \begin{aligned} & \frac{{dU}}{{d\Omega }} = \Phi , \\ & \frac{{d\Phi }}{{d\Omega }} = \Re _{1} U^{3} \left( \Omega \right) - \Re _{2} U\left( \Omega \right) + \vartheta \sin \left( {\gamma t} \right). \\ \end{aligned} \right.$$
(43)

In the revised perturbed system (42) mentioned above, the parameters \(\vartheta\) and \(\gamma\) play crucial roles. They signify the magnitude and frequency of an external force applied to the dynamical system, respectively. We showcase both 2D and 3D phase portraits for the disturbed system. Upon examining the phase portraits, intricate and captivating patterns emerge. Observations from Figs. 2 and 3 reveal diverse dynamics. These findings highlight the system’s dynamics’ sensitivity to variations in the parameter γ, providing deep insights into the impact of the perturbed term \(\vartheta \sin \left( {\gamma t} \right)\) on the system’s overall behavior. This enhanced understanding of how the system responds to changes in parameters deepens our knowledge of the complex interplay between γ, the perturbation term, and the system’s dynamics. Such insights are invaluable, significantly enriching our understanding of how minor parameter adjustments can influence the system’s path, thereby facilitating more precise predictions of its behavior under different scenarios.

Fig. 2
figure 2

2D and 3D chaotic visual representations of Eq. (43), with the following parameters assumed \(\vartheta =-0.1, \gamma =\pi , m=0.1, \omega =-0.3, n=0.5, \varepsilon = -0.5, \text{and}\, c=0.2\)

Full size image
Fig. 3
figure 3

2D and 3D chaotic visual representations of Eq. (43), with the following parameters assumed \(\vartheta =0.1, \gamma =\pi , m=0.1, \omega =-0.3, n=0.5, \varepsilon = -0.5, \text{and}\, c=0.2\)

Full size image

3.3 Sensitivity analysis

In this section, we demonstrate the sensitivity behavior of the dynamical system (41) using various sets of initial conditions. The system’s initial conditions are specified as follows: \(U\left( 0 \right) = 0.1,\;\Phi \left( 0 \right) = 0\), \(U\left( 0 \right) = 0,\;\Phi \left( 0 \right) = 0.1\), \(U\left( 0 \right) = 0.2,\;\Phi \left( 0 \right) = 0\), and \(U\left( 0 \right) = 0, \;\Phi \left( 0 \right) = 0.2\). The outcomes derived from this efficient approach are illustrated in Fig. 4. From examining the figures, it becomes evident that minor modifications in the initial conditions can result in significant alterations in the system’s dynamics.

Fig. 4
figure 4

Numerical illustrations of the state variables versus time, with parameters set as \(m=0.1, \omega =0.3, n=0.5, \varepsilon = 0.5, \text{and} c=0.2\) with various initial conditions

Full size image

4 Exact solution of the Shynaray IIA equation by IMGREMM

Substitute Eqs. (8 and 40) in Eq. (38), we obtain the following equation using Maple.

$$\begin{aligned} \frac{1}{m} & (\omega ma_{0} + \omega ma_{1} Q\left( \Omega \right) - \omega m\delta a_{0} - \omega m\delta a_{1} Q\left( \Omega \right) - \delta \varepsilon cn^{2} a_{0}^{3} - 3\delta \varepsilon cn^{2} a_{0}^{2} a_{1} Q\left( \Omega \right) \\ & \quad - 3\delta \varepsilon cn^{2} a_{0} a_{1}^{2} Q^{2} \left( \Omega \right) - \delta \varepsilon cn^{2} c_{1}^{3} Q^{3} \left( \Omega \right) + ca_{1} m\beta_{0} \beta_{1} + 2ca_{1} m\beta_{0} \beta_{2} Q\left( \Omega \right) \\ & \quad + ca_{1} m\beta_{1}^{2} Q\left( \Omega \right) + 2ca_{1} m\beta_{1} Q^{2} \left( \Omega \right)\beta_{2} + 2ca_{1} m\beta_{2}^{2} Q^{3} \left( \Omega \right) + 2ca_{1} m\beta_{0} \beta_{2} Q\left( \Omega \right) \\ & \quad + ca_{1} m\beta_{1}^{2} Q\left( \Omega \right) + 3ca_{1} m\beta_{1} \beta_{2} Q^{2} \left( \Omega \right) + 2ca_{1} m\beta_{1} \beta_{2}^{2} Q^{2} \left( \Omega \right) = 0 \\ \end{aligned}$$
(44)

By equating the coefficients of various power of \(Q^{i} \left( \Omega \right)\) to zero, we derive a system of equations with the following forms:

$$Q^{0} \left( \Omega \right):\frac{1}{m}\left( {\omega ma_{0} - \omega m\delta a_{0} - \delta \varepsilon cn^{2} a_{0}^{3} + ca_{1} ma_{0} a_{1} } \right) = 0$$
(45)
$$Q^{1} \left( \Omega \right):\frac{1}{m}\left( {\omega ma_{1} - \omega m\delta a_{1} - 3\delta \varepsilon cn^{2} a_{0}^{2} a_{1} + 1ca_{1} n\beta_{0} \beta_{2} + ca_{1} m\beta_{1}^{2} } \right) = 0$$
(46)
$$Q^{2} \left( \Omega \right):\frac{1}{m}\left( { - 3\delta \varepsilon cn^{2} a_{0} a_{1}^{2} + 3ca_{1} m\beta_{1} \beta_{2} } \right) = 0$$
(47)
$$Q^{3} \left( \Omega \right): \frac{1}{m}\left( { - \delta \varepsilon cn^{2} a_{1}^{3} + 2ca_{1} m\beta_{2}^{2} } \right) = 0\left( {48} \right)$$
(48)

By solving the above system of equations with the help of Maple, we find the following values of coefficients:

$${a}_{0}=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n\sqrt{\frac{m}{\delta \varepsilon }}},$$
(49)
$${a}_{1}=\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n},$$
(50)
$${\upbeta }_{1}={\upbeta }_{1},$$
(51)
$${\upbeta }_{2}={\upbeta }_{2},$$
(52)
$${\upbeta }_{0}=\frac{1}{2}\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}.$$
(53)

For \({\beta }_{0}={\beta }_{1}=0, {\beta }_{2}\ne 0,\) the rational solution is

$${w}_{1}\left(\text{x},\text{t}\right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{1}{{\upbeta }_{2}(\Omega +\text{C})}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{1}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{1}{{\upbeta }_{2}\left(\Omega +\text{C}\right)}\right)\right)}^{2}.$$

For \({\beta }_{0}=0,\) the solutions in the form of exponential are

$${w}_{2}\left(\text{x},\text{t}\right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{{\beta }_{1}\phi }{{{\beta }_{2}(e}^{-{\beta }_{1}\left(\Omega +C\right)}+\varphi ) }\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{2}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{{\beta }_{1}\phi }{{{\beta }_{2}(e}^{-{\beta }_{1}\left(\Omega +C\right)}+\varphi ) }\right)\right)}^{2},$$
$${w}_{3}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{{\beta }_{1}{e}^{{\beta }_{1}\left(\Omega +C\right)}}{{{\beta }_{2}(e}^{{\beta }_{1}\left(\Omega +C\right)}+\varphi ) }\right){e}^{i\left(-\delta x+\omega t+\theta \right)},$$
$${v}_{3}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{{\beta }_{1}{e}^{{\beta }_{1}\left(\Omega +C\right)}}{{{\beta }_{2}(e}^{{\beta }_{1}\left(\Omega +C\right)}+\varphi ) }\right)\right)}^{2}.$$

For \(\rho ={\beta }_{1}^{2}-4{\beta }_{0}{\beta }_{2}>0, {\beta }_{1}{\beta }_{2}\ne 0\) or \({\beta }_{0}{\beta }_{2}\ne 0\) where \(p\) and \(q\) are real constants, the solutions in the form of trigonometric hyperbolic are given as

$${w}_{4}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{2\beta }_{2}}\mathit{tan}h\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}} \right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{4}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\begin{array}{c}\\ \pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{2\beta }_{2}}\mathit{tan}h\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}} \right)\end{array}\right)}^{2},$$
$${w}_{5}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{2\beta }_{2}}\mathit{cot}h\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{5}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{2\beta }_{2}}\mathit{cot}h\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right)\right)}^{2}$$
$${w}_{6}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{2\beta }_{2}}(\mathit{tan}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\pm isech\left(\sqrt{\rho }\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{{2\beta }_{2}}\right){e}^{i\left(-\delta x+\omega t+\theta \right)},$$
$${v}_{6}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\begin{array}{c}\\ \pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{2\beta }_{2}}(\mathit{tan}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\pm isech\left(\sqrt{\rho }\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{{2\beta }_{2}}\right)\end{array}\right)}^{2}$$
$${w}_{7}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{2\beta }_{2}}\left(\mathit{cot}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\pm \mathit{csc}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\right)-\frac{{\beta }_{1}}{{2\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{7}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{2\beta }_{2}}\left(\mathit{cot}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\pm \mathit{csc}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\right)-\frac{{\beta }_{1}}{{2\beta }_{2}}\right)\right)}^{2}$$
$${w}_{8}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}} \mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{4\beta }_{2}}(\mathit{tan}h\left(\frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)+coth\left( \frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{{2\beta }_{2}}\right){e}^{i\left(-\delta x+\omega t+\theta \right)},$$
$${v}_{8}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\begin{array}{c}\\ \pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho }}{{4\beta }_{2}}(\mathit{tan}h\left(\frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)+coth\left( \frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{{2\beta }_{2}}\right)\end{array}\right)}^{2}$$
$${w}_{9}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho \left({p}^{2}+{q}^{2}\right)}-p\sqrt{\rho }\mathit{cos}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)}{{2\beta }_{2}\left(p sinh\left(\sqrt{\rho }\left(\Omega +C\right)\right)+q\right)} -\frac{{\beta }_{1}}{{2\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{9}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{\rho \left({p}^{2}+{q}^{2}\right)}-p\sqrt{\rho }\mathit{cos}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)}{{2\beta }_{2}\left(p sinh\left(\sqrt{\rho }\left(\Omega +C\right)\right)+q\right)} -\frac{{\beta }_{1}}{{2\beta }_{2}}\right)\right)}^{2}$$
$${w}_{10}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}\mathit{cos}h\left( \frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)}{\sqrt{\rho } sinh\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)-{\beta }_{1}cosh\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{10}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}\mathit{cos}h\left( \frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)}{\sqrt{\rho } sinh\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)-{\beta }_{1}cosh\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)}\right)\right)}^{2}$$
$${w}_{11}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}\mathit{sin}h\left( \frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)}{\sqrt{\rho }\mathit{cos}h\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)-{\beta }_{1}\mathit{sin}h\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{11}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}\mathit{sin}h\left( \frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)}{\sqrt{\rho }\mathit{cos}h\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)-{\beta }_{1}\mathit{sin}h\left(\frac{\sqrt{\rho }}{2}\left(\Omega +C\right)\right)}\right)\right)}^{2}$$
$${w}_{12}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{2{\beta }_{0}\mathit{cos}h\left( \sqrt{\rho }\left(\Omega +C\right)\right)}{\sqrt{\rho }\mathit{sin}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)-{\beta }_{1}\mathit{cos}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\pm i\sqrt{\rho }}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{12}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\begin{array}{c}\\ \pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{2{\beta }_{0}\mathit{cos}h\left( \sqrt{\rho }\left(\Omega +C\right)\right)}{\sqrt{\rho }\mathit{sin}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)-{\beta }_{1}\mathit{cos}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\pm i\sqrt{\rho }}\right)\end{array}\right)}^{2}$$
$${w}_{13}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}sinh\left( \sqrt{\rho }\left(\Omega +C\right)\right)}{\sqrt{\rho }cosh\left(\sqrt{\rho }\left(\Omega +C\right)\right)-{\beta }_{1}\mathit{sin}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\pm \sqrt{\rho }}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{13}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}sinh\left( \sqrt{\rho }\left(\Omega +C\right)\right)}{\sqrt{\rho }cosh\left(\sqrt{\rho }\left(\Omega +C\right)\right)-{\beta }_{1}\mathit{sin}h\left(\sqrt{\rho }\left(\Omega +C\right)\right)\pm \sqrt{\rho }}\right)\right)}^{2},$$
$${w}_{14}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}sinh\left(\frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)cosh\left(\frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)}{2\sqrt{\rho }{cosh}^{2}\left(\frac{\sqrt{\rho }}{4}\left(\xi +C\right)\right)-2{\beta }_{1}\mathit{sin}h\left(\frac{\sqrt{\rho }}{4}\sqrt{\rho }\left(\Omega +C\right)\right)\mathit{cos}h\left(\frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)-\sqrt{\rho } }\right){e}^{i(-\delta x+\omega t+\theta )},$$

\({v}_{14}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}sinh\left(\frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)cosh\left(\frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)}{2\sqrt{\rho }{cosh}^{2}\left(\frac{\sqrt{\rho }}{4}\left(\xi +C\right)\right)-2{\beta }_{1}\mathit{sin}h\left(\frac{\sqrt{\rho }}{4}\sqrt{\rho }\left(\Omega +C\right)\right)\mathit{cos}h\left(\frac{\sqrt{\rho }}{4}\left(\Omega +C\right)\right)-\sqrt{\rho } }\right)\right)}^{2}\).

For \(\rho ={\beta }^{2}-4{\beta }_{0}{\beta }_{2}<0, {\beta }_{1}{\beta }_{2}\ne 0,\) or \(({\beta }_{0}{\beta }_{2}\ne 0)\) with \({p}^{2}-{q}^{2}>0,\) the solutions of trigonometric form are given as

$${w}_{15}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{2{\beta }_{2}}\mathit{tan}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{15}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{2{\beta }_{2}}\mathit{tan}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right)\right)}^{2}$$
$${w}_{16}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{2{\beta }_{2}}\mathit{cot}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{16}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{2{\beta }_{2}}\mathit{cot}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right)\right)}^{2}$$
$${w}_{17}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{2{\beta }_{2}} \left(\mathit{tan}\left(\sqrt{-\rho }\left(\Omega +C\right)\right) \pm \mathit{sec}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{17}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{2{\beta }_{2}} \left(\mathit{tan}\left(\sqrt{-\rho }\left(\Omega +C\right)\right) \pm \mathit{sec}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right)\right)}^{2}$$
$${w}_{18}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{2{\beta }_{2}}\left(\mathit{cot}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\pm \mathit{csc}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{18}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{2{\beta }_{2}}\left(\mathit{cot}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\pm \mathit{csc}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right)\right)}^{2}$$
$${w}_{19}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}} \pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{4{\beta }_{2}}\left(\mathit{tan}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)-cot\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{19}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho }}{4{\beta }_{2}}\left(\mathit{tan}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)-cot\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)\right)-\frac{{\beta }_{1}}{2{\beta }_{2}}\right)\right)}^{2}$$
$${w}_{20}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}} \pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho ({p}^{2}-{q}^{2})}-p\sqrt{-\rho }\mathit{cos}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)}{2{\beta }_{2}\left(psin(\sqrt{-\rho }\left(\Omega +C\right)+q\right)}-\frac{{\beta }_{1}}{2{\beta }_{2}}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{20}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\sqrt{-\rho ({p}^{2}-{q}^{2})}-p\sqrt{-\rho }\mathit{cos}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)}{2{\beta }_{2}\left(psin(\sqrt{-\rho }\left(\Omega +C\right)+q\right)}-\frac{{\beta }_{1}}{2{\beta }_{2}}\right)\right)}^{2}$$
$${w}_{21}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}\mathit{cos}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)}{\sqrt{-\rho }\mathit{sin}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)+{\beta }_{1}\mathit{cos}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{21}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}\mathit{cos}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)}{\sqrt{-\rho }\mathit{sin}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)+{\beta }_{1}\mathit{cos}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)}\right)\right)}^{2}$$
$${w}_{22}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}\mathit{sin}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)}{\sqrt{-\rho }\mathit{cos}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)-{\beta }_{1}\mathit{sin}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{22}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\omega \delta }{{m}_{2}c}\mathit{sin}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)}{\sqrt{-\rho }\mathit{cos}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)-{\beta }_{1}\mathit{sin}\left(\frac{\sqrt{-\rho }}{2}\left(\Omega +C\right)\right)}\right)\right)}^{2}$$
$${w}_{23}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\mathit{\omega \delta }}{{m}_{2}c}\mathit{cos}\left(\sqrt{-\rho }\left(\Omega +C\right)\right) }{{\beta }_{1}cos\left(\sqrt{-\rho }\left(\Omega +C\right)\right)+\sqrt{-\rho }sin\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\pm \sqrt{-\rho }}\right){e}^{i\left(-\delta x+\omega t+\theta \right)},$$
$${v}_{23}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\mp \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\mathit{\omega \delta }}{{m}_{2}c}\mathit{cos}\left(\sqrt{-\rho }\left(\Omega +C\right)\right) }{{\beta }_{1}cos\left(\sqrt{-\rho }\left(\Omega +C\right)\right)+\sqrt{-\rho }sin\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\pm \sqrt{-\rho }}\right)\right)}^{2}$$
$${w}_{24}^{\pm }\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\mathit{\omega \delta }}{{m}_{2}c}\mathit{sin}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)}{{\beta }_{1}sin\left(\sqrt{-\rho }\left(\Omega +C\right)\right)-\sqrt{-\rho }cos\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\pm \sqrt{-\rho }}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{24}^{\pm }\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\mathit{\omega \delta }}{{m}_{2}c}\mathit{sin}\left(\sqrt{-\rho }\left(\Omega +C\right)\right)}{{\beta }_{1}sin\left(\sqrt{-\rho }\left(\Omega +C\right)\right)-\sqrt{-\rho }cos\left(\sqrt{-\rho }\left(\Omega +C\right)\right)\pm \sqrt{-\rho }}\right)\right)}^{2}$$
$${w}_{25}\left(\Omega \right)=\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\mathit{\omega \delta }}{{m}_{2}c}\mathit{sin}\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)\mathit{cos}\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)}{\sqrt{-\rho }{cos}^{2}\left(\frac{\sqrt{-\rho }}{4}(\Omega +C)\right)-{\beta }_{1}\mathit{sin}\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)\mathit{cos}\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)-\frac{1}{2}\sqrt{-\rho }}\right){e}^{i(-\delta x+\omega t+\theta )},$$
$${v}_{25}\left(\text{x},\text{t}\right)=-\frac{c\epsilon {n}^{2}}{m}{\left(\pm \frac{1}{2}\frac{m{m}_{1}\sqrt{2}}{\delta \varepsilon n \sqrt{\frac{m}{\delta \varepsilon }}}\pm \frac{\sqrt{2}\sqrt{\frac{m}{\delta \varepsilon }}{m}_{2}}{n}\left(\frac{\frac{c{m}_{1}^{2}-2\omega +2\mathit{\omega \delta }}{{m}_{2}c}\mathit{sin}\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)\mathit{cos}\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)}{\sqrt{-\rho }{cos}^{2}\left(\frac{\sqrt{-\rho }}{4}(\Omega +C)\right)-{\beta }_{1}\mathit{sin}\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)\mathit{cos}\left(\frac{\sqrt{-\rho }}{4}\left(\Omega +C\right)\right)-\frac{1}{2}\sqrt{-\rho }}\right)\right)}^{2}$$

5 Graphical representation

This section graphically describes the structures of the solutions derived in Sect. 3 using suitable values for the free parameters. For Figs. 5 and 6, we assigned \(\delta =2, \theta =0.5, {m}_{1}=1, \omega =0.1, {m}_{0}=1,\) and \({m}_{2}=2\) for the solutions \({w}_{2}\left(\Omega \right)\) and \({v}_{2}\left(\Omega \right)\) to obtain the dark, bright kink, and multiple soliton wave propagation in 3D and 2D at \(t=0.2\). Figure 7 presents the rogue soliton waves in 3D and 2D plots for the absolute and real parts of \({v}_{7}(\Omega )\) for \(\delta =-0.2, \theta =0.5, {m}_{1}=1, \omega =1.5, {m}_{0}=1,\) and \({m}_{2}=-2\). In Figs. 8 and 9, we set \(\delta =-2, \theta =0.5, {m}_{1}=1, \omega =2, {m}_{0}=1,\) and \({m}_{2}=2\) to obtain dark, kink, anti-kink soliton and multiple wave propagations in 3D form and 2D at \(t=0.2\) for the solutions \({w}_{9}\left(\Omega \right),\) and \({w}_{10}(\Omega ).\) The different solitary wave structures could justify that the method is robust on the considered model and will enhance the practical applications in industries and other important places. These solutions will be of high significance in all areas of applications of shynaray IIA equation such as optical communications, tsunami and tidal wave phenomena The solutions obtained in this work are more accurate, concise and more general compared to the solutions obtained using the direct algebra method (Faridi et al. 2024), the improved Sardar method (Faridi et al. 2024; Khan et al. 2024) and the Φ6-model expansion approach (Tipu et al. 2024). The employed approach in this work yields the rational function exponential solutions, different periodic function solutions, and numerous hyperbolic function solutions. Also, the graphical visualization further illustrates the breather soliton, envelope soliton, dark-wave soliton, multiple soliton, and bright-wave soliton propagations in both 2D and 3D.

Fig. 5
figure 5

The dark and kink soliton waves in 3D and 2D plots for the absolute, real and imaginary parts of \({w}_{2}(\Omega )\)

Full size image
Fig. 6
figure 6

The dark and bright soliton waves in 3D and 2D plots for the absolute and real parts of \({v}_{2}(\Omega )\)

Full size image
Fig. 7
figure 7

The peakon soliton waves in 3D and 2D plots for the absolute and real parts of \({v}_{7}(\Omega )\)

Full size image
Fig. 8
figure 8

The multiple soliton waves in 3D and 2D plots for the absolute, real and imaginary parts of \({w}_{9}(\Omega )\)

Full size image
Fig. 9
figure 9

The envelope soliton waves in 3D and 2D plots for the absolute, real and imaginary parts of \({w}_{10}(\Omega )\)

Full size image

6 Conclusion

In this research article, we successfully construct new exact solutions for the Shynaray-IIA equation applying IGREMM. Through the investigation, a set of exact solutions including rational, exponential, trigonometric and hyperbolic trigonometric forms are established, providing insight into the dynamics and behavior of S-IIAE. The intricate dynamics of the equation have been unveiled by employing a meticulous derivation of the associated dynamical system through the Galilean transformation, together with a careful examination of bifurcation events using planar dynamical system theory. By introducing perturbations, it became feasible to perform a comprehensive analysis of chaotic phenomena, which were clearly illustrated in phase pictures. The sensitivity analysis, conducted using the Runge–Kutta method, offered a compelling demonstration of the robustness of the solutions. Even slight modifications in initial conditions did not change this outcome. The aforementioned findings have wide significance in many different areas of applied mathematics and physics such as optical communications, tsunami and tidal wave phenomena.. Some of the obtained solutions are plotted in various dimensional graphs that show the direct analysis of solution behaviors. The suggested approach creates new opportunities for solving other complex nonlinear equations in addition to providing insights into S-IIAE. This is an interesting path for advancement in future investigations. Analytical, semi-analytical, and numerical solutions could be explored in future research on S-IIAE with the goal of revealing a variety of fascinating model outcomes. These studies could cover topics consisting of lie symmetry analysis, consistency of solutions, modulation instability, and physical viability.