1 Introduction

Telegraph equations have great significance in areas of physics [1, 2], mathematics [3,4,5], wave propagation [6], signal analysis [7], random walk theory [8] and other disciplines. These are used to produce and design high frequency and voltage transmission lines.

In particular, fractional space telegraph equation has been analysed explicitly in [9,10,11,12,13,14,15,16,17,18,19,20]. Neville et al [9] obtained numerical solution of fractional telegraph equation using finite difference method and also established its stability. Orsingher and Zhao [11] studied the same type of problem and obtained the Fourier transform of the obtained solution. Adomain decomposition method (ADM) is used by Momani [10] to obtain the solution of space and time-fractional telegraph problem. Same type of problem has been solved by Ahmad and Ibrahim [12] using the method of separation of variables. Zhao and Li [13] used difference method and finite element method to find the approximate solution of the space–time fractional telegraph equation. A new perturbative Laplace method has been developed by Khan et al [14] for solving space–time fractional telegraph equations. Garg et al [15] implemented transform method to obtain the solution of space–time fractional telegraph equation. The homotopy perturbation method has successfully been incorporated by Yıldırım [16] to obtain an approximate solution. Sevimlican [17] used variational iteration method (VIM) for the solution of governing equation. Ford et al [18] developed quadrature formula approach and also obtained the stability condition. Alkahtani et al [19] applied VIM and Sumudu transform to get the solution. A new technique based on Laplace and VIM has been established by Alawad et al [20] for space–time fractional telegraph equations.

In the aforementioned works, one may observe that the parameters, variables, initial and boundary conditions etc. are defined exactly. But in real life, rather than the exact value, one may have only incomplete information or vague estimations, because in general those are found by some experiment, observation, experience etc. So, to model these types of uncertainties and vagueness, one may use fuzzy parameters and variables [21,22,23].

Both uncertainty and fractional differential equations play important roles in real-life applications. Various contributions can be seen to the theory of fuzzy differential equation [24,25,26,27,28] and fuzzy fractional differential equations [29,30,31,32,33,34,35,36,37]. The idea of fuzzy fractional differential equation has been first introduced by Agarwal et al [29]. Using the concept of [29], Arshad and Lupulescu [30] established some results on the existence and uniqueness of solutions.

Souahi et al [33] discussed the existence of solution and uniqueness properties of higher-order equations. Allahviranloo et al [31] studied explicit solution of fuzzy/uncertain fractional differential equations. VIM is used by Khodadadi and Celik [32] for the solution. Recently, Chakraverty and Tapaswini [34, 35] used homotopy perturbation method with double parametric form for solving fuzzy fractional Fornberg–Whitham and diffusion equations. Very recently, Behera et al [36] successfully obtained the responses of fuzzy fractionally damped beam using homotopy perturbation method. Rivaz et al [37] used the generalised differential transform method for the solution of fuzzy fractional ordered equation.

In the present work, ADM [38, 39] has been used to solve imprecisely defined space-fractional telegraph equation. Uncertainties involved in the initial and boundary conditions are modelled in terms of Gaussian and triangular fuzzy numbers. Using this method, one can write the solution in power series form or compact form, which is the main advantage of this method. Also it converges rapidly. Convergence analysis of ADM can be found in [38, 39]. Some researchers have successfully executed ADM for differential equations with uncertainty [40,41,42,43,44]. However, the existing methods applied splitting approach to convert the main equation into two crisp differential equations for the solution, whereas the present approach converts the main equation into a single crisp form using double parametric for the solution.

Organisation of this paper is given as follows. The proposed procedure is discussed in §2. In §3, ADM has been implemented to find the general solution. Different cases have been studied in §4 depending upon the value of the function or variable involved. In §5, numerical results have been presented with analysis. Finally, §6 gives the conclusions.

2 Double parametric form of fuzzy space-fractional telegraph equation

Let us consider the fuzzy space-fractional telegraph equation as

$$\begin{aligned}&\frac{\partial ^{\alpha }{\tilde{p}}(y,t)}{\partial y^{\alpha }}\nonumber \\&\quad =\frac{\partial ^{2}{\tilde{p}}(y,t)}{\partial t^{2}}+\frac{\partial {\tilde{p}}(y,t)}{\partial t} +{\tilde{p}}(y,t)+{\tilde{g}}(y,t),\quad \nonumber \\&\qquad t\ge 0,\quad 0 <\alpha \le 2, \end{aligned}$$
(1)

subjected to fuzzy initial and boundary conditions as

$$\begin{aligned}&{\tilde{p}}(0,t)={\tilde{\delta }}_{1} f_{1} (t),\quad t\ge 0, \\&\frac{\partial {\tilde{p}}(0,t)}{\partial y}={\tilde{\delta }}_{2} f_{2} (t),\quad t\ge 0 \end{aligned}$$

and

$$\begin{aligned} {\tilde{p}}(y,0)={\tilde{\delta }}_{3} s(y),\quad 0<y<1, \end{aligned}$$

where \({\partial ^{\alpha }}/{\partial y^{\alpha }}\) is the Caputo derivative [45] of order \(\alpha \) and \({\tilde{p}}(y,t)\) denotes the causal fuzzy function of space.

Equation (1) may be rewritten as

$$\begin{aligned}&\frac{\partial ^{2}{\tilde{p}}(x,t)}{\partial y^{2}}\nonumber \\&\quad =\frac{\partial ^{2-\alpha }}{\partial y^{2-\alpha }}\left( {\frac{\partial ^{2}{\tilde{p}}(y,t)}{\partial t^{2}}+\frac{\partial {\tilde{p}}(y,t)}{\partial t}+{\tilde{p}}(y,t)+{\tilde{g}}(y,t)} \right) ,\nonumber \\&\qquad t\ge 0,\quad 0 <\alpha \le 2. \end{aligned}$$
(2)

Using the single parametric form, the above fuzzy space-fractional differential equation (eq. (2)) can be written as

$$\begin{aligned}&\left[ {\frac{\partial ^{2}{\underline{p}}(y,t)}{\partial y^{2}},\frac{\partial ^{2}\bar{{p}}(y,t)}{\partial y^{2}}} \right] =\frac{\partial ^{2-\alpha }}{\partial y^{2-\alpha }}\nonumber \\&\qquad \times \left( {\begin{array}{l} \left[ {\dfrac{\partial ^{2}{\underline{p}}(y,t)}{\partial t^{2}},\dfrac{\partial ^{2}\bar{{p}}(y,t)}{\partial t^{2}}} \right] \\ +\left[ {\dfrac{\partial {\underline{p}}(y,t)}{\partial t},\dfrac{\partial \bar{{p}}(y,t)}{\partial t}} \right] \\ +[ {{\underline{p}}(y,t),\bar{{p}}(y,t)} ]+[ {{\underline{g}}(y,t),\bar{{g}}(y,t)} ] \\ \end{array}} \right) , \end{aligned}$$
(3)

subject to fuzzy initial and boundary conditions

$$\begin{aligned}&[ {{\underline{p}}(0,t;r),\bar{{p}}(0,t;r)} ]\nonumber \\&\quad = [{\underline{\delta } }_{1} (r), \bar{{\delta }}_{1} (r)]f_{1} (t),\quad t\ge 0, \nonumber \\&\left[ {\frac{\partial {\underline{p}}(0,t;r)}{\partial y},\frac{\partial \bar{{p}}(0,t;r)}{\partial y}} \right] \nonumber \\&\quad = [{\underline{\delta } }_{2} (r), \bar{{\delta }}_{2} (r)]f_{2} (t),\quad t\ge 0, \nonumber \\&[ {{\underline{p}}(y,0;r), \bar{{p}}(y,0;r)} ]\nonumber \\&= [{\underline{\delta } }_{3} (r), \bar{{\delta }}_{3} (r)]s(y), \end{aligned}$$
(4)

where \(r\in [0, 1], 0<y<1.\)

After that, using double parametric form [36], eq. (3) can be expressed as

$$\begin{aligned}&\left( {\beta \left( {\frac{\partial ^{\alpha }\bar{{p}}(y,t;r)}{\partial y^{\alpha }}-\frac{\partial ^{\alpha }{\underline{p}}(y,t;r)}{\partial y^{\alpha }}} \right) +\frac{\partial ^{\alpha }{\underline{p}}(y,t;r)}{\partial y^{\alpha }}} \right) \nonumber \\&\quad = \frac{\partial ^{2-\alpha }}{\partial y^{2-\alpha }}\nonumber \\&\qquad \times \left( {\begin{array}{l} \left( \beta \left( {\dfrac{\partial ^{2}\bar{{p}}(y,t;r)}{\partial t^{2}}-\dfrac{\partial ^{2}{\underline{p}}(y,t;r)}{\partial t^{2}}} \right) \right. \\ \qquad \left. +\dfrac{\partial ^{2}{\underline{p}}(y,t;r)}{\partial t^{2}} \right) \\ +\left( \beta \left( {\dfrac{\partial \bar{{p}}(y,t;r)}{\partial t}-\dfrac{\partial {\underline{p}}(y,t;r)}{\partial t}} \right) \right. \\ \qquad \left. +\dfrac{\partial {\underline{p}}(y,t;r)}{\partial t} \right) \\ +( {\beta ( {\bar{{p}}(y,t;r)-{\underline{p}}(y,t;r)} )+{\underline{p}}(y,t;r)} )\\ +( {\beta ( {\bar{{g}}(y,t;r)-{\underline{g}}(y,t;r)} )+{\underline{g}}(y,t;r)} ) \\ \end{array}} \right) \nonumber \\ \end{aligned}$$
(5)

subject to the initial and boundary conditions

$$\begin{aligned}&( {\beta ( {\bar{{p}}(0,t;r)-{\underline{p}}(0,t;r)} )+{\underline{p}}(0,t;r)} )\nonumber \\&\quad =( {( {\bar{{\delta }}_{1} (r)-{\underline{\delta } }_{1} (r)} )+{\underline{\delta } }_{1} (r)} )f_{1} (t) \nonumber \\&\beta \left( {\frac{\partial \bar{{p}}(0,t;r)}{\partial y}-\frac{\partial {\underline{p}}(0,t;r)}{\partial y}} \right) +\frac{\partial {\underline{p}}(0,t;r)}{\partial y}\nonumber \\&\quad =( {( {\bar{{\delta }}_{2} (r)-{\underline{\delta } }_{2} (r)} )+{\underline{\delta } }_{2} (r)} )f_{2} (t),\quad t\ge 0 \nonumber \\&( {\beta ( {\bar{{p}}(y,0;r)-{\underline{p}}(y,0;r)} )+{\underline{p}}(y,0;r)} )\nonumber \\&\quad =( {( {\bar{{\delta }}_{3} (r)-{\underline{\delta } }_{3} (r)} )+{\underline{\delta } }_{3} (r)} )s(y),\quad 0<y<1 \end{aligned}$$
(6)

where \(r\hbox {, }\beta \in [0,1]\).

Let

$$\begin{aligned}&\left( {\beta \left( {\frac{\partial ^{2}\bar{{p}}(y,t;r)}{\partial y^{2}}-\frac{\partial ^{2}{\underline{p}}(y,t;r)}{\partial y^{2}}} \right) +\frac{\partial ^{2}{\underline{p}}(y,t;r)}{\partial y^{2}}} \right) \\&\quad =\frac{\partial ^{2}{\tilde{p}}(y,t;r,\beta )}{\partial y^{2}}, \\&\left( {\beta \left( {\frac{\partial ^{2}\bar{{p}}(y,t;r)}{\partial t^{2}}-\frac{\partial ^{2}{\underline{p}}(y,t;r)}{\partial t^{2}}} \right) +\frac{\partial ^{2}{\underline{p}}(y,t;r)}{\partial t^{2}}} \right) \\&\quad =\frac{\partial ^{2}{\tilde{p}}(y,t;r,\beta )}{\partial t^{2}}, \\&\left( {\beta \left( {\frac{\partial \bar{{p}}(y,t;r)}{\partial t}-\frac{\partial {\underline{p}}(y,t;r)}{\partial t}} \right) +\frac{\partial {\underline{p}}(y,t;r)}{\partial t}} \right) \\&\quad =\frac{\partial {\tilde{p}}(y,t;r,\beta )}{\partial t}, \\&( {\beta (\bar{{p}}(y,t;r)-{\underline{p}}(y,t;r))+{\underline{p}}(y,t;r)} )\\&\quad ={\tilde{p}}(y,t;r,\beta ), \\&( {\beta ( {\bar{{g}}(y,t;r)-{\underline{g}}(y,t;r)} )+{\underline{g}}(y,t;r)} )\\&\quad ={\tilde{g}}(y,t;r,\beta ), \\&( {\beta ( {\bar{{p}}(0,t;r)-{\underline{p}}(0,t;r)} )+{\underline{p}}(0,t;r)} )\\&\quad ={\tilde{p}}(0,t;r,\beta ), \\&\beta \left( {\frac{\partial \bar{{p}}(0,t;r)}{\partial y}-\frac{\partial {\underline{p}}(0,t;r)}{\partial y}} \right) +\frac{\partial {\underline{p}}(0,t;r)}{\partial y}\\&\quad =\frac{\partial {\tilde{p}}(0,t;r,\beta )}{\partial y}, \\&( {\beta ( {\bar{{p}}(y,0;r)-{\underline{p}}(y,0;r)} )+{\underline{p}}(y,0;r)} )\\&\quad ={\tilde{p}}(y,0;r,\beta ), \\&( {( {\bar{{\delta }}_{1} (r)-{\underline{\delta } }_{1} (r)} )+{\underline{\delta } }_{1} (r)} )={\tilde{\delta }}_{1} (r;\beta ),\\&\qquad ( {( {\bar{{\delta }}_{2} (r)-{\underline{\delta } }_{2} (r)} )+{\underline{\delta } }_{2} (r)} )={\tilde{\delta }}_{2} (r;\beta )\\&\hbox {and}\\&( {( {\bar{{\delta }}_{3} (r)-{\underline{\delta } }_{3} (r)} )+{\underline{\delta } }_{3} (r)} )={\tilde{\delta }}_{3} (r;\beta ). \end{aligned}$$

Substituting these values in eqs (5) and (6) we get

$$\begin{aligned}&\frac{\partial ^{2}{\tilde{p}}(y,t;r,\beta )}{\partial y^{2}}\nonumber \\&\quad =\frac{\partial ^{2-\alpha }}{\partial y^{2-\alpha }}\left( \frac{\partial ^{2}{\tilde{p}}(y,t;r,\beta )}{\partial t^{2}}\right. \nonumber \\&\qquad \left. +\frac{\partial {\tilde{p}}(y,t;r,\beta )}{\partial t}+{\tilde{p}}(y,t;r,\beta )+{\tilde{g}}(y,t;r,\beta ) \right) \nonumber \\ \end{aligned}$$
(7)

with initial and boundary conditions

$$\begin{aligned}&{\tilde{p}}(0,t;r,\beta )={\tilde{\delta }}_{1} (r;\beta )f_{1} (t), \nonumber \\&\frac{\partial {\tilde{p}}(0,t;r,\beta )}{\partial y}={\tilde{\delta }}_{2} (r;\beta )f_{2} (t), \nonumber \\&{\tilde{p}}(y,0;r,\beta )={\tilde{\delta }}_{3} (r;\beta )s(y). \end{aligned}$$
(8)

Hence, solving the above one may get the solution as \({\tilde{p}}(y,t;r,\beta )\). Substituting \(\beta =0\hbox { and }1\) gives the lower and upper bounds of the solution respectively in single parametric form. This can be expressed as

$$\begin{aligned} {\tilde{p}}(y,t;r,0)=\underline{p}(y,t;r) \end{aligned}$$

and

$$\begin{aligned} {\tilde{p}}(y,t;r,1)=\bar{{p}}(y,t;r). \end{aligned}$$

3 Solution using proposed methodology along with ADM

ADM has been applied to solve eq. (7), and so we have

$$\begin{aligned}&L_{yy} {\tilde{p}}(y,t;r,\beta )\nonumber \\&\quad =L_{y}^{2-\alpha } \left( L_{tt} {\tilde{p}}(y,t;r,\beta )+L_{t} {\tilde{p}}(y,t;r,\beta )\right. \nonumber \\&\qquad \left. +\,{\tilde{p}}(y,t;r,\beta )+{\tilde{g}}(y,t;r,\beta ) \right) \end{aligned}$$
(9)

where

$$\begin{aligned}&L_{t} \equiv \partial /{\partial t},\quad L_{tt} \equiv {\partial ^{2}}/{\partial t^{2}}, \quad \\&L_{y}^{2-\alpha } \equiv {\partial ^{2-\alpha }}/{\partial y^{2-\alpha }}\\&\hbox {and }\\&L_{yy} \equiv {\partial ^{2}}/{\partial y^{2}}. \end{aligned}$$

Apply the operator \(L_{yy}^{-1} \) on both sides of eq. (9), to yield

$$\begin{aligned}&L_{yy}^{-1} L_{yy} {\tilde{p}}(y,t;r,\beta )\nonumber \\&\quad =L_{yy}^{-1} ( L_{y}^{2-\alpha } ( L_{tt} {\tilde{p}}(y,t;r,\beta )\nonumber \\&\qquad \left. \left. +\,L_{t} {\tilde{p}}(y,t;r,\beta )+{\tilde{p}}(y,t;r,\beta )\right. \right. \nonumber \\&\qquad \left. \left. +\,{\tilde{g}}(y,t;r,\beta ) \right) \right) . \end{aligned}$$
(10)

Here \(L_{yy}^{-1} \) is the inverse operator of \(L_{yy} \).

This may then be written as

$$\begin{aligned}&L_{yy}^{-1} L_{yy} {\tilde{p}}(y,t;r,\beta )\\&\quad ={\tilde{p}}(y,t;r,\beta )-{\tilde{p}}(0,t;r,\beta )-y{\tilde{u}}_{y} (0,t;r,\beta ). \end{aligned}$$

Equation (9) becomes

$$\begin{aligned}&{\tilde{p}}(y,t;r,\beta )\nonumber \\&\quad ={\tilde{p}}(0,t;r,\beta )+y{\tilde{p}}_{y} (0,t;r,\beta )\nonumber \\&\qquad +\,L_{y}^{-\alpha } \left[ {\begin{array}{l} L_{tt} {\tilde{p}}(y,t;r,\beta )+L_{t} {\tilde{p}}(y,t;r,\beta ) \\ +{\tilde{p}}(y,t;r,\beta )+{\tilde{g}}(y,t;r,\beta ) \\ \end{array}} \right] . \end{aligned}$$
(11)

According to Adomian decomposition [38, 39] we assume an infinite series solution for unknown function \({\tilde{p}}(y,t;r,\beta )\) as

$$\begin{aligned} {\tilde{p}}(y,t;r,\beta )=\sum _{n=0}^\infty {{\tilde{p}}_{n} (y,t;r,\beta )} \end{aligned}$$
(12)

with

$$\begin{aligned}&{\tilde{p}}_{0} (x,t;r,\beta )\\&\quad ={\tilde{p}}(0,t;r,\beta )+y{\tilde{p}}_{y} (0,t;r,\beta )+L_{y}^{-\alpha } g(y,t;r,\beta ) \end{aligned}$$

and the components \({\tilde{p}}_{n} (y,t;r,\beta )\) where \(n>0\) are usually determined by

$$\begin{aligned}&{\tilde{p}}_{n} (x,t;r,\beta )\\&\quad =L_{y}^{-\alpha } \left( L_{tt} {\tilde{p}}_{n-1} (y,t;r,\beta )+L_{t} {\tilde{p}}_{n-1} (y,t;r,\beta )\right. \\&\qquad \left. +\,{\tilde{p}}_{n-1} (y,t;r,\beta ) \right) . \end{aligned}$$

Substituting these terms in eq. (12) one may get the approximate solution of eq. (7) as

$$\begin{aligned} {\tilde{p}}(y,t;r,\beta )= & {} {\tilde{p}}_{0} (y,t;r,\beta )+{\tilde{p}}_{1} (y,t;r,\beta )\\&+\,{\tilde{p}}_{2} (y,t;r,\beta )+{\tilde{p}}_{3} (y,t;r,\beta )+\cdots . \end{aligned}$$

The above series converges very rapidly [46,47,48,49], and rapid convergence means that only a few terms are required to get the approximate solutions.

4 Solution bounds for particular cases

In this section, two different cases are considered [10] depending upon the function \(f_{1} (t)\), \(f_{2} (t)\), s(y) and \({\tilde{g}}(y,t;r,\beta )\) as discussed in the following cases to find uncertain bounds for fuzzy fractional telegraph equations using the proposed technique. For Cases 1 and 2, the uncertainties are modelled through triangular and Gaussian fuzzy number respectively.

Case 1: For this case, let us consider

$$\begin{aligned}&f_{1} (t)=\mathrm{e}^{-t}, \quad f_{2} (t)=\mathrm{e}^{-t}, \quad \\&s(y)=\mathrm{e}^{-y}\quad \hbox { and }\quad {\tilde{g}}(y,t;r,\beta )=0 \end{aligned}$$

along with

$$\begin{aligned}&{\tilde{\delta }}_{1} (r,\beta )={\tilde{\delta }}_{2} (r,\beta )={\tilde{\delta }}_{3} (r,\beta )\\&\quad =\beta (0.4-0.4r) +(0.2r+0.8)={\tilde{\delta }}(r,\beta ). \end{aligned}$$

Hence, eq. (7) will become

$$\begin{aligned}&\frac{\partial ^{2}{\tilde{p}}(y,t;r,\beta )}{\partial y^{2}}=\frac{\partial ^{2-\alpha }}{\partial y^{2-\alpha }}\nonumber \\&\quad \times \left( {\frac{\partial ^{2}{\tilde{p}}(y,t;r,\beta )}{\partial t^{2}}+\frac{\partial {\tilde{p}}(y,t;r,\beta )}{\partial t}+{\tilde{p}}(y,t;r,\beta )} \right) \nonumber \\ \end{aligned}$$
(13)

with the initial and boundary conditions as

$$\begin{aligned}&{\tilde{p}}(0,t;r,\beta )={\tilde{\delta }}(r,\beta )\mathrm{e}^{-t}, \nonumber \\&\frac{\partial {\tilde{p}}(0,t;r,\beta )}{\partial y}={\tilde{\delta }}_{2} (r,\beta )\mathrm{e}^{-t}, \nonumber \\&{\tilde{p}}(y,0;r,\beta )={\tilde{\delta }}_{3} (r,\beta )\mathrm{e}^{-y}. \end{aligned}$$
(14)

By using ADM we have

$$\begin{aligned}&{\tilde{p}}_{0} (y,t;r,\beta )\nonumber \\&\quad = {\tilde{\delta }}(r,\beta )\mathrm{e}^{-t}(1+y), \end{aligned}$$
(15)
$$\begin{aligned}&{\tilde{p}}_{1} (y,t;r,\beta )\nonumber \\&\quad = {\tilde{\delta }}(r,\beta )\mathrm{e}^{-t}\left( {\frac{y^{\alpha }}{\Gamma (\alpha +1)}+\frac{y^{\alpha +1}}{\Gamma (\alpha +2)}} \right) , \end{aligned}$$
(16)
$$\begin{aligned}&{\tilde{p}}_{2} (y,t;r,\beta )\nonumber \\&\quad = {\tilde{\delta }}(r,\beta )\mathrm{e}^{-t}\left( {\frac{y^{2\alpha }}{\Gamma (2\alpha +1)}+\frac{y^{2\alpha +1}}{\Gamma (2\alpha +2)}} \right) , \end{aligned}$$
(17)
$$\begin{aligned}&{\tilde{p}}_{3} (y,t;r,\beta )\nonumber \\&\quad = {\tilde{\delta }}(r,\beta )\mathrm{e}^{-t}\left( {\frac{y^{3\alpha }}{\Gamma (3\alpha +1)}+\frac{y^{3\alpha +1}}{\Gamma (3\alpha +2)}} \right) , \end{aligned}$$
(18)
$$\begin{aligned}&{\tilde{p}}_{4} (y,t;r,\beta )\nonumber \\&\quad = {\tilde{\delta }}(r,\beta )\mathrm{e}^{-t}\left( {\frac{y^{4\alpha }}{\Gamma (4\alpha +1)}+\frac{y^{4\alpha +1}}{\Gamma (4\alpha +2)}} \right) \end{aligned}$$
(19)

and so on.

Therefore, the general solution can be written as

$$\begin{aligned}&{\tilde{p}}(y,t;r,\beta )={\tilde{\delta }}(r,\beta )\mathrm{e}^{-t}\nonumber \\&\qquad \times \left( {\sum _{i=0}^\infty {\frac{y^{i\alpha }}{\Gamma (i\alpha +1)}} +\sum _{j=0}^\infty {\frac{y^{j\alpha +1}}{\Gamma (j\alpha +2)}} } \right) , \end{aligned}$$
(20)

or

$$\begin{aligned}&{\tilde{p}}(y,t;r,\beta )\nonumber \\&\quad =\left( {\beta (0.4-0.4r)+(0.2r+0.8)} \right) \mathrm{e}^{-t}\nonumber \\&\qquad \times \left( {\sum _{i=0}^\infty {\frac{y^{i\alpha }}{\Gamma (i\alpha +1)}} +\sum _{j=0}^\infty {\frac{y^{j\alpha +1}}{\Gamma (j\alpha +2)}} } \right) . \end{aligned}$$
(21)

To obtain the solution bounds in single parametric form we may put \(\beta =0\hbox { and }1\) in eq. (21) for lower and upper bounds of the solution respectively. So we get

$$\begin{aligned} {\underline{p}}(y,t;r,0)= & {} (0.2r+0.8)\mathrm{e}^{-t}\nonumber \\&\times \left( {\sum _{i=0}^\infty {\frac{y^{i\alpha }}{\Gamma (i\alpha +1)}} +\sum _{j=0}^\infty {\frac{y^{j\alpha +1}}{\Gamma (j\alpha +2)}} } \right) \nonumber \\ \end{aligned}$$
(22)

and

$$\begin{aligned} \bar{{p}}(y,t;r,1)= & {} (1.2-0.2r)\mathrm{e}^{-t}\nonumber \\&\times \left( {\sum _{i=0}^\infty {\frac{y^{i\alpha }}{\Gamma (i\alpha +1)}} +\sum _{j=0}^\infty {\frac{y^{j\alpha +1}}{\Gamma (j\alpha +2)}} } \right) .\nonumber \\ \end{aligned}$$
(23)

One may note that in the special case when \(r=1\), the crisp results obtained by the proposed method are exactly the same as that of the solution obtained by Momani [10] and Yıldırım [16].

Case 2: In this case, the values \(f_{1} (t)\), \(f_{2} (t)\) and s(y) are considered the same as that of Case 1. Along with these it is also assumed that

$$\begin{aligned} {\tilde{g}}(y,t;r,\beta )=-y^{2}-t+1 \end{aligned}$$

and

$$\begin{aligned} {\tilde{\delta }}_{1} (r,\beta )= & {} {\tilde{\delta }}_{2} (r,\beta )={\tilde{\delta }}_{3} (r,\beta )\\= & {} \beta ( {0.4\sqrt{-2\log _{e} r}} )\\&+\,( {1-0.2\sqrt{-2\log _{e} r}} )={\tilde{\delta }}(r,\beta ). \end{aligned}$$

Using ADM for this case again, one may have

$$\begin{aligned} {\tilde{p}}_{0} (y,t;r,\beta )= & {} {\tilde{\delta }}(r,\beta )t-\frac{2y^{\alpha +2}}{\Gamma (\alpha +3)}\nonumber \\&+(1-t)\frac{y^{\alpha }}{\Gamma (\alpha +1)}, \end{aligned}$$
(24)
$$\begin{aligned} {\tilde{p}}_{1} (y,t;r,\beta )= & {} {\tilde{\delta }}(r,\beta )\left( {1+t} \right) \frac{y^{\alpha }}{\Gamma (\alpha +1)}-\frac{2y^{2\alpha +2}}{\Gamma (2\alpha +3)}\nonumber \\&-\,t\frac{y^{2\alpha }}{\Gamma (2\alpha +1)}, \end{aligned}$$
(25)
$$\begin{aligned} {\tilde{p}}_{2} (y,t;r,\beta )= & {} {\tilde{\delta }}(r,\beta )(2+t)\frac{y^{2\alpha }}{\Gamma (2\alpha +1)}\nonumber \\&-(1+t)\frac{y^{3\alpha }}{\Gamma (3\alpha +1)} -\,\frac{2y^{3\alpha +2}}{\Gamma (3\alpha +3)}, \end{aligned}$$
(26)
$$\begin{aligned} {\tilde{p}}_{3} (y,t;r,\beta )= & {} {\tilde{\delta }}(r,\beta )(3+t)\frac{y^{3\alpha }}{\Gamma (3\alpha +1)}\nonumber \\&-(2+t)\frac{y^{4\alpha }}{\Gamma (4\alpha +1)} -\,2\frac{y^{4\alpha +2}}{\Gamma (4\alpha +3)}\nonumber \\ \end{aligned}$$
(27)

and so on.

The solution in general form may be obtained as

$$\begin{aligned}&{\tilde{p}}(y,t;r,\beta )\nonumber \\&\,\, ={\tilde{\delta }}(r,\beta )\left( t+(1+t)\frac{y^{\alpha }}{\Gamma (\alpha +1)}+(2+t)\frac{y^{2\alpha }}{\Gamma (2\alpha +1)}\right. \nonumber \\&\quad \left. +\,(3+t)\frac{y^{3\alpha }}{\Gamma (3\alpha +1)} +\frac{y^{3\alpha }}{\Gamma (3\alpha +1)}+\cdots \right) \nonumber \\&\quad +\,\left( {\begin{array}{l} -2\dfrac{y^{\alpha +2}}{\Gamma (\alpha +3)}+(1-t)\dfrac{y^{\alpha }}{\Gamma (\alpha +1)}-\dfrac{2y^{2\alpha +2}}{\Gamma (2\alpha +3)}\\ -t\dfrac{y^{2\alpha }}{\Gamma (2\alpha +1)}-(1+t)\dfrac{y^{3\alpha }}{\Gamma (3\alpha +1)} \\ -\dfrac{2y^{3\alpha +2}}{\Gamma (3\alpha +3)}-(2+t)\dfrac{y^{4\alpha }}{\Gamma (4\alpha +1)}-2\dfrac{y^{4\alpha +2}}{\Gamma (4\alpha +3)}\\ -\cdots \\ \end{array}} \right) ,\nonumber \\ \end{aligned}$$
(28)

or

$$\begin{aligned}&{\tilde{p}}(y,t;r,\beta )\nonumber \\&\,\,=\beta ( {0.2\sqrt{-2\log r}} )+( {1-0.1\sqrt{-2\log r}} ) \nonumber \\&\quad \times \left( t+(1+t)\frac{y^{\alpha }}{\Gamma (\alpha +1)}+(2+t)\frac{y^{2\alpha }}{\Gamma (2\alpha +1)}\right. \nonumber \\&\quad \left. +\,(3+t)\frac{y^{3\alpha }}{\Gamma (3\alpha +1)}+\frac{y^{3\alpha }}{\Gamma (3\alpha +1)}+\cdots \right) \nonumber \\&\quad +\,\left( {\begin{array}{l} -2\dfrac{y^{\alpha +2}}{\Gamma (\alpha +3)}+(1-t)\dfrac{y^{\alpha }}{\Gamma (\alpha +1)}-\dfrac{2y^{2\alpha +2}}{\Gamma (2\alpha +3)}\\ -t\dfrac{y^{2\alpha }}{\Gamma (2\alpha +1)}-(1+t)\dfrac{y^{3\alpha }}{\Gamma (3\alpha +1)} \\ -\dfrac{2y^{3\alpha +2}}{\Gamma (3\alpha +3)}-(2+t)\dfrac{y^{4\alpha }}{\Gamma (4\alpha +1)}-2\dfrac{y^{4\alpha +2}}{\Gamma (4\alpha +3)}\\ -\cdots \\ \end{array}} \right) .\nonumber \\ \end{aligned}$$
(29)

Putting \(\beta =0\hbox { and }1\) in \({\tilde{p}}(y,t;r,\beta )\) we get the lower and upper bounds of the fuzzy solutions respectively as

$$\begin{aligned}&{\underline{p}}(y,t;r,0)\nonumber \\&\,\, =( {1-0.1\sqrt{-2\log r}} )\nonumber \\&\quad \times \left( {\begin{array}{l} t+(1+t)\dfrac{y^{\alpha }}{\Gamma (\alpha +1)}+(2+t)\dfrac{y^{2\alpha }}{\Gamma (2\alpha +1)} \\ +(3+t)\dfrac{y^{3\alpha }}{\Gamma (3\alpha +1)}+\dfrac{y^{3\alpha }}{\Gamma (3\alpha +1)}+\cdots \\ \end{array}} \right) \nonumber \\&\quad +\,\left( {\begin{array}{l} -2\dfrac{y^{\alpha +2}}{\Gamma (\alpha +3)}+(1-t)\dfrac{y^{\alpha }}{\Gamma (\alpha +1)}-\dfrac{2y^{2\alpha +2}}{\Gamma (2\alpha +3)} \\ -t\dfrac{y^{2\alpha }}{\Gamma (2\alpha +1)} -(1+t)\dfrac{y^{3\alpha }}{\Gamma (3\alpha +1)}\\ -\dfrac{2y^{3\alpha +2}}{\Gamma (3\alpha +3)} -(2+t)\dfrac{y^{4\alpha }}{\Gamma (4\alpha +1)}-2\dfrac{y^{4\alpha +2}}{\Gamma (4\alpha +3)}\\ -\cdots \\ \end{array}} \right) \nonumber \\ \end{aligned}$$
(30)

and

$$\begin{aligned}&\bar{{p}}(y,t;r,1)=( {1+0.1\sqrt{-2\log r}} )\nonumber \\&\quad \times \left( {\begin{array}{l} t+(1+t)\dfrac{y^{\alpha }}{\Gamma (\alpha +1)}+(2+t)\dfrac{y^{2\alpha }}{\Gamma (2\alpha +1)} \\ +(3+t)\dfrac{y^{3\alpha }}{\Gamma (3\alpha +1)}+\dfrac{y^{3\alpha }}{\Gamma (3\alpha +1)}+\cdots \\ \end{array}} \right) \nonumber \\&\quad +\,\left( {\begin{array}{l} -2\dfrac{y^{\alpha +2}}{\Gamma (\alpha +3)}+(1-t)\dfrac{y^{\alpha }}{\Gamma (\alpha +1)}\\ -\dfrac{2y^{2\alpha +2}}{\Gamma (2\alpha +3)}-t\dfrac{y^{2\alpha }}{\Gamma (2\alpha +1)} \\ -(1+t)\dfrac{y^{3\alpha }}{\Gamma (3\alpha +1)}-\dfrac{2y^{3\alpha +2}}{\Gamma (3\alpha +3)}\\ -(2+t)\dfrac{y^{4\alpha }}{\Gamma (4\alpha +1)} -2\dfrac{y^{4\alpha +2}}{\Gamma (4\alpha +3)} -\cdots \\ \end{array}} \right) .\nonumber \\ \end{aligned}$$
(31)

Solution obtained by the proposed method for \(r=1\) is again found to be exactly the same as that of (crisp result) Momani [10].

Fig. 1
figure 1

Triangular fuzzy solution (Case 1) for \(\alpha =0.5\) and \(t=2\) by varying y from 0.1 to 0.9.

Full size image

5 Numerical results and discussions

Here numerical solutions of fuzzy space-fractional telegraph equations have been computed with different values of \({\tilde{g}}(y,t;r,\beta )\), fuzzy initial and boundary conditions. Comparison has been made with Momani [10] and Yıldırım [16] in special cases with the present solution for validation. The obtained results are represented as plots.

Fig. 2
figure 2

Gaussian fuzzy solution (Case 2) for \(\alpha =0.5\) and \(t=2\) by varying y from 0.1 to 0.9.

Full size image
Fig. 3
figure 3

Triangular fuzzy solution (Case 1) for \(\alpha =1.25\) and \(y=0.6\) by varying t from 0 to 0.5.

Full size image
Fig. 4
figure 4

Gaussian fuzzy solution (Case 2) for \(\alpha =1.25\) and \(y=0.6\) by varying t from 0 to 0.5.

Full size image
Fig. 5
figure 5

Interval solution (Case 1) for \(r=0.3\), 0.6 and 1, \(\alpha =1.5\), \(t=2\) and y from 0.1 to 0.9.

Full size image
Fig. 6
figure 6

Interval solution (Case 2) for \(r=0.3\), 0.6 and 1, \(\alpha =1.5\), \(t=2\) and by varying y from 0.1 to 0.9.

Full size image
Fig. 7
figure 7

Interval solution (Case 1) for \(r=0.3\), 0.6 and 1, \(\alpha =1.75\), \(y=0.6\) by varying t from 0 to 2.

Full size image
Fig. 8
figure 8

Interval solution (Case 2) for \(r=0.3\), 0.6 and 1, \(\alpha =1.75\), \(y=0.6\) by varying t from 0 to 2.

Full size image
Fig. 9
figure 9

Interval solution (Case 1) for \(\alpha = 1.25\), 1.5 and 1.75, \(r=0.5\), \(y=0.6\) by varying t from 0 to 2.

Full size image
Fig. 10
figure 10

Interval solution (Case 2) for \(\alpha = 1.25\), 1.5 and 1.75, \(r=0.5\), \(y=0.6\) by varying t from 0 to 2.

Full size image
Fig. 11
figure 11

Interval solution (Case 1) for \(\alpha = 1.25\), 1.5 and 1.75, \(r=0.3\), \(t=2\) by varying y from 0 to 0.9.

Full size image
Fig. 12
figure 12

Interval solution (Case 2) for \(\alpha = 1.25\), 1.5 and 1.75, \(r=0.3\), \(t=2\) by varying y from 0 to 0.9.

Full size image

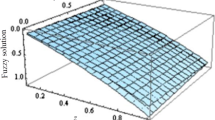
Fuzzy solutions are given in figures 1 and 2 for Cases 1 and 2 respectively by varying y from 0.1 to 0.9 and for fixed values of \(\alpha =0.5\) and \(t=2\). Similarly, figures 3 and 4 represent the results for Cases 1 and 2 by varying t from 0 to 0.5 for fixed values of \(\alpha =1.25\) and \(y=0.6\) respectively. Next, interval solutions for both Cases 1 and 2 are given in figures 5 and 6 respectively for \(r=0.3\), 0.6 and 1. In these solutions, \(\alpha =1.5\), \(t=2\) and the values of y vary from 0.1 to 0.9. After that, similar observations have also been made to find the interval solution for Cases 1 and 2 by considering \(\alpha =1.75, y=0.6\) and varying t from 0 to 2. Here also we have considered \(r=0.3\), 0.6 and 1, and the obtained results for Cases 1 and 2 are plotted in figures 7 and 8 respectively. Moreover, the results by varying t from 0 to 2 for Cases 1 and 2 along with \(r=0.5\) and \(y=0.6\) are shown in figures 9 and 10 respectively. In figures 9 and 10, the results have been included for \(\alpha = 1.25\), 1.5 and 1.75. Lastly, figures 11 and 12 denote the results for Cases 1 and 2 respectively by varying y from 0 to 0.9 along with \(r=0.3\), \(t=2\). Here the values of \(\alpha \) have been considered the same as that of figures 9 and 10.

It can be observed from figures 9 and 10 that the lower and upper bounds of the uncertain solution \({\tilde{p}}(y,t)\) gradually decrease by increasing the fractional-order derivative \(\alpha \) with increase in time (here r and y are constant). And similar observations have been made from figures 11 and 12 that solution bounds of the uncertain solution \({\tilde{p}}(y,t)\) (with constant r and t) gradually decrease by increasing the fractional-order derivative \(\alpha \) with increase of y.

6 Conclusions

Fractional-order telegraphic equation with fuzzy uncertainty has been solved using ADM. Here, in the solution process, a newly developed equivalent form of fuzzy number known as double parametric form has been implemented. Gaussian and triangular convex normalised fuzzy sets are used to model the uncertainty presents in the initial and boundary conditions. It can be seen that for the core, that is for \(r=1\), right- and left-hand side solutions are equal as expected. Using this method, one can get the solution in terms of infinite series. The obtained results are compared in the special cases with Momani [10] and Yıldırım [16] which are found to be in good agreement. It can be observed that the left and right bounds of the uncertain solutions gradually decrease by increasing the fractional-order derivative with increase in time. And also the left and right bounds of the uncertain solution gradually decrease by increasing the fractional-order derivative with increase of y. The future aim is to study the problem by considering all the parameters as uncertain.