Abstract
Analytical studies of fuzzy fractional differential equations (FFDEs) of two different independent fractional orders are often complex and difficult. It is essential to develop comprehensive schemes for the solutions of FFDEs with independent orders. This article introduces and investigates the fully closed-form analytical solutions of FFDEs involving two different independent fractional orders under the strongly generalized Hukuhara differentiability (SGHD). Based on the concept of SGHD, we extract two possible solutions of FFDEs in terms of the Mittag-Leffler function. Potential solutions for homogeneous and inhomogeneous FFDEs are obtained using the definition of the fuzzy Laplace transform technique. Some interesting properties and results for the FFDEs are introduced using the concepts of SGHD. We illustrate some examples as applications to explain the effectiveness of our proposed results. FFDE has a variety of applications in science and engineering. To enhance the functional significance of this work, we solve the RLC circuit using the proposed technique in a fuzzy setting to analyze and interpret the theoretical results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
1.1 Fuzzy differential equations
Every real-world problem is inherently based on uncertainty. In a world full of uncertainty, it is often necessary to accurately identify problems, modify and solve, infer and interpret results. Generally speaking, there are several problems in science and engineering that are completely solved by fuzzy differential equations (FDE). Dubios and Prade (1982) initially introduced the the concept of FDEs. These differential equations are based on the definition of fuzzy derivative which is called the Dubois-Prade derivative. Subsequently, a number of definitions of fuzzy derivatives were introduced including Puri and Ralescu (1983) derivative (for short H-derivative), the Goetschel and Voxman (1986) derivative, Seikkala (1987) derivative and Friedman et al. (1996) derivative. Although these derivatives are defined in different forms from one another, but all of them gave equivalent results for fuzzy functions. The most common derivatives are the Seikkala and Puri-Ralescu derivative. The Puri-Ralescu derivative is defined using H-difference while the Seikkala derivative defined by \(\alpha\)-level set of fuzzy functions. Yue and Guangyuan (1998) introduced the ’same and reverse’ order derivative approach to solve the challenges caused from H-derivative. Bede and Gal (2005) developed the concept of SGHD. This structure provides two types of differentiability from the fuzzy function. These two types of differentiability are usually called the first and second forms of differentiability. The first form is corresponding to the H-differentiability and the second form corresponds to the non-decreasing diameter of fuzzy function. Allahviranloo and Ghanbari (2020), Haq et al. (2022) and Wasques et al. (2020) introduced the reliable and ABC approach to extract the fuzzy solutions of FFDEs with their applications.
1.2 Fuzzy fractional differential equations
Fractional calculus is a branch of mathematics that investigates the different properties of derivatives and integrals with fractional order (or non-integer orders). A broader understanding for fractional calculus allows us to evaluate the dynamic behavior of real-world problems both in theoretical and practical point of view. Fractional calculus has been effectively applied for modeling to solve many complicated problems. In this field of study, the idea and techniques for solving non-integer differential equations with the unknown function are particularly important. Several researchers, including Miller and Ross (1993), Kilbas et al. (2006) and Magin (2006) investigated new techniques for solving many complicated problems related to the real-world. The revolution of non-integer orders (or fractional orders) has been found to be useful in representing complicated systems, despite the fact that the computational effects are vague. In many areas of fractional calculus, the computational process is not straightforward. For this reason, Ahmad et al. (2021) developed the solution procedure for solving the fuzzy fractional dimensionless Fisher equation. Ghaffari et al. (2021) introduced the analytical technique for time-fractional problems in uncertain environments. Ezadi and Allahviranloo (2020) proposed an efficient technique to solve FFDEs. Khakrangin et al. (2021) developed a numerical scheme for the fuzzy solution of FFDEs. Melliani et al. (2021) analyzed the Ulam–Hyers–Rassias stability to solve fuzzy fractional integral-differential equations in the sense of Caputo gH-differentiability. Vu and Hoa (2019) studied FFDEs on time scales using granular differentiability. Agarwal et al. (2010) studied the solution of FFDEs using Riemann–Liouville (R–L) derivative. Fuzzy fractional initial value problem using Caputo derivative was introduced by Ngo et al. (2018). Generalized Hukuhara fractional differentiation using interval numbers was developed by Hoa et al. (2017). Laplace transform in fuzzy environments was established by Allahviranloo and Ahmadi (2010). In addition, Salahshour and Allahviranloo (2013) discussed the application of fuzzy Laplace transform. Allahviranloo et al. (2014) developed the solution procedure for FFDEs using Caputo’s definition. Akram et al. (2022, 2022); Akram and Ihsan (2022) interpreted the solution of Pythagorean fuzzy ordinary and partial differential equations using SGHD. Furthermore, Akram et al. (2022, 2023) extracted the solution procedure for fuzzy Langevin and two dimensional system of differential equations in Caputo’s derivative sense with their applications. Rahaman et al. (2021) and Dong et al. (2022) investigated the solution procedure for finding the exact solution and finite-time stability of FFDEs.
1.3 Motivation of the proposed technique
Many authors have drawn readers’s attention when solving fractional differential equations (FrDE) involving independent fractional orders discussed the existence of solutions for FrDE. Ahmad et al. (2012) and Ahmad and Nieto (2010) investigated the solution of FrDEs on different Dirichlet boundary conditions and intervals. Moreover, Mahmudov (2020) and Baghani and Nieto (2019) studied the FrDEs containing two fractional independent orders on various intervals. Fazli et al. (2020) determined the existence and uniqueness of FrDEs with different independent fractional orders. So, determining the solution of FrDEs with independent fractional order becomes more important because of their cross-discipline research. On the other hand, fuzzy models are used to represent the dynamical behaviors that do not include randomness but do contain some uncertain parameters. Some of these models naturally result in FFDEs. FFDEs have received extensive attention due to the vast majority in real-life problems including science and engineering (Blackwell and Beck (2010)). This uncertainty in FFDEs may cause due to measurement, observation, environmental facts, or lack of information. There are some mathematical models in the literature that can deal with the uncertainty such as stochastic, or fuzzy sets. Wang et al. (2015) studied that some problems exist in the literature that can only analyzed using fuzzy mathematical models. Here, we extract the fully closed-form analytical solution of FDEs with fractional orders to overcome and analyze the uncertainty that arises in the fuzzy mathematical model. Although, Diethelm et al. (2002) and Diethelm and Ford (2004) determine the approximate solution of FrDEs using various numerical approaches and algorithms. We investigate the analytical fuzzy solution of FFDEs with independent fractional orders in terms of the M-LF using the tool of fuzzy Laplace transform.
1.4 Novelty of the work
Nonetheless, some authors have developed many interesting methods and schemes to address FFDE and its applications. This article emphasizes its uniqueness from the following perspectives:
-
(i)
A solution to an FFDE involving two independent fractional orders.
-
(ii)
Two possible solutions of FFDE are extracted on the basis of SGHD.
-
(iii)
M-LF closed-form solutions for homogeneous and heterogeneous FFDEs are discussed.
-
(iv)
The fuzzy solution is determined using the fuzzy Laplace transform technique.
-
(v)
Several important concepts, facts and relationships and their applications are analyzed.
-
(vi)
Solution of RLC circuits in uncertain environments using the proposed method.
1.5 Structure of paper
The rest of this article is arranged as: Section 2 presents some preliminaries and the basic concepts of fractional calculus, fuzzy fractional calculus, and fractional differential operators in crisp and fuzzy environments. In Sect. 3, we describe the concept of fuzzy Caputo SGHD using H-difference. Section 4 contains the solution procedure for FFDEs involving independent fractional order in terms of the M-LF using first and second differentiability. In Sect. 5, some examples are solved to check the validity and efficiency of our proposed technique. The conclusions and future directions are given in Sect. 6.
2 Basic concepts
We start this section by reviewing some fundamental concepts and terminologies that are necessary for this article.
\(\mathscr {F}^{\Re }={\big \{\hslash : \varOmega \longrightarrow :[0,1]\big \}}\) denotes the class of fuzzy subset on \(\Re\). Firmly, \(\hslash\) is convex because
where, \(\hslash\) is semi-continuous on upward such that \(\{x_{1}\in \Re |~\hslash (x_{1})\ge \lambda \}\) is closed for every \(0\le \lambda \le 1\); and there exist \(x_{1}\in \Re\) such that \(\hslash (x_{1})=1\); \([\hslash ]^{0}=\overline{\{x_{1}\in \Re |~\hslash (x_{1})>0\}}\) is compact. The support of \(\hslash\) is \(\{x\in \Re |~\hslash (x)>0\}\).
Definition 1
Smadi et al. (2021) The \(\alpha\)-level set of \(\hslash \in \mathscr {F}^{\Re }\) is defined as
\([\hslash ]^{\alpha }\) is bounded and closed interval such that \([\hslash ]^{\alpha }=\big [\hslash _{1}(\alpha ), \hslash _{2}(\alpha )\big ], \forall \alpha \in [0,1]\).
Definition 2
Goetschel and Voxman (1986) The triangular fuzzy number (TFN) \(\upsilon \in \mathscr {F}^{\Re }\) is characterized in the parametric form \(\big (\hslash _{1}(\alpha ), \hslash _{2}(\alpha )\big )\), \(0\le \alpha \le 1\). The functions \(\hslash _{1}(\alpha )\) and \(\hslash _{2}(\alpha )\) fulfil the following axioms:
-
(i)
The lower parametric fuzzy function \(\hslash _{1}(\alpha )\) is left continuous, bounded and monotonic increasing.
-
(ii)
The upper parametric fuzzy function \(\hslash _{2}(\alpha )\) is left continuous, bounded and monotonic decreasing.
-
(iii)
\(\hslash _{1}(\alpha )\le \hslash _{2}(\alpha )\).
Definition 3
Ngo et al. (2018) Suppose \(\hslash _{1}, \hslash _{2}\in \mathscr {F}^{\Re }\), if there exist \(\hslash _{3}\in \mathscr {F}^{\Re }\) such that \(\hslash _{1}=\hslash _{2}+\hslash _{3}\). Then \(\hslash _{3}\) will be the H-difference of \((\hslash _{1},\hslash _{2})\). We will compose the standard notation of H-difference as \(\hslash _{1}\ominus _{H}\hslash _{2}\). Indeed, if H-difference \(\hslash \ominus _{H}\mathfrak {j}\) exists, then \([\hslash \ominus _{H}\mathfrak {j}]^{\alpha }=[\hslash _{1}(\alpha )-\mathfrak {j}_{1}(\alpha ),\hslash _{2}(\alpha )-\mathfrak {j}_{2}(\alpha )]\). Throughout this article, we depict the sign \(``\ominus ''\) to denote H-difference.
Let \(\mathfrak {C}^{\mathscr {F}^{\Re }}\) and \(\mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\) be the class of continuous and integrable fuzzy-valued functions (FVFs) on \(\mathscr {E}=[a,b]\), respectively.
Definition 4
Ngo et al. (2018) Suppose \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). The fuzzy R–L fractional integral of order \(\vartheta \in \mathbb {C}\), Re\((\vartheta )>0\) is defined
Recall that the \(\alpha\)-level form of fuzzy-valued function (FVF) \(\hslash\) is defined as: \([\hslash (x)]^{\alpha }=\big [\hslash _{1}(x;\alpha ),\hslash _{2}(x;\alpha )\big ]\).
On the base of lower and upper FVF, we describe the fuzzy R–L fractional integral as:
Definition 5
Salahshour et al. (2012) Let \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). The fuzzy R–L fractional integral for FVF \(\hslash\) of order \(\vartheta \in \mathbb {C}\), Re\((\vartheta )>0\) is defined as
where the lower and upper FVFs is defined as
3 Caputo’s SGH-differentiability
In this section, we define fuzzy Caputo SGH-differentiability under H-difference. We attempt to develop some basic definitions and terminologies which are similar to the classical context in fuzzy environment.
Definition 6
Bede and Gal (2005) Assume \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\) and \(\psi (x)=\dfrac{1}{\varGamma (1-\vartheta )}\int ^{x}_{a}\dfrac{\hslash (q)\ominus \hslash (0)}{(x-q)^{\vartheta }}dq\). The FVF \(\hslash (x)\) is said to be the Caputo fuzzy fractional differentiable function (CFFDF) of order \(0<\vartheta \le 1\) at \(x\in (a,b)\) in the first form, if there exists \({^{C}\mathbf {D}^{\vartheta }}\hslash (x)\in \mathscr {F}^{\Re }\) such that:
-
(i)
For every \(\tau\) positive, the functions \(\psi (x+\tau )\ominus \psi (x)\) and \(\psi (x)\ominus \psi (x-\tau )\) both exists such that
$$\begin{aligned} {^{C}\mathbf {D}^{\vartheta }}\hslash (x)=\lim \limits _{\tau \searrow 0^{+}}\dfrac{\psi (x+\tau )\ominus \psi (x)}{\tau }= \lim \limits _{\tau \searrow 0^{+}}\dfrac{\psi (x)\ominus \psi (x-\tau )}{\tau }. \end{aligned}$$(3)Or, \(\hslash (x)\) is called CFFDF of order \(0<\vartheta <1\) at \(x\in (a,b)\) in the second form, if there exists \({^{C}\mathbf {D}^{\vartheta }}\hslash (x)\in \mathscr {F}^{\Re }\) such that
-
(ii)
For every \(\tau\) positive, the expressions \(\psi (x)\ominus \psi (x+\tau )\) and \(\psi (x-\tau )\ominus \psi (x)\) both exists such that
$$\begin{aligned} {^{C}\mathbf {D}^{\vartheta }}\hslash (x)&=\lim \limits _{\tau \searrow 0^{+}}\dfrac{\psi (x)\ominus \psi (x+\tau )}{-\tau }\nonumber \\&= \lim \limits _{\tau \searrow 0^{+}}\dfrac{\psi (x-\tau )\ominus \psi (x)}{-\tau }. \end{aligned}$$(4)
Indeed, \(\hslash\) is differentiable on the open interval (a, b) if \(\hslash\) is differentiable for every point in the interval (a, b).
Note 1
Fuzzy R–L fractional derivative of FVF \(\hslash (x)\) is denoted by \({^{RL}\mathbf {D}^{\vartheta }}\hslash (x)\) and is defined same as the above Definition 6.
For the sake of convenient, we depict the following definition as:
Definition 7
Let \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\) such that the following status can be obtained:
-
(i)
\(\hslash\) is first differentiable on \(\mathscr {E}\), if \(\hslash\) is differentiable at first status of the Definition 6.
-
(ii)
\(\hslash\) is second differentiable on \(\mathscr {E}\), if \(\hslash\) is differentiable at second status (ii) of the Definition 6.
Based on Allahviranloo et al. (2012), we define the following theorem without its proof.
Theorem 1
Let \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\) such that the following status can be achieved:
-
(i)
If \(\hslash\) is CFFDF of the first form, then their lower and upper FVF is also fractional differentiable and
$$\begin{aligned} {[}{^{C}\mathbf {D}^{\vartheta }}\hslash (x)]^{(\alpha )}=\bigg [\big ({^{C}\mathbf {D}^{\vartheta }}\hslash _{1}\big )(x;\alpha ), \big ({^{C}\mathbf {D}^{\vartheta }}\hslash _{2}\big )(x;\alpha )\bigg ]. \end{aligned}$$ -
(ii)
If \(\hslash\) is CFFDF of the second form, then their lower and upper FVF is also fractional differentiable and
$$\begin{aligned} {[}{^{C}\mathbf {D}^{\vartheta }}\hslash (x)]^{(\alpha )}=\bigg [\big ({^{C}\mathbf {D}^{\vartheta }}\hslash _{2}\big )(x;\alpha ), \big ({^{C}\mathbf {D}^{\vartheta }}\hslash _{1}\big )(x;\alpha )\bigg ], \end{aligned}$$
where,
and
The fuzzy R–L fractional derivative is defined as:
Definition 8
Salahshour et al. (2012) Let \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). If a FVF \(\hslash\) is fractional differentiable function of first form. Then the fuzzy R–L fractional derivative of order \(\vartheta \in \mathbb {C}\), Re\((\vartheta )\ge 0\) is defined as
If a FVF \(\hslash\) is fractional differentiable function of second form. Then the fuzzy R–L fractional derivative of order \(\vartheta \in \mathbb {C}\), Re\((\vartheta )\ge 0\) is defined as
where, the integral in Eqs. (5) and (6) is defined in Definition 5 and \(m-1\le Re(\vartheta )<m\) such that m is natural number. If \(0<\vartheta <1\) and \(a=0\) then the above definition is defined for first and second differentiability as
and
Definition 9
Podlubny (1999) Let \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). If a FVF \(\hslash\) is differentiable in the first form. Then the CFFDF of order \(\vartheta \in \mathbb {C}\), Re\((\vartheta )\ge 0\) is defined as
If a FVF \(\hslash\) is differentiable in second form. Then the CFFDF of order \(\vartheta \in \mathbb {C}\), Re\((\vartheta )\ge 0\) is defined as
where, the integral in Eqs. (5) and (6) is defined in Definition 5 and \(m-1\le Re(\vartheta )<m\) such that m is natural number. If \(0<\vartheta <1\) and \(a=0\) then the above definition is defined for first and second differentiability as
and
Definition 10
Let \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). The fuzzy fractional integral (base on Ahmadova et al. (2021)) in terms of M-LF is defined as
where \(\mu , \nu >0\) and \(\epsilon , \eta _{1}\) are real parameters.
Definition 11
Allahviranloo and Ahmadi (2010) Let \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). Assume that \(\int _{0}^{\infty }e^{-qu}\hslash (u)du\) is fuzzy Riemann integrable. Then this integral is called the fuzzy Laplace transform of \(\hslash\) and their symbolic representation
Since,
Therefore, Eq. (9) takes the following form
where,
and \(l (\hslash (x))\) is the classical notation in crisp environment of the function \(\hslash (x)\).
In the following section, we develop an analytical technique to solve FFDEs with independent fractional order.
4 Solution procedure for FFDEs involving independent fractional order
In this section, first we develop some categorial structure for closed-form fuzzy solutions of FFDEs with independent fractional orders. To this end, we demonstrate the following results, which are required to find the fuzzy Laplace transform (FLT) of the fuzzy fractional derivative. Although, the following theorem has already proof using fuzzy R–L fractional derivative ( Salahshour et al. (2012)). We proof in the sense of Caputo derivative as:
Theorem 2
Let \(\hslash : \mathscr {E}\longrightarrow {\mathscr {F}^{\Re }}\), \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). If \(\hslash (x)\) is CFFDF of first form. Then
If \(\hslash (x)\) is CFFDF of second form. Then
Proof
Suppose \(\hslash (x)\) is CFFDF of first form. Then
By linearity of \(\mathscr {L}\), we have
This leads to the following expression
Since \(\alpha\)-values are arbitrary. Therefore, we get the above equation as
If \(\hslash (x)\) is CFFDF of second form. Then
By linearity of \(\mathscr {L}\), we have
This leads to the following expression
Since \(\alpha\)-level values are arbitrary. Therefore, we get the above equation as
This completes the proof. \(\square\)
FFDEs with independent fractional orders play a significant role to deal the uncertainty in uncertain fractional model. Let us we assume the functional fuzzy structure of FFDEs with independent fractional order in a general form
where, \(x\in [x_{0},X]\) and \(0<\vartheta _{1}, \vartheta _{1}<1\). The mapping \(\mathbb {Z}: [x_{0},X]\times \Re \rightarrow \Re\) is continuous and the initial condition\(\hslash (0)\) is the fuzzy number. Here \({{^{C}}\mathbf {D}}_{0^{+}}^{\vartheta _{1}}\) and \({{^{C}}\mathbf {D}}_{0^{+}}^{\vartheta _{2}}\) are the Caputo derivatives with arbitrary non-integer order. A mapping \(\hslash : [x_{0},X]\times \Re \rightarrow \mathscr {F}^{\Re }\) such that \(\hslash\) is absolutely continuous in the domain, then we call \(\hslash\) is the solution of FFDEs with independent fractional order. According to Zadeh’s extension principle when \(\hslash\)=\(\hslash (x)\) is a fuzzy number
where, \(t\in \Re\). It follows that
with lower and upper FVF defined as
and
Moreover, Ahmad et al. (2013) studied the existence and uniqueness of FFDEs using extension principle.
-
Case I. To deterministic the solution of system 24. Taking fuzzy Laplace transform on both sides of Eq. (24), we get
$$\begin{aligned} \mathscr {L}\big [{{^{C}}\mathbf {D}}_{0^{+}}^{\vartheta _{1}}\hslash (x)\big ]+\mathscr {L}\big [{{^{C}}\mathbf {D}}_{0^{+}}^{\vartheta _{2}}\hslash (x)\big ]=\mathscr {L}\big [ \mathbb {Z}(x, \hslash (x))\big ]. \end{aligned}$$(13)If \(\hslash\) is CFFDF of first form. Then using the status first of Theorem 3.1 (Akram et al. 2022), it yields that
$$\begin{aligned}&q^{\vartheta _{1}}\mathscr {L}\big [\hslash (x)\big ]{\ominus } q^{\vartheta _{1}-1}\hslash _{0}(0)+q^{\vartheta _{2}}\mathscr {L}\big [\hslash (x)\big ]{\ominus } q^{\vartheta _{2}-1}\hslash _{1}(0)\nonumber \\&\qquad =\mathscr {L}\big [ \mathbb {Z}(x, \hslash (x))\big ]. \end{aligned}$$(14)Now we extend the aforementioned expression into the following lower and upper FVF as:
$$\begin{aligned}&q^{\vartheta _{1}} l \big [\hslash _{1}(x;\alpha )\big ]-q^{\vartheta _{1}-1}\hslash _{(0)1}(0;\alpha )\nonumber \\&\qquad +q^{\vartheta _{2}} l \big [\hslash _{1}(x;\alpha )\big ]\nonumber \\&\qquad -q^{\vartheta _{2}-1}\hslash _{(1)1}(0;\alpha )=\mathscr {L}\big [ \mathbb {Z}_{1}(x, \hslash (x);\alpha )\big ] \end{aligned}$$(15)and
$$\begin{aligned}&q^{\vartheta _{1}} l \big [\hslash _{2}(x;\alpha )\big ]-q^{\vartheta _{1}-1}\hslash _{(0)2}(0;\alpha )+ q^{\vartheta _{2}} l \big [\hslash _{2}(x;\alpha )\big ]\nonumber \\&\qquad -q^{\vartheta _{2}-1}\hslash _{(1)2}(0;\alpha )=\mathscr {L}\big [ \mathbb {Z}_{2}(x, \hslash (x);\alpha )\big ], \end{aligned}$$(16)where,
$$\begin{aligned} \mathbb {Z}_{1}(x,\hslash (x);\alpha )=\min \big \{\mathbb {Z}(x, u):~u\in [\hslash _{1}(x;\alpha ), \hslash _{2}(x;\alpha )]\big \} \end{aligned}$$and
$$\begin{aligned} \mathbb {Z}_{2}(x,\hslash (x);\alpha )=\max \big \{\mathbb {Z}(x, u):~u\in [\hslash _{1}(x;\alpha ), \hslash _{2}(x;\alpha )]\big \}. \end{aligned}$$To solve the linear system of Eqs. (15-16) and after some manipulation, we have
$$\begin{aligned} l \big [\hslash _{1}(x;\alpha )\big ]=\eta _{1}(p;\alpha )~~~\mathrm{and}~~~ l \big [\hslash _{2}(x;\alpha )\big ]=\eta _{2}(p;\alpha ) \end{aligned}$$(17)Taking inverse Laplace transform to the Eq. (17), we get
$$\begin{aligned} \hslash _{1}(x;\alpha )= l ^{-1}\big [\eta _{1}(p;\alpha )\big ]~~~\mathrm{and}~~~ \hslash _{2}(x;\alpha )= l ^{-1}\big [\eta _{2}(p;\alpha )\big ]. \end{aligned}$$(18) -
Case II. If \(\hslash\) is CFFDF of second form. Then using the second status of Theorem 3.1 Akram et al. (2022), we have
$$\begin{aligned}&-\big (q^{\vartheta _{1}-1}\hslash _{0}(0)\big ){\ominus }\big (-q^{\vartheta _{1}}\mathscr {L}\big [\hslash (x)\big ]\big ) -\big (q^{\vartheta _{2}-1}\hslash _{1}(0)\big ){\ominus }\nonumber \\&\qquad \big (-q^{\vartheta _{2}}\mathscr {L}\big [\hslash (x)\big ]\big )=\mathscr {L}\big [ \mathbb {Z}(x, \hslash (x))\big ]. \end{aligned}$$(19)The above expression can be written in form of lower and upper FVFs as
$$\begin{aligned}&q^{\vartheta _{1}} l \big [\hslash _{2}(x;\alpha )\big ]-q^{\vartheta _{1}-1}\hslash _{(0)2}(0;\alpha )+ q^{\vartheta _{2}} l \big [\hslash _{2}(x;\alpha )\big ]\nonumber \\&\qquad -q^{\vartheta _{2}-1}\hslash _{(1)2}(0;\alpha )=\mathscr {L}\big [ \mathbb {Z}_{1}(x, \hslash (x);\alpha )\big ] \end{aligned}$$(20)and
$$\begin{aligned}&q^{\vartheta _{1}} l \big [\hslash _{1}(x;\alpha )\big ]-q^{\vartheta _{1}-1}\hslash _{(0)1}(0;\alpha )+ q^{\vartheta _{2}} l \big [\hslash _{1}(x;\alpha )\big ]\nonumber \\&\qquad -q^{\vartheta _{2}-1}\hslash _{(1)1}(0;\alpha )=\mathscr {L}\big [ \mathbb {Z}_{2}(x, \hslash (x);\alpha )\big ], \end{aligned}$$(21)where,
$$\begin{aligned} \mathbb {Z}_{1(\alpha )}(x,\hslash (x))=\min \big \{\mathbb {Z}(x, u):~u\in [\hslash _{1}(x;\alpha ), \hslash _{2}(x;\alpha )]\big \} \end{aligned}$$and
$$\begin{aligned} \mathbb {Z}_{2(\alpha )}(x,\hslash (x))=\max \big \{\mathbb {Z}(x, u):~u\in [\hslash _{1}(x;\alpha ), \hslash _{2}(x;\alpha )]\big \}. \end{aligned}$$To solve the linear system of Eqs. (20-21) and after some manipulation, we have
$$\begin{aligned} l \big [\hslash _{1}(x;\alpha )\big ]=\eta _{1}(p;\alpha )~~~\mathrm{and}~~~ l \big [\hslash _{2}(x;\alpha )\big ]=\eta _{2}(p;\alpha ). \end{aligned}$$(22)Taking inverse Laplace transform to the Eq. (22), we get
$$\begin{aligned} \hslash _{1}(x;\alpha )= l ^{-1}\big [\eta _{1}(p;\alpha )\big ]~~~\mathrm{and}~~~ \hslash _{2}(x;\alpha )= l ^{-1}\big [\eta _{2}(p;\alpha )\big ]. \end{aligned}$$(23)
Consider the general non-homogeneous fuzzy fractional initial value problem
4.1 Deterministic the analytical solution of FFDEs with independent fractional order
To solve the aforementioned problem 24, we restrict our concentration to the analysis of the following cases:
where, \(0<\vartheta _{1}, \vartheta _{1}<1\). We discuss these cases in the form of the following results.
Theorem 3
Let \(\hslash : \mathscr {E}\longrightarrow {\mathscr {F}^{\Re }}\), \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). If \(\vartheta _{1}<\vartheta _{2}\) and \(\hslash\) is Caputo differentiable function of first form. Then the system (24) have the following solution
If \(\vartheta _{1}<\vartheta _{2}\) and \(\hslash\) is Caputo differentiable function of the second form. Then the system (24) have the following solution Since \(\alpha\)-level values are arbitrary. Therefore, above expression completely be written as
Proof
First we assume \(\vartheta _{1}<\vartheta _{2}\). Applying fuzzy Laplace transformation on both sides of Eq. (24), we obtain the following
-
If \(\hslash\) is CFFDF of first form, Then using the status first of Theorem 3.1 Akram et al. (2022), we get
Now we extend the Eq. (27) into the following lower and upper FVF as following
and
From Eqs. (28) and (29), we get
and
The solution of aforementioned equations after taking inverse fuzzy Laplace transform and using Definition 10, we get the following
and
or
In the form of \(\alpha\)-level values, we have
Since \(\alpha\)-values are arbitrary. Therefore, above expression completely be written as
-
If \(\hslash\) is CFFDF of second form. Then using the status second of Theorem 3.1 Akram et al. (2022), we have
Now we split the aforementioned expression into the following upper and lower FVFs as
and
From Eqs. (38) and (39), we get
and
The solution of aforementioned equations after taking inverse Laplace transform, we have
and
or
In the form of \(\alpha\)-level values, we have
Since \(\alpha\)-level values are arbitrary. Therefore, above expression completely be written as
This completes the proof. \(\square\)
Theorem 4
Let \(\hslash : \mathscr {E}\longrightarrow {\mathscr {F}^{\Re }}\), \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). If \(\vartheta _{1}>\vartheta _{2}\) and \(\hslash\) is Caputo differentiable function of first form. Then the system (24) have the following solution
If \(\vartheta _{1}<\vartheta _{2}\) and \(\hslash\) is Caputo differentiable function of the second form. Then the system (24) have the following solution Since \(\alpha\)-level values are arbitrary. Therefore, above expression completely be written as
Proof
First we assume \(\vartheta _{2}<\vartheta _{1}\). Applying fuzzy Laplace transformation on both sides of Eq. (24), we obtain the following
-
If \(\hslash\) is CFFDF of first form, Then using the status first of Theorem 3.1 Akram et al. (2022), we get
Now we extend the Eq. (48) into the following lower and upper FVF as following
and
From Eqs. (49) and (50), we get
and
The solution of aforementioned equations after taking inverse fuzzy Laplace transform and using Definition 10, we get the following
and
or
In the form of \(\alpha\)-level values, we have
Since \(\alpha\)-values are arbitrary. Therefore, above expression completely be written as
-
If \(\hslash\) is CFFDF of second form. Then using the status second of Theorem 3.1 Akram et al. (2022), we have
Now we split the aforementioned expression into the following upper and lower FVFs as
and
From Eqs. (59) and (60), we get
and
The solution of aforementioned equations after taking inverse Laplace transform, we have
and
or
In the form of \(\alpha\)-level values, we have
Since \(\alpha\)-level values are arbitrary. Therefore, above expression completely be written as
This completes the proof. \(\square\)
Theorem 5
Let \(\hslash : \mathscr {E}\longrightarrow {\mathscr {F}^{\Re }}\), \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). If \(\vartheta _{1}=\vartheta _{2}=\flat\) and \(\hslash\) is CFFDF of first form. Then the system (24) have the following solution
If \(\vartheta _{1}=\vartheta _{2}=\flat\) and \(\hslash\) is CFFDF of second form. Then the system (24) have the following solution
Proof
Suppose that \(\vartheta _{1}=\vartheta _{2}=\flat\). Taking fuzzy LT on both sides of Eq. (24), we have
-
If \(\hslash\) is CFFDF of first form, then Eq. (68) can be written as
Now we extend the aforementioned expression into the following lower and upper FVFs as
and
From Eqs. (70) and (71), we get
and
The solution of aforementioned equations after taking inverse fuzzy Laplace transform, we have
and
The above expression takes the following form
In the form of \(\alpha\)-level values, we have
Since \(\alpha\)-values are arbitrary. Therefore, above expression completely be written as
-
If \(\hslash\) is CFFDF of second form, then the Eq. (68) can be written as
The above equation can be written in the upper and lower form
and
From Eqs. (80) and (81), we get
and
Taking inverse fuzzy Laplace transform, we get
and
The aforementioned Eq. (85) in the form of FVF
In \(\alpha\)-level form, we have
Since \(\alpha\)-values are arbitrary. Therefore, above expression completely be written as
This completes the proof. \(\square\)
5 Applications
Application 1
As an application of Theorem 3, for \(\vartheta _{1} <\vartheta _{2}\). For instance \(\vartheta _{1}=\dfrac{1}{3}\) and \(\vartheta _{2}=\dfrac{1}{2}\). We consider the non-homogeneous FFDEs with independent fractional order
If \({\frac{1}{3}}<\frac{1}{2}\). In accordance with Theorem 3, analytical solutions for the initial value problem are given as follows:
and
As an application of Theorem 4, for \(\vartheta _{1} >\vartheta _{2}\). For instance \(\vartheta _{1}=\dfrac{1}{2}\) and \(\vartheta _{2}=\dfrac{1}{3}\).
Application 2
We consider the non-homogeneous FFDEs with independent fractional order
If \({\frac{1}{4}}>\frac{1}{5}\). In accordance with Theorem 4, analytical solutions for the initial value problem are given as follows:
and
If \(\vartheta _{1}=\vartheta _{2}\). Then the following application converges to the Theorem 5. For instance \(\vartheta _{1}=\vartheta _{2}=\dfrac{1}{4}\).
Application 3
We consider the non-homogeneous FFDEs with independent fractional order
If \(\flat ={\frac{1}{4}}\). In accordance with Theorem 5, analytical solutions for the initial value problem are given as follows:
and
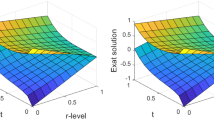
The underlying annotations can be seen in the graphs of Figs. 1, 2, 3, 4 and 5. All plots behave the same. The plots fit each other very well. Especially when considering FFDEs with independent fractional order. The solution is a fuzzy function for each point in the domain, and FFDEs with independent fractional order has a strong connection to the model profile. To determine the general solution for homogeneous FFDEs with independent fractional order, we consider the following homogeneous FFDEs with independent fractional order with fuzzy initial-value problem.
We give the following corollaries regarding the homogeneous system without these proofs. The reader can find their solution easily using above analysis.
Graphical presentation of the solution of Application 1 taking \(\mathfrak {f}(x)=x\) and \(\mathfrak {f}(x)=x^{2}\), \(m=0\), different values for \(\alpha\) and space variable \(\hslash (x)\),respectively
At \(x=0:0.01:1\) and \(\alpha =0,0.1,0.2,0.3,\cdots ,1\). We depict the graph of \(\hslash (x)\) in Fig. 2. If we change the value of \(\alpha\) continuously, we have the graph of the given fuzzy functions in crisp environment
Graphical presentation of the solution of Application 2 taking \(\mathfrak {f}(x)=x\) and \(\mathfrak {f}(x)=x^{2}\), \(m=0\), different values for \(\alpha\) and space variable \(\hslash (x)\), respectively
Graphical presentation of the solution of Application 3 taking \(\mathfrak {f}(x)=x\) and \(\mathfrak {f}(x)=x^{2}\) with different values for \(\alpha\) and space variable \(\hslash (x)\)
Corollary 1
Let \(\hslash : \mathscr {E}\longrightarrow {\mathscr {F}^{\Re }}\), \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). If \(\vartheta _{1}>\vartheta _{2}\). Then the aforementioned system (92) have the following solution
Corollary 2
Let \(\hslash : \mathscr {E}\longrightarrow {\mathscr {F}^{\Re }}\), \(\hslash \in \mathfrak {C}^{\mathscr {F}^{\Re }}(\mathscr {E})\cap \mathfrak {L}^{\mathscr {F}^{\Re }}(\mathscr {E})\). If \(\vartheta _{1}<\vartheta _{2}\). Then the aforementioned system (92) have the following solution
Now, we solve an RLC electrical circuit in fuzzified version that already studied Devi and Jakhar (2020) in classical environment. An inductor, resistor and capacitor are connected in the form of series with electromotive force of \(\mathcal {E}\) volts. Suppose the current (and charge on the capacitor) in the circuit is zero. Now, we determine and analyze the uncertainty in charge and current when time increase. Suppose \(\mathcal {Q}\) and \(\mathcal {I}\) is the charge and current at a specific time. Second-order ordinary differential equation is
We construct a fuzzified form of the above Eq. (93). So, the fractional model of the above initial-value problem can be represented as
with the uncertain initial condition \(\mathcal {Q}(0)=\mathcal {Q}_{0}\) and \(\mathcal {Q}^{(1)}(0)=\mathcal {Q}^{(1)}_{0}\) are fuzzy number. The model given in Eq. (94) is a special case of the model given in Eq. (4) with fractional orders \(0<\alpha _{1}\le 2\) and \(0<\alpha _{2}\le 1\).
Suppose \(\mathcal {Q}(t)=\hslash (x)\), \(\mathcal {E}(t)=\mathfrak {f}(x)\) and assume arbitrary values for each parameter as: \(\alpha _{1}=0.7\), \(\alpha _{2}=0.5\), \(\mathcal {Q}(0)=(\alpha , 2-\alpha )\), \(\mathcal {Q}^{(1)}(0)=(\alpha , 2-\alpha )\), \(\mathcal {L}=\mathcal {R}=1\). Let us consider that the value of \(\mathcal {C}\) is large enough. Then the above problem (94) can be written as
The system (95) is an application of the Theorem 4. The solution of the system (95) for the first form of differentiability is given by
The solution of the system (95) for the second form of differentiability
This solution is almost close to the crisp solution, and we obtain the exact solution in the crisp environment by taking \(\alpha\) equal to 1. In a broader sense, uncertainty in FFDE may be due to measurements, observations, environmental facts, or lack of information. Since the initial conditions have some uncertainty due to the measurement. This solution also satisfies the solution in a crisp environment with a slight modification of the initial conditions. This study shows how fuzzification of non-integer order differential equations can help researchers maintain tolerance. The research also has important implications for dealing with uncertainty in Brownian motion.
6 Conclusions
Fractional calculus is a useful subfield of mathematical analysis. This is a generalization of usual calculus that allows non-integer order. It has become the focus of attention of mathematicians, physicists and engineers. In this article, we have analyzed and investigated a fully closed-form solution for FFDEs with independent fractional order in terms of the Mittage-Leffler function using SGHD. We have classified this solution into first and second differentiability according to the concept of SGHD. A potential solution of homogeneous and inhomogeneous FFDEs with independent fractional order has been determined using a fuzzy Laplace transform approach. Several significant concepts, facts, and relationships have been introduced and analyzed. To grasp the considered technique, some illustrative examples have been studied and analyzed to visualize and support the theoretical results. The proposed technique has some sort of drawbacks which can be explained as follows: The SGHD generates two types of differentiability which are usually called the first and second forms of differentiability. The H-derivative corresponds to the first form, and the non-decreasing diameter of a differentiable fuzzy function is the second form of differentiability (if it exists). However, when we apply the fuzzy Laplace transform approach to arrive at a proposed solution, the second differentiability adds the difficulty. In general, certain results are only valid in specific conditions when we use the second differentiability. In future, one can discuss the uncertainty and vagueness of Brownian motion using the proposed approach.
Data availability
No data were used to support this study.
References
Agarwal RP, Lakshmikantham V, Nieto JJ (2010) On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal Theory Methods Appl 72(6):2859–2862
Ahmad MZ, Hassan MK, Abbasbanday S (2013) Solving fuzzy fractional differential equations using Zadeh’s extension principle. Sci World J 2013:1–11
Ahmad A, Nieto JJ (2010) Solvability of nonlinear Langevin equation involving two fractional orders with Dirichlet boundary conditions. Int J Differ Equ 1649486
Ahmad B, Nieto JJ, Alsaedi A, El-Shahed M (2012) A study of nonlinear Langevin equation involving two fractional orders in different intervals. Nonlinear Anal Real World Appl 13:599–606
Ahmad S, Ullah A, Ullah A, Akgül A, Abdeljawad T (2021) Computational analysis of fuzzy fractional order non-dimensional Fisher equation. Phys Scr 96(8):084004
Ahmadova A, Huseynov IT, Fernandez A, Mahmudov NI (2021) Trivariate Mittag-Leffler functions used to solve multi-order systems of fractional differential equations. Commun Nonlinear Sci Numer Simul 97:105735
Akram M, Allahviranloo T, Pedrycz W, Ali M (2021) Methods for solving \(LR\)-bipolar fuzzy linear systems. Soft Comput 25:85–108
Akram M, Ihsan T, Allahviranloo T (2022) Solving Pythagorean fuzzy fractional differential equations using Laplace transform. Granul Comput. https://doi.org/10.1007/s41066-022-00344-z
Akram M, Ihsan T, Allahviranloo T, Al-Shamiri MMA (2022) Analysis on determining the solution of fourth-order fuzzy initial value problem with Laplace operator. Math Biosci Eng 19(12):11868–11902
Akram M, Ihsan T (2022) Solving Pythagorean fuzzy partial fractional diffusion model using the Laplace and Fourier transforms. Granul Comput. https://doi.org/10.1007/s41066-022-00349-8
Akram M, Muhammad G, Allahviranloo T, Ali G (2022) New analysis of fuzzy fractional Langevin differential equations in Caputo’s derivative sense. AIMS Math 7(10):18467–18496
Akram M, Muhammad G, Allahviranloo T, Ali G (2023) A solving method for two-dimensional homogeneous system of fuzzy fractional differential equations. AIMS Math 8(1):228–263
Allahviranloo T, Ahmadi MB (2010) Fuzzy laplace transforms. Soft Comput 14(3):235
Allahviranloo T, Armand A, Gouyandeh Z (2014) Fuzzy fractional differential equations under generalized fuzzy Caputo derivative. J Intell Fuzzy Syst 26(3):1481–1490
Allahviranloo T, Ghanbari B (2020) On the fuzzy fractional differential equation with interval Atangana-Baleanu fractional derivative approach. Chaos Solit Fractals 130:109397
Allahviranloo T, Salahshour S, Abbasbandy S (2012) Explicit solutions of fractional differential equations with uncertainty. Soft Comput 16(2):297–302
Baghani H, Nieto JJ (2019) On fractional Langevin equation involving two fractional orders in different intervals. Nonlinear Anal Model 24:884–897
Bede B, Gal SG (2005) Generalizations of the differentiability of fuzzy-number-valued functions with applications to fuzzy differential equations. Fuzzy Sets Syst 151(3):581–599
Blackwell B, Beck J (2010) A technique for uncertainty analysis for inverse heat conduction problems. Int J Heat Mass Transf 53(4):753–759
Chen A, Chen Y (2011) Existence of solutions to nonlinear Langevin equation involving two fractional orders with boundary value conditions. Bound Value Probl 3:1–17
Devi A, Jakhar M (2020) Analytic solution of fractional order differential equation arising in RLC electrical circuit. Malaya J Matematik 8(2):421–426
Diethelm K (2010) The analysis of fractional differential equations: an application-oriented exposition using differential operators of Caputo type. Series on complexity, nonlinearity and chaos. Springer, Heidelberg
Diethelm K, Ford NJ (2004) Multi-order fractional differential equations and their numerical solution. Appl Math Comput 154:621–640
Diethelm K, Ford NJ, Freed AD (2002) A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn 29:3–22
Dong NP, Son NTK, Allahviranloo T, Tam HTT (2022) Finite-time stability of mild solution to time-delay fuzzy fractional differential systems under granular computing. Granul Comput. https://doi.org/10.1007/s41066-022-00325-2
Dubios D, Prade H (1982) Towards fuzzy differential calculus part 3: differentiation. Fuzzy Sets Syst 8(3):225–233
Ezadi S, Allahviranloo T (2020) Artificial neural network approach for solving fuzzy fractional order initial value problems under \(gH\)-differentiability. Math Methods Appl Sci
Friedman M, Ming M, Kandel A (1996) Fuzzy derivatives and fuzzy Cauchy problems using LP metric. Fuzzy Logic Found Ind Appl 8:57–72
Fazli H, Sun H, Nieto JJ (2020) Fractional Langevin equation involving two fractional orders: existence and uniqueness. Mathematics 8(5):743
Ghaffari M, Allahviranloo T, Abbasbandy S, Azhini M (2021) On the fuzzy solutions of time-fractional problems. IJFS 18(3):51–66
Goetschel R Jr, Voxman W (1986) Elementary fuzzy calculus. Fuzzy Sets Syst 18(1):31–43
Haq EU, Hassan QMU, Ahmad J, Ehsan K (2022) Fuzzy solution of system of fuzzy fractional problems using a reliable method. Alex Eng J 61(4):3051–3058
Hoa NV, Lupulescu V, O’Regan D (2017) Solving interval-valued fractional initial value problems under Caputo \(gH\)-fractional differentiability. Fuzzy Sets Syst 309:1–34
Khakrangin S, Allahviranloo T, Mikaeilvand N, Abbasbandy S (2021) Numerical solution of fuzzy fractional differential equation by Haar wavelet. Int J Appl Math 16(1):14
Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations, 20th edn, vol 204. Elsevier Science, Amsterdam, pp 1–523
Magin RL (2006) Fractional calculus in bioengineering. Begell House Publisher Inc, Connecticut
Mahmudov NI (2020) Fractional Langevin type delay equations with two fractional derivatives. Appl Math Lett 106215
Melliani S, Arhrrabi E, Elomari MH, Chadli LS (2021) Ulam-Hyers-Rassias stability for fuzzy fractional integrodifferential equations under Caputo \(gH\)-differentiability. Int J Optim Appl 51
Miller KS, Ross B (1993) An introduction to the fractional calculus and differential equations. Wiley, New York
Ngo HV, Lupulescu V, O’Regan D (2018) A note on initial value problems for fractional fuzzy differential equations. Fuzzy Sets Syst 347:54–69
Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier, Amsterdam
Podlubny I (1999) Fractional differential equations. Academic Press, San Diego
Prabhakar TR (1971) A singular integral equation with a generalized Mittag-Leffler function in the kernel. Yokohama Math J
Puri ML, Ralescu DA (1983) Differentials of fuzzy functions. J Math Anal Appl 91(2):552–558
Rahaman M, Mondal SP, Alam S, Khan NA, Biswas A (2021) Interpretation of exact solution for fuzzy fractional non-homogeneous differential equation under the Riemann-Liouville sense and its application on the inventory management control problem. Granul Comput 6(4):953–976
Salahshour S, Allahviranloo T (2013) Applications of fuzzy Laplace transforms. Soft comput 17(1):145–158
Salahshour S, Allahviranloo T, Abbasbandy S (2012) Solving fuzzy fractional differential equations by fuzzy Laplace transforms. Commun Nonlinear Sci Numer Simul 17(3):1372–1381
Samko SG, Kilbas AA, Marichev OI (1993) Fractional integrals and derivatives: theory and applications. Gordon & Breach Science Publishers, Yverdon
Seikkala S (1987) On the fuzzy initial value problem. Fuzzy Sets Syst 24(3):319–330
Smadi MA, Arqub OA, Zeidan D (2021) Fuzzy fractional differential equations under the Mittag-Leffler kernel differential operator of the ABC approach: Theorems and applications. Chaos Solit Fractals 146:110891
Vu H, Hoa NV (2019) Uncertain fractional differential equations on a time scale under granular differentiability concept. Comput Appl Math 38(3):1–22
Wang C, Qiu Z, He Y (2015) Fuzzy interval perturbation method for uncertain heat conduction problem with interval and fuzzy parameters. Int J Numer Methods Eng 104(5):330–34
Wasques V, Laiate B, Pedro FS, Esmi E, Barros LCD (2020) Interactive fuzzy fractional differential equation: application on HIV dynamics. In: International conference on information processing and management of uncertainty in knowledge-based systems. Springer, Cham, pp 198–211
Yue Z, Guangyuan W (1998) Time domain methods for the solutions of \(N\)-order fuzzy differential equations. Fuzzy Sets Syst 94(1):77–92
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Akram, M., Muhammad, G. Analysis of incommensurate multi-order fuzzy fractional differential equations under strongly generalized fuzzy Caputo’s differentiability. Granul. Comput. 8, 809–825 (2023). https://doi.org/10.1007/s41066-022-00353-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41066-022-00353-y