Stability and chaotic dynamics of forced $\phi ^8$ generalised Liénard systems

Abstract

This work studies a forced generalised Liénard oscillator with $\phi ^8$ potential with order 8 dissipation. The fixed points and their stability have been analysed for autonomous and non-dissipative Liénard oscillator. The system can exhibit three, five or seven fixed points and the corresponding stability diagram is checked and analysed. The effect of restoring parameters on the potential is also studied. Periodic, multiperiodic and chaotic monostable and bistable attractors and their coexistence have been checked through the bifurcation diagram, Lyapunov exponent, phase space and Poincaré section using the fourth-order Runge–Kutta algorithm. The results obtained by the analytical methods are validated and complemented by the numerical simulations.

1 Introduction

From ancient times till today, many life-like phenomena are based on nonlinearities. The knowledge and mastery of these phenomena require a good understanding of the related laws of nonlinear sciences. It is in this sense that many researchers are doing research in fields such as mathematics, physics, chemistry, finance, epidemiology, aeronautics, engineering, etc. where these nonlinear sciences are applied. The equations of nonlinear oscillators are based on the equations which are often used to globalise these nonlinear phenomena. To understand the behaviour of oscillators, we often focus on theoretical, numerical and experimental investigations. Theoretical investigations reveal their rich and complex behaviours, and the experimental investigations (self-excited oscillators) describe the evolution of many biological, chemical, electrical, mechanical, optical, aeronautical and other engineering systems [1,2,3,4,5,6]. Among the nonlinear oscillators, we can cite the Liénard oscillator with its various variants that model several phenomena in electronics, electricity and mechanics [7,8,9,10,11,12,13,14]. For these different oscillators, the researchers have studied the existence and the number of limit cycles using different techniques [7,8,9,10,11,12]. In the meantime, we have studied Melnikov’s chaos for Rayleigh–Liénard’s two-well oscillators subjected to parametric excitation and then to an amplitude modulation force [13, 14]. In these studies, we note the importance of limit cycles, chaos in engineering and other fields of science. On the other hand, Chudzik et al [15], Kuiate et al [16] and Kingni et al [17] have studied multistability and coexistence of periodic, multiperiodic and chaotic attractors for nonlinear oscillators using numerical methods. They have proved the importance of the presence of these attractors and their coexistence in biological, physical and non-physical systems. It is pointed out that the chaos analysis of the four-well oscillator has not yet been done in the literature. In this work we consider the generalised oscillator of Liénard oscillator whose equation is as follows:

$$\begin{aligned}&\ddot{x}-(a_0+a_1x^2+a_2x^4+a_3x^6+a_4x^8)\dot{x}\nonumber \\&\quad +(x-x^3)(b_2x^4+b_1x^2+b_0)=f\cos \Omega t. \end{aligned}$$

(1)

$a_i, i=0\hbox {--}4$, are coefficients of the damping terms while $b_j, j=0\hbox {--}2$, are the coefficients of the stiffness terms. f and $\Omega$, respectively, denote the amplitude and the frequency of the external periodic excitation. This oscillator has been the subject of research and the Hopf bifurcation is studied by Wu et al [18]. In their study, they considered the case where the generalised oscillator of Liénard is $Z_2$-equivariant. In addition, the generalised forced Liénard equations appear in a number of physical models and an important question is whether these equations can support periodic solutions. This problem has been studied extensively by a number of researchers. In fact, they investigated the existence of periodic solutions for a class of second-order generalised forced Liénard equations using Schauder’s fixed point theorem and Green’s function (see e.g. [19,20,21,22,23,24]). The objective of this work is to look for all the fixed points of the undamping and autonomous system and to study their nature and stability. This work is also concerned with the conditions for which the $\phi ^8$ potential of the Liénard oscillator is a four well considering the importance of sinks in the variation of energy for physical and biological oscillators. The variation of the depth of each well under the influence of the parameters $b_j$ is also analysed. Finally, multistability, chaos and hysteresis are numerically studied and the nature of damping terms is derived.

Our work is motivated by the physical significance of the generalised Liénard oscillator. Indeed, in addition to its many applications in electronics and mechanics, Liénard systems are frequently used to model many biological regulatory and physiological systems (single-organ systems, such as the cardiac, respiratory or neural systems, and multiorgan systems, such as the vegetative system, by coupling of Liénard systems) [25,26,27,28]. In these systems, the interest of knowing the potential and Hamiltonian contributions in understanding their mechanisms is crucial. For example, in metabolic models, the potential and Hamiltonian parts have precise biological meanings. In practice, nonlinear systems, in general, and particularly the dynamic, electronic, mechanical, biological, physiological and chemical systems modelled by Liénard equations have interesting properties in the neighbourhood of their equilibrium points. Thus, locating the fixed points of a dynamic system and controlling their stability can predict the dynamics of the system. For example, knowledge of the nature of a point of equilibrium of a system may lead to the determination not only of a certain symmetry of the problem studied but also of the types of bifurcations that the system may present. Specifically, in practice, when the dynamics systems are in the vicinity of one of its stable fixed points or one of its stable limit cycles, it is not too sensitive to the initial conditions. This makes it possible to choose parameters to avoid chaos. On the other hand, the control of the depth of the wells of the potential of a nonlinear dynamic system allows to have an idea of the energy that the system will put in play to enter or leave the well according to the application that one wants to do it. Finally, the systems that undergo hysteresis phenomena are memory systems and are very much in demand in technologies. So looking for stability and multistability, chaotic behaviour, hysteresis and evolution of the depth of the four wells of a generalised Liénard oscillator at potential $\phi ^8$ is important. This work on the generalised Liénard oscillator with potential $\phi ^8$ (this case is studied very little so far because of the great difficulty related to the high nonlinearity of the equation) opens doors to the research on four-well potential systems with significant engineering applications.

The paper is structured as follows: §2 provides the study of the equilibrium points and the stability of the unperturbed generalised Liénard oscillator. This section also deals with the analysis of the effect of parameters $b_j$ on the number and depth of the wells of the $\phi ^8$ potential. In §3, the bifurcation sequences, route to chaos and multistability using numerical simulations are analysed. We provided a conclusion in the last section.

2 Fixed points of the unperturbed system

In this section, we consider the unperturbed system

$$\begin{aligned} \dot{x}&=y, \nonumber \\ \dot{y}&=-(x-x^3)(b_2x^4+b_1x^2+b_0). \end{aligned}$$

(2)

The undamped autonomous system Hamiltonian is

$$\begin{aligned} H(x,y)=&\frac{1}{2}y^2+\frac{1}{2}b_0x^2+\frac{1}{4}(b_1-b_0)x^4\nonumber \\&+\frac{1}{6}(b_2-b_1)x^6-\frac{1}{8}b_2x^8. \end{aligned}$$

(3)

The associated potential is

$$\begin{aligned} V(x)= & {} \frac{1}{2}b_0x^2+\frac{1}{4}(b_1-b_0)x^4\nonumber \\&+\frac{1}{6}(b_2-b_1)x^6-\frac{1}{8}b_2x^8. \end{aligned}$$

(4)

The research and analysis of fixed points of the unperturbed system (2) shows that the system can exhibit three, five or seven fixed points which can be saddle nodes or centres according to the values of the parameters $b_0, b_1,$ and $b_2$. The following lemma (whose proof is given in Appendix A) summarises this result.

Lemma

We consider the undamped autonomous Liénard oscillator described by system (2).

• 1. We assume that $b_0<0$:

  • (a) For $b_1^2<4b_0b_2$, system (2) possesses three fixed points $P_0, P_1$ and $P_2$. $P_0$ is a saddle node if $b_0<0$ and a centre if $b_0>0$; $P_1$ and $P_2$ are symmetrical with respect to $P_0$ and are saddle nodes if $b_0+b_1+b_2<0$ and centre if $b_0+b_1+b_2>0$.

  • (b) When $b_1^2=4b_0b_2$,

    • i. there exists three fixed points $P_0, P_1$ and $P_2$ which can be saddle nodes or centres if $b_1$ and $b_2$ have the same sign;

    • ii. if $b_1$ and $b_2$ have opposite sign, the system has five fixed points $P_0, P_1, P_2, C_1$ and $C_2$.

  • (c) For $b_1^2>4b_0b_2$, the system possesses:

    • i. seven fixed points $P_0, P_1, P_2, P_3, P_4, P_5$ and $P_6$ if $b_0<0, b_1>0$ and $b_2<0$. $P_0$ is a saddle node; $P_1$ and $P_2$ are saddle nodes if $b_0+b_1+b_2>0$ and centre if $b_0+b_1+b_2<0$. $P_3$ and $P_4$ are saddle nodes if $\alpha >0$ and centres when $\alpha <0$. In the same vein, $P_5$ and $P_6$ are saddle nodes if $\beta >0$ and centres when $\beta <0$;

    • ii. three or five fixed points $P_0, P_1, P_2, P_3, P_4, P_5$ and $P_6$ which can be coll points or centres if $b_1<0$, and $b_0$ and $b_2$ do not have a same sign.

• 2. Consider now $b_0>0$. The results are symmetrical with the case of $b_0<0$ with respect to $O$.

The different fixed points are given by

$$\begin{aligned}&P_0(0,0),\quad P_1(-1,0),\quad P_2(1,0),\\{}&P_3\left( -\sqrt{\frac{-b_1+\sqrt{\Delta }}{2b_2}},0 \right) ,\quad P_4\left( \sqrt{\frac{-b_1+\sqrt{\Delta }}{2b_2}},0 \right) ,\\{}&P_5\left( -\sqrt{\frac{-b_1-\sqrt{\Delta }}{2b_2}},0 \right) , \quad P_6\left( \sqrt{\frac{-b_1-\sqrt{\Delta }}{2b_2}},0 \right) ,\\{}&C_1\left( -\sqrt{\frac{-b_1}{2b_2}},0 \right) ,\quad C_2\left( \sqrt{\frac{-b_1}{2b_2}},0 \right) \end{aligned}$$

with $\Delta =b_1^2-4b_0b_2$. $\alpha$ and $\beta$ are given by

$$\begin{aligned} \alpha&=-b_0-3(b_1-b_2)\left( \frac{-b_1+\sqrt{\Delta }}{2b_2}\right) \\&\qquad -5(b_2-b_1)\left( \frac{-b_1+\sqrt{\Delta }}{2b_2}\right) ^{2}\\&\qquad + 7b_2\left( \frac{-b_1+\sqrt{\Delta }}{2b_2}\right) ^{3},\\ \beta&=-b_0-3(b_1-b_2)\left( \frac{-b_1-\sqrt{\Delta }}{2b_2}\right) \\&\qquad - 5(b_2-b_1)\left( \frac{-b_1-\sqrt{\Delta }}{2b_2}\right) ^{2}\\&\qquad + 7b_2\left( \frac{-b_1-\sqrt{\Delta }}{2b_2}\right) ^{3}. \end{aligned}$$

Fig. 1

Existence and stability domains of fixed points of the unperturbed Liénard system with$b_0=-0.6$.

Fig. 2

Existence and stability domains of fixed points of unperturbed Liénard system with $b_0=0.6$.

Fig. 3

Four-well potential of unperturbed Liénard system with $b_0=-0.6$, $b_1=0.5$ and $b_2=-0.1$.

Fig. 4

Effect of different parameters on the four-well potential with parameters of figure 3: (a) effect of $b_0$, (b) effect of $b_1$ and (c) effect of $b_2$.

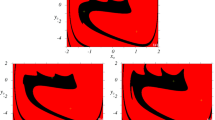
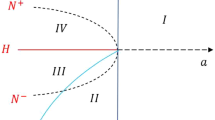
Figures 1 and 2 resume Lemma and show the stability diagram, respectively, for $b_0=-0.6$ and 0.6. For example, figure 1 shows 15 domains in which the number of fixed points and the stability are not the same. Exactly, in domain A, there exists three fixed points $P_0, P_1$ and $P_2$ where $P_0$ is a stitch point and the other two are centres. Domains $B_1$ and $B_2$ have three fixed points $P_0, P_1$ and $P_2$; $B_3$ is the place where seven fixed points coexist: $P_0, P_3, P_4$ are saddle nodes and $P_1, P_2, P_5, P_6$ are centres. $B_4$ is the place where seven fixed points, $P_0, P_1,P_2, P_3, P_4, P_5, P_6$ coexist. $P_0, P_3, P_4, P_5, P_6$ are saddle nodes and $P_1, P_2$ are centres. Domains $C_1$ and $C_2$ represent the place where only fixed points $P_0$ (coll point) and $P_1, P_2$ (centres) coexist. In domain $C_3$, seven fixed points exist: $P_0, P_1,P_2, P_3, P_4$ are saddle nodes and $P_5, P_6$ are centres. In domains $D_1$ and $D_2$, $\Delta <0$ and the undamped autonomous system has three fixed points $P_0, P_1,P_2$ which are all saddle nodes. Then there exist, in domain E, seven fixed points $P_0, P_1,P_2, P_3, P_4, P_5, P_6$, where $P_0$ is a coll and the other six are centres. Domain $F_1$ is the place where the undamped autonomous system has equilibrium points $P_0, P_1,P_2, P_3, P_4, P_5, P_6$, where $P_0, P_1, P_2$ are sells and $P_3, P_4, P_5, P_6$ are centres because $\Delta>0, b_0+b_1+b_2>0, \alpha<0, \beta <0$ (see figure 1). In domain $F_2$, $\Delta>0, b_1>0, b_2>0$ and $b_0+b_1+b_2>0$ so that eq. (2) admits three fixed points: $P_0$ (saddle node) and $P_1, P_2$ (centres). G is the place of existence of the seven fixed points $P_0, P_1,P_2, P_3, P_4, P_5, P_6$ which are stitch because $\Delta>0, b_0+b_1+b_2>0, \alpha>0, \beta >0$ (see figure 1). At last, in domain H, eq. (2) possesses seven fixed points $P_0, P_1,P_2, P_3, P_4, P_5, P_6$, where $P_0, P_3, P_4, P_5, P_6$ are stitch and $P_1,P_2$ are centres because $\Delta>0, b_0+b_1+b_2<0, \alpha>0, \beta >0$ (see figure 1). The same analysis can be made for figure 2 while each domain is symmetrical with its corresponding domain of figure 1 with respect to O.

Fig. 5

Bifurcation diagram of the generalised Liénard system without damping force when $b_0=-0.6, b_1=0.5$ $b_2=-0.1$, $\delta =0.003$ and $\Omega =1$.

Fig. 6

Chaotic phase space (a) and its corresponding Poincaré section (b) of the generalised Liénard system with parameters of figure 5 and $f=0.3$.

Now, we shall consider the case where the system has seven fixed points. Hence, as long as $b_0<0, b_1>0, b_2<0$ and $b_1^2>4b_0b_2$, the undamped autonomous system has a four-well potential. For example, when $b_0=-0.6, b_1=0.5$ and $b_2=-0.1$, we are in the domain H, and one observes clearly in figure 3 that the undamped autonomous system has seven fixed points $P_0, P_1,P_2, P_3, P_4, P_5, P_6$ and a four-well potential. Figures 4a–4c show, respectively, the effects of $b_0, b_1$ and $b_2$ on the four wells of the potential. Indeed, through these figures, we note that the depth of each of the extreme wells increases with each of the parameters $b_0, b_1$ and $b_2$, and that of the intermediate wells decrease when $b_0$ or $b_1$ increases. The increase of $b_2$ has almost no action on intermediate wells. It is also noted that the system has three or five fixed points $P_0, P_1, P_2, P_3, P_4, P_5$ and $P_6$ which can be coll points or centres if $b_1<0$, and $b_0$ and $b_2$ do not have the same sign. In this case, the potential is not four wells.

Fig. 7

Bifurcation diagram (a) and its corresponding Lyapunov exponent (b) of the generalised Liénard system with $a_0=0.001, a_1=0.01, a_2=0, a_3=0.01, a_4=0, b_0=-0.6, b_1=0.5$, $b_2=-0.1$ and $\Omega =1$.

3 Bifurcation and route to chaos

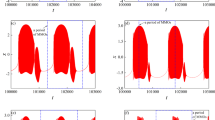
In this section, we are interested in finding the parameters which lead to chaos, and those which can make chaos disappear. The tools used for this purpose are the bifurcation diagram, the Lyapunov exponent, the phase portrait and the Poincaré section. We set $b_0=-0.6, b_1=0.5, b_2=-0.1, \Omega =1$ and the initial conditions are $x_0=0.5$ and $y_0=0.5$. We plot the bifurcation diagram and its corresponding Lyapunov exponent by taking as the bifurcation parameter the amplitude f of the periodic excitation force and also the order 4, 6 and 8 damping parameters. Figure 5 shows the bifurcation diagram of the undamped Liénard oscillator. It is observed from this figure that the undamped system is chaotic over a large range of amplitude of the external force and that the domain of regular behaviour is small compared to that of the chaotic one. The phase portrait (figure 6) obtained for $f=0.3$ confirms the chaotic behaviour of the system. Figure 7 represents the bifurcation diagram and the corresponding Lyapunov exponent for $a_0=0.002, a_1=0.01, a_2=0, a_3=0.01, a_4=0$ and $\delta =0.003$ when $f\in [0,10]$. We note that for these values of damping parameters, the oscillator exhibits periodical behaviours with the periods $1T, 2T, 3T,\ldots$ and also chaotic behaviours. Comparing figures 5 and 7, it can be seen that the presence of damping force considerably reduces the area of chaotic behaviour. Figures 8 and 9 show, respectively, the phase portraits and their corresponding Poincaré sections and have been obtained by choosing the parameters of figure 7 with values of f in the appropriate domains. Through these figures, we note that the periodic, multiperiodic and chaotic behaviours predicted by the bifurcation diagram are confirmed. In addition, there is the coexistence of several attractors (see figure 8c). The influence of order 4, 6 and 8 damping on the chaotic behaviour is analysed and the study of multistability  of the damped oscillator is performed. The obtained results are plotted in figures 10–14. Figures 10 and 13 have been obtained with various values of $a_2$ in [0, 0.04] (figure 10), $a_3$ in [0, 0.01] (figure 13a) and $a_4$ in [0, 0.006] (figure 13b). The blue colour corresponds to an increase of the bifurcation parameter and the red one to a decrease of the same bifurcation parameter. These figures show oscillations for the oscillator with periods 1T, 2T, 3T, .., nT and chaotic oscillations. We also observe the presence of a variety of periodic, multiperiodic and chaotic attractors confirmed by the phase portraits and their corresponding Poincaré sections (see figures 11, 12 and 14). As can be seen in figures 10 and 13, the bifurcation parameters ($a_2, a_3, a_4$) evolve in the increasing or decreasing direction, the dynamics of the generalised Liénard oscillator are the same for the same parameter. Irrespective of the damping parameter, the system is either monostable or bistable. For example, in figure 10, when $a_2$ increases (blue diagram) or decreases (red diagram) in the domain [0, 0.0099041], the dynamic remains the same, corresponding to a value of x. On the remains of the domain, we have different values of x with the same dynamic (figure 10). We then conclude that the Liénard generalised oscillator is monostable if $a_2\in [0, 0.0099041]$ and bistable if $a_2\ge 0.0099041$. The possible dynamics of the system obtained for $a_2$ have been confirmed by the Lyapunov exponent (see figures 10a and 10b). The monostability and bistability are confirmed by the phase spaces (figures 11 and 12). We can then conclude that these monostable and bistable attractors obtained by taking two different directions from variations of the damping parameters can give rise to the phenomenon of hysteresis. This phenomenon is often obtained in the physical and non-physical systems in general and in particular in the electronic systems modelled by the Liénard equation.

Fig. 8

Various phase spaces and the corresponding Poincaré sections of the generalised Liénard system with parameters of figure 7: (a) $f=0.3$, (b) $f=1.2$, (c) $f=5.3$ and (d) $f=6.5$.

Fig. 9

Various Poincaré sections of the generalised Liénard system with parameters of figure 8: (a) $f=0.3$, (b) $f=5.3$ and (c) $f=6.5$.

Fig. 10

Bifurcation diagram vs. $a_2$ (a) and its corresponding Lyapunov exponent (b) of the generalised Liénard system with $a_0\,{=}\,0.001$, $a_1\,{=}\,0.001$, $a_3\,{=}\,0.001$, $a_4\,{=}\,0.0022$, $b_0\,{=}\,-0.6$, $b_1\,{=}\,0.5,$ $b_2=-0.1, f=4.5$ and $\Omega =1$. Bifurcation diagrams and their corresponding Lyapunov exponents are obtained by scanning the parameter $a_2$ upwards (blue) and downwards (red).

Fig. 11

Chaotic attractor in the phase space of the generalised Liénard system with parameters of figure 10 and $a_2=0.002$. (a) Initial conditions (0.5, 0.5) and (b) initial conditions $(-0.5, -0.5)$.

Fig. 12

Period-3T attractor in the phase space of the generalised Liénard system with parameters of figure 10 and $a_2=0.01$. (a) Initial conditions (0.5, 0.5) and (b) initial conditions $(-0.5, -0.5)$.

Fig. 13

Bifurcation diagram vs. $a_3$ (a) and bifurcation diagram vs. $a_4$ (b) of the generalised Liénard system with $a_0=0.001, a_1=0.001, a_2=0.001, b_0=-0.6, b_1=0.5$, $b_2=-0.1, f=4.5$ and $\Omega =1$. Bifurcation diagrams and their corresponding Lyapunov exponents are obtained by scanning each parameter $a_3$ (a) and $a_4$, (b) upwards (blue) and downwards (red).

Fig. 14

Various phase spaces and the corresponding Poincaré section of the generalised Liénard system with parameters of figure 13b. (a) and (b) $a_4=0.0003$, (c) and (d) $a_4=0.0007$, (e) and (f) $a_4=0.0031$.

4 Conclusion

In this work, we have studied the forced generalised Liénard oscillator with a four-well potential and an eight-degree damping. We searched for the number of fixed points and the stability of the autonomous oscillator without damping with an order eight potential. From the conditions of existence and stability obtained, it appears that the oscillator considered in this case can have three, five or seven fixed points which can be stitch points or centres. These different important results are summarised in a lemma and the proof is given in Appendix A and these are supported by stability diagrams (figures 1 and 2). An analysis of the effect of various parameters on the number of wells and their depth has shown that the depth of each of the extreme wells increases with each of the parameters $b_0, b_1$ and $b_2$ and that of the intermediate wells decreases when $b_0$ or $b_1$ increases; the increase of $b_2$ has almost no action on the intermediate wells. It is also noted that when one of the parameters $b_0, b_1, b_2$ varies with $b_1< 0$ and $b_0, b_2$ do not have the same sign, the system has three or five fixed points. Subsequently, a numerical study is performed using a fourth-order Runge–Kutta algorithm and bifurcation diagrams, Lyapunov’s exponent, phase portrait and Poincaré sections are plotted. From the analysis of the results obtained, we showed that the forced damped Liénard oscillator considered in this work presents periodic, multiperiodic and chaotic behaviours for appropriate values of different parameters. Periodic, multiperiodic and chaotic attractors obtained are monostable and bistable proving the presence of the phenomenon of hysteresis. From this study, it appears that the generalised Liénard oscillator with $\phi ^8$ potential is very rich in dynamics and presents important phenomena such as monostability, bistability and hysteresis. Finally, we can conclude that the different important results such as, the fixed points and their stability, the four-well potential and their depth, obtained in this work can help the researchers to investigate the horseshoes chaos for high nonlinear oscillators with $\phi ^8$ potential which is not found right now.

Appendix A: Proof of the lemma

We consider the undamped autonomous system (2). The fixed points are given by $x-x^{3}=0$ and $b_{2}x^{4}+b_{1}x^{2}+b_{0} =0$:

$$\begin{aligned} x-x^{3}=0 \Leftrightarrow x=0\quad \text{ and } \quad x=\pm 1. \end{aligned}$$

Thus, we have $P_0(0,0), P_1(-1,0)$ and $P_2(-1,0)$. We note that $P_0,\, P_1$ and $P_2$ exist always. Now, we resolve $b_{2}X^{2}+b_{1}X+b_{0} =0$ with $x^{2}=X$. The discriminant is $\Delta = b_{1}^2 -4b_{0}b_{2}.$

• If $b_{1}^2 -4b_{0}b_{2}> 0$, $X\pm =-(b_{1}\pm \sqrt{\Delta })/{2b_{2}}$.

  $Sign\; of\; X\pm$:

  $X\pm > 0$ $\Leftrightarrow$ $[-(b_{1}\pm \sqrt{\Delta })/{2b_{2}}] > 0$.

  If $b_{2}>0$, then

  $$\begin{aligned} -b_{1}\pm \sqrt{\Delta }>0 \Leftrightarrow {\left\{ \begin{array}{ll} \sqrt{\Delta } > b_{1}, \\ \sqrt{\Delta } <- b_{1}. \end{array}\right. } \end{aligned}$$

  This implies

  $$\begin{aligned} {\left\{ \begin{array}{ll} b_{0}< 0, \\ b_{1}< 0, \\ b_{2}>0, \\ b_{1}^2 > 4b_{0}b_{2} \end{array}\right. } \end{aligned}$$

  or

  $$\begin{aligned} {\left\{ \begin{array}{ll} b_{0}< 0, \\ b_{1}> 0, \\ b_{2}>0, \\ b_{1}^2 > 4b_{0}b_{2} \end{array}\right. } \end{aligned}$$

  or

  $$\begin{aligned} {\left\{ \begin{array}{ll} b_{0}> 0, \\ b_{1}< 0, \\ b_{2} <0, \\ b_{1}^2 > 4b_{0}b_{2}. \end{array}\right. } \end{aligned}$$

  Thus, in these conditions $x^2_{\pm }$ exist.

  If $b_{2} < 0$, then

  $$\begin{aligned} -b_{1}\pm \sqrt{\Delta }<0&\Rightarrow \pm \sqrt{\Delta }<b_{1} \\&\Rightarrow \sqrt{\Delta } <b_{1}\; \mathrm {or}\; \sqrt{\Delta } >-b_{1}. \end{aligned}$$

  If $b_{1} >0$ and then $x_{\pm }$ exist when

  $$\begin{aligned} {\left\{ \begin{array}{ll} b_{0}< 0,\\ b_{1}>0, \\ b_{2} < 0, \\ b_{1}^{2}-4b_{0}b_{2} >0 \end{array}\right. } \end{aligned}$$

  or

  $$\begin{aligned} {\left\{ \begin{array}{ll} b_{0}> 0,\\ b_{1} <0, \\ b_{2}> 0, \\ b_{1}^{2}-4b_{0}b_{2} >0. \end{array}\right. } \end{aligned}$$

  Then, the unperturbed system admits a trivial double solution (0; 0) and six symmetrical fixed points two by two:

  $$\begin{aligned}&P_1(-1,0) \; \mathrm{and} \; P_2(1,0), \\&\displaystyle P_3\left( -\sqrt{\frac{-b_{1}+ \sqrt{\Delta }}{2b_{2}}},0 \right) \;\mathrm{and} \; P_4\left( \sqrt{\frac{-b_{1}+ \sqrt{\Delta }}{2b_{2}}},0\right) , \\&\displaystyle P_5\left( -\sqrt{ \frac{-b_{1}- \sqrt{\Delta }}{2b_{2}}},0\right) \; \mathrm{and} \;P_6\left( \sqrt{ \frac{-b_{1}- \sqrt{\Delta }}{2b_{2}}},0\right) . \end{aligned}$$

  Consider now the case where $x_{\pm }$ are not simultaneously positive:

  $$\begin{aligned} X_{\pm } =\frac{-b_{1}\pm \sqrt{\Delta }}{2b_{2}}, \quad X_{+}X_{-} =\frac{b_{0}}{b_{2}}. \end{aligned}$$

  There are the three cases:

  • $b_{0} < 0$, $b_{2} < 0.$ This case is discussed above.

  • If $b_{0} > 0$, $b_{2} > 0.$ This case is also discussed above.

  • If $b_{0} < 0$, $b_{2} > 0$ and $b_{2} < 0$, $b_{0} > 0$, $X_{+}\cdot X_{-} < 0$. Then $X_{+}$ and $X_{-}$ have opposite signs and the system admits five fixed points.

• * $b_{0} < 0$ and $b_{2} > 0$:

  $\Delta = b_{1}^{2} -4b_{0}b_{2} > 0$,

  $X_{+} ={-(b_{1}+ \sqrt{\Delta })}/{2b_{2}}$ and $X_{-} = {-(b_{1}- \sqrt{\Delta })}/{2b_{2}}$.

  In this case, $X_{\pm } >0$ have the numerator sign and we have

  $$\begin{aligned} {\left\{ \begin{array}{ll} \sqrt{\Delta }> b_{1}\\ \sqrt{\Delta }< -b_{1} \end{array}\right. }&\;\mathrm{or}\;&{\left\{ \begin{array}{ll} \sqrt{\Delta }< b_{1},\\ \sqrt{\Delta }< -b_{1}. \end{array}\right. } \end{aligned}$$

• * $b_{0}>0$ and $b_{2} <0$: $X_{+}$ and $X_{-}$ have opposite signs of $-b_{1}+\sqrt{\Delta }$ and $-b_{1}-\sqrt{\Delta }$, respectively.

  In the same vein,

  $$\begin{aligned}&{\left\{ \begin{array}{ll} b_{1}-\sqrt{\Delta }< 0\\ b_{1}+\sqrt{\Delta }> 0 \end{array}\right. } \;\mathrm{or}\; {\left\{ \begin{array}{ll} -b_{1}+\sqrt{\Delta }< 0,\\ -b_{1}-\sqrt{\Delta }> 0 \end{array}\right. } \\&{\left\{ \begin{array}{ll} b_{1}< \sqrt{\Delta } \\ \sqrt{\Delta } > -b_{1} \end{array}\right. } \;\mathrm{or}\; {\left\{ \begin{array}{ll} \sqrt{\Delta }< b_{1},\\ \sqrt{\Delta } < -b_{1}. \end{array}\right. } \end{aligned}$$

  Then

  $$\begin{aligned} {\left\{ \begin{array}{ll} b_{1}>0, \\ b_{2} <0, \\ b_{1}^{2} > 4b_{0}b_{2}. \end{array}\right. } \end{aligned}$$

  In these conditions, ${X}_{+} <0$ and $X_{-}>0$:

  $$\begin{aligned} X_{-}>0 \Leftrightarrow X_{-}^{1}= \frac{-b_{1}-\sqrt{\Delta }}{2b_{2}} \end{aligned}$$

  and

  $$\begin{aligned}&X_{-}^{2}= \frac{-b_{1}-\sqrt{\Delta }}{2b_{2}},\\&x_{-}^{1}=\sqrt{\frac{-b_{1}-\sqrt{\Delta }}{2b_{2}}} \\&\mathrm{and}\\&x_{-}^{2}=-\sqrt{\frac{-b_{1}-\sqrt{\Delta }}{2b_{2}}}. \end{aligned}$$

  The fixed points are:

  (0; 0); (1; 0); $(-1;0)$; $(x_{-}^{1};0)$ and $(x_{-}^{2};0)$.

• * $\Delta <0$, i.e. $b_{1}^{2} -4b_{0}b_{2} <0$: The system admits three fixed points (0; 0), (1; 0) and $(-1;0)$.

• * $\Delta =0$, i.e. $b_{1}^{2} -4b_{0}b_{2} =0$:

  $$\begin{aligned} b_{1}^{2} -4b_{0}b_{2} = 0 \Leftrightarrow b_{1}^{2} =4b_{0}b_{2} \end{aligned}$$

  $b_{0}$ and $b_{2}$ have the same sign.

  So $X_{0}={-b_{1}}/{2b_{2}}$.

  • If $b_{0}<0$, $b_{2} <0$:

    $$\begin{aligned}&X_{0}>0\quad \Rightarrow \quad b_{1} >0,\\&x_{0}^{1} =\sqrt{\frac{-b_{1}}{2b_{2}}} \end{aligned}$$

    and

    $$\begin{aligned} x_{0}^{2} =-\sqrt{\frac{-b_{1}}{2b_{2}}}. \end{aligned}$$

    Then the system admits five fixed points (0; 0), (1; 0), $(-1;0)$, $(x_{0}^{1};0)$ and $(x_{0}^{2};0)$.

  • If $b_{0}>0$, $b_{2} >0$:

    $$\begin{aligned} X_{0} >0\quad \Rightarrow \quad b_{1} < 0\\ \end{aligned}$$

    and

    $$\begin{aligned} x_{0}^{1} =\sqrt{\frac{-b_{1}}{2b_{2}}} \end{aligned}$$

    and

    $$\begin{aligned} x_{0}^{2} =-\sqrt{\frac{-b_{1}}{2b_{2}}}. \end{aligned}$$

    The system possesses five fixed points (0; 0), (1; 0), $(-1;0)$, $(x_{0}^{1};0)$ and $(x_{0}^{2};0)$.

  • $b_{1}$ and $b_{2}$ have the same sign, $X_{0} <0$ then the system has three fixed points.

    Nature and stability of fixed points when $\Delta >0$:

    $$\begin{aligned} {\left\{ \begin{array}{ll} b_{0}<0, \\ b_{1}>0, \\ b_{2} <0, \\ b_{1}^{2} - 4b_{0}b_{2} >0. \end{array}\right. } \end{aligned}$$

    The fixed points of the system are

    $$\begin{aligned}&P_{0}(0,0),\,\, P_{1}(-1,0), \\&P_{2}(1,0), \,\, P_{3} \left( -\sqrt{\frac{-b_{1}+ \sqrt{\Delta }}{2b_{2}}},0\right) , \\&P_{4} \left( \sqrt{\frac{-b_{1}+ \sqrt{\Delta }}{2b_{2}}},0 \right) ,\\&P_{5} \left( -\sqrt{\frac{-b_{1}- \sqrt{\Delta }}{2b_{2}}},0\right) , \\&P_{6} \left( \sqrt{\frac{-b_{1}- \sqrt{\Delta }}{2b_{2}}},0\right) . \end{aligned}$$

    The Jacobian matrix at the equilibrium point $E_*(x_*,0)$ gives

    $$\begin{aligned} {\mathcal J} = \left( \begin{array}{c@{\quad }l} 0 &{} 1 \\ -b_{0} - 3(b_{1}-b_{0})x_*^{2}-5(b_{2}- b_{1})x_*^{4}+7b_{2}x_*^{6} &{} 0 \end{array} \right) . \end{aligned}$$

• $\textit{Case of}\; P_{0}(0;0)$

  $$\begin{aligned} {\mathcal J} = \left( \begin{array}{cl} 0 &{} 1 \\ -b_{0} &{} 0 \end{array} \right) . \end{aligned}$$

  The characteristic equation is

  $$\begin{aligned} \lambda ^{2} + b_{0} =0 \end{aligned}$$

  and the eigenvalues are $\lambda _{\pm } = \pm \sqrt{-b_{0}}$ if $b_{0}<0$. $\lambda _{+}$ and $\lambda _{-}$ are real with opposite sign and then the fixed point $P_{0}$ is a semistable saddle node.

  If $b_{0}>0$, $\lambda _{\pm } = \pm \mathrm {i} \sqrt{-b_{0}}$, the fixed point $P_{0}$ is a centre.

• * $\textit{Case of}\; P_{1}\; and\; P_{2}$

  $$\begin{aligned}&{\mathcal J} _{P_{1}} = {\mathcal J} _{P_{2}}\\&\quad = \left( \begin{array}{ll} 0 &{} 1 \\ -b_{0} - 3(b_{1}-b_{0})-5(b_{2}- b_{1})+7b_{2} &{} 0 \end{array} \right) . \end{aligned}$$

  The characteristic equation

  $$\begin{aligned} \lambda ^{2} + 3(b_{1}-b_{0})-5(b_{2}- b_{1})+7b_{2}=0 \end{aligned}$$

  and is reduced as

  $$\begin{aligned} \lambda ^{2} =2(b_{0}+b_{1}+b_{2}). \end{aligned}$$

  • If $b_{0}+b_{1}+b_{2} >0,$

    $$\begin{aligned} b_{1}>-b_{0}-b_{2}, \quad \lambda _{\pm } =\pm \sqrt{2(b_{0}+b_{1}+b_{2})}. \end{aligned}$$

    The fixed points $P_{1}$ and $P_{2}$ are saddle nodes and semistable.

  • If $b_{0}+b_{1}+b_{2}<0$, then

    $$\begin{aligned} \lambda _{\pm } =\pm \mathrm {i} \sqrt{-2(b_{0}+b_{1}+b_{2}).} \end{aligned}$$

    So, $P_{1}$ and $P_{2}$ are centres.

• * $\textit{Case of}\; P_{3}$ and $P_{4}$

  $$\begin{aligned}&{\mathcal J} _{P_{3}},{\mathcal J} _{P_{4}} = \left( \begin{array}{c@{\quad }l} 0 &{} 1 \\ -b_{0} - 3(b_{1}-b_{0})x^{2}-5(b_{2}- b_{1})x^{4}+7b_{2}x^{6} &{} 0 \end{array} \right) _{P_{3},P_{4}}. \end{aligned}$$

  The characteristic equation is

  $$\begin{aligned} \lambda ^{2} -\alpha =0 \end{aligned}$$

  with

  $$\begin{aligned} \alpha =&-b_{0} - 3(b_{1}-b_{0})\left( \frac{-b_{1}+\sqrt{\Delta }}{2b_{2}}\right) \\&-5(b_{2}-b_{1})\left( \frac{-b_{1}+ \sqrt{\Delta }}{2b_{2}}\right) ^{2}\\&+7b_{2}\left( \frac{-b_{1}+\sqrt{\Delta }}{2b_{2}}\right) ^{3}. \end{aligned}$$

  If $\alpha >0$, $\lambda _{\pm } = \pm \sqrt{\alpha }$ and $P_{3}$ and $P_{4}$ are saddle nodes.

  If $\alpha <0$, $\lambda _{\pm } = \pm \mathrm {i} \sqrt{\alpha }$ and $P_{3}$ and $P_{4}$ are centres.

• * $\textit{Case of}\; P_{5}$ and $P_{6}$

  $$\begin{aligned}&{\mathcal J} _{P_{5}},{\mathcal J} _{P_{6}}= \left( \begin{array}{c@{\quad }l} 0 &{} 1 \\ -b_{0} - 3(b_{1}-b_{0})x^{2}-5(b_{2}- b_{1})x^{4}+7b_{2}x^{6} &{} 0 \end{array} \right) _{P_{5},P_{6}}. \end{aligned}$$

  The characteristic equation is

  $$\begin{aligned} \lambda ^{2} -\beta =0 \end{aligned}$$

  with

  $$\begin{aligned} \beta =&-b_{0} - 3(b_{1}-b_{0})\left( \frac{-b_{1}-\sqrt{\Delta }}{2b_{2}}\right) \\&-5(b_{2}-b_{1})\left( \frac{-b_{1}- \sqrt{\Delta }}{2b_{2}}\right) ^{2}\\&+7b_{2}\left( \frac{-b_{1}-\sqrt{\Delta }}{2b_{2}}\right) ^{3}. \end{aligned}$$

• If $\beta >0$, $\lambda _{\pm } = \pm \sqrt{\beta }$, $P_{5}$ and $P_{6}$ are saddle nodes and are semistable.

• If $\beta <0$, $\lambda ^{2}=-\mathrm {i}^{2}\beta$ $\Leftrightarrow$ $\lambda _{\pm } = \pm \mathrm {i} \sqrt{\beta }$, $P_{5}$ and $P_{6}$ are centres.