1 Introduction

The theory of oscillators has shown that many dynamics phenomena can be modeled by oscillators in engineering, biochemistry, biophysics, and communications. Nonlinear oscillations and its applications in physics, chemistry, and engineering are studied with some analytical, numerical, and experimental methods [1,2,3,4,5]. The most interesting nonlinear oscillators are self-excited, and the study of their dynamics is often difficult. Duffing–Van der Pol–Rayleigh oscillators have been studied by many researchers. Nowadays, much research has accomplished the composition of these oscillators. Multiresonance, chaotic behavior and its control, bifurcations, limit cycle stability, hysteresis and jump phenomena, analytic solutions, plasma oscillations, and noise effect...are seriously analyzed [6,7,8,9,10,11,12,13,14]. Among the many fields of application of the system, we have the nonlinear dynamics of ship rolling. Roll motion has been attracting considerable attention over the years because of it being the most critical motion leading to a capsize, out of the six motions of a ship. Since so many casualties have continued to be reported due to severe rolling, it seems that it will retain its popularity for many years to come. Linear and nonlinear formulation of the motion can be found in the literature [15, 16]. Linearity of the motion is often violated by the nonlinear features of damping and restoring. Thus, most of the time nonlinearity is introduced into the equation through these two parameters. Various models of roll motion containing nonlinear terms in damping and restoring have been studied by many researchers [17,18,19,20,21]. Several techniques are used by many researchers to identify different behaviors of a ship (see [13,14,15,16,17,18,19,20,21,22,23,24,25,26]). The most important are the phenomena of resonance and jump amplitude, regular, chaotic, hyperchaotic behaviors, etc. For example, ultraharmonics, subharmonics, and superharmonics oscillations in ship rolling motion are studied with different models by many researchers [27,28,29,30]. Holappa and Falzarano [26] have established the ship motions general equation, and Contento et al. [31] obtained the effectiveness of constant coefficients roll motion equation.

The nonlinear oscillator considered in this paper is an hybrid Rayleigh–Van der Pol–Duffing oscillator. The equation of motion of the system is written as

$$\begin{aligned}&\ddot{x} + 2\tilde{\mu } \dot{x} + \tilde{\delta _2} \dot{x}^3 + \tilde{\beta _1} x \dot{x} + \tilde{\beta _2}\dot{x}^2 +\tilde{\delta _1} x^2\dot{x}+ \omega _0^2 x \nonumber \\&+ \tilde{\lambda } x^3 + \tilde{\gamma } x^5=F\cos \omega t, \end{aligned}$$
(1)

where \(\tilde{\mu }, \tilde{\beta _1}, \tilde{\beta _2}, \tilde{\delta _1}, \tilde{\delta _2}\) are linear, impure quadratic, pure quadratic, impure cubic, and pure cubic nonlinear damping coefficients respectively; which represent Rayleigh and Van der Pol terms. \(\tilde{\lambda }\) and \(\tilde{\gamma }\) are cubic and quintic nonlinear Duffing coefficients, respectively; \(\omega _0\) and \(\omega \) are natural and external forcing frequencies respectively and F represents the external forcing amplitude. Our goal is to find the different behaviors of physical systems simultaneously taking into account the Rayleigh–Van der Pol–Duffing terms and also quadratic (pure and hybrid) damping parameters. We also seek the mutual influence of these parameters on the behaviors obtained. Since this kind of equation can model ship rolling motions, knowledge of these phenomena will enable the practical naval architect to know when they occur and understand their consequences so that it will be able to avoid design that promotes capsizing, to evaluate the sea worthiness of a craft and recommend appropriate measures to control or minimize large amplitudes motions.

The paper is organized as follows: Sect. 2 addresses the different resonances states, analyzes the effect of different parameters of the system. Section 3 deals with the analyses of the bifurcations sequences and transition to chaos using the numerical simulations. The conclusion is presented in the last section.

2 Resonant oscillatory states

In this section, we investigate theoretically and numerically analysis of the nonlinear responses of our model equation to primary resonance, superharmonic resonances, and subharmonic resonances of the vibration mode. Since these oscillations rise up at different timescales, the best tool to be used for their investigation is the multiple timescale method [6, 32]. We set \(\tilde{\mu }=\epsilon \mu , \tilde{\beta _1}=\epsilon \beta _1, \tilde{\beta _2}=\epsilon \beta _2, \tilde{\delta _1}=\epsilon \delta _1, \tilde{\delta _2}=\epsilon \delta _2, \tilde{\lambda }=\epsilon \lambda \) and \(\tilde{\gamma }=\epsilon \gamma \). In such a situation, an approximate solution is generally sought as follows:

$$\begin{aligned} x( \epsilon ,t)=x_0(T_0,T_1)+ \epsilon x_0(T_0,T_1) +\dots . \end{aligned}$$
(2)

The first and second times derivatives are defined as follow:

$$\begin{aligned}&\frac{d}{dt}=D_0+\epsilon D_1 +\dots . \end{aligned}$$
(3)
$$\begin{aligned}&\frac{d^2}{dt^2}=D_0^2+2\epsilon D_1 D_0+\dots , \end{aligned}$$
(4)

where \( D_n^m= \frac{\partial ^m}{\partial T_n^m}\) and \(T_n = \epsilon ^n t\).

2.1 Primary resonance

In the case of primary resonant state, the amplitude F of the external excitation is small, that is \(F=\epsilon F_0\). The closeness between both internal and external frequencies is given by \(\omega = \omega _0+ \epsilon \sigma \), where \(\sigma \) is the detuning parameter. With Eqs. (2), (3), and (4 ), Eq. (1) gives

Order \(\epsilon ^0 \):

$$\begin{aligned} D_0^2 x_0+ \omega _0^2 x_0=0, \end{aligned}$$
(5)

Order \(\epsilon ^1\):

$$\begin{aligned}&D_0^2 x_1+ \omega _0^2 x_1= F_0\cos \omega t - 2D_1 D_0 x_0- 2 \mu D_0 x_0\nonumber \\&-\,\delta _2 (D_0 x_0)^3-\beta _1 x_0 D_0 x_0\nonumber \\&-\,\beta _2 (D_0 x_0)^2 -\delta _1 x_0^2 D_0 x_0\nonumber \\&-\,\lambda x_0^3 -\gamma x_0^5 . \end{aligned}$$
(6)

We set \( \omega _0=1\). The general solution of Eq. (5) is

$$\begin{aligned} x_0=A(T_1)e^{(jT_0)}+ cc, \end{aligned}$$
(7)

where \(''cc''\) is the complex conjugate of the previous terms. Inserting this solution into Eq. (6), eliminating the secular terms, we found after somme algebraic manipulations the primary resonant amplitude equation as follows:

$$\begin{aligned}&\left( \sigma ^2 +\mu ^2\right) +\left[ \mu \left( \frac{3\delta _2}{4}+\frac{\delta _1}{2} \right) -\frac{\sigma }{4}\left( 3\lambda -\frac{\delta _1}{2} \right) \right] a_0^4 \nonumber \\&\quad +\left[ \left( \frac{3\delta _2}{8}+\frac{\delta _1}{4} \right) ^2 -\frac{5\gamma \sigma }{8}+ \frac{1}{64} \left( 3\lambda -\frac{\delta _1}{2} \right) ^2 \right] a_0^6 \nonumber \\&\quad +\frac{5\gamma }{64}\left( 3\lambda -\frac{\delta _1}{2} \right) a_0^8 + \frac{25\gamma ^2 }{256}a_0^{10}-\frac{F_0}{4} =0. \end{aligned}$$
(8)

We plotted in Fig. 1 the primary amplitude response curves obtained from Eq. (8). One can observe that the resonance amplitude and frequency are affected only by cubic damping coefficients and amplitude of external force. Thereby, it is observed that the model goes from resonance to a hysteresis state when the cubics damping descrease and the amplitude of external force increases.

Fig. 1
figure 1

Primary resonant state curves a effect of \(\delta _1\), b effect of \(\delta _2\) and c effect of \(F_0\) with \(\lambda =-0.6, \gamma =0.05, F_0=0.5, \omega _0=1\)

Full size image

2.2 Superharmonic and subharmonic resonances

When the amplitude of the sinusoidal external force is large \((F=\epsilon ^0 F_0)\), other type of oscillations can be displayed by the model, namely the superharmonic and the subharmonic oscillatory states. Using the multiple timescale method, we obtain:

Order \(\epsilon ^0 \):

$$\begin{aligned} D_0^2 x_0+ \omega _0^2 x_0= F\cos \omega t , \end{aligned}$$
(9)

Order \(\epsilon ^1\):

$$\begin{aligned} D_0^2 x_1+ \omega _0^2 x_1= - 2D_1 D_0 x_0- 2 \mu D_0 x_0-\delta _2 (D_0 x_0)^3-\nonumber \\ \beta _1 x_0 D_0 x_0-\beta _2 (D_0 x_0)^2 -\delta _1 x_0^2 D_0 x_0-\lambda x_0^3 -\gamma x_0^5 .\nonumber \\ \end{aligned}$$
(10)

The general solution of Eq. (7) is

$$\begin{aligned} x_0=A(T_1)e^{(jT_0)}+ \varLambda e^{j\omega T_0}+ cc, \end{aligned}$$
(11)

where \( \varLambda =\frac{F}{2\left( 1-\omega ^2\right) }\), and \(\omega _0=1\).

Inserting this solution into Eq. (10), we obtain after some algebraic manipulations the following equation:

$$\begin{aligned}&D_0^2 x_1+ x_1= \left[ -2jA' -3j\delta _2 | A|^2A - 6j\delta _2 \omega ^2 \varLambda ^2 A\right. \nonumber \\&\left. \quad - 3 \lambda | A|^2 A -6\lambda A\varLambda ^2\right] e^{jT_0}\nonumber \\&\quad +\left[ - 10\gamma |A|^4A -60 \gamma \varLambda ^2 |A|^2A-30\gamma A \varLambda ^4\right] e^{jT_0}\nonumber \\&\quad + \left[ - j \delta _1 |A|^2 A-2j\delta _1 A\varLambda ^2-2j\mu A\right] e^{jT_0}\nonumber \\&\quad +\left( \beta _2 A^2-j\beta _1 A^2 \right) e^{2jT_0}\nonumber \\&\quad \times \left[ j\delta _2 A^3 -\lambda A^3 -5\gamma | A|^2 A^3\right. \nonumber \\&\left. \quad -20 \gamma \varLambda ^2 A^3-j\delta _1 A^3 \right] e^{3jT_0}- \gamma A^5 e^{5jT_0}\nonumber \\ \end{aligned}$$
$$\begin{aligned}&\quad +\left[ -6j\delta _2 \omega \varLambda |A|^2-3j\delta _2 \omega ^3 \varLambda ^3-6\lambda \varLambda |A|^2\right. \nonumber \\&\left. \quad - 3\lambda \varLambda ^3 -30\gamma \varLambda |A|^4\right] e^{j\omega T_0}\nonumber \\&\quad +\left[ -60\gamma \varLambda ^3|A|^2-10\gamma \varLambda ^5-2j\omega \delta _1\varLambda |A|^2-j\omega \delta _1 \varLambda ^3\right. \nonumber \\&\left. \quad - 2j\omega \mu \varLambda \right] e^{j\omega T_0} \left( \beta _2 \omega ^2 \varLambda ^2-j\beta _1 \omega \varLambda ^2 \right) e^{2j\omega T_0} \nonumber \\&\quad \times \left[ j\delta _2 \varLambda ^3 \omega ^3 - \lambda \varLambda ^3 - 20\gamma \varLambda ^3 |A|^2 - 5\gamma \varLambda ^5- j \omega \delta _1 \varLambda ^3 \right] e^{3j\omega T_0}\nonumber \\&\quad -\gamma \varLambda ^5 e^{5j\omega T_0} + \left[ -2\beta _2 \omega \varLambda A - j\beta _1 \varLambda A +j \omega \beta _1 \varLambda A \right] \nonumber \\&\quad \times e^{j(1-\omega )T_0} + \left[ -2 \beta _2 \omega \varLambda \bar{A} + j\beta _1 \varLambda \bar{A} -j\omega \beta _1 \varLambda \bar{A} \right] e^{j(-1+\omega )T_0}\nonumber \\&\quad +\left[ -3j\delta _2 \omega \varLambda A^2 - 3\lambda \varLambda A^2 - 20 \gamma \varLambda |A|^2 A^2 \right] e^{j(2-\omega )T_0}\nonumber \\&\quad +\left[ -30 \gamma \varLambda ^3 A^2 -2j\delta _1 \varLambda A^2+ j\omega \delta _1 \varLambda A^2 \right] e^{j(2-\omega )T_0}\nonumber \\&\quad \times \left[ 3j\delta _2 \omega \varLambda \bar{A}^2 -3\lambda \varLambda \bar{A}^2 - 20 \gamma \varLambda |A|^2 \bar{A}^2 \right] e^{j(2-\omega )T_0}\nonumber \\&\quad +\left[ -30 \gamma \varLambda ^3 \bar{A}^2 +2j\delta _1 \varLambda \bar{A}^2 -j\omega \delta _1 \varLambda \bar{A}^2 \right] e^{j(-2+\omega )T_0}\nonumber \\&\quad + \left[ 3j\delta _2 \omega ^2 A \varLambda ^2 - 3 \lambda A \varLambda ^2 -30 \gamma |A|^2 {A} \varLambda ^2\right] e^{j(1-2\omega )T_0}\nonumber \\&\quad +\left[ -20 \gamma A \varLambda ^4 - j\delta _1 A \varLambda ^2 + 2j\omega \delta _1 \varLambda ^2 A \right] e^{j(1-2\omega )T_0}\nonumber \\&\quad + \left[ - 3j\delta _2 \omega ^2 \bar{A} \varLambda ^2 - 3 \lambda \bar{A} \varLambda ^2 -30 \gamma |A|^2 \bar{A} \varLambda ^2\right] e^{j(1-2\omega )T_0}\nonumber \\&\quad +\left[ -20 \gamma \bar{A} \varLambda ^4 + j\delta _1 \bar{A} \varLambda ^2 - 2j\omega \delta _1 \varLambda ^2 \bar{A}\right] e^{j(-1+2\omega )T_0}\nonumber \\&\quad -10 \gamma A^3 \varLambda ^2 e^{j(3-2\omega )T_0} -10 \gamma \bar{A}^3 \varLambda ^2 e^{j(-3+2\omega )T_0} \nonumber \\&\quad -10\gamma A^2 \varLambda ^3 e^{j(2-3\omega )T_0} + -10\gamma \bar{A}^2 \varLambda ^3 e^{j(-2+3\omega )T_0}\nonumber \\&\quad -5\gamma A^4 \varLambda e^{j(4-\omega )T_0} -5\gamma \bar{A}^4 \varLambda e^{j(-4+\omega )T_0}\nonumber \\&\quad -5\gamma A \varLambda ^4 e^{j(1-4\omega )T_0} -5\gamma \bar{ A} \varLambda ^4 e^{j(-1+4\omega )T_0}\nonumber \\&\quad -2|A|^2\beta _2- 2\omega \beta _2 \varLambda ^2 + NST + cc, \end{aligned}$$
(12)

where “NST” is non secular terms and “cc” is the complex conjugate of the previous terms.

We noticed that the system can presented four superharmonic resonant states and four subharmonic resonant states, when the following conditions are satisfied:

  • Subharmonic

    \( \omega = 2 + \epsilon \sigma \); \(\omega = 3 + \epsilon \sigma \); \(\omega = 4 + \epsilon \sigma \) and \( \omega = 5 + \epsilon \sigma \)

  • Superharmonic:

    \( 2\omega = 1 + \epsilon \sigma \); \(3\omega = 1 + \epsilon \sigma \); \(4\omega = 1 + \epsilon \sigma \) and \(5 \omega = 1 + \epsilon \sigma \)

2.2.1 Superharmonic resonant states

Considering \(5\omega = 1+ \epsilon \sigma \), and injecting this condition into Eq. (12) and setting secular terms to 0, we obtained

$$\begin{aligned}&-2jA' -3j\delta _2 | A|^2A - 6j\delta _2 \omega ^2 \varLambda ^2 A - 3 \lambda | A|^2 A -6\lambda A\varLambda ^2\nonumber \\&\quad - 10\gamma |A|^4 A -60 \gamma \varLambda ^2 |A|^2 A-30\gamma A \varLambda ^4 \nonumber \\&\quad -j\delta _1 |A|^2 A -2j\delta _1 A \varLambda ^2-2j\mu A-\gamma \varLambda ^5 e^{\sigma T_1}=0. \nonumber \\ \end{aligned}$$
(13)

The polar form of A is

$$\begin{aligned} A= & {} \frac{1}{2} a(T_1) e^{j\varPhi (T_1)}. \end{aligned}$$
(14)

Inserting Eq. (14) into Eq. (13), after puting \(\theta = \sigma T_1- \varPhi \), we neglect the reals and imaginary parts and we obtained

$$\begin{aligned}&a'=-\frac{3}{8} \delta _2 a^3 - 3 \delta _2 \omega ^2 \varLambda ^2 a -\frac{1}{8} \delta _1 a^3\nonumber \\&\quad - \delta _1 a \varLambda ^2 -\mu a - \gamma \varLambda ^5 \sin \theta , \end{aligned}$$
(15)
$$\begin{aligned}&a \theta '= a\sigma -\frac{3}{8} \lambda a^3 - 3 \lambda \varLambda ^2 a -\frac{5}{16} \gamma a^5 \nonumber \\&\quad -\frac{15}{2} \gamma \varLambda ^2 a^3 - 15\gamma \varLambda ^4 a -\gamma \varLambda ^5 a\cos \theta . \end{aligned}$$
(16)

In the steady-state case \( a'=0 \) and \( a\theta '=0\), we obtained the following nonlinear equation:

$$\begin{aligned}&\left( \frac{3}{8} \delta _2 a^3 + 3 \delta _2 \omega ^2 \varLambda ^2 a +\frac{1}{8} \delta _1 a^3+ \delta _1 a \varLambda ^2 +\mu a\right) ^2\nonumber \\&\quad +\left( a\sigma -\frac{3}{8} \lambda a^3 - 3 \lambda \varLambda ^2 a -\frac{5}{16} \gamma a^5 \right. \nonumber \\&\quad \left. -\frac{15}{2} \gamma \varLambda ^2 a^3 - 15\gamma \varLambda ^4 a \right) ^2=\gamma ^2 \varLambda ^{10}. \end{aligned}$$
(17)

Using the appropriate algorithm, the amplitude a is plotted as a function of the detuning parameter \(\sigma \) for different values of the nonlinear parameters. With the appropriate set of parameters, the response curves are obtained and presented in Fig. 2. As the primary resonance state, the quadratic damping coefficients have no effect on the superharmonic resonance state. Figure 2c shows that the external force is the origin of the phenomenon called bistability or jump phenomenon. The same effects are obtained when the nonlinear cubic damping coefficients descrease (see Fig. 2a, b). The parameters \(\delta _1\) and \( \delta _2\) can be used to eliminate or control the bistability or jump phenomenon.

Fig. 2
figure 2

Order 5 superharmonic resonant state curves a effect of \(\delta _1\), b effect of \(\delta _2\) and c effect of F with \(\lambda =-0.6, \gamma =0.05, \omega _0=1\)

Full size image

To analyze the 1 : 3 superharmonic resonance, we set \(3\omega =1+\epsilon \sigma \).

Substituting the superharmonic resonance relation in Eq. (12), the condition for eliminating secular terms in the problem is given by

$$\begin{aligned}&-2jA' -3j\delta _2 | A|^2A \nonumber \\&\quad - 6j\delta _2 \omega ^2 \varLambda ^2 A - 3 \lambda | A|^2 A -6\lambda A\varLambda ^2\nonumber \\&\quad - 10\gamma |A|^4 A -60 \gamma \varLambda ^2 |A|^2 A-30\gamma A \varLambda ^4\nonumber \\&\quad -j\delta _1 |A|^2 A -2j\delta _1 A \varLambda ^2-2j\mu A \nonumber \\&\quad +\left[ j \delta _2 \varLambda ^3 \omega ^3 - \lambda \varLambda ^3 - 20\gamma \varLambda ^3 |A|^2\right. \nonumber \\&\quad \left. - 5\gamma \varLambda ^5-j\omega \delta _1 \varLambda ^3\right] e^{\sigma T_1}=0. \end{aligned}$$
(18)

The 1 : 3 superharmonic resonance equation is:

$$\begin{aligned}&\left( \frac{3}{8} \delta _2 a^3 + 3 \delta _2 \omega ^2 \varLambda ^2 a +\frac{1}{8} \delta _1 a^3+ \delta _1 a \varLambda ^2 +\mu a\right) ^2 \nonumber \\&\quad +\left( a\sigma -\frac{3}{8} \lambda a^3 - 3 \lambda \varLambda ^2 a -\frac{5}{16} \gamma a^5\right. \nonumber \\&\quad -\left. \frac{15}{2} \gamma \varLambda ^2 a^3 - 15\gamma \varLambda ^4 a \right) \nonumber \\&\quad =\left( \delta _2 \varLambda ^3 \omega ^3 - \omega \delta _1 \varLambda ^3 \right) ^2 \nonumber \\&\quad + \left( \lambda \varLambda ^3 + 5 \gamma \varLambda ^3 a^2 + 5 \gamma \varLambda ^5 \right) ^2 . \end{aligned}$$
(19)

Figure 3 presents the frequency response curves of the third order superharmonic resonance. The same observations are obtained as in the previous case, but the amplitude and the frequency are lower and also vary less than in the previous case.

Fig. 3
figure 3

Order 3 superharmonic resonant state curves a effect of \(\delta _1\), b effect of \(\delta _2\) and c effect of F with \(\lambda =-0.6, \gamma =0.05, \omega _0=1\)

Full size image

Now, we consider 1 : 2 superharmonic resonance state \( 2\omega = 1+ \epsilon \sigma \). Inserting \( 2\omega = 1+ \epsilon \sigma \) into Eq. (12) and eliminating the secular terms, we obtained

$$\begin{aligned}&-2jA' -3j\delta _2 | A|^2A - 6j\delta _2 \omega ^2 \varLambda ^2 A\nonumber \\&\quad - 3 \lambda | A|^2 A -6\lambda A\varLambda ^2\nonumber \\&\quad - 10\gamma |A|^4 A -60 \gamma \varLambda ^2 |A|^2 A-30\gamma A \varLambda ^4 -j\delta _1 |A|^2 A \nonumber \\&\quad -2j\delta _1 A \varLambda ^2-2j\mu A \nonumber \\&\quad + \left( \beta _2 \omega ^2 \varLambda ^2 - j \beta _1 \omega \varLambda ^2\right) e^{\sigma T_1}=0. \end{aligned}$$
(20)

In this case, the resonance equation is governed by

$$\begin{aligned}&\left( \frac{3}{8} \delta _2 a^3 + 3 \delta _2 \omega ^2 \varLambda ^2 a +\frac{1}{8} \delta _1 a^3+ \delta _1 a \varLambda ^2 +\mu a\right) ^2 \nonumber \\&\quad +\left( a\sigma -\frac{3}{8} \lambda a^3 - 3 \lambda \varLambda ^2 a -\frac{5}{16} \gamma a^5 \right. \nonumber \\&\left. \quad -\frac{15}{2} \gamma \varLambda ^2 a^3 - 15\gamma \varLambda ^4 a \right) ^2 \nonumber \\&\quad =\left( \beta _1^2+ \beta _2^2 \omega ^2 \right) \omega ^2 \varLambda ^4. \end{aligned}$$
(21)

The frequency response curves of second-order superharmonic oscillations are plotted in Fig. 4. In this case, the influences of the impure and pure quadratic parameters on the oscillations have been checked (see Fig. 4a, b respectively). From these figures, we conclude that the range of frequency where a response can be obtained is more important in the case of \(\beta _1\) than in the case of \(\beta _2\). It is also noticed that the bistability or jump phenomenon occurs when the nonlinear quadratic parameters increase.

Fig. 4
figure 4

Effects of quadratic damping on 1 : 2 superharmonic resonant state curves a effect of \(\delta _1\), b effect of \(\delta _2\) and c effect of F with \(\lambda =-0.6, \gamma =0.05, F=2, \omega _0=1\)

Full size image
Fig. 5
figure 5

Order 5 subharmonic resonant state curves a effect of \(\delta _1\), b effect of \(\delta _2\) and c effect of F with \(\lambda =-0.6, \gamma =0.05, F=1, \omega _0=1\)

Full size image
Fig. 6
figure 6

Order 3 subharmonic resonant state curves a effect of \(\delta _1\), b effect of \(\delta _2\) and c effect of F with \(\lambda =-0.6, \gamma =0.05, \omega _0=1\)

Full size image
Fig. 7
figure 7

Effects of quadratic damping on 2 : 1 subharmonic resonant state curves a effect of \(\delta _1\), b effect of \(\delta _2\) and c effect of F with \(\lambda =-0.6, \gamma =0.05, F=2, \omega _0=1\)

Full size image

2.2.2 Subharmonic resonant states

In this part, we treat three cases: \( \omega = 5+ \epsilon \sigma , \omega = 3+ \epsilon \sigma \) and \( \omega = 2+ \epsilon \sigma \). In the first case ( \( \omega = 5+ \epsilon \sigma \)), the secular terms are eliminated when

$$\begin{aligned}&-2jA' -3j\delta _2 | A|^2A - 6j\delta _2 \omega ^2 \varLambda ^2 A - 3 \lambda | A|^2 A \nonumber \\&\quad -\ 6\lambda A\varLambda ^2 - 10\gamma |A|^4 A -60 \gamma \varLambda ^2 |A|^2 A-30\gamma A \varLambda ^4 \nonumber \\&\quad -\ j\delta _1 |A|^2 A -2j\delta _1 A \varLambda ^2-2j\nonumber \\&\quad \times \ \mu A-5\gamma \varLambda \bar{A}^4 e^{\sigma T_1}=0. \end{aligned}$$
(22)

Inserting the polar form of A and putting \( \theta = \sigma T_1 - 5\varPhi \), we obtained

$$\begin{aligned} a'= & {} \frac{3}{8} \delta _2 a^3 + 3 \delta _2 \omega ^2 \varLambda ^2 a +\frac{1}{8} \delta _1 a^3\nonumber \\&+ \delta _1 a \varLambda ^2 +\mu a +\frac{5\varLambda }{16} a^4 \sin \theta , \end{aligned}$$
(23)
$$\begin{aligned} a \theta '= & {} a\sigma -15 \lambda \varLambda ^2 a-\frac{25}{16} \gamma a^5 -\frac{75}{2}\gamma \varLambda ^2 a^3 \nonumber \\&-75\gamma \varLambda ^4-\frac{15}{8} \lambda a^3 -\frac{5}{16}\varLambda a^5 \cos \theta . \end{aligned}$$
(24)

We set \(a'=0, \theta '=0\) and we eliminate the phase \(\theta \), and then we obtained after some algebraic manipulations

$$\begin{aligned}&\left( \frac{3}{8} \delta _2 a^3 + 3 \delta _2 \omega ^2 \varLambda ^2 a +\frac{1}{8} \delta _1 a^3+ \delta _1 a \varLambda ^2 +\mu a\right) ^2 \nonumber \\&\quad +\left( a\frac{\sigma }{5}-\frac{3}{8} \lambda a^3-3\lambda \varLambda ^2 a -\frac{5}{16}\gamma a^5\right. \nonumber \\&\quad \left. -\frac{15}{2}\gamma \varLambda ^2a^3-15 \gamma \varLambda ^4\right) ^2= \frac{25}{256}\varLambda ^2 a^8. \end{aligned}$$
(25)

Figure 5 shows frequency response curves for different values of the nonlinear parameters. We noticed that the quadratic damping parameters effects are not significant as those of cubic damping parameters and external force. The cubic damping parameters have the same effects which are the contrary to the external force effects.

Fig. 8
figure 8

Bifurcation diagram and corresponding Lyapunov exponents of a modified Duffing oscillator with \(\delta _1=1.05, \delta _2=0.85, \beta _1=3.5, \beta _2=0.125, \mu =0.0005, \lambda =-0.6, \gamma =0.05, \omega _0=1, \omega =1\)

Full size image
Fig. 9
figure 9

Phase portraits of the modified Duffing oscillator with parameters of Fig. 8. a F = 0.25, b F = 0.75, c F = 0.965, d F = 1.5

Full size image
Fig. 10
figure 10

Times histories corresponding to phase portraits of the modified Duffing oscillator with parameters of Fig. 8. a F = 0.25, b F = 0.75, c F = 0.965, d F = 1.5

Full size image
Fig. 11
figure 11

Bifurcation diagram and corresponding Lyapunov exponents of a modified Duffing oscillator with \(\delta _1=1.05, \delta _2=0.85, \beta _1=3.5, \beta _2=0.125, \mu =0.0005, \lambda =-0.6, \gamma =0.05, \omega _0=1, F=0.965\)

Full size image
Fig. 12
figure 12

Phase portraits showing periodic orbits of the modified Duffing oscillator with parameters of Fig. 11. a \(\omega =1/3\), b \(\omega =0.5\), c \(\omega =2\), d \(\omega =3\)

Full size image
Fig. 13
figure 13

Phase portraits showing chaotic motions of the modified Duffing oscillator with parameters of Fig. 11. a \(\omega =0.2\), b \(\omega =0.66\), c \(\omega =1\), d \(\omega =1.88\)

Full size image
Fig. 14
figure 14

Effect of damping parameters on bifurcation diagram of a modified Duffing oscillator with parameters of Fig. 8. a \(\beta _2=0.75\), b \(\delta _2=0.05\), c \(\delta _1=0.05\), d \(\beta _1=0, \beta _2=0, \delta _1=0, \delta _2=0\)

Full size image

We consider the 3 : 1 subharmonic resonant state \( \omega = 3+ \epsilon \sigma \). The resonance equation is governed by

$$\begin{aligned}&\left( \frac{3}{8} \delta _2 a^3 + 3 \delta _2 \omega ^2 \varLambda ^2 a +\frac{1}{8} \delta _1 a^3+ \delta _1 a \varLambda ^2 +\mu a\right) ^2 \nonumber \\&\quad +\left( a\frac{\sigma }{5}-\frac{3}{8} \lambda a^3-3\lambda \varLambda ^2 a -\frac{5}{16}\gamma a^5\right. \nonumber \\&\quad \left. -\frac{45}{2}\gamma \varLambda ^2a^3-45 \gamma \varLambda ^4a ^3\right) ^2\nonumber \\&\quad =\left( \frac{3}{4} \delta _2 \omega +\frac{1}{2} \delta _1 - \frac{1}{4}\delta _1 \omega \right) ^2 \varLambda ^2 a^4 \nonumber \\&\quad + \left( \frac{3}{4} \lambda +\frac{5}{4}\gamma a^2 +\frac{15}{2} \gamma \varLambda ^2 \right) ^2 \varLambda ^2a^4. \end{aligned}$$
(26)

Figure 6 displays the amplitude response curves obtained from Eq. (26) for different values of the nonlinear parameters. As the third superharmonic resonance state, the damping coefficients have the same effects in the 3 : 1 subharmonic resonance state (see Fig. 6a, b). In Fig. 6c, as the amplitude of the external force increases as far as \(F=3\), bistability and jump phenomenon are observed. For other values of F, these phenomena disappear. We conclude that the parameters \(F, \delta _1\) and \( \delta _2\) can be used to eliminate or control the bistability and jump phenomena.

The system enter the second-order subharmonic resonant state when \(\omega = 2 + \epsilon \sigma \). In this case, the resonance equation is given by

$$\begin{aligned}&\left( \frac{3}{8} \delta _2 a^3 + 3 \delta _2 \omega ^2 \varLambda ^2 a +\frac{1}{8} \delta _1 a^3+ \delta _1 a \varLambda ^2 +\mu a\right) ^2 \nonumber \\&\quad +\left( a\frac{\sigma }{5}-\frac{3}{8} \lambda a^3-3\lambda \varLambda ^2 a -\frac{5}{16}\gamma a^5-15\gamma \varLambda ^2a^3-15 \gamma \varLambda ^4a ^3\right) ^2\nonumber \\&\quad =\frac{1}{4}\left( 1-\omega \right) ^2 \beta _1^2 \varLambda ^2 a^2 + \beta _2^2 \omega ^2 \varLambda ^2 a^2. \end{aligned}$$
(27)

The frequency response curves of second-order subharmonic oscillations are plotted in Fig. 7, and the regions where such behaviors occur are obtained. In this case, the influences of the impure and pure quadratic parameters on such oscillations have been checked (see Fig. 7a, b respectively). From these figures, we conclude that the range of frequency where a response can be obtained is more important in the case of \(\beta _2\) than in the case of \(\beta _1\).

3 Bifurcation and transition to chaos

The aim of this section is to investigate the way under which chaotic motions arise in the model described by Eq. (9) since they are of interest in many physics phenomena. We use the bifurcation diagram and its corresponding Lyapunov exponent (defined in Ref. [32]), the phase portraits, and times histories. From the bifurcation diagram and its corresponding Lyapunov exponents, various types of motions are displayed. For instance, in Fig. 8, quasiperiodic motions are obtained for \(F\in [0, 0.709]\cup [1.08, 1.103]\cup [1.126, 1.145]\). A period-1 orbit exists for \(F > 1.347\), while a period-3 orbit exists for \([0.719, 0.807]\cup [0.987, 1.02]\). A period-4 orbit exists for \([0.807, 0.827]\cup [0.8619, 0.906]\cup [1.02, 1.037]\). On the other hand, chaotic motions exist for \(F\in [0.709, 0.719]\cup [0.827, 0.8619] \cup [0.906, 0.987]\cup [1.037, 1.08]\cup [1.103, 1.126]\cup [1.145, 1.347]\). For several different values of F chosen in the above-mentioned regions, various phase portraits and its corresponding times histories are plotted respectively in Figs. 9 and 10. Figure 11 presents the bifurcation diagram and its corresponding Lyapunov exponent for \(\delta _1=1.05, \delta _2=0.85, \beta _1=3.5, \beta _2=0.125, \mu =0.0005, \lambda =-0.6, \gamma =0.05, \omega _0=1, F=0.965\) and \(\omega \) varying from 0 to 5. For these parameters values, it can be noticed that the chaotic behavior occurs when the external frequency is near to primary and 1 : 2 superharmonic resonance frequencies, while the periodic or quasiperiodic behaviors occur when the external frequency is near to 1 : 3, 1 : 5 superharmonic resonance frequencies and 2 : 1, 3 : 1, 5 : 1 subharmonic resonance frequencies. For instance, periodic orbits and chaotic motions obtained for appropriate choice of \(\omega \) from Fig. 11 are reported in Figs. 12 and 13, respectively. The influences of both the nonlinear quadratic and cubic dissipative parameters on the bifurcation sequences are also investigated, and the results are reported in Fig. 14. From Figs. 8 and 14, it can be pointed out that the nonlinear damping parameters can be used to control the presence of chaotic oscillations. From these results, we can conclude that the dissipation parameters have a real impact on the dynamics of the model. Therefore, it is useful to forecast domains in which such effects could be of interest or not.

4 Conclusion

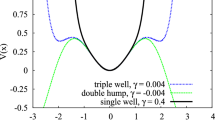
In this work, we have investigated the dynamics behaviors of a modified Duffing oscillator. The originality of the work is related to the presence of pure and impure nonlinear damping terms and the \(\phi ^6\)-potential and then to their effects on the system behaviors. By the multiple timescale method, an exhaustive study of various resonance states is done, and nine resonance states were obtained of which seven were studied. We have obtained resonance, hysteresis, and jump phenomena. The appearance of each of these phenomena depends on the nonlinear damping and stiffness parameters. The study of the effects of different nonlinear damping parameters showed that these resonances phenomena can be controlled or even eliminated. These parameters can also generate the bistability phenomenon in the evolution of the amplitude of the system oscillations. Some bifurcation structures and transition to chaos of the model have been investigated. The model presented several dynamics motions which are influenced by nonlinear damping parameters and external excitation. For example, multiperiodic orbits, quasiperiodic and chaotic motions are obtained. It can be concluded that the dissipation parameters have a real impact on the dynamics of the model. In the ship motion case, the detection of each phenomenon due to the nonlinearities is very capital. Practical naval architect must be able to recognize these phenomena when they occur and should understand their consequences so that it will be able to avoid design that promotes capsizing, to evaluate the sea worthiness of a craft and recommend appropriate measures to control or minimize large amplitudes motions.