1 Introduction

More generalised forms of differential equations are described as fractional differential equations (FDEs). The FDEs have been found to be effective to describe some physical phenomena and social science fields such as engineering, geology, economics, chemistry, engineering, biology, fluid flow, signal processing, control theory, systems identification and fractional dynamics [1,2,3,4]. As a result, numerous influential methods have been proposed. Some of these include the fractional sub-equation method [5, 6], the tanh–sech method [7], the \(({G{'}}/{G})\)-expansion method [8, 9], the first integral method [10], the modified Kudryashov method [11], the exponential function method [12, 13] and others [14,15,16].

The novelties of this paper are mainly exhibited in three aspects: first, we use a new method, which is not so familiar, the so-called Riccati–Bernoulli sub-ODE method [17,18,19]. The space–time fractional modified equal width (mEW) equation and generalised time-fractional Hirota–Satsuma coupled Korteweg–de Vries (KdV) system are chosen to illustrate the verity of this method. Second, we also show that the proposed method gives an infinite sequence of solutions, using a Bäcklund transformation. Third, we obtain new types of exact analytical solutions. Moreover, by comparing our results with other results, one can see that our results are new and most extensive.

Assume that f(t) denotes a continuous \({\mathbb {R}} \rightarrow {\mathbb {R}}\) function (but not necessarily first-order differentiable) [20]. The Jumarie modified Riemann–Liouville derivative is defined as

$$\begin{aligned} D_{t}^{\alpha }f(t) ={\left\{ \begin{array}{ll} \dfrac{1}{\Gamma (1-\alpha )}\dfrac{\mathrm{d}}{\mathrm{d}t}\int _{0}^{t}(t-\xi )^{-\alpha -1}(f(\xi )-f(0))\mathrm{d}\xi ,&{}{ } \alpha< 0,\\ \dfrac{1}{\Gamma (1-\alpha )}\dfrac{\mathrm{d}}{\mathrm{d}t}\int _{0}^{t}(t-\xi )^{-\alpha }(f(\xi )-f(0))\mathrm{d}\xi ,&{}{ } 0<\alpha< 1,\\ (f^{(n)}(t))^{(\alpha -n)}, &{} { }n~\le \alpha < n+1,~ n\ge 1,\, \end{array}\right. }~~~~~~ \end{aligned}$$
(1.1)

where

$$\begin{aligned} \Gamma (x)=\int _{o}^{\infty }\mathrm{e}^{-t}t^{x-1}\mathrm{d}t. \end{aligned}$$

An important property of the fractional modified Riemann–Liouville derivative is

$$\begin{aligned} D_{t}^{\alpha }t^{r}=\frac{\Gamma (1+r)}{\Gamma (1+r-\alpha )}t^{r-\alpha }. \end{aligned}$$
(1.2)

The rest of the paper is arranged as follows: In §2, we give a description of the Riccati–Bernoulli sub-ODE method. We also give a Bäcklund transformation of the Riccati–Bernoulli equation. In §3, we apply the Riccati–Bernoulli sub-ODE method to solve the space–time fractional mEW equation and the time-fractional Hirota–Satsuma coupled KdV system. In §4, we compare our results with other results in order to show that the Riccati–Bernoulli sub-ODE is efficacious, robust and adequate. That is, we clarify that this method is superior to other methods. Finally, in §5, we give the conclusions.

2 Method descriptions

We give abbreviation of the Riccati–Bernoulli sub-ODE method. Any nonlinear FDE in two independent variables x and t can be expressed in the following form:

$$\begin{aligned} G(\psi ,D^{\alpha }_{t}\psi ,D^{\alpha }_{x}\psi ,D^{\alpha }_{t}D^{\alpha }_{x}\psi ,D^{\alpha }_{x}D^{\alpha }_{x}\psi ,\ldots )=0, \end{aligned}$$
(2.1)

where \(0<\alpha \le 1\) and G is a polynomial in \( \psi (x,t) \) and its partial fractional derivatives. We introduce a fractional complex transformation as follows:

$$\begin{aligned} \psi (x,t)=\psi (\xi ),\quad \xi =\frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}. \end{aligned}$$

This transformation transform eq. (2.1) into the following ODE:

$$\begin{aligned} H(\psi ,\psi ',\psi '',\psi ''',\ldots )=0, \end{aligned}$$
(2.2)

where prime denotes the derivation with respect to \(\xi \).

Step 1. Assume that eq. (2.2) has the following solution:

$$\begin{aligned} \psi '=a\psi ^{2-n}+b\psi +c\psi ^{n}, \end{aligned}$$
(2.3)

where a, b, c and n are constants which are to be calculated later. Using eq. (2.3), we obtain the following:

$$\begin{aligned} \psi ''&=a(2-n)\psi ^{1-n}\psi '+b\psi '+c\psi ^{n-1}\psi ' \nonumber \\&=a(2-n)\psi ^{1-n}(a\psi ^{2-n}+b\psi +c\psi ^{n})\nonumber \\&\quad +\,b(a\psi ^{2-n}+b\psi +c\psi ^{n})\nonumber \\&\quad +\,c\psi ^{n-1}(a\psi ^{2-n}+b\psi +c\psi ^{n})\nonumber \\&=ab(3-n)\psi ^{2-n}+a^{2}(2-n)\psi ^{3-2n}+nc^{2}\psi ^{2n-1}\nonumber \\&\quad +\,bc(n+1)\psi ^{n}+(2ac+b^2)\psi . \end{aligned}$$
(2.4)

Similarly, we can obtain

$$\begin{aligned} \displaystyle \psi '''= & {} (ab(3-n)(2-n)\psi ^{1-n}\nonumber \\&+a^{2}(2-n)(3-2n)\psi ^{2-2n} \nonumber \\&\displaystyle +\, n(2n-1)c^{2}\psi ^{2n-2}+bc n(n+1)\psi ^{n-1}\nonumber \\&+\,(2ac+b^2))\psi ', \end{aligned}$$
(2.5)

\(\ldots \)

Remark 1

Equation (2.3) is called the Riccati–Bernoulli equation. When \(ac \ne 0\) and \(n = 0\), eq. (2.3) is a Riccati equation. When \(a \ne 0\), \(c = 0\) and \(n \ne 0\), eq. (2.3) is a Bernoulli equation.

Step 2. Exact solutions to eq. (2.3), for an arbitrary constant \(\mu ,\) are given as follows:

  1. 1.

    For \(n = 1\), the solution is

    $$\begin{aligned} \psi (\xi )=\mu \mathrm {e}^{(a+b+c)\xi }. \end{aligned}$$
    (2.6)
  2. 2.

    For \(n \ne 1\), \(b=0\) and \(c=0\), the solution is

    $$\begin{aligned} \psi (\xi )=\left( a(n-1)(\xi +\mu )\right) ^{{1}/({n-1})}. \end{aligned}$$
    (2.7)
  3. 3.

    For \(n \ne 1\), \(b\ne 0\) and \(c=0\), the solution is

    $$\begin{aligned} \psi (\xi )=\left( \frac{-a}{b}+ \mu \mathrm {e}^{b(n-1)\xi } \right) ^{{1}/({n-1})}. \end{aligned}$$
    (2.8)
  4. 4.

    For \(n \ne 1\), \(a\ne 0\) and \(b^2-4ac < 0\), the solutions are

    $$\begin{aligned} \psi (\xi )= & {} \left( \frac{-\,b}{2a}+ \frac{\sqrt{4ac-b^2}}{2a} \right. \nonumber \\&\left. \times \tan \!\left( \!\frac{(1-n)\sqrt{4ac-b^2}}{2} (\xi +\mu ) \!\right) \!\right) ^{\!{1}/({1-n})}\,\nonumber \\ \end{aligned}$$
    (2.9)

    and

    $$\begin{aligned} \psi (\xi )= & {} \left( \frac{-\,b}{2a}- \frac{\sqrt{4ac-b^2}}{2a} \right. \nonumber \\&\left. \times \cot \left( \!\frac{(1-n)\sqrt{4ac-b^2}}{2} (\xi +\mu ) \!\right) \!\!\right) ^{\!\!{1}/({1-n})}\!\!.\nonumber \\ \end{aligned}$$
    (2.10)
  5. 5.

    For \(n \ne 1\), \(a\ne 0\) and \(b^2-4ac > 0\), the solutions are

    $$\begin{aligned} \psi (\xi )\!=\! & {} \left( \!\frac{-\,b}{2a} - \frac{\sqrt{b^2-4ac}}{2a} \right. \nonumber \\&\quad \left. \times \coth \left( \!\!\frac{(1-n)\sqrt{b^2-4ac}}{2} (\xi +\mu ) \!\!\right) \!\!\right) ^{\!\!{1}/({1-n})}\nonumber \\ \end{aligned}$$
    (2.11)

    and

    $$\begin{aligned} \psi (\xi )\!=\! & {} \left( \frac{-\,b}{2a}- \frac{\sqrt{b^2-4ac}}{2a} \right. \nonumber \\&\left. \times \!\tanh \!\left( \!\frac{(1\!-\!n)\sqrt{b^2\!-\!4ac}}{2} (\xi \!+\!\mu ) \!\right) \!\!\right) ^{\!\!{1}/({1-n})}\!\!.\nonumber \\ \end{aligned}$$
    (2.12)
  6. 6.

    For \(n \ne 1\), \(a\ne 0\) and \(b^2-4ac=0\), the solution is

    $$\begin{aligned} \psi (\xi )=\left( \frac{1}{a(n-1)(\xi +\mu )}-\frac{b}{2a}\right) ^{{1}/({1-n})}. \end{aligned}$$
    (2.13)

2.1 Bäcklund transformation

When \(\psi _{m-1}(\xi )\) and \(\psi _{m}(\xi )\,(\psi _{m}(\xi )=\psi _{m}(\psi _{m-1}(\xi )))\) are solutions of eq. (2.3), we get

$$\begin{aligned} \frac{\mathrm{d}\psi _{m}(\xi )}{\mathrm{d}\xi }&=\frac{\mathrm{d}\psi _{m}(\xi )}{\mathrm{d}\psi _{m-1}(\xi )} \frac{\mathrm{d}\psi _{m-1}(\xi )}{\mathrm{d}\xi }\\&=\frac{\mathrm{d}\psi _{m}(\xi )}{\mathrm{d}\psi _{m-1}(\xi )}(a\psi _{m-1}^{2-n}+b\psi _{m-1}+c\psi _{m-1}^{n}), \end{aligned}$$

that is,

$$\begin{aligned} \frac{\mathrm{d}\psi _{m}(\xi )}{a\psi _{m}^{2-n}+b\psi _{m}+c\psi _{m}^{n}}= \frac{\mathrm{d}\psi _{m-1}(\xi )}{a\psi _{m-1}^{2-n}+b\psi _{m-1}+c\psi _{m-1}^{n}}. \end{aligned}$$
(2.14)

Integrating eq. (2.14) once with respect to \(\xi \), we get Bäcklund transformation of eq. (2.3) as follows:

$$\begin{aligned} \psi _{m}(\xi )=\left( \frac{-cK_{1}+aK_{2}\left( \psi _{m-1}(\xi )\right) ^{1-n}}{bK_{1}+aK_{2}+aK_{1} \left( \psi _{m-1}(\xi )\right) ^{1-n}}\right) ^{{1}/({1-n})}, \end{aligned}$$
(2.15)

where \(K_1\) and \(K_2\) are arbitrary constants. If we get a solution to this equation, we use eq. (2.15) to get an infinite sequence of solutions to eq. (2.3) as well as to eq. (2.1).

A complete derivation of this method is given in [18].

3 Applications

The Riccat–Bernoulli sub-ODE technique is presented for solving the space–time fractional mEW equation and time-fractional Hirota–Satsuma coupled KdV equation.

3.1 The fractional mEW equation

Here, we apply the Riccat–Bernoulli sub-ODE method to solve the space–time fractional mEW equation [21], which is presented by a model for nonlinear dispersive waves, of the form:

$$\begin{aligned} D_{t}^{\alpha }\psi (x,t)+\epsilon D_{x}^{\alpha }\psi ^3(x,t)-\delta D_{xxt}^{3\alpha }\psi (x,t)=0, \end{aligned}$$
(3.1)

where \(\epsilon \) and \(\delta \) are positive parameters.

$$\begin{aligned} \phi ({x},{t})= & {} \frac{1}{\kappa }{v}^2(\xi ), \chi ({x}, {t})=-\kappa +{v}(\xi ),\nonumber \\ \psi ({x},{t})= & {} 2 \kappa ^{2}-2 \kappa {v}(\xi ),\quad \xi = {x}-\frac{\kappa {t}^{\alpha }}{\Gamma (1+\alpha )},\nonumber \\ \end{aligned}$$
(3.2)

where \(\kappa \) is a non-zero constant and \(0<\alpha \le 1\), to transform eq. (3.1) into the following ODEs:

$$\begin{aligned} \kappa v^{\prime \prime } + 2v^3 - 2{\kappa }^2v = 0. \end{aligned}$$
(3.3)

Substituting eq. (2.4) into eq. (3.3), we obtain

$$\begin{aligned}&\delta \lambda k^2(ab(3-m)\psi ^{2-m}+a^{2}(2-m)\psi ^{3-2m}\nonumber \\&\quad +mc^{2}\psi ^{2m-1}+bc(m+1)\psi ^{m}\nonumber \\&\quad +(2ac+b^2)\psi )+\epsilon k \psi ^3-\lambda \psi =0. \end{aligned}$$
(3.4)

If \(m = 0\), then eq. (3.4) is reduced to

$$\begin{aligned}&3\delta \lambda k^{2}ab\psi ^2+2\delta \lambda k^{2}a^{2}\psi ^{3}+\delta \lambda k^{2}bc\nonumber \\&\quad +\delta \lambda k^{2}(2ac+b^2)\psi +\epsilon k \psi ^3-\lambda \psi =0. \end{aligned}$$
(3.5)

Equating all the coefficients of \(\psi ^i\ (i = 0, 1, 2, 3)\) to zero, we, respectively, get

$$\begin{aligned}&\delta \lambda k^{2} bc=0, \end{aligned}$$
(3.6)
$$\begin{aligned}&\delta \lambda k^{2}(2ac+b^2)-\lambda =0, \end{aligned}$$
(3.7)
$$\begin{aligned}&3\delta \lambda k^{2}ab=0, \end{aligned}$$
(3.8)
$$\begin{aligned}&2\delta \lambda k^{2}a^{2}+\epsilon k=0. \end{aligned}$$
(3.9)

Solving eqs (3.22)–(3.25), we obtain

$$\begin{aligned} b= & {} 0, \end{aligned}$$
(3.10)
$$\begin{aligned} c= & {} \pm \frac{1}{k}\sqrt{\frac{\lambda }{-\,2\delta k\epsilon }}, \end{aligned}$$
(3.11)
$$\begin{aligned} a= & {} \pm \sqrt{\frac{-\,\epsilon }{2\delta \lambda k}}. \end{aligned}$$
(3.12)

Hence, we give cases of solutions for eq. (3.3) as well as eq. (3.1) as follows:

  1. 1.

    When \(\delta > 0\), substituting eqs (3.10)–(3.12) and (3.2) into eqs (2.9) and (2.10), we obtain travelling wave solutions to eq. (3.1) as

    $$\begin{aligned} \psi _{1,2}(x,t)= & {} \pm \sqrt{\frac{\lambda }{-\varepsilon k}} \tan \frac{\sqrt{2}}{\sqrt{\delta }k}\nonumber \\&\times \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) \nonumber \\ \end{aligned}$$
    (3.13)

    and

    $$\begin{aligned} \psi _{3,4}(x,t)= & {} \pm \sqrt{\frac{\lambda }{-\varepsilon k}} \cot \frac{\sqrt{2}}{\sqrt{\delta }k}\nonumber \\&\times \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) ,\nonumber \\ \end{aligned}$$
    (3.14)

    where \(\lambda \), \(\varepsilon \), k, \(\delta \) and \(\mu \) are arbitrary constants. Figure 1 illustrates solution \(\psi _2\).

  2. 2.

    When \(\delta < 0\), substituting eqs (3.10)–(3.12) and (3.2) into eqs (2.11) and (2.12), we obtain travelling wave solutions to eq. (3.1) as

    $$\begin{aligned} \psi _{5,6}(x,t)= & {} \pm \sqrt{\frac{\lambda }{\varepsilon k}} \tanh \frac{\sqrt{2}}{\sqrt{-\delta }k}\nonumber \\&\times \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) \nonumber \\ \end{aligned}$$
    (3.15)

    and

    $$\begin{aligned} \psi _{7,8}(x,t)= & {} \pm \sqrt{\frac{\lambda }{\varepsilon k}} \coth \frac{\sqrt{2}}{\sqrt{-\delta }k}\nonumber \\&\times \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) ,\nonumber \\ \end{aligned}$$
    (3.16)

    where \(\lambda \), \(\varepsilon \), k, \(\delta \) and \(\mu \) are arbitrary constants. Figure 2 illustrates solution \(\psi _6\).

Remark 2

Applying eq. (2.15) to \(\psi _i(x,t)\), \(i =1,2,\ldots ,9\), we obtain an infinite sequence of solutions of eq. (3.3). Consequently, we obtain an infinite sequence of solutions to eq. (3.1). For illustration, by applying eq. (2.15) into \(\psi _i(x,t)\), \(i =1,2,\ldots ,9\), once, we have new solutions to eq. (3.3)

$$\begin{aligned} \psi ^{\star }_{1,2}(x,t)= & {} \frac{\pm \frac{1}{k}\sqrt{\frac{\lambda }{-2\delta k\epsilon }}\pm B_{3} \sqrt{\frac{\lambda }{-\varepsilon k}} \tan \frac{\sqrt{2}}{\sqrt{\delta }k} \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) }{B_{3}\pm \sqrt{\frac{\lambda }{-\varepsilon k}} \tan \frac{\sqrt{2}}{\sqrt{\delta }k} \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) }, \\ \psi ^{\star }_{3,4}(x,t)= & {} \frac{\pm \frac{1}{k}\sqrt{\frac{\lambda }{-2\delta k\epsilon }}\pm B_{3} \sqrt{\frac{\lambda }{-\varepsilon k}} \cot \frac{\sqrt{2}}{\sqrt{\delta }k} \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) }{B_{3}\pm \sqrt{\frac{\lambda }{-\varepsilon k}} \cot \frac{\sqrt{2}}{\sqrt{\delta }k} \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) }, \\ \psi ^{\star }_{5,6}(x,t)= & {} \frac{\pm \frac{1}{k}\sqrt{\frac{\lambda }{-2\delta k\epsilon }}\pm B_{3} \sqrt{\frac{\lambda }{\varepsilon k}} \tanh \frac{\sqrt{2}}{\sqrt{-\delta }k} \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) }{B_{3}\pm \sqrt{\frac{\lambda }{\varepsilon k}} \tanh \frac{\sqrt{2}}{\sqrt{-\delta }k} \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) }, \\ \psi ^{\star }_{7,8}(x,t)= & {} \frac{\pm \frac{1}{k}\sqrt{\frac{\lambda }{-2\delta k\epsilon }}\pm B_{3} \sqrt{\frac{\lambda }{\varepsilon k}} \coth \frac{\sqrt{2}}{\sqrt{-\delta }k} \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) }{B_{3}\pm \sqrt{\frac{\lambda }{\varepsilon k}} \coth \frac{\sqrt{2}}{\sqrt{-\delta }k} \left( \frac{kx^{\alpha }}{\Gamma (1+\alpha )}-\frac{\lambda t^{\alpha }}{\Gamma (1+\alpha )}+\mu \right) }, \end{aligned}$$

where \(B_{3}\), \(\lambda \), \(\varepsilon \), k, \(\delta \) and \(\mu \) are arbitrary constants.

3.1.1 Physical interpretation

Here, we explain the physical interpretation of the solution for the fractional mEW equation. This equation has different types of travelling wave solutions, which play an important role in solitary wave theory. These types of waves depend on the variation of physical parameters. We also introduce both 2D and 3D plots, using the mathematical software MATLAB 15, to give a full illustration in 3D and 2D at a certain time. That is, these figures are presented to clarify the behaviour of the solution in a completely unified way.

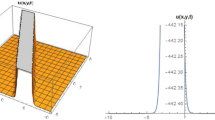
Indeed, figure 1 shows solution (3.13) of the fractional mEW equation, which represents the shape of the multiple periodic solution wave when \(\lambda =0.8\), \(\epsilon =-2\), \(k=1.6\), \(\delta =2.5\), \(\alpha = 1\), \(\mu =1\), \(0\le t \le 6\) and \(-6\le x \le 6\). Figure 1a presents the 3D plot and figure 1b presents the 2D plot for \(t = 1\).

Figure 2 shows solution (3.15) of the fractional mEW equation, which represents the kink-type travelling wave solution when \(\lambda =1.8\), \(\epsilon =3\), \(k=1.4\), \(\delta =-\,1.5\), \(\alpha = 1\), \(\mu =1\), \(0\le t \le 5\) and \(-\,5\le x \le 5\). Figure 2a presents the 3D plot and figure 2b presents the 2D plot for \(t = 0\).

Fig. 1
figure 1

The solution \(\psi = \psi _1(x, t)\) in (3.13) with \(\lambda =0.8\), \(\epsilon =-2\), \(k=1.6\), \(\delta =2.5\), \(\alpha = 1\), \(\mu =1\), \(0\le t \le 6\) and \(-6\le x \le 6\): (a) the 3D plot and (b) the 2D plot for \(t = 1\).

Full size image
Fig. 2
figure 2

The solution \(\psi = \psi _5(x, t)\) in (3.15) when \(\lambda =1.8\), \(\epsilon =3\), \(k=1.4\), \(\delta =-\,1.5\), \(\alpha = 1\), \(\mu =1\), \(0\le t \le 5\) and \(-\,5\le x \le 5\): (a) the 3D plot and (b) the 2D plot for \(t = 0\).

Full size image

3.2 The time-fractional generalised Hirota–Satsuma coupled KdV system

The time-fractional generalised Hirota–Satsuma coupled KdV system appears in mathematical modelling of physical phenomena, which describes the interaction of two long waves with different dispersion relations. Moreover, the travelling wave solutions of these equations have been studied in [8, 14, 15, 22]. These equations are given in the following form:

$$\begin{aligned} \begin{array}{l} \displaystyle D_{t}^{\alpha }\phi =\frac{1}{4}\phi _{xxx}+3\phi \phi _x+3(-\chi ^2+\psi )_x,\\ \displaystyle D_{t}^{\alpha }\chi =-\frac{1}{2}\chi _{xxx}-3\phi \chi _x,\\ \displaystyle D_{t}^{\alpha }\psi =-\frac{1}{2}\psi _{xxx}-3\phi \psi _x,\\ \end{array} \end{aligned}$$
(3.17)

where \(\phi = \phi (x, t)\), \(\chi = \chi (x, t)\) and \(\psi = \psi (x, t)\), \(t > 0\), \(0 < \alpha \le 1\). This system models the interaction between two long waves that have distinct dispersion relations.

Using the transformation

$$\begin{aligned} \phi (x,t)&=\frac{1}{\kappa }\upsilon ^2(\xi ),\quad \chi (x,t)=-\,\kappa +\upsilon (\xi ),\nonumber \\ \psi (x,t)&=2\kappa ^2-2\kappa \upsilon (\xi ), \quad \xi =x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )}, \end{aligned}$$
(3.18)

where \(\kappa \) is the non-zero constant and \(0<\alpha \le 1\).

Equation (3.17) transforms into the following RODEs, using (3.18):

$$\begin{aligned} \kappa \upsilon ''+2 \upsilon ^3-2\kappa ^2 \upsilon =0. \end{aligned}$$
(3.19)

Substituting eq. (2.4) into eq. (3.19), we obtain

$$\begin{aligned}&\kappa (ab(3-m)\upsilon ^{2-m}+a^{2}(2-m)\upsilon ^{3-2m}\nonumber \\&\quad +mc^{2}\upsilon ^{2m-1}+bc(m+1)\upsilon ^{m}\nonumber \\&\quad +(2ac+b^2)\upsilon )+2\upsilon ^3-2\kappa ^2 \upsilon =0. \end{aligned}$$
(3.20)

Setting \(m = 0\), eq. (3.20) is reduced to

$$\begin{aligned} \kappa (3 ab^2\upsilon ^2+2 a^{2}\upsilon ^{3}+ bc+ (2ac+b^2)\upsilon ) +2\upsilon ^3-2\kappa ^2 \upsilon =0. \end{aligned}$$
(3.21)

Setting each coefficient of \(\upsilon ^i\ (i = 0, 1, 2, 3)\) to zero, we get

$$\begin{aligned}&\kappa bc=0, \end{aligned}$$
(3.22)
$$\begin{aligned}&\kappa (2ac+b^2)-\,2\kappa ^2=0, \end{aligned}$$
(3.23)
$$\begin{aligned}&3 \kappa ab=0, \end{aligned}$$
(3.24)
$$\begin{aligned}&2\kappa a^{2}+2=0. \end{aligned}$$
(3.25)

Solving eqs (3.22)–(3.25), we get

$$\begin{aligned}&b=0, \end{aligned}$$
(3.26)
$$\begin{aligned}&c=\pm \kappa \sqrt{-\,\kappa }, \end{aligned}$$
(3.27)
$$\begin{aligned}&a=\pm \frac{1}{\sqrt{-\,\kappa }}. \end{aligned}$$
(3.28)

Hence, we give cases of solutions for eqs (3.19) and (3.17), respectively:

  1. 1.

    When \(\kappa > 0\), substituting eqs (3.26)–(3.28) and (3.18) into eqs (2.9) and (2.10), we obtain the exact wave solutions of eq. (3.17)

    $$\begin{aligned} \upsilon _{1,2}(x,t)=\pm \mathrm {i}\sqrt{\kappa }\tan \sqrt{\kappa } \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) \end{aligned}$$
    (3.29)

    and

    $$\begin{aligned} \upsilon _{3,4}(x,t)=\pm \mathrm {i}\sqrt{\kappa }\cot \sqrt{\kappa } \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) . \end{aligned}$$
    (3.30)

    Using eqs (3.29), (3.30) and (3.18) the solutions of eq. (3.17) take the forms:

    $$\begin{aligned} \phi _{1,2}(x,t)= & {} \tan ^2 \sqrt{\kappa } \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) ,\nonumber \\ \end{aligned}$$
    (3.31)
    $$\begin{aligned} \phi _{3,4}(x,t)= & {} \cot ^2\sqrt{\kappa } \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) , \nonumber \\ \end{aligned}$$
    (3.32)
    $$\begin{aligned} \chi _{1,2}(x,t)= & {} -\,\kappa \pm \mathrm {i}\sqrt{\kappa }\,\tan \, \sqrt{\kappa } \nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) , \end{aligned}$$
    (3.33)
    $$\begin{aligned} \chi _{3,4}(x,t)= & {} -\,\kappa \pm \mathrm {i}\sqrt{\kappa }\,{\cot }\,\sqrt{\kappa }\nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) , \end{aligned}$$
    (3.34)
    $$\begin{aligned} \psi _{1,2}(x,t)= & {} 2\kappa ^2\mp 2 \mathrm {i} \kappa \sqrt{\kappa }\,{\tan }\, \sqrt{\kappa }\nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) \end{aligned}$$
    (3.35)

    and

    $$\begin{aligned} \psi _{3,4}(x,t)= & {} 2\kappa ^2 \mp 2 \mathrm {i} \kappa \sqrt{\kappa }\,{\cot }\,\sqrt{\kappa }\nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) , \end{aligned}$$
    (3.36)

    where \(\kappa \) and \(\mu \) are arbitrary constants and \(0<\alpha \le 1\). Figure 3 illustrates solution \(\phi _1\).

  2. 2.

    When \(\kappa < 0\), substituting eqs (3.26)–(3.28) and (3.18) into eqs (2.11) and (2.12), we obtain the exact travelling wave solutions to eq. (3.17)

    $$\begin{aligned} \upsilon _{5,6}(x,t)= & {} \pm \mathrm {i}\sqrt{\,-k}\,{\tanh }\,\sqrt{-\,k}\nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) \end{aligned}$$
    (3.37)

    and

    $$\begin{aligned} \upsilon _{7,8}(x,t)= & {} \pm \mathrm {i}\sqrt{-\,k}\,{\coth }\,\sqrt{-\,k} \nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) . \end{aligned}$$
    (3.38)

    Using eqs (3.37), (3.38) and (3.18), the solutions to eq. (3.17) take the following forms:

    $$\begin{aligned}&\phi _{5,6}(x,t)\nonumber \\&= \tanh ^2 \left( \sqrt{-\,k} \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) \right) ,\nonumber \\ \end{aligned}$$
    (3.39)
    $$\begin{aligned}&\phi _{7,8}(x,t)\nonumber \\&=\coth ^2 \left( \sqrt{-\,k} \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) \right) ,\nonumber \\ \end{aligned}$$
    (3.40)
    $$\begin{aligned} \chi _{5,6}(x,t)= & {} -\,\kappa \pm \mathrm {i}\sqrt{-\,k}\,{\tanh }\, \sqrt{-\,k}\nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) , \end{aligned}$$
    (3.41)
    $$\begin{aligned} \chi _{7,8}(x,t)= & {} -\,\kappa \pm \mathrm {i}\sqrt{-\,k}\,{\coth }\, \sqrt{-\,k}\nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) , \end{aligned}$$
    (3.42)
    $$\begin{aligned} \psi _{5,6}(x,t)= & {} 2\kappa ^2 \mp 2 \mathrm {i}\sqrt{-\,k}\,{\tanh }\, \sqrt{-\,k}\nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) \end{aligned}$$
    (3.43)

    and

    $$\begin{aligned} \psi _{7,8}(x,t)= & {} 2\kappa ^2 \mp 2 \mathrm {i}\sqrt{-\,k}\,{\coth }\, \sqrt{-\,k}\nonumber \\&\times \left( x-\frac{\kappa t^{\alpha }}{\Gamma (1+\alpha )} +\mu \right) , \end{aligned}$$
    (3.44)

    where \(\kappa \) and \(\mu \) are arbitrary constants and \(0<\alpha \le 1\). Figure 4 illustrates solution \(\phi _5\).

Fig. 3
figure 3

The solution \(\phi = \phi _1(x, t)\) in (3.31) when \(\kappa =1\), \(\alpha = 1\), \(\mu =0\), \(0\le t\le 5\) and \(-\,5\le x \le 5\): (a) the 3D plot and (b) the 2D plot for \(t= 1\).

Full size image
Fig. 4
figure 4

The solution \(\phi = \phi _5(x, t)\) in (3.39) when \(\kappa = -\,1\), \(\alpha = 1\), \(\mu =1\), \(0\le t\le 5\) and \(-\,5\le x \le 5\): (a) the 3D plot and (b) the 2D plot for \(t = 0\).

Full size image

Remark 3

As in Remark 2, we can get an infinite sequence of solutions to eq. (3.17), by applying eq. (2.15) once to \(\upsilon _i(x, t)\) \((i =1,2, \ldots ,8)\).

3.2.1 Physical interpretation

We discuss the physical interpretation of the results for the time-fractional generalised Hirota–Satsuma coupled KdV system. The graphical demonstrations of some of the obtained solutions are shown in figures 3 and 4. These figures have the following physical explanations.

The shapes of eqs (3.31) and (3.39) are represented in figures 3 and 4. Equation (3.31) is a trigonometric function solution. Figures 3a and 3b present the exact periodic travelling wave solutions of the solitary wave solution in 3D and 2D, respectively, with the fractional order and the wave speed is within \(0\le t\le 5\) and \(-\,5\le x \le 5\). Equation (3.39) is a hyperbolic function solution. Figures 4a and 4b present the bell-shaped solitary wave solutions in 3D and 2D, respectively, with the fractional order and the wave speed within \(0\le t\le 5\) and \(-\,5\le x \le 5\).

4 Comparisons

Here, we compare our results with other results in order to show that the Riccati–Bernoulli sub-ODE is efficacious, robust and adequate. We clarify that this method is superior to other methods:

  1. 1.

    First, we discuss the comparison between the solutions given in [21, 23] and our solutions for the space–time fractional mEW equation. Kaplan et al [23] have presented only one solution to the mEW equation, using the modified simple equation method, whereas Korkmaz [21] gave two solutions to the space–time fractional mEW equation, using the ansatz method. The main advantage of the Riccati–Bernoulli sub-ODE method over the modified simple equation technique and ansatz method is that it supplies many new exact travelling wave solutions along with additional free parameters. If we also compare between these two methods and the proposed method in this paper, the Riccati–Bernoulli sub-ODE method is more effective in providing many new solutions than these two methods.

  2. 2.

    Second, we discuss the comparison between the solutions given in [15, 24, 25] and our solutions. Guo et al [25] used the improved fractional sub-equation method and obtained only three solutions. Furthermore, Liu and Chen [15] studied the time-fractional Hirota–Satsuma coupled KdV equations to find exact solutions via the functional variable method and achieved only two solutions. In contrast, we provide more general and a huge amount of new exact travelling wave solutions with numerous free parameters. Neirameh [24] used a direct algebraic method for solving the time-fractional Hirota–Satsuma coupled KdV equations. Actually, the method proposed by him is simple, flexible, easy to use and produces very accurate results. His result is much better than the results given in [15, 25].

Based on the above discussions, we deduce that the Riccati–Bernoulli sub-ODE method is very effective, powerful and vital in providing many new solutions. Moreover, the Riccati–Bernoulli sub-ODE technique has a very important feature that admits an infinite sequence of solutions to equations, which are explained clearly in §2.1. In fact, this feature has never been given for any other method, as shown in [15, 21, 23,24,25].

5 Conclusions

In this work, we have proposed a Riccati–Bernoulli sub-ODE technique to solve nonlinear fractional differential equations (NFDEs). By this way, the degree of auxiliary polynomials is increased and more solutions provide an opportunity for some models. The space–time fractional mEW equation and generalised time-fractional Hirota–Satsuma coupled KdV system are handled to demonstrate the effectiveness of the proposed method. In comparison with the other classical methods, more travelling wave solutions are obtained. The graphs of some solutions are depicted for suitable coefficients. Actually, this method can be applied to many other NFDEs appearing in mathematical physics and natural sciences.