Higher dimensional Bianchi type-III string cosmological models with dark energy in Saez–Ballester scalar-tensor theory of gravitation

Abstract

We have investigated the five-dimensional Bianchi type-III string cosmological models with dark energy using the Saez–Ballester scalar-tensor theory of gravitation. To solve the field equations, we applied the laws of volumetric expansions and assumed a scaling relation between the shear scalar $\sigma$ and the expansion scalar $\theta$, which leads to a relationship between the metric potentials, i.e., $D=C^{r}$ (where r is a non-zero constant). We have considered both power-law model and exponential model and have discussed the physical and kinematical parameters of these models.

1 Introduction

According to multiple observations, including studies of type Ia supernovae (Filippenko & Riess 1998; Perlmutter et al. 1999), the Sloan Digital Sky Survey (Tegmark et al. 2004) and the cosmic microwave background data, the universe is currently undergoing accelerated expansion. These findings provide strong evidence for the existence of an accelerating universe. According to these studies, the acceleration of the universe is caused by dark energy, a fluid with negative pressure, even though it dominates the universe, more research is needed to understand its mysterious origins and behavior. The cosmological constant is described as the energy density linked to empty space or as vacuum energy with a net pressure that drives the universal expansion. The cosmological constant has been used to represent a part of dark energy, although there are issues with cosmic coincidence and fine-tuning. To comprehend the universal cosmic acceleration, scalar field theories, such as quintessence, phantom, k-essence, tachyon and quintom have been investigated. The variable equation of state parameter ($\omega$) can be used to describe different dark energy theories. In the case of $\omega =-1$, it is mathematically evolved into the cosmological constant. Researchers have recently shown an interest in many scalar-tensor theories. The analysis of the scalar-tensor theories of gravity proposed by Brans & Dicke (1961) and Saez & Ballester (1986), as well as the f(R) and f(R, T) theories of gravitation, are important in explaining the dark energy models. In the Brans & Dicke (1961) theory of gravity, we introduced a scalar field ($\phi$) that is coupled to the mass density of the universe and is reciprocal to the time-varying gravitational constant, G. In Saez & Ballester (1986) theory of gravitation, the metric potentials are simply connected to a dimensionless scalar field ($\phi$). They have demonstrated that the weak fields are adequately described by this minimal coupling. Additionally, the Saez–Ballester theory presents a possible solution to the problem of missing matter in non-flat FRW cosmologies. A lot of researchers have studied Saez–Ballester theory of gravitation. Aditya & Reddy (2018) proposed an anisotropic new holographic dark energy model within the framework of Saez–Ballester theory of gravitation. They investigated the implications of holographic dark energy on the dynamics and expansion of the universe, considering an anisotropic behavior. Chand & Mishra (2016) investigated the Bianchi type-III cosmological model within the framework of Saez–Ballester theory of gravity in the presence of bulk viscous dark fluid. The study explores the dynamics of the universe and the impact of bulk viscosity on the evolution of the cosmic scale factor. Naidu et al. (2012) studied a Bianchi type-III cosmological model with dark energy within the framework of Saez–Ballester scalar-tensor theory. They investigated the dynamical behavior of the universe and the influence of dark energy on its evolution. Pradhan et al. (2013) investigated the dynamics of accelerating Bianchi type-V cosmological models with perfect fluid and heat flow within the framework of Saez–Ballester theory of gravitation. The study explores the role of perfect fluid and heat flow in the evolution of the universe and the possibility of achieving accelerated expansion. Rao & Divya Prasanthi (2017) investigated Bianchi type-I and type-III cosmological models with modified holographic Ricci dark energy in the framework of Saez–Ballester theory of gravitation. The findings contribute to our understanding of the interplay between modified holographic dark energy, geometry and evolution of the universe.

The field equations for Saez–Ballester theory are provided below:

$$\begin{aligned} G_{ij}-\omega \phi ^{n}\big (\phi ,_{i}\phi ,_{j} -\tfrac{1}{2}g_{ij}\phi ,_{k}\phi ^{,k}\big )=-T_{ij} \end{aligned}$$

(1)

and the equations are satisfied by the scalar field:

$$\begin{aligned} 2\phi ^{n}\phi ^{,i}_{;i}+n\phi ^{n-1}\phi _{,k}\phi ^{,k}=0, \end{aligned}$$

(2)

where $G_{ij}$ is the Einstein tensor, $T_{ij}$ represents the energy-momentum tensor, $\omega$ is a dimensionless coupling constant and the term’s comma (,) and semicolon (;) denote partial and covariant differentiations, respectively.

The equation for the conservation of energy can be expressed as:

$$\begin{aligned} T_{;j}^{ij}=0. \end{aligned}$$

(3)

The analysis of data from WMAP and CMB suggests that a small amount of anisotropy may be visible during the early stages of the universe. Consequently, the spatially homogeneous and anisotropic universe has become a subject of interest among researchers. Bianchi’s models have proven to be valuable tools in understanding the anisotropic universe. The concept of extra dimensions was discovered by Kaluza (1921) and Klein (1926) through their work on unifying gravitation and electromagnetism. Although the fifth dimension remains small, resulting in our universe appearing four-dimensional, it has become challenging to explain the early evolution of the universe after the Big Bang explosion. To address this issue, higher-dimensional models have been developed to understand the early evolution of the universe. The presence of extra dimensions can help to solve problems related to flatness and horizon by generating a large amount of entropy. Furthermore, higher dimensions play a vital role in the development of string theories and can affect the unification of fundamental forces. This outcome is seen in lots of authors who have studied higher-dimensional models. The study by Trivedi & Bhabor (2021) explores the interplay among cosmic strings, dark energy and the scalar field, providing insights into the dynamics of the universe in higher dimensional framework. Katore et al. (2010) studied the dynamics of domain walls and their implications in the context of scalar-tensor theories, shedding light on the behavior of gravity and matter interactions in higher-dimensional scenarios. Samanta et al. (2013) explored the dynamics and evolution of the universe considering the effects of bulk viscosity, providing insights into the behavior of string cosmologies in higher-dimensional spacetimes.

Building on the research mentioned above, we have conducted a study of the Bianchi type-III string cosmological universe with dark energy using the Saez–Ballester theory of gravitation. The structure of this paper is as follows: Section 2 provides the field equation for the Bianchi type-III universe, while Section 3 presents the solutions of the field equations obtained in Section 2. Subsections 3.1 and 3.2 estimate the physical parameters of power-law and exponential models, respectively. Section 4 offers a discussion of our findings and finally, Section 5 presents the conclusions of both power-law and exponential models.

2 Metric and field equations

The spacetime described by the Bianchi type-III metric as:

$$\begin{aligned} ds^{2}&=dt^{2}-A^{2}dx^{2}-B^{2} e^{-2mx}dy^{2}\nonumber \\&\quad -C^{2}dz^{2}-D^{2}d\psi ^{2}, \end{aligned}$$

(4)

here, the metric potentials A, B, C and D in the Bianchi type-III metric are functions of cosmic time t, while the constant m is non-zero. We have assumed that $x^{1}= x$, $x^{2}=y$, $x^{3}=z$, $x^{4}=\psi$ and $x^{5}=t$.

The energy-momentum tensor for the derived model is expressed as:

$$\begin{aligned} T_{ij}=T_{ij}^{CS}+T_{ij}^{DE}, \end{aligned}$$

(5)

where the energy-momentum tensor is composed of the energy-momentum tensors of cosmic string ($T_{ij}^{CS}$) and dark energy ($T_{ij}^{DE}$). The energy-momentum tensor of cosmic string is defined as:

$$\begin{aligned} T_{ij}^{CS}=(\rho +p) u_{i}u_{j}-pg_{ij}+\lambda x_{i}x_{j}, \end{aligned}$$

(6)

here, $u^{i}u_{i}=- x^{i}x_{i}=1$ and $u^{i}x_{i}=0$, where $x^{i}$ represents the direction of cosmic strings along x-direction and $u^{i}$ denotes the four-velocity vector. The fluid’s pressure is denoted by p, the tension density of the string is represented by $\lambda$ and the rest energy density of strings is given by $\rho$. Now:

$$\begin{aligned} T_{i}^{j (CS)}=\textrm{diag}[-(p+\lambda ),-p,-p,-p,\rho ]. \end{aligned}$$

(7)

The energy-momentum tensor of dark energy is defined as:

$$\begin{aligned} T_{ij}^{DE}=(\rho +p) u_{i}u_{j}-pg_{ij}, \end{aligned}$$

(8)

which finally takes the form of:

$$\begin{aligned} T_{i}^{j (DE)}&=\textrm{diag}[-\omega _{x},-\omega _{y},-\omega _{z},-\omega _{\psi },1] \rho _{de}, \end{aligned}$$

(9)

$$\begin{aligned} T_{i}^{j (DE)}&=\textrm{diag}[-\omega _{de},-(\omega _{de}+\beta ),\nonumber \\&\quad -(\omega _{de}+\gamma ),-(\omega _{de}+\gamma ),1] \rho _{de}. \end{aligned}$$

(10)

In the above equation, the parameter $\omega _{de}$ denotes the equation of state (EoS) for dark energy and $\rho _{de}$ represents the density of dark energy. Additionally, there are two skewness parameters $\beta$ and $\gamma$, which describe the deviations from $\omega _{de}$ along the y, z and $\psi$ axes. The inclusion of deviations from the equation of state parameter of dark energy along specific axes in cosmological models serves to incorporate the possibility of anisotropy in the distribution of dark energy (Yadav et al. 2011; Aditya & Reddy 2018). For simplification of the solution, we assume $\omega _{de_x}= \omega _{de}$ and $\omega _{de_z}= \omega _{de_\psi }=\omega _{de}+\gamma$. The Saez–Ballester field Equations (1) and (2) for the metric (4) by using (5), (7) and (10) can be written as:

$$\begin{aligned}&\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\ddot{D}}{D}+\frac{\dot{B}\dot{C}}{BC} +\frac{\dot{C}\dot{D}}{CD}+\frac{\dot{B}\dot{D}}{BD}-\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =-((p+\lambda )+\omega _{de}\rho _{de}), \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\ddot{D}}{D}+\frac{\dot{C}\dot{D}}{CD} +\frac{\dot{A}\dot{D}}{AD}+\frac{\dot{A}\dot{C}}{AC}-\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =-(p+(\omega _{de}+\beta )\rho _{de}), \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\ddot{D}}{D}+\frac{\dot{A}\dot{B}}{AB} +\frac{\dot{B}\dot{D}}{BD}+\frac{\dot{A}\dot{D}}{AD}-\frac{m^{2}}{A^{2}}-\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =-(p+(\omega _{de}+\gamma )\rho _{de}), \end{aligned}$$

(13)

$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\dot{A}\dot{B}}{AB} +\frac{\dot{B}\dot{C}}{BC}+\frac{\dot{A}\dot{C}}{AC}-\frac{m^{2}}{A^{2}}-\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =-(p+(\omega _{de}+\gamma )\rho _{de}), \end{aligned}$$

(14)

$$\begin{aligned}&\frac{\dot{A}\dot{B}}{AB}+\frac{\dot{B}\dot{C}}{BC}+\frac{\dot{C}\dot{D}}{CD} +\frac{\dot{A}\dot{D}}{AD}+\frac{\dot{A}\dot{C}}{AC}+\frac{\dot{B}\dot{D}}{BD}\nonumber \\&\quad -\frac{m^{2}}{A^{2}}+\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}=\rho +\rho _{de}, \end{aligned}$$

(15)

$$\begin{aligned}&\frac{\dot{A}}{A}-\frac{\dot{B}}{B}=0, \end{aligned}$$

(16)

$$\begin{aligned}&\ddot{\phi }+\dot{\phi }\Bigg (\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}+\frac{\dot{D}}{D}\Bigg )+\frac{n}{2} \frac{\dot{\phi ^{2}}}{\phi }=0. \end{aligned}$$

(17)

The notation used in the equation implies that the derivative with respect to cosmic time, t is denoted by a dot above the corresponding variable.

2.1 Physical parameters

Spatial volume:

$$\begin{aligned} V = a^{4}(t)=ABCD. \end{aligned}$$

(18)

Hubble parameter:

$$\begin{aligned} H=\frac{\dot{a}}{a}=\frac{1}{4}\Bigg (\frac{\dot{A}}{A}+\frac{\dot{B}}{B} +\frac{\dot{C}}{C}+\frac{\dot{D}}{D}\Bigg ). \end{aligned}$$

(19)

The deceleration parameter:

$$\begin{aligned} q=\frac{d}{dt}\Bigg (\frac{1}{H}\Bigg ) -1. \end{aligned}$$

(20)

Scalar expansion:

$$\begin{aligned} \theta =4H=\Bigg (\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}+\frac{\dot{D}}{D}\Bigg ). \end{aligned}$$

(21)

Shear scalar:

$$\begin{aligned} \sigma ^{2}=\frac{1}{2}\left( \sum _{i=1}^{4} H_{i}^{2}-4H^{2}\right) . \end{aligned}$$

(22)

Mean anisotropy parameter:

$$\begin{aligned} A_{h}=\frac{1}{4}\sum _{i=1}^{4} \Bigg (\frac{H_{i}-H}{H}\Bigg )^{2}, \end{aligned}$$

(23)

here, the directional Hubble parameter in the x, y, z and $\psi$ directions is denoted by $H_{i}$.

3 Solution of field equations

By Equation (16), we get:

$$\begin{aligned} B=kA, \end{aligned}$$

(24)

where k is the constant of integration. If we take $k=1$, then we get:

$$\begin{aligned} B=A. \end{aligned}$$

(25)

By using Equation (25), the field Equations (11)–(17) and the energy conservation Equation (3) lead to the following equations:

$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\ddot{D}}{D} +\frac{\dot{A}\dot{C}}{AC}+\frac{\dot{C}\dot{D}}{CD} +\frac{\dot{A}\dot{D}}{AD}-\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =-((p+\lambda )+\omega _{de}\rho _{de}), \end{aligned}$$

(26)

$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C} +\frac{\ddot{D}}{D}+\frac{\dot{A}\dot{C}}{AC} +\frac{\dot{C}\dot{D}}{CD}+\frac{\dot{A}\dot{D}}{AD} -\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =-(p+(\omega _{de}+\beta )\rho _{de}), \end{aligned}$$

(27)

$$\begin{aligned}&2\frac{\ddot{A}}{A}+\frac{\ddot{D}}{D} +2\frac{\dot{A}\dot{D}}{AD}+\Bigg (\frac{\dot{A}}{A}\Bigg )^{2} -\frac{m^{2}}{A^{2}}-\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =-(p+(\omega _{de}+\gamma )\rho _{de}), \end{aligned}$$

(28)

$$\begin{aligned}&2\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+2\frac{\dot{A}\dot{C}}{AC} +\Bigg (\frac{\dot{A}}{A}\Bigg )^{2}-\frac{m^{2}}{A^{2}}-\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =-(p+(\omega _{de}+\gamma )\rho _{de}), \end{aligned}$$

(29)

$$\begin{aligned}&2\frac{\dot{A}\dot{C}}{AC}+2\frac{\dot{A}\dot{D}}{AD} +\frac{\dot{C}\dot{D}}{CD}+\Bigg (\frac{\dot{A}}{A}\Bigg )^{2} -\frac{m^{2}}{A^{2}}+\frac{\omega }{2} \dot{\phi }^{2}\phi ^{n}\nonumber \\&\quad =\rho +\rho _{de}, \end{aligned}$$

(30)

$$\begin{aligned}&\ddot{\phi }+\dot{\phi }\Bigg (2\frac{\dot{A}}{A} +\frac{\dot{C}}{C}+\frac{\dot{D}}{D}\Bigg )+\frac{n}{2} \frac{\dot{\phi ^{2}}}{\phi }=0, \end{aligned}$$

(31)

$$\begin{aligned}&\dot{\rho }+4H(p+\rho )+\lambda H_{1}+\dot{\rho _{de}}+4H(\omega _{de}+1)\rho _{de} \nonumber \\&\quad +(\beta H_{2}+\gamma (H_{3}+H_{4}) ) \rho _{de}=0. \end{aligned}$$

(32)

By subtracting Equation (27) from Equation (26), we have:

$$\begin{aligned} \beta \rho _{de}=\lambda . \end{aligned}$$

(33)

Equation (32) represents the energy conservation equation involving cosmic strings (with energy density $\rho$) and dark energy (with energy density $\rho _{de}$). Assuming non-interacting behavior between cosmic strings and dark energy, Equation (32) can be separated into three individual Equations (34)–(36).

$$\begin{aligned}&\dot{\rho }+4H(p+\rho )+\lambda H_{1}=0, \end{aligned}$$

(34)

$$\begin{aligned}&\dot{\rho _{de}}+4H(\omega _{de}+1)\rho _{de}=0, \end{aligned}$$

(35)

$$\begin{aligned}&\beta H_{2}+\gamma (H_{3}+H_{4})=0. \end{aligned}$$

(36)

Equation (34) corresponds to the energy conservation equation for cosmic strings. Equation (35) represents the energy conservation equation for dark energy. Equation (36) represents a constraint equation that arises when assuming non-interacting behavior between cosmic strings and dark energy. These equations describe the energy conservation and interaction properties of cosmic strings and dark energy in the universe (Aditya & Reddy 2018; Trivedi & Bhabor 2021).

By subtracting Equation (29) from Equation (28) and solving it, we get:

$$\begin{aligned} \frac{\dot{D}}{D}-\frac{\dot{C}}{C}=\frac{k_{1}}{a^{4}}, \end{aligned}$$

(37)

where $k_{1}$ is the constant of integration.

The system of field Equations (26)–(31) consists of six independent equations with eleven unknowns. These equations are highly non-linear, making it challenging to find a determinate solution. To simplify the problem, we make two physical plausible assumptions:

• 1. We have assumed a scaling relation between the shear scalar $\sigma$ and the expansion scalar $\theta$ (Collins et al. 1980), which leads to a relationship between the metric potentials. As a result, we can take:

  $$\begin{aligned} D=C^{r}, \end{aligned}$$

  (38)

  where $r\ne 0$ is a constant.

• 2. We have used two different volumetric expansion laws (Akarsu & Kılınç 2010). Volume (V) for power-law model:

  $$\begin{aligned} V = c_{1}t^{4m} \end{aligned}$$

  (39)

  and volume (V) for the exponential model:

  $$\begin{aligned} V= c_{1}e^{4mt}, \end{aligned}$$

  (40)

  where $c_{1}$ and m are positive constants. These models cover all possible expansion histories, including exponential (Koivisto & Mota 2008) and power-law expansion (Golovnev et al. 2008). The models with the power-law for $m < 1$ exhibit accelerating volumetric expansion, while those for $m = 1$ exhibit volumetric expansion with constant velocity. The models for $m > 1$ exhibit decelerating volumetric expansion. Therefore, the anisotropic fluid studied in this work can be considered in the context of DE in the models with power-law expansion for $m > 1$.

3.1 Power-law model

Using Equations (25), (37)–(39), we get the metric potentials:

$$\begin{aligned}&A=B=c_{1}^{2} t^{2m}k_{2}^{\frac{r+1}{2(1-r)}} \exp \left\{ \frac{k_{1}(r+1)t^{1-4m}}{2c_{1}(1-r)(1-4m)}\right\} , \end{aligned}$$

(41)

$$\begin{aligned}&C=k_{2}^{\frac{1}{r-1}} \exp \left\{ \frac{k_{1}t^{1-4m}}{c_{1}(r-1)(1-4m)}\right\} , \end{aligned}$$

(42)

$$\begin{aligned}&D=k_{2}^{\frac{r}{r-1}} \exp \left\{ \frac{k_{1}r t^{1-4m}}{c_{1}(r-1)(1-4m)}\right\} . \end{aligned}$$

(43)

The Hubble parameter:

$$\begin{aligned} H=\frac{m}{t}. \end{aligned}$$

(44)

The directional Hubble parameters are:

$$\begin{aligned}&H_{1}= H_{2}=\frac{2m}{t}+\frac{k_{1}(r+1)t^{-4m}}{2c_{1}(1-r)}, \end{aligned}$$

(45)

$$\begin{aligned}&H_{3}=\frac{k_{1}t^{-4m}}{c_{1}(r-1)}, \end{aligned}$$

(46)

$$\begin{aligned}&H_{4}=\frac{k_{1}rt^{-4m}}{c_{1}(r-1)}. \end{aligned}$$

(47)

The deceleration parameter:

$$\begin{aligned} q=\frac{1}{m}-1, \qquad \textrm{where} \ m>1. \end{aligned}$$

(48)

The expansion scalar:

$$\begin{aligned} \theta =4H=\frac{4m}{t}. \end{aligned}$$

(49)

The shear scalar:

$$\begin{aligned} \sigma ^{2}&=\frac{2m^{2}}{t^{2}} +\frac{k_{1}^{2}(3r^{2}+2r+3)t^{-8m}}{4c_{1}^{2}(r-1)^{2}}\nonumber \\&\quad \;\; +\frac{2mk_{1}(r+1)t^{-1-4m}}{c_{1}(1-r)}. \end{aligned}$$

(50)

The anisotropy parameter:

$$\begin{aligned} A_{h}&=\frac{\sigma ^{2}}{2H^{2}}=1 +\frac{k_{1}^{2}(3r^{2}+2r+3)t^{2(1-4m)}}{8c_{1}^{2}m^{2}(r-1)^{2}}\nonumber \\&\quad \;\;+\frac{k_{1}(r+1)t^{1-4m}}{c_{1}m(1-r)}. \end{aligned}$$

(51)

The ratio:

$$\begin{aligned} \frac{\sigma ^{2}}{\theta ^{2}}&=\frac{1}{8}+\frac{k_{1}^{2}(3r^{2}+2r+3)t^{2(1-4m)}}{64c_{1}^{2}m^{2}(r-1)^{2}}\nonumber \\&\quad \;\;+\frac{k_{1}(r+1)t^{1-4m}}{8c_{1}m(1-r)}. \end{aligned}$$

(52)

By Equations (2) and (44), the scalar field ($\phi$) is given by:

$$\begin{aligned} \phi ^{\frac{n+2}{2}}=\phi _{0}\frac{(n+2) t^{1-4m}}{2(1-4m)}+\frac{k_{3}(n+2)}{2}, \end{aligned}$$

(53)

where $\phi _{0}$ and $k_{3}$ are constant of integration.

To determine the string density, we make use of the assumption. These assumptions allow us to get simpler equations and easier analytical solutions (Reddy & Rao 2006; Adhav et al. 2009).

$$\begin{aligned}&\lambda =\alpha \rho , \end{aligned}$$

(54)

$$\begin{aligned}&p=\chi \rho , \end{aligned}$$

(55)

where $\alpha$ and $\chi$ are non-evolving state parameters.

Solving Equation (34) by using Equations (44), (45), (54) and (55), we get:

$$\begin{aligned} \rho =\rho _{0}t^{-2m(2\chi +\alpha +2)}\exp \left\{ \frac{\alpha k_{1}(r+1)t^{1-4m}}{2c_{1}(r-1)(1-4m)}\right\} , \end{aligned}$$

(56)

$\rho _{0}$ represents the rest energy density at the present epoch.

String pressure:

$$\begin{aligned} p&=\chi \rho _{0}t^{-2m(2\chi +\alpha +2)}\nonumber \\ {}&\quad \times \exp \left\{ \frac{\alpha k_{1}(r+1)t^{1-4m}}{2c_{1}(r-1)(1-4m)}\right\} . \end{aligned}$$

(57)

String tension density:

$$\begin{aligned} \lambda =\alpha \rho _{0}t^{-2m(2\chi +\alpha +2)} \exp \left\{ \frac{\alpha k_{1}(r+1)t^{1-4m}}{2c_{1}(r-1)(1-4m)}\right\} . \end{aligned}$$

(58)

Solving Equation (30), by using Equations (41), (44)–(47), (53) and (56), the dark energy density is given by:

$$\begin{aligned}&\rho _{de} =\frac{4m^{2}}{t^{2}}-\frac{2mk_{1}(r+1)t^{-1-4m}}{c_{1}(r-1)}\nonumber \\&\quad +t^{-8m}\Bigg (\frac{\omega \phi _{0}^{2}}{2} -\frac{k_{1}^{2}(3r^{2}+2r+3)}{4c_{1}^{2}(r-1)^{2}}\Bigg ) \nonumber \\ {}&\quad - \frac{m^{2}k_{2}^{\frac{r+1}{r-1}}t^{-4m}}{c_{1}}\exp \left\{ \frac{k_{1}(r+1)t^{1-4m}}{c_{1}(r-1)(1-4m)}\right\} \nonumber \\&\quad -\rho _{0}t^{-2m(2\chi +\alpha +2)}\exp \left\{ \frac{\alpha k_{1}(r+1)t^{1-4m}}{2c_{1}(r-1)(1-4m)}\right\} . \end{aligned}$$

(59)

Solving Equation (35), by using Equations (44) and (59), the EoS parameter is given by:

$$\begin{aligned}&\omega _{de} =\frac{1}{\rho _{de}}\Biggl [-\frac{4m^{2}}{t^{2}} +\frac{2m}{t^{2}}-t^{-4m}\Bigg (\frac{m^{2}k_{2}^{\frac{r+1}{r-1}}}{c_{1}}\nonumber \\&\quad +\frac{k_{1}(r+1)(1+4m)}{2c_{1}(r-1)t} -\frac{2mk_{1}(r+1)}{c_{1}(r-1)t}\Bigg )\nonumber \\&\quad +t^{-8m}\Bigg (\frac{\omega \phi _{0}^{2}}{2} -\frac{k_{1}^{2}(3r^{2}+2r+3)}{4c_{1}^{2}(r-1)^{2}}\Bigg )\nonumber \\&\quad +t^{1-8m}\frac{mk_{1}(r+1)k_{2}^{\frac{r+1}{r-1}}}{4c_{1}^{2}(r-1)}+\frac{mk_{1}(r+1)k_{2}^{\frac{r+1}{r-1}}t^{1-8m}}{4c_{1}^{2}(r-1)}\nonumber \\&\quad \times \left( 1+\exp \left\{ \frac{k_{1}(r+1)t^{1-4m}}{c_{1}(r-1)(1-4m)}\right\} \right) \nonumber \\&\quad -\rho _{0}\left( \chi +\frac{\alpha }{2}-\frac{\alpha k_{1}(r+1)t}{8mc_{1}(r-1)}\right) \nonumber \\ {}&\quad \times t^{-2m(2\chi +\alpha +2)} \exp \left\{ \frac{\alpha k_{1}(r+1)t^{1-4m}}{2c_{1}(r-1)(1-4m)}\right\} \Biggr ]. \end{aligned}$$

(60)

By Equations (33) and (36), using Equations (45)–(47), (58) and (59), the skewness parameters are given by:

$$\begin{aligned} \beta&=\frac{\rho _{0}}{\rho _{de}}\alpha t^{-2m(2\chi +\alpha +2)} \exp \left\{ \frac{\alpha k_{1}(r+1)t^{1-4m}}{2c_{1}(r-1)(1-4m)}\right\} , \end{aligned}$$

(61)

$$\begin{aligned} \gamma&=\frac{\rho _{0}}{\rho _{de}}\alpha t^{-2m(2\chi +\alpha +2)}\Bigg (\frac{1}{2}-\frac{2mc_{1}(r-1)t^{4m-1}}{k_{1}(r+1)}\bigg )\nonumber \\&\quad \times \exp \left\{ \frac{\alpha k_{1}(r+1)t^{1-4m}}{2c_{1}(r-1)(1-4m)}\right\} . \end{aligned}$$

(62)

3.2 Exponential model

Using Equations (25), (37), (38) and (40), we get the metric potentials:

$$\begin{aligned}&A=B=c_{1}^{\frac{1}{2}} k_{2}^{\frac{r+1}{2(1-r)}} \exp \left\{ 2mt+\frac{k_{1}(r+1)e^{-4mt}}{8mc_{1}(r-1)}\right\} , \end{aligned}$$

(63)

$$\begin{aligned}&C=k_{2}^{\frac{1}{r-1}} \exp \left\{ \frac{k_{1}e^{-4mt}}{4mc_{1}(1-r)}\right\} , \end{aligned}$$

(64)

$$\begin{aligned}&D=k_{2}^{\frac{r}{r-1}} \exp \left\{ \frac{k_{1}r e^{-4mt}}{4mc_{1}(1-r)}\right\} . \end{aligned}$$

(65)

The Hubble parameter:

$$\begin{aligned} H= m. \end{aligned}$$

(66)

The directional Hubble parameters are:

$$\begin{aligned}&H_{1}= H_{2}=2m-\frac{k_{1}(r+1)e^{-4mt}}{2c_{1}(r-1)}, \end{aligned}$$

(67)

$$\begin{aligned}&H_{3}=\frac{k_{1}e^{-4mt}}{c_{1}(r-1)}, \end{aligned}$$

(68)

$$\begin{aligned}&H_{4}=\frac{k_{1}re^{-4mt}}{c_{1}(r-1)}. \end{aligned}$$

(69)

The deceleration parameter:

$$\begin{aligned} q=-1. \end{aligned}$$

(70)

The expansion scalar:

$$\begin{aligned} \theta =4H=4m. \end{aligned}$$

(71)

The shear scalar:

$$\begin{aligned} \sigma ^{2}&=\frac{1}{2} \Bigg (4m^{2}+\frac{k_{1}^{2}(3r^{2}+2r+3) e^{-8mt}}{2c_{1}^{2}(r-1)^{2}}\nonumber \\&\quad -\frac{4mk_{1}(r+1)e^{-4mt}}{c_{1}(r-1)}\Bigg ). \end{aligned}$$

(72)

The anisotropy parameter:

$$\begin{aligned} A_{h}&=\frac{\sigma ^{2}}{2H^{2}}=1+\frac{k_{1}^{2}(3r^{2}+2r+3) e^{-8mt}}{8c_{1}^{2}m^{2}(r-1)^{2}}\nonumber \\&\quad -\frac{k_{1}(r+1)e^{-4mt}}{c_{1}m(r-1)}. \end{aligned}$$

(73)

The ratio:

$$\begin{aligned} \frac{\sigma ^{2}}{\theta ^{2}}=\frac{1}{8}+ \frac{k_{1}^{2}(3r^{2}+2r+3)e^{-8mt}}{64c_{1}^{2}m^{2}(r-1)^{2}}-\frac{k_{1}(r+1)e^{-4mt}}{8c_{1}m(r-1)}. \end{aligned}$$

(74)

By Equation (2) and using Equation (66), the scalar field ($\phi$) is given by:

$$\begin{aligned} \phi ^{\frac{n+2}{2}}=-\phi _{0}\frac{(n+2)e^{-4mt}}{8m}+\frac{k_{3}(n+2)}{2}, \end{aligned}$$

(75)

where $\phi _{0}$ and $k_{3}$ are constant of integration.

To determine the string density, we make use of the assumption (Reddy & Rao 2006; Adhav et al. 2009).

$$\begin{aligned}&\lambda =\alpha \rho , \end{aligned}$$

(76)

$$\begin{aligned}&p=\chi \rho , \end{aligned}$$

(77)

where $\alpha$ and $\chi$ are non-evolving state parameters.

Solving Equation (34) by using Equations (66), (67), (76) and (77), we get:

$$\begin{aligned} \rho&=\rho _{0}\exp \!\left\{ -2m(2\chi +\alpha +2)t-\frac{\alpha k_{1}(r+1)e^{-4mt}}{8mc_{1}(r-1)}\right\} , \end{aligned}$$

(78)

where $\rho _{0}$ denotes the rest energy density at the present epoch.

String pressure:

$$\begin{aligned} p&=\chi \rho _{0} \exp \!\bigg \{\!-2m(2\chi +\alpha +2)t \nonumber \\&\quad -\frac{\alpha k_{1}(r+1)e^{-4mt}}{8mc_{1}(r-1)}\bigg \}. \end{aligned}$$

(79)

String tension density:

$$\begin{aligned} \lambda =\alpha \rho _{0} \exp \!\left\{ \!-2m(2\chi +\alpha +2)t\!-\!\frac{\alpha k_{1}(r+1)e^{-4mt}}{8mc_{1}(r-1)}\!\right\} . \end{aligned}$$

(80)

Solving Equation (30), by using Equations (63), (66)–(69), (75) and (78), the dark energy density is given by:

$$\begin{aligned} \rho _{de}&=4m^{2}+\frac{2mk_{1}(r+1)e^{-4mt}}{c_{1}(r-1)} \nonumber \\&\quad +e^{-8mt}\Bigg (\frac{\omega \phi _{0}^{2}}{2}-\frac{k_{1}^{2}(3r^{2}+2r+3)}{4c_{1}^{2}(r-1)^{2}}\Bigg )\nonumber \\&\quad -\frac{m^{2}k_{2}^{\frac{r+1}{r-1}}}{c_{1}}\exp \left\{ -4mt-\frac{k_{1}(r+1)e^{-4mt}}{4mc_{1}(r-1)}\right\} \nonumber \\&\quad -\rho _{0}\exp \bigg \{-2m(2\chi +\alpha +2)t\nonumber \\&\quad -\frac{\alpha k_{1}(r+1)e^{-4mt}}{8mc_{1}(r-1)}\bigg \}. \end{aligned}$$

(81)

Solving Equation (35), by using Equations (66) and (81), the EoS parameter is given by:

$$\begin{aligned} \omega _{de}&=\frac{1}{\rho _{de}}\Biggl [-4m^{2} +e^{-8mt}\Bigg (\frac{\omega \phi _{0}^{2}}{2} \nonumber \\ {}&\quad -\frac{k_{1}^{2}(3r^{2}+2r+3)}{4c_{1}^{2}(r-1)^{2}}\Bigg ) +\frac{mk_{1}(r+1)k_{2}^{\frac{r+1}{r-1}}e^{-4mt}}{4c_{1}^{2}(r-1)}\nonumber \\&\quad \times \exp \!\left\{ \!-4mt\!-\!\frac{k_{1}(r+1)e^{-4mt}}{4mc_{1}(r-1)}\right\} \nonumber \\&\quad -\rho _{0}\left( \chi +\frac{\alpha }{2}-\frac{\alpha k_{1}(r+1)e^{-4mt}}{8mc_{1}(r-1)}\right) \nonumber \\&\quad \times \exp \bigg \{-2m(2\chi +\alpha +2)t\nonumber \\&\quad -\frac{\alpha k_{1}(r+1)e^{-4mt}}{8mc_{1}(r-1)}\bigg \}\Biggl ]. \end{aligned}$$

(82)

By Equations (33) and (36), and using Equations (67)–(69), (80) and (81), the skewness parameters are given by:

$$\begin{aligned} \beta&=\alpha \frac{\rho _{0}}{\rho _{de}}\exp \bigg \{-2m(2\chi +\alpha +2)t\nonumber \\&\quad -\frac{\alpha k_{1}(r+1)e^{-4mt}}{8mc_{1}(r-1)}\bigg \}, \end{aligned}$$

(83)

$$\begin{aligned} \gamma&=\frac{\rho _{0}}{\rho _{de}}\alpha \Bigg (\frac{1}{2} -\frac{2mc_{1}(r-1)e^{4mt}}{k_{1}(r+1)}\bigg )\nonumber \\&\quad \times \exp \left\{ -2m(2\chi +\alpha +2)t-\frac{\alpha k_{1}(r+1) e^{-4mt}}{8mc_{1}(r-1)}\right\} . \end{aligned}$$

(84)

4 Results and discussion

Fig. 1

For the power-law model, the graph between string tension density, $\lambda$ and cosmic time, t (giga years) for $m=2$, $r=2$, $\chi =-1$, $k_{1}=-1$, $c_{1}=1$ and $\rho _{0}= -1$.

Fig. 2

For the exponential model, the graph between string tension density, $\lambda$ and cosmic time, t (giga years) for $m=2$, $r=2$, $\chi =-1$, $k_{1}=-1$, $c_{1}=1$ and $\rho _{0}= 1$.

The variations of the string tension density ($\lambda$) over time, t are depicted in Figures 1 and 2. These figures demonstrate that at the early stage of the universe, when time t approaches zero, the value of $\lambda$ can be either negative or positive, depending on the value of $\alpha$. At a later time, as $t \rightarrow \infty$, $\lambda$ converges towards zero. It is noteworthy that when $\alpha = 0$ then $\lambda = 0$ for both models. Based on these observations, we can infer that the universe was initially dominated by strings, and that at a later time, strings will become less dominant, eventually vanishing in the universe.

These findings provide important insights into the evolution of the universe, particularly during the string-dominated era. The results suggest that the effects of strings were significant in the early universe, but their influence has decreased over time (Letelier 1981, 1983; Akarsu & Kılınç 2010).

Fig. 3

For the power-law model, the graph between dark energy density, $\rho _{de}$ and cosmic time, t (giga years) for $m=2$, $r=2$, $\chi =-\frac{1}{2}$, $\alpha =1$, $\omega =2$ and $k_{1}=k_{2}=c_{1}=\phi _{0}=\rho _{0}= 1$.

Fig. 4

For the exponential model, the graph between dark energy density, $\rho _{de}$ and cosmic time, t (giga years) for $m=2$, $r=2$, $\chi =-\frac{1}{2}$, $\alpha =1$, $\omega =2$ and $k_{1}=k_{2}=c_{1}=\phi _{0}=\rho _{0}= 1$.

Equations (59) and (81) express the dark energy density ($\rho _{de}$) in the power-law and exponential models, respectively. In the power-law model, $\rho _{de}\rightarrow {-}\infty$ at the initial epoch of time, and converges towards zero as time $t\rightarrow \infty$. These findings are supported by Letelier (1981, 1983) and are shown in Figure 3. Similarly, in the exponential model, the dark energy density approaches 20.67 at the initial epoch of time and eventually converges towards 16 as $t\rightarrow \infty$ (Figure 4). Notably, in both the models, the dark energy density remains positive throughout the evolution. This suggests that the dark energy density dominates the string density.

Overall, these findings suggest that the universe is dominated by dark energy density, and at an early stage, the universe was driven by a negative dark energy density (Bonnor 1989; Farnes 2018; Malekjani et al. 2023). However, as time progressed, the universe transitioned towards a positive dark energy density. In the case of $\alpha =0$, our model predicts the existence of a universe dominated solely by dark fluid, which provides a valuable framework for further exploration of the nature of dark energy density and its relationship to other fundamental aspects of the universe.

Fig. 5

For the power-law model, the graph between the EoS parameter, $\omega _{de}$ and cosmic time, t (giga years) for $m=2$, $r=2$, $\chi =-\frac{1}{2}$, $\alpha =1$, $\omega =2$ and $k_{1}=k_{2}=c_{1}=\phi _{0}=\rho _{0}= 1$.

Fig. 6

For the exponential model, the graph between the EoS parameter, $\omega _{de}$ and cosmic time, t (giga years) for $m=2$, $r=2$, $\chi =-\frac{1}{2}$, $\alpha =1$, $\omega =2$ and $k_{1}=k_{2}=c_{1}=\phi _{0}=\rho _{0}= 1$.

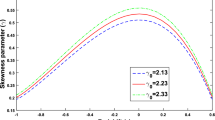
In both the power-law and exponential models, the EoS parameter of dark energy ($\omega _{de}$) varies with time, which is consistent with recent observations of Tegmark et al. (2004). Figures 5 and 6 demonstrate that in both models, $\omega _{de}$ initially has positive values that gradually decrease over time and eventually approach values of $- 0.75$ and $-1$, respectively. This indicates that the universe has undergone different phases, such as matter-dominated ($\omega _{de}=0$), quintessence ($\omega _{de}> 1$) and phantom fluid-dominated ($\omega _{de}< 1$) phases.

Therefore, we can conclude that at an early stage, the universe was dominated by matter, and as time progressed, it underwent a transition to a vacuum fluid-dominated universe.

Fig. 7

For the power-law model, the graph among Hubble parameter (H), expansion scalar ($\theta$), shear scalar ($\sigma$) and cosmic time, t (giga years) for $m=2$, $r=2$, $k_{1}=1$ and $c_{1}=1$.

Our analysis of the power-law and exponential models reveals interesting insights into the expansion and shear properties of the universe. In the power-law model, we found that the expansion scalar ($\theta$) and Hubble parameter (H) are infinite at time $t = 0$, indicating the maximum value of Hubble’s parameter and accelerated expansion of the universe. However, as time progresses, both $\theta$ and H decrease gradually and eventually become zero when $t \rightarrow \infty$. This implies that the universe expands with time, but the rate of expansion decreases as time increases. Additionally, we found that the shear scalar $\sigma \rightarrow \infty$ at the initial epoch, but decreases with time and becomes zero in the late universe, indicating that the universe obtained in this model is shear-free at the late time. Also, as $t \rightarrow \infty$, the ratio $\frac{\sigma ^{2}}{\theta ^{2}} = \frac{1}{8} \ne 0$ for $m > \frac{1}{4}$. Hence, this model is anisotropic for large values of t when $m > \frac{1}{4}$ (Figure 7) (Priyokumar & Jiten 2021; Daimary & Roy Baruah 2022; Mete & Deshmukh 2022).

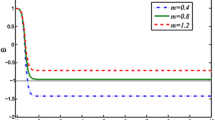
On the other hand, in the exponential model, we found that the expansion scalar ($\theta$) and Hubble parameter (H) are constant, indicating that the universe is expanding at the same rate from the beginning. Additionally, we found that the shear scalar ($\sigma$) is 0.75 at the initial epoch, increases with time, and becomes constant in the late universe, indicating that the universe obtained in this model is neither shear-free at the initial epoch nor will be in the late time. Also as $t \rightarrow \infty$, the ratio $\frac{\sigma ^{2}}{\theta ^{2}} = \frac{1}{8} \ne 0$ for $m > 0$, indicating the model does not attain isotropy (Figure 8) (Priyokumar & Jiten 2021; Daimary & Roy Baruah 2022; Mete & Deshmukh 2022).

Fig. 8

For the exponential model, the graph among Hubble parameter (H), Expansion scalar ($\theta$), Shear scalar ($\sigma$) and cosmic time, t (giga years) for $m=2$, $r=2$, $k_{1}=1$ and $c_{1}=1$.

Fig. 9

The graph between the deceleration parameter (q) and variable, m.

The deceleration parameter (q) is related to the rate at which the expansion of the universe is slowing down. If q is negative, as in both models, this means that the expansion of the universe is accelerating rather than slowing down.

In the power-law model, since $1+q > 0$, the expansion is accelerating from the initial singularity at $t=0$ and continues to accelerate as time increases (Figure 9). In the exponential model, the value of q remains constant and negative ($q = -0.5$), which means that the universe is expanding at a constant rate from the beginning of its expansion (Figure 9). The power-law model describes a universe that begins at an initial singularity with zero volume at time $t = 0$. As time progresses, the universe expands and when t approaches infinity, the volume V also approaches infinity. This behavior is described by Equation (39) for volume V in the power-law model. In the exponential model, the expression of volume, V as obtained in Equation (40), shows that the model universe does not start from zero volume at the initial epoch, but expands as time increases. Additionally, when $t \rightarrow \infty$, $V \rightarrow \infty$.

This difference in the behavior of the volume in two models is a significant distinction. The power-law model predicts that the universe started from a singularity and then expanded, while the exponential model does not have an initial singularity. This has important implications for the nature and origin of the universe. The power-law model suggests a finite age of the universe, while the exponential model suggests an infinite age. The absence of an initial singularity in the exponential model may be seen as a more appealing feature since it avoids the conceptual difficulties associated with a singularity.

5 Conclusions

From the analysis of the power-law and exponential models, we can draw the following conclusions:

• Both models show that dark energy density dominates the string density throughout the evolution of the universe.

• The equation of state parameter, $\omega _{de}$ is found to be time-varying in both models, $\omega _{de}$ initially has positive values that gradually decrease over the time and eventually approach $\omega _{de}\ge -1$. This is consistent with recent observations.

• The power-law model shows that the universe begins with an initial singularity at time $t=0$ and expands with time, but the rate of expansion slows down as time increases, and the expansion stops at $t \rightarrow \infty$. The model also exhibits accelerated expansion when $1+q>0$.

• The exponential model shows that the universe starts from a non-zero volume at the initial epoch and expands at a constant rate from the beginning. The model exhibits constant acceleration when $1+q=0$.

• Both models predict different phases of the universe based on the value of the equation of state parameter, $\omega _{de}$, i.e., matter-dominated universe ($\omega _{de}=0$), quintessence ($\omega _{de}>{1}$) and phantom fluid-dominated universe ($\omega _{de}<{1}$).

In summary, the power-law and exponential models provide insight into the behavior of the universe’s evolution and expansion under the influence of dark energy. These models can help in understanding the current state of the universe and provide a framework for further studies and observations.