1 Introduction

Our universe is experiencing accelerated expansion that has been validated by many cosmological observations such as Type 1a Supernova [1, 2]. According to data from CMB and large-scale structure, a fluid with negative pressure, known as dark energy, is causing cosmic acceleration. Though dark energy dominates the universe, yet its origin is still mystic. Moreover, WMAP estimates that nearly 73, 23, and \(4\%\) of our universe filled up with dark energy, dark matter and normal matter, respectively. Cosmological constant is defined as energy density associated with vacant space or as vacuum energy having negative pressure which causes expansion of the universe. \(\Lambda \) has proven best candidate to represents as dark energy component but \(\Lambda \mathrm{CDM}\) has some serious issues given by cosmological constant fine- tuning problem and cosmic coincident problem [3]. Hence, Scalar field models such as quintessence [4,5,6], phantom [7], k-essence [8, 9], Tachyon [10], and Quintom [11] have been explored to understand the universe following cosmic acceleration. The Dark Energy can be represented by the equation of state (EoS) \(\omega =\frac{p}{\rho }\) where p is the pressure and \(\rho \) is energy density. It has become mathematically equivalent to the cosmological constant \(\Lambda \) in the case of \((\omega =-1)\). Peebles and Ratra [12] have given a brief review on the cosmological constant and dark energy. Nojiri and Odintsov [13] have given a detailed review of different modified gravities. Also, the Big rip and other singularities have been discussed with their solutions. Bamba et al. [14] have reviewed different dark energy models, namely the \(\Lambda \)CDM model with a fluid description of dark energy. Moreover, they analyzed the various cosmological observation tests and modified gravity models.

Several scalar-tensor theories have been a matter of interest to researchers in the last few years. After the formation of the scalar-tensor theories proposed by Brans and Dicke [15], Nordvedt [16], Barber [17], Saez and Ballester [18] introduced a scalar-tensor theory in which the metric is coupled with a dimensionless scalar field in a simple manner. Whereas, in Brans–Dicke’s theory, simply a scalar field \(\phi \) is coupled to the mass density of the universe and it is reciprocal of time-varying gravitational constant G. The Saez-Ballester theory gives a good enough description of the weak fields and thought-provoking results of scalar field. Despite having the dimensionless character of the scalar field, the antigravity regime appears in weak fields. Furthermore, the theory offers a feasible approach to figuring out the missing matter problem in non-flat FRW models. Rao et al. [19], Rao et al. [20], Pradhan et al. [21], Reddy et al. [22] have worked upon different aspects of this theory. Moreover, Naidu et al. [23], Ghate and Sontakke [24], Vinutha et al. [25] have investigated dark energy models in Saez-Ballester theory of gravitation.

WMAP and CMB data suggest that the inclusion of a small amount of anisotropy can be seen in the early phase of the universe. The spatially homogeneous and anisotropic universe became the area of interest to the researchers. Bianchi models had proved very useful to understand the anisotropic universe. Bianchi type-I models are the most understandable model of the universe because of their ability to explain the spatially homogeneous, anisotropic, and flat universe. Also, Bianchi-I cosmology can explain the flat FLRW universe as a special case. A desirable feature of these models is the field equations used in these models are very simplified. A tremendous amount of work has been done on Bianchi-I cosmologies. In the literature, Pradhan and singh [26], Saha [27], Singh and Tiwari [28], Adhav et. al. [29], Mahanta and Biswal [30], Katore and Kapse [31] worked upon Bianchi -I models in different theories of gravitation. Aditya and Reddy [32] have studied Bianchi -I model in saez-ballester theory of gravitation. Recently, Mishra and Dua [33] have studied Bianchi type-I cosmological model in Saez-Ballester theory with variable deceleration parameter.

Kaluza and Klein [34, 35] developed the idea of the extra dimension by unifying gravitation and electromagnetism. But the fifth dimension remains small which leads to our universe effectively looking four dimensional. It was hard to explain the early-stage evolution of the universe just After the Big Bang explosion. Hence, higher-dimensional models came out with the aim to understand early-stage evolution. The flatness and horizon problems can be solved by generating large amount of entropy, which is possible in the presence of the extra dimension [36, 37]. Marciano [38] has invesigated how the low-energy couplings and masses are related. The parameters are found time varying which may indicate the presence of extra dimensions. In the 1980s, many authors explained the idea of how external dimensions expand while internal dimensions contract [39,40,41]. Recently, Akarsu et al. [42] have studied the impact of the unobservable universe on the evolution of the possible anisotropy of the observable universe by considering a five-dimensional Bianchi type-I metric within the framework of extension of the conventional general theory of relativity with a five-dimensional cosmological constant. Moreover, higher dimensions play a significant role in the development of string theories. The existence of higher dimensions can influence the unification of fundamental forces. This results in many authors have studied higher-dimensional models [39, 43, 44]. Katore et al. [45] and Reddy et al. [46] studied higher-dimensional models within the framework of Saez-balletser theory of gravitation. Reddy and Ramesh [47] have investigated five-dimensional dark energy model in the presence of scalar-meson fields in general relativity. Zimdahl and Pavo’n [48] have investigated that the coincidence problem can be solved by an interaction between dark energy and dark matter. Barrow and Clifton [49] have given a mathematical model which describes the energy transfer between two fluids in an expanding Friedmann universe with zero spatial curvature. The interacting and non-interacting behavior of barotropic fluid and dark energy is capable of explaining cosmic acceleration. Hence, Reddy et al. [50, 51] have discussed two fluid scenario for dark energy model in Saez-Ballester and Brans-Dicke theories of gravitation. Singh and Chaubey [52] have investigated an interacting scenario of Dark energy and Barotropic fluid in Bianchi-I cosmologies. Also, Singh and Chaubey [53] studied interacting scenario of two fluids in Bianchi-V cosmological model. Amirhashchi et al. [54] have studied interacting two-fluid viscous dark energy models in a non-flat universe. Moreover, Vinutha et al. [55], Tiwari et al. [56] have discussed both interacting and non-interacting behavior of dark energy and barotropic fluid. Rao et al. [57] have discussed two-fluid scenario for dark energy cosmological model in higher dimension in the framework of Saez-Ballester theory of gravitation. Recently, Goswami et al. [70] have obtained Bianchi-I models with dark energy and barotropic fluid in general relativity.

Inspired by the above research work, in this paper we will discuss Bianchi-I universe filled with dark energy and barotropic fluids in saez-ballester theory of gravitation. We have structured this paper as follows. Section 2 contains the field equation for Bianchi Type-I universe. Section 3 represents non-interacting two fluid model. Physical parameters for case I and case II are estimated in subsections 3.1 and 3.2. In Sect. 4, interacting two fluid model is described and subsecs. 4.1, 4.2 contain Physical parameters for case I and case II. Graphs and concluding remarks are presented in Sect. 5.

2 Metric and field equations

Here, we have taken five-dimensional Bianchi type-I metric in the form

$$\begin{aligned} \begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+A^{2}\mathrm{d}x^{2}+B^{2}\mathrm{d}y^{2}+C^{2}\mathrm{d}z^{2}+D^{2}\mathrm{d}\psi ^{2} \end{aligned} \end{aligned}$$
(1)

where the metric potentials A, B, C and D are functions of cosmic time t. The field equation in scalar-tensor theory proposed by Saez and Ballester are given by

$$\begin{aligned} \begin{aligned} G_{ij}-\omega \phi ^{n}\left( \phi _{,i}\phi _{,j}-\frac{1}{2}g_{ij}\phi _{,k}\phi ^{,k}\right) =-T_{ij} \end{aligned} \end{aligned}$$
(2)

and the scalar field \(\phi \) satisfies the equation

$$\begin{aligned} \begin{aligned} 2\phi ^{n}\phi ^{,i}_{;i}+n\phi ^{n-1}\phi _{,k}\phi ^{,k}=0 \end{aligned} \end{aligned}$$
(3)

where \(G_{ij}\) is Einstein tensor, n is an arbitrary constant, \(\omega \) is a dimensionless coupling constant, comma and semicolon denotes partial and covariant differentiation, respectively.

The equation of motion is given by

$$\begin{aligned} T^{ij}_{,j}=o \end{aligned}$$
(4)

It is a consequence of the field Eqs. (2) and (3). Now, the energy momentum tensor for the obtained model of two fluids is defined as

$$\begin{aligned} T_{ij}=T^{(\mathrm{de})}_{ij}+T^{(m)}_{ij} \end{aligned}$$
(5)

where \(T^{(\mathrm{de)}}_{ij}\) and \(T^{(m)}_{ij}\) represent the energy momentum tensors of dark energy and ordinary matter (barotropic uid), respectively, and defined as

$$\begin{aligned} \begin{aligned} T^{(\mathrm{de)}}_{ij}&=diag[-\rho _\mathrm{de},p_\mathrm{de},p_\mathrm{de}, p_\mathrm{de}, p_\mathrm{de}]\\&=diag[-1,\omega _\mathrm{de},\omega _\mathrm{de}+\alpha , \omega _\mathrm{de}+\beta ,\omega _\mathrm{de}+\beta ]\rho _{de} \end{aligned} \end{aligned}$$
(6)

and

$$\begin{aligned} \begin{aligned} T^{(m)}_{ij}&=diag[-\rho _{m},p_\mathrm{de},p_{m}, p_{m}, p_{m}]\\&=diag[-1,\omega _{m},\omega _{m}, \omega _{m},\omega _{m}]\rho _{m} \end{aligned} \end{aligned}$$
(7)

where \(\omega _\mathrm{de}=\frac{p_\mathrm{de}}{\rho _\mathrm{de}}\) represents the equation of state parameter (EoS) for dark energy. \(p_\mathrm{de}\) and \(\rho _\mathrm{de}\) are the pressure and energy density of dark energy. \(\alpha \) and \(\beta \) are considered as skewness parameters, which represent the deviations from \(\omega _\mathrm{de}\) on y and \(z,\psi \) axis, respectively. Similarly, \(p_{m}\) and \(\rho _{m}\) denote, respectively, the pressure and energy density of the barotropic uid component while \(\omega _{m}=\frac{p_{m}}{\rho _{m}}\) is the corresponding EoS parameter.

The field equations (2), (3) and (4) for the metric (1), with the help of (5),(6) and (7), lead to

$$\begin{aligned}&\frac{{\ddot{B}}}{B}+\frac{{\ddot{C}}}{C}+\frac{{\ddot{D}}}{D}+\frac{{\dot{B}}{\dot{C}}}{BC}+\frac{{\dot{B}}{\dot{D}}}{BD}+\frac{{\dot{C}}{\dot{D}}}{CD}-\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}\nonumber \\&\quad =-\omega _\mathrm{de}\rho _\mathrm{de}-\omega _{m}\rho _{m} \end{aligned}$$
(8)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+\frac{{\ddot{C}}}{C}+\frac{{\ddot{D}}}{D}+\frac{{\dot{A}}{\dot{C}}}{AC}+\frac{{\dot{A}}{\dot{D}}}{AD}+\frac{{\dot{C}}{\dot{D}}}{CD}-\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}\nonumber \\&\quad =-\left( \omega _\mathrm{de}+\alpha \right) \rho _\mathrm{de}-\omega _{m}\rho _{m} \end{aligned}$$
(9)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+\frac{{\ddot{B}}}{B}+\frac{{\ddot{D}}}{D}+\frac{{\dot{A}}{\dot{B}}}{AB}+\frac{{\dot{A}}{\dot{D}}}{AD}+\frac{{\dot{B}}{\dot{D}}}{BD}-\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}\nonumber \\&\quad =-\left( \omega _\mathrm{de}+\beta \right) \rho _\mathrm{de}-\omega _{m}\rho _{m} \end{aligned}$$
(10)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+\frac{{\ddot{B}}}{B}+\frac{{\ddot{C}}}{C}+\frac{{\dot{A}}{\dot{B}}}{AB}+\frac{{\dot{B}}{\dot{C}}}{BC}+\frac{{\dot{A}}{\dot{C}}}{AC}-\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}\nonumber \\&\quad =-\left( \omega _\mathrm{de}+\beta \right) \rho _\mathrm{de}-\omega _{m}\rho _{m} \end{aligned}$$
(11)
$$\begin{aligned}&\frac{{\dot{A}}{\dot{B}}}{AB}+\frac{{\dot{B}}{\dot{C}}}{BC}+\frac{{\dot{A}}{\dot{C}}}{AC}+\frac{{\dot{A}}{\dot{D}}}{AD}+\frac{{\dot{B}}{\dot{D}}}{BD}+\frac{{\dot{C}}{\dot{D}}}{CD}+\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}\nonumber \\&\quad =\rho _\mathrm{de}+\rho _{m} \end{aligned}$$
(12)
$$\begin{aligned}&\ddot{\phi }+{\dot{\phi }}\left( \frac{{\dot{A}}}{A}+\frac{{\dot{B}}}{B}+\frac{{\dot{C}}}{C}+\frac{{\dot{D}}}{D}\right) +\frac{n}{2}\frac{{\dot{\phi }}^{2}}{\phi }=0 \end{aligned}$$
(13)

where overhead dot represents differentiation with respect to the cosmic time t. Also, the energy conservation equation (4) leads to

$$\begin{aligned} \begin{aligned}&\dot{\rho _\mathrm{de}}+4\rho _\mathrm{de}(\omega _\mathrm{de}+1)H+\rho _\mathrm{de}\left( \alpha H_{2}+\beta H_{3}+\gamma H_{4}\right) +\dot{\rho _{m}}\\&\quad +4\rho _{m}(\omega _{m}+1)H=0 \end{aligned} \end{aligned}$$
(14)

where H is average Hubble parameter and \(H_{2}, H_{3}, H_{4}\) are directional Hubble parameters.

3 Non-interacting two-fluid model

We consider that two fluids do not interact with each other in the universe. The assumption of non-interacting behavior of dark energy and barotropic fluid is represented by these two separate equations as obtained from eq.(14).

$$\begin{aligned} \begin{aligned} \dot{\rho _\mathrm{de}}+4\rho _\mathrm{de}(\omega _\mathrm{de}+1)H+\rho _\mathrm{de}\left( \alpha H_{2}+\beta (H_{3}+H_{4})\right) =0 \end{aligned} \end{aligned}$$
(15)

and

$$\begin{aligned} \dot{\rho _{m}}+4\rho _{m}(\omega _{m}+1)H=0 \end{aligned}$$
(16)

EoS parameter of barotropic uid \(\omega _{m}\) is constant (Akarsu [59] and Kilinc [60]), that is

$$\begin{aligned} \omega _{m}=\frac{p_{m}}{\rho _{m}}=\mathrm{constant} \end{aligned}$$
(17)

whereas, \(\omega _\mathrm{de}\) is considered as a function of cosmic time. Hence, integrating Eq.(16) we get,

$$\begin{aligned} \rho _{m}=\rho _{0}a^{-4(1+\omega _{m})} \end{aligned}$$
(18)

where \(\rho _{0}\) is constant of integration and a is scale factor.

In order to solve highly nonlinear field Eqs. (8)-(13), we will use the assumption, that is,

$$\begin{aligned} A=B=C=t^{n} and\;\; D=t^{n_{1}} \end{aligned}$$
(19)

Bhabor et al. [61] have used this transformation to find solution of the highly nonlinear field equations. where n and \(n_{1}\) are constants.

Now, using Eq. (19), the field Eqs. (8)–(12) reduce to the following equations

$$\begin{aligned}&\frac{3n^{2}+n_{1}^{2}+2nn_{1}-2n-n_{1}}{t^{2}}-\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}=-\omega _\mathrm{de}\rho _\mathrm{de}\nonumber \\&\quad -\omega _{m}\rho _{m} \end{aligned}$$
(20)
$$\begin{aligned}&\frac{3n^{2}+n_{1}^{2}+2nn_{1}-2n-n_{1}}{t^{2}}-\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}=-\left( \omega _\mathrm{de}+\alpha \right) \rho _\mathrm{de}\nonumber \\&\quad -\omega _{m}\rho _{m} \end{aligned}$$
(21)
$$\begin{aligned}&\frac{3n^{2}+n_{1}^{2}+2nn_{1}-2n-n_{1}}{t^{2}}-\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}=-\left( \omega _\mathrm{de}+\beta \right) \rho _\mathrm{de}\nonumber \\&\quad -\omega _{m}\rho _{m} \end{aligned}$$
(22)
$$\begin{aligned}&\frac{6n^{2}-3n}{t^{2}}-\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}=-\left( \omega _\mathrm{de}+\beta \right) \rho _\mathrm{de}\nonumber \\&\quad -\omega _{m}\rho _{m} \end{aligned}$$
(23)
$$\begin{aligned}&\frac{3n^{2}+3nn_{1}}{t^{2}}+\frac{1}{2}\omega \phi ^{n}{\dot{\phi }}^{2}\nonumber \\&\quad =\rho _\mathrm{de}+\rho _{m} \end{aligned}$$
(24)

Subtracting Eq. (22) from Eq. (23), we get two values of \(n_{1}\)

$$\begin{aligned}&n_{1}=n \end{aligned}$$
(25)
$$\begin{aligned}&n_{1}=-3n+1 \end{aligned}$$
(26)

Hence, dark energy model with barotropic fluid for two different scenarios can be obtained for the above two values of \(n_{1}\).

3.1 Case 1: when \(n_{1}=n\)

The metric (1) can be written as

$$\begin{aligned} \begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+t^{2n}\left( \mathrm{d}x^{2}+\mathrm{d}y^{2}+\mathrm{d}z^{2}+\mathrm{d}\psi ^{2}\right) \end{aligned} \end{aligned}$$
(27)

and from Eq. (19), we have

$$\begin{aligned} A=B=C=D=t^{n} \end{aligned}$$
(28)

The directional Hubble parameters are as follows,

$$\begin{aligned} H_{1}=H_{2}=H_{3}=H_{4}=\frac{n}{t} \end{aligned}$$
(29)

Average Hubble parameter,

$$\begin{aligned} H=\frac{n}{t} \end{aligned}$$
(30)

Spatial Volume,

$$\begin{aligned} V=ABCD=a^{4}=t^{4n} \end{aligned}$$
(31)

The expansion scalar,

$$\begin{aligned} \theta =\frac{4n}{t} \end{aligned}$$
(32)

The shear scalar,

$$\begin{aligned} \sigma ^{2}=0 \end{aligned}$$
(33)

The Anisotropy parameter,

$$\begin{aligned} A_{h}=0 \end{aligned}$$
(34)

The ratio,

$$\begin{aligned} \frac{\sigma ^{2}}{\theta ^{2}}=0 \end{aligned}$$
(35)

Deceleration parameter,

$$\begin{aligned} q=\frac{1-n}{n} \end{aligned}$$
(36)

Now, using Eq.(28) in Eq. (13) and integrating, we get

$$\begin{aligned} \begin{aligned} \phi =\left( \frac{n+2}{2}\right) \frac{\phi _{0}}{1-4n}t^{1-4n}+c \end{aligned} \end{aligned}$$
(37)

where \(\phi _{0}\) and c are constants of integration.

using Eqs. (18), (25), (37) in Eq. (24), we obtain dark energy density as

$$\begin{aligned} \begin{aligned} \rho _\mathrm{de}=\frac{6n^{2}}{t^{2}}+\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{8n}}-\frac{\rho _{0}}{t^{4n(1+\omega _{m})}} \end{aligned} \end{aligned}$$
(38)

The deviation free part of Eq. (15) with the help of Eq. (38), gives the value of EoS parameter of dark energy,

$$\begin{aligned} \begin{aligned} \omega _\mathrm{de}=-\left[ \frac{\frac{3n}{t^{2}}\left( 2n-1\right) -\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{8n}}+\frac{\omega _{m}\rho _{0}}{t^{4n(1+\omega _{m})}}}{\frac{6n^{2}}{t^{2}}+\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{8n}}-\frac{\rho _{0}}{t^{4n(1+\omega _{m})}}}\right] \end{aligned} \end{aligned}$$
(39)

the pressure of dark energy is given by,

$$\begin{aligned} \begin{aligned} p_\mathrm{de}=-\left[ \frac{3n}{t^{2}}\left( 2n-1\right) -\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{8n}}+\frac{\omega _{m}\rho _{0}}{t^{4n(1+\omega _{m})}}\right] \end{aligned} \end{aligned}$$
(40)

The skewness parameters,

$$\begin{aligned} \alpha =\beta =0 \end{aligned}$$
(41)

Dark energy density parameter can be defined as

$$\begin{aligned} \begin{aligned} \Omega _\mathrm{de}=\frac{\rho _\mathrm{de}}{3H^{2}}=2+\frac{\omega \phi _{0}^{2}}{6n^{2}}t^{2(1-4n)}-\frac{\rho _{0}}{3n^{2}}t^{2(1-2n(1+\omega _{m}))} \end{aligned} \end{aligned}$$
(42)

density parameter of barotropic fluid can be defined as

$$\begin{aligned} \Omega _{m}=\frac{\rho _{m}}{3H^{2}}=\frac{\rho _{0}}{3n^{2}}t^{2(1-2n(1+\omega _{m}))} \end{aligned}$$
(43)

Hence, the overall density parameter can be obtained as

$$\begin{aligned} \begin{aligned} \Omega =\Omega _\mathrm{de}+\Omega _{m}=2+\frac{\omega \phi _{0}^{2}}{6n^{2}}t^{2(1-4n)} \end{aligned} \end{aligned}$$
(44)

jerk parameter,

$$\begin{aligned} j=q+2q^{2}-\frac{{\dot{q}}}{H}=\frac{(1-n)(2-n)}{n^{2}} \end{aligned}$$
(45)

3.2 Case 2: when \(n_{1}=-3n+1\)

The metric (1) can be written as

$$\begin{aligned} \begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+t^{2n}\left( \mathrm{d}x^{2}+\mathrm{d}y^{2}+\mathrm{d}z^{2}\right) +t^{2(-3n+1)}\mathrm{d}\psi ^{2} \end{aligned} \end{aligned}$$
(46)

and from Eq. (19), we have

$$\begin{aligned} A=B=C=t^{n}, D=t^{-3n+1} \end{aligned}$$
(47)

The directional Hubble parameters are as follows,

$$\begin{aligned} H_{1}=H_{2}=H_{3}=\frac{n}{t}, H_{4}=\frac{(-3n+1)}{t} \end{aligned}$$
(48)

Average Hubble parameter,

$$\begin{aligned} H=\frac{1}{4t} \end{aligned}$$
(49)

Spatial Volume,

$$\begin{aligned} V=ABCD=a^{4}=t \end{aligned}$$
(50)

The expansion scalar,

$$\begin{aligned} \theta =\frac{1}{t} \end{aligned}$$
(51)

The shear scalar,

$$\begin{aligned} \sigma ^{2}=\frac{3}{8t^{2}}(4n-1)^{2} \end{aligned}$$
(52)

The Anisotropy parameter,

$$\begin{aligned} A_{h}=\frac{3}{2}(4n-1)^{2} \end{aligned}$$
(53)

The ratio,

$$\begin{aligned} \frac{\sigma ^{2}}{\theta ^{2}}=\frac{3}{8}(4n-1)^{2} \end{aligned}$$
(54)

Deceleration parameter,

$$\begin{aligned} q=3 \end{aligned}$$
(55)

Now, using Eq.(46) in Eq. (13) and integrating, we get

$$\begin{aligned} \begin{aligned} \phi =\left( \frac{n+2}{2}\right) \phi _{0}logt+c \end{aligned} \end{aligned}$$
(56)

where \(\phi _{0}\) and c are constants of integration.

using Eqs. (18), (26), (56) in Eq. (24), we obtain dark energy density which is given by

$$\begin{aligned} \begin{aligned} \rho _\mathrm{de}=\frac{3n}{t^{2}}(1-2n)+\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{2}}-\frac{\rho _{0}}{t^{(1+\omega _{m})}} \end{aligned} \end{aligned}$$
(57)

The deviation free part of Eq. (15) with the help of Eq. (57), gives the value of EoS parameter of dark energy,

$$\begin{aligned} \begin{aligned} \omega _\mathrm{de}=-\left[ \frac{\frac{3n}{t^{2}}\left( 2n-1\right) -\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{2}}+\frac{\omega _{m}\rho _{0}}{t^{(1+\omega _{m})}}}{\frac{3n}{t^{2}}(1-2n)+\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{2}}-\frac{\rho _{0}}{t^{(1+\omega _{m})}}}\right] \end{aligned} \end{aligned}$$
(58)

the pressure of dark energy is given by,

$$\begin{aligned} \begin{aligned} p_\mathrm{de}=-\left[ \frac{3n}{t^{2}}\left( 2n-1\right) -\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{2}}+\frac{\omega _{m}\rho _{0}}{t^{(1+\omega _{m})}}\right] \end{aligned} \end{aligned}$$
(59)

The skewness parameters,

$$\begin{aligned} \alpha =\beta =0 \end{aligned}$$
(60)

Dark energy density parameter can be defined as

$$\begin{aligned} \begin{aligned} \Omega _\mathrm{de}=\frac{\rho _\mathrm{de}}{3H^{2}}=16n(1-2n)+\frac{8\omega \phi _{0}^{2}}{3}-\frac{16\rho _{0}}{3}t^{(2-(1+\omega _{m}))} \end{aligned} \end{aligned}$$
(61)

density parameter of barotropic fluid can be expressed as

$$\begin{aligned} \Omega _{m}=\frac{\rho _{m}}{3H^{2}}=\frac{16\rho _{0}}{3}t^{(2-(1+\omega _{m}))} \end{aligned}$$
(62)

Hence, the overall density parameter is given by

$$\begin{aligned} \begin{aligned} \Omega =\Omega _\mathrm{de}+\Omega _{m}=16n(1-2n)+\frac{8\omega \phi _{0}^{2}}{3} \end{aligned} \end{aligned}$$
(63)

jerk parameter,

$$\begin{aligned} j=q+2q^{2}-\frac{{\dot{q}}}{H}=21 \end{aligned}$$
(64)

4 Interacting two-fluid model

In this section, we examine the framework when dark energy and barotropic fluid are interacting. In this regard, the continuity equations for dark energy and barotropic fluid is as follows,

$$\begin{aligned}&\dot{\rho _\mathrm{de}}+4H(\omega _\mathrm{de}+1)=-Q \end{aligned}$$
(65)
$$\begin{aligned}&\dot{\rho _{m}}+4H(\omega _{m}+1)=Q \end{aligned}$$
(66)

where the quantity Q stands for the interaction between dark energy and barotropic fluids. We consider a positive value of Q because we want energy transformation from dark energy to barotropic fluid. In this way, the second postulate of thermodynamics is also satisfied [62]. Following Amendola et al. [63] and Gau et al. [64], we have

$$\begin{aligned} Q=3H\sigma \rho _{m} \end{aligned}$$
(67)

where \(\sigma \) is coupling constant. Using Eq. (67) in Eq. (66) and integrating, we obtain

$$\begin{aligned}&\rho _{m}=\rho _{0}t^{-4n\left( (1+\omega _{m})-\frac{3}{4}\sigma \right) }\;\; when\;\; n_{1}=n \end{aligned}$$
(68)
$$\begin{aligned}&\rho _{m}=\rho _{0}t^{-\left( (1+\omega _{m})-\frac{3}{4}\sigma \right) }\;\; when\;\; n_{1}=-3n+1 \end{aligned}$$
(69)

where \(\rho _{0}\) is constant of integration.

using Eqs. (25), (37) and (68) in Eq. (24), we obtain dark energy density for case I defined as

$$\begin{aligned} \begin{aligned} \rho _\mathrm{de}=\frac{6n^{2}}{t^{2}}+\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{8n}}-\frac{\rho _{0}}{t^{4n\left( (1+\omega _{m})-\frac{3}{4}\sigma \right) }} \end{aligned} \end{aligned}$$
(70)

The deviation free part of Eq. (15) with the help of Eq. (70), gives the value of EoS parameter of dark energy,

$$\begin{aligned} \begin{aligned} \omega _\mathrm{de}=-\left[ \frac{\frac{3n}{t^{2}}\left( 2n-1\right) -\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{8n}}+\frac{\omega _{m}\rho _{0}}{t^{4n\left( (1+\omega _{m})-\frac{3}{4}\sigma \right) }}}{\frac{6n^{2}}{t^{2}}+\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{8n}}-\frac{\rho _{0}}{t^{4n\left( (1+\omega _{m})-\frac{3}{4}\sigma \right) }}}\right] \end{aligned} \end{aligned}$$
(71)

the pressure of dark energy is given by,

$$\begin{aligned} \begin{aligned} p_\mathrm{de}=-\left[ \frac{3n}{t^{2}}\left( 2n-1\right) -\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{8n}}+\frac{\omega _{m}\rho _{0}}{t^{4n\left( (1+\omega _{m})-\frac{3}{4}\sigma \right) }}\right] \end{aligned} \end{aligned}$$
(72)

using Eqs. (26), (56) and (69) in Eq. (24), dark energy density for case II are given by

$$\begin{aligned} \begin{aligned} \rho _\mathrm{de}=\frac{3n}{t^{2}}(1-2n)+\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{2}}-\frac{\rho _{0}}{t^{\left( 1+\omega _{m}-\frac{3}{4}\sigma \right) }} \end{aligned} \end{aligned}$$
(73)

The deviation free part of Eq. (15) with the help of Eq. (73), gives the value of EoS parameter of dark energy for case II,

$$\begin{aligned} \begin{aligned} \omega _\mathrm{de}=-\left[ \frac{\frac{3n}{t^{2}}\left( 2n-1\right) -\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{2}}+\frac{\omega _{m}\rho _{0}}{t^{\left( 1+\omega _{m}-\frac{3}{4}\sigma \right) }}}{\frac{3n}{t^{2}}(1-2n)+\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{2}}-\frac{\rho _{0}}{t^{\left( 1+\omega _{m}-\frac{3}{4}\sigma \right) }}}\right] \end{aligned} \end{aligned}$$
(74)

the pressure of dark energy can be expressed as

$$\begin{aligned} \begin{aligned} p_\mathrm{de}=-\left[ \frac{3n}{t^{2}}\left( 2n-1\right) -\frac{\omega }{2}\frac{\phi _{0}^{2}}{t^{2}}+\frac{\omega _{m}\rho _{0}}{t^{\left( 1+\omega _{m}-\frac{3}{4}\sigma \right) }}\right] \end{aligned} \end{aligned}$$
(75)

The matter density (\(\Omega _\mathrm{de}\)) and dark energy density (\(\Omega _{m}\)) (case I) are given by

$$\begin{aligned}&\Omega _\mathrm{de}=\frac{\rho _{de}}{3H^{2}}=2+\frac{\omega \phi _{0}^{2}}{6n^{2}}t^{2(1-4n)}-\frac{\rho _{0}}{3n^{2}}t^{2\left( 1-2n\left( 1+\omega _{m}-\frac{3}{4}\sigma \right) \right) } \end{aligned}$$
(76)
$$\begin{aligned}&\Omega _{m}=\frac{\rho _{m}}{3H^{2}}=\frac{\rho _{0}}{3n^{2}}t^{2\left( 1-2n\left( 1+\omega _{m}-\frac{3}{4}\sigma \right) \right) } \end{aligned}$$
(77)

the overall density parameter can be obtained as

$$\begin{aligned} \begin{aligned} \Omega =\Omega _\mathrm{de}+\Omega _{m}=2+\frac{\omega \phi _{0}^{2}}{6n^{2}}t^{2(1-4n)} \end{aligned} \end{aligned}$$
(78)

Hence, the total density parameter of interacting fluids is the same as non-interacting fluids for the value \(n_{1}=n\). The matter density (\(\Omega _\mathrm{de}\)) and dark energy density (\(\Omega _{m}\)) and total density parameter for case II are found to be

$$\begin{aligned}&\Omega _\mathrm{de}=\frac{\rho _\mathrm{de}}{3H^{2}}=16n(1-2n)+\frac{8\omega \phi _{0}^{2}}{3}-\frac{16\rho _{0}}{3}t^{\left( 2-\left( 1+\omega _{m}-\frac{3}{4}\sigma \right) \right) } \end{aligned}$$
(79)
$$\begin{aligned}&\Omega _{m}=\frac{\rho _{m}}{3H^{2}}=\frac{16\rho _{0}}{3}t^{\left( 2-\left( 1+\omega _{m}-\frac{3}{4}\sigma \right) \right) } \end{aligned}$$
(80)
$$\begin{aligned}&\Omega =\Omega _\mathrm{de}+\Omega _{m}=16n(1-2n)+\frac{8\omega \phi _{0}^{2}}{3} \end{aligned}$$
(81)

The expression for \(\Omega \) is same as the obtained value of the average density parameter in the non-interacting scenario for \(n_{1}=-3n+1\).

5 Results and discussion

Fig. 1
figure 1

The plot of dark energy density as a function of cosmic time t (Gyr) for non-interacting two fluid scenario (CASE I) with \(\omega =2,\rho _{0}=\phi _{0}=\omega _{m}=1\)

Full size image
Fig. 2
figure 2

The plot of EoS parameter as a function of cosmic time t (Gyr) for non-interacting two fluid scenario (CASE I) with \(\omega =2,\rho _{0}=\phi _{0}=\omega _{m}=1\)

Full size image

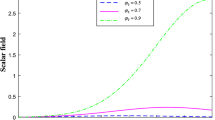
The behavior of dark energy density and EoS parameter for non-interacting two-fluid scenarios has represented in Figs. 1, 2, 3 and 4. For the case I, it is observed that dark energy density is positive and decreasing function of time for different values of n. Hence, both weak energy conditions (WEC) and null energy conditions (NEC) are satisfied in our model. Later on, it converges to zero for a large value of cosmic time t which implies that the barotropic fluid is a little affective on dark energy density (see Fig. (1)). We have taken the different value of n (\(n=0.1\)) for case II because dark energy density is found negative throughout the evolution for \(n>1\). We have observed that for case II, dark energy density depends on the barotropic EoS parameter. Therefore, We have taken different values of \(\omega _{m}\) to see how they affect the energy density and EoS parameter. We observed that the energy density is negative and increasing with time for \(\omega _{m}=0.05, 0\). So, we can conclude that universe is matter dominated in the early phase of the evolution for these two values of \(\omega _{m}\). Whereas it stays positive and decreasing function of time for \(\omega _{m}=1,2\) (see Fig. (3)) which indicates that dark energy density dominates over the matter fluid.

Fig. 3
figure 3

The plot of dark energy density as a function of cosmic time t (Gyr) for non-interacting two fluid scenario (CASE II) with \(\omega =2,\rho _{0}=\phi _{0}=1, n=0.1\)

Full size image
Fig. 4
figure 4

The plot of EoS parameter as a function of cosmic time t (Gyr) for non-interacting two fluid scenario (CASE II) with \(\omega =2,\rho _{0}=\phi _{0}=1, n=0.1\)

Full size image

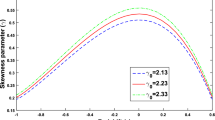
For case I, the value of EoS parameter is considered a function of time and lies between quintessence region \(\biggl (-\frac{2}{3}\le \omega _{de}\le -\frac{1}{3}\biggr )\) for \(n=1\). Also, it attains constant values which is independent of time for different values of n. The model shows consistency with \(\Lambda \)CDM model as it is tending to \(-1\) for large values of n. Moreover, it does not crosses the phantom divided region, i.e., \(\omega _{de}<-1\) (see Fig. (2)). For \(\omega _{m}=0.05, 0\), It is observed that the value of \(\omega _{de}\) starts in the phantom region, increases and tends to \(-1\). Later on, it passes through the quintessence region and tends to a constant value. The behavior of EoS parameter is found positive and tends to 1 for \(\omega _{m}=2\). For \(\omega _{m}=1\), \(\omega _{de}\) attains the constant value 1 (see Fig. (4)). Also, for \(\omega _{m}=0.05,0\), EoS parameter lies between \(-1.44 \le \omega _\mathrm{de} \le -0.92\) which shows resemblance with the latest results from Planck collaboration and CMBR anisotropy [65, 66].

Fig. 5
figure 5

The plot of dark energy density as a function of cosmic time t (Gyr) for interacting two fluid scenario (CASE I) with \(\omega =2, \rho _{0}=\phi _{0}=\omega _{m}=1, \sigma =1.34\)

Full size image
Fig. 6
figure 6

The plot of EoS parameter as a function of cosmic time t (Gyr) for interacting two fluid scenario (CASE I) with \(\omega =2, \rho _{0}=\phi _{0}=\omega _{m}=1, \sigma =1.34\)

Full size image

Figures (5) and (6) describe the behavior of the density of dark energy and EoS parameter of dark energy in the interacting two-fluid scenario for case I. We concluded that both the parameters show almost similar behavior as case I of a non-interacting scenario. For \(n_{1}= -3n+1\), a little variation can be seen in the character of these parameters in comparison to case II of a non-interacting scenario (see Figs. (7) and (8)). Dark energy density is negative for \(\omega _{m}=0.05, 0, 1\) and positive for \(\omega _{m}=2\). Also, it tends to a small positive value for \(\omega _{m}=2\). The value of the EoS parameter begins in the phantom region for \(\omega _{m}\)=2. Furthermore, it crosses the phantom region, varies between quintessence region and tends to 0 for \(\omega _{m}=0.05, 0\). for \(\omega _{m}=1\), it shows the same constant value 1 (see Fig. (8)).

Fig. 7
figure 7

The plot of dark energy density as a function of cosmic time t (Gyr) for interacting two fluid scenario (CASE II) with \(\omega =2, \rho _{0}=\phi _{0}=1, n=0.1, \sigma =1.34\)

Full size image
Fig. 8
figure 8

The plot of EoS parameter as a function of cosmic time t (Gyr) for interacting two fluid scenario (CASE II) with \(\omega =2, \rho _{0}=\phi _{0}=1, n=0.1, \sigma =1.34\)

Full size image
Fig. 9
figure 9

The plot of average density parameter as a function of cosmic time t (Gyr) for non-interacting two fluid scenario (CASE I) with \(\omega =2,\phi _{0}=1\)

Full size image
Fig. 10
figure 10

The plot of average density parameter as a function of n for non-interacting two fluid scenario (CASE II) with \(\omega =2,\phi _{0}=1\)

Full size image

The behavior of the average density parameter as a function of t in the case I of non-interacting model is shown in Fig. (9). \(\Omega \) is decreasing function of time and its value will always be \(\Omega >2\). From Eq. (63), it can be seen that \(\Omega \) is independent of time and depends on n in the context of case II of a non-interacting scenario. Figure (10) demonstrates that \(\Omega \) is positive for \(0.1\le n \le 0.7\) and than it becomes negative for \(n\ge 0.8\). The Average density parameter of interacting model exhibits identical values with the average density parameter of non-interacting scenario (see Eqs. (78) and (81)).

Fig. 11
figure 11

The plot of Hubble parameter as a function of redshift z for non-interacting two fluid scenario (CASE I) with \(n=70\)

Full size image
Fig. 12
figure 12

The plot of Hubble parameter as a function of redshift z for non-interacting two fluid scenario (CASE II)

Full size image

The variation of the Hubble parameter over the variation of redshift z is represented in Figs. (11) and (12). From Fig. (11), for \(n=70\) the numeric value of Hubble’s parameter is measured to be \(H = 69.37\) at \(z=-0.5\). Also for case II, the calculated value of the Hubble parameter is \(H=66.66\) at \(z=3\). These values are very close to \(H_{0} = 67.36\pm 0.54\, \mathrm{kms^{-1}\,Mpc^{-1}}\), the value estimated by the latest Planck 2018 result [67].

Fig. 13
figure 13

The plot of deceleration parameter as a function of n for non-interacting two fluid scenario (CASE I)

Full size image

We can see from Fig. (13) that our model is accelerating in case I of the non-interacting scenario as the value of the deceleration parameter is negative throughout the evolution. Whereas in case II, our model is decelerating at all times as the value of the deceleration parameter is constant and positive.

6 Conclusions

In this paper, we have examined a five-dimensional Bianchi type-I cosmological model filled with barotropic fluid and dark energy in a scalar-tensor theory of gravitation proposed by Saez-Ballester (1986). We have derived physical and kinematical parameters for both the interacting and non-interacting scenarios. The observations and conclusions are as follows:

For case I, the spatial volume \(V=0\) at \(t=0\) and it expands exponentially as \(t\rightarrow \infty \) for \(n>0\). Hubble parameter \(H, H_{1}, H_{2}, H_{3}, H_{4}\) and expansion scalar diverge at \(t=0\). Also, they will vanish as t tends to \(\infty \). Since \(\sigma ^{2}=0\), universe is shear free. The model becomes isotropic at all times as \(\frac{\sigma ^{2}}{\theta ^{2}}=0\). Deceleration parameter \(q=0\) for \(n=1\) represents expanding universe with constant velocity. Also, the negative value of deceleration parameter \(q<0\) for \(n>1\) represents accelerated universe. The skewness parameters are zero. jerk parameter becomes zero at \(n=1, 2\) and it becomes positive for \(n>2\). Hence, the model begins with zero volume and than it becomes expanding, shear free, accelerating and isotropic. Singh and Chaubey [52] have investigated four-dimensional Bianchi type-I model with dark energy and barotropic fluid in general relativity which leads to shear free and isotropic model. Although method of solving the field equations is different from what they have adapted in LRS Bianchi-I space-time yet we observed that our model shows similarities with the results obtained by them.

For case II, the spatial volume \(V=0\) at \(t=0\) and it expands as \(t\rightarrow \infty \). Hubble parameters and shear scalar diverges at \(t=0\) and get vanish as \(t \rightarrow \infty \) which is same as case I. Shear scalar also diverges as t tends to \(\infty \) and for \(n=\frac{1}{4}\) it vanishes. Model is anisotropic as \(\frac{\sigma ^{2}}{\theta ^{2}}\) is constant. It will become isotropic for \(n=\frac{1}{4}\). The value of deceleration parameter is positive, therefore the model is decelerating. Jerk parameter stays constant and positive.

The calculated value of the EoS parameter of dark energy for case I and case II shows resemblance with current observational data. Mishra et al. [68, 69] have concluded that compared with string fluid, viscous fluid has a slighter effect on dark energy density as dark energy density attains a small positive value rather than reaches zero. In our model, dark energy density is decreasing function of cosmic time and tends to zero for the case I. Also, this indicates string and barotropic fluids are a little more effective on dark energy comparatively to viscous fluid. But, Dark energy dominates the universe in late times. For case II, the universe is matter dominated for some values of the barotropic EoS parameter. In particular, dark energy dominates the universe in both scenarios. The behavior of dark energy density and EoS parameter of dark energy is almost same in both interacting and non-interacting scenarios. It can be observed that the behavior of these physical parameters is consistent with the results already obtained in the five-dimensional Kaluza-Klien model with dark energy and barotropic fluid in Saez-Ballester theory [57]. Recently, Goswami et al. [70] have studied four-dimensional Bianchi-I universe filled with barotropic fluid and dark energy in general relativity. The cosmological parameters have been estimated by using 38 OHD points and 581 SN Ia data.

Here, the fifth dimensional plays a significant role to understand early evolution of the universe. These two models investigated here are physically stable and show good agreement with recent cosmological data. Thus, the consequences of this investigation might be valuable to get a better understanding of anomalies about the cosmic evolution and existence of dark energy in the universe.