1 Introduction

Over the last two decades, substantial progress has been made in observations of MHD waves in the solar atmosphere due to appearance of new observational facilities. Slow MHD waves have been detected in coronal loops by SOHO/EIT (Berghmans & Clette 1999; De Moortel et al. 2002) and SOHO/SUMER observations (Ofman & Wang 2002; Wang et al. 2003), in polar plumes by UVCS/SOHO (Ofman et al. 1997) and EIT/SOHO observations (Ofman et al. 1999). These observations of MHD waves motivate the development of various theoretical models. In the absence of coronal heating, plasma starts to cool by various mechanisms. The damping mechanisms for slow waves are caused by dissipative effects, namely, thermal conduction, compressive viscosity and radiation. De Moortel & Hood (2003) studied the damping of slow MHD waves in a homogeneous medium by taking into account thermal conduction and compressive viscosity as the damping mechanisms. The behaviour of propagating slow MHD waves in a radiatively cooling homogeneous plasma is investigated by Morton et al. (2010). They found that cooling causes the damping of propagating slow MHD waves. Al-Ghafri et al. (2014) studied the effect of cooling on standing slow MHD waves in hot coronal loops in the presence of thermal conduction and showed that the oscillation period increases with time due to the effect of plasma cooling. The amplitude of oscillations increases in relatively cool coronal loops due to plasma cooling but damping rate enhances in very hot coronal loop oscillations by the cooling. The effect of varying temperature or density background on slow MHD waves has been investigated by several researchers (Aschwanden & Terradas 2008; Ruderman 2011; Al-Ghafri & Erdélyi 2013). The propagation and damping of slow MHD waves in flowing viscous coronal plasma have been studied by Kumar et al. (2016). They showed that the amplitude of velocity perturbation and damping time of slow waves decrease with increase in the value of Mach number. Flow causes an increase in the period of slow waves and phase shift in the perturbed velocity amplitude. Ballester et al. (2016) studied the effect of time-dependent background temperature on prominence oscillations and found that the period of slow waves decreases with time and amplitude of velocity perturbations is damped when background temperature increases with time whereas the period of slow waves increases with time and amplitude of velocity perturbations grows when background temperature decreases with time. Kolotkov et al. (2019) studied the mechanism for the damping of standing slow waves in the solar corona by the misbalance of some heating and cooling processes. They discussed the wave dynamics in the presence of heating, radiative cooling and thermal conduction and found that the wave dynamics is highly sensitive to the characteristic timescales of heating–cooling function. Zavershinskii et al. (2019) studied the role of heating–cooling imbalance in the formation of quasi-periodic slow MHD waves. They have shown that a broadband impulsive driver may excite the formation of quasiperiodicity in slow MHD modes. Recently, Prasad et al. (2021a) have explored the effect of thermal conductivity, compressive viscosity and radiative cooling with and without heating–cooling imbalance on the phase shift of slow waves and found that phase difference is highly dependent on the form of heating function chosen. In an another study, Prasad et al. (2021b) discussed the role of compressive viscosity and thermal conduction on damping of slow waves with and without heating–cooling imbalance in solar coronal loops. They found that damping of fundamental mode of oscillations in shorter and super-hot loops enhances significantly with the inclusion of compressive viscosity along with thermal conductivity and pointed out that in the presence of heating–cooling, thermal conductivity plays a dominant role. So, we aim to extend the work of Ballester et al. (2016) to investigate the effect of heating–cooling imbalance on the behaviour of slow MHD waves in an unbounded solar plasma in which background temperature varies with time by considering thermal conduction and optically thin radiation as damping mechanisms.

In this paper, we study the effect of heating–cooling imbalance on slow magnetohydrodynamic waves in solar coronal loops taking into account time-varying background temperature and optically thin radiation and thermal conduction. The plan of the paper is as follows. In Section 2, we model the problem for studying slow waves in solar coronal loops in terms of basic governing equations. We linearise the basic equations and then Fourier decompose to solve them. In Section 3, we numerically solve the equations to show the temporal behaviour of normalised velocity amplitude of slow waves for time-varying background temperature in interesting typical situations arising in solar coronal loops and discuss the results obtained.

2 The model and governing equations

We consider solar coronal plasma with time-varying background temperature in the presence of thermal conduction, optically thin radiation and heating permeated by a uniform magnetic field which is aligned along the z-axis. The governing MHD equations describing the solar coronal plasma motion are mass conservation equation, momentum conservation equation, induction equation, energy equation, ideal gas equation and solenoid constraint are given as follows (Priest 2014; Ballester et al. 2016).

The mass conservation equation:

$$\begin{aligned} \frac{\partial \rho }{\partial t}+ \nabla \cdot ({\rho \mathbf{v}})=0. \end{aligned}$$
(1)

The momentum conservation equation:

$$\begin{aligned} \rho \left( \frac{\partial }{\partial t}+\mathbf{v}\cdot \nabla \right) \mathbf{v}+\nabla p= \frac{(\nabla \times \mathbf{B})\times \mathbf{B}}{\mu _0}. \end{aligned}$$
(2)

The induction equation:

$$\begin{aligned} \frac{\partial \mathbf{B}}{\partial t}=\nabla \times (\mathbf{v} \times \mathbf{B}). \end{aligned}$$
(3)

The energy equation:

$$\begin{aligned} \frac{R}{\tilde{\mu }}\rho ^{\gamma }\left[ \frac{\partial }{\partial t}\frac{T}{\rho ^{\gamma -1}}+(\mathbf{v}\cdot \nabla )\frac{T}{\rho ^{\gamma -1}}\right] =-(\gamma -1)L. \end{aligned}$$
(4)

The ideal gas equation:

$$\begin{aligned} p=\frac{R}{\tilde{\mu }}\rho T. \end{aligned}$$
(5)

Solenoidal constrain:

$$\begin{aligned} \nabla \cdot \mathbf{B}=0. \end{aligned}$$
(6)

Here \(\mathbf{v}\), \(\mathbf{B}\), \(\rho \), p and T denote the velocity, magnetic field, density, gas pressure and temperature, respectively; R is gas constant, \(\tilde{\mu }\) is mean molecular weight, \(\gamma \) is the ratio of specific heats and \(\mu _0\) is the magnetic permeability of free space. The symbol L is given by

$$\begin{aligned} L=-\nabla \cdot (\kappa _\parallel \nabla T)+L_r - H, \end{aligned}$$
(7)

comprising radiation and heating terms \(L_r\) and H, respectively. The first term in Equation (7) represents the thermal conduction term where the symbol \(\kappa _\parallel \) denotes the component of conductivity tensor along the magnetic field and it is approximated in solar atmosphere as \(\kappa _\parallel =\kappa _0 T_0^{5/2}=10^{-11}T_0^{5/2}\) W m\(^{-1}\) K\(^{-1}\). Following Ballester et al. (2016), we assume that radiation term \(L_r\) is proportional to plasma temperature, that is, \(L_r=aT\). The heating term is \(H=h\rho ^b T^c\), where b and c are constants. For heating by coronal current dissipation (\(b=1\) and \(c=1\)), the heating function H can be written as \(H=h\rho T\). The background magnetic field \(\mathbf{B}_\mathbf{0}\) is considered to be uniform and horizontal, \(\mathbf{B}_\mathbf{0} = B_0 \hat{z}\). The background state for this problem can be described as

$$ T_0= T_0(t), \ p_0=p_0(t), \ \rho _0=\mathrm{const.}, \ B_0=\mathrm{const.} $$
(8)

Here \(T_0\), \(p_0\), \(\rho _0\) and \(B_0\) are the background quantities representing the temperature, pressure, density and magnetic field, respectively. Assuming that there is no background flow, the MHD equations determining the background plasma state reduce to

$$\rho _0=\mathrm{const.}, \ \mathbf{v}_\mathbf{0}=0, \ \nabla p_0 =0, \ p_0=\frac{R}{\tilde{\mu }}\rho _0 T_0, $$
$$\begin{aligned}&\frac{R}{\tilde{\mu }}\rho _0\frac{\mathrm{d}T_0}{\mathrm{d}t}=-(\gamma -1)L. \end{aligned}$$
(9)

In equilibrium state, \( L_r=aT_0(t)\). Imposing \(T_{0i}\) as the initial temperature, we obtain from Equation (9)

$$\begin{aligned} T_0=T_{0i} {\exp }\left( \frac{-t}{\tau }\right) , \end{aligned}$$
(10)

where \(\tau =({R\rho _0})/({(\gamma -1)\tilde{\mu }(a-h\rho _0)})\) is the characteristic time that governs the rate at which plasma temperature is changing.

Considering small perturbations from the equilibrium, the field quantities can be written as

$$\mathbf{B=B_0+B_1(r,t)}, \ \mathbf{v}=\mathbf{0}+ {\mathbf{v_1}}({\mathbf{r}},t), \ p=p_0(t)+p_1({\mathbf{r}},t),\ \rho =\rho _0+\rho _1({\mathbf{r}},t), \ {T}=T_0(t)+T_1({\mathbf{r}},t) $$

where the subscripts ‘0’ and ‘1’ refer to equilibrium and perturbed quantities, respectively.

Taking into consideration the motion and propagation in the plane, the linearised MHD equations are

$$\begin{aligned}&\frac{\partial \rho _1}{\partial t}+ \rho _0\left( \frac{\partial v_{1x}}{\partial x}+\frac{\partial v_{1z}}{\partial z}\right) =0, \end{aligned}$$
(11)
$$\begin{aligned}&\rho _0 \frac{\partial \mathbf{v_1}}{\partial t}=-\nabla p_1+ \frac{1}{\mu _0}(\nabla \times \mathbf{B_1})\times \mathbf{B_0}, \end{aligned}$$
(12)
$$\begin{aligned}&\frac{\partial B_{1x}}{\partial t}=B_0 \frac{\partial v_{1x}}{\partial z},\end{aligned}$$
(13)
$$\begin{aligned}&\frac{\partial B_{1z}}{\partial t}=-B_0\frac{\partial v_{1x}}{\partial x},\end{aligned}$$
(14)
$$\begin{aligned}&\frac{R}{\tilde{\mu }}\left[ \rho _1\frac{\partial T_0}{\partial t}+\rho _0\frac{\partial T_1}{\partial t}+(\gamma -1)\rho _0T_0 \left( \frac{\partial v_{1x}}{\partial x}+\frac{\partial v_{1z}}{\partial z}\right) \right] \nonumber \\&=-(\gamma -1)(aT_1-\kappa _0T_0^{5/2}\nabla ^2 T_1-h\rho _0T_1-h\rho _1T_0),\end{aligned}$$
(15)
$$\begin{aligned}&p_1=\frac{R}{\tilde{\mu }}(\rho _0 T_1+\rho _1 T_0). \end{aligned}$$
(16)

Here we have considered the heating by coronal current dissipation so the heating function H is taken as \(H=h\rho T\). As we aim to study slow waves, we consider the perturbed velocity component \(v_{1z}\), parallel wave number \(k_z\) and \(T_0(t)\) only and take perpendicular wave number \(k_x=0\) in the following analysis. So the spatial and temporal dependence of the perturbed quantities can be expressed as

$$\begin{aligned} f_1(x, z, t)=f_1(t) \,\mathrm{e}^{\mathrm{i}k_z z}, \end{aligned}$$
(17)

where \(f_1(t)\) is time-dependent amplitude of the perturbations. Using Equation (17), the linearised Equations (11)–(16) become

$$\begin{aligned}&\frac{\partial \rho _1}{\partial t}=-\mathrm{i}k_z \rho _0 v_{1z},\end{aligned}$$
(18)
$$\begin{aligned}&\frac{\partial v_{1z}}{\partial t}=\frac{-\mathrm{i}k_z p_1}{\rho _0},\end{aligned}$$
(19)
$$\begin{aligned}&\rho _1\frac{\partial T_0}{\partial t}+\rho _0\frac{\partial T_1}{\partial t}+\mathrm{i}(\gamma -1)\rho _0T_0 k_z v_{1z}=-\frac{\rho _0 T_1}{\tau }\nonumber \\&\quad -(\gamma -1)\frac{\tilde{\mu }\kappa _0T_0^{5/2}k_z^2T_1}{R} +(\gamma -1)\frac{\tilde{\mu }h \rho _1T_0}{R}, \end{aligned}$$
(20)
$$\begin{aligned}&p_1=\frac{R}{\tilde{\mu }}(\rho _0 T_1+\rho _1 T_0). \end{aligned}$$
(21)

System of Equations (18)–(21) is the required set of equations in order to study the effect of heating–cooling imbalance on slow waves propagating in time-varying background temperature plasma with thermal conduction and optically thin radiation. If we consider the constant heating, the above system of Equations (18)–(21) reduces to the system of Equations (19)–(22) of Ballester et al. (2016).

3 Results and discussion

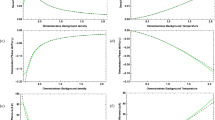
We solve the above set of Equations (18)–(21) numerically for an interesting situation in coronal loops having density \(\rho _0 = 5 \times 10^{-11}\) kg m\(^{-3}\) and temperature \(T_{0i} = 10,000\) K. We set the initial conditions as \(v_{1z}(0)= 1\), \(\rho _1(0) = 0\) and \(T_1(0) =0\) to study the effect of heating–cooling imbalance on slow waves. We consider heating function H for two cases by taking (i) \(H =\mathrm{constant}\) and (ii) \(H=h\rho T \). Variations of normalised velocity amplitudes with time for increasing and decreasing time-dependent background temperatures with characteristic time \(\tau =1000\) s, 3000 s taking heating \(H = \mathrm{constant}\) (blue) and \( H=h\rho T\) (red) in the presence of thermal conduction are shown in Figures 1–4.

Figure 1
figure 1

Temporal behaviour of normalised velocity amplitude when background temperature increases with time, \(\tau =3000\) s, \(H =\mathrm{constant}\) (blue) and \(H=h\rho ^b T^c\) \((b=1, c=1)\) (red).

Full size image

The temporal behaviour of normalised perturbed velocity of slow wave for considered coronal plasma structure whose background temperature increases with time in the case of \(\tau =3000\) s, \(H = \mathrm{constant}\) and \(H=h\rho T\) is shown in Figure 1. It is observed from Figure 1 that heating–cooling imbalance for different H influences the damping of slow mode and it does not alter the period of slow mode. Amplitudes of velocity decrease with the increase in time. Figure 2 shows the behaviour of normalised perturbed velocity amplitude of slow wave with time in the case of decaying background temperature, \(\tau =3000\) s, \(H = \mathrm{constant}\), \( H=h\rho T\). In this case, it is found that the amplitudes of perturbed velocity are growing with time but period of slow waves remains the same for both the values of heating function H. It can be seen from Figures 1 and 2 that the amplitude of normalised velocity for constant heating function H is smaller than the amplitude of normalised velocity for heating function \(H=h\rho T\).

Figure 2
figure 2

Temporal behaviour of normalised velocity amplitude when background temperature decreases with time, \(\tau =3000\) s, \(H = \mathrm{constant}\) (blue) and \( H=h\rho ^b T^c\) \((b=1, c=1)\) (red).

Full size image
Figure 3
figure 3

Temporal behaviour of normalised velocity amplitude when background temperature increases with time, \(\tau =1000\) s, \(H =\mathrm{constant}\) (blue) and \(H=h\rho ^b T^c\) \((b=1, c=1)\) (red).

Full size image

Figures 3 and 4 are plotted for showing the temporal behaviour of normalised velocity amplitudes of slow waves for increasing and decreasing time-dependent background temperature with \(\tau =1000\) s and heating \(H =\mathrm{constant}\), \( h\rho T\). Figure 3 depicts that amplitudes of normalised velocity of slow wave decrease sharply with time when we consider \(\tau =1000\) s instead of \(\tau =3000\) s as taken in Figure 1. In this case, the damping of slow wave is more prominent than the damping shown in Figure 1. For \(H = \mathrm{constant}\), amplitude of velocity is smaller than the amplitude of velocity for \(H = h\rho T\). Figure 4 shows that the damping of waves for \(\tau =1000\) s is stronger than the damping of waves in the case \(\tau =3000\) s for decaying-background temperature plasma.

Figure 4
figure 4

Temporal behaviour of normalised velocity amplitude when background temperature decreases with time, \(\tau =1000\) s, \(H = \mathrm{constant}\) (blue) and \(H= h\rho ^b T^c\) \((b=1, c=1)\) (red).

Full size image