1 Introduction

Observation made by SUMER instrument on board SoHO confirms that longitudinal standing (slow) magneto-acoustic waves have been seen to suffer a rapid damping (Kliem et al. 2002; Wang et al. 2002, 2003). Modelling for observed oscillations by SUMER have been carried out by Taroyan et al. (2007), where excitation and damping mechanisms are investigated. It also presents how standing and propagating slow MHD waves can be differentiated from each other. The issue of fast damping is still obscure and attracts a remarkable attention to understand the dominant method of damping. The most nominated mechanisms for damping the standing longitudinal oscillations are thermal conduction, radiation and viscosity (Ofman & Wang 2002; De Moortel & Hood 2003; Mendoza-Briceño et al. 2004; Taroyan et al. 2005; Sigalotti et al. 2007; Al-Ghafri & Erdélyi 2013; Al-Ghafri et al. 2014). Radiation is found to dominate the damping of cool coronal loops, whereas hot loops are damped by thermal conduction. For a recent review of standing slow waves in coronal loops, see Wang (2011).

Plasma cooling has been detected everywhere in the solar atmosphere (Viall & Klimchuk 2012; 2013). In the absence of coronal heating, the plasma starts to cool by radiation and thermal conduction (Klimchuk 2012). For example, Aschwanden & Terradas (2008) have shown that the coronal loops are cooling with the characteristic cooling time of the order of a few oscillation periods. Morton & Erdélyi (2009, 2010) and Ruderman (2011a, b) investigated the effect of cooling on kink oscillations of coronal loop. They found that the kink oscillations experience an amplification due to cooling. Further to this, propagating slow MHD waves in a homogeneous, radiatively cooling plasma was studied by Morton et al. (2010). Essentially, plasma cooling is reported to cause a strong damping for longitudinal slow MHD waves. Recently, Erdélyi et al. (2011) investigated the behaviour of longitudinal magneto-acoustic oscillations in slowly varying coronal plasma. In particular, the damping rate is found to undergo a reduction by the emergence of cooling.

Al-Ghafri & Erdélyi (2013) and Al-Ghafri et al. (2014) have studied the effect of cooling on standing slow MHD waves in hot coronal loops that are damped due to thermal conduction. In particular, the plasma cooling is assumed by unspecified thermodynamic source. The individual effect of cooling is found to amplify the amplitude of oscillating loops. Although the rate of damping caused by thermal conduction increases at the beginning, it is noticed to reduce gradually in a hot corona because of plasma cooling. As thermal conduction approaches infinity, the damping rate tends to zero. Hence, slow magnetosonic waves propagate almost without damping at the slower, isothermal sound speed.

The present article discusses the combined effects of radiative cooling and thermal conduction on damping longitudinal standing MHD waves. A function with a simple form representing the radiation mechanism is taken to ensure that the plasma temperature decreases exponentially with time according to observations. The cooling is assumed to be weak, with the characteristic cooling time scale much larger than the oscillation period. The paper is structured as follows: In Section 2 we present our model and derive the main governing equation with boundary conditions. The analytical results are obtained with the aid of the WKB theory in Section 3. In Section 4 the individual and combined effects of radiation and thermal conduction are studied by displaying the analytical solution numerically. Our discussions and conclusions are presented in Section 5.

2 The model and governing equations

We model a straight coronal loop, in which the magnetic field is uniform and in the z-direction, i.e. \(\mathbf {B}_{0}=B_{0}\hat {\mathbf {z}}\). The magnetic loop is of length L, with its ends at z=±L/2 . The background plasma temperature (pressure) is assumed to change as a function of time due to radiative cooling; the density is a constant.

The governing MHD equations for the background plasma take the following form

$$\begin{array}{@{}rcl@{}} &&\frac{\partial{\rho}}{\partial{t}}+\nabla.(\rho\mathbf{v}) =0, \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} &&\rho\frac{\partial{\mathbf{v}}}{\partial{t}}+\rho(\mathbf{v}.\nabla)\mathbf{v}=-\nabla{p}+\frac{1}{\mu_{0}}(\nabla\times\mathbf{B})\times\mathbf{B}, \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} &&\frac{R}{\tilde\mu}\frac{\rho^{\gamma}}{(\gamma-1)}\left[\frac{\partial{}}{\partial{t}}\frac{T}{\rho^{\gamma-1}} +(\mathbf{v}.\nabla)\frac{T}{\rho^{\gamma-1}}\right]=\nabla(\kappa_{\|}\nabla{T})-\rho^{2}Q(T) , \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} &&{p}=\frac{R}{\tilde\mu}\rho{T}, \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} &&\frac{\partial{\mathbf{B}}}{\partial{t}}=\nabla\times(\mathbf{v}\times\mathbf{B}). \end{array} $$
(5)

Here, v, B, ρ, p and T represent the flow velocity, magnetic field, density, pressure and temperature, respectively; μ 0 is the magnetic permeability of free space, R is the gas constant, \(\tilde {\mu }\) is the mean molecular weight and γ is the ratio of specific heats. The thermal conduction term is ∇(κ ∥∇T), where κ ∥=κ 0 T 5/2 and ρ 2 Q(T) is the general radiation term for optically thin losses.

Note that the radiative loss function is approximated by a piecewise continuous function (Rosner et al. 1978; Priest 2000), but it is assumed here to take a simple form to match the observed cooling as described below. The observation shows that the radiative cooling coronal loops are cooling exponentially (Aschwanden & Terradas 2008; Morton & Erdélyi 2009, 2010) and the cooling profile has the form

$$ T=T_{0i}\exp\left( -\frac{t}{\tau_{\mathrm{c}}}\right), $$
(6)

where T 0i is the initial temperature at t=0 and τ c is the cooling time scale.

In order to match the observed exponential cooling of the background plasma, Erdélyi et al. (2011) assigned thermal conduction to be the essential cause of cooling in their model. Further to this, an unspecified thermodynamic source for creating the plasma cooling was suggested by Al-Ghafri & Erdélyi (2013) and Al-Ghafri et al. (2014), to investigate longitudinal MHD waves in dissipative time-dependent plasma. Moreover, Morton et al. (2010) assumed that the plasma is cooling radiatively and the radiative loss function has the form δ p, where the loss term is assumed to follow the Newton cooling. Hence, we assume here that the radiation term ρ 2 Q(T)∼δ p. Therefore, the background plasma state with no background flow satisfies the equations

$$\begin{array}{@{}rcl@{}} &&v_{0}=0,\;\qquad\rho_{0}=\text{const}.,\;\Longrightarrow\; \nabla p_{0}=0, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} &&p_{0}=\frac{R}{\tilde{\mu}}\rho_{0}T_{0},\qquad {\text{i.e.}}\quad p_{0}\sim T_{0}, \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} &&\frac{R}{\tilde\mu}\rho_{0}\frac{\mathrm{d}{T_{0}}}{\mathrm{d}{t}} =-\delta p_{0}, \;\Longrightarrow\; \frac{\mathrm{d}{T_{0}}}{\mathrm{d}{t}}=-\delta T_{0}, \end{array} $$
(9)

where the 0 index denotes background quantity and δ is a small quantity. Equation (9) gives the solution

$$ T_{0}=T_{0i}\exp(-\delta t). $$
(10)

Comparing eq. (10) with eq. (6), it is obtained that δ=1/τ c and this gives a justification of taking δ to be small, where the observed cooling times are 500 s<τ c<2000 s (Morton et al. 2010).

Now, we linearise the governing eqs (1)–(5) about the background state by writing all the variables in the form

$$f(z,t)=f_{0}(t)+f_{1}(z,t), $$

and neglecting nonlinear terms, where the subscript 1 indicates the perturbed quantities. Thus, the linearised MHD equations for the longitudinal motion can be reduced to

$$ \frac{\partial^{2}{v}_{1}}{\partial t^{2}}-\frac{\gamma p_{0}}{\rho_{0}}\frac{\partial^{2}{v}_{1}}{\partial z^{2}} =-(\gamma-1)\frac{\kappa_{0} T_{0}^{5/2}}{\rho_{0}}\frac{\partial^{3}T_{1}}{\partial z^{3}}-\delta\frac{\partial v_{1}}{\partial t}. $$
(11)

It is more convenient to use the non-dimensional variables to solve the governing eq. (11). Hence, we introduce the dimensionless quantities

$$ \tilde{t}=\frac{t}{P},\quad \tilde{z}=\frac{z}{L},\quad \tilde{c}_{s} = \sqrt{\frac{T_{0}}{T_{0i}}}, \quad \tilde{v}_{1} = \frac{{v}_{1}}{c_{si}}, \quad \tilde{T}_{1}=\frac{T_{1}}{T_{0i}}, \quad c_{si}^{2} = \frac{\gamma RT_{0i}}{\tilde{\mu}}, $$
(12)

where P is the period of the loop oscillation, \(\tilde {c}_{s}\) is the dimensionless sound speed, c s i is the initial sound speed, and we put P=L/c s i . In what follows, we drop the tilde.

Applying non-dimensionalisation for eq. (11), we arrive at

$$ \frac{\partial^{2}{v}_{1}}{\partial t^{2}}-{c_{s}^{2}}\frac{\partial^{2}{v}_{1}}{\partial z^{2}} =-\frac{\sigma}{\gamma}{c_{s}^{5}}\frac{\partial^{3}T_{1}}{\partial z^{3}}-\epsilon\frac{\partial v_{1}}{\partial t}. $$
(13)

Here, the dimensionless constants σ and 𝜖 represent the strength of thermal conduction and radiation, and are defined by

$$ \sigma=\frac{(\gamma-1)\tilde{\mu}\kappa_{0}\,T^{5/2}_{0i}} {RL\sqrt{\gamma\, p_{0i}\,\rho_{0}}}, \qquad \epsilon=P\delta. $$
(14)

Both quantities σ and 𝜖 are found to be small under standard coronal conditions, in which γ=5/3, \(\tilde {\mu } \approx 0.6\), R=8.3×103 m2 s−2 K−1, and \(\kappa _{0} \approx 10^{-11}\,\textmd {m}^{2}\,\textmd {s}^{-1}\,\textmd {K}^{-5/2}\). If we take L=100 Mm and T 0i =0.6– 5 MK as typical coronal values, then we obtain \(0.0068 \lesssim \sigma \lesssim 0.48\).

Now, the governing eq. (13) can be written in the form of wave-like equation as

$$ \frac{\partial}{\partial t}\left[\frac{1}{{c^{7}_{s}}}\left( \frac{\partial^{2}{v}_{1}}{\partial t^{2}}-{c_{s}^{2}}\frac{\partial^{2}{v}_{1}}{\partial z^{2}}\right)\right] = \frac{\sigma}{\gamma}\frac{\partial}{\partial z^{2}} \left[\gamma\frac{\partial}{\partial t}\left( \frac{1}{{c_{s}^{2}}}\frac{\partial v_{1}}{\partial t}\right)-\frac{\partial^{2}v_{1}}{\partial z^{2}}\right] - \epsilon\frac{\partial}{\partial t} \left( \frac{1}{{c_{s}^{7}}}\frac{\partial v_{1}}{\partial t}\right). $$
(15)

Because we are interested in investigating the damping of standing waves, it is necessary to introduce the boundary conditions at z=±1/2. Therefore, as the loop ends are embedded in the dense photosphere, it is suitable to assume that the perturbed velocity vanishes at these ends,

$$ v_{1} = 0 \quad \text{at} ~ z = \pm 1/2 . $$
(16)

In case of 𝜖=σ=0 (i.e. in the absence of radiative cooling and thermal conduction), eq. (15) represents a simple wave equation with constant sound speed (see Al-Ghafri & Erdélyi 2013). The effect of cooling and thermal conduction on longitudinal slow MHD waves will be investigated in the next section.

3 Analytical solution

Now, we aim to solve the governing eq. (15) using the WKB method. Thus, we need to introduce two slow variables, t 1=𝜖 t and \(\sigma =\epsilon \tilde {\sigma }\), so eq. (15) becomes

$$\begin{array}{@{}rcl@{}} \frac{\partial}{\partial t_{1}}\left[\frac{1}{{c^{7}_{s}}}\left( \epsilon^{2}\frac{\partial^{2}{v}_{1}}{\partial {t_{1}^{2}}}-{c_{s}^{2}}\frac{\partial^{2}{v}_{1}}{\partial z^{2}}\right)\right] &=& \frac{\tilde{\sigma}}{\gamma}\frac{\partial}{\partial z^{2}} \left[\gamma\epsilon^{2}\frac{\partial}{\partial t_{1}}\left( \frac{1}{{c_{s}^{2}}}\frac{\partial v_{1}}{\partial t_{1}}\right)-\frac{\partial^{2}v_{1}}{\partial z^{2}}\right]\\ &&-\epsilon^{2}\frac{\partial}{\partial t_{1}} \left( \frac{1}{{c_{s}^{7}}}\frac{\partial v_{1}}{\partial t_{1}}\right). \end{array} $$
(17)

Then, the WKB theory implies that the solution to eq. (17) has the form

$$ v_{1}(z,t_{1}) = Q(z,t_{1})\exp(\mathrm{i}\epsilon^{-1}{\Theta}(t_{1})), $$
(18)

where the function Q is expanded in power series with respect to 𝜖, i.e.,

$$ Q = Q_{0} + \epsilon\, Q_{1} + {\cdots} . $$
(19)

Substituting eqs (18) and (19) into eq. (17), and taking the largest order terms in 𝜖 (order of 𝜖 −3) we obtain

$$ \frac{\partial^{2}Q_{0}}{\partial z^{2}}+\frac{\omega^{2}}{{c_{s}^{2}}}Q_{0}=0, $$
(20)

where ω=dΘ/dt 1 and Q 0 is subject to the boundary conditions

$$ Q_{0}=0 \qquad \text{at}~ z=\pm\frac{1}{2}, $$
(21)

according to eq. (16). The general solution to the boundary-value problem, eqs (20) and (21), can be given by the Fourier series, in the form

$$ Q_{0}(z,t_{1})=\sum\limits_{n=0}^{\infty} A_{n}(t_{1})\cos\left( (2n+1)\pi z\right), \quad \omega_{n}=(2n+1)\pi c_{s},\quad n=0,1,2,\ldots. $$
(22)

In this study, we are only interested in the fundamental longitudinal mode corresponding to n=0. Thus, eq. (22) reduces to

$$ Q_{0}(z,t_{1})=A(t_{1})\cos\left( \pi z\right), \qquad \omega=\pi c_{s}, $$
(23)

where A=A 0 and ω=ω 0. Function A(t 1) refers to the amplitude of standing oscillation. In order to find the function A(t 1), we collect terms of the order of 𝜖 −2. Then, we obtain the equation

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}Q_{1}}{\partial z^{2}}+\frac{\omega^{2}}{{c_{s}^{2}}}Q_{1}&=&\frac{\mathrm{i}}{{c_{s}^{2}}}\left[\left( \frac{9}{2}\omega+3\frac{\mathrm{d}\omega}{\mathrm{d} t_{1}}+ \tilde{\sigma}\omega^{3} {c_{s}^{3}} \right)Q_{0}+3\omega\frac{\partial Q_{0}}{\partial t_{1}}\right.\\ &&\left.+\frac{5}{2}\frac{{c^{2}_{s}}}{\omega}\frac{\partial^{2}Q_{0}}{\partial z^{2}}+\frac{{c^{2}_{s}}}{\omega}\frac{\partial^{3}Q_{0}}{\partial t_{1}\partial z^{2}}- \frac{\tilde{\sigma}}{\gamma}\frac{{c^{7}_{s}}}{\omega}\frac{\partial^{4}Q_{0}}{\partial z^{4}} \right], \end{array} $$
(24)

where the function Q 1 satisfies the boundary conditions

$$ Q_{1}=0 \qquad \text{at}~ z=\pm\frac{1}{2}. $$
(25)

The Sturm-Lioville problem, eqs (24) and (25), has a non-trivial solution when the right-hand side of eq. (24) satisfies the compatibility condition. To obtain the compatibility condition, we multiply eq. (24) by Q 0, integrate with respect to z over [−1/2,1/2], and use the integration by parts. Hence, we arrive at

$$\begin{array}{@{}rcl@{}} &&{\int}_{-1/2}^{1/2}\frac{\mathrm{i}}{{c_{s}^{2}}}\left[\left( \frac{9}{2}\omega+3\frac{\mathrm{d}\omega}{\mathrm{d} t_{1}}+ \tilde{\sigma}\omega^{3} {c_{s}^{3}}\right){Q_{0}^{2}}+3\omega\, Q_{0}\frac{\partial Q_{0}}{\partial t_{1}} +\frac{5}{2}\frac{{c^{2}_{s}}}{\omega}Q_{0}\frac{\partial^{2}Q_{0}}{\partial z^{2}}\right.\\ &&\qquad\qquad\qquad\left.+\frac{{c^{2}_{s}}}{\omega}Q_{0}\frac{\partial^{3}Q_{0}}{\partial t_{1}\partial z^{2}}- \frac{\tilde{\sigma}}{\gamma}\frac{{c^{7}_{s}}}{\omega}Q_{0}\frac{\partial^{4}Q_{0}}{\partial z^{4}}\right]\mathrm{d} z=0. \end{array} $$
(26)

The solution to eq. (26), with the aid of eq. (23), gives the amplitude of standing wave in the form

$$ A(t_{1})=A(0)\exp\left( \frac{-1}{4}t_{1}+\frac{\tilde{\sigma}}{5}\left( \frac{\gamma-1}{\gamma}\right)\pi^{2}\,[{c_{s}^{5}}(t_{1})-1]\right). $$
(27)

This equation in terms of the scaled variables can be written as

$$ A(t)=A(0)\exp\left( \frac{-\epsilon}{4}t+\frac{\sigma}{5\epsilon}\left( \frac{\gamma-1}{\gamma}\right)\pi^{2}\,[{c_{s}^{5}}(t)-1]\right), $$
(28)

where \({c_{s}^{5}}(t)=\exp (-5\epsilon t/2)\). In case of 𝜖=0, it can be rid of the quantity 𝜖, in the denominator of the second term in the exponent, using Taylor expansion for the sound speed.

4 Numerical evaluations

In this section, the analytical solution describing the temporal evolution of longitudinal standing-mode amplitude are studied using numerical evaluations. Typical coronal conditions are exploited to calculate the wave amplitude numerically. Then, the results are depicted to show the behaviour of MHD waves in radiatively cooling coronal loops.

4.1 The effect of radiative cooling

In the absence of thermal conduction (σ=0), eq. (28) reduces to

$$ A(t)=A(0)\exp\left( \frac{-\epsilon}{4}t\right). $$
(29)

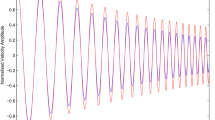
It is clear from eq. (29), that the amplitude of oscillating loops decreases with time due to radiative cooling. To give more insight into amplitude variations, we take 𝜖∈[0,0.5] as typical values for solar corona. Figure 1 shows that the cooling causes a strong damping for the coronal loops. This result is applicable to TRACE loops with temperature T 0=1 − 2 MK, where radiation is the dominant damping mechanism.

Figure 1
figure 1

The amplitude of the standing wave with different values of 𝜖 (0.0,0.1,0.3,0.5) representing the effect of the cooling on the amplitude of standing wave. The time is measured in units of L/c s i .

Full size image

In contrast with the result obtained by Al-Ghafri & Erdélyi (2013), who assumed the cooling by unspecified thermodynamic source, the cooling by radiation brings about an attenuation in the amplitude of waves, where a strong cooling (𝜖=0.5) leads to a strong damping.

4.2 The effect of thermal conduction

In the absence of cooling (𝜖=0) eq. (28), after using Taylor expansion for the sound speed, becomes

$$ A(t)=A(0)\exp\left( -\frac{\sigma}{2}\left( \frac{\gamma-1}{\gamma}\right)\pi^{2}\,t\right). $$
(30)

This expression is consistent with its counterpart in Al-Ghafri & Erdélyi (2013). The amplitude of oscillation is damped and the strength of damping depends on the value of thermal conduction, σ. Taking into account that thermal conduction, σ, is calculated in an order of 𝜖 to obtain the amplitude expression, eq. (30) is physically applicable for a small σ. This means that eq. (30) determines the influence of weak thermal conduction, σ≪1. The variations of amplitude are studied on initial temperatures T 0=[0.6,1,3,5]6 K, which correspond to σ=[0.0068, 0.019,0.17,0.48].

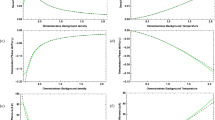
In Figure 2, we present the effect of varying the magnitude of the thermal conduction, σ, on the damping rate of the standing acoustic wave. As we can see, the increase of thermal conduction gives rise to a strong decline in the amplitude of standing oscillations, due to the presence of thermal conduction. This result is mostly expected because thermal conduction is the essential cause of damping for the observed hot coronal loops, especially in the region of temperature T 0≥3 MK.

Figure 2
figure 2

The amplitude of the standing wave with different values of σ (0.0068,0.019, 0.17,0.48) representing the effect of thermal conduction on the amplitude of standing wave. The time is measured in units of L/c s i .

Full size image

4.3 Combined effects of radiative cooling and thermal conduction

We now investigate the combined effects of radiation and thermal conduction on damping the amplitude of standing slow magneto-acoustic oscillations in radiatively cooling coronal loops using eq. (28).

The temporal evolution of longitudinal standing-mode amplitude for various values of 𝜖 and the initial loop temperature is exhibited in Figure 3. We can see a remarkable change in the wave amplitude for different temperature regions. For example, Figures 3(a) and 3(b) indicate that the emergence of cooling enhances the rate of damping caused by thermal conduction for loops with temperature T 0≤1 MK. On the other hand, the damping rate of wave amplitude starts to decrease due to the plasma cooling when the loop temperature approaches 3 MK onwards, and the reduction in damping grows quickly by increasing the amount of cooling. However, the state of damping is still rising strongly with time, in the absence of cooling, as displayed in Figures 3(c) and 3(d).

Figure 3
figure 3

The dependence of the oscillation amplitude on time. Panels (a), (b), (c) and (d) correspond to T 0i =0.6 MK (σ=0.0068), T 0i =1 MK (σ=0.019), T 0i =3 MK (σ=0.17) and T 0i =5 MK (σ=0.48), respectively. The time is measured in units of L/c s i .

Full size image

Overall, the scenario of damping in loops with temperature more than 3 MK is in agreement with that obtained by Al-Ghafri et al. (2014).

5 Discussion and conclusion

In this paper, we have investigated the damping of standing longitudinal MHD waves due to radiation and thermal conduction in cooling coronal loops. The plasma cooling is assumed because of radiation method. The radiative function is postulated to have the form δ p, to match the observed cooling, which has approximately an exponential profile. Subsequently, the temperature in the loop decreases exponentially with the characteristic time scale, which is much longer than the characteristic oscillation period. The assumption of the low-beta plasma reduces the MHD equations to one-dimensional system for standing acoustic waves. We have used the WKB theory to obtain an analytic solution for the governing MHD equations.

Typical coronal conditions are applied to evaluate the evolution of amplitude with time numerically. The results show that the radiative cooling enhances the damping rate of coronal loops with temperature T 0≤1 MK, while in the region of temperature T 0≥3 MK, the damping is reduced gradually by cooling. In comparison with radiation mechanism, it is found that thermal conduction is not sufficient to cause a strong damping for very cool loops. However, the damping of hot coronal loops are mainly dominated by thermal conduction, where the amplitude of standing slow MHD waves experiences a rapid damping with time due to lack of cooling.

According to the results, the rate of damping of coronal oscillations seems to increase continuously with time, until reaching its maximum in the region of temperature \(4\lesssim T \lesssim 6\) MK, and then decreases afterward. Eventually, slow magnetosonic waves will propagate almost without damping when thermal conduction approaches infinity.