1 Introduction

The mathematical aspects related to the variational formulation, existence and uniqueness, finite element discretization of boundary value problems for elastodynamics can be found in [12, 23, 37, 61, 64, 76]. General mechanical formulations in computational structural dynamics, vibration and substructuring techniques can be found in [6, 8, 10, 22, 29, 52]. In structural dynamics and coupled problems such as fluid-structure interaction, general computational methods can also be found in [11, 19, 28, 32, 45, 57, 88] and algorithms for solving large eigenvalue problems in [18, 70, 75]. For computational structural dynamics in the low- and medium-frequency ranges and extensions to structural acoustics, we refer the reader to [62, 65] and for uncertainty quantification (UQ) in computational structural dynamics to [78].

The problem considered here is the construction of a reduced-order model for linear vibration of a dissipative structure subjected to prescribed forces and composed of two main linear dissipative substructures connected through a physical flexible viscoelastic interface (linking substructure).

Let us recall that the concept of substructures was first introduced by Argyris and Kelsey in [5] and by Przemieniecki in [71] and was extended by Guyan and Irons in [30, 41]. In Hurty [38, 39] considered the case of two substructures coupled through a geometrical interface, for which the first substructure is represented using its elastic modes with fixed geometrical interface and the second substructure is represented using its elastic modes with free geometrical interface completed by static boundary functions of the first substructure. Finally, Craig and Bampton in [21] adapted the Hurty method in order to represent each substructure of the same manner consisting in using the elastic modes of the substructure with fixed geometrical interface and the static boundary functions on its geometrical interface. Improvements have been proposed with many variants [1, 7, 9, 15, 17, 27, 31, 35, 47, 53, 54, 83, 87], in particular for complex dynamical systems with many appendages considered as substructures (such as disk with blades) Benfield and Hruda in [13] proposed a component mode substitution using the Craig and Bampton method for each appendage. Another type of methods has been introduced in order to use the structural modes with free geometrical interface for two coupled substructures instead of the structural modes with fixed geometrical interface (elastic modes) as used in the Craig and Bampton method. In this context, MacNeal in [50] introduced the concept of residual flexibility which has then been used by Rubin in [74]. The Lagrange multipliers have also been used to write the coupling on the geometrical interface [51, 67, 68, 73]. Dynamic substructuring in the medium-frequency range has been analyzed [33, 43, 77, 81]. On the other hand, UQ is nowadays recognized as playing an important role in order to improve the robustness of the models for the low-frequency range and especially, in the medium-frequency range in the context of substructuring techniques [16, 34, 36, 55, 63, 79, 80]. Reviews have also been performed [20, 24, 45]. It should be noted that all these above dynamic substructuring methodologies, which have been developed for the discrete case (computational model), have also been reanalyzed in the framework of the continuous case (continuum mechanics) by Morand and Ohayon in [56] for which details can be found in [57] for conservative systems and by Ohayon and Soize in [62] for the dissipative systems.

A physical flexible interface (the linking substructure) between two coupled substructures, modeled by an elastic medium, has been considered by Kuhar and Stahle [44] considering a static behavior of the junction. In this paper, a generalization of this work is presented in a more general framework for a viscoelastic dynamic behavior of the junction using existing component mode synthesis methods (see [66] for computational details). We consider a structure composed of two dissipative main substructures coupled through a physical flexible viscoelastic linking substructure by two geometrical interfaces. The boundary value problem is written in the frequency domain. The linking substructure is modeled in the context of the general linear viscoelasticity theory [14, 84], yielding damping and stiffness sesquilinear forms depending on the frequency, while the two main dissipative substructures are modeled in the context of linear elasticity with an additional classical viscous damping modeling which is assumed to be independent of the frequency.

We present a variational-based reduced-order model in dynamic substructuring, adapted to computational dynamics, for linear elastodynamic of a dissipative structure composed of two main dissipative substructures coupled through a physical flexible viscoelastic interface constituting the linking substructure. A reduced-order model is constructed using the structural modes of the two main substructures with free geometrical interfaces and, for the linking substructure, using an adapted frequency-dependent vector basis with fixed geometrical interfaces and an appropriate static lifting operator with respect to the geometrical interfaces. It should be noted that the linking substructures models which are used, generally correspond to a rough modeling of the real linking systems and consequently, uncertainties induced by modeling errors can be introduced [55]. Another interest of using free structural modes of the two main substructures is also to allow a direct dynamical identification of the main substructures using experimental modal analysis [2, 3, 26, 42, 49, 58–60, 72, 86]. Such a reduced-order model is very useful for sensitivity analysis, design optimization and controller design for vibration active control [25, 40, 46, 69, 85].

2 Displacement Variational Formulation for Two Substructures Connected with a Linking Substructure

2.1 Description of the Mechanical System and Hypotheses

This paper deals with the linear vibration of a free structure, around a static equilibrium configuration which is taken as a natural state (for the sake of brevity, prestresses are not considered but could be added without changing the presentation), submitted to prescribed external forces which are assumed to be in equilibrium at each instant. The displacement field of the structure is then defined up to an additive rigid body displacement field. In this paper, we are only concerned in the part of the displacement field due to the structural deformation.

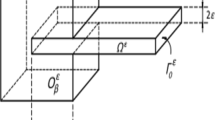
Let \(\varOmega _1\), \(\varOmega _2\) and \(\varOmega _L\) be three open bounded domains in \({{\mathchoice{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }}}^3\) with sufficiently smooth boundaries. The structure \(\varOmega \) is composed of two substructures \(\varOmega _1\) and \(\varOmega _2\) perfectly connected through interfaces \(\varGamma _{1L}\) and \(\varGamma _{2L}\) by a linking substructure \(\varOmega _L\) (see Fig. 1). The boundaries are such that \(\partial \varOmega _1=\varGamma _{1L}\cup \varGamma _1\), \(\partial \varOmega _2=\varGamma _{2L}\cup \varGamma _2\), \(\partial \varOmega _L=\varGamma _{1L}\cup \varGamma _L\cup \varGamma _{2L}\). We then have \(\varOmega =\varOmega _1\cup \varGamma _{1L}\cup \varOmega _L\cup \varGamma _{2L}\cup \varOmega _2\) and \(\partial \varOmega =\varGamma _1\cup \varGamma _L\cup \varGamma _2\). The physical space is referred to a cartesian reference system and the generic point is denoted as \(\mathbf{x }= (x_1,x_2,x_3)\). A frequency domain formulation is used, the convention for the Fourier transform being \(v(\omega )=\int _{{\mathchoice{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }}}e^{-i\omega t} \, v(t)\, dt\) where \(\omega \) denotes the real circular frequency, \(v(\omega )\) is in \({{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}\) and where \(\overline{v}(\omega )\) denotes its conjugate. The convention of summation over repeated indices is used and \(v_{,j}\) denotes the partial derivative of \(v\) with respect to \(x_j\). In \(\mathbf{u }\cdot \mathbf{v }\), the dot denotes the usual Euclidean inner product on \({{\mathchoice{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }}}^3\) extended to \({{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}^3\).

Fig. 1
figure 1

Two substructures \(\varOmega _1\) and \(\varOmega _2\) connected with a linking substructure \(\varOmega _L\)

Full size image

For \(r\) in \(\{1,L,2\}\), the space of admissible displacement fields defined on \(\varOmega _r\) with values in \({{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}^3\) (resp. in \({{\mathchoice{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }}}^3\)) is denoted by \({ {{{\mathcal {C}}}}_{\varOmega _r}} \) (resp. \({ {{{\mathcal {R}}}}_{\varOmega _r} }\)). For substructure \(\varOmega _r\), the test function (weighted function) associated with \(\mathbf{u }^r\) is denoted by \(\delta \mathbf{u }^r\in { {{{\mathcal {C}}}}_{\varOmega _r}} \) (or in \({ {{{\mathcal {R}}}}_{\varOmega _r} })\). The space \({ {{{\mathcal {R}}}}_{\varOmega _r} }\) is the real Sobolev space \((H^1(\varOmega _r))^3\) and the space \({ {{{\mathcal {C}}}}_{\varOmega _r}} \) is defined as the complexified Hilbert space of \({ {{{\mathcal {R}}}}_{\varOmega _r} }\). Let \( {{{{\mathcal {R}}}}_{\small \textit{rig}}}^r\) be the subspace (of dimension 6) of \({ {{{\mathcal {C}}}}_{\varOmega _r}} \) spanned by all the \({{\mathchoice{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }}}^3\)-valued rigid body displacement fields which are written as \(\mathbf{u }^r(\mathbf{x })= \mathbf{t }+ {\varvec{\theta }}\times \mathbf{x }\) for all \(\mathbf{x }\) in the closure \(\overline{\varOmega }_r\) of \(\varOmega _r\), in which \(\mathbf{t }\) and \({\varvec{\theta }}\) are two arbitrary constant vectors in \({{\mathchoice{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }}}^3\). Let \( {{{{\mathcal {R}}}}_{\varOmega } }\) be the space of admissible displacement fields defined on \(\varOmega \) with values in \({{\mathchoice{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }}}^3\). Let \( {{{{\mathcal {R}}}}_{\small \textit{rig}}}\) be the subspace (of dimension 6) of \( {{{{\mathcal {R}}}}_{\varOmega } }\) spanned by all the \({{{\mathchoice{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }{\mathop {\hbox {R}}\nolimits }}}}^3\)-valued rigid body displacement fields which are written as \(\mathbf{u }(\mathbf{x })= \mathbf{t }+ {\varvec{\theta }}\times \mathbf{x }\) for all \(\mathbf{x }\).

Each substructure is a three-dimensional dissipative elastic medium. The linking substructure \(\varOmega _L\) is modeled in the context of the general linear viscoelasticity theory while the two main dissipative substructures \(\varOmega _1\) and \(\varOmega _2\) are modeled in the context of linear elasticity with an additional classical viscous damping modeling which is assumed to be independent of the frequency. For \(r\) in \(\{1,L,2\}\), for all fixed \(\omega \) and for each point \(\mathbf{x }\), the displacement field is denoted by \(\mathbf{u }^r(\mathbf{x },\omega )=(u^r_1(\mathbf{x },\omega ),u^r_2(\mathbf{x },\omega ),u^r_3(\mathbf{x },\omega ))\), the external given body and surface force density fields applied to \(\varOmega _r\) and \({\varGamma _{\! r}}\) are denoted by \(\mathbf{g }^{\varOmega _r}(\mathbf{x },\omega ) =( g^{\varOmega _r}_1(\mathbf{x },\omega ), g^{\varOmega _r}_2(\mathbf{x },\omega ), g^{\varOmega _r}_3(\mathbf{x },\omega ))\) and \(\mathbf{g }^{\varGamma _r}(\mathbf{x },\omega ) = (g^{\varGamma _r}_1(\mathbf{x },\omega ), g^{\varGamma _r}_2(\mathbf{x },\omega ),g^{\varGamma _r}_3(\mathbf{x },\omega ))\) respectively. Let be

(1)
(2)

in which is the indicator function of set \(B\). Since we are only concerned in the part of the displacement field due to the structural deformation, it will be assumed that the given external forces are such that, for all \(\mathbf{u }\) in \( {{{{\mathcal {R}}}}_{\small \textit{rig}}}\),

$$\begin{aligned} \int _{\varOmega } \mathbf{g }^{\varOmega }(\mathbf{x },\omega ) \cdot {\mathbf{u }(\mathbf{x })}\, d\mathbf{x }+ \int _{\partial \varOmega } \mathbf{g }^{\partial \varOmega }(\mathbf{x },\omega ) \cdot {\mathbf{u }(\mathbf{x })} \, ds(\mathbf{x }) = 0. \end{aligned}$$
(3)

2.1.1 Constitutive Equations

For \(r\) in \(\{1,L,2\}\), the linearized strain tensor is defined by

$$\begin{aligned} \varepsilon _{ij}(\mathbf{u }^r)= {1\over 2} (u^r_{i,j} + u^r_{j,i}). \end{aligned}$$
(4)

(i) For \(r\) in \(\{1,2\}\), the constitutive equation for substructure \(\varOmega _r\), which is assumed to be made up of an elastic material with linear viscous term, is written as

$$\begin{aligned} \sigma _\mathrm{tot}^r = \sigma ^r + i\omega \, s^r, \end{aligned}$$
(5)

where \(\sigma ^r\) is the elastic stress tensor defined by \(\sigma ^r_{ij}(\mathbf{u }^r)=a_{ijkh}^r(\mathbf{x })\, \varepsilon _{kh}(\mathbf{u }^r)\) and where \(i\omega \, s^r\) is the viscous part of the total stress tensor such that \(s^r_{ij}(\mathbf{u }^r)=b_{ijkh}^r(\mathbf{x })\, \varepsilon _{kh}(\mathbf{u }^r)\). The mechanical coefficients \(a_{ijkh}^r(\mathbf{x })\) and \(b_{ijkh}^r(\mathbf{x })\) depend on \(\mathbf{x }\) but are independent of frequency \(\omega \) and verify the usual properties of symmetry, positiveness and boundedness (lower and upper).

(ii) For \(r = L\), the constitutive equation for linking substructure \(\varOmega _L\), which is assumed to be made up of a linear viscoelastic material, is written as

$$\begin{aligned} \sigma _\mathrm{tot}^L = \sigma ^L + i\omega \, s^L, \end{aligned}$$
(6)

where \(\sigma ^L\) is the elastic part of the total stress tensor defined by \(\sigma ^L_{ij}(\mathbf{u }^L)=a_{ijkh}^L(\mathbf{x },\omega )\, \varepsilon _{kh}(\mathbf{u }^L)\) and where \(i\omega \, s^L\) is the viscous part of the total stress tensor such that \(s^L_{ij}(\mathbf{u }^L)=b_{ijkh}^L(\mathbf{x },\omega )\, \varepsilon _{kh}(\mathbf{u }^L)\). The mechanical coefficients \(a_{ijkh}^L(\mathbf{x },\omega )\) and \(b_{ijkh}^L(\mathbf{x },\omega )\) depend on \(\mathbf{x }\) and on frequency \(\omega \) and, for all fixed \(\omega \), verify the usual properties of symmetry, positiveness and boundedness (lower and upper). At zero frequency, \(a_{ijkh}^L(\mathbf{x },0)\) is the equilibrium modulus tensor (which differs from the initial elasticity tensor). For more details concerning the properties of tensors \(a_{ijkh}^L(\mathbf{x },\omega )\) and \(b_{ijkh}^L(\mathbf{x },\omega )\), see [23, 62, 84].

2.2 The Boundary Value Problem

2.2.1 Equilibrium Equations in the Frequency Domain for Each Substructure

For all fixed \(\omega \) and for \(r\) in \(\{1,L,2\}\), the equilibrium equation for substructure \(\varOmega _r\) is written as

$$\begin{aligned} -\omega ^2\, \rho ^r \, u^r_i - \{{\sigma _\mathrm{tot}^r}\}_{ij,j} = g^{\varOmega _r}_i \hbox { in } \varOmega _r \quad \hbox {for} \quad i=1,2,3, \end{aligned}$$
(7)

in which \(\rho ^r\) is the mass density depending on \(\mathbf{x }\) (which is assumed to be strictly positive and bounded), with the boundary condition,

$$\begin{aligned} \{{\sigma _\mathrm{tot}^r}\}_{ij} \, n^r_j = g^{\varGamma _r}_i \quad \hbox {on} \quad \varGamma _r \quad \hbox {for} \quad i=1,2,3, \end{aligned}$$
(8)

in which the vector \(\mathbf{n }^r =(n_1^r,n_2^r,n_3^r)\) is the unit normal to \(\partial \varOmega _r\), external to \(\varOmega _r\).

2.2.2 Coupling Conditions

The coupling conditions of the linking substructure \(\varOmega _L\) with substructures \(\varOmega _1\) and \(\varOmega _2\) on \(\varGamma _{1L}\) and \(\varGamma _{2L}\) are written as

$$\begin{aligned}&\mathbf{u }^1 =\mathbf{u }^L \quad \hbox {on} \quad \varGamma _{1L}, \nonumber \\&\mathbf{u }^2 =\mathbf{u }^L \quad \hbox {on} \quad \varGamma _{2L}.\end{aligned}$$
(9)
$$\begin{aligned}&\sigma _\mathrm{tot}^1\, \mathbf{n }^1 =-\sigma _\mathrm{tot}^L\, \mathbf{n }^L \quad \hbox {on} \quad \varGamma _{1L}, \nonumber \\&\sigma _\mathrm{tot}^2\, \mathbf{n }^2 =-\sigma _\mathrm{tot}^L\, \mathbf{n }^L \quad \hbox {on} \quad \varGamma _{2L}. \end{aligned}$$
(10)

2.2.3 Boundary Value Problem in Displacement

For all fixed \(\omega \), the boundary value problem consists in finding the displacement fields \(\mathbf{u }^1\), \(\mathbf{u }^L\) and \(\mathbf{u }^2\), verifying, for each \(r\) equal to \(1\), \(L\) or \(2\), the equilibrium equation Eq. (7) with the constitutive equation defined by Eq. (5) (for \(r=1,2\)) or by Eq. (6) (for \(r=L\)), with the Neumann boundary condition defined by Eq. (8) and with the coupling conditions defined by Eqs. (9) and (10).

2.3 Variational Formulation of the Boundary Value Problem

2.3.1 Definition of the Sesquilinear Forms of the Problem

For \(r\) in \(\{1,L,2\}\), a sesquilinear form on \({ {{{\mathcal {C}}}}_{\varOmega _r}} \!\times { {{{\mathcal {C}}}}_{\varOmega _r}} \) is defined by

$$\begin{aligned} m^r(\mathbf{u }^r, \delta \mathbf{u }^r)= \int _{\varOmega _r} \rho ^r\, \mathbf{u }^r\cdot \overline{\delta \mathbf{u }^r} \, d\mathbf{x }. \end{aligned}$$
(11)

The sesquilinear form \(m^r\) is continuous positive definite Hermitian on \({ {{{\mathcal {C}}}}_{\varOmega _r}} \!\times { {{{\mathcal {C}}}}_{\varOmega _r}} \).

(i) For \(r\) in \(\{1,2\}\), two sesquilinear forms on \({ {{{\mathcal {C}}}}_{\varOmega _r}} \!\times { {{{\mathcal {C}}}}_{\varOmega _r}} \), independent of frequency \(\omega \) are defined by

$$\begin{aligned} k^r(\mathbf{u }^r, \delta \mathbf{u }^r)&= \int _{\varOmega _r} a_{ijkh}^r(\mathbf{x })\, \varepsilon _{kh}(\mathbf{u }^r)\, \varepsilon _{ij}(\, \overline{\delta \mathbf{u }^r}\, ) \, d\mathbf{x }, \end{aligned}$$
(12)
$$\begin{aligned} d^r(\mathbf{u }^r, \delta \mathbf{u }^r)&= \int _{\varOmega _r} b_{ijkh}^r(\mathbf{x })\, \varepsilon _{kh}(\mathbf{u }^r)\, \varepsilon _{ij}(\, \overline{\delta \mathbf{u }^r}\, ) \, d\mathbf{x }. \end{aligned}$$
(13)

(ii) For \(r = L\), two sesquilinear forms on \({ {{{\mathcal {C}}}}_{\varOmega _r}} \!\times { {{{\mathcal {C}}}}_{\varOmega _r}} \), depending on frequency \(\omega \), are defined by

$$\begin{aligned} k^L(\mathbf{u }^L, \delta \mathbf{u }^L;\omega )&= \int _{\varOmega _L} a_{ijkh}^L(\mathbf{x },\omega )\, \varepsilon _{kh}(\mathbf{u }^L)\, \varepsilon _{ij}(\, \overline{\delta \mathbf{u }^L}\, ) \, d\mathbf{x }, \end{aligned}$$
(14)
$$\begin{aligned} d^L(\mathbf{u }^L, \delta \mathbf{u }^L;\omega )&= \int _{\varOmega _L} b_{ijkh}^L(\mathbf{x },\omega )\, \varepsilon _{kh}(\mathbf{u }^L)\, \varepsilon _{ij}(\, \overline{\delta \mathbf{u }^L}\, ) \, d\mathbf{x }. \nonumber \\ \end{aligned}$$
(15)

Taking into account the usual assumptions related to the constitutive equations, for \(r\) in \(\{1,L,2\}\), the sesquilinear forms \(k^r\) and \(d^r\) are continuous semi-definite positive Hermitian on \({ {{{\mathcal {C}}}}_{\varOmega _r}} \!\times { {{{\mathcal {C}}}}_{\varOmega _r}} \), the semi-definite positiveness being due to the presence of rigid body displacement fields.

(i) For \(r\) in \(\{1,2\}\), for all \(\delta \mathbf{u }^r\) in \({ {{{\mathcal {C}}}}_{\varOmega _r}} \), \(\, k^r(\mathbf{u }^r, \delta \mathbf{u }^r)\) and \(d^r(\mathbf{u }^r, \delta \mathbf{u }^r)\) are equal to zero for any \(\mathbf{u }^r\) in \( {{{{\mathcal {R}}}}_{\small \textit{rig}}}^r\).

(ii) For \(r=L\), for all fixed frequency \(\omega \) and for all \(\delta \mathbf{u }^L\) in \( {{{{\mathcal {C}}}}_{\varOmega _L}} \), \(\, k^L(\mathbf{u }^L, \delta \mathbf{u }^L;\omega )\) and \(d^L(\mathbf{u }^L, \delta \mathbf{u }^L;\omega )\) are equal to zero for any \(\mathbf{u }^L\) in \( {{{{\mathcal {R}}}}_{\small \textit{rig}}}^L\).

2.3.2 Definition of the Antilinear Forms of the Problem

For \(r\) in \(\{1,L,2\}\) and for all fixed frequency \(\omega \), it is assumed that \(\mathbf{g }^{\varOmega _r}\) and \(\mathbf{g }^{\varGamma _r}\) are such that the antilinear form \(\delta \mathbf{u }^r \mapsto f^r (\delta \mathbf{u }^r;\omega )\) on \({ {{{\mathcal {C}}}}_{\varOmega _r}} \), defined by

$$\begin{aligned} f^r (\delta \mathbf{u }^r;\omega ) = \int _{\varOmega _r} \mathbf{g }^{\varOmega _r}(\mathbf{x },\omega ) \cdot \overline{\delta \mathbf{u }^r(\mathbf{x })}\, d\mathbf{x }\nonumber \\ + \int _{\varGamma _r} \mathbf{g }^{\varGamma _r}(\mathbf{x },\omega ) \cdot \overline{\delta \mathbf{u }^r(\mathbf{x })}&\, ds(\mathbf{x }), \end{aligned}$$
(16)

is continuous.

2.3.3 Definition of the Complex Bilinear Forms of the Problem

(i) For \(r\) in \(\{1,2\}\) and for all fixed \(\omega \), the complex bilinear form \(z^r\) on \({ {{{\mathcal {C}}}}_{\varOmega _r}} \!\times { {{{\mathcal {C}}}}_{\varOmega _r}} \) is defined by

$$\begin{aligned} z^r(\mathbf{u }^r, \delta \mathbf{u }^r;\omega ) = -\omega ^2\, m^r(\mathbf{u }^r, \delta \mathbf{u }^r) \nonumber \\ +i\omega \, d^r(\mathbf{u }^r, \delta \mathbf{u }^r)&+ k^r(\mathbf{u }^r, \delta \mathbf{u }^r). \end{aligned}$$
(17)

(ii) For \(r=L\) and for all fixed frequency \(\omega \), the complex bilinear form \(z^L\) on \( {{{{\mathcal {C}}}}_{\varOmega _L}} \!\times {{{{\mathcal {C}}}}_{\varOmega _L}} \) is defined by

$$\begin{aligned} z^L(\mathbf{u }^L, \delta \mathbf{u }^L;\omega )&= -\omega ^2\, m^L(\mathbf{u }^L, \delta \mathbf{u }^L) \nonumber \\&+i\omega \, d^r(\mathbf{u }^L, \delta \mathbf{u }^L;\omega ) + k^L(\mathbf{u }^L, \delta \mathbf{u }^L;\omega ). \nonumber \\ \end{aligned}$$
(18)

2.3.4 Variational Formulation of the Boundary Value Problem

The variational formulation of the boundary value problem in \(\mathbf{u }^1\), \(\mathbf{u }^L\) and \(\mathbf{u }^2\) is defined as follows. For all fixed real \(\omega \), find \((\mathbf{u }^1(\omega ), \mathbf{u }^L(\omega ), \mathbf{u }^2(\omega ))\) in \( {{{{\mathcal {C}}}}_{\varOmega _1}} \!\times {{{{\mathcal {C}}}}_{\varOmega _L}} \!\times { {{{\mathcal {C}}}}_{\varOmega _2}} \) verifying the linear constraints \(\mathbf{u }^1(\omega )=\mathbf{u }^L(\omega )\) on \(\varGamma _{1L}\) and \(\mathbf{u }^2(\omega )=\mathbf{u }^L(\omega )\) on \(\varGamma _{2L}\), such that, for all \((\delta \mathbf{u }^1,\delta \mathbf{u }^L,\delta \mathbf{u }^2)\) in \( {{{{\mathcal {C}}}}_{\varOmega _1}} \!\times {{{{\mathcal {C}}}}_{\varOmega _L}} \!\times { {{{\mathcal {C}}}}_{\varOmega _2}} \) verifying the linear constraints \(\delta \mathbf{u }^1 =\delta \mathbf{u }^L\) on \(\varGamma _{1L}\) and \(\delta \mathbf{u }^2 =\delta \mathbf{u }^L\) on \(\varGamma _{2L}\), we have

$$\begin{aligned}&z^1(\mathbf{u }^1(\omega ), \delta \mathbf{u }^1;\omega ) + z^L(\mathbf{u }^L(\omega ), \delta \mathbf{u }^L;\omega ) + z^2(\mathbf{u }^2(\omega ), \delta \mathbf{u }^2;\omega ) \nonumber \\&\quad = f^1 (\delta \mathbf{u }^1;\omega ) + f^L (\delta \mathbf{u }^L;\omega ) + f^2 (\delta \mathbf{u }^2;\omega ). \end{aligned}$$
(19)

Under the given hypotheses relative to the constitutive equations and the hypothesis on the external given forces defined by Eq. (3), the existence and uniqueness of a solution can be proven for all real \(\omega \). This solution corresponds only to deformation of the structure (i.e. without rigid body displacements).

3 Reduced-Order Model

The method is based on the use of the variational formulation defined by Eq. (19). The reduced-order model is carried out using (i) for \(r=1,2\), the eigenmodes of substructure \(\varOmega _r\) with free interface \(\varGamma _{rL}\), (ii) a frequency-dependent family of eigenfunctions for linking substructure \(\varOmega _L\) with fixed interface \(\varGamma _{1L}\cup \varGamma _{2L}\) and (iii) the elastostatic lifting operator of \(\varOmega _L\) with respect to interface \(\varGamma _{1L}\cup \varGamma _{2L}\) at zero frequency.

3.1 Eigenmodes of Substructure \(\varOmega _r\) with Free Interface \(\varGamma _{rL}\) for \(r=1,2\)

For \(r=1,2\), a free-interface mode of substructure \(\varOmega _r\) is defined as an eigenmode of the conservative problem associated with free substructure \(\varOmega _r\), subject to zero forces on \(\partial \varOmega _r\). The real eigenvalues \(\lambda ^r \ge 0\) and the corresponding eigenmodes \(\mathbf{u }^r\) in \({ {{{\mathcal {R}}}}_{\varOmega _r} }\) are then the solutions of the following spectral problem: find \(\lambda ^r\ge 0\), \(\mathbf{u }^r\in { {{{\mathcal {R}}}}_{\varOmega _r} }(\mathbf{u }^r\not = \mathbf{0 })\) such that for all \(\delta \mathbf{u }^r\in { {{{\mathcal {R}}}}_{\varOmega _r} }\), one has

$$\begin{aligned} k^r(\mathbf{u }^r, \delta \mathbf{u }^r) = \lambda ^r\, m^r(\mathbf{u }^r, \delta \mathbf{u }^r) \, . \end{aligned}$$
(20)

It can be shown that there exist six zero eigenvalues \(0= \lambda ^r_{-5} = \cdots = \lambda ^r_0\) (associated with the rigid body displacement fields) and that the strictly positive eigenvalues (associated with the displacement field due to structural deformation) constitute the increasing sequence \(0< \lambda ^r_1\le \lambda ^r_2,\ldots \). The six eigenvectors \(\{\mathbf{u }^r_{-5},\ldots ,\mathbf{u }^r_{0}\}\) associated with zero eigenvalues span \( {{{{\mathcal {R}}}}_{\small \textit{rig}}}\) (space of the rigid body displacement fields). The family \(\{ \mathbf{u }^r_{-5},\ldots ,\) \(\mathbf{u }^r_0\); \(\mathbf{u }^r_1,\ldots \}\) of all the eigenmodes forms a complete family in \({ {{{\mathcal {R}}}}_{\varOmega _r} }\). For \(\alpha \) and \(\beta \) in \(\{-5,\ldots , 0 ; 1,\ldots \}\), we have the orthogonality conditions

$$\begin{aligned} m^r(\mathbf{u }^r_\alpha , \mathbf{u }^r_\beta )&= \delta _{\alpha \beta }, \end{aligned}$$
(21)
$$\begin{aligned} k^r(\mathbf{u }^r_\alpha , \mathbf{u }^r_\beta )&= \delta _{\alpha \beta }\, \lambda ^r_\alpha , \end{aligned}$$
(22)

in which each eigenmode \(\mathbf{u }^r_\alpha \) is normalized to \(1\) with respect to \(m^r\) and where \(\omega ^r_\alpha =\sqrt{\lambda ^r_\alpha }\) is the eigenfrequency of mode \(\alpha \).

3.2 Frequency-Dependent Family of Eigenfunctions for Linking Substructure \(\varOmega ^L\) with Fixed Interface \(\varGamma _{1L}\cup \varGamma _{2L}\)

Let us introduce the following admissible space,

$$\begin{aligned} { {{{\mathcal {R}}}}_{\varOmega _L}^{0} }=\left\{ \, \mathbf{u }^L\in { {{{\mathcal {R}}}}_{\varOmega _L} }\,\, \big \vert \,\,\mathbf{u }^L = 0 \quad \hbox {on} \quad \varGamma _{1L}\cup \varGamma _{2L} \right\} . \end{aligned}$$
(23)

At given frequency \(\omega \), a fixed-interface vector basis of linking substructure \(\varOmega _L\) is defined as an eigenfunction of the conservative problem associated with \(\varOmega _L \) with fixed interface \(\varGamma _{1L}\cup \varGamma _{2L}\), subject to zero forces on \(\partial \varOmega _L\). A real eigenvalue \(\lambda ^L(\omega ) > 0\) and the corresponding eigenfunction \(\mathbf{u }^L(\omega )\) in \({ {{{\mathcal {R}}}}_{\varOmega _L} }\) are then the solution of the following spectral problem: find \(\lambda ^L(\omega ) > 0\) and nonzero \(\mathbf{u }^L(\omega )\) in \({ {{{\mathcal {R}}}}_{\varOmega _L}^{0} }\) such that for all \(\delta \mathbf{u }^L\in { {{{\mathcal {R}}}}_{\varOmega _L}^{0} }\), we have

$$\begin{aligned} k^L(\mathbf{u }^L(\omega ), \delta \mathbf{u }^L;\omega ) = \lambda ^L(\omega )\,\, m^L(\mathbf{u }^L(\omega ), \delta \mathbf{u }^L). \end{aligned}$$
(24)

It can be shown that there exist a strictly positive increasing sequence of eigenvalues, \(0< \lambda ^L_1(\omega )\le \lambda ^L_2(\omega ),\ldots \), and a corresponding family \(\{ \mathbf{u }^L_1(\omega ) , \mathbf{u }^L_2(\omega ),\ldots \}\) of eigenfunctions which constitutes a complete family in \({ {{{\mathcal {R}}}}_{\varOmega _L}^{0} }\). For \(\alpha \) and \(\beta \) in \(\{1,2,\ldots \}\), we have the orthogonality conditions

$$\begin{aligned} m^L(\mathbf{u }^L_\alpha (\omega ), \mathbf{u }^L_\beta (\omega ))&= \delta _{\alpha \beta }, \end{aligned}$$
(25)
$$\begin{aligned} k^L(\mathbf{u }^L_\alpha (\omega ), \mathbf{u }^L_\beta (\omega );\omega )&= \delta _{\alpha \beta }\, \lambda ^L_\alpha (\omega ), \end{aligned}$$
(26)

in which each eigenfunction \(\mathbf{u }^L_\alpha (\omega )\) is normalized to \(1\) with respect to \(m^L\).

Remarks The reduced-order model will be constructed in using a finite family \({{\mathcal {U}}}^L(\omega ) = \{\mathbf{u }^L_1(\omega ), \ldots ,\) \(\mathbf{u }^L_{N_L}(\omega )\}\) of the sequence \(\{ \mathbf{u }^L_1(\omega ) , \mathbf{u }^L_2(\omega ),\ldots \}\) of the eigenfunctions associated with the first \(N_L\) eigenvalues \(0< \lambda ^L_1(\omega )\le \ldots \le \lambda ^L_{N_L}(\omega )\). In addition, such a reduced-order model will be constructed for analyzing the response of the structure for frequency \(\omega \) belonging to a given frequency band of analysis, \(\mathrm {B}=[{\omega _\mathrm{{{min}}}}, {\omega _\mathrm{{{max}}}}]\), with \(0\le {\omega _\mathrm{{{min}}}}< {\omega _\mathrm{{{max}}}}\). In practice, the response is calculated for the frequencies belonging to the finite subset \({{\mathcal {B}}}= \{ \omega _1, \omega _2, \ldots , \omega _{\mu }\}\) of \(\mu \) sampling frequencies of band \(\mathrm {B}\), for which \(\mu \) can be of several hundreds or of the order of one thousand.

(i) In the above formulation, the generalized eigenvalue problem defined by Eq. (24) must be solved for all \(\omega \) in \({{\mathcal {B}}}\). If the number \(\mu \) of frequencies is not too high (that is generally the case for the linking substructure), such a computation remains feasible. It should be noted that the use of massively parallel computers facilitates the analysis of such numerical problem depending on continuous parameter \(\omega \).

(ii) For solving the generalized eigenvalue problem defined by Eq. (24) for all \(\omega \) in \({{\mathcal {B}}}\), the numerical cost can be reduced using the following procedure. First, Eq. (24) is solved for \(\omega \) belonging to the subset \({{\mathcal {B}}}' = \{\omega '_1,\ldots , \omega '_{\mu '}\}\) of chosen frequency points in \({{\mathcal {B}}}\) with \(\mu ' \ll \mu \), called master frequency points. Then, an approximation \(\widetilde{{\mathcal {U}}}^L(\omega )\) of \({{\mathcal {U}}}^L(\omega )\) is calculated for all \(\omega \) in \({{\mathcal {B}}}\backslash {{\mathcal {B}}}'\) by using an interpolation procedure based on the values \({{\mathcal {U}}}^L(\omega '_1), \ldots ,{{\mathcal {U}}}^L(\omega '_{\mu '})\) at the \(\mu '\) frequency points. Finally, for each \(\omega \) in \({{\mathcal {B}}}\backslash {{\mathcal {B}}}'\) , the generalized eigenvalue problem defined by Eq. (24) is projected on the subspace spanned by the finite family \(\widetilde{{\mathcal {U}}}^L(\omega )\) which yields a reduced-order generalized eigenvalue problem of dimension \(N_L\) and which allows an approximation \(\widetilde{\lambda }^L_1(\omega ),\ldots ,\) \(\widetilde{\lambda }^L_{N_L}(\omega )\) of \(\lambda ^L_1(\omega ),\ldots ,\lambda ^L_{N_L}(\omega )\) to be calculated. Such a procedure can be found in [4].

(iii) Another way consists in replacing the above interpolation procedure by the following construction of a frequency-independent basis adapted to band \(\mathrm {B}\). It consists in extracting the larger family of linearly independent functions from the family \({{\mathcal {U}}}^L(\omega '_1), \ldots ,{{\mathcal {U}}}^L(\omega '_{\mu '})\) at the \(\mu '\) master frequency points.

(iv) If \(k^L( \cdot , \cdot \, ;\omega )\) slowly varies for \(\omega \) in band \(\mathrm {B}\), a well adapted frequency-independent basis for all \(\omega \) in \(\mathrm {B}\), consists in choosing \({{\mathcal {U}}}^L(\omega )\) for an arbitrary \(\omega \) in \(\mathrm {B}\) but in such a case convergence with respect to \(N_L\) must be carefully checked.

(v) More generally, any subset of \(N_L\) functions extracted from a Hilbertian basis of the admissible space \({ {{{\mathcal {R}}}}_{\varOmega _L}^{0} }\) can be used.

3.3 Elastostatic Lifting Operator of \(\varOmega _L\) with Respect to Interface \(\varGamma _{1L}\cup \varGamma _{2L}\) at Zero Frequency

We consider the solution \(\mathbf{u }^L_S\) of the elastostatic problem at zero frequency for linking substructure \(\varOmega _L\) subjected to prescribed displacement fields \(\mathbf{u }_{\varGamma _{1L}}\) on \(\varGamma _{1L}\) and \(\mathbf{u }_{\varGamma _{2L}}\) on \(\varGamma _{2L}\), and zero force on \(\varGamma _L\). We introduce the following sets of functions,

$$\begin{aligned}&{ {{{\mathcal {R}}}}_{\varGamma _{1L},\varGamma _{2L}}} = (H^{1/2}(\varGamma _{1L}))^3 \times (H^{1/2}(\varGamma _{2L}))^3, \end{aligned}$$
(27)
$$\begin{aligned}&{ {{{\mathcal {R}}}}_{\varOmega _L}^{ \mathbf{u }_{\varGamma _{1L}},\mathbf{u }_{\varGamma _{2L}} } }= \{ \, \mathbf{u }^L\in { {{{\mathcal {R}}}}_{\varOmega _L} }\,\, \big \vert \,\, \mathbf{u }^L = \mathbf{u }_{\varGamma _{1L}} \,\, \hbox {on} \,\, \varGamma _{1L} \,\, ;\nonumber \\&\mathbf{u }^L = \mathbf{u }_{\varGamma _{2L}} \,\, \hbox {on} \,\,\varGamma _{2L} \hbox {with}\,(\mathbf{u }_{\varGamma _{1L}},\mathbf{u }_{\varGamma _{2L}}) \in { {{{\mathcal {R}}}}_{\varGamma _{1L},\varGamma _{2L}}} \}.\nonumber \\ \end{aligned}$$
(28)

Displacement field \(\mathbf{u }^L_S\) satisfies the following variational formulation,

$$\begin{aligned} k^L(\mathbf{u }^L_S, \delta \mathbf{u }^L_S;0) = 0 \quad , \quad \mathbf{u }^L_S\in { {{{\mathcal {R}}}}_{\varOmega _L}^{ \mathbf{u }_{\varGamma _{1L}},\mathbf{u }_{\varGamma _{2L}} } }, \nonumber \\ \forall \, \delta \mathbf{u }^L_S \in { {{{\mathcal {R}}}}_{\varOmega _L}^{0} }, \end{aligned}$$
(29)

corresponding to the following boundary value problem,

$$\begin{aligned} \{a_{ijkh}^L(\mathbf{x },0)\, \varepsilon _{kh}(\mathbf{u }^L)\}_{,j} = 0 \quad \hbox {in} \quad \varOmega _L \quad \hbox {for} \quad i=1,2,3, \end{aligned}$$
(30)

with the Neumann and Dirichlet boundary conditions,

$$\begin{aligned}&a_{ijkh}^L(\mathbf{x },0)\, \varepsilon _{kh}(\mathbf{u }^L) \, n^L_j = 0 \quad \hbox {on} \quad \varGamma _L \quad \hbox {for} \quad i=1,2,3, \end{aligned}$$
(31)
$$\begin{aligned}&\mathbf{u }^L = \mathbf{u }_{\varGamma _{1L}} \,\, \hbox {on} \,\, \varGamma _{1L} \, ; \nonumber \\&\mathbf{u }^L = \mathbf{u }_{\varGamma _{2L}} \,\, \hbox {on} \,\, \varGamma _{2L}. \end{aligned}$$
(32)

The problem defined by Eq. (29) has a unique solution \(\mathbf{u }^L_S\) which defines the linear continuous operator \(S^L\) from \({ {{{\mathcal {R}}}}_{\varGamma _{1L},\varGamma _{2L}}}\) into \({ {{{\mathcal {R}}}}_{\varOmega _L}^{ \mathbf{u }_{\varGamma _{1L}},\mathbf{u }_{\varGamma _{2L}} } }\) (called the elastostatic lifting operator at zero frequency),

$$\begin{aligned} (\mathbf{u }_{\varGamma _{1L}},\mathbf{u }_{\varGamma _{2L}} ) \mapsto \mathbf{u }^L_S = S^L(\mathbf{u }_{\varGamma _{1L}},\mathbf{u }_{\varGamma _{2L}} ). \end{aligned}$$
(33)

Let \({ {{{\mathcal {R}}}}_{\varOmega _L}^{\small \text {stat}} }\) be the subspace of \({ {{{\mathcal {R}}}}_{\varOmega _L}^{ \mathbf{u }_{\varGamma _{1L}},\mathbf{u }_{\varGamma _{2L}} } }\) constituted of all the solutions of Eq. (29) (i.e. the range of operator \(S^L\)). It can then be proven that \({ {{{\mathcal {R}}}}_{\varOmega _L} }= { {{{\mathcal {R}}}}_{\varOmega _L}^{\small \text {stat}} }\oplus { {{{\mathcal {R}}}}_{\varOmega _L}^{0} }\). Finally, introducing the complexified spaces \({ {{{\mathcal {C}}}}_{\varOmega _L}^{\small \text {stat}} }\) and \({ {{{\mathcal {C}}}}_{\varOmega _L}^{0} }\) of \({ {{{\mathcal {R}}}}_{\varOmega _L}^{\small \text {stat}} }\) and \({ {{{\mathcal {R}}}}_{\varOmega _L}^{0} }\), it can be proven that

$$\begin{aligned} {{{{\mathcal {C}}}}_{\varOmega _L}} = { {{{\mathcal {C}}}}_{\varOmega _L}^{\small \text {stat}} }\oplus { {{{\mathcal {C}}}}_{\varOmega _L}^{0} }. \end{aligned}$$
(34)

3.4 Construction of a Reduced-Order Model

The following reduced-order model can then be constructed using the elastostatic lifting operator and performing a Ritz-Galerkin projection with the free-interface modes of substructures \(\varOmega _1\) and \(\varOmega _2\), and the fixed interface modes of linking substructure \(\varOmega _L\). Let \(N_1\), \(N_L\) and \(N_2\) be finite integers. For all fixed \(\omega \), the following finite projections \(\mathbf{u }^{1,N_1}(\omega )\), \(\mathbf{u }^{L,N_L}(\omega )\) and \(\mathbf{u }^{2,N_2}(\omega )\) of \(\mathbf{u }^{1}(\omega )\), \(\mathbf{u }^{L}(\omega )\) and \(\mathbf{u }^{2}(\omega )\) are introduced as follows,

$$\begin{aligned} \mathbf{u }^{1,N_1}(\omega )&= \sum _{\alpha =-5}^{N_1} q^1_\alpha (\omega ) \, \mathbf{u }^1_\alpha ,\end{aligned}$$
(35)
$$\begin{aligned} \mathbf{u }^{L,N_L}(\omega )&= S^L(\mathbf{u }^{N_1}_{\varGamma _{1L}}(\omega ),\mathbf{u }^{N_2}_{\varGamma _{2L}}(\omega )) + \sum _{\alpha =1}^{N_L} q^L_\alpha (\omega ) \, \mathbf{u }^L_\alpha (\omega ), \end{aligned}$$
(36)
$$\begin{aligned} \mathbf{u }^{2,N_2}(\omega )&= \sum _{\alpha =-5}^{N_2} q^2_\alpha (\omega ) \, \mathbf{u }^2_\alpha , \end{aligned}$$
(37)

in which \(\mathbf{u }^{N_1}_{\varGamma _{1L}}(\omega )\) and \(\mathbf{u }^{N_2}_{\varGamma _{2L}}(\omega )\) are such that

$$\begin{aligned} \mathbf{u }^{N_1}_{\varGamma _{1L}}(\omega )&= \sum _{\alpha =-5}^{N_1} q^1_\alpha (\omega ) \, \mathbf{u }^1_{\alpha \vert \varGamma _{1L}} \, , \end{aligned}$$
(38)
$$\begin{aligned} \mathbf{u }^{N_2}_{\varGamma _{2L}}(\omega )&= \sum _{\alpha =-5}^{N_2} q^2_\alpha (\omega ) \, \mathbf{u }^2_{\alpha \vert \varGamma _{2L}} \, . \end{aligned}$$
(39)

Note that Eq. (36) is due to the property defined by Eq. (34). The corresponding test functions are then written as,

$$\begin{aligned}&\delta \mathbf{u }^{1,N_1} = \sum _{\alpha =-5}^{N_1} \delta q^1_\alpha \, \mathbf{u }^1_\alpha , \end{aligned}$$
(40)
$$\begin{aligned}&\delta \mathbf{u }^{L,N_L}(\omega ) = S^L(\delta \mathbf{u }^{N_1}_{\varGamma _{1L}},\delta \mathbf{u }^{N_2}_{\varGamma _{2L}}) + \sum _{\alpha =1}^{N_L} \delta q^L_\alpha \, \mathbf{u }^L_\alpha (\omega ) \, ,\end{aligned}$$
(41)
$$\begin{aligned}&\delta \mathbf{u }^{2,N_2}= \sum _{\alpha =-5}^{N_2} \delta q^2_\alpha \, \mathbf{u }^2_\alpha , \end{aligned}$$
(42)

in which \(\delta \mathbf{u }^{N_1}_{\varGamma _{1L}}\) and \(\delta \mathbf{u }^{N_2}_{\varGamma _{2L}}\) are such that

$$\begin{aligned} \delta \mathbf{u }^{N_1}_{\varGamma _{1L}}&= \sum _{\alpha =-5}^{N_1} \delta q^1_\alpha \, \mathbf{u }^1_{\alpha \vert \varGamma _{1L}},\end{aligned}$$
(43)
$$\begin{aligned} \delta \mathbf{u }^{N_2}_{\varGamma _{2L}}&= \sum _{\alpha =-5}^{N_2} \delta q^2_\alpha \, \mathbf{u }^2_{\alpha \vert \varGamma _{2L}}. \end{aligned}$$
(44)

Substituting Eqs. (35) to (44) into Eq. (19) yields the following variational reduced-order model of order \(N =\) \(N_1 +\) \(6 + N_L + N_2 + 6\). For all fixed \(\varOmega \), find \(({\mathbf{q }}^1(\omega ),\) \({\mathbf{q }}^L(\omega ),\) \({\mathbf{q }}^2(\omega ))\) in \({{{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}}^{N_1+6}\times {{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}^{N_L}\times {{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}^{N_2+6}\) such that, for all \((\delta \mathbf{q }^1,\delta \mathbf{q }^L,\delta \mathbf{q }^2)\) in \({{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}^{N_1+6}\times {{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}^{N_L}\times {{\mathchoice{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }{\mathop {\hbox {C}}\nolimits }}}^{N_2+6}\), we have

$$\begin{aligned}&z^{\small \text {red}}_N(\mathbf{q }^1(\omega ),\mathbf{q }^L(\omega ),\mathbf{q }^2(\omega ), \delta \mathbf{q }^1,\delta \mathbf{q }^L,\delta \mathbf{q }^2; \omega ) \nonumber \\&\quad = f^{N}(\delta \mathbf{q }^1,\delta \mathbf{q }^L,\delta \mathbf{q }^2;\omega ), \end{aligned}$$
(45)

in which \(\mathbf{q }^1 = (q^1_{-5}, \ldots , q^1_{0},q^1_{1}\ldots q^1_{N_1})\), \(\mathbf{q }^L = (q^L_{1}, \ldots ,\) \(q^L_{N_L})\), \(\mathbf{q }^2 = (q^2_{-5}, \ldots , q^2_{0},\) \(q^2_{1}\ldots q^2_{N_2})\), \(\delta \mathbf{q }^1 = (\delta q^1_{-5}, \ldots ,\) \(\delta q^1_{0},\) \(\delta q^1_{1}\ldots \delta q^1_{N_1})\), \(\delta \mathbf{q }^L = (\delta q^L_{1}, \ldots , \delta q^L_{N_L})\) and \(\delta \mathbf{q }^2 = (\delta q^2_{-5}, \ldots , \delta q^2_{0},\) \(\delta q^2_{1}\ldots \delta q^2_{N_2})\).

4 Concluding Remarks and Research Perspectives

A continuum-based substructuring techniques has been presented for the linear dynamic analysis of two substructures connected with a physical flexible viscoelastic interface, for which each substructure is reduced using its free-interface elastic modes. Concerning the research perspectives, for such a dynamical system, the physical flexible viscoelastic interface generally presents model uncertainties induced by imperfect coupling boundary conditions with the substructures, the viscoelastic model used for of the material and the geometrical parameters. The complexity of such physical interface model can require advanced dynamic multiscale methods in micro-macro mechanics for materials [48] and requires to take into account model uncertainties induced by modeling errors. Such implementation using the nonparametric probabilistic approach of model uncertainties, coupling recent advanced research concerning uncertainty quantification for viscoelastic structures [65, 82] and uncertain coupling interface methodologies [55], is in progress. In addition, the introduction of smart materials in the physical interface would be of prime interest for micromechanical systems.