Abstract
The chapter is addressed at phenomenological mapping and mathematical analogies of oscillatory regimes in hybrid discrete-continuum systems of coupled deformable bodies. Systems consist of connected deformable bodies like plates, beams, belts, or membranes that are coupled through visco-elastic non-linear layer. The layer is modeled by continuously distributed elements of Kelvin–Voigt type with non-linearity of third order. Using the mathematical analogies, the similarities of structural models in systems of plates, beams, belts, or membranes are explained. The mathematical models consist by a set of two coupled non-homogenous partial non-linear differential equations. The proposed solution is divided into space and time domains by classical Bernoulli–Fourier method. In the time domains, the systems of coupled ordinary non-linear differential equations are completely analog for different systems of deformable bodies and are solved using the Krilov–Bogolyubov–Mitropolski asymptotic method. This paper presents the power of mathematical analytical calculus which is similar for physically different systems. The mathematical numerical experiments are a great and useful tool for making the final conclusions between many input and output values. The conclusions about non-linear phenomena in multi-body systems dynamics are revealed from the specific example of double plate’s system stationery and no stationary oscillatory regimes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The investigation of dynamics and vibration of coupled plates as new qualitative systems has grown exponentially over the last few years due to their practical importance and the theoretical challenges involved in their non-linear analysis. As an introduction, a review of first author’s research results in area of transversal vibrations of different double-plate systems is presented (see References [1,2,3,4,5,6,7]). Main result of the contribution [1,2,3,4,5,6,7] is analytical approximation of solution of the coupled homogeneous and non-homogeneous partial differential equations of the free and forced vibrations of the double rectangular or circular plates system coupled by elastic or visco-elastic layer. This solution is obtained by use of the method of Bernoulli’s particular integral as well as Lagrange’s method of the constant’s variation. Some numerical examples are presented along with visualizations of the double-plate free and forced vibrations. Obtained analytical and numerical result is very valuable for university teaching process for the area of structural system elastodynamics as well as of hybrid deformable body system vibrations.
The paper by Poltorak and Nagaya [8] was concerned with a method for solving forced vibration problems of solid sandwich plates with irregular boundaries. The exact, general solution of the equation of motion in terms of Bessel functions is found. The boundary problem is solved using the Fourier expansion collocation method. Damping properties of an intermediate, visco-elastic layer are taken into consideration by means of a concept of a complex shear modulus. The paper by Poltorak and Nagaya [9] deals with a method for solving free vibration problems of three-layered isotropic plates of arbitrary shape with clamped edges. The direct solution of the Yan and Dowell equation of motion, in terms of Bessel functions, is found.
Recent technological innovations, especially in microelectromechanical systems and nanomaterials structures, have caused a considerable interest in the study of components and hybrid dynamical processes of coupled rigid and deformable bodies (plates, beams, membranes, and belts) denoted as hybrid systems. These coupled structures are characterized by the interaction between subsystem dynamics, governed by coupled partial differential equations with appropriate boundary and initial conditions. In the papers [7, 10], the method for obtaining frequency equations of small oscillations is presented using hybrid systems with a statical as well as dynamically coupled discrete subsystem of rigid bodies and continuous subsystem as an example. Also, series of theorems of small oscillations frequency equations are defined. Based on presented examples, the analogy between frequency equations for some classes of these systems is identified. Special cases of discretization and continouization of coupled subsystems in the light of these sets of proper circular frequencies and frequency equations of small oscillations are analyzed [11, 12].
The research of vibrational behavior of an elastically connected double plates system is important for both theoretical and pragmatic reasons (see Refs. [1, 2, 13]). Many important structures are modeled as composite structure. As a conceptual model of such structure, it is convenient to use the model of a visco-elastically connected double plates system. The elements for acoustic and vibrations’ isolation, such as the walls or grounds, all can be modeled and analysed with these suggested coupled structure systems. These models and analysis are the subjects of our presented research which follows gradually explained in the next sections.
The obtained results have particular practical importance especially if the models refer to structures maid of material with creeping features (see Ref. [14]).
Theory of Petrović Alas, presented in two books [15, 16] in Serbian, contains elements of mathematical phenomenology and phenomenological mapping. Since in Serbian, the books have been only approachable for a certain number of his disciples. The idea of mathematical phenomenology of Petrović, was presented in his works entitled “Phenomenological Mapping” [16], containing the following chapters: The mapping of facts; General notation of mapping; Conventional mapping; Natural mapping; Mutual particularities of facts and Elements and properties (essentials) of facts. Alas’s theory defines two tips of analogies: qualitative and mathematical analogy. Since Alas was a student of H. Poincaré, P. Painlevé, Ch. Hermite, and É. Picard and his theory of “Phenomenological Mapping” can be considered as the continuation of the ideas of Poincare’s mapping. Poincare was forerunner to modern researchers of non-linear dynamics and dynamical systems mapping, especially contributed to nowadays spreadly used Poincaré section and map. Also, similar concept of mapping is used by Smale’s horseshoe mapping in the vicinity of the homoclinic unstable point.
The similar ideas were later applied in graphical-computer techniques by Penrose [17], and Glaick [18]. This had a great importance in the time of computer and software tool expansion.
Based on this theory, it is possible to integrate the immense contemporary knowledge from the disparate fields of sciences and identify analogous dynamics and phenomena. Phenomenological mapping of phenomenon and models permit the description of dynamics of multiple system models, even of disparate nature, by a single mathematical model. The recognisable example is mechanical–electrical analogy of electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series or in parallel with simple harmonic oscillator. J. Maxwell brought in analogies of this sort in the 19th century and Rašković [19, 20] gave a series of examples for electro-mechanical mathematically analogous vibration systems mathematically described and solved for free vibrations. Additionally, as electrical network analysis matured, it was realized that certain mechanical complex problems could be easily explained through an electrical analogy based on a prescribed frequency function that is analogue for both systems.
Based on the Petrović‘s ideas [15, 16], an analogy between vector models of stress and strain states and model of the state of the body mass inertia moments were introduced and applied, in the paper [21], for explanation in the possible phenomenological mapping of these different kinds of states.
Ideas of phenomenology and phenomenological mapping were used for the formulation of the frequency’s equation theorems of small oscillations, see for instance [12, 21]. These theorems found their application for investigating the dynamics, and vibration phenomena of resonance and dynamical absorption. These findings have great importance in research, understanding, and control of the dynamics for various kinds of chains and multi-body systems.
To our knowledge, only a few studies by different authors are available with discussing phenomenological mapping: in mathematics [21,22,23,24], from the area of neuroscience [25] or as a part of string theory and its applications [26]. String theory is an independent mathematical model that explains all elementary forces and forms of matter.
The undesirable phenomena in vibrational behavior of deformable structures are sudden amplitude jumps, non-linear hysteresis, modulation, beating, and phase shifting. Such phenomena originate from inherently non-linear material and geometrical properties of deformable structures. The most important step in the description of the dynamics of such a structures and structural model formulation is an adequate mathematical model of mechanical system. Where by the description of the system represents all the levels of researching the kinetics characteristics of the systems and abilities of their improvement, control, regulation, or some other usage of mechanical systems. Speaking diversely, mathematical modeling regards on the usage of mathematical equations to present the behavior of practical systems. It helps in better understanding of systems features. Since the non-linearity appears inherently as an object’s natural characteristic, it is important to describe, model, solve, and control it by available methods. The usual linear approximation of the system does not give the satisfactory results especially in the contemporary application of micro- and nanostructures where the aforementioned behaviors overcome the dimensions of the structures and imperil the stable work conditions. Thus, the issue is to explore and in some plausible way to control system non-linearities.
Starting hypothesis is always examined with theoretical models which are useful for presenting the general conclusions to the simple models. The adjoint numerical calculations give conclusions for specific and even complicated systems of the observed parameter sets. However, between the conceptual model and structural form that consists of a set of mathematical equations addressing the complex system behaviors, we are forced to introduce a number of assumptions, simplifications, neglect, or possible measurement errors. Consequently, our structural model can have significantly different dynamics from real physical models. Reasonably, it is useful to note the similarities in the different physical phenomena. Mathematical descriptions of that phenomena usually are described with the analogue sets of equations. Thus, it is possible to take advantage of the general conclusions from understanding generalized mathematical models.
In this paper, we will present mathematical models of several complex mechanical systems, introduce its analogies, and explain non-linear phenomena of passing through resonant regions. Systems consist of coupled deformable bodies like plates, beams, or membranes that are connected through discrete-continuum layer with non-linear elastic and translator and rotator inertia properties. Visco-elastic non-linear layer, with properties of translation and rotation of added mass elements, was rheological modeled by continuously distributed elements of Kelvin–Voigt type with non-linearity of third order with addition of rotatory elements.
The investigation of dynamics of multi bodies systems with different rheological coupling steadily enlarges over the last few years due to their practical importance especially in microelectromechanical systems and nanomaterials structures. Moreover, it is evident the existing considerable interest in the study of component and hybrid dynamical processes of coupled rigid and deformable bodies (plates, beams, membranes, and belts) (see Refs. [27,28,29,30]). Such systems are denoted as hybrid mechanical systems and are characterized by the interaction between subsystem dynamics. Their structural models comprise a set of coupled partial differential equations with boundary and initial conditions.
The research of small transversal vibrations of deformable bodies connected with elastic, visco-elastic, or creep connections has as much theoretical as practical importance. Their mathematical model can be used to describe the dynamic behavior of a considerable number of coupled multi-body systems. The results and conclusions of the analysis of such mathematical models are used in the presentation of non-linear dynamics behavior for a number of real structures. For instance, in civil engineering for roofs, floors, walls, in thermo and acoustics isolation systems of walls and floors constructions, orthotropic bridge decks or for building any structural application in which the traditional method of construction uses stiffened steel.
In this paper, we show that the model of a visco-elastically connected double deformable bodies system with non-linearity in the elastic layer is apt for modeling sandwich construction behavior. The sandwich constructions consist of two or more facing layers that are structurally bonded to a core made of material with small specific weight. This type of construction provides a structural lightweight system that acts as a crack arrest layer and that can join two dissimilar metals without welding. Such construction provides equivalent in-plane and transverse stiffness and strength, reduces fatigue problems, minimizes stress concentrations, improves thermal and acoustical insulation, and provides vibration control.
2 Theoretical problem formulation and governing equations of the basic problem of double circular plate system vibrations
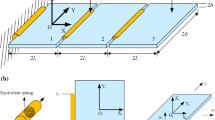
The example to start consideration is the system of two isotropic, elastic, thin circular plates. The material and geometrical properties of plates are denoted as: widths \( h_{i} \), \( i=1,2 \), modulus of elasticity \( E_{i} \), Poisson’s ratios \( \mu _{i} \), shear modulus \( G_{i} \), and plate mass distributions \( \rho _{i} \). The plates are of constant thickness in the z-direction (see Fig. 1a). The contours of the plates are parallel. The plates are interconnected by a linear elastic Winkler-type layer with constant surface stiffness c. This elastically connected double-plate system is a composite structure type, or sandwich plate, or layered plate, and here, it is a first considered problem.
The origins of the two coordinate systems are located at the corresponding centers in the undeformed plate’s middle surfaces, as shown in Fig. 1a, and have parallel corresponding axes. The problem at hand is to determine solutions and the own vibration frequencies for such a double-plate system elastically connected by an elastic spring layer distributed along plates contour surfaces.
The use of Love–Kirchhoff approximation makes the classical plate theory essentially a two-dimensional model, in which the normal and transverse forces and bending and twisting moments on plate cross sections (see Ref. [19]) can be found in term of the displacement \( w_{i} \left( {r,\varphi ,t} \right) \), \( i=1,2 \) of the middle surface points, which is assumed to be a function of two coordinates, r and \( \varphi \) in polar–cylindrical coordinate system, and time t.
The plates are assumed to have the same contour forms and boundary conditions.
Let us suppose that the plate middle surfaces are plane in the undeformed state. If the plates transverse deflections \( w_{i} \left( {r,\varphi ,t} \right) \), \( i=1,2 \) are small compared to the plates thicknesses, \( h_{i} \), \( i=1,2 \) (see Ref. [19]) and that plate vibrations occur only in the vertical direction.
Let us denote with \({D}_{\left( i \right) } =\frac{{\mathbf{E }}_{i} h_{i}^{3} }{12\left( {1-\mu _{i}^{2} } \right) } \), \( i=1,2 \) the bending cylindrical rigidity of plates. On the basis of previous assumptions, we suppose that plate displacements \( u_{i} \left( {r,\varphi ,z,t} \right) \), \( i=1,2 \) and \( v_{i} \left( {r,\varphi ,z,t} \right) \), \( i=1,2 \) of the generic plate point \( N_{i} \left( {r,\varphi ,z} \right) \), \( i=1,2 \) in the radial and circular direction can be expressed in function of its distance z from the corresponding plate middle surface and its transversal displacement \( w_{i} \left( {r,\varphi ,t} \right) \), \( i=1,2 \) in direction of the axis z, and also the same displacement of the corresponding point \( N_{i0} \left( {r,\varphi ,0} \right) \), \( i=1,2 \) in the plate middle surface.
The governing equations (see Ref. [1]) are formulated in terms of two unknowns: the transversal displacements \( w_{i} \left( {r,\varphi ,t} \right) \), \( i=1,2 \) in direction of the axis z, of a point \( N_{i} \left( {r,\varphi } \right) \), \( i=1,2 \) of the upper plate middle surface and of the lower plate middle surface. The system of two coupled partial differential equations is derived using d’Alembert’s principle or by variational principle (see Ref. [19]). These partial differential equations of the elastically connected double-plate system, by discrete-continuum layer, are in the following forms:
where c is the constant surface mechanical stiffness of discrete-continuum elastic layer.
Let us introduce the following notations: \( a_{\left( i \right) }^{2} =\frac{c}{\rho _{i} h_{i} } \), \( i=1,2 \) and \( c_{\left( i \right) }^{4} =\frac{D_{i} }{\rho _{i} h_{i} } \), \( i=1,2 \). By decoupling the equations of the previous system (1), we obtain the corresponding two partial differential equations of the decoupled plate system, which describe two partial plates founded on the elastic foundation of the Winkler type. These partial differential equations are in the following forms:
2.1 Particular solutions of governing basic decoupled equations of double-plate system oscillations
Solution of the previous system of partial differential equations can be looked for by Bernoulli’s method of particular integrals in the form of multiplication of two functions, of which the first \( {{\textit{W}}}_{\left( i \right) } \left( {r,\varphi } \right) \), \( i=1,2 \) depends only on space coordinates r and \( \varphi \), and the second is a time function \( T_{(i)}\left( t \right) \), \( i=1,2 \) (see Refs. [1, 2, 19])
The assumed solution is introduced in the previous system of Eq. (1), and after transformation, we obtain the following:
Thus, we obtain in the space cylindrical–polar coordinates r, \( \varphi \) and z the following differential equations:
where eigen circular frequencies of the corresponding basic system of decoupled plates are
It is easy to find the following time functions:
2.2 Space coordinate eigen amplitude functions
Let us consider the space coordinate amplitude functions \( {{\textit{W}}}_{\left( i \right) } \left( {r,\varphi } \right) \), \( i=1,2 \). For the plates in circular form, the set of the partial differential equations in the space cylindrical–polar coordinates r, \( \varphi \), and z is
where \( \Delta \) is the differential operator \( \Delta =\frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}}{\partial \varphi ^{2}} \).
We write the solutions of previous equations in the form \( {{\textit{W}}}_{\left( i \right) } \left( {r,\varphi } \right) =\Phi _{\left( i \right) } \left( \varphi \right) {\mathbf{R }}_{\left( i \right) } \left( r \right) \), and after applying this solution, we obtain the following system of ordinary differential equations:
The second equation of previous system has particular solutions in the form of Neumann’s and Bessel’s functions [31], but Neumann’s functions for \( r=0 \) have infinite value, than particular solutions of this problem are only Bessel’s function of the first kind with real argument \( {\mathbf{J }}_{n} \left( x \right) \) as well as with imaginary arguments \( {\mathbf{I }}_{n} \left( x \right) \), where \( x=kr \). Modified Bessel’s function of the first kind with imaginary arguments \( {\mathbf{I }}_{n} \left( x \right) \), with order n, is in the following form:
If n is an integer number, than this function satisfies the following differential equation:
Using previous considerations and the study of Eq. (9), we can write their solutions in the polar coordinates as follows:
Therefore, the solutions for the space coordinate amplitude functions are in the following forms:
which are the space coordinate–eigen amplitude normal functions for boundary conditions in the form constrained along the contour circular plate. The characteristic numbers are roots of the next characteristic transcendent equation (see Ref. [19])
The family (14) of characteristic equations for each n has an infinite number of solutions (roots) and we are going to mark them with \( k_{nm} \), \( m=1,2,3,\ldots \), denoting a family of eigen values for each \( n=1,2,3,4,\ldots \), sets of Eq. (14) of eigen values for each \( n=1,2,3,4,\ldots \), can be rewritten in the form
As the solutions (roots) of this equation are \( \lambda _{nm} \), \( n=1,2,3,4,\ldots \), \( n=1,2,3,\ldots \), so we have \( k_{nm} =\frac{\lambda _{\text{ nm }} }{a} \) where a is the plate radius. The graphics of characteristic transcendent equations for \( n=0 \), \( n=1 \) and \( n=2 \) are reported in Fig. 2a*–c*.
The graph of characteristic transcendent Eq. (14) for: ...\( n=0 \), where we can see only eight solutions (roots) \( \lambda _{0m} \), \( m=1,2,\ldots ,8 \); of the set with infinite number of roots, b* \( n=1 \), where we can see only eleven solutions (roots) \( \lambda _{1m} \), \( m=1,2,\ldots ,11 \); of the set with infinite number of roots, and c* \( n=2 \) where we can see only eleven solutions (roots) \( \lambda _{2m} \), \( m=1,2,\ldots ,11 \) of the set with infinite number of roots
In Fig. 2a*, we can see from the set with infinite number of roots, corresponding to various n only a certain number of solutions (roots) denoted with \( \lambda _{nm} \). For example in Fig. 2a*, we find the following roots \( \lambda _{01} =3.196;\,\lambda _{02} =6.306;\,\lambda _{03} =9.439,\ldots \), in Fig. 2b* the following roots \( \lambda _{11} =4.61,\,\lambda _{12} =7.8,\,\lambda _{13} =10.96,\,\ldots \), and in Fig. 2c* the following roots \( \lambda _{21} =5.9,\,\lambda _{22} =9.2,\,\lambda _{23} =12.4,\ldots \). For those values of characteristic numbers, the space coordinate eigen amplitude functions are represented in Fig. 3.
Last but not least, we obtain the general solutions for the transversal plates middle surface point displacement in the following forms:
or
The space coordinate eigen amplitude functions \( {{\textit{W}}}_{\left( i \right) nm} \left( {r,\varphi } \right) , i=1,2 , n,m=1,2,3,4,\ldots \infty \) satisfy the following conditions of orthogonality:
where \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \), \( s,r=1,2,3,4,\ldots \infty \), which is easily derived using system equation (9).
2.3 Particular solutions of governing system of coupled partial differential equations for free system oscillations
For the solutions of the governing system of the coupled partial differential equations (1) for free double plates’ oscillations in the form of expansion (17), the eigen amplitude function \( {{\textit{W}}}_{\left( i \right) nm} \left( {r,\varphi } \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) are the same as in the case of decoupled plates problem and \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) are unknown time functions describing their time evolution.
After introducing (17) into the following system of the coupled partial differential equations for free double plate’s oscillations:
The space coordinate eigen amplitude functions \( W_{nm} (r,\varphi ) \) for: a \( \lambda _{11} =4.61,\,\lambda _{12} =7.8,\,\lambda _{13} =10.96,\ldots \); b \( \lambda _{21} =5.9,\,\lambda _{22} =9.2,\,\lambda _{23} =12.4,\,\ldots \) are presented above and the corresponding cross sections are presented below
we obtain
By multiplying the first and second equation with \({W}_{\left( i \right) sr} \left( {r,\varphi } \right) rdrd\varphi \), integrating along middle plate surface and taking into account orthogonality conditions (18) and equal boundary conditions of the plates, we obtain the mn-family of systems containing two coupled ordinary differential equations for determination of the unknown time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) in the following form:
or in the form
Eliminating the time function \( {T}_{\left( 2 \right) nm} \left( t \right) \) from previous mn-family of system of coupled second-order ordinary differential equations, we obtain the mn-family of one fourth-order equation in the form of
with the corresponding mn-family frequency equation in the form of polynomial, biquadratic equation with respect to unknown own circular frequencies \( {\tilde{\omega }}_{nm}^{2} \), \( n,m=1,2,3,4,\ldots \infty \)
Having the two roots \( {\tilde{\omega }}_{nm\left( s \right) }^{2} \), \( n,m=1,2,3,4,\ldots \infty \), \( s=1,2 \)
or in the form
Formally, we can write the system equation (20) by the following matrices of inertia \( {\mathbf{A }}_{nm} \) and of quasielastic coefficients \( {\mathbf{C }}_{nm} \) of the dynamical system corresponding to the mn-family, with two degrees of freedom:
and using the solutions in the form of
where \( {\tilde{\omega }}_{nm}^{2} \), \( n,m=1,2,3,4,\ldots \infty \) are unknown eigen circular frequencies, \( A_{\left( i \right) nm} \) unknown amplitudes, and \( \alpha _{nm} \) unknown phases. Then, the frequency equation of the mn-family is in the form of
which is equal to Eq. (22) with the sets of two roots \( {\tilde{\omega }}_{nm\left( s \right) }^{2} \), \( n,m=1,2,3,4,\ldots \infty \), \( s=1,2 \), (23).
The relations of the amplitudes of each set are in the form
If we take into account that it is \({A}_{\left( 1 \right) nm}^{\left( 1 \right) } ={A}_{\left( 1 \right) nm}^{\left( 2 \right) } =1 \), then we obtain
The solutions of the mn-family mode time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) are in the form of
where the mn-family mode \( n,m=1,2,3,4,\ldots \infty \) contains the set of unknown constants \( {A}_{nm},\,{B}_{nm},\,{C}_{nm},{D}_{nm} \) defined by plates initial conditions.
Then, the particular solutions of the governing system of coupled partial differential equations for free system oscillations corresponding to plate displacements read
The initial conditions are
where \( g_{i} \left( {r,\varphi } \right) \) and \( {\tilde{g}}_{i} \left( {r,\varphi } \right) \), \( i=1,2 \) are initial condition functions for middle plate points displacement and velocity, satisfying boundary conditions. Then, by initial conditions (32) and frequency Eq. (27), the unknown coefficients are defined by no homogeneous algebra equation system. Using Cramer formula, the set of the unknown constants \( {A}_{nm},\,{B}_{nm},\,{C}_{nm},\,{D}_{nm} \) for mn -family mode \( n,m=1,2,3,4,\ldots \infty \) are defined in the following form:
The solutions (31) are the first main analytical result of our research of transversal vibrations of elastically connected double circular plates’ system. From analytical solutions (31), and corresponding expressions (33) of the constant, we can conclude that for one mn-family mode \( n,m=1,2,3,4,\ldots \infty \), to one eigen amplitude function corresponds two own circular frequencies and corresponding two-frequency time function \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \). We can conclude that the elastical Winkler type of discrete-continuum layer duplicates the number of system circular frequencies corresponding to one eigen amplitude function of the mn-family mode \( n,m=1,2,3,4,\ldots \infty \).
3 Theoretical problem formulation and governing equations of forced oscillation of the visco-elastically connected double-plate system
Let us consider the same system of plates, but connected with a visco-elastic discrete-continuum layer (see Fig. 1b* and external excitation force distributed along upper and lower surface. This visco-elastically connected double-plate system is a composite visco-elastic structure type.
If we present the interconnecting discrete-continuum layer as a model of one visco-elastic element with starting element’s length \( l_{0} \) whose ends have displacements \( w_{1} \left( {r,\varphi ,t} \right) \) and \( w_{2} \left( {r,\varphi ,t} \right) \), and velocities \( {{\dot{w}}}_{1} \left( {r,\varphi ,t} \right) \) and \( {{\dot{w}}}_{2} \left( {r,\varphi ,t} \right) \), like shown in at Fig. 1c*, using visco-elastic element’s constitutive relation of force, displacements, and velocities in that layer (see [1]), we will formulate governing equations for this problem in terms of two unknowns: the transversal displacements \( w_{i} \left( {r,\varphi ,t} \right) \), \( i=1,2 \) in direction of the axis z of the upper plate middle surface and of the lower plate middle surface. Then, the system of two coupled partial differential equations of the forced visco-elastically connected double-plate system is in the following form [4, 7]:
where we use the same notations as in previous parts and define: \( 2\delta _{\left( i \right) } =\frac{b}{\rho _{i} h_{i} } \)—constant surface damping coefficient of visco-elastic layer; \( {\tilde{q}}_{\left( i \right) } (r,\varphi ,t) \), \( i=1,2 \)—function of continual distributed transversal forces which we use like external excitation of plates.
Solution of the previous system (34) of partial differential equations can be looked for by Bernoulli’s method of particular integrals in the form (17) of multiplication of two functions, of which the first \( {{\textit{W}}}_{\left( i \right) } \left( {r,\varphi } \right) \), \( i=1,2 \) depends only on space coordinates r and \( \varphi \), and the second is a time function \( T_{(i)nm}\left( t \right) \), \( i=1,2 \). Here, we use the same space coordinate eigen amplitude functions \( {{\textit{W}}}_{\left( i \right) } \left( {r,\varphi } \right) \), \( i=1,2 \) as in the case of decoupled system and for the example of mentioned boundary conditions in form (13).
3.1 Analytical solutions of the time functions of the forced transversal vibrations of a double circular plate system with visco-elastic discrete-continuum layer
Our next defined task is to derive analytical solution of the governing system of coupled partial differential equations for forced system oscillations, Eq. (35). We consider the eigen amplitude functions \( {{\textit{W}}}_{\left( i \right) nm} \left( {x,y} \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) expansion with unknown time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) describing their time evolution [4, 7] as mentioned above in the case of decoupled plates problem. Then, after introducing (17) into (34), we obtain the following system of no homogeneous second-order ordinary differential equations with respect to the unknown time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) for the mn -family mode:
where known time functions \( f_{\left( 1 \right) nm} \left( t \right) \) and \( f_{\left( 2 \right) nm} \left( t \right) \) are defined by the following expressions:
We can obtain the basic linear unperturbed equations of the coupled system of differential Eq. (35) neglecting the external excitations. Also, for the linear system, we can formally define the following matrices: mass inertia moment matrix \( {\mathbf{A }} \), damping coefficient matrix \( {\mathbf{B }} \), and quasielastic coefficients matrix \( {\mathbf{C }} \) (see Ref. [7]):
and the characteristic equation of the linearized coupled system is in the following form:
with four roots for every eigen amplitude function mode nm:
We obtain own amplitude numbers from (see Refs. [7, 19]):
and we rewrite the solution of linear coupled system in the form:
where amplitudes and phases \( R_{0i} \) and \( \alpha _{0i} \) are constants, defined by the initial conditions.
To obtain an approximation of the solution of the coupled ordinary differential equations (35) for the forced vibrations by using the Lagrange’s method of constant variations, we propose solutions in the following forms:
where two amplitudes \( R_{inm} \left( t \right) \) and two phases \( \Phi _{inm} \left( t \right) ={\hat{p}}_{inm} t+\phi _{i} \left( t \right) \), \( i=1,2 \) are unknown functions. By introducing the condition that the first derivatives of the time functions \( {{\dot{T}}}_{\left( i \right) nm} \left( t \right) \):
have the same forms as in the case where amplitudes \( R_{inm} \left( t \right) \) and difference of phases \( \phi _{inm} \left( t \right) \) are constants:
we obtained first two conditions for the derivatives of the unknown functions \( {{\dot{R}}}_{i} \left( t \right) \) and \( {{\dot{\Phi }}}_{i} \left( t \right) \).
After multiplying first Eq. (44) with cofactors \( K_{22}^{\left( 1 \right) } \) or \( K_{22}^{\left( 2 \right) } \) and second with \( -K_{21}^{\left( 1 \right) } \) or \( -K_{21}^{\left( 2 \right) } \) and summing these two equation the system of equations follows:
The second derivatives \( {{\ddot{T}}}_{\left( i \right) nm} \left( t \right) \) are in the forms:
After introducing derivatives, the first \( {{\dot{T}}}_{\left( i \right) nm} \left( t \right) \), expressions (43) and second \( {{\ddot{T}}}_{\left( i \right) nm} \left( t \right) \), expressions (46) derivatives of the proposed solutions (42) in the system of non-homogeneous differential equations (42) we obtain two new equations in the derivatives of the unknown functions \( {{\dot{R}}}_{inm} \left( t \right) \) and \( {{\dot{\phi }}}_{inm} \left( t \right) \):
After multiplying first equation with cofactor \( K_{22}^{\left( 1 \right) } \) or \( K_{22}^{\left( 2 \right) } \) and second with \( -K_{21}^{\left( 1 \right) } \) or \( -K_{21}^{\left( 2 \right) } \) and summing these two equations the system of equations follows:
Solving the obtained subsystems of four non-homogeneous algebraic Eqs. (45) and (47) with respect to the derivatives \( {{\dot{R}}}_{inm} \left( t \right) \) and \( {\dot{\Phi }}_{inm} \left( t \right) \), we can write the system of first-order differential equations as follows:
where we denoted \( \Phi _{inm} \left( t \right) ={\hat{p}}_{inm} t+\phi _{inm} \left( t \right) \).
If we use trigonometrical transformation of mentioned solutions (39) and define four more variables like:
and integrate the system of Eq. (44), using the obtained solutions we can rewrite the solutions in following final forms:
The solutions (50) are the main analytical result for eigen time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) of forced transversal vibrations of visco-elastically connected double circular plates system, so the solutions for middle surface points displacements in functions of \( r,\varphi \) and t are in forms (17) where the space coordinate eigen amplitude functions \( {{\textit{W}}}_{\left( i \right) } \left( {r,\varphi } \right) \), \( i=1,2 \) are in forms (13). From the analytical solutions (50), we can conclude that for one mn-family mode \( n,m=1,2,3,4,\ldots \infty \), to one eigen amplitude function corresponds two circular-damped frequencies and corresponding two-frequency time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \), in the case of free oscillations of the system, and that for forced oscillations in those functions contain terms corresponding to different combinations (sums and differences) between frequencies of forced external excitations and eigen circular-damped frequencies.
Choosing for external excitation periodic forces, we can rewrite the functions \( f_{\left( i \right) nm} \left( t \right) =h_{\left( {0i} \right) } \cos \Omega _{i} t \), \( i=1,2 \) in the following forms:
and
where \( {\tilde{q}}_{i} \left( {r,\varphi ,t} \right) ={\tilde{F}}_{\left( {0i} \right) } {\tilde{{\tilde{F}}}}_{\left( i \right) } \left( {r,\varphi } \right) \cos \Omega _{i} t \) are known specific area distributed external transversal excitations along upper plate upper contour surface as well lower plate lower contour surface.
In the special observed cases of homogeneous double-plate system with equal plate mass distributions and thicknesses, and considering external excitation only in the upper plate we obtained the following solutions:
3.2 Numerical results
For numerical experiment and analysis, we take into consideration a homogeneous double-plate system containing two equal circular plates with radius \( a=1[m] \) and graded from steel material. Using Maple and possibilities of visualizing these numerical results, we present them as space surfaces of the plate middle surface during the time, and also as time-history diagrams of the plate middle surface points displacements. On the basis of numerical results, series of characteristic middle surface forms of coupled plates during the time are presented in the Figs. 4, 5 and 6.
In Fig. 4, characteristic transversal displacements of the middle surface points of lower and upper plates are presented in function of \( r,\varphi \) and t, in three different time moments for:
a* one eigen amplitude function form of oscillations (\( n=1, m=0)\);
b* two eigen amplitude function forms of oscillations (\( n=0, m=1 \) summed with forms for \( n=1,m=1 \)) and
c* three eigen amplitude function forms of oscillations (\( n=0,m=1 \) summed with forms for \( n=1,m=1 \) and \( n=2, m=1 \)).
In Fig. 5 characteristic transversal displacements of the middle surface points on characteristic diameters for lower and upper plates in function of r for \( \varphi _{j} =const \) at characteristic forms along time t, three eigen amplitude function forms of oscillations (\( n=0,m=1 \) summed with forms for \( n=1,m=1 \) and \( n=2,m=1)\) are presented for: three different values of the external excitation frequency, when external distributed force is applied to upper plate \({a}^* \Omega \approx {\tilde{\omega }}_{11} =\sqrt{\omega _{11}^{2} -a^{2}} \) ; \({b}^* \Omega \approx {\tilde{\omega }}_{21} =\sqrt{\omega _{21}^{2} -a^{2}} \) and \({c}^* \Omega \approx {\tilde{\omega }}_{31} =\sqrt{\omega _{31}^{2} -a^{2}} \).
Characteristic transversal displacements of the middle surface points of lower and upper plates in function of \( r,\varphi \) and t, in three different time moments, for: a* one eigen amplitude function form of oscillations (\( n=1,m=0) \); b* two eigen amplitude function forms of oscillations (\( n=0,m=1\) summed with forms for \( n=1,m=1 \)) and c* three eigen amplitude function forms of oscillations (\( n=0,m=1 \) summed with forms for \( n=1,m=1 \) and \( n=2,m=1 \))
Characteristic transversal displacements of the middle surface points on characteristic diameters for lower and upper plates in function of r for \( \varphi _{j} =const \) at characteristic forms along time t, three eigen amplitude function forms of oscillations (\( n=0,m=1 \) summed with forms for \( n=1,m=1 \) and \( n=2,m=1 \)) for: three different values of the external excitation frequency, when external distributed force is applied to upper plate a* \( \Omega \approx {\tilde{\omega }}_{11} =\sqrt{\omega _{11}^{2} -a^{2}} \); b* \( \Omega \approx {\tilde{\omega }}_{21} =\sqrt{\omega _{21}^{2} -a^{2}} \) and c* \( \Omega \approx {\tilde{\omega }}_{31} =\sqrt{\omega _{31}^{2} -a^{2}} \)
Characteristic transversal displacements of the middle surface points: 6.1: on the series of characteristic diameters and cycles in function of \( r,\varphi \) for \( \varphi _{j} =\) const and \( r=\) const, at characteristic forms along time t; 6.2: on the series of characteristics diameters in function of r, for \( \varphi _{j} =\) const at characteristic forms along time t, for lower and upper plates three eigen amplitude function forms of oscillations (\( n=0,m=1 \) summed with forms for \( n=1,m=1 \) and \( n=2,m=1 \)) for: three different values of the external excitation frequency, when external distributed force is applied to upper plate a* \( \Omega \approx {\tilde{\omega }}_{11} =\sqrt{\omega _{11}^{2} -a^{2}} \) ; b* \( \Omega \approx {\tilde{\omega }}_{21} =\sqrt{\omega _{21}^{2} -a^{2}} \) and c* \( \Omega \approx {\tilde{\omega }}_{31} =\sqrt{\omega _{31}^{2} -a^{2}} \)
In Fig. 6, characteristic transversal displacements of the middle surface points are presented:
6.1: on the series of characteristics diameters and cycles in function of \( r,\varphi \) for \( \varphi _{j} =const \) and \( r=const \), at characteristic forms along time t;
6.2: on the series of characteristics diameters in function of r, for \( \varphi _{j} =const \) at characteristic forms along time t, for lower and upper plates three eigen amplitude function forms of oscillations (\( n=0,m=1 \) summed with forms for \( n=1,m=1 \) and \( n=2,m=1) \) for: three different values of the external excitation frequency, when external distributed force is applied to upper plate a* \( \Omega \approx {\tilde{\omega }}_{11} =\sqrt{\omega _{11}^{2} -a^{2}} \) ; b* \( \Omega \approx {\tilde{\omega }}_{21} =\sqrt{\omega _{21}^{2} -a^{2}} \) and c* \( \Omega \approx {\tilde{\omega }}_{31} =\sqrt{\omega _{31}^{2} -a^{2}} \).
3.3 Concluding remarks
The analytical solutions of system coupled partial differential equations in every of nm-family of corresponding dynamical free (unperturbed by external excitation) processes are obtained using method of Bernoulli’s particular integral and Lagrange’s method of constants variations for solution of forced transversal oscillations.
From the obtained ordinary differential equations and corresponding analytical solutions for time functions corresponding to one eigen amplitude function mode, we can conclude that they are uncoupled from other eigen amplitude time functions.
From the analytical solutions for the case of pure elastic layer between plates, we can conclude that for one mn-family mode \( n,m=1,2,3,4,\ldots \infty \), to one eigen amplitude function correspond two circular frequencies and corresponding two-frequency time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \), in the case of free oscillations of the system, and that for forced oscillations these functions contain terms corresponding to different combinations (sums and differences) between frequencies of forced external excitations and eigen circular frequencies.
We can see that integral part, i.e., particular analytical solutions of coupled partial differential equations, of derived solutions corresponds to the coupled forced and free middle surface vibrations regimes, and describes multi-frequency vibrations with frequencies which are different combinations (sums and differences) between frequencies of forced external excitations and eigen circular-damped frequencies [see solutions (54)]. These analytical solutions can be used for analyses of possible regimes of resonances or phenomena of dynamical absorption. Using Maple program, visualizations of the characteristic forms of the plate middle surfaces through time are presented.
Obtained analytical and numerical result is very valuable for university teaching process in the area of structural system elastodynamics as well as of hybrid deformable body system vibrations.
Comparison between system of ordinary differential equations (20) or (35) along eigen time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) in corresponding eigen amplitude function \( {{\textit{W}}}_{\left( i \right) nm} \left( {r,\varphi } \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) of the plates shape form of free (or forced) oscillations with corresponding ordinary differential equations of the free (or forced) displacements of mass particle free (or forced) oscillation in chain system with two degrees of freedom; it is easier to indicate a mathematical and qualitative analogy. Then obtained solution for chain system free (or forced no conservative) oscillations are analogous with solutions f time functions. Also, mathematical and qualitative analogies are between time functions in each of infinite number of eigen amplitude shapes of double beam system, as well as double membrane system and double membrane system. Then obtained results for eigen time functions \( T_{(i)nm}\left( t \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) in corresponding eigen amplitude function \( {{\textit{W}}}_{\left( i \right) nm} \left( {r,\varphi } \right) \), \( i=1,2 \), \( n,m=1,2,3,4,\ldots \infty \) in the form (53)–(54) is possible to use for explanation vibrations of listed analogous double-body system transversal vibrations.
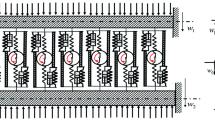
a* Double circular plate system with discrete-continuum layer; b* multi-plate system with discrete-continuum layer; c* the rheological model of rolling visco-elastic and non-linear discrete element with rotator and translator inertia properties; d* the rheological scheme of rolling visco-elastic and non-linear discrete element with rotator and translator inertia properties; e* double membrane system with discrete-continuum layer; f* double beam system with discrete-continuum layer
3.4 Partial differential equations of transversal vibrations of a double deformable bodies system containing discrete-continuum layer with inertia and non-linear properties
For standard rolling visco non-linear elastic element with translator and rotator inertia properties, Fig. 1c*, d* lighted on a way of the rheological models [32], we write the expressions for the velocity of translation for the center of mass C in the form: \( {{\dot{w}}}_{C} ={\left( {{{\dot{w}}}_{2} +{{\dot{w}}}_{1} } \right) } \big / 2 \), and for the angular velocity around center of mass in the form: \( \omega _{C} ={\left( {{{\dot{w}}}_{2} -{{\dot{w}}}_{1} } \right) } \big / {2R} \). The constitutive relations for forces on the ends of this element are in the following form:
where c and \( c_{1} \) are stiffness of linear springs, \( b_{1} \) is coefficient of damping force, \( \beta \) is stiffness of non-linear springs, m is mass of disc, and \( i_{C}^{2} ={J_{C} } \big / m \) is the square of radius of axial mass inertia moment for the rolling element around central axis. If the rolling element is the disc, then mass axial moment of inertia is \( {J_{C} =R^{2}m} \big / 2 \) and \( i_{C}^{2} ={R^{2}} \big / 2 \).
The governing equations of the double body-plate system [27, 28, 33], Fig. 7a*, b*, e*, and d*, are formulated in terms of two unknowns: the transversal displacement \( w_{i} \left( {\wp ,t} \right) \), \( i=1,2 \) in direction of the z axis, of the upper body-plate middle surface and of the lower body-plate middle surface, respectively. We present the interconnecting layer as a model of distributed discrete rheological rolling visco-elastic elements with non-linearity in the elastic part of the layer and translatory and rotatory inertia properties, as shown in Fig. 1c*, d*. Since that elements are continually distributed on plates middle surfaces, the generalized resulting forces (55) are, also, continually distributed onto plate middle surface points. Our assumptions for the plates are: they are thin with same contours and with equal type of the boundary conditions and they have small transversal displacements. The system of two coupled partial differential equations is derived using d’Alembert’s principle of dynamic equilibrium in the following forms:
For plates, we have \( \wp \equiv r,\varphi \) space middle surface coordinates; operator \( \prod \equiv \Delta ^{2}=\left( {\frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}}{\partial \varphi ^{2}}} \right) ^{2} \). Reductions of coefficients are \( {\tilde{a}}_{ii} ={{\hat{a}}_{ii} } \big / {\rho _{i} h{ }_{i}} \); \( {\tilde{a}}_{12\left( i \right) } ={{\hat{a}}_{12} } \big / {\rho { }_{i}h_{i} } \) ; \( a_{\left( i \right) }^{2} ={\left( {c+{c_{1} } \big / 4} \right) } \big / {\rho _{i} h_{i} } \) ; \( D_{i} ={E_{i} h_{i}^{3} } \big / {12\left( {1-\mu _{i}^{2} } \right) } \); flexural plate rigidity \( c_{\left( i \right) }^{4} ={D_{i} } \big / {\rho _{i} h_{i} } \); \( 2\delta _{i} ={b_{1} } \big / {\rho _{i} h_{i} } \) and \( \varepsilon \beta _{\left( i \right) } =\beta \big / {\rho _{i} h_{i} } \); for \( i=1,2 \); \( h_{i} = \) height of plates. The form of the external loads on the bodies surfaces are given as \( {\tilde{q}}_{\left( i \right) } ={q_{\left( i \right) } \left( {r,\varphi ,t} \right) } \big / {\rho _{i} h_{i} } \).
For circular membranes, we have \( \wp \equiv r,\varphi \) space surface coordinates; \( \prod \equiv \Delta =\frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}}{\partial \varphi ^{2}} \) is Laplacian operator. Reductions of the coefficients are: \( {\tilde{a}}_{ii} ={{\hat{a}}_{ii} } \big / {\rho _{i} } \); \( {\tilde{a}}_{12\left( i \right) } ={{\hat{a}}_{12} } \big / {\rho { }_{i}} \); \( c_{\left( i \right) }^{2} ={\sigma _{i} } \big / {\rho _{i} } \); \( a_{\left( i \right) }^{2} ={c_{e} } \big / {\rho _{i} } \); \( \varepsilon \beta _{\left( i \right) } =\beta \big / {\rho _{i} } \) ; \( 2\delta _{i} ={b_{i} } \big / {\rho _{i} } \); \( {\tilde{q}}_{\left( i \right) } ={q_{\left( i \right) } \left( {r,\varphi ,t} \right) } \big / {\rho _{i} } \).
For beams, we have \( \wp \equiv z \) line coordinate along neutral line of the beams; operator \( \prod \equiv \frac{\partial ^{4}}{\partial z^{4}} \); \(\textsf {B}_{i} =E_{i} I_{x} \) flexural beam rigidity. Reductions of the coefficients are \( {\tilde{a}}_{ii} ={{\hat{a}}_{ii} } \big / {\rho _{i} A{ }_{i}} \); \( {\tilde{a}}_{12\left( i \right) } ={{\hat{a}}_{12} } \big / {\rho { }_{i}A_{i} }\); \( c_{\left( i \right) }^{2} =\sqrt{{B_{i} } \big / {\rho _{i} A_{i} }}\); \( a_{\left( i \right) }^{2} ={c_{e} } \big / {\rho _{i} }A_{i} \); \( \varepsilon \beta _{\left( i \right) } =\beta \big / {\rho _{i} A_{i} } \); \( 2\delta _{i} ={b_{i} } \big / {\rho _{i} }A_{i} \); \( {\tilde{q}}_{\left( i \right) } ={q_{\left( i \right) } \left( {z,t} \right) } \big / {\rho _{i} A_{i} } \).
For belts, we have \( \wp \equiv x \) line coordinate along neutral line length of belts; \( \prod \equiv \Delta =\frac{\partial ^{2}}{\partial x^{2}} \) is Laplacian operator. Reduction coefficients are \( {\tilde{a}}_{ii} ={{\hat{a}}_{ii} } \big / {\rho _{i} } \); \( {\tilde{a}}_{12\left( i \right) } ={{\hat{a}}_{12} } \big / {\rho { }_{i}} \); \( c_{\left( i \right) }^{2} ={\sigma _{i} } \big / {\rho _{i} } \); \( a_{\left( i \right) }^{2} ={c_{e} } \big / {\rho _{i} } \); \( \varepsilon \beta _{\left( i \right) } =\beta \big / {\rho _{i} } \) ; \( 2\delta _{i} ={b_{i} } \big / {\rho _{i} } \); \( {\tilde{q}}_{\left( i \right) } ={q_{\left( i \right) } \left( {r,\varphi ,t} \right) } \big / {\rho _{i} } \).
For all four cases on has denotation \( {\hat{a}}_{12} =m \big / 4-{J_{C} } \big / {4R^{2}}=m \big / 8 \); \( {\hat{a}}_{ii} =m \big / 4+{J_{C} } \big / {4R^{2}}={3m} \big / 8 \); \( E = \) Young’s modulus of bodies materials; \( \mu _{i} = \) Poisson’s coefficient; \( \rho _{i} = \) density of bodies material.
The sign \( \pm \) on the right-hand side of partial differential equations (56) corresponds to the soft (sign \(+ \)) or hard (sign −) properties of the non-linear elastic layer.
The asymptotic approximation of solutions, in a single eigen-mode of oscillations, where a number of eigen-modes are \( n,m=1,2,3\ldots \infty \) for plates or membranes, and \( n=1,2,3\ldots \infty \) for beams or belts for the system (56) of partial differential equations are taken in the form of the eigen amplitude functions \( W_{i\left( \mathrm{eign} \right) } \left( \wp \right) \), generalized form of (31), satisfying the same boundary conditions and orthogonally conditions, multiplied with time coefficients in the form of unknown time functions \( T_{i} \left( t \right) \), \( i=1,2 \) and describing their time evolution (see References [27, 28, 33])
where
* \( K_{2i,k\left( \mathrm{eign} \right) }^{\left( s \right) } \) cofactors of elements of second row and corresponding column of determinant corresponding to basic linear coupled system, for proper eigen characteristic number (for details, see References [19, 27, 28, 33]), also see procedure (37)–(40) with different mass inertia moment matrix \( {\mathbf{A }} \) according to the presence of rolling elements;
* \( -{\hat{\delta }}_{i\left( \mathrm{eign} \right) } \) real parts of the appropriate pair of the roots of the characteristic equation [33, 34];
* Unknown amplitudes \( R_{i\left( \mathrm{eign} \right) } \left( t \right) \) and phases \( \Phi _{i\left( \mathrm{eign} \right) } \left( t \right) =\Omega _{i\left( \mathrm{eign} \right) } t+\phi _{i\left( \mathrm{eign} \right) } \left( t \right) \); \( i=1,2 \); of unknown time functions \( T_{\left( i \right) k\left( \mathrm{eign} \right) } \left( t \right) \) which we are going to obtain using the Krilov–Bogolyubov–Mitropolski asymptotic method (see References [33, 35, 36]). We assume that the non-linearity is small and that the interactions between the eigen amplitude modes are negligible, and we take into account the interactions between two time eigen-modes in the single-amplitude mode.
After substituted this proposed asymptotic approximation of solutions (57) in system of partial non-linear differential equations (56), keeping in mind orthogonality conditions of body eigen amplitude functions \( W_{i\left( \mathrm{eign} \right) } \left( \wp \right) \) and \( W_{j\left( \mathrm{eign} \right) } \left( \wp \right) \), \( i\ne j \), it turns out system of ordinary non-linear differential equations for eigen time functions \( T_{\left( i \right) k\left( \mathrm{eign} \right) } \left( t \right) \) of one eigen amplitude mode of considered class of the bodies transversal oscillations
where
is coefficient of non-linearity influence of elastic layer
are the known function of external forces and coefficients of reduction are
We introduce denotation of \( \omega _{\left( i \right) }^{2} =k_{\left( i \right) eign}^{4} c_{\left( i \right) }^{4} +a_{\left( i \right) }^{2} \), \( i=1,2 \) for the square of eigen circular frequency of coupled body free linear vibrations, correspond to one eigen amplitude mode and corresponding time functions, procedure similar to (37)–(39), obtained form system of ordinary differential equations (58) by omitting non-linear terms and terms correspond to external excitation distributed along body middle surface in transversal directions.
The system of ordinary non-linear differential equations (58) is completely, pure mathematically, the same type for plate, beam, membrane, or belt system of two coupled deformable bodies. The mathematical analogy is complete. Based on phenomenological mapping, a mathematical analogy between eigen time functions \( T_{\left( i \right) k\left( \mathrm{eign} \right) } \left( t \right) \), \( i=1,2 \) in a single-amplitude mode of hybrid system dynamics is identified for corresponding multi-beam, multi-plate, multi-membrane, and multi-belt system dynamics with layers of same properties. Summarizes that solutions for one type of dynamics of a hybrid system can be used for another for qualitative analysis of linear or non-linear phenomena that have occurred in dynamics.
It is considered that defined task satisfies all necessary conditions for applying asymptotic Krilov–Bogolyubov–Mitropolyski method [35, 36] concerning small parameter of discrete-continuum layer between bodies. We suppose that the functions of external excitation at one eigen-mode of oscillations are the two-frequency process in the form
\( h_{(0i)} \) are given in Appendix A. The external force frequencies \( \Omega _{i\left( \mathrm{eign} \right) } \), \( i=1,2 \) are in the range of two corresponding eigen-linear-damped coupled system frequencies \( \Omega _{1\left( \mathrm{eign} \right) } \approx {\hat{\text{ p }}}_{1\left( \mathrm{eign} \right) } \) and \( \Omega _{2\left( \mathrm{eign} \right) } \approx {\hat{\text{ p }}}_{2\left( \mathrm{eign} \right) } \), (39), of the corresponding linear and free system to system (58) and that initial conditions of the double-body system permit appearance of the two-frequency like vibrations regimes of in one eigen amplitude mode of the system. \( {\hat{\text{ p }}}_{i\left( \mathrm{eign} \right) } \) are frequencies of visco-elastic coupling obtained like imaginary parts of solution \( \lambda _{i,j\left( \mathrm{eign} \right) } =-{\hat{\delta }}_{i\left( \mathrm{eign} \right) } {\mp } \text{ i }{\hat{\text{ p }}}_{i\left( \mathrm{eign} \right) } \), \( i=1,2 \) for characteristic equations of system, (37)–(39), (58). For details, see References [27, 28, 33].
The observed case is that external distributed two-frequencies force acts at upper surfaces of upper body with frequencies near circular frequencies of coupling \( \Omega _{i\left( \mathrm{eign} \right) } \approx {\hat{\text{ p }}}_{i\left( \mathrm{eign} \right) } \), \( i=1,2 \) and that the lower body is free of excitation \( {\tilde{q}}_{\left( 2 \right) eign} \left( t \right) =0 \). Then, the first asymptotic averaged approximation of the system of differential equations for amplitudes \( R_{i\left( \mathrm{eign} \right) } \left( t \right) \) and difference of phases \( \phi _{i\left( \mathrm{eign} \right) } \left( t \right) \) is obtained in the following general form [27, 28, 33, 35, 36]:
where \( a_{i} \left( t \right) =R_{i} \left( t \right) e^{-{\hat{\delta }}_{i} t} \) is the change of variables; hence, \( {{\dot{a}}}_{i} \left( t \right) =\left( {{{\dot{R}}}_{i} \left( t \right) -{\hat{\delta }}_{i} R_{i} \left( t \right) } \right) e^{-{\hat{\delta }}_{i} t} \). The full forms of constants \( \delta _{i} \), \( \alpha _{i} \), \( \beta _{i} \) and \( P_{i} \) were presented in [33]. Here, it was underlined that these constants all rely on coefficients of coupling properties via cofactors \( \text{ K}_{2i}^{\left( s \right) } \), that \( \delta _{i} \) depends of damping coefficients of visco-elastic layer \( {\tilde{\delta }}_{\left( i \right) } \), \( \varepsilon \text{ P}_{i} \) depend of excited amplitudes, and \( \alpha _{i} \), \( \beta _{i} \) of non-linearity layer properties. Coefficients \( \alpha _{i} \), \( \beta _{i} \) are coefficients of eigen time mode mutual interactions.
It was observed the case when external distributed two-frequencies force in one eigen-body amplitude mode acts at normal direction and along middle plain (line) of upper body with frequencies near eigen circular frequencies of corresponding coupled linearized body systems \( \Omega _{i} \approx {\hat{p}}_{i} \). In that case, the lower body is free of load. This means that we were observed the passing thought main resonant states by discrete changing the values of the forced frequencies. Using the first asymptotic approximation of the amplitudes and phases of multi-frequency particular solutions of eigen time functions of one eigen amplitude shape as well as of the non-linear system dynamics (64)–(65), we are in position to make analytical analysis of the stability of non-linear modes in stationary regimes and to present results of theirs numerical solutions, for particular eigen time modes in single eigen amplitude mode of oscillations, \( n,m=1,2,3\ldots \infty \) for plates (membranes) or \( n=1,2,3\ldots \infty \) for beams (belts).
3.5 Multi-frequency analysis of the stationary resonant regimes of transversal vibrations of a double body system
For the analysis of the stationary resonant regimes of eigen time function mode oscillations correspond to one eigen amplitude function, we were used analysis of amplitudes and phases for system of differential equations (5) in the first approximation, obtained by Krilov–Bogolyubov–Mitropolyski method [35, 36]. For that reason, we equal the right-hand sides of differential equations (64)–(65) in the first asymptotic approximation along amplitudes \( R_{i\left( \mathrm{eign} \right) } \left( t \right) \), \( a_{i} \left( t \right) =R_{i} \left( t \right) e^{-{\hat{\delta }}_{i} t} \), \( i=1,2 \), and difference of phases \( \phi _{i\left( \mathrm{eign} \right) } \left( t \right) \), \( i=1,2 \) with null. Eliminating the phases \( \phi _{1} \) and \( \phi _{2} \), we obtained system of two non-linear algebraic equations by unknown amplitudes \( a_{1} \) and \( a_{2} \) (for detail, see Refs. [7, 15]). Also, with elimination of amplitudes \( a_{1} \) and \( a_{2} \), we obtained the algebraic equations for phases \( \phi _{1} \) and \( \phi _{2} \) in the case of two-frequencies forced oscillations in stationary regime of one eigen (nm for plates or mode n for beams) mode of double bodies’ system oscillations. Solving these algebraic systems by numerical Newton–Kantorovic’s method in computer program Mathematica, we obtained stationary amplitude and phase-frequency curves of two frequency vibrating regims. Each curve corresponds to resonant regime of one of eigen amplitude mode oscillations in double bodies’ system coupled with rolling visco-elastic non-linear discrete-continuum layer with translator and rotator inertia properties, depending on frequencies of external excitation force in single-amplitude mode and distributed along upper middle plate surface. If we fixed the value of one external excitation frequency by two possible, we obtained amplitude– and phase–frequency curves of stationary resonant vibration regime in the following forms:
1* for \( \Omega _{2} =const \) proper amplitude and phase–frequency curves of eigen time function modes in one amplitude mode are denoted by
2* for \( \Omega _{1} =const \) proper amplitude and phase–frequency curves of eigen time function modes in one amplitude mode are denoted by
Amplitude–frequency characteristic curves for the amplitudes of the first time harmonics \( a_{1nm} =f_{1} \left( {\Omega _{1nm} } \right) \) of eigen time function modes in one amplitude mode on the different value of the excited frequency \( \Omega _{1nm} \) for the discrete value of the excited frequency \( \Omega _{2nm} =\) const with noted corresponding one or more resonant jumps for \( m =240\) kg. The arrows designate the directions of the resonant jumps
For any different discrete value of external force frequencies, we get characteristic diagram of that amplitude and phase–frequency curves of eigen time function modes in single-amplitude modes. Figure 8 illustrates a series of diagrams of the regimes of eigen temporal functions that represent the passage through discrete stationary states in resonant frequency intervals. We may track the changes of amplitude and phase of eigen time functions in a single-amplitude mode at specific value of the frequencies of external force which is close to the value of eigen frequencies of coupling in accompanied linearized system of oscillations.
The phenomena of the resonant transition for stationary regime are evident from diagrams. These are the distinctive jumps of the amplitude and phase response (see Figs. 9 and 10) in the vicinity of the resonant values \( \Omega _{i} \approx {\hat{\text{ p }}}_{i} \), appearance of the new stable and unstable branches causing the multi-value-system response and the emergence of two stable solutions of the system around those new branches, the mutual interaction of the time harmonics, and the jumps of the system energies.
Phase–frequency characteristic curve for the phase of the first time harmonics \( \phi _{1nm} =f_{3} \left( {\Omega _{1nm} } \right) \) of eigen time function modes in one amplitude mode on the different value of the excited frequency \( \Omega _{1nm} \), for the discrete value of the excited frequency \( \Omega _{2nm} =\) const with noted corresponding one or more resonant jumps for \( m = 240\) kg. The arrows designate the directions of the resonant jumps
Amplitude–frequency characteristic curves for the amplitudes of the first time harmonics \( a_{1} =f_{1} \left( {\Omega _{1} } \right) \) of eigen time function modes in one amplitude mode for hard characteristics of interconnected layer and for the different discrete values of excited frequency \( \Omega _{2} = \) const with noted proper one or more resonant jumps, for \( m = 0\) kg
From both series of the amplitude–frequency and phase–frequency curves of eigen time function modes in single-amplitude mode, Figs. 8 and 9, it is notable that more than one pair of the resonant jumps exist; some of them are notified with arrows. Also, these jumps are followed by the appearance of new instability branches, which appear at the unstable side of the original curve. The instable parts of branches are presented by dashed line in the listed figures. Their onset is followed with growth and merging, while original curves slowly disappear. The newly born branches after resonant region form the shifted frequency response.
Amplitude–frequency characteristic curve for the amplitudes of the second time harmonics \( a_{2nm} =f_{2} \left( {\Omega _{1nm} } \right) \) of eigen time function modes in one amplitude mode on the different value of the excited frequency \( \Omega _{1nm} \), for the discrete value of the excited frequency \( \Omega _{2nm} =\) const with noted corresponding one or more resonant jumps for m = 0 kg
For the case when \( m=\text{0 }\,\text{ kg } \) that there are no rolling elements at the connected layer of the two plates, on Figs. 10 and 11 for the select numerical values of the system parameters, the interactions between two-time modes, in single nmth amplitude mode of body two frequency stationary like vibrations regime, are presented. From Fig. 10, it is noticable that amplitude–frequency curve of the first harmonic of eigen time function mode in single-amplitude mode pass through resonant regime of the second frequency of external excitation without characteristic onsets of new branches. However, the amplitude response of the second harmonic has resonant jumps in the resonant range of the second frequency of external excitation \( \Omega _{2nm} \in \left[ {185,\,201} \right] \,\text{ s}^{-1} \) and during resonant passage take changes of both values and shape. It stems from this that first harmonic has bigger impact on the second then vice versa. For such a selection of all other system parameters, the hardening effect, right-side inclination, of non-linearity is prominent. The hardening or softening effects of non-linearity in the interconnected layer may be less or more present which depend also on the other parameters of the system. For the set of parameters from paper [34], by changing the value of the amplitude of the external excitations or coefficient of damping, we may find the same phenomena of resonant transition, the resonant jumps, and mutual modes interactions but with more noticable hardening effect. By looking at the first and the last diagrams in Fig. 10, we may notice that the amplitude (same is for phase) responses of the first harmonic of eigen time function modes in single-amplitude mode have small changes after transient regime. At the same time, Fig. 11, the amplitude (phase) responses of the second harmonic have significant changes of the values and the shapes. Therefore, we suggest that the first time harmonic has a greater influence on the second harmonic in the resonant region of the frequencies \( \Omega _{1nm} \) of external excitation.
Frequency characteristic curves for the amplitude of the first time harmonic \( a_{1} =f_{1} \left( {\Omega _{1} } \right) \), for the amplitude of the second time harmonic \( a_{2} =f_{2} \left( {\Omega _{1} } \right) \), for the phase of the first time harmonic \( \phi _{1} =f_{3} \left( {\Omega _{1} } \right) \), and for the phase of the second time harmonic \( \phi _{2} =f_{4} \left( {\Omega _{1} } \right) \) of eigen time function modes in single-amplitude mode on discrete value of excited frequency \( \Omega _{2} =132\,\left[ {s^{-1}} \right] \), with marked corresponding five stationary values by star points A, B, C, D and E
The data of stability or instability of the stationary amplitude and phase of eigen time function modes in single-amplitude mode are explored by linearization of the system of first approximation of solutions (64)–(65) in each discrete stationary vibration state and by composing corresponding characteristic equations and obtaining corresponding roots. The local stability problem is defined by Jacobian matrix of system (64)–(65); the procedure was performed for similar mathematical model in [33]. For obtaining eigen values of that matrix, the corresponding characteristic equation is of the form
Equation (68) is the polynomial of the fourth-order \( \lambda ^{4}+A\lambda ^{3}+B\lambda ^{2}+C\lambda +D=0 \), which coefficients are given in the Appendix B. If eigenvalues \( \lambda \) have negative real parts than that stationary two-frequency like non-linear vibration regimes of eigen time function modes in single shape mode are stable. The values of these coefficients have to be checked for any value of \( \Omega _{is} \) and determined values of \( a_{is} \) for \( i=1,2 \) from the above diagrams and of \( \phi _{is} \) from proper diagrams of phase–frequencies’ curves. For instance, the stared points A, B, C or any else, on the diagrams at Fig. 12 has coordinate stationary values \( \left( {a_{1} ;\phi _{1} ;a_{2} ;\phi _{2} ;\Omega _{1} ;\Omega _{2} } \right) \). With these values, corresponding coefficients from Appendix B are calculated and then roots of the characteristic equation (68) are numerically determined. For point A, the roots are all complex with negative real parts, and thus, this point is on the stable part of the frequency curve. All stationary values were numerically treated, and if all real parts of the all roots of the characteristic equation are negative, then stationary resonant regime is stable. The solution is unstable for at least one positive real part of all roots. Branches presented with dashed line correspond to the expected unstable stationary vibration resonant regimes.
Here, we may add that obtained solutions in time domain of oscillations for couple plates may be used for description of non-linear phenomenon in any of coupled beams, belts, or membranes systems with layer of same features. Their mathematical models in the time domain of their dynamics are just the same.
Using phenomenological analogy approach from [15, 16, 37], and comparing the results from the papers [12, 38, 39] with results in this paper, there are analogies between non-linear phenomena in particular multi-frequency stationary resonant regimes of multi-circular plate system non-linear dynamics and proper resonant forced regimes in chain system non-linear dynamics. Also, we underlined here that non-linear phenomena in particular multi-frequency stationary resonant regimes can be analogously explained in the proper forced resonant regimes of multi-beam, membrane, or belt system non-linear dynamics.
3.6 Concluding remarks
A mathematical model of small transverse oscillations of the hybrid mechanical system class has been established. The hybrid structure of the presented systems consists of connected deformable isotropic bodies of different shapes connected by a layer of evenly distributed discrete systems. Discrete layer elements have different properties of rheological elements by which the forces on ends are defined from the proposed cases of elements. The common characteristics of all elements are the presence of non-linear elasticity of the third order. The general system of coupled partial differential equations of transversal oscillations (56) for systems is derived from D’Alembert’s principle of dynamic equilibrium. We apply separation of variables and divide the proposed solutions into two domains of space and time variables. The shape of body together with boundary conditions determines the form of the space domain in the form of amplitude (shape) functions. The time functions have the same forms for any of considered class of multi-body system forced dynamics. The overall analogy of systems of coupled ordinary non-linear non-homogeneous differential time equations (58) of inherent time functions in the single-amplitude regime is obvious for different physically connected multiple deformable body systems. For each possible nmth amplitude mode, it is possible to determine two related time functions in double-body systems. The existence of mathematical analogies of model for different body shapes indicates the phenomenological analogy too. The whole range of facts present due to the designed non-linearity in the resonant regimes of forced oscillation is applicable for different coupled structures, no matter if they are plates, beams, membranes, or belts. The results of our research are practicable for the qualitative discussion and clarification of dynamical behavior for whole range of mechanical systems with analogue non-linear properties without solving them. In the time domain of the system of coupled non-linear inhomogeneous ordinary differential equations (58), we used the asymptotic method Krylov–Bogoliubov–Mitropolski. It enabled us to analytically determine the first asymptotic approximation of the solution for changes in amplitude and phase in both interrelated time modes, Eqs. (64-5). This system is further numerically processed, and as a solution, we presented the amplitude and phase–frequency characteristics of eigen time functions in the vibration mode of single-amplitude function. We then analyzed the stability of stationary regimes of forced resonant non-linear oscillations for the presented model of a double-plate system. We gave the representation of passage through resonant regimes of forced oscillation for one class of coupled structures, namely the double-plate system connected with system of non-linear visco-elastic discrete elements with rolling properties. However, it is clear that the same phenomena exist within non-linear forced dynamics of system of coupled beams, membranes, or belts with modeled non-linearities.
Non-linearity in the interconnected layer is a cause of resonant jumps in the amplitude and phase–frequency response of time functions corresponding to the single shape mode of oscillation. Among the two jumps, there is an odd number of singular values of stationary amplitudes and phases. They alternate stable and unstable values and build coupled singularities. The trigger of coupled singularities comprises two stables about one unstable stationary value of amplitude or phase. While the frequencies of the external excitation pass through resonant regimes, the value of the stationary amplitude or phase loses stability and is divided into a trigger of three connected singularities—two stable and one unstable saddle-type values. This is a scenario for a simple case where the interaction of time modes is insignificant; for example, Fig. 10. However, if there are mutual interaction between time modes, Figs. 8 and 9, then more than one pair of coupled singularities exist. These instabilities of stationary vibration regimes are related with Hopf bifurcations of the solution (64-65). The bifurcations of saddle point emerges on inflection points or on points of resonant jumps at the amplitude– or phase–frequency curves in system of the averaged system of Duffing type. These points correspond to the bifurcation saddle points of periodic orbits of whole system, [34]. This is valid also for more complex bifurcation of multi-parametric system (64-65) of averaged approximations in presented complex structures. Thus, there exists the unique point from the \( a,\Omega \) space for which this system has degenerative fixed point that is separable into one, two, or more points. At that point, two turns of the amplitude (phase)–frequency curves, see Figs. 8, 9, 10, 11, or 12, unite at the point of vertical tangent. This means that near that point, the starting system of equations (58) has a bifurcation of three periodic orbits.
This review paper shows the power of mathematical analytical calculus which is the same even for physically different systems. The numerical experiments, allowing numerous parameters changes, are strong and useful tool for making the final conclusions between too many input and output variables of complex structure dynamics. The proposed analytical solution for changes in amplitude and phase in the first asymptotic approximation of solution for complex systems dynamics is very useful for in-silico experimentation with different sets of kinetic parameters, initial conditions, and external excitation properties. Hence, the multi-parametric analysis of hybrid deformable bodies dynamics is attainable and conceivable based of our approaches and that opens the new avenues in potential next research [39].
References
K.R. Hedrih (Stevanović), Transversal vibrations of double-plate systems. Acta Mech. Sin. 22, 487–501 (2006). (Springer (hard cower and on line))
K.R. Hedrih (Stevanović), Double plate system with discontinuity in the elastic bounding layer. Acta Mech. Sin. (2007). https://doi.org/10.1007/s10409-007-0061-x ((corrected proof, in press))
K.R. Hedrih (Stevanović), Integrity of dynamical systems. J. Nonlinear Anal. 63, 854–871 (2005)
K.R. Hedrih (Stevanović), Partial fractional order differential equations of transversal vibrations of creep-connected double plate systems, in Monograph—Fractional Differentiation and Its Applications, ed. by A. Le Mahaute, J.A.T. Machado, J.C. Trigeassou, J. Sabatier (U-Book, 2005), p. 289–302
K.R. Hedrih (Stevanović), Transversal vibrations of the axially moving sandwich belts. Arch. Appl. Mech. (2007). https://doi.org/10.1007/s00419-006-0105-x
K.R. Hedrih (Stevanović), The frequency equation theorems of small oscillations of a hybrid system containing coupled discrete and continuous subsystems. Facta Univ. Ser. Mech. Autom. Control Robot. 5(1), 25–41 (2006). http://facta.junis.ni.ac.yu/facta/
K.R. Hedrih (Stevanović), J. Simonović, Transversal Vibrations of a non-conservative double circular plate system. Facta Univ. Ser. Mech. Autom. Control Robot. (2006)
K. Poltorak, K. Nagaya, A method for solving free vibration problems of three-layered plates with arbitrary shape. J. Acoust. Soc. Am. 78–6, 2042–2048 (1985)
K. Poltorak, K. Nagaya, A method for solving forced vibration problems of three-layered plates with arbitrary shape. J. Acoust. Soc. Am. 80–5, 1408–1413 (1986)
K.R. Hedrih (Stevanović), Frequency equations of small oscillations mixed systems of the coupled discrete and continuous subsystems, Mehanika tverdogo tela (Rigid Body Mechanics), Donetsk, Ukraine, vol. 33, pp. 174–189 (2003) (UDC 531.1:534.012:534.013: ISSN 0321-1975)
K.R. Hedrih (Stevanović), Discrete continuum method, in Computational Mechanics, WCCM VI in Conjunction with APCOM’04, Sept. 5–10, 2004, Beijing, China (Tsinghua University Press & Springer-Verlag, 2004), pp. 1–11
K. R. Hedrih (Stevanović), Modes of the homogeneous chain dynamics. Signal Process. 86, 2678–2702 (2006). www.sciencedirect.com/science/journal/01651684(ISSN: 0165-1684)
K.R. Hedrih (Stevanović), J. Simonović, Characteristic Eigen numbers and frequencies of the transversal vibrations of sandwich system, in SEECCM 06—First South-East European Conference on Computational Mechanics, Proceedings, ed. by M. Kojic, M. Papadrakakis (Kragujevac, 2006), pp. 90–94. http://www.seeccn.kg.ac.yu(ISBN 86-81037-13-7, COBISS.SR-ID 131758092, udc 531/533(082))
K. R. Hedrih (Stevanović), Transveral vibrations of creep connected multi plate homogeneous systems, in CD Proceedings, Fifth EUROMECH Nonlinear Dynamics Conference, Eindhoven University of Technology, ed. by D.H. van Campen, M.D. Lazurko, W.P.J.M. van den Over (2005), pp. 1445–1454 (ID 11-428)
M. Petrović, Fenomenološko Preslikavanje (Phenomenological Mapping) (Srpska kraljevska akademija, Štamparija Planeta, Beograd, 1933). http://elibrary.matf.bg.ac.rs/handle/123456789/475
M. Petrović, Elementi Matematičke Fenomenologije, (Elements of Mathematical Phenomenology) (Srpska kraljevska akademija, Državna Štamparija Kraljevine Srbije, Beograd, 1911). http://elibrary.matf.bg.ac.rs/handle/123456789/476
R. Penrose, The Emperors New Mind: Concerning Computers, Minds and The Laws of Physics (Oxford University Press, Oxford, 1989)
J. Gleick, Chaos: Making a New Science (Vintage, 1987)
D.P. Rašković, Teorija oscilacija, (Theory of oscillations), in Naučna knjiga (1965), p. 503 (in Serbian). http://elibrary.matf.bg.ac.rs/handle/123456789/4754
D.P. Rašković, Analitička mehanika (Analytical Mechanics). Mašinski fakultet Kragujevac (1974). http://elibrary.matf.bg.ac.rs/handle/123456789/3778
K.R. Hedrih (Stevanović), Analogy between models of stress state, strain state and state of the body mass inertia moments. Facta Univ. Ser. Mech. Autom. Control Robot. Nis 1(1), 105–120 (1991)
K.R. Hedrih (Stevanović), Mathematical analogy and phenomenological mapping: vibrations of multi plate and multi beam homogeneous systems, in Scientific Buletletin of the “Politehnica” University of Timisoara, Romania, Transaction on Mechanics, Editura Politenica, Tom 50 (64), Special Issue, 11–18 (2005) (ISSN 1224-6077)
H. Freudenthal, Didactical Phenomenology of Mathematical Structures (Springer, Berlin, 1986)
F. Pfeiffer, P. Fritz, J. Srnik, Nonlinear vibrations of chains. J. Vib. Control 3(4), 397–410 (1997)
R. Walsh, Phenomenological mapping: a method for describing and comparing states of consciousness. J. Transpers. Psychol. 27, 125–5 (1995)
R.I. Kelebanov, M.J. Maldacena, Solving quantum field theories via curved space-times. Phys. Today 68, 28–33 (2009)
K.R. Hedrih (Stevanović), J. Simonović, Multi-frequency analysis of the double circular plate system non-linear dynamics. Nonlinear Dyn. 67(3), 2299–2315 (2012)
K.R. Hedrih (Stevanović), J. Simonović, Non-linear dynamics of the sandwich double circular plate system. Int. J. Non-Linear Mech. 45(9), 902–918 (2010)
K.R. Hedrih (Stevanović), Energy analysis in the nonlinear hybrid system containing linear and nonlinear subsystem coupled by hereditary element. Nonlinear Dyn. 51(1), 127–140 (2007). https://doi.org/10.1007/s11071-007-9197-2
K.R. Hedrih (Stevanović), Energy transfer in the hybrid system dynamics (energy transfer in the axially moving double belt system), Special Issue. Arch. Appl. Mech. 79(6–7), 529–540 (2009). https://doi.org/10.1007/s00419-008-0285-7
D.S. Mitrinović, D.Ž Djoković, Special functions (Specijalne gunkcije) (Gradjevinska knjiga, Beograd, 1964), p. 267
O. A. Goroško, K.R. Hedrih (Stevanović), Analitička dinamika (mehanika) diskretnih naslednih sistema, (Analytical Dynamics (Mechanics) of Discrete Hereditary Systems) (University of Niš, Monograph, 2001), p. 426 (ISBN 86-7181-054-2)
J. Simonović, Dynamics and Stability of Dynamics Hybrid Systems. Doctoral dissertation on Serbian, Faculty of Mechanical Engineering, University of Niš (2012), p. 341
K.R. Hedrih (Stevanović), J. Simonović, Structural analogies on systems of deformable bodies coupled with non-linear layers. Int. J. Non-Linear Mech. 73, 18–24 (2015). https://doi.org/10.1016/j.ijnonlinmec.2014.11.004
Yu.A. Mitropolski, Nelinyeynaya mehanika-Asimptoticcheskie metodi (Institut matematiki NAN Ukraini, Kiev, 1995), p. 397
Yu.A. Mitropolski, N.V. Dao, Lectures on Asymptotic Methods of Nonlinear Dynamics (Vietnam National University Publishing House, Hanoi, 2003), p. 494
M. Petrović, Mecanismes communs aux phenomenes disparates. Paris (1921). http://en.wikipedia.org/wiki/Mihailo_Petrovi%C4%87
K. R. Hedrih (Stevanović), Modes of the homogeneous chain dynamics. Signal Process. 86, 2678–2702 (2006)
K.R. Hedrih (Stevanović), A.N. Hedrih, Phenomenological mapping and dynamical absorptions in chain systems with multiple degrees of freedom. J. Vib. Control. https://doi.org/10.1177/1077546314525984. http://jvc.sagepub.com.proxy.kobson.nb.rs:2048/. http://www.sagepub.co.uk/journal.aspx?pid=105701(ISSN 1077-5463)
Acknowledgements
The paper is a part of the research done within the project OI 174001 of the Serbian Ministry of Education, Science and Technological Development. Five excerpts and Figs. 8, 9, 10, 11, 12 were reprinted from [34] International Journal of Non-Linear Mechanics, 73/7, Katica R. (Stevanovic) Hedrih and Julijana D. Simonovic, Structural analogies of deformable bodies coupled with non-linear layers, Pages No. 18-24, Copyright (2015), with permission from Elsevier (License Number 5114790114946).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
Appendix B
Rights and permissions
About this article
Cite this article
(Stevanović) Hedrih, K.R., Simonović, J.D. Structural analogies for hybrid discrete-continuum systems of deformable bodies coupled with non-linear layers. Eur. Phys. J. Spec. Top. 230, 3705–3729 (2021). https://doi.org/10.1140/epjs/s11734-021-00250-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjs/s11734-021-00250-6