1 Introduction

Despite their vast variation of applications and design bases, wavelets have a common property of de-correlation. The typical implementation of the discrete wavelet transform (DWT) is subband filtering. Due to its design flexibility and immediate relation to classical subband filtering, the lifting style decomposition is popular [7, 8, 11, 12]. Besides, the synthesis operation is completely symmetric and the de-correlation concept is automatically implemented in the “prediction” scheme (P) of the lifting decomposition. Obviously, other types of transforms, including the classical matrix-based transforms, also aim for the de-correlation of the input random vector. The relation between a (multi-level) subband decomposition and a transform matrix was explained in [2], where a technique to define a wavelet decomposition structure in terms of a block transform matrix (hence the name; block wavelet transform—BWT) was devised. In that work, the generation method of the corresponding BWT from any DWT filter bank was explained, and various numerical examples of such transforms were provided [2]. The original methodology of BWT generation was feeding the balanced subband tree with shifted unit sample trains, each with a period of \(L=2^N\), where N is the number of decomposition levels. The outputs of each branch in the subband tree naturally become constant, rendering a column of the BWT.

In the previous research by the authors, the iterative determination of a \(2^N \times 2^N\) BWT matrix generating algorithm (from smaller BWT counterparts) was developed, a filter design technique using the orthogonality constraints of BWT matrices for the lifting scheme (envisaged by Sweldens [11, 12]) was proposed together with another filter design technique which yield BWT matrices that would mimic statistically optimal Karhunen–Loéve transform (KLT) matrices, which are, by construction, best de-correlating matrices [9, 10]. In essence, the previous research is the dual problem of the method in [2], instead of generating a BWT from DWT, to try to determine filter coefficients of DWT, which is expected to produce a particular BWT (that is close to KLT in a Frobenius norm). One attempting method was investigated by Dogan and Gerek [4–6] for orthogonal wavelets using orthogonal QMF subband structures. However, QMF subband filters are too restrictive, and the distance between a KLT matrix and the BWT of a QMF DWT cannot be made arbitrarily close.

The drawback of author’ s previous research is the wavelets’ dependence to the test images, i.e., wavelets varied for each test image [9, 10]. Questions are, would one wavelet of a certain test image work on the other test images or is there a possibility of the existence of a general wavelet? This research deals with the second question. Signal-specific wavelets bring problems with them, and a general solution must be found. This paper concludes the previous research [9] by generalizing the signal-specific wavelets described in [9]. Thus, the aim of this paper is to achieve a general solution by designing the general wavelet. Hence, in this work, the more flexible case of biorthogonal lifting style wavelet parametrization is not considered through the same KLT approximation idea as in the previous research [9, 10], but a general wavelet is introduced which is only based on the KLT approximation idea.

The paper starts by briefly explaining the lifting scheme in Sect. 2. In the lifting scheme, the author describes the motivation behind. Next, the general wavelet is introduced in Sect. 3, and finally in Sect. 4, conclusions are provided.

2 Lifting scheme

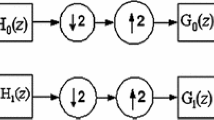
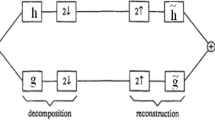
Lifting is a smart method to implement a 2-channel decomposition in the polyphase domain (Fig. 1). For the 1-level lifting decomposition structure, the polyphase matrix is defined as

$$\begin{aligned} \mathbf H _{p}=\left[ \begin{array}{cc} H_{0,ev}(z) &{} H_{0,od}(z) \\ H_{1,ev}(z) &{} H_{1,od}(z) \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} H_{0,ev}(z)&= 1 - P(z)U(z)\\ H_{0,od}(z)&= U(z)\\ H_{1,ev}(z)&= - P(z)\\ H_{1,od}(z)&= 1\\ \end{aligned} \end{aligned}$$

and the subband decomposition filters are

$$\begin{aligned} H_{0}(z)= & {} H_{0,ev}(z^{2}) + zH_{0,od}(z^{2})\\ H_{1}(z)= & {} H_{1,ev}(z^{2}) + zH_{1,od}(z^{2}) \end{aligned}$$

In order to design a regularized wavelet having at least one vanishing moment so that its corresponding scaling and wavelet dilation equations converge iteratively, \(H_{0}(z=-1)\) and \(H_{1}(z=1)\) must equal to 0. This condition automatically imposes that, when the prediction filter is in the form: \(P(z) = \sum _{i}a_{-i}z^{i}\) and the update filter is in the form: \(U(z) = \sum _{i}b_{i}z^{-i}\), the coefficients must obey the following conditions:

$$\begin{aligned} \begin{aligned} \alpha&=\sum _{i}a_{-i}=1\\ \beta&=\sum _{i}b_{i}=0.5 \end{aligned} \end{aligned}$$
(1)

These filter coefficient constraints are, therefore, adopted as an initial condition for the BWT construction algorithms, while the minimization of the difference between the BWT and KLT matrices remains the optimization criterion.

Fig. 1
figure 1

1-level lifting structure

Full size image

Daubechies 5-tap/3-tap (Daub 5/3) wavelet has the following prediction (P(z)) and update (U(z)) filters

$$\begin{aligned} \begin{aligned} P(z)&=\frac{1}{2}+\frac{1}{2}z\\ U(z)&=\frac{1}{4}+\frac{1}{4}z{^-1} \end{aligned} \end{aligned}$$
(2)

where it must be underlined that the Daub 5/3 wavelet has a major advantage. Its implementation consists of bitwise shifts and additions [1, 3]. Hence, it would be better if the general wavelet to be proposed possesses such properties.

The basic methodology starts with the observation of 32 wavelet samples contained from 16 test images in the author’s previous study [9]. Then, a general wavelet is proposed, which possesses the shifting and addition operations of Daubechies 5/3 wavelet. In the author’s previous research, it has been described in detail that \(8 \times 8\) design works worse than the \(4 \times 4\) case [9]. So it must be noted that the author’s operations are on \(4 \times 4\) BWTs, i.e., 5-tap/3-tap biorthogonal wavelets.

3 Results and discussion

When the 32 wavelets of the previous research are investigated [9], it is seen that the update filter approximated for Barbara’s column KLT matrix is of length 1, i.e., \(U(z)=0.5\). This is due to the fact that Barbara’s column KLT matrix has second and third rows where the magnitudes of the elements are close to each other forcing the differences and summations of filter the coefficients to be equal. When the summation and difference of two variables are close to each other, one variable approaches to 0. In this case, Barbara’ s column KLT approximation resulted an update filter \(U(z)=0.5000\), and the prediction filter was no different, which was \(P(z)=0.9932+0.0068z\).

However, for the rest of the 31 cases (including 8 cases given in Table 4 of [9]), \(a_{0}\) varies around 0.75, whereas \(a_{-1}\) varies around 0.25. Similarly, \(b_{0}\) varies around 0.4375, whereas \(a_{-1}\) varies around 0.0625 [9]. These picked pivot numbers are the closest coefficients that can be described by shifting and addition bitwise operations.

3.1 Definition of a general wavelet using the \(4 \times 4\) KLT approximation wavelets

Using these filter coefficient results obtained in our previous research [9], we have devised general wavelet coefficients as shown in Eq. 3

$$\begin{aligned} \begin{aligned} P&=\frac{3}{4}+\frac{1}{4}z\\ U&=\frac{7}{16}+\frac{1}{16}z^{-1} \end{aligned} \end{aligned}$$
(3)

The importance of these prediction and update filters is not only their character to be generalized definitions, but also they include bitwise additions and shifts as in Daubechies 5/3.

The delayer components (i.e., z/4 and \(z^{-1}\)/16) are plain bitwise shifting and addition operations. Compared to the Daubechies’ delayer shiftings of 1 for P and 2 for U (i.e., z/2 and \(z^{-1}\)/4), the wavelet introduced in this paper has delayer shiftings of 2 for P and 4 for U.

Likewise, the wavelet introduced in this paper has scalar shiftings of 2 for P (1/4) and 4 for U (1/16) compared to Daubechies’ scalar shiftings of 1 for P (1/2) and 2 for U (1/4). On the other hand, using parallel architecture, it is possible to achieve bitwise shifting and addition operations for scalar components, which are 3/4 and 7/16. Off course, this adds 3 addition operations for P and 7 addition operations to U realizations.

The lifting filters of Eq. 3 result analysis subband filters such as

$$\begin{aligned} \begin{aligned} H_{0}(z)&=\frac{1}{64}\left( -7z^{2}+28z+42+4z^{-1}-3z^{-2}\right) \\ H_{1}(z)&=\frac{1}{4}\left( -z^{2}+4z-3\right) \end{aligned} \end{aligned}$$
(4)

and the synthesis subband filters become

$$\begin{aligned} G_{0}(z)= & {} -z^{-1}H_{1}(-z)\nonumber \\= & {} \frac{\left( z+4+3z^{-1}\right) }{4}\end{aligned}$$
(5)
$$\begin{aligned} G_{1}(z)= & {} z^{-1}H_{0}(-z)\nonumber \\= & {} \frac{\left( -7z-28+42z^{-1}-4z^{-2}-3z^{-3}\right) }{64} \end{aligned}$$
(6)

The variances of the wavelet tree images are listed in Table 1. As can be seen, the wavelet introduced in this research gives better variance results with better coding gain and energy unbalance.

Table 1 Variances of the wavelet tree images for the Daubechies 5/3 and the general wavelet
Full size table

4 Conclusions

In this research, a general wavelet is presented based on a signal-specific methodology to design lifting wavelets at certain sizes (5/3 for this case). The described general wavelet is inspired by wavelets which construct a \(4 \times 4\) orthogonal BWT matrix that mimic a \(4 \times 4\) KLT matrix corresponding to a time series. Experimentally, the general wavelet was tested on the 16 different typical test images, and it was observed that the designed wavelet has good regularity properties and also provides plausible de-correlation performances as compared to the Daubechies 5/3 wavelet.