Abstract—A new biorthogonal system of wavelet bases has been constructed, which is oriented toward reconstructing the useful signal of a measuring system if the measurement process is represented as a convolution model. New biorthogonal wavelet bases are obtained by using a instrumental function to modify a Kravchenko orthogonal wavelet system with a finite spectrum. The properties of new biorthogonal frequency-modified wavelets are studied, and digital filters that realize fast computational algorithms are constructed. Schemes for multiresolution analysis are proposed, which, during discrete wavelet transform, immediately solve the problem of reconstructing the useful signal, as well as effective noise suppression, which can significantly speed up computations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 FORMULATION OF THE PROBLEM
In various fields of physics (radio astronomy, radar, infrared radar, various types of microscopy, etc.), it is necessary to take into how the measuring path of the technical system and the communication channel (the inertia of the medium through which the signal propagates) influence recorded signals or images. In this case, there are distortions in the real signal distribution that depend on the instrumental function (response of the apparatus) of the technical system, and noise is added. If the form of the instrumental function is known, then the problem of reconstructing the useful signal or at least the problem of improving the distribution quality of the recorded signal is reduced to solving an integral equation that relates the recorded and initial distribution of the sought value. In the mathematical description of this problem, the convolution model of representing the measuring process is widely used, which considers the solution to Fredholm convolution integral equation of the first kind. As is known, such a problem is ill-posed, i.e., unstable to arbitrarily small measurement errors. Therefore, when solving it, the useful signal is estimated based on available a priori information about the signal, noise, instrumental function, and technical requirements for the processing system.
The general form of the convolution integral equation has the form
The convolution operator \(\mathcal{L}\) is determined as follows:
For practical application, the following problem statement is the most interesting: to estimate the useful signal x(t) initially distorted by the impulse response λ (t) of a linear stationary system followed by noise n(t):
The noise n(t) is assumed to be additive and white Gaussian noise (AWGN) with variance σ2. AWGN is a model well suited to mathematically describe many physical processes.
There are many different methods for solving (1) [1–7]. For Fourier transform (FT), the most widely used are FT methods with Tikhonov regularization and the Wiener filtering method, which use a regularizing component R(ω).
Amplified noise \({{\hat {n}(\omega )} \mathord{\left/ {\vphantom {{\hat {n}(\omega )} {\hat {\lambda }(\omega )}}} \right. \kern-0em} {\hat {\lambda }(\omega )}}\) is reduced by a filter with a frequency response [1–7]
Note that for R → 0, the spectrum \(\hat {K}(\omega )\) becomes the expression for inverse or pseudoinverse filtering. Thus, the problem becomes ill-posed, and the solution is unstable.
The following relation holds for FT estimation of the useful signal xr, calculated by FT regularization methods:
Here \({{\hat {x}}_{{\text{r}}}}\) and \({{{{{\hat {n}}}_{{\text{r}}}}} \mathord{\left/ {\vphantom {{{{{\hat {n}}}_{{\text{r}}}}} {\hat {\lambda }}}} \right. \kern-0em} {\hat {\lambda }}}\) are the terms of the solution spectrum \({{\hat {\tilde {x}}}_{{\text{r}}}}\), respectively, of the FT of the cleaned signal xr and past noise \({{\mathcal{L}}^{{ - 1}}}{{n}_{{\text{r}}}},\) entering into the estimate of the useful signal \({{\tilde {x}}_{{\text{r}}}}\).
A distinctive feature of using FT to solve (1) is compact representation of noise \({{\mathcal{L}}^{{ - 1}}}n,\) since FT acts as a Karhunen–Loeve expansion [10–12] and decorrelates the noise \({{\mathcal{L}}^{{ - 1}}}n.\) Therefore, among all linear transformations with FT, the main noise energy \({{\mathcal{L}}^{{ - 1}}}n\) is concentrated in the smallest possible number of coefficients. The best results in solving the convolution integral equation by FT methods can be achieved when an undistorted signal x(t) is uniformly smooth and effectively approximated by a Fourier basis.
However, although the Fourier basis distinguishes frequencies well, it does not provide information on sharp and short bursts, drops, discontinuity points, isolated singularities, nor generally on the local behavior of the function, since the basis exp(jωt) covers the entire real line, and FT of the function \(\hat {x}(\omega )\) depends on the x(t) values for all \(t \in \mathbb{R}\) [13–23]. In the best case, a local singularity will have a very wide spectrum and the signal energy will be concentrated in a significant number of Fourier coefficients. Estimation of the useful signal x(t) is concentrated in a neighborhood of singular points. In this case, for a compact representation of the signal x(t) with the indicated singularities, it is desirable that the basis elements be localized as best as possible in time and frequency. Wavelet bases satisfy this requirement. As well, additional conditions are imposed, such as orthogonality of the basis, compactness of wavelet supports, etc. Subsequently, by performing threshold processing of the expansion coefficients in a suitable wavelet basis according to [13, 14, 24], a near-optimal estimate of the useful signal x(t) can be achieved.
The use of wavelet transform (WT) assumes that the choice of the wavelet basis is based on its properties. Since the solution to the convolution integral equation is realized in the spectral domain, it is necessary to choose a wavelet basis with a compact support in the frequency domain, a fairly rapid decrease, and a small number of wavelet filter coefficients. From this aspect, Kravchenko wavelets are optimal [25–28]; they have better characteristics compared to known wavelet systems with a finite spectrum (Meyer, Kotelnikov–Shannon wavelets). In addition, it is possible to use finite wavelets in the time domain (e.g., Daubechies wavelets), which have good steepness of fronts in the frequency domain. The resulting systematic error should be estimated for each specific case.
Thus, Fourier and wavelet bases have several advantages in the representation and processing of signals. These advantages can be used to create a combined approach to solving convolution integral equation (1), which should consist of separate blocks [29]: fast FT (FFT), deconvolution, inverse fast FT (IFFT), discrete WT (DWT), threshold processing of the coefficients, and inverse discrete WT (IDWT). This inevitably leads to additional hardware and time costs. To ensure maximum efficiency with minimal computational resources, it is necessary to combine the solutions of several processing problems in one wavelet transform. This is done via DWT using a modification of the selected orthogonal Kravchenko wavelet system [25–28]. The modified Kravchenko wavelets must also meet all the requirements of multiresolution analysis (MRA) theory so that it is possible to construct filter blocks for fast wavelet transforms. Such a modification gives rise to a nonstationary MRA based on the family of Kravchenko biorthogonal wavelet bases.
2 WAVELET APPROXIMATION OF THE SOLUTION TO THE CONVOLUTION INTEGRAL EQUATION
Let the scaling functions and wavelets \(\{ {{\varphi }_{{{{j}_{0}},k}}}(t),{{\psi }_{{j,k}}}(t):j \geqslant {{j}_{0}},k \in \mathbb{Z}\} \) form an orthogonal multiresolution expansion L2(\(\mathbb{R}\)) (\( - \infty \),\(\infty \)). Let us consider a short-scale approximation of a piecewise continuous function f(x) \( \in \)\({{L}^{2}}(\mathbb{R}),\) which has limited variation
In the case of nondifferentiability of the function, the total variation f(x) can be calculated by considering the derivatives in the sense of generalized functions [13, 30–32]. At scale J, the orthogonal projection f(t) on \({{{\mathbf{V}}}_{J}} \subset {{L}^{2}}(\mathbb{R})\) has the form
where \({{P}_{{{{j}_{0}}}}},\)\({{Q}_{j}}\) are the subspace orthogonal projection operators \({{{\mathbf{V}}}_{{{{j}_{0}}}}}\) and Wj, parameter j = j0, …, J – 1, and j0 is the roughest scale; \({{\varphi }_{{j,k}}}(t) = {{2}^{{j/2}}}\varphi ({{2}^{j}}t - k),\)\({{\psi }_{{j,k}}}(t) = {{2}^{{j/2}}}\psi ({{2}^{j}}t - k)\) are shifts/compression of the scaling and wavelet functions; \({{a}_{{j,k}}} = \int {f(t)} {{\varphi }_{{j,k}}}(t)dt,\)\({{b}_{{j,k}}} = \int {f(t)} {{\psi }_{{j,k}}}(t)dt\) are the expansion coefficients of the basis of the scaling and wavelet functions.
Because VJ admits an orthonormal basis \(\{ {{\varphi }_{{J,k}}}(t):k \in \mathbb{Z}\} ,\) this projection can be rewritten as the finite sum of scaling functions at scale J with a uniform shift k:
Wavelets can efficiently approximate uniformly smooth signals by a finite number of basis functions. The approximation error is related to the Sobolev differentiability [30, 31]. It can be calculated for discontinuous signals with limited variation [39, 40]. The spaces of the Sobolev functions \({{H}^{s}}(\mathbb{R}),\) which are s times differentiable, are the spaces of functions \(f \in {{L}^{2}}(\mathbb{R})\), the Fourier transform of which satisfies the inequality
Here we consider the wavelet  having a quick decrease and q zero moments. This means that for any 0 ≤ p ≤ q and \(m \in \mathbb{Z}\) there is a constant Cm such that
having a quick decrease and q zero moments. This means that for any 0 ≤ p ≤ q and \(m \in \mathbb{Z}\) there is a constant Cm such that
The wavelet transform can be considered a multiscale differential operator of order q [13, 14]. This establishes the relationship between the differentiability of the function f and the decrease of its wavelet transform at small scales [13]. Therefore, efficient approximation \(f \in {{H}^{s}}(\mathbb{R})\) requires q > s. According to [13], the Sobolev smoothness is equivalent to a fast decrease in the wavelet coefficients |(f, ψj,k)| for a decrease in scale j. If f is a piecewise smooth function, the nonlinear wavelet approximation is more efficient, in which the approximation scale is refined in the vicinity of each singularity. Then, the approximation is calculated by the coefficients of the wavelet expansion with the largest amplitude, which can be obtained by threshold processing of the wavelet coefficients of the linear approximation. To study the implementation of nonlinear wavelet approximations, Besov spaces \(B_{{\beta ,\gamma }}^{s},\) are used, which are a natural generalization of Sobolev spaces for a fractional order of differentiation. The corresponding embedding theorems have been obtained in many cases [13, 33, 34]:
Besov spaces contain functions that are not differentiable s times at all points. Even if f is discontinuous, but the number of discontinuities is finite and f satisfies the uniform Lipschitz condition α between these discontinuities, then \(f \in B_{{\beta ,\gamma }}^{s}\) (at 1/p <α +1/2, p = β = γ).
For convenience of notation, we assume that the sequence of scales j and shifts k is not violated in (5) and a nonlinear approximation is obtained when some of the coefficients bj, k take zero values as a result of threshold processing.
Equation (5) in the frequency domain has the form
Here \({{\hat {\varphi }}_{{{{j}_{0}}}}}(\omega ) = {{2}^{{ - j/2}}}\hat {\varphi }\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{0}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{0}}}}}}}} \right),\)\({{\hat {\psi }}_{j}}(\omega ) = {{2}^{{ - j/2}}}\hat {\psi }\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{j}}}}} \right. \kern-0em} {{{2}^{j}}}}} \right),\) and \({{a}_{{{{j}_{0}}}}}(\omega )\) and \({{b}_{j}}(\omega )\) are periodic frequency functions with a period \({{2}^{{{{j}_{0}} + 1}}}\pi \) and 2j + 1π, obtained from the expansion coefficients \({{a}_{{{{j}_{0}},k}}}\) and \({{b}_{{j,k}}}\)
We write (6) in the frequency domain:
Using the scaling equations [13–20]
we show that aJ(ω) can be obtained from the frequency functions aJ – 1(ω) and bJ – 1(ω). In (9) and (10), \({{H}_{0}}(\omega ) = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}\sum\nolimits_k {{{h}_{k}}\exp ( - ik\omega )} \) =  is the frequency response function of the scaling function with filter coefficients \(\{ {{h}_{k}}:k \in \mathbb{Z}\} \); \({{G}_{0}}(\omega ) = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}\sum\nolimits_k {{{g}_{k}}\exp ( - ik\omega )} \) = \({1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}G(\omega )\) is the wavelet function of the frequency response with filter coefficients \(\{ {{g}_{k}}:k \in \mathbb{Z}\} .\)
is the frequency response function of the scaling function with filter coefficients \(\{ {{h}_{k}}:k \in \mathbb{Z}\} \); \({{G}_{0}}(\omega ) = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}\sum\nolimits_k {{{g}_{k}}\exp ( - ik\omega )} \) = \({1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}G(\omega )\) is the wavelet function of the frequency response with filter coefficients \(\{ {{g}_{k}}:k \in \mathbb{Z}\} .\)
The Fourier transform \({{\hat {f}}_{J}}(\omega )\) is determined by Eq. (8) at scale J and by \(\hat {\varphi }(\omega )\), \(\hat {\psi }(\omega )\) at scale J – 1:
Then,
Thus, the formula for reconstructing aJ(ω) by aJ – 1(ω) and bJ – 1(ω) has the form
In a similar way, using scaling equations (9), (10), we can obtain an expansion algorithm in the frequency domain [13–20]:
Let us consider the wavelet approximation of the solution to convolution integral equation (1) in the frequency domain in the case \(\lambda \in {{L}^{1}}(\mathbb{R}),\)\(\hat {\lambda }(\omega ) \ne 0\) with a limited right-hand side \(y(t) \in {{H}^{p}}\):
When Kravchenko wavelets with a finite spectrum are applied, the following theorem holds.
Theorem 1. Let \(y(t) \in {{{\mathbf{V}}}_{J}},\)\(\lambda \in {{L}^{1}}(\mathbb{R})\) and \(\hat {\lambda }(\omega ) \ne 0\) for \({{\hat {\varphi }}_{J}}(\omega ) \ne 0,\)\(\sup {\kern 1pt} {\text{p}}{\kern 1pt} \,{{\hat {\varphi }}_{J}}(\omega )\) = \(\left[ { - {{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3});{{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right].\) Then, convolution integral equation (1) has a unique solution in the subspace VJ +1.
Proof. If \(y\, \in {{{\mathbf{V}}}_{J}}\), then \(y(t) = {{P}_{J}}y(t)\) = \({{y}_{J}}(t) = \sum\nolimits_k {a_{{J,k}}^{y}{{\varphi }_{{j,k}}}(t)dt} ,\) where \(a_{{J,k}}^{y} = \int {y(t)} {{\varphi }_{{J,k}}}(t)dt,\)\(\{ a_{{J,k}}^{y}\} \in {{l}^{2}},k \in \mathbb{Z}{\kern 1pt} {\kern 1pt} .\) Hence, in the frequency domain \({{\hat {y}}_{J}}(\omega ) = a_{J}^{y}(\omega ){{\hat {\varphi }}_{J}}\left( \omega \right),\)\(k \in \mathbb{Z}\,,\) where \(a_{J}^{y}(\omega )\) is a periodic function with a period 2J+ 1π.
Using the frequency function \(\hat {K}(\omega )\), the FT of the regularized solution to convolution integral equation (1) has the form
Since
Function \({{H}_{0}}\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}}} \right)\) is periodic with a period 2J + 2π and is not zero in the intervals \(\left[ { - {{2}^{J}}\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right) + {{2}^{{J + 2}}}\pi k;{{2}^{J}}\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right) + {{2}^{{J + 2}}}\pi k} \right],\)\(k \in \mathbb{Z}\).
Because \(a_{J}^{y}(\omega )\) has a period of 2J+ 1π, the product \(a_{J}^{y}(\omega ){{H}_{0}}\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}}} \right)\) is a 2J+ 2π-periodic function. If \(\hat {K}(\omega )\) will be periodically continued with a period of 2J+ 2π, then this will not change (17):
where \({{\left[ {{{{\left. {\hat {K}(\omega )} \right|}}_{{\omega \in \left[ { - {{2}^{J}}\frac{{4\pi }}{3};{{2}^{J}}\frac{{4\pi }}{3}} \right]}}}} \right]}_{{{{2}^{{J + 2}}}\pi }}}\) is a 2J + 2π-periodic continuation of the function \(\hat {K}(\omega )\) limited to the interval \(\left[ { - {{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3});{{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right].\)
Thus, the product of the first three terms in expression (18) is a 2J+ 2π-periodic function (Fig. 1).
Position of Fourier transforms of functions for use of Kravchenko wavelets {\(\widetilde {up}\)}: curve 1, \({{H}_{0}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}})\); curve 2, \({{\left[ {{{{\left. {\hat {K}(\omega )} \right|}}_{{\omega \in \left[ { - {{2}^{J}}\frac{{4\pi }}{3};{{2}^{J}}\frac{{4\pi }}{3}} \right]}}}} \right]}_{{{{2}^{{J + 2}}}\pi }}}\); curve 3, \(a_{J}^{y}(\omega )\).
We introduce the following notation:
\(a_{{J + 1}}^{{{{{\tilde {x}}}_{P}}}}(\omega ) = {{\left[ {{{{\left. {\hat {K}(\omega )} \right|}}_{{\omega \in \left[ { - {{2}^{J}}\frac{{4\pi }}{3};{{2}^{J}}\frac{{4\pi }}{3}} \right]}}}} \right]}_{{{{2}^{{J + 2}}}\pi }}}a_{J}^{y}(\omega ){{H}_{0}}\left( {\frac{\omega }{{{{2}^{{J + 1}}}}}} \right)\) is a 2J+ 2π-periodic frequency function.
We find that
Consequently, \({{\tilde {x}}_{{\text{r}}}} \in {{{\mathbf{V}}}_{{J + 1}}}.\) However, if the frequency response \(\hat {\lambda }(\omega )\) is continuous and nonzero at \(\left[ { - {{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3});{{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right],\) then the frequency function \(\hat {K}(\omega )\) has the same properties. Then (1) has a unique solution, as required.
If \(y(t) \notin {{{\mathbf{V}}}_{J}}\), then y(t) is projected on the space of the scaling functions of the finest scale VJ. As a result, the convolution equation is transforms to
This equation has a unique solution \({{\tilde {x}}_{{J + 1}}}(t) \in {{{\mathbf{V}}}_{{J + 1}}}\) such that \(\left( {\lambda {\text{*}}{{{\tilde {x}}}_{{J + 1}}}} \right)(t) = {{y}_{J}}(t).\) Thus, \(\tilde {x}_{{J + 1}}^{{}}(t)\) is a wavelet approximation of the exact solution \(\bar {x}\) and an estimate can be obtained.
Theorem 2. Let the kernel of the convolution integral equation \(\lambda \in {{L}^{1}}(\mathbb{R})\) have a nonzero Fourier transform, \(\hat {\lambda }(\omega ) \ne 0\) on \({\text{supp(}}\hat {\varphi }{\text{)}}\), where φ (t) is the scaling function from the Kravchenko wavelet systems. If α, β are real numbers such that 1 ≤ α ≤ β \(\hat {\lambda }(\omega ) \geqslant C{{\left( {1 + {{\omega }^{2}}} \right)}^{{ - \alpha /2}}},\)\(y \in {{H}^{\beta }}\), then the following estimate holds:
Proof. Using the unitarity of the Fourier transform, we write
Since the regularizing component R(ω) is always positive and \(\hat {\lambda }(\omega ) \ne 0,\) then the stabilizing factor takes a value of \(0 < \frac{{{{{\left| {\hat {\lambda }(\omega )} \right|}}^{2}}}}{{{{{\left| {\hat {\lambda }(\omega )} \right|}}^{2}} + R(\omega )}} \leqslant 1.\)
Then,
The theorem is proved.
According to Theorem 1, if the function of the right-hand side \(y(t) \in {{{\mathbf{V}}}_{J}},\) then
Since there is no signal x(t) or its linear transformation \(\mathcal{L}x(t)\), the expansion coefficients in (22) cannot be calculated immediately. Therefore, we will use the sequence of functions {\({{\xi }_{{J,k}}}(t)\): k\( \in \mathbb{Z}\)} such that
Since the transformation \(\mathcal{L}\) is uniform, the function \({{\xi }_{{J,k}}}(t)\) also represents shifts and tension/compression of some function \(\xi (t)\). Moreover, the family of functions \(\{ {{\xi }_{{J,k}}}(t):k \in \mathbb{Z}\} \) no longer has the property of orthonormality, but forms a stable basis. Therefore, such constants 0 < A ≤ B <∞ should exist that
for all quadratically summable sequences  (see proof below).
(see proof below).
The problem of constructing functions \({{\xi }_{{J,k}}}(t)\) can be solved using a dual basis \({{\tilde {\xi }}_{{J,k}}}(t)\) in \({{L}^{2}}(\mathbb{R})\). It is known [13–15] that a basis \({{\tilde {\xi }}_{{J,k}}}(t)\) satisfying the duality relations \(\left( {{{\xi }_{{J,n}}}(t),{{{\tilde {\xi }}}_{{J,k}}}(t)} \right) = {{\delta }_{{n,k}}},\) exists; moreover, it admits construction of a biorthogonal wavelet system [13–15] that can be used to estimate the useful signal x(t) initially distorted by the impulse response λ (t) followed by noise n(t).
3 CONSTRUCTION OF BIORTHOGONAL FREQUENCY-MODIFIED WAVELETS
Let an unknown function \(x\,(t)\) in (1) belong to the space of scaling functions \({{{\mathbf{V}}}_{{J + 1}}} = \overline { \cup \{ {{\varphi }_{{J + 1,k}}}:k \in \mathbb{Z}\} } ,\) where \(\varphi (t)\) is the orthonormal scaling function with a finite spectrum. As \(\varphi (t)\), in accordance with the previously described advantages, we take the scaling function from the family of Kravchenko wavelet bases {\(\widetilde {up}(\omega )\)} [25–28]. If we represent the estimate of the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\) from the observed signal \(y(t)\) in the form of an expansion over \(\{ {{\varphi }_{{J + 1,k}}}:k \in \mathbb{Z}\} ,\) then
If (4) is written as \(\hat {K}{{(\omega )}^{{ - 1}}}{{\hat {\tilde {x}}}_{{\text{r}}}}(\omega ) = \hat {y}(\omega ),\) we obtain
We denote
then Eq. (24) takes the following form:
Thus, the solution to convolution integral equation (1) with respect to the unknown function \(x\,(t)\) corresponds to solution (26) with respect to an unknown sequence of expansion coefficients \(\{ a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}:k \in \mathbb{Z}\} \), which are found as the scalar product of a known function y(t) and functions \(\{ {{\tilde {\xi }}_{{J,k}}}(t):k \in \mathbb{Z}\} \), which are a dual basis in relation to \(\{ {{\xi }_{{J,k}}}(t):k \in \mathbb{Z}\} .\)
Taking into account that in signal processing, there are different ways to set the stabilizing factor \(\hat {K}(\omega )\), and sometimes additional correction of this frequency response of the signal is required, we introduce the function \(\hat {D}(\omega )\) modifying \(\hat {\varphi }_{{j,k}}^{{}}(\omega )\), which admits representation (25) in the form \({{\hat {\xi }}_{{j,k}}}(\omega ) = \hat {D}(\omega )\hat {\varphi }_{{j,k}}^{{}}(\omega )\).
To solve (1) using DWT, a new biorthogonal wavelet system is needed, which includes scaling functions and wavelets modified in the frequency domain that form two pairs of functions \(\xi (t)\), \(\gamma (t)\) and \(\tilde {\xi }(t)\), \(\tilde {\gamma }(t)\) such that \({{\xi }_{{j,k}}}(t)\), \({{\gamma }_{{j,k}}}(t)\) give rise to a space of scaling functions \({{{\mathbf{U}}}_{j}}\) and wavelet space \({{{\mathbf{S}}}_{j}}\), and functions \({{\tilde {\xi }}_{{j,k}}}(t)\), \({{\tilde {\gamma }}_{{j,k}}}(t)\) form dual bases. As follows from [13–21, 35], the subspaces \({{{\mathbf{S}}}_{j}},\,\,{{\widetilde {\mathbf{S}}}_{j}}\) are obtained as an orthogonal complement to the embedded subspace system \({{{\mathbf{U}}}_{j}},\,\,{{\widetilde {\mathbf{U}}}_{j}}\)
Subspaces \({{{\mathbf{S}}}_{j}},\,\,{{\widetilde {\mathbf{S}}}_{j}}\) are mutually orthogonal and form an orthogonal expansion \({{L}^{2}}(\mathbb{R}).\) Let us consider the functions \({{\xi }_{{j,k}}}(t) = {{\xi }_{j}}(t - {{2}^{{ - j}}}k),\)\({{\gamma }_{{j,k}}}(t) = {{\gamma }_{j}}(t - {{2}^{{ - j}}}k),\)\(j,k \in \mathbb{Z}\) such that
where \(\hat {\varphi }(\omega )\), \(\hat {\psi }(\omega )\) is the spectrum of functions from an orthonormal wavelet system (Kravchenko wavelets {\(\widetilde {up}(\omega )\)}). Transformations (27), (28) perform a linear mapping of the MRA subspaces Vj and Wj into new subspaces Uj and Sj. New functions ξj, k, γj, k are transforms of the scaling function φj, k and wavelet ψj, k in subspaces Uj and Sj. According to the MRA requirements [13–21, 35], these functions should form a Riesz basis.
Lemma 1. If j < jmax, then systems of functions \(\{ {{\xi }_{{j,k}}}(t):k \in \mathbb{Z}\} ,\)\(\{ {{\gamma }_{{j,k}}}(t):k \in \mathbb{Z}\} \) are the Riesz basis of subspaces Uj and Sj.
Proof. The linear shell \(\{ {{\xi }_{{j,k}}}(t):j,k \in \mathbb{Z}\} \) is dense in L2(\(\mathbb{R}\)). To prove that \({{\xi }_{{j,k}}}(t)\) forms a Riesz basis, we show that there are positive constants A and B (0 < A ≤ B <∞) in U0 such that
for all infinite square-summable sequences {\({{c}_{k}}\)}.
According to the definition of the norm and Parseval’s identity, we have
Let for some \(\left| \omega \right| \geqslant \Omega ,\)\(\hat {\varphi }(\omega ) \approx 0.\) Then
With scale values j ≥ jmax (jmax > 0), a situation may arise when \(B = {{\sup }_{{\omega \in \left[ { - {{2}^{{{{j}_{{\max }}}}}}\Omega ,\,{{2}^{{{{j}_{{\max }}}}}}\Omega } \right]}}}\left| {\hat {D}(\omega )} \right|_{{}}^{2}\) becomes infinitely large and stability condition (29) is violated. In another case, when j ≤ jmin (jmin <0) it may turn out that
and system of functions \({{\xi }_{{j,k}}}(t)\) degenerates into an orthonormal basis. For \(j \ne 0\) the lemma is similarly proved. Repeating the above steps for the case \({{\gamma }_{{j,k}}}(t)\), it can be proved that \({{\gamma }_{{j,k}}}(t)\) forms a Riesz basis.
The following lemma shows that the subspaces {Uj} form an embedded sequence and satisfy such points in the definition of the MRA:
Lemma 2. The sequence of embedded subspaces {Uj} satisfies all the requirements of the MRA and \({{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}.\)
Proof. Transformation (27) translates any function \(f(t) \in {{{\mathbf{V}}}_{j}}\) into the corresponding single element \(u(t) \in {{{\mathbf{U}}}_{j}}.\) Because {Vj} form an embedded system of subspaces, \(f(t) \in {{{\mathbf{V}}}_{{j + 1}}},\) therefore, it is true that \(u(t) \in {{{\mathbf{U}}}_{{j + 1}}}\) and there is a chain
Thus, {Uj} form a sequence of embedded subspaces.
The requirement \(\bigcap\nolimits_{j \in Z} {{{{\mathbf{U}}}_{j}}} = \{ 0\} \) from the definition of MRA is checked against the opposite.
Confirmation of the MRA \(\overline {\bigcup\nolimits_{j \in Z} {{{{\mathbf{V}}}_{j}}} } = {{L}^{2}}\) will be proved if \({{{\mathbf{V}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}\) and \({{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}.\)
Let some function \(f(t) \in {{{\mathbf{V}}}_{j}},\) then \(f(t) \in {{{\mathbf{U}}}_{{j + 1}}}\) if
where \(a_{{j + 1}}^{f}(\omega )\) should be a 2j + 2π-periodic function. Since \(f(t) \in {{{\mathbf{V}}}_{j}},\)
where \(b_{j}^{f}(\omega )\) is a 2j+ 1π-periodic function and the scaling function φ belongs to the Kravchenko wavelet system. Given the scaling equation in the frequency domain, we have
where the product of the first two terms is a 2j + 2π-periodic function, since function \({{H}_{0}}\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}}} \right)\) is periodic with a period 2j+ 2π, as well as nonzero in intervals \(\left[ { - {{2}^{J}}\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right) + {{2}^{{J + 2}}}\pi k;} \right.\)\(\left. {{{2}^{J}}\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right) + {{2}^{{J + 2}}}\pi k} \right],\)\(k \in \mathbb{Z}\).
From (18) and (27), we obtain
Equalities (34) and (35) are equivalent when \(a_{{j + 1}}^{f}(\omega )\) is a 2j + 2π-periodic function, and \(\hat {D}(\omega )\) is periodically continued with a period of 2j + 2π (Fig. 2). Consequently, \({{{\mathbf{V}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}.\)
Graphs of functions: curve 1, \(a_{{j + 1}}^{f}(\omega )\); curve 2, \(b_{j}^{f}(\omega )\); curve 3, \({{\left[ {{{{\left. {\hat {D}(\omega )} \right|}}_{{\omega \in \left[ { - {{2}^{J}}\frac{{4\pi }}{3};{{2}^{J}}\frac{{4\pi }}{3}} \right]}}}} \right]}_{{{{2}^{{J + 2}}}\pi }}}\); curve 4, \({{H}_{0}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}})\).
The validity of embedding of subspaces \({{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}\) can be demonstrated by assuming that some function \(f(t) \in {{{\mathbf{U}}}_{j}}.\) Then \(f(t) \in {{{\mathbf{V}}}_{{j + 1}}},\) if
where \(b_{{j + 1}}^{f}(\omega )\) is a 2j + 2π-periodic function and the function φ is also from the Kravchenko wavelet system. Since \(f(t) \in {{{\mathbf{U}}}_{j}},\)\(\hat {f}(\omega ) = a_{j}^{f}(\omega )\hat {\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{j}}}}} \right. \kern-0em} {{{2}^{j}}}}),\) where \(a_{j}^{f}(\omega )\) is a 2j+ 1π-periodic function. After the transformation, this equality takes the form
where the product of the first three terms is the 2j+ 2π-periodic function \(b_{{j + 1}}^{f}(\omega )\) (Fig. 3). Consequently, \({{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}\) and the MRA requirement is met \(\overline {\bigcup\nolimits_{j \in Z} {{{{\mathbf{U}}}_{j}}} } = {{L}^{2}},\) because \(\overline {\bigcup\nolimits_{j \in Z} {{{{\mathbf{V}}}_{j}}} } = {{L}^{2}}.\)
Graphs of functions: curve 1,\(a_{j}^{f}(\omega )\); curve 2,\(b_{{j + 1}}^{f}(\omega )\); curve 3, \({{\left[ {{{{\left. {\hat {D}(\omega )} \right|}}_{{\omega \in \left[ { - {{2}^{J}}\frac{{4\pi }}{3};{{2}^{J}}\frac{{4\pi }}{3}} \right]}}}} \right]}_{{{{2}^{{J + 2}}}\pi }}}\), curve 4,\({{H}_{0}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}})\).
Summarizing the conditions \({{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{U}}}_{j}}\) and \({{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}},\) we obtain the proof of the statement \({{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}.\) Fulfillment of the condition that shifts of the frequency-modified scaling function \(\{ {{\xi }_{j}}(t - {{2}^{{ - j}}}k):k \in \mathbb{Z}\} \) formed a Riesz basis follows from Lemma 1.
Let us show the validity of the scalability relation. Let some function \(f(t) \in {{{\mathbf{U}}}_{j}}.\) Then
where \(a_{j}^{f}(\omega )\) is a 2j+ 1π-periodic function.
If \(f(2t) \in {{{\mathbf{U}}}_{{j + 1}}},\) then
where \(a_{{j + 1}}^{f}(\omega )\) should be a 2j + 2π-periodic function.
Indeed, by changing the variable w = ω/2 in (38), we obtain \(a_{{j + 1}}^{f}(\omega ) = a_{j}^{f}\left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-0em} 2}} \right).\) Consequently, \(a_{{j + 1}}^{f}(\omega )\) is a 2j + 2π-periodic function. The scalability ratio \(f(t) \in {{{\mathbf{U}}}_{j}} \Leftrightarrow f(2t) \in {{{\mathbf{U}}}_{{j + 1}}}.\) This differs from the scalability relation of classical MRA in that the spaces {Uj} form functions nonstationary with respect to the scale \({{\xi }_{j}}\), which follows from (27). For each value of scale j, the function \({{\xi }_{j}}(t)\) is no longer the result of tension/compression of one function, as in the case of classical MRA. Depending of the scale j, the support of the function changes \({{\hat {\varphi }}_{j}}(\omega ),\) as well as the frequency subrange of the function \(\hat {D}(\omega )\) encompassing \({{\hat {\varphi }}_{j}}(\omega )\). Therefore, functions \({{\xi }_{j}}\) exist only in a range of scales limited by the frequency range of the function \(\hat {D}(\omega )\). In practice, other scale values are not used, since the spectrum of the observed signal is always within the spectral range of the function \(\hat {D}(\omega )\). Let us formulate the requirements for the subspace of modified wavelet functions.
Lemma 3. If j < jmax, then subspaces Sj are an orthogonal complement to the embedded subspace system Uj
Proof. Transformation (27) translates any function \(f(t) \in {{{\mathbf{V}}}_{{j + 1}}}\) into the corresponding single element \(u(t) \in {{{\mathbf{U}}}_{{j + 1}}}\). Because {Vj} form the MRA, for each j there is an orthogonal complement Wj to the space Vj in the space Vj +1:
Therefore,
Since \(\{ {{{\mathbf{U}}}_{j}}\} \) satisfy all MRA requirements and \(u(t) \in {{{\mathbf{U}}}_{{j + 1}}}\) is the projection of \(f(t)\) from \({{{\mathbf{V}}}_{{j + 1}}} = {{{\mathbf{V}}}_{j}} \oplus {{{\mathbf{W}}}_{j}},\) the representation \({{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}},\)\({{{\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}},\)\({{{\mathbf{S}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}\) takes place. The basis for subspace Sj consists of shifts and scaling of one function \(\gamma \).
Thus, taking into account the nonstationarity with respect to the scale, we write
With similar reasoning, we can show that \({{{\mathbf{U}}}_{j}} = {{{\mathbf{U}}}_{{j - 1}}} \oplus {{{\mathbf{S}}}_{{j - 1}}}.\) Consequently, \({{{\mathbf{U}}}_{{j + 1}}}\) = \({{{\mathbf{U}}}_{{j - 1}}} \oplus {{{\mathbf{S}}}_{{j - 1}}} \oplus {{{\mathbf{S}}}_{j}}.\) Continuing this procedure, we obtain the orthogonal expansion of the space \({{{\mathbf{U}}}_{{j + 1}}}:{{{\mathbf{U}}}_{{j + 1}}}\) = \({{\overline { \oplus _{{k = - \infty }}^{j}{\mathbf{S}}} }_{k}}.\) The property of the MRA \(\overline {\bigcup\nolimits_{j \in Z} {{{{\mathbf{U}}}_{j}}} } = {{L}^{2}}\) formally makes it possible to represent \({{L}^{2}} = {{\overline { \oplus _{{k = - \infty }}^{{ + \infty }}{\mathbf{S}}} }_{k}}.\) Just like for modified scaling functions \(\xi (t)\), wavelet functions \(\gamma (t)\) have a restriction on the scale j < jmax, greater than which the stability condition is violated. Figure 4 shows the relative position of the Fourier transforms of functions \(\hat {\varphi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}}),\)\(\hat {\psi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}}),\)\(\hat {D}(\omega ).\)
Graphs of functions: curve 1,\(\hat {\varphi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}})\); curve 2,\(\hat {\psi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}})\); curve 3,\(\hat {D}(\omega )\); curve 4,\(\hat {f}\left( \omega \right)\).
It turns out that even if the product \(\hat {D}(\omega )\hat {\varphi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}})\) is limited, \(\hat {D}(\omega )\hat {\psi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}})\) may go beyond the dynamic measurement range.
Using the dual basis theorem [13–15] and taking into account the lemmas proved above, we find the remaining modified functions \({{\tilde {\xi }}_{{j,k}}}(t),\)\({{\tilde {\gamma }}_{{j,k}}}(t),\) which form dual bases to \({{\xi }_{{j,k}}}(t),\)\({{\gamma }_{{j,k}}}(t)\) and generate a space of scaling functions \({\mathbf{\tilde {U}}}{}_{j}\) and space of wavelets \({{{\mathbf{\tilde {S}}}}_{j}}\) such that \({{{\mathbf{U}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{j}},\)\({\mathbf{\tilde {U}}}{\kern 1pt} {}_{j} \bot {{{\mathbf{S}}}_{j}},\)\({{{\mathbf{S}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{l}}\) for \(j \ne l,\)\({{{\mathbf{\tilde {U}}}}_{{j + 1}}} = {{{\mathbf{\tilde {U}}}}_{j}} \oplus {{{\mathbf{\tilde {S}}}}_{j}},\)\({{{\mathbf{\tilde {U}}}}_{j}} \cap {{{\mathbf{\tilde {S}}}}_{j}} = \{ 0\} ,\)\({{{\mathbf{\tilde {U}}}}_{j}} \subset {{{\mathbf{\tilde {U}}}}_{{j + 1}}}\), \({{{\mathbf{\tilde {S}}}}_{j}} \subset {{{\mathbf{\tilde {U}}}}_{{j + 1}}}\).
Direct application of the dual basis theorem from [13–15] determines the Fourier transform of the basis function, which is dual to \({{\xi }_{j}}(t)\) in the sense that \(\left( {{{\xi }_{{j,n}}}(t),{{{\tilde {\xi }}}_{{j,k}}}(t)} \right) = {{\delta }_{{n,k}}},\) as follows:
The denominator in (42) is bounded almost everywhere by Riesz boundaries [13–15] A and B, 0 < A ≤ B <∞, which were obtained in the proof of Lemma 1:
Since \(\sum\nolimits_{p \in Z} {{{{\left| {{{{\hat {\xi }}}_{j}}(\omega + 2\pi p)} \right|}}^{2}}} \) is bounded from below by a positive constant, it is obvious that \({1 \mathord{\left/ {\vphantom {1 {\sum\nolimits_{p \in Z} {{{{\left| {{{{\hat {\xi }}}_{j}}(\omega + 2\pi p)} \right|}}^{2}}} }}} \right. \kern-0em} {\sum\nolimits_{p \in Z} {{{{\left| {{{{\hat {\xi }}}_{j}}(\omega + 2\pi p)} \right|}}^{2}}} }}\) is also a 2π-periodic function belonging to \({{L}^{1}}(0,2\pi ).\)
In the same way [13–15], we determine the Fourier transform dual to wavelet function \({{\gamma }_{j}}(t)\) of the basis \({{\tilde {\gamma }}_{j}}(t),\) for which the equality \(\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{l,k}}}(t)} \right) = {{\delta }_{{j,l}}}{{\delta }_{{n,k}}}\) holds:
Since the duality relation \(\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{l,k}}}(t)} \right) = {{\delta }_{{j,l}}}{{\delta }_{{n,k}}}\) is commutative \({{\tilde {\gamma }}_{j}}(t)\), the dual wavelet \({{\gamma }_{j}}(t),\) itself is a dual wavelet \({{\gamma }_{j}}(t).\)
The resulting pairs of modified functions satisfy the biorthogonality relations \(\left( {{{\xi }_{{j,n}}}(t),{{{\tilde {\xi }}}_{{j,k}}}(t)} \right) = {{\delta }_{{n,k}}},\)\(\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{l,k}}}(t)} \right)\) = \({{\delta }_{{j,l}}}{{\delta }_{{n,k}}},\) but the prerequisites for the existence of a biorthogonal wavelet system are violated \(\left( {{{\xi }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{j,k}}}(t)} \right) = 0,\)\(\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\xi }}}_{{j,k}}}(t)} \right) = 0.\) Therefore, it is necessary to switch to a new strategy for the formation of modified dual bases.
To do this, we introduce the 2π-periodic function \(E_{j}^{\xi }(\omega ) \in {{L}_{1}}(0,2\pi ){\kern 1pt} :\)
It follows from (44) that \(\sum\nolimits_{p \in Z} {{{{\left| {{{{\hat {\xi }}}_{j}}(\omega + 2\pi p)} \right|}}^{2}}} \) = \(E_{j}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{j}}}}} \right. \kern-0em} {{{2}^{j}}}})\) and \(E_{j}^{\xi }\left( \omega \right)\) are also bounded almost everywhere by constants A and B, 0 < A ≤ B <∞, \(A \leqslant E_{j}^{\xi }\left( \omega \right) \leqslant B.\) Then \({1 \mathord{\left/ {\vphantom {1 {E_{j}^{\xi }\left( \omega \right)}}} \right. \kern-0em} {E_{j}^{\xi }\left( \omega \right)}}\) is a bounded 2π-periodic function in \({{L}^{1}}(0,2\pi ),\)\({1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-0em} B} \leqslant {1 \mathord{\left/ {\vphantom {1 {E_{j}^{\xi }\left( \omega \right)}}} \right. \kern-0em} {E_{j}^{\xi }\left( \omega \right)}} \leqslant {1 \mathord{\left/ {\vphantom {1 A}} \right. \kern-0em} A}.\) Turning to scaling equations in the frequency domain, we formulate the following theorem.
Theorem 3. Let the scaling function \({{\xi }_{{j,k}}}(t) \in {{{\mathbf{U}}}_{j}},\) determined by (27), generate a MRA in space \({{L}^{2}}(\mathbb{R})\) and the wavelet \({{\gamma }_{{j,k}}}(t) \in {{{\mathbf{S}}}_{j}}\) during expansion \({{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}}\) be given by (28). Then there exist dual bases \({{\tilde {\xi }}_{{j,k}}}(t),\)\({{\tilde {\gamma }}_{{j,k}}}(t),\) given by the formulas
where \(E_{j}^{\xi }(\omega ) = \sum\nolimits_{n \in Z} {{{{\left| {\hat {D}\left( {{{2}^{j}}(\omega + 2\pi n)} \right)\hat {\varphi }(\omega + 2\pi n)} \right|}}^{2}}} ,\)
such that
(a) systems of functions \(\left\{ {{{{\tilde {\xi }}}_{{j,k}}}(t){\kern 1pt} :k \in \mathbb{Z}} \right\}\), \(\left\{ {{{{\tilde {\gamma }}}_{{j,k}}}(t){\text{:}}\,\,k \in \mathbb{Z}} \right\}\) are Riesz bases of subspaces \({{\widetilde {\mathbf{U}}}_{j}}\) and \({{\widetilde {\mathbf{S}}}_{j}}\);
(b) an embedded system of basis subspaces {\({{\widetilde {\mathbf{U}}}_{j}}\)} with orthogonal complements \({{\widetilde {\mathbf{S}}}_{j}}\) possibly forms a new MRA and \({{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{\tilde {U}}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}},\)\({{{\mathbf{\tilde {U}}}}_{{j + 1}}} = {{{\mathbf{\tilde {U}}}}_{j}} \oplus {{{\mathbf{\tilde {S}}}}_{j}};\)
(c) the scalability ratio \(f(t) \in {{{\mathbf{\tilde {U}}}}_{j}} \Leftrightarrow f(2t) \in {{{\mathbf{\tilde {U}}}}_{{j + 1}}};\)
(d) there are the properties
Thus, \({{{\mathbf{U}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{j}},\)\({\mathbf{\tilde {U}}}{}_{j} \bot {{{\mathbf{S}}}_{j}}\) and \({{{\mathbf{S}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{l}}\) for \(j \ne l.\) Therefore, two pairs of functions \(\xi \)(t), \(\gamma \)(t) and \(\tilde {\xi }(t)\),\(\tilde {\gamma }(t)\) form a biorthogonal wavelet system.
Proof. First, we show that \({{\tilde {\xi }}_{{j,k}}}(t),\)\({{\tilde {\gamma }}_{{j,k}}}(t)\) are dual bases. From direct application of the Parseval’s identity and periodicity of functions \({{H}_{0}}\left( \omega \right),\)\({1 \mathord{\left/ {\vphantom {1 {E_{{j + 1}}^{\xi }\left( \omega \right)}}} \right. \kern-0em} {E_{{j + 1}}^{\xi }\left( \omega \right)}}\), for p = k – n we obtain
Hence,
Based on the fact that \({{H}_{0}}(\omega )\) = \(\frac{1}{{\sqrt 2 }}\sum\nolimits_{n \in Z} {{{h}_{n}}\exp ( - in\omega )} ,\) we obtain
The biorthogonality of the shift for modified wavelets \({{\gamma }_{{j,n}}}(t)\) and \({{\tilde {\gamma }}_{{l,k}}}(t)\) is also proved. For j = l and p = k – n,
Orthogonality with respect to scale at \(j \ne l\) will be proved below.
Proof that \({{\tilde {\xi }}_{{j,k}}}(t)\) forms a Riesz basis as in Lemma 1. Let there exist positive constants \(\tilde {A}\) and \(\tilde {B}\) (\(0 < \tilde {A} \leqslant \tilde {B} < \infty \)) in \({{\widetilde {\mathbf{U}}}_{0}}\) such that
for all \(\left\| {{\text{\{ }}{{c}_{{j,k}}}{\text{\} }}} \right\|_{{{{l}_{2}}}}^{2} = \sum\nolimits_k {{{{\left| {{{c}_{{j,k}}}} \right|}}^{2}}} < 0.\) Consequently,
Let for some \(\left| \omega \right| \geqslant \Omega ,\)\(\hat {\varphi }(\omega ) \approx 0\). Then
In a similar way,
For \(j \ne 0\), the proof is similar. For \({{\tilde {\xi }}_{{j,k}}}(t)\) there will also be a restriction on scale values j ≥ jmax (jmax > 0) under which the stability condition (47) is violated. In a similar way, it is proved that \({{\tilde {\gamma }}_{{j,k}}}(t)\) forms a Riesz basis.
The validity that the sequence of embedded subspaces {\({{\widetilde {\mathbf{U}}}_{j}}\)} forms a new MRA and \({{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{\tilde {U}}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}},\) as well as the fact that the subspaces \({{{\mathbf{\tilde {S}}}}_{j}}\) are an orthogonal complement to the base system {\({{\widetilde {\mathbf{U}}}_{j}}\)} and \({{\widetilde {\mathbf{U}}}_{{j + 1}}} = {{\widetilde {\mathbf{U}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}}\), is proved, just like in Lemmas 2 and 3.
We show the validity of the scalability relation in accordance with the previous proof in Lemma 2. Let some function \(f(t) \in {{{\mathbf{\tilde {U}}}}_{j}}.\) Consequently
where \(a_{j}^{f}(\omega )\) is a 2j + 1π-periodic function.
Then \(f(2t) \in {{{\mathbf{\tilde {U}}}}_{{j + 1}}},\) if
where \(a_{{j + 1}}^{f}(\omega )\) should be a 2j + 2π-periodic function.
By replacing variable w = ω/2 in (48) we obtain \(a_{{j + 1}}^{f}(\omega ) = a_{j}^{f}\left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-0em} 2}} \right).\) Consequently, \(a_{{j + 1}}^{f}(\omega )\) is a 2j + 2π‑periodic function and the scalability ratio \(f(t) \in {{{\mathbf{\tilde {U}}}}_{j}} \Leftrightarrow f(2t) \in {{{\mathbf{\tilde {U}}}}_{{j + 1}}}.\)
Note that spaces \(\{ {{\widetilde {\mathbf{U}}}_{j}}\} \) also form functions nonstationary with respect to scale \({{\tilde {\xi }}_{j}}\).
To show that the orthogonality property of the subspaces is satisfied \({{{\mathbf{U}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{j}}\) and \({\mathbf{\tilde {U}}}{\kern 1pt} {}_{j} \bot {{{\mathbf{S}}}_{j}},\) we determined the corresponding scalar product of the generating functions
By doing the same to prove the orthogonality \({\mathbf{\tilde {U}}}{\kern 1pt} {}_{j} \bot {{{\mathbf{S}}}_{j}},\) we have
We show biorthogonality with respect to scale for modified wavelets \(\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{l,k}}}(t)} \right)\) = \({{\delta }_{{n,k}}}{{\delta }_{{j,l}}}.\) The case was previously considered for j = l. If \(j \ne l\) then for l < j we have \({{\tilde {\gamma }}_{{l,k}}} \in {{{\mathbf{\tilde {S}}}}_{l}},\)\(k \in \mathbb{Z}\) and \({{{\mathbf{\tilde {S}}}}_{l}} \subset {{{\mathbf{\tilde {U}}}}_{{l + 1}}}\)\( \subset ... \subset \)\({{{\mathbf{\tilde {U}}}}_{{j - 1}}} \subset {{{\mathbf{\tilde {U}}}}_{j}}.\) Based on the statement \({\mathbf{\tilde {U}}}{\kern 1pt} {}_{j}\, \bot {{{\mathbf{S}}}_{j}}\) we obtain \(({{\gamma }_{{j,n}}}(t),{{\tilde {\gamma }}_{{l,k}}}(t)) = 0,\)\(n,k \in \mathbb{Z}.\) For l > j the same conclusions can be made using the second statement \({{{\mathbf{U}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{j}}.\)
This completes the proof of the theorem. Thus, it follows from the theorem that two pairs of functions \(\xi \),\(\gamma \) and \(\tilde {\xi }\),\(\tilde {\gamma }\) form a biorthogonal wavelet system (Fig. 5).
Graphs of biorthogonal frequency-modified wavelets Kravchenko \(\{ \widetilde {up}\} \): \({{\xi }_{{j,0}}}(t),{{\gamma }_{{j,0}}}(t)\) (a), \({{\tilde {\xi }}_{{j,0}}}(t),{{\tilde {\gamma }}_{{j,0}}}(t)\) (b), \({{\xi }_{{j - 2,0}}}(t),{{\gamma }_{{j - 2,0}}}(t)\) (c), \({{\tilde {\xi }}_{{j - 2,0}}}(t),{{\tilde {\gamma }}_{{j - 2,0}}}(t)\) (d).
This ensures fulfillment of the following necessary conditions for the wavelet and scaling functions [13–21]:
Thus, the new modified basis functions of the obtained wavelet system:
—form a biorthogonal system of basis functions forming a nonstationary multiresolution signal analysis in \({{L}^{2}}(\mathbb{R})\);
—are nonstationary in relation to scale j, since depending on j, the support of the spectrum of the functions changes \({{\varphi }_{j}}(t),\)\({{\psi }_{j}}(t)\), as does, accordingly, the interval of the frequency subrange of the function \(\hat {D}(\omega )\) encompassed by them;
—degenerate for \(\hat {D}(\omega )\) = const in the corresponding source functions \({{\varphi }_{j}}(t)\) and \({{\psi }_{j}}(t)\).
4 SCALING EQUATIONS OF BIORTHOGONAL FREQUENCY-MODIFIED WAVELETS
Since the basis subspaces \({\mathbf{U}}{}_{j}\) and \({\mathbf{\tilde {U}}}{}_{j}\) form the MRA, the functions \({{\xi }_{j}} \in {\mathbf{U}}{}_{j},\)\({{\gamma }_{j}} \in {{{\mathbf{S}}}_{j}},\)\({{\tilde {\xi }}_{j}} \in {\mathbf{\tilde {U}}}{}_{j},\)\({{\tilde {\gamma }}_{j}} \in {{{\mathbf{\tilde {S}}}}_{j}}\) are similar to the classical scaling equations [13‒21, 35], and they can be expressed as a linear combination of their scaling functions \({{\xi }_{{j + 1}}} \in {\mathbf{U}}{}_{{j + 1}}\) or \({{\tilde {\xi }}_{{j + 1}}} \in {\mathbf{\tilde {U}}}{}_{{j + 1}}.\)
For the function \({{\xi }_{{j,k}}}(t)\) we have the relation
The scalar product under the sum sign will be equal to
Consequently,
or in the frequency domain
We determine the scalar product for the scaling relation in a similar way
Thus,
Let us construct the scaling relations that the modified wavelet functions \({{\gamma }_{{j,n}}}\) and \({{\tilde {\gamma }}_{{j,n}}}\) must satisfy. For \({{\gamma }_{{j,n}}}\) we have
As a result of calculating the filter coefficients, we obtain
Now we rewrite (56) as
After the Fourier transform, this relation takes the form
Similarly, for \({{\tilde {\gamma }}_{{j,n}}}\) we obtain
In the frequency domain, this relation takes the form
The properties of the frequency functions of the constructed biorthogonal wavelet system are well known [13–21, 35], since they are also the corresponding frequency functions of the original wavelet bases H(ω) for \(\hat {\varphi }(\omega )\) and G(ω) for \(\hat {\psi }(\omega )\). The condition for the biorthogonal frequency functions

is fully confirmed by the condition for the orthonormal case [13–21, 35]

According to the statements of Lemma 2 and Theorem 3 on embedded subspaces
other scaling relationships can be obtained. Because \({\mathbf{U}}{}_{j} \subset {{{\mathbf{V}}}_{{j + 1}}},\)\({{\xi }_{j}} \in {\mathbf{U}}{}_{j},\)\({{\varphi }_{{j + 1}}} \in {\mathbf{V}}{}_{{j + 1}},\) there is a 2j + 2π-periodic function \({{\Theta }_{{j + 1}}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}),\) such that
To determine \({{\Theta }_{{j + 1}}}\) we use the equation
Here the product of the first two terms should form a 2j + 2π-periodic function. For this, we introduce a 2j + 2π-periodic continuation of the function \(\hat {D}(\omega )\) with a gap \(\left[ { - {{2}^{j}}(4{\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3});{{2}^{j}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right]\) on \(\mathbb{R}\) (when Kravchenko wavelets are used).
Then,
Here \({{D}_{{j + 1}}}*(\omega )\) is a 2π-periodic function determined by the equality
where \({{\chi }_{{\omega \in \left[ { - {{2}^{j}}\frac{{4\pi }}{3};{{2}^{j}}\frac{{4\pi }}{3}} \right]}}}(\omega )\) is the characteristic function of the interval \(\left[ { - {{2}^{j}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3});{{2}^{j}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right],\) for which equality holds \(\hat {D}(\omega ) = {{D}_{{j + 1}}}^{*}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}).\)
Consequently,
As a result of inverse Fourier transform of expression (64), taking into account an arbitrary value of the shift in n , we have
Based on (66), the formula for calculating \({{\theta }_{{j + 1,k}}}\) will be
In a similar way, we obtain the expression for the Fourier transform of a modified wavelet \({{\gamma }_{{j,n}}}(t)\)
where \({{{\rm N}}_{{j + 1}}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})\) is a 2j + 2π-periodic function.
It follows that
Then, the scaling relation with the filter coefficients can be represented as
Shifts of the biorthogonal to \({{\xi }_{j}} \in {\mathbf{U}}{}_{j}\) scaling function \({{\tilde {\xi }}_{j}}\) generate the subspace \({\mathbf{\tilde {U}}}{}_{j}\), and according to Theorem 3, the condition of embedded subspaces \({\mathbf{\tilde {U}}}{\kern 1pt} {}_{j}\, \subset {{{\mathbf{V}}}_{{j + 1}}}\) is fulfilled. Therefore, there exists a 2j + 2π-periodic function \(\tilde {\Theta }(\omega ),\) such that
After the corresponding transformations, we have
Then the following equality is valid:
In (74) we represent \({{\tilde {\Theta }}_{{j + 1}}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})\) as expansion in a Fourier series:
where
As a result of the Fourier transform, we obtain the scaling relation
Similarly for the wavelet function \({{\tilde {\gamma }}_{{j,n}}}\), the corresponding expressions in the frequency domain will have the form
where 2j + 2π-periodic function \({{\widetilde {\rm N}}_{{j + 1}}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}),\) which is determined as follows:
After the inverse Fourier transform, the scaling relation (80) in the time domain can be represented as
where
Let us consider some properties of the filter coefficients \(\{ {{\theta }_{{j,k}}}:k \in \mathbb{Z}\} ,\)\(\{ {{\tilde {\theta }}_{{j,k}}}:k \in \mathbb{Z}\} ,\)\(\{ {{\eta }_{{j,k}}}:k \in \mathbb{Z}\} ,\)\(\{ {{\tilde {\eta }}_{{j,k}}}:k \in \mathbb{Z}\} .\) The coefficients \(\{ {{\theta }_{{j,k}}}:k \in \mathbb{Z}\} \) and \(\{ {{\tilde {\theta }}_{{j,k}}}:k \in \mathbb{Z}\} \) are biorthogonal with respect to the double shift
This follows from the equality \(\left( {{{\xi }_{{j - 1,0}}}(t),{{{\tilde {\xi }}}_{{j - 1,p}}}(t)} \right) = {{\delta }_{{p,0}}}.\)
The scaling \(\{ {{\theta }_{{j,k}}}:k \in \mathbb{Z}\} \) and wavelet \(\{ {{\tilde {\eta }}_{{j,k}}}:k \in \mathbb{Z}\} \) coefficients of the filters have the following properties:
In addition, the following conditions on the sum of the coefficients are fulfilled:
The corresponding frequency functions must satisfy a relation similar to (61):
Let us consider the scalar product for p = k – n
We use the Parseval’s identity and \({\text{the}}\) scaling relations obtained above:
The resulting equality takes place only when
This equality holds for an arbitrary value of the scale j < jmax.
Another new complex of scaling equations can be obtained from the constructed biorthogonal system of functions if the formula for dual bases (45) is transformed using relation (52)
Here \(H({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})\) and \({1 \mathord{\left/ {\vphantom {1 {E_{{j + 1}}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})}}} \right. \kern-0em} {E_{{j + 1}}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})}}\) are 2j + 2π-periodic functions and their product is also a 2j + 2π-periodic function. Hence follows the validity of the scaling equation in the frequency domain for \({{\tilde {\xi }}_{j}} \in \widetilde {\mathbf{U}}{}_{j}\) and \({{\xi }_{{j + 1}}} \in {\mathbf{U}}{}_{{j + 1}}\):
where
If we rewrite the relation for the dual basis (45) in the form \({{\hat {\xi }}_{j}}(\omega ) = E_{{j + 1}}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}){{\hat {\tilde {\xi }}}_{j}}(\omega )\), then in the same way, taking into account (55), we obtain a scaling equation in the frequency domain that expresses the function \({{\xi }_{j}} \in {\mathbf{U}}{}_{j}\) through a scaled version of its dual basis \({{\tilde {\xi }}_{{j + 1}}} \in \widetilde {\mathbf{U}}{}_{{j + 1}}\)
where the 2j+ 2π-periodic function has the form
Rewriting relation (46) as \({{\hat {\gamma }}_{j}}(\omega )\) = \(E_{{j + 1}}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}){{\hat {\tilde {\gamma }}}_{j}}(\omega )\), we similarly construct new scaling equations for the wavelet functions \({{\tilde {\gamma }}_{j}} \in {{{\mathbf{\tilde {S}}}}_{j}}\) and \({{\gamma }_{j}} \in {{{\mathbf{S}}}_{j}}\)
where
and
where
Applying the obtained scaling equations in the frequency domain, we can formulate a theorem.
Theorem 4. If j < jmax, then the embedding of subspaces is true
and subspaces \({{{\mathbf{S}}}_{j}}\) and \({{{\mathbf{\tilde {S}}}}_{j}}\) are also an orthogonal complement to the embedded subspace system \({{{\mathbf{U}}}_{j}}\) and \({{\widetilde {\mathbf{U}}}_{j}}\) before \({{\widetilde {\mathbf{U}}}_{{j + 1}}}\) and \({{{\mathbf{U}}}_{{j + 1}}}\), respectively
Proof. To show the embedding of the scalable subspaces, it suffices to verify that \({{\widetilde {\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}\) and \({{{\mathbf{U}}}_{j}} \subset {{\widetilde {\mathbf{U}}}_{{j + 1}}}.\) For proof \({{\widetilde {\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}\), we assume that some function \(f(t) \in {{\widetilde {\mathbf{U}}}_{j}}.\) Then \(f(t) \in {{{\mathbf{U}}}_{{j + 1}}},\) if \(\hat {f}(\omega ) = \tilde {a}_{{j + 1}}^{f}(\omega ){{\xi }_{{j + 1}}}\left( \omega \right),\) and \(\tilde {a}_{{j + 1}}^{f}(\omega )\) should be a 2j + 2π‑periodic function. Since \(f(t) \in {{\widetilde {\mathbf{U}}}_{j}},\)\(\hat {f}(\omega ) = a_{j}^{f}(\omega ){{\hat {\tilde {\xi }}}_{j}}\left( \omega \right).\) Transformation of this equality gives
where the product of the first two terms is a 2j + 2π-periodic function \(\tilde {a}_{{j + 1}}^{f}(\omega )\). Consequently, \({{\widetilde {\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}.\) In a similar way it is proved that \({{{\mathbf{U}}}_{j}} \subset {{\widetilde {\mathbf{U}}}_{{j + 1}}}\). Generalizing these conditions, we obtain the proof of the statements \({{{\mathbf{U}}}_{{j - 1}}} \subset {{\widetilde {\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}\) and \({{\widetilde {\mathbf{U}}}_{{j - 1}}} \subset {{{\mathbf{U}}}_{j}} \subset {{\widetilde {\mathbf{U}}}_{{j + 1}}}.\)
To prove the second part of the theorem \({{\widetilde {\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}}\), it is necessary to show that the family of functions \(\{ {{\xi }_{{j,n}}}(t),{{\gamma }_{{j,k}}}(t):n,k \in \mathbb{Z}\} \) forms the basis of the entire subspace \({{\widetilde {\mathbf{U}}}_{{j + 1}}}\). According to Theorem 3, the condition \({{\widetilde {\mathbf{U}}}_{{j + 1}}} = {{\widetilde {\mathbf{U}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}},\) holds if \(f(t) \in {{\widetilde {\mathbf{U}}}_{{j + 1}}}\), then \(\hat {f}(\omega ) = a_{{j + 1}}^{f}(\omega ){{\tilde {\xi }}_{{j + 1}}}\left( \omega \right)\), where \(a_{{j + 1}}^{f}(\omega )\) is a 2j + 2π-periodic function.
Thus,
where \(a_{j}^{f}(\omega )\) and \(b_{j}^{f}(\omega )\) are 2j + 1π-periodic functions. We transform the dual bases of the scaling function and the wavelet on the right-hand side of this expression
Then,
and the product of the first two terms on the right-hand side is still a 2j + 2π-periodic function, which proves \({{\widetilde {\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}}\) and \({{{\mathbf{S}}}_{j}} \subset {{\widetilde {\mathbf{U}}}_{{j + 1}}}.\)
Similarly, if \(f(t) \in {{{\mathbf{U}}}_{{j + 1}}}\) and \(\hat {f}(\omega ) = \tilde {a}_{{j + 1}}^{f}(\omega ){{\xi }_{{j + 1}}}\left( \omega \right),\) then according to the hypothesis of Lemma 3
where \(\tilde {a}_{{j + 1}}^{f}(\omega )\) is a 2j + 2π-periodic function and \(\tilde {a}_{j}^{f}(\omega )\) and \(\tilde {b}_{j}^{f}(\omega )\) are 2j + 1π-periodic functions.
Consequently,
Then \({{{\mathbf{U}}}_{{j + 1}}} = {{\widetilde {\mathbf{U}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}}\), \({{{\mathbf{\tilde {S}}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}\), which required.
The scaling and wavelet filter coefficients will be sought on the basis that the frequency functions of the modified wavelet system in (91), (93), (95), (97) are the product of the frequency function of the original orthonormal wavelet system with filter coefficients \(\{ {{h}_{k}}:k \in \mathbb{Z}\} \), \(\{ {{g}_{k}}:k \in \mathbb{Z}\} \), which are known, and the periodic function \(E_{{j + 1}}^{\xi }(\omega )\). For \(E_{{j + 1}}^{\xi }(\omega )\), the filter coefficients are determined as follows:
The filter coefficients for \({1 \mathord{\left/ {\vphantom {1 {E_{{j + 1}}^{\xi }(\omega )}}} \right. \kern-0em} {E_{{j + 1}}^{\xi }(\omega )}}\) can obtained this way:
Then scaling equation (91) is written as
We introduce the notation of the filter coefficients for (100), which are a convolution of known numerical sequences
Then,
In the time domain, the scaling equation has the form
Similarly for (93) we have
where
After performing inverse Fourier transform, the scaling equation (104) takes the form
Similarly, for wavelet functions, we have
where
In the time domain (107) has the form
Similarly, for the expression
we obtain
where
In the time domain (111) takes the form
The filter coefficients \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} _{{j,k}}^{\xi }:k \in \mathbb{Z}\} ,\)\(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} _{{j,k}}^{\xi }:k \in \mathbb{Z}\} ,\)\(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} _{{j,k}}^{\xi }:k \in \mathbb{Z}\} ,\)\(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} _{{j,k}}^{\xi }:k \in \mathbb{Z}\} \) have the following properties:
In the biorthogonal case the frequency functions \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{H} _{j}^{\xi }\left( \omega \right)\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} _{j}^{\xi }\left( \omega \right)\) satisfy the equality
Fulfillment of this equality is easily shown by directly substituting relations (92) and (94) in (121).
5 MULTIRESOLUTION APPROXIMATION OF THE SOLUTION TO THE CONVOLUTION INTEGRAL EQUATION USING BIORTHOGONAL FREQUENCY-MODIFIED KRAVCHENKO WAVELETS
As shown earlier, the solution to convolution integral equation (1) involves estimation of the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\) from an observed signal \(y(t)\) based on the regularized spectrum of the solution [1–7]
where \(\hat {D}(\omega )\) is the stabilizing factor, which can be given as \(\hat {D}(\omega ) = \;{{\hat {K}}^{{ - 1}}}(\omega )\).
Using the convolution integral equation in the frequency domain \(\hat {y}(\omega ) = \hat {\lambda }(\omega )\hat {x}(\omega ) + \hat {n}(\omega ),\) we obtain from (122) the estimate \({{\hat {\tilde {x}}}_{{\text{r}}}}(\omega ) = \hat {\lambda }(\omega ){{\hat {D}}^{{ - 1}}}(\omega )\hat {x}(\omega )\) + \({{\hat {D}}^{{ - 1}}}(\omega )\hat {n}(\omega ).\) If \(\hat {D}(\omega ) = \hat {\lambda }(\omega ),\) then the estimate of the useful signal has the form of an inverse filter. In the absence of noise solution (122) makes it possible to accurately reconstruct the signal \(\hat {x}(\omega )\) distorted by the impulse response \(\hat {\lambda }(\omega )\) of the linear stationary system. In the presence of noise, it is infinitely amplified at frequencies at which \(\hat {\lambda }(\omega ) \to 0,\) which necessitates mathematical approaches to effectively suppress noise, which include wavelet filtering [13–21].
According to (22), the estimate of the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\) is thus determined:
where \({{\varphi }_{{J + 1,k}}}(t) \in {{{\mathbf{V}}}_{{J + 1}}}\;\) are the initial scaling functions selected from Kravchenko orthonormal wavelet systems; \(a_{{J + 1,k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}}\) = \(\left( {x(t),{{\varphi }_{{J + 1,k}}}(t)} \right)\) are the coefficients of expansion of x(t) over the scaling functions \(\{ {{\varphi }_{{J + 1,k}}}(t):k \in \mathbb{Z}\} .\)
Thus, the solution to convolution integral equation (1) with respect to the function \(x\,(t)\) reduces to finding an unknown sequence of expansion coefficients {\(a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}\): \(k \in \mathbb{Z}\)} [29, 36–41]. Let us represent (22) in the frequency domain
Multiplying (123) on the left and right by \(\hat {D}(\omega )\), we obtain
Taking into account (27), (122) it can be shown that the coefficients {\(a_{{J + 1,k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}}\): \(k \in \mathbb{Z}\)} are determined as the expansion of the observed signal \(y(t)\) over the basis system of functions \({{\xi }_{{j,k}}}(t),k \in \mathbb{Z},\) in which \(a_{{J + 1,k}}^{y} = a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}.\) Indeed, since
then
Consequently, \(y(\omega ) \in {{{\mathbf{U}}}_{{j + 1}}}\) and the condition of Theorem 1 is satisfied, since \({{{\mathbf{V}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}\) according to Lemma 2.
Thus, the estimate of the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\) will be determined by the following expansion over the basis \({{\varphi }_{{J + 1,k}}},\,\,k \in \mathbb{Z}\,:\)
The coefficients to be determined {\(a_{{J + 1,k}}^{y}\): \(k \in \mathbb{Z}\)} are found based on the existence of a biorthogonal system of functions \({{\xi }_{{j,k}}}(t),\,\,{{\tilde {\xi }}_{{j,k}}}(t),\,\,k \in \mathbb{Z}\)
Here, the estimate of the approximate solution to convolution integral equation (1) in the form of (127) is reduced to determining the coefficients (128). Based on the fact that the proposed and substantiated biorthogonal system of wavelet functions \({{\xi }_{{j,k}}}(t),\)\({{\gamma }_{{j,k}}}(t)\) and \({{\tilde {\xi }}_{{j,k}}}(t),\)\({{\tilde {\gamma }}_{{j,k}}}(t)\), \(k \in \mathbb{Z}\) generates two MRA chains, any function from \({{{\mathbf{U}}}_{{J + 1}}}\) can be represented as an orthogonal expansion over the bases of subspaces of a lower scale \({{{\mathbf{U}}}_{j}}\), \({{{\mathbf{S}}}_{j}}\) so that \({{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}}.\) Then to create computational algorithms for estimating the useful signal we search for \({{\tilde {x}}_{{\text{r}}}}(t)\) in the form of an expansion
which describes the DWT of the classical MRA by wavelets with a compact support in the frequency domain, in particular, Kravchenko wavelets [25–28].
In the frequency domain (129) has the form
Coefficients {\(a_{{{{j}_{0}},k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}},\,\,b_{{j,k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}}\): \(k \in \mathbb{Z}\)} are the result of DWT \({{\tilde {x}}_{{\text{r}}}}(t)\) when expanded to some scale j0 so that \({{\tilde {x}}_{{\text{r}}}}(t)\) is represented as the sum of a rough approximation \({{P}_{{{{j}_{0}}}}}{{\tilde {x}}_{{{\text{r}}\,}}}(t) \in {{{\mathbf{V}}}_{{{{j}_{0}}}}}\) and set of details \(\;{{Q}_{j}}{{\tilde {x}}_{{\text{r}}}}(t) \in {{{\mathbf{W}}}_{j}}\)
According to the MRA concept, the coefficients of the wavelet expansion can be obtained recursively with a rougher approximation. Indeed, let some signal f(t) be given by samplings at time instants \({{t}_{m}} = m{{2}^{{ - N}}},\)\(m \in \mathbb{Z}{\kern 1pt} .\) Then, by multiplying the scalar scaling equations \({{\varphi }_{{j,n}}}(t)\) = \(\sum\nolimits_k {{{h}_{{k - 2n}}}} {{\varphi }_{{j + 1,k}}}(t),\)\({{\psi }_{{j,n}}}(t)\) = \(\sum\nolimits_k {{{g}_{{k - 2n}}}} {{\varphi }_{{j + 1,k}}}(t)\) left and right on \(f(t)\) for an arbitrary scale j it is possible to obtain recursive formulas for calculating the wavelet expansion coefficients from the more accurate scale j + 1 to a rougher scale j [13–21]
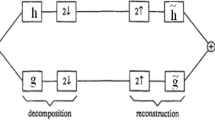
Graphically the wavelet expansion algorithm f(t) can be represented as a diagram (Fig. 6a). This algorithm is realized via a multistage serial connection of filter blocks providing fast DWT calculations.
The initial values of the coefficients \(a_{{j,k}}^{f}\) determined by formulas \(a_{{j,k}}^{f} = (f(t),{{\varphi }_{{j,k}}}(t)),\)\(\,b_{{j,k}}^{f} = (f(t),{{\psi }_{{j,k}}}(t))\) at this value of scale j, in which within the spectral range of the signal \(\hat {f}(\omega )\) function \({{\hat {\varphi }}_{j}}(\omega )\) remains almost constant, i.e. such that the wavelet approximation sufficiently accurately reflects the signal f(t). Such a calculation is labor-consuming and may not provide the necessary calculation accuracy. Since the signal f(t) is practically given by its values, at a large scale j, the coefficients \(\{ {{a}_{{j,k}}}:k \in \mathbb{Z}\} \) can be set equal to the samplings of the function:
It follows that when choosing the Kravchenko wavelet system \(a_{{j,k}}^{f} \approx {{\left. {f(t)} \right|}_{{t = k{{2}^{{ - j}}}}}} = {{f}_{k}}.\)
Therefore, fast DWT calculation makes it possible to represent the estimate of approximate solution (1) in discrete form as a sequence of coefficients \(\{ a_{{{{j}_{0}},k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}},b_{{j,k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}}:\)\({{j}_{0}} \leqslant j \leqslant J,k \in \mathbb{Z}\} ,\) over which \({{\tilde {x}}_{{\text{r}}}}(t)\) is expanded in (129).
As shown in (122), the estimate of the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\) determined by processing the observed signal y(t) by a filter with a frequency response \({{\hat {D}}^{{ - 1}}}(\omega )\) corresponds to wavelet expansion of the observed signal y(t) over the basis \({{\xi }_{{j,k}}}(t)\), \(k \in \mathbb{Z}\) at the finest scale J. Similarly we obtain the expansion \({{\hat {\tilde {x}}}_{{\text{r}}}}(t)\) in DWT form, multiplying the expression (130) on the left and right by \(\hat {D}(\omega )\)
With allowance for (27), (28) we have
Therefore, the coefficients {\(a_{{J + 1,k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}}\), \(b_{{J + 1,k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}}\): \(k \in \mathbb{Z}\)} are obtained by expanding the observed signal \(y(t)\) over the basis system of functions \({{\xi }_{{j,k}}}(t),{{\gamma }_{{j,k}}}(t),\)\(k \in \mathbb{Z},\)\({{j}_{0}} \leqslant j \leqslant J\), in which \(a_{{{{j}_{0}},k}}^{y} = a_{{{{j}_{0}},k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}}\), \(b_{{j,k}}^{y} = b_{{j,k}}^{{{{{\tilde {x}}}_{{\text{r}}}}}}\). Thus, the estimate of approximate solution (1) will be determined \({\text{by}}\) the following expansion over bases \({{\varphi }_{{{{j}_{0}},k}}}(t),{{\psi }_{{j,k}}}(t),\)\(k \in \mathbb{Z},{{j}_{0}} \leqslant j \leqslant J\):
where \(\{ a_{{{{j}_{0}},k}}^{y},b_{{j,k}}^{y}:k \in \mathbb{Z},{{j}_{0}} \leqslant j \leqslant J\} \) are the coefficients of expansion of the observed signal \(y(t)\) over frequency-modified biorthogonal wavelets \({{\xi }_{{j,k}}}(t),{{\gamma }_{{j,k}}}(t),\)\(k \in \mathbb{Z},{{j}_{0}} \leqslant j \leqslant J.\)
The proposed and substantiated biorthogonal system of functions \({{\xi }_{{j,k}}}(t)\), \({{\gamma }_{{j,k}}}(t)\) and \({{\tilde {\xi }}_{{j,k}}}(t)\), \({{\tilde {\gamma }}_{{j,k}}}(t)\), \(k \in \mathbb{Z}\) generates the MRA; therefore, for the effective solution of problem (1) on estimating the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\) distorted by the impulse response \(\lambda (t)\), it is necessary to develop an algorithm for fast calculation of the wavelet coefficients {\(a_{{{{j}_{0}},k}}^{y}\), \(b_{{j,k}}^{y}\): \(k \in \mathbb{Z},{{j}_{0}} \leqslant j \leqslant J\)} based on the previously obtained scaling equations (51), (54), (57), (59), (67), (72), (79), (82), (103), (106), (109) , (113), as well as the scaling and wavelet filter coefficients \(\{ h\} \), \(\{ g\} \), \(\{ {{\theta }_{j}}\} \), \(\{ {{\eta }_{j}}\} \), \(\{ {{\tilde {\theta }}_{j}}\} \), \(\{ {{\tilde {\eta }}_{j}}\} \), \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} _{j}^{\xi }\} \), \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} _{j}^{\xi }\} \), \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} _{j}^{\xi }\} \), \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} _{j}^{\xi }\} \). Then, effective noise suppression is performed and its infinite amplification is compensated using mathematical approaches to process the wavelet coefficients [13–21, 42, 43].
The developed frequency-modified biorthogonal wavelets make it possible to obtain recursive algorithms for calculating the DWT coefficients taking into account the localization and compensation of the time–frequency singularities of the observed signal y(t), frequency response function \(\hat {\lambda }(\omega )\), or filter with the frequency response \(\hat {D}(\omega )\) due to the existence of scaling equations (51), (54), (57), (59), (67), (72), (79), (82), (103), (106), (109), (113). Scaling equations (103), (106), (109), (113) allow transitions during wavelet expansion of the observed signal y(t) from the basis \({{\xi }_{{j + 1,k}}}(t)\) to the bases \({{\tilde {\xi }}_{{j,k}}}(t)\), \({{\tilde {\gamma }}_{{j,k}}}(t)\) or from the basis \({{\tilde {\xi }}_{{j + 1,k}}}(t)\) to the bases \({{\xi }_{{j,k}}}(t)\), \({{\gamma }_{{j,k}}}(t)\) (the next level of expansion is performed along the biorthogonal basis) using single DWT in the necessary frequency ranges, where the properties of the wavelet bases \({{\xi }_{{j,k}}}(t)\), \({{\gamma }_{{j,k}}}(t)\) or \({{\tilde {\xi }}_{{j,k}}}(t)\), \({{\tilde {\gamma }}_{{j,k}}}(t)\) allow better approximation of the signal y(t). It follows that in a unified DWT algorithm, it becomes possible to optimize the process of obtaining wavelet expansion coefficients for further processing in order to efficiently recover the signal x(t), suppress noise, and compensate for its infinite amplification. For subspace scaling functions \({\mathbf{U}}{}_{j}\) and corresponding subspace wavelet functions \({{{\mathbf{S}}}_{j}}\), the scaling relations (51), (57), (67), (72), (106), (113) hold, and for subspaces \({\mathbf{\tilde {U}}}{}_{j}\) and \({{{\mathbf{\tilde {S}}}}_{j}}\), the scaling relations (54), (59), (79), (82), (103), (109).
Expansion coefficients \(\{ a_{{j,k}}^{y},b_{{j,k}}^{y}:k \in \mathbb{Z}\} \) in (137) for an arbitrary value of the scale j are determined by the formulas
We obtain recursive algorithms for calculating these coefficients by substituting in (138), (139) instead of \({{\tilde {\xi }}_{{j,k}}}(t)\) and \({{\tilde {\gamma }}_{{j,k}}}(t)\) scaling relations (54), (59), (79), (82), (103), (109). Using (54), (59) we obtain
From scaling equations (51), (57), (67), (72), (79), (82), (103), (106), (109), (113) it also follows that other recursive calculation algorithms are possible as the coefficients of expansion \(\{ a_{{{{j}_{0}},k}}^{y},b_{{j,k}}^{y}:k \in \mathbb{Z}\} \) of the observed signal y(t) over basis functions \({{\xi }_{{j,k}}}(t),\)\({{\gamma }_{{j,k}}}(t)\) and coefficients of expansion y(t) over functions biorthogonal to these bases \({{\tilde {\xi }}_{{j,k}}}(t),\)\({{\tilde {\gamma }}_{{j,k}}}(t).\)
We introduce the notation for the coefficients of expansion of the observed signal y(t) for basis functions \({{\tilde {\xi }}_{{j,k}}}(t)\), \({{\tilde {\gamma }}_{{j,k}}}(t)\) at an arbitrary scale j
and for the coefficients of expansion of the observed signal y(t) on the original wavelet bases \({{\varphi }_{{j,k}}}(t)\), \({{\psi }_{{j,k}}}(t)\)
From (79), (82) follow
Using (103), (109), we have
The recursive algorithm for calculating the coefficients of expansion \(\{ \tilde {a}_{{{{j}_{0}},k}}^{y},\tilde {b}_{{j,k}}^{y}:k \in \mathbb{Z}\} \) of the observed signal y(t) over the basis functions \({{\tilde {\xi }}_{{j,k}}}(t)\)\({{\tilde {\gamma }}_{{j,k}}}(t)\) seems similar to the above cases
As in the case of the classical MRA, the obtained recursive algorithms for calculating the coefficients \(\{ a_{{{{j}_{0}},k}}^{y},b_{{j,k}}^{y}:k \in \mathbb{Z}\} \) or \(\{ \tilde {a}_{{{{j}_{0}},k}}^{y},\tilde {b}_{{j,k}}^{y}:k \in \mathbb{Z}\} \) require that the corresponding initial values of the expansion coefficients \(a_{{J,k}}^{y}\) or \(\tilde {a}_{{J,k}}^{y}\) be known at the finest scale J. To calculate the initial coefficients \(\{ a_{{J,k}}^{y}:k \in \mathbb{Z}\} \) from the known samplings of the observed signal y(t), we substitute scaling relation (79) in (138)
Hence, it follows that when choosing the Kravchenko wavelet system, we obtain
Similarly, according to (82), (139), we write
Hence, when choosing the Kravchenko wavelet system, we have
The initial coefficients \(\{ \tilde {a}_{{J,k}}^{y}:k \in \mathbb{Z}\} \) are calculated similarly from known samplings of the observed signal y(t) using (67) and (142), (72) and (143)
Thus, using formulas (140), (141), (146)–(159) we can obtain different variants of the recursive algorithm for expansion of the observed signal y(t) over its samplings from a finer resolution J to a rough resolution j0. To calculate each subsequent coefficient from the previous ones with a large scale characterizing a wider-band process, it is better to use the basis functions and their scaling and wavelet filters in (140), (141), (146)–(159), which take into account and compensate for the frequency–time singularities of the observed signal y(t) and frequency functions \(\hat {\lambda }(\omega ),\hat {D}(\omega )\) in the corresponding range. Figure 7a shows a diagram of one possible algorithm for wavelet expansion of the observed signal y(t).
In contrast to the classical wavelet expansion scheme [13–21] the samplings of the observed signal y(t) at the first stage are processed by low- and high-pass filters \(\{ {{\tilde {\theta }}_{{J + 1}}}\} \), \(\{ {{\tilde {\eta }}_{{J + 1}}}\} \). The filters in subsequent processing steps do not change.
Next, we obtain a recursive algorithm for reconstructing the approximating coefficients characterizing the low-frequency signal component with a large scale from the wavelet expansion coefficients of a smaller scale (one IDWT level). Then, given that \({{{\mathbf{\tilde {U}}}}_{{j + 1}}} = {{{\mathbf{\tilde {U}}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}}\), the scaling function \({{\tilde {\xi }}_{{j,k}}}(t)\), \(k \in \mathbb{Z}\) can be represented as the sum
Multiplying (160) scalarly on the left and right by y(t), we obtain
which corresponds to the following representation of the expansion coefficients \(a_{{j + 1,k}}^{y}\):
Thus, using formula (161), a recursive algorithm for reconstructing the estimate is obtained \({{\tilde {x}}_{P}}(t)\) from to the wavelet expansion coefficients from a rough to exact resolution using the filters of the original wavelet bases \(\{ {{h}_{k}}\} \) and \(\{ {{g}_{k}}\} \). The scheme for reconstructing the samplings of the estimate \({{\tilde {x}}_{P}}(t)\) does not differ from the classical MRA scheme (see Fig. 7b).
Due to the proposed and substantiated constructive approach for obtaining frequency-modified wavelet bases, the scheme for expansion of the observed signal y(t) and reconstruction of the wavelet expansion coefficients of the estimate \({{\tilde {x}}_{{\text{r}}}}(t)\) is not the only one. In the scheme for expansion of the observed signal y(t), other recursive formulas (148)–(159) can be used. Based on the resulting wavelet expansion coefficients the estimate should be reconstructed \({{\tilde {x}}_{{\text{r}}}}(t)\).
For subspaces \({{{\mathbf{U}}}_{{j + 1}}}\) and \({{{\mathbf{\tilde {U}}}}_{{j + 1}}}\) scaling functions \({{\xi }_{{j + 1,k}}}(t)\) and \({{\tilde {\xi }}_{{j + 1,k}}}(t)\), \(k \in \mathbb{Z}\) the orthogonal expansions \({{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}},\)\({{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{\tilde {U}}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}},\)\({{{\mathbf{\tilde {U}}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus \;{{{\mathbf{S}}}_{j}}\) are valid. Then, scaling functions \({{\xi }_{{j + 1,k}}}(t)\), \({{\tilde {\xi }}_{{j,k}}}(t)\), \(k \in \mathbb{Z}\) can be represented as the sums
from which follow the formulas for the expansion coefficients \(a_{{j + 1,k}}^{y}\) and \(\tilde {a}_{{j + 1,k}}^{y}\):
Therefore, using the recursive relations (161) and (165) it is possible to recover the coefficients of expansion of a larger scale from the coefficients of expansion of the same basis of a smaller scale, and using the relations (166) and (167), the coefficients of expansion of a larger scale from the coefficients of expansion of a biorthogonal basis of a smaller scale. In addition, mixed recursive relations are possible, where the coefficients of expansion of a larger scale are obtained from the coefficients of expansion of the scaling functions of the same or biorthogonal wavelet system and the wavelet functions of the biorthogonal or the same wavelet system at a smaller scale. Indeed, if we use (160), and then (45), (46) and (92), (96), then in the time domain we obtain
Similarly, from (163) with (45) (46) and (94), (98) in the time domain we have
Then, mixed recursive reconstruction formulas for approximating expansion coefficients \(a_{{j + 1,k}}^{y},\)\(\tilde {a}_{{j + 1,k}}^{y}\) have the following form:
Thus, recursive formulas are obtained for one level of DWT and IDWT, which make it possible to construct flexible computational schemes for multiresolution approximation of the solution to convolution integral equation (1) taking into account the time–frequency singularities of the observed signal y(t), frequency response function \(\hat {\lambda }(\omega )\), or filter with a frequency response \(\hat {D}(\omega )\). Figure 8 shows the generalized scheme realizing a multiresolution algorithm for reconstructing the estimate of the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\).
The useful signal x(t) initially distorted by the impulse response λ(t) followed by noise n(t) in the form of time samplings yn= y(tn) is subjected to wavelet expansion with a low-pass filter \(\{ \overline {{{{\tilde {\theta }}}_{{J + 1,k}}}} \} \) (or \(\{ \overline {{{\theta }_{{J + 1,k}}}} \} \)) and high-pass filter \(\{ \overline {{{{\tilde {\eta }}}_{{J + 1,k}}}} \} \) (or \(\{ \overline {{{\eta }_{{J + 1,k}}}} \} \)). As a result the approximating wavelet expansion coefficients \(c{{A}_{J}} = \{ a_{J}^{y}\} \) (or \(c{{A}_{J}} = \{ \tilde {a}_{J}^{y}\} \)) and detailed wavelet expansion coefficients \(c{{D}_{J}} = \{ b_{J}^{y}\} \) (or \(c{{D}_{J}} = \{ \tilde {b}_{J}^{y}\} \)) of scale J are obtained. Next, each of the approximating coefficients of the wavelet expansion \(c{{A}_{j}} = \{ a_{j}^{y}\} \) (or \(c{{A}_{j}} = \{ \tilde {a}_{j}^{y}\} \)) for \({{j}_{0}} - 1 \leqslant j \leqslant J\) must be processed by a low-pass filter \(\{ \overline {{{h}_{k}}} \} \) (or \(\{ \overline {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} {{{_{{}}^{\xi }}}_{{j,k}}}} \} \), or \(\{ \,\overline {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} {{{_{{}}^{\xi }}}_{{j,k}}}} \} \)) and high-pass filter \(\{ \overline {{{g}_{k}}} \} \) (or \(\{ \overline {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} {{{_{{}}^{\xi }}}_{{j,k}}}} \} \), or \(\{ \,\overline {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} {{{_{{}}^{\xi }}}_{{j,k}}}} \} \)). Thus, a discrete sequence of wavelet expansion coefficients \(\{ c{{A}_{{{{j}_{0}}}}},c{{D}_{j}}:\)\({{j}_{0}} \leqslant j \leqslant J\} .\) is formed. The detailed coefficients \(\{ c{{D}_{j}}:\,{{j}_{0}} \leqslant j \leqslant J\} \) are subsequently subjected to threshold processing. After that, the IFT is performed with a low-pass filter \(\left\{ {{{h}_{k}}} \right\}\) (or \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} {{_{{}}^{\xi }}_{{j,k}}}\} \), or \(\{ \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} {{_{{}}^{\xi }}_{{j,k}}}\} \)) and high-pass filter \(\left\{ {{{g}_{k}}} \right\}\) (or \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} {{_{{}}^{\xi }}_{{j,k}}}\} \), or \(\{ \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} {{_{{}}^{\xi }}_{{j,k}}}\} \)). In this case, the wavelet reconstruction scheme should yield a solution to integral equation (1).
Estimation of the useful signal \({{\tilde {x}}_{{\text{r}}}}\) with a multiresolution algorithm using the new biorthogonal frequency-modified wavelets is done in several stages.
1. Choice of the frequency-modifying function\(\hat {D}(\omega )\). At this stage to select the frequency-modifying function \(\hat {D}(\omega )\) a priori information about the useful and observed signals \(x(t)\), \(y(t)\), impulse response λ (t), and noise parameters n(t) is taken into account.
In practice, to suppress infinite noise amplification, a filter is used that regularizes amplification at high frequencies (3), which can be used to construct the function \(\hat {D}(\omega )\) in the form \(\hat {D}(\omega ) = \hat {K}{{(\omega )}^{{ - 1}}}.\) Suppression of infinite noise amplification can also be achieved by applying a window function w(ω), which includes the scaling function \({{\hat {\varphi }}_{J}}(\omega )\), which at the finest resolution J must satisfy the following requirements:
—an infinite increase of the high-frequency part of the spectrum \(\hat {\lambda }{{(\omega )}^{{ - 1}}}\) must be compensated by a decrease in the high-frequency part of the scaling function;
—the spectrum of the scaling function \({{\hat {\varphi }}_{J}}(\omega )\) within the spectral band \(\hat {y}(\omega )\) should be as flat as possible;
—the scaling function \({{\hat {\varphi }}_{J}}(\omega )\) should be smooth enough to eliminate the Gibbs phenomenon (continuously differentiable by as many times as possible).
The scaling functions from Kravchenko wavelet systems possess such properties [25–28].
Additionally, the frequency response of the system can be corrected. For this, function \(\hat {D}(\omega )\) must be multiplied by a suitable polynomial of ω.
2. Choice of an orthonormal wavelet basis\(\varphi (t)\),\(\psi (t)\)with optimal properties. To achieve greater accuracy and computational advantages, the wavelet basis must have a compact spectrum, a small number of filter coefficients \(\{ h_{k}^{{}}\} ,\,\,\,\{ g_{k}^{{}}\} \), and continuous differentiability by as many times as possible. The scaling functions from the Kravchenko wavelet systems have such properties [25–28].
From the time–frequency properties of the selected wavelet basis, the scale values \(J \geqslant j \geqslant {{j}_{0}},\) are determined at which DWT should be performed.
3. Obtaining a biorthogonal frequency-modified wavelet system\({{\xi }_{{j,k}}}(t),\)\({{\gamma }_{{j,k}}}(t)\),\({{\tilde {\xi }}_{{j,k}}}(t)\),\({{\tilde {\gamma }}_{{j,k}}}(t)\). Initially from the selected orthonormal wavelet basis \({{\varphi }_{{j,k}}}(t)\), \({{\psi }_{{j,k}}}(t)\) and modifying function \(\hat {D}(\omega )\) functions \({{\xi }_{{j,k}}}(t)\), \({{\gamma }_{{j,k}}}(t)\) should be obtained by formulas (27), (28). Next the function \(E_{j}^{\xi }(\omega )\) from formula (44) is introduced, with the use of which biorthogonal wavelet bases \({{\tilde {\xi }}_{{j,k}}}(t)\), \({{\tilde {\gamma }}_{{j,k}}}(t)\) are constructed by (45), (46). Additionally, the modifying function \(\hat {D}(\omega )\) may be subjected to frequency correction.
4. Calculation of the discrete filters of the new biorthogonal frequency-modified wavelet system. To conduct forward DWT of the observed signal y(t) and obtain an estimate of the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\) using IDWT, the known discrete filters \(\{ h_{k}^{{}}\} ,\,\,\,\{ g_{k}^{{}}\} \) of the orthonormal wavelet basis \(\varphi (t)\), \(\psi (t)\) are supplemented with calculation of the following filters:
—using formulas (68), (73), (78), (83), the filter coefficients \(\{ {{\tilde {\theta }}_{{J + 1,k}}}\} \), \(\{ {{\tilde {\eta }}_{{J + 1,k}}}\} \) and \(\{ {{\theta }_{{J + 1,k}}}\} \), \(\{ {{\eta }_{{J + 1,k}}}\} \) are calculated, which determine the first level of DWT;
—using formulas (101), (105), (108), (112) the filter coefficients \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} {{_{{}}^{\xi }}_{{j,k}}}\} \), \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} _{{j,k}}^{\xi }\} \) and \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} {{_{{}}^{\xi }}_{{j,k}}}\} \), \(\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} _{{j,k}}^{\xi }\} \) are calculated, which along with \(\{ h_{k}^{{}}\} ,\,\,\,\{ g_{k}^{{}}\} \) can be used in calculating subsequent levels of DWT and in the IDWT. It should be noted that the coefficients of these filters do not require IFT calculation for each resolution. They are calculated by discrete convolution of the known filter coefficients \(\{ {{h}_{k}}\} ,\{ {{g}_{k}}\} \) with a precalculated sequence of coefficients of a 2j + 2π-periodic function \(E_{{j + 1}}^{\xi }(\omega )\) and its inverse function \({1 \mathord{\left/ {\vphantom {1 {E_{{j + 1}}^{\xi }(\omega )}}} \right. \kern-0em} {E_{{j + 1}}^{\xi }(\omega )}}\), respectively, \(\{ {{\varsigma }_{{j + 1,\;n}}}\} \), \(\{ {{\tilde {\varsigma }}_{{j + 1,\;n}}}\} \). Moreover, the coefficients \(\{ {{\tilde {\varsigma }}_{{j + 1,\;n}}}\} \) can be calculated from the coefficients \(\{ {{\varsigma }_{{j + 1,\;n}}}\} \). Thus, the largest computational cost requires single calculation of the filter coefficients \(\{ {{\tilde {\theta }}_{{J + 1,k}}}\} \), \(\{ {{\tilde {\eta }}_{{J + 1,k}}}\} \) and \(\{ {{\theta }_{{J + 1,k}}}\} \), \(\{ {{\eta }_{{J + 1,k}}}\} \).
5. Obtaining the initial expansion coefficients of the observed signaly(t). At the first stage of expansion of the observed signal y(t), the coefficients \(\{ a_{{J,n}}^{y},b_{{J,n}}^{y}:n \in \mathbb{Z}\} \) or \(\{ \tilde {a}_{{J,n}}^{y},\tilde {b}_{{J,n}}^{y}:n \in \mathbb{Z}\} \) are calculated using discrete filters \(\{ {{\tilde {\theta }}_{{J + 1,k}}}:k \in \mathbb{Z}\} \), \(\{ {{\tilde {\eta }}_{{J + 1,k}}}:k \in \mathbb{Z}\} \) or \(\{ {{\theta }_{{J + 1,k}}}:k \in \mathbb{Z}\} \), \(\{ {{\eta }_{{J + 1,k}}}:k \in \mathbb{Z}\} \) by formulas (156)–(159). These filters were obtained in the frequency domain by formulas (66), (71), (76), (81) and take into account the singularities of the modifying function \(\hat {D}(\omega )\), which can increase significantly in the high-frequency region. Moreover, it follows from (66), (71), (76), (81) that frequency filters \({{\tilde {\Theta }}_{j}}(\omega ),{{\tilde {{\rm N}}}_{j}}(\omega )\) can provide an increase in the frequency components of the processed signal for \(\hat {\lambda }(\omega ) \to 0\) (in the frequency band of the observed signal \(\hat {y}(\omega )\)), if these singularities are not sufficiently compensated by the appropriate choice of \(\hat {D}(\omega )\). In particular, the high-frequency component of the signal containing the main noise can be significantly increased. Filters \({{\Theta }_{j}}(\omega ),{{{\rm N}}_{j}}(\omega )\), conversely, do not amplify such frequency components of the processed signal and can serve as an alternative approach for calculating the expansion coefficients of the observed signal y(t) at the first stage of DWT. Subsequent stages are carried out with filters with a lower passband, where in the high-frequency part, the increase in the modifying function \(\hat {D}(\omega )\), as a rule, is significantly less. Therefore, subsequent DWT stages are most often less critical toward the choice of the expansion filters.
6. DWT of the observed signaly(t). During DWT the optimal scheme for wavelet expansion of the observed signal is selected y(t) using formulas (140), (141), (148)–(151), (154), (155) for the selected scale values \({{j}_{0}}\,\, \geqslant j \geqslant J\) taking into account the time–frequency singularities of the observed signal y(t), frequency response function \(\hat {\lambda }(\omega )\), or filter with frequency response \(\hat {D}(\omega )\). Excess DWT is also used (wavelet coefficients are not discarded as a result of decimation), for which better noise reduction can be achieved.
7. Threshold processing of the wavelet coefficients. Cleaning up the observed signal from noise using wavelets can be performed by threshold processing of the wavelet coefficients [13–21, 42, 43]. The advantage of nonlinear methods for threshold processing of the wavelet coefficients is the speed of the algorithms for constructing the estimates and the possibility of better adaptation to functions with varying degrees of regularity in different areas. In addition to the noise removal problem, threshold processing makes it possible to solve the signal compression problem. In threshold processing the level of the detailing coefficients is limited by the threshold function  . Instead of argument x in the function
. Instead of argument x in the function  the detailing coefficients for each expansion level are substituted by j (\(c{{D}_{j}}\), \({{j}_{0}} \leqslant j \leqslant J\)).
the detailing coefficients for each expansion level are substituted by j (\(c{{D}_{j}}\), \({{j}_{0}} \leqslant j \leqslant J\)).
A hard or soft threshold function with a threshold T is commonly used. The hard threshold processing function is described by the following expression:

Obviously, the hard threshold processing function has a gap. This can lead to undesirable processing singularities of a sufficiently smooth signal function. Soft threshold processing is set by a continuous threshold function

Figure 9 shows the hard and soft threshold processing functions.
Therefore, with this approach, the most effective noise removal will be achieved when the signal energy as a result of DWT is concentrated in the minimum number of coefficients above the threshold and the noise energy is distributed in the maximum number of coefficients below the threshold. This occurs when the selected wavelet basis is well correlated with the signal. For every scale j, a threshold Tj is selected, which in accordance with [42, 43] is determined as
This threshold is called “universal,” since it does not depend on the observed data (it depends only on the noise variance). When choosing a threshold TU, the closeness of the root-mean-square risk to the minimum is ensured [42–45], and almost all noise is removed from the signal. The noise variance \({{\sigma }^{2}}\) can be calculated using the calibration procedure of the signal recording device. However, often the variance \({{\sigma }^{2}}\) is unknown and instead of its exact value, it is necessary to use some estimate \(\sigma _{{\text{O}}}^{2}\). The variance estimate can be obtained from the observed yn= y(tn) by calculating the median Mb wavelet coefficients \(c{{D}_{j}}\) at the finest scale J since, by virtue of (157) (or (159)), these coefficients actually contain only noise \({{\sigma }_{{\text{O}}}} = {{{{M}_{b}}} \mathord{\left/ {\vphantom {{{{M}_{b}}} {0.6745}}} \right. \kern-0em} {0.6745}}.\) In addition, selective variance can be used as the variance \(\sigma _{{\text{O}}}^{2}\). Selective variance is the most widely used estimate for \(\sigma _{{\text{O}}}^{2}\) and in the absence of rejects, it is most preferable. Then, if the signal yn has a length N of the N/2 wavelet coefficients \(c{{D}_{j}}\) of the smallest scale j = J−1, then \(\sigma _{{\text{O}}}^{2}\) is estimated as follows:
8. Reconstruction of the estimate of the useful signal\({{\tilde {x}}_{P}}(t)\)using IDWT. During IDWT, the discrete values of the estimate of the signal \({{\tilde {x}}_{{{\text{r}}\,,n}}} = {{\tilde {x}}_{{\text{r}}}}({{t}_{n}})\) are reconstructed from the wavelet expansion coefficients of the observed signal yn= y(tn) that have undergone threshold processing. Since for the given approximating and detailed coefficients at each scale j (\({{j}_{0}} \leqslant j \leqslant J\)) it is possible to reconstruct the approximating coefficients \(\{ a_{{j + 1}}^{y}\} \) or \(\{ \tilde {a}_{{j + 1}}^{y}\} \) depending on the filters in formulas (161), (165)–(167), (172)–(175), the next stage of IDWT can be carried out taking into account the time–frequency singularities of the observed signal y(t), frequency response function \(\hat {\lambda }(\omega )\), or filter with frequency response \(\hat {D}(\omega )\). At the last stage of reconstruction, formulas should be applied that ensure reconstruction of \({{\tilde {x}}_{{{\text{r}}\,,n}}}\).
9. Visualization and interpretation of the results. Estimating the error in solving the problem. The obtained result is visualized and subjected to further processing (statistical, comparative, empirical, etc.) in order to more fully study the object and evaluate the error in solving the problem.
6 CONCLUSIONS
We have validated the use of wavelet approaches in reconstructing the useful signal in the case of representing the measurement process as a convolution model. To realize the algorithm for solving problem (1), it is proposed to use Kravchenko orthogonal wavelets with a finite spectrum [25–28]. It is demonstrated that it is possible to modify wavelets with a compact support in the frequency domain so that it becomes possible to estimate the useful signal \({{\tilde {x}}_{{\text{r}}}}(t)\) from the observed signal \(y(t)\) using fast DWT-based algorithms. A method for obtaining new biorthogonal frequency-modified wavelets that form two MRA chains based on a modifying function with a frequency response \(\hat {D}(\omega )\) is proposed and validated. The function \(\hat {D}(\omega )\) allows the construction of wavelets taking into account stabilization of the solution to convolution integral equation (1) and effective noise suppression. Several types of scaling equations and formulas for calculating the wavelet coefficients for these equations are obtained. The proposed biorthogonal frequency-modified wavelets are nonstationary with respect to scale; i.e., they are not the result of a shift and scaling of one scaling and wavelet functions. However, they form an effective multiresolution algorithm for approximating the solution to convolution integral equation (1). The obtained wavelet systems make it possible for DWT and IDWT to optimize the process of obtaining and reconstructing wavelet coefficients to compensate time–frequency singularities of the observed signal y(t), frequency response function \(\hat {\lambda }(\omega )\), or filter with frequency response \(\hat {D}(\omega )\). Several variants of DWT and IDWT are proposed based on new biorthogonal frequency-modified wavelets, which can be used in various physical applications.
REFERENCES
A. N. Tikhonov and V. Ya. Arsenin, Solutions of Ill-Posed Problems (Nauka, Moscow, 1979; Wiley, New York, 1977).
A. F. Verlan’ and V. S. Sizikov, Integral Equations: Methods, Algorithms, Programs. A Handbook (Naukova Dumka, Kiev, 1986) [in Russian].
A. F. Verlan’ and V. S. Sizikov, Methods of Solution of Integral Equations and Computer Programs (Naukova Dumka, Kiev, 1978) [in Russian].
V. S. Sizikov, Integral Equations and MatLab in Problems of Tomography, Iconics and Spectroscopy (LAMBERT Academic Publ., Saarbrucken, 2011).
Yu. P. Petrov and V. S. Sizikov, Correct, Incorrect and Intermediate Tasks with Appendices: Studies. Manual for Higher Education Institutions (Politekhnika, St. Petersburg, 2012) [in Russian].
V. S. Sizikov, Direct and Return Problems of Recovery of Images, Spectroscopy and a Tomography with MatLab (Lan’, St. Petersburg, 2017) [in Russian].
V. S. Sizikov, Return Applied Tasks and MatLab (Lan’, St. Petersburg, 2011) [in Russian].
A. B. Sergienko, Digital Signal Processing (BKhV-Peterburg, St. Petersburg, 2011) [in Russian].
A. V. Oppenheim and R. W. Schafer, Discrete-Time Signal Processing (Prentice Hall, 1999; Tekhnosfera, Moscow, 2006).
L. Yaroslavsky, Digital Holography and Digital Image Processing: Principles, Methods, Algorithms (Sovetskoe Radio, Moscow, 1979; Springer Science & Business Media, 2013).
L. E. Franks, Signal Theory (Prentice-Hall, Englewood Cliffs, 1969; Sovetskoe Radio, Moscow, 1974).
A. V. Bumagin, A. V. Gondar’, V. B. Steshenko, et al., Kompon. & Tekhnol. 105 (4), 113 (2010).
S. G. Mallat, A Wavelet Tour of Signal Processing (Academic, San Diego, 1998; Mir, Moscow, 2005).
I. Daubechies, Ten Lectures on Wavelets (SIAM, Philadelphia, 1992; NITS RKHD, Izhevsk–Moscow, 2001).
C. Chui, An Introduction to Wavelets (Academic, Boston, 1992; Mir, Moscow, 2001).
I. Ya. Novikov, V. Yu. Protasov, and M. A. Skopina, Theory of Splashes (Fizmatlit, Moscow, 2006) [in Russian].
C. Blatter, Wavelets: A Primer (A. K. Peters, Massachusetts, 1998; Tekhnosfera, Moscow, 2004).
N. K. Smolentsev, Fundamental Theory of Wavelets. Wavelets in MATLAB (DMK Press, Moscow, 2014) [in Russian].
V. I. Vorob’ev and V. G. Gribunin, The Theory and Practice of Wavelets Transformations (VUS, St. Petersburg, 1999) [in Russian].
V. P. D’yakonov, Wavelets. From Theory to Practice (SOLON-R, Moscow, 2002) [in Russian].
H.-G. Stark, Wavelets and Signal Processing. An Application-Based Introduction (Springer-Verlag, New York, 2005; Tekhnosfera, Moscow, 2007).
A. A. Koronovskii and A. E. Khramov, Continuous Wavelet Analysis and Its Applications (Fizmatlit, Moscow, 2003) [in Russian].
Yu. E. Voskoboinikov, A. V. Gochakov, and A. B. Kolker, Filterings of Signals and Images: Fourier also Wavelet Algorithms (with Examples in Mathcad) (NGASU (Sibstrin), Novosibirsk, 2010) [in Russian].
D. Donoho and I. Johnstone, Biometrika 81, 425 (1994).
V. F. Kravchenko and O. V. Kravchenko, Constructive Methods of Algebra of Logic, Atomic Functions, Wavelets, Fractals in Problems of Physics and the Technique, Ed. by V. F. Kravchenko (Tekhnosfera, Moscow, 2018) [in Russian].
V. F. Kravchenko and D. V. Churikov, Digital Processing of Signals Atomic Functions and Wavelets, Ed. by V. F. Kravchenko (Tekhnosfera, Moscow, 2019), additional circulation 300 [in Russian].
V. F. Kravchenko, O. V. Kravchenko, V. I. Pustovoit, D. V. Churikov, and A. V. Yurin, J. Communications. Technol. Electron. 60, 103 (2015).
V. F. Kravchenko and A. V. Yurin, Usp. Sovr. Radioelektron. 13 (5), 3 (2008).
R. Neelamani, H. Choi, and R. Baraniuk, “ForWaRD: Fourier-Wavelet Regularized Deconvolution for Ill-Conditioned,” IEEE Trans. Signal Process. 52, 418 (2004).
W. P. Ziemer, Weakly Differentiable Functions. Sobolev Spaces and Function of Bounded Variation (Springer-Verlag, New York, 1989).
M. O. Korpusov and A. A. Panin, Lectures on the Linear and Nonlinear Functional Analysis (Mos. Gos. Univ., Moscow, 2016) [in Russian].
M. V. Falaleev, Generalized Functions and Actions over Them: Methodology (Irkut. Gos. Univ., Irkutsk, 2011) [in Russian].
W. Härdle, G. Kerkyacharian, D. Picard, and A. Tsybakov, Wavelets, Approximation and Statistical Applications (Springer-Verlag, New York, 1998).
H. Triebel, Theory of Function Spaces (Akad. Verl.-Ges. Geest& Porting, Leipzig, 1983; Mir, Moscow, 1986).
L. V. Novikov, Bases of the Wavelet-Analysis of Signals: Manual (MODUS+, St. Petersburg, 1999) [in Russian].
D. L. Donoho, Appl. Comput. Harmonic Analys 2 (2), 101 (1995).
F. Abramovich and B. Silverman, Biometrika 85 (1), 115 (1998).
R. Neelamani, H. Choi, and R. Baraniuk, IEEE Int. Conf. Acoustics, Speech, and Signal Processing 6, 3241 (1999).
I. Johnstone, G. Kerkyacharian, D. Picard, and M. Raimondo, J. R. Statist. Soc. Ser. B (Statistical Methodology) 66, 547 (2004).
L. V. Novikov, Instrum. Exp. Tech. 50, 61 (2007).
L. V. Novikov, Instrum. Exp. Tech. 48, 711 (2005).
D. L. Donoho, IEEE Trans. Inf. Theory 41, 613 (1995).
D. L. Donoho and I. M. Johnstone, Bernoulli 2 (1), 39 (1996).
O. V. Shestakov, Inf. Primen. 6, 122 (2012).
J. Bigot and S. Van Bellegem, Scand. J. Statistics 36, 749 (2009).
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Kravchenko, V.F., Pustovoit, V.I. & Yurin, A.V. Signal Reconstruction Using New Biorthogonal Frequency-Modified Kravchenko Wavelets When Representing the Measurement Process as a Convolution Model. J. Commun. Technol. Electron. 65, 423–448 (2020). https://doi.org/10.1134/S106422692004004X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S106422692004004X